极坐标与参数方程PPT课件
- 格式：ppt
- 大小：2.11 MB
- 文档页数：26
下载文档原格式
合集下载
参数方程与极坐标
来表示，使点 P ( x , y ) 随着变量 t 在某一范围内变化而 描出曲线C ，且只描出 C， 则方程 ( * * ) 称为曲线 C 的参数方程，变量 t 称为参变量。
常用的曲线的参数方程
1. 圆 x2 y2 R2 的参数方程
x R cos , y R sin
a
0
a a
x
4. 摆线的参数方程
y
x a ( t sin t ) , y a (1 cos t )
t ( , )
x
4、摆线
半径为a(a 0)的圆沿直线滚动无滑动), (
研究圆周上一定点的运 动轨迹.
y
aP
t
T
o P
x
一拱 x at a sin t a(t sin t ), y a a cos t a(1 cos t ).
2、极坐标及心形线
画图 : r a(1 cos )(a 0).
y
y
r
P(x,y) θ
y
( r , )
o
x
x
o
x
直角坐标与极坐标的关系 : x r cos . y r sin
常用曲线的极坐标方程 1. 圆
a
O
圆心在极点 O上，半径为 a 的
圆的极坐标方程为
参数方程与极坐标方程
（1）参数方程 原点为圆心，半径为R的 圆方程为： x 2 y 2 R 2
RyBiblioteka R yP( x, y)
xR
R
o
x R cos
y R sin
x
(*)
显然，对于圆上的任一点 P ( x , y ) ，总存在一 [0, 2 ) 满足(*). 反之，当任取 [0, 2 ) 时，(*)式就确定了相应
数学选修4第二轮复习课件：极坐标与参数方程
我们把这一形式称为直线参数方程的标准形式，其中t 表示直线l上以定点M0为起点，任意一点M(x,y)为终点的 有向线段的数量M0M。当点M在点M0的上方时，t>0；当 点M在点M0的下方时，t<0；当点M与点M0重合时，t=0。 很明显，我们也可以参数t理解为以M0为原点，直线l向上 的方向为正方向的数轴上点M的坐标，其长度单位与原直 角坐标系的长度单位相同。 用坐标的观点理解上述直线参数方程中的参数t，在 解决有关直线问题时，可以自然地将新旧知识联系起来。
所成的弦的弦长．
21
例 11． （2008 宁夏银川一中）已知椭圆 C
2
金太阳教育网
品质来自专业 信赖源于诚信 的极坐标方
12 程为 ，点 F1、F2 为其左， 2 2 3 cos 4 sin
2 t x 2 2 (t 为参 右焦点，直线 l 的参数方程为 y 2 t 2
x 2 2t , (t 为参数)． Ox 为极轴建立极坐标系， 以 y 1 4t ,
圆 C 的极坐标方程为 2 2 sin(
4
).
(1)写出直线 l 的普通方程和圆 C 的直角坐标方程； (2)判断直线 l 和圆 C 的位置关系.
23
五、考点预测
金太阳教育网
15
3．极坐标方程研究两曲线的位置关系
金太阳教育网
品质来自专业 信赖源于诚信
x 1 2t , 例 5． 江苏省南通市 2008-2009） （ 求直线 （t y 1 2t x 3cos , 为参数）被圆 （α 为参数）截得的弦长． y 3sin
11
金太阳教育网
品质来自专业 信赖源于诚信
所成的弦的弦长．
21
例 11． （2008 宁夏银川一中）已知椭圆 C
2
金太阳教育网
品质来自专业 信赖源于诚信 的极坐标方
12 程为 ，点 F1、F2 为其左， 2 2 3 cos 4 sin
2 t x 2 2 (t 为参 右焦点，直线 l 的参数方程为 y 2 t 2
x 2 2t , (t 为参数)． Ox 为极轴建立极坐标系， 以 y 1 4t ,
圆 C 的极坐标方程为 2 2 sin(
4
).
(1)写出直线 l 的普通方程和圆 C 的直角坐标方程； (2)判断直线 l 和圆 C 的位置关系.
23
五、考点预测
金太阳教育网
15
3．极坐标方程研究两曲线的位置关系
金太阳教育网
品质来自专业 信赖源于诚信
x 1 2t , 例 5． 江苏省南通市 2008-2009） （ 求直线 （t y 1 2t x 3cos , 为参数）被圆 （α 为参数）截得的弦长． y 3sin
11
金太阳教育网
品质来自专业 信赖源于诚信
高考数学一轮复习选修44坐标系与参数方程课件新人教A版理
3
cos +sin
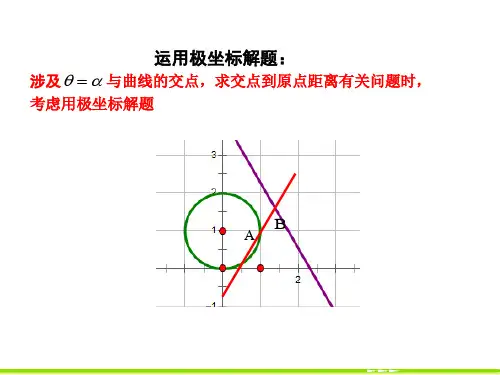
(2)C3 是一条过原点且斜率为正值的直线,
C3 的极坐标方程为 θ=α,α∈ 0,
π
2
,
= 2cos,
联立 C1 与 C3 的极坐标方程
= ,
得 ρ=2cos α,即|OA|=2cos α.
3
= cos +sin ,
联立 C1 与 C2 的极坐标方程
= ,
-11知识梳理
1
双基自测
2
3
4
5
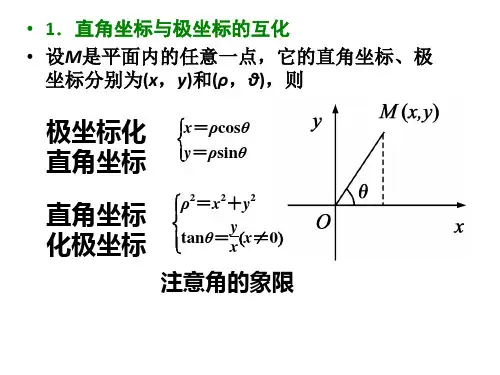
2.若原点与极点重合,x 轴正半轴与极轴重合,则点(-5,-5√3)的极
坐标是(
)
π
A. 10, 3
2π
C. -10,- 3
4π
B. 10, 3
2π
D. 10, 3
关闭
设点(-5,-5√3)的极坐标为(ρ,θ),
-5 √3
则 tan θ=
-5
= √3.
4π
因为 x<0,所以最小正角 θ= ,
由圆 C1 与圆 C2 的方程相减可得公共弦所在的直线方程为
4x-2y+1=0.
圆心(1,1)到直线 4x-2y+1=0 的距离 d=
故弦长|AB|=2 1-
3 2
√20
=
√55
5
.
|4-2+1|
42 +(-2)2
=
3
,
√20
-24考点1
考点2
考点3
考点4
考点5
(2)解 ①圆 O:ρ=cos θ+sin θ,即 ρ2=ρcos θ+ρsin θ,
3
3
得 ρ=cos +sin ,即|OB|=cos +sin ,
12-2坐标系与参数方程教学课件
2020/6/24
2020/6/24
(2)空间点 P 的直角坐标(x，y，z)与球坐标(r，φ，θ)之 x＝rsinφcosθ
间的变换关系为y＝rsinφsinθ . z＝rcosφ
2020/6/24
二、参数方程 1．参数方程的概念 在平面直角坐标系中，如果曲线上任意一点的坐标 x、 y 都是某个变数 t 的函数xy＝＝gftt (*)，如果对于 t 的每一 个允许值，由方程组(*)所确定的点 M(x，y)都在这条曲线 上，则方程组(*)就叫做这条曲线的参数方程，变数 t 叫做 参数．
2020/6/24
解析：由条件知点12x，3y在方程 x2＋y2＝1 的曲线 上，∴12x2＋(3y)2＝1，即曲线 C 的方程为：x42＋9y2＝1.
答案：x42＋9y2＝1
2020/6/24
点评：在坐标变换式yx′′＝＝μλxy 中，点(x′，y′)是变 换后点的坐标，应满足变换后的曲线方程 x2＋y2＝1(x，y) 是变换前点的坐标，应满足变换前曲线的方程x42＋9y2＝1.
答案：2 或－8
2020/6/24
• (文)(2010·广东理)在极坐标系(Ρ，Θ)(0≤Θ<2Π) 中，曲线Ρ＝2SINΘ与ΡCOSΘ＝－1的交点的 极坐标为________．
2020/6/24
解析：由 ρ＝2sinθ 与 ρcosθ＝－1 得 2sinθcosθ＝－1， ∴sin2θ＝－1，∵0≤θ<2π 且 sinθ>0，cosθ<0， ∴θ＝34π，∴ρ＝2sin34π＝ 2. 答案：( 2，34π)
x′＝λxλ>0 y′＝μyμ>0
的作用下，点 P(x，y)对应到点 P′(x′，
y′)，称 φ 为平面直角坐标系中的伸缩变换．
2020/6/24
(2)空间点 P 的直角坐标(x，y，z)与球坐标(r，φ，θ)之 x＝rsinφcosθ
间的变换关系为y＝rsinφsinθ . z＝rcosφ
2020/6/24
二、参数方程 1．参数方程的概念 在平面直角坐标系中，如果曲线上任意一点的坐标 x、 y 都是某个变数 t 的函数xy＝＝gftt (*)，如果对于 t 的每一 个允许值，由方程组(*)所确定的点 M(x，y)都在这条曲线 上，则方程组(*)就叫做这条曲线的参数方程，变数 t 叫做 参数．
2020/6/24
解析：由条件知点12x，3y在方程 x2＋y2＝1 的曲线 上，∴12x2＋(3y)2＝1，即曲线 C 的方程为：x42＋9y2＝1.
答案：x42＋9y2＝1
2020/6/24
点评：在坐标变换式yx′′＝＝μλxy 中，点(x′，y′)是变 换后点的坐标，应满足变换后的曲线方程 x2＋y2＝1(x，y) 是变换前点的坐标，应满足变换前曲线的方程x42＋9y2＝1.
答案：2 或－8
2020/6/24
• (文)(2010·广东理)在极坐标系(Ρ，Θ)(0≤Θ<2Π) 中，曲线Ρ＝2SINΘ与ΡCOSΘ＝－1的交点的 极坐标为________．
2020/6/24
解析：由 ρ＝2sinθ 与 ρcosθ＝－1 得 2sinθcosθ＝－1， ∴sin2θ＝－1，∵0≤θ<2π 且 sinθ>0，cosθ<0， ∴θ＝34π，∴ρ＝2sin34π＝ 2. 答案：( 2，34π)
x′＝λxλ>0 y′＝μyμ>0
的作用下，点 P(x，y)对应到点 P′(x′，
y′)，称 φ 为平面直角坐标系中的伸缩变换．
极坐标与参数方程1运用极坐标解题市公开课一等奖课件名师大赛获奖课件
(2)曲线C3的极坐标方程为
= (0
2
)
设A(1, ), B(2 , ), 则
1 =
3
4
cos
sin
,
2
2 sin
A
B
OB 2 1 2sin 3 cos sin OA 1 4
1 4
3 sin 2 cos 2 1
1 4
2
sin
2
6
1
又0 , 2 5 ,
2 1 a2 0 5
【解析】：（Ⅰ）由
x
y
a 1
cost, a sin
t,
(t
为参数，
a
0)
可得
x
y
a cost, 1 a sin
t,
所以
x
2
( y
(a cos t)2 1)2 (a sin t)2
，即
x2
(y
1)2
a2
故曲线 C1 是以 (0,1) 为圆心，半径为 a 的圆.一般方程为 x2 y2 2 y 1 a2 0(*)
将
x2 y2 2
y
sin
代入
(*)
式子可得 C1 的极坐标方程为
2
2
sin
1
a2
0
.
（Ⅱ）由题意联立
2
2
2 sin 1 4 cos
a2
0
可得曲线 C1 与 C2 的公共点所在的方程为 4 cos 2 sin 1 a2 0 ，
因为曲线 C1 与 C2 的公共点都在 C3 : 0 上，
A
B
直角坐标系 xOy 中，直线 l : 3x y b 0 。在以坐标原点为极点， x 轴
极坐标与参数方程ppt课件
当 θ1=θ2，|AB|＝/ρ1—-ρ2/
• 3．直线的极坐标方程：若直线过点M(ρ0，θ0)，且极 轴到此直线的角为α，则它的方程为：
• ρsin(θ－α)＝ρ0sin(θ0－α)． • 几个特殊位置的直线的极坐标方程 • (1)直线过极点：θ＝θ0和θ＝π+θ0； • (2)直线过点M(a,0)且垂直于极轴：ρcosθ＝a；
若 M1，M2 是 l 上的两点，其对应参数分别为 t1，t2，则 (1)M1，M2 两点的坐标分别是(x0＋t1cos α，y0＋t1sin α)，(x0 ＋t2cos α，y0＋t2sin α)． (2)|M1M2|＝|t1－t2|. (3)若线段 M1M2 的中点 M 所对应的参数为 t，则 t＝t1＋2 t2， 中点 M 到定点 M0 的距离|MM0|＝|t|＝t1＋2 t2. (4)若 M0 为线段 M1M2 的中点，则 t1＋t2＝0.
[解] (1)直线 l 的普通方程为 xsin α－ycos α＋cos α＝0. 曲线 C 的极坐标方程为 ρcos2θ＝4sin θ， 即 ρ2cos2θ＝4ρsin θ，∵ρcos θ＝x，ρsin θ＝y， ∴曲线 C 的直角坐标方程为 x2＝4y.
x＝tcos α， (2)将 l: y＝1＋tsin α 代入曲线 C∶x2＝4y 中， 得 t2cos2α－4tsin α－4＝0.
意判断点P所在的象限(即角θ的终边的位置)，以 便正确地求出角θ. • (2)注意“双坐标系”是直角坐标与极坐标互化的 前提．若要判断曲线的形状，通常是先将极坐标 方程化为直角坐标方程，再判断．
(3)极坐标系中两点间的距离公式：已知点 A(ρ1，θ1)，
B(ρ2，θ2)，那么|AB|＝ ρ12＋ρ22－2ρ1ρ2cosθ1－θ2.
• 3．直线的极坐标方程：若直线过点M(ρ0，θ0)，且极 轴到此直线的角为α，则它的方程为：
• ρsin(θ－α)＝ρ0sin(θ0－α)． • 几个特殊位置的直线的极坐标方程 • (1)直线过极点：θ＝θ0和θ＝π+θ0； • (2)直线过点M(a,0)且垂直于极轴：ρcosθ＝a；
若 M1，M2 是 l 上的两点，其对应参数分别为 t1，t2，则 (1)M1，M2 两点的坐标分别是(x0＋t1cos α，y0＋t1sin α)，(x0 ＋t2cos α，y0＋t2sin α)． (2)|M1M2|＝|t1－t2|. (3)若线段 M1M2 的中点 M 所对应的参数为 t，则 t＝t1＋2 t2， 中点 M 到定点 M0 的距离|MM0|＝|t|＝t1＋2 t2. (4)若 M0 为线段 M1M2 的中点，则 t1＋t2＝0.
[解] (1)直线 l 的普通方程为 xsin α－ycos α＋cos α＝0. 曲线 C 的极坐标方程为 ρcos2θ＝4sin θ， 即 ρ2cos2θ＝4ρsin θ，∵ρcos θ＝x，ρsin θ＝y， ∴曲线 C 的直角坐标方程为 x2＝4y.
x＝tcos α， (2)将 l: y＝1＋tsin α 代入曲线 C∶x2＝4y 中， 得 t2cos2α－4tsin α－4＝0.
意判断点P所在的象限(即角θ的终边的位置)，以 便正确地求出角θ. • (2)注意“双坐标系”是直角坐标与极坐标互化的 前提．若要判断曲线的形状，通常是先将极坐标 方程化为直角坐标方程，再判断．
(3)极坐标系中两点间的距离公式：已知点 A(ρ1，θ1)，
B(ρ2，θ2)，那么|AB|＝ ρ12＋ρ22－2ρ1ρ2cosθ1－θ2.
§12.2极坐标与参数方程
22 5 5 2 5 当sin(θ+α)=1时,|PA|取得最小值,最小值为 . 5
当sin(θ+α)=-1时,|PA|取得最大值,最大值为 .
栏目索引
1.化参数方程为普通方程的基本思路是消去参数,常用的消参方法有代入 消去法、加减消去法、恒等式(三角的或代数的)消去法. 2.在将曲线的参数方程化为普通方程时,不仅仅是要把参数消去,还要注 意x、y的取值范围,即在消去参数的过程中一定要注意普通方程与参数方 程的等价性.
栏目索引
4.已知圆的极坐标方程为ρ=2cos θ,则圆心的直角坐标是 .
答案 解析
;半径为
(1,0);1
由ρ2=2ρcos θ得x2+y2=2x,即圆的直角坐标方程为(x-1)2+y2=1.于是圆
心坐标为(1,0),半径为1.
栏目索引
x 1 t, 5.若直线l的参数方程为 (t为参数),则直线l的斜率为 y 2 3 t
(2)因为ρ=6cos θ ,
3
,即 所以ρ=6 cos θ cos sin θ sin
3 3
ρ2=3ρcos θ+3 3 ρsin θ,
栏目索引
所以x2+y2=3x+3 3 y, 即x2+y2-3x-3 3 y=0. ∴直角坐标方程为x2+y2-3x-3 3 y=0.
轴正半轴为极轴建立极坐标系,则直线l的极坐标方程是
6
6
.
(2)(2014陕西,15C,5分)在极坐标系中,点 到直线 ρ sin θ 2, =1的距离
是
.
பைடு நூலகம் θ 2 (1) ρcos =1 4
高三第二轮专题复习极坐标与参数方程课件.ppt
x
y
a b
r r
cos sin
(为参数)
其中参数的几何意义为: θ为圆心角
4.椭圆
x2 a2
y2 b2
1(a
b
0)的参数方程为:
x
y
a b
cos sin
(为参数)
双基自测
1．极坐标方程 ρ＝cos θ 和参数方程xy＝ ＝2－＋1t－t， (t 为参
数)所表示的图形分别是( )．
A．直线、直线
答案 (－4,0)
4．(2013·广州调研)已知直线 l 的参数方程为：xy＝＝12＋t，4t (t 为参数)， 圆 C 的极坐标方程为 ρ＝2 2sin θ，则直线 l 与圆 C 的位置关系为 ________．
x＝2t，
解析 将直线 l 的参数方程：
化为普通方程得，y＝1＋2x，
y＝1＋4t
圆 ρ＝2 2sin θ 的直角坐标方程为 x2＋(y－ 2)2＝2，圆心(0， 2)到
重点方法：<1>消参的方法；<2>极 坐标方程化为直角坐标方程的方法； <3>设参的方法。
1、过定点 M 0 (x0 , y0 ) 、倾斜角为 的直线 l 的参
数方程为
x
y
x0 y0
t cos t sin
，(t
为参数)
我们把这一形式称为直线参数方程的标准形式，其
中t表示直线l上以定点M0为起点，任意一点M(x,y)为终 点的有向线段的数量M0M。当点M在点M0的上方时， t>0；当点M在点M0的下方时，t<0；当点M与点M0重合 时，t=0。很明显，我们也可以参数t理解为以M0为原点， 直线l向上的方向为正方向的数轴上点M的坐标，其长度
极坐标与参数方程
为(3,1) 3.已知点(1， 经过伸缩变换后的点的坐标 2) 1 y′ = 2 y 则该伸缩变换为 .
Ⅱ.曲线的伸缩变换 Ⅱ.曲线的伸缩变换
x ′ = 2 x， 1.直 线 x + 2 y + 1 = 0经 过 伸 缩 变 换 y′ = 3 y 后的曲线方程为 3 x′ + 4 y′ + 6 = 0 . x ′ = 3 x， 2.曲 线 C 经 过 伸 缩 变 换 后的曲线C ′ y′ = y ′ 2 − 9 y ′ 2 = 1, 则 曲 线 C的 方 程 为 1 的方程为x ′
ρ cos θ = a
( a > 0)且 与 极 轴 平 行 . ρ sin θ = − a
ρ cos θ = − a
4.写出下列曲线的极坐标方程： π (1)过点 3， 且垂直于极轴的直线； 3 3 6 ρ cos θ = 2 π (2)过点 3， 且平行于极轴的直线； 3 6 ρ sin θ = 2 π π (3)过点 3， 且与极轴所成角为 的直线； 3 π 6 3 ρ sin − θ = 3 2 π (4)以点 3， 为圆心,半径长为2的圆. π 2 6 ρ − 6 ρ cos θ − +5=0
t A + tB 2．A、B 两点的中点所对应的参数为 ， 2
若点 M0 是线段 AB 的中点，则 tA+tB=0，反之亦然。
直线参数方程的应用
(1)求 线 段 AB的 长 度; (2)求 A、 B中 点 的 坐 标;
eg .已 知 直 线 l : x + y − 3 = 0与 抛 物 线 y = x 2交 于 A, B两 点 , 点 P ( −1, 4)为 直 线 l 上 一 点 .
2015高考总复习数学(文)课件：18.2 极坐标与参数方程
5cosθ， π (θ 是参数， 0≤θ≤2) 5sinθ
2 x＝1－ 2 t， 和 C2： (t 是参数)， 它们的交点坐标为________． y＝－ 2t 2 解析：C1：x2＋y2＝5(0≤x≤ 5)，C2：y＝x－1，
2cosθ， (θ 是参数)，它们的交点坐标为________． 2sinθ
解析：C1：y2＝x(y>0)，C2：x2＋y2＝2，得交点坐标为(1,1)． 答案：(1,1)
(2)(2013 年湖南)在平面直角坐标系 xOy 中， 若 (t 为参数)过椭圆
x＝3cos φ， C： y＝2sin φ
3 )，则点M的极坐标为
π D.2，2kπ＋3(k∈Z)
2．极坐标方程 ρ＝cosθ 化为直角坐标方程为( D )
12 2 1 A.x＋2 ＋y ＝4
B．x
2
12 1 ＋y＋2 ＝4
C．x
2
12 1 ＋y－2 ＝4
12 2 1 D.x－2 ＋y ＝4
x＋y＝1， y－x＝1， π 1， . 2
π 答案：1，2
x＝0， 解得 y＝1，
则 交 点 为 (0,1) ， 对 应 的 极 坐 标 为
(2)曲线C的极坐标方程 ρ＝2cosθ，直角坐标系中的点 M的 坐 标 为 (0,2) ， P 为 曲线 C 上 任 意 一 点 ， 则 |MP| 的最 小 值 是 ________． 解析：由题设知：曲线C的直角坐标方程是x2＋y2＝2x，
第2讲
极坐标与参数方程
考纲要求 1.理解坐标系的作用；了解在平面直角坐标系伸 缩变换作用下平面图形的变化情况． 2．能在极坐标系中用极坐标表示点的位置，理 解在极坐标系和平面直角坐标系中表示点的位 置的区别，能进行极坐标和直角坐标的互化． 3．能在极坐标系中给出简单图形(如过极点的直 线、过极点或圆心在极点的圆)的方程．通过比 较这些图形在极坐标和平面直角坐标系中的方 程，理解用方程表示平面图形时选择适当坐标系 的意义． 4．了解柱坐标系、球坐标系中表示空间中点的 位置的方法，并与空间直角坐标系表示点的位置 的方法相比较，了解它们的区别． 5．了解参数方程，了解参数的意义；能选择适 当的参数写出直线、圆和圆锥曲线的参数方程.
数学优质课件精选选修系列极坐标与参数方程课件
(t 为参数)．
极坐标、参数方程的综合应用
利用极坐标、参数方程与普通方程间的转化，把 点、线和曲线等问题转化为熟知内容，进而解决 有关问题．
例3 (2011 年盐城市高三调研)已知直线 l 的参数方 程xy＝＝1t ＋2t (t 为参数)和圆 C 的极坐标方程 ρ＝
2 2sin(θ＋π4)． (1)将直线 l 的参数方程化为普通方程，圆 C 的极 坐标方程化为直角坐标方程； (2)判断直线 l 和圆 C 的位置关系．
参数)，
所以曲线 C 的直线坐标方程为 y＝12x2(x∈[－
2,2])，
联立解方程组得xy＝＝00，，
或x＝2 3， y＝6.
根据 x 的范围应舍去x＝2 3， y＝6，
故 P 点的直角坐标为(0,0)．
考点探究·挑战高考
考点突破 极坐极系与直角坐标系的互化
1．极坐标的四要素：(1)极点；(2)极轴；(3)长 度单位；(4)角度单位和它的正方向，四者缺一 不可．
y)，极坐标是(ρ，θ)，可以得出它们之间的
关系：x＝_______，y＝_______.又可得到关
系 ρcosθ
ρsinθ
• 式：ρ2＝_______，tanθ＝ ___y_ (x≠0)．
x2＋y2
x
• 3．常见曲线的极坐标方程
• (1)直线的极坐标方程
• •
过 方 (2)点 程圆M为的(ρ_极ρs_0i_，n坐_(θ_θ标－_0)_方且α__)程倾＝__斜ρ_0_角s_in_为(_θ_α0_－的__α直_)_线_．l的极坐标
第三节 坐标系与参数方程
双基研习·面对高考 第 三 节
坐
标
考点探究·挑战高考
系
与
参数方程ppt课件
考虑多种情况
注意单位的统一
在求解参数方程时，需要注意单位的 统一，避免出现单位不匹配的情况。
对于某些参数方程，可能需要考虑多 种情况，分别进行讨论和求解。
03 参数方程的应用实例
物理中的参数方程应用
总结词
描述物理中参数方程的应用，如行星运动、电磁波传播等。
详细描述
在物理学中，参数方程被广泛应用于描述各种现象，如行星运动轨迹、电磁波 传播路径等。这些参数方程通过引入一些变化的参数，能够精确地描述物理量 之间的关系，帮助我们更好地理解物理规律。
参数方程在其他领域的应用将有助于 推动相关领域的技术进步和理论发展 。
随着科技的发展，参数方程在数据科 学、机器学习等领域的应用也将逐渐 增多，为解决实际问题提供更多思路 和方法。
如何提高参数方程的应用水平
加强数学教育和普及工作，提高公众对参数方程的认识和理解，培养更多的数学人才和应用 型人才。
加强学科交叉和合作，促进参数方程与其他学科的融合和应用，共同推动相关领域的发展。
理解。
参数方程与线性代数的关联
参数方程可以用于描述线性代 数中的向量和矩阵的变化规律 。
通过参数方程，可以理解线性 变换的概念，以及矩阵的运算 和性质。
参数方程在解决线性代数问题 中也有一定的应用，例如求解 线性方程组、矩阵的逆和行列 式等。
参数参数方程与复变函数的关系
复变函数是一种描述复数域上的函数的方法，而参数方程可以用于描述复数域上的 函数的变化规律。
参数方程ppt课件
ቤተ መጻሕፍቲ ባይዱ
• 参数方程的基本概念 • 参数方程的求解方法 • 参数方程的应用实例 • 参数方程与其他数学知识的关联 • 参数方程的未来发展与展望
01 参数方程的基本概念
第十章 极坐标和参数方程第二节 参数方程
为了与曲线的参数方程有所区别，我们把表示曲线上点 的坐标之间的直接关系的方程叫做曲线的普通方程.
二、参数方程的作图
在所给曲线的参数方程
x = x t
y
=
y
t
，a t b
中, 先给参数t以某些可能取的值,求出x和y的对应值,这样就
确定了曲线上的点,将这些点连成光滑的曲线,就是参数方程
的图像.
0t
cos
, 纵坐标为0t
sin
1 2
gt
2
,因此我们就以方程组
:
x
0t
cos
y
0 t
sin
1 2
gt 2
，0 t t1
y
v0t sin
T •
v0t
M x, y
•
O
Q
x
v0t cos
图10-17 炮弹运动规律的轨迹
来表示炮弹运动的轨迹方程,其中 g是重力加速度g=9.8m/s2 ,t1
下面我们分别在直角坐标系与极坐标系内建立圆的渐开线 的参数方程.
(1)直角坐标参数方程 如图10-22所示,设基圆的圆心为O, 半径为 r, 绳子全部绕在圆圈上时,端点为 A. 取 O 为原点, 过 OA 的直线为 x 轴,建立直角坐标系.
设M x, y是渐开线上任意一点, BM 是切线,连接 OB,取
0来表示炮弹运动的轨迹方程是比较困难的.但是我们知道, 炮弹
运动的轨迹是由炮弹在各个时刻的位置所决定的.下面就来分析
炮弹在任意位置的坐标x和y分别与时刻t之间的关系.如果不考
虑地心引力,则经过时刻t,炮弹运动到T ,于是OT =0t.但事实上,
炮弹受地心引力的影响,不在点T而在点M .由于点M的横坐标为
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
例 1 在极坐标系中，已知圆 C 的圆心坐标为 C (2，
π )，半径 R= 5 ，求圆 C 的极坐标方程. P
3
C
O
x
思路 2：运用直接法，寻求点 P 的极径与 极角的关系，即是圆的极坐标方程.
8
题5 型一 极坐标、参数方程、直角坐标互化
法二：解 设 P( ρ，θ )是圆 C 上的任意一点，则
x
14
知识点回顾：
4．直线的参数方程
过定点 M(x0，y0)，倾斜角为 α 的直线 l 的参数方程为
x＝x0＋tcos α， y＝y0＋tsin α
(t 为参数)．
y
M(x,y)
注意：直线参数方程中
参数t的绝对值等于直 线上动点M到定点M0的
距离 |t|=|M0M|
M0(x0,y0)
O
t1 t2
（值3为）若M0是AB的中点，则t1+t2=0
2
16
题型二 参数方程的应用
例 4 在平面直角坐标系 xOy 中，直线 l 的参数方程为
x＝－2＋53t，
y＝2＋45t
(t
为参数)，它与曲线
设点
P
PC= R= 5 .
ρ5
在△POC 中，由余弦定理，
C
θ2
O
x
列 式 得 ρ2+22－2×2×ρcos ( θ－ ) = 5. 3
化 简 化简，得 ρ2－4ρcos ( θ－ )－1 = 0， 3
检 验 此即为所求的圆 C 的方程.
9
回顾反思
（1）基本思路：( 求曲线的极坐标方程 ) ①转化为直角坐标． ②直接法；
12
2019/12/23
13
知识点回顾：
4．直线的参数方程
解: 已 知 直 线 过 点 M 0( x 0 , y 0 ) ， 倾 斜 角 ，
在直线上任取一点M(x,y),则
M 0M (x x0, y y0)
y
设 e是 直 线 l的 单 位 方 向 向 量 ， 则
e (cos ,sin )
因 为 M 0 M / / e , 所 以 存 在 实 数 t R , 使 M 0 M t e , 即
(x x0, y y0 ) t(co s ,sin )
O
x x0 t cos , y y0 t sin
M(x,y) M0(x0,y0)
(co s ,sin )
参数方程与极坐标
迁安一中西校区 周荣荣
1
知识脉络
2
考纲要求
1 了解坐标系的作用，了解在平面直角坐标系伸缩变换作用下 平面图形的变化情况.
2 了解极坐标的基本概念，会在极坐标系中用极坐标刻画点的 位置，能进行极坐标和直角坐标的互化.
3 能在极坐标系中给出简单图形（如过极点的直线、过极点或 圆心在极点的圆）表示的极坐标方程.
解析 ∵C1：(x－3)2＋(y－4)2＝1，C2：x2＋y2＝1， ∴两圆心之间的距离为 d＝ 32＋42＝5.
∵A∈曲线 C1，B∈曲线 C2， ∴ABmin＝5－2＝3.
11
题型二 参数方程的应用
例3
（1）在曲线
C
：
x2 4
y2 9
1上找一点 M，使其到直线
l ： 2x y 6 0 的距离最小，并求最小距离。
ρ2＝x2＋y2 ， tan θ＝y(x≠0)
x
.
4
知识点回顾：
2.圆的参数方程
圆心在点 M(x0，y0)，半径为 r 的圆的参数方程为
x＝x0＋rcos θ， y＝y0＋rsin θ
(θ 为参数，0≤θ≤2π)．
3. 椭圆的参数方程
xa22＋by22＝1
的参数பைடு நூலகம்程为yx＝＝bascions
θ θ
(θ 为参数)．
5
题型一 极坐标、参数方程、直角坐标互化
例 1 在极坐标系中，已知圆 C 的圆心坐标为
C (2， π )，半径 R= 5 ，求圆 C 的极坐标方程. 3
P
思路 1：化为直角坐标研究.
C x
O
6
题型一 极坐标、参数方程、直角坐标互化
法一：将圆心 C(2，π) 化成直角坐标为（1，3）. 3
（2）动点 P(x,y)在曲线上变化 ，求 3x+2y 的最大值和最小值
变式：（2014 全国卷Ⅰ）23.（2）过曲线 C 上任一点 P 作与l 夹 角为 30o 的直线，交l 于点 A ，求| PA | 的最大值与最小值.
反思： （1）思维策略：涉及圆、椭圆的最值问题，常利用圆或 椭圆的参数方程，转化为三角函数的有界性问题． （2）思想方法：参数思想、化归转化思想
半径 R= 5 , 故圆 C 的直角坐标方程为
(x－1)2＋(y－ 3 )2 = 5.
y
再将 C 化成极坐标方程，
C
O
x
得( ρcosθ－1)2 + ( ρsinθ－ 3 )2=5.
化简，得 ρ2－4ρcos(θ－ π )－1=0， 3
此即为所求的圆 C 的方程.
7
题型一 极坐标、参数方程、直角坐标互化
M0M te
x
15
15
· 知识点y 回顾： B
· A
M（x，y）
·· M0（x0，y0）
x y
x0 y0
t cos t sin
(t是 参 数 ）
O
x
设A,B为直线上任意两点，它们所对应的参
数值分别为t1,t2.
（1）|AB|＝t1 t 2
（2）若M是AB的中点，M对应的参数
4 了解参数方程，了解参数的意义.
5 能选择适当的参数写出直线、圆和圆锥曲线的参数方程.
3
知识点回顾：
1．直角坐标与极坐标的互化
把直角坐标系的原点作为极点，x 轴
正半轴作为极轴，且在两坐标系中取
相同的长度单位. 设 M 是平面内的任
意一点，它的直角坐标、极坐标分别
ρ
为(x，y)和(ρ，θ)，则
x＝ρcos θ y＝ρsin θ
（2）思想方法：化归转化思想． 直接法求曲线的极坐标方程的一般步骤： ① （建系）建立适当的极坐标系；
② （设点）在曲线上任取一点 P( ， ) ；
③ （列式）根据曲线上的点所满足的条件写出等式；
④ （化简）用极坐标 ， 表示上述等式，并化简；
⑤ （检验）证明所得的方程是曲线的极坐标方程．
10
题型一 极坐标、参数方程、直角坐标互化
例 2 (2011·陕西)在直角坐标系 xOy 中，以原点为极点，x 的
正半轴为极轴建立极坐标系，设点 A，B 分别在曲线 C1：
x＝3＋cos θ， y＝4＋sin θ
(θ 为参数)和曲线 C2：ρ＝1 上，则 AB 的最
3 小值为________．