高二数学极坐标与参数方程PPT教学课件

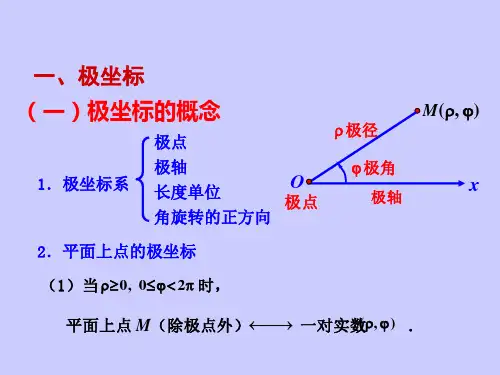
解 如图10 -12所示,设M , 是直线上任意一点.连接OM ,
则OM =, AOM .又因为
OAM ,所以有cos a ,
2
即
a cos
• M ,
O
•
A a, 0
x
这就是所求直线的极坐标方程.
图10-12 例8图形
第23页
例9 设有一圆经过极点O,圆心C在极轴上,半径为a,求它 的极坐标方程.
第11页
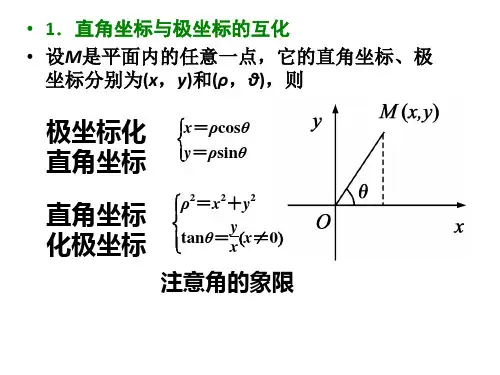
例2 设点M的直角坐标为1,-1,求它的极坐标.
解 由公式10-2可得 :
12 12 2, tan 1 1.
1
因为点M 1, 1在第IV象限,所以 7 ,于是可得点M的
4
极坐标为
2,
7 4
.
第12页
二、曲线极坐标方程
1.曲线极坐标方程概念
在平面上的一条曲线, 在
直角坐标系中可以用含有 x 和 y 的方程来表示.同样,在极坐
x O
M0 0,0
图10-14 等速螺线极坐标系
第25页
极角为: t
由于 t
所以
0
令a ,得 :
0 a a, 0为常数,且a 0.
这就是等速螺线的极坐标方程.
如果0 0,即动点M由极点O开始运动,那么 a.这时,极 径与极角成正比.
下面我们来作等速螺线 a a 0的图像.
x
5 cos
3
5 2
,
y
5
sin
3Leabharlann 53 2.
第10页
于是得点M的直角坐标为
5 2
,
5
3 2
.我们也可以把点M的
直角坐标化为极坐标,由公式10 1变化可得 :

所以，经过伸缩变换后，直线 2x＋4y＝1 变成直线 x′＋y′＝1. (2)将 ①代入 x ＋ y ＝ 4，得到经过伸缩变换后的图形的方程为 x′2 y′2 ＋ ＝4. 4 16
2 2 x ′ y ′ 所以，圆 x2＋y2＝4 经过伸缩变换后变成椭圆 ＋ ＝1. 16 64 2 2
x ′ y′ 答案：(1)x′＋y′＝1 (2) ＋ ＝4 4 16
2
2
5x＇＝x 例 3 在平面直角坐标系中，经过伸缩变换 曲线 C 变 4y＇＝y，
为曲线 x′2＋y′2＝1，求曲线 C 的方程． 解析：设曲线 C 上任意一点为(x，y)，经过伸缩变换后对应点的 坐标为(x′，y′)，
5x′＝x， 由 得 4y′＝y
x y 1 代入 x′ ＋y′ ＝1，得25＋16＝1. y′＝4y.
题型二 伸缩变换
例 2 在平面直角坐标系中， 求下列方程所对应的图形经过伸缩
x＇＝2x， 变换 后的图形． y′＝4y
(1)2x＋4y＝1；(2)x2＋y2＝4.
x′＝2x， 解析：由伸缩变换式 得 y′＝4y
1 y＝4y′.
1 x＝ x′， 2
①
(1)将①代入 2x＋4y＝1，得到经过伸缩变换后的图形方程为 x′ ＋y′＝1.
2.平面直角坐标系中的伸缩变换 (1)平面直角坐标系中方程表示图形,那么平面图形的伸缩变换 就可归纳为坐标伸缩变换,这就是用代数方法研究几何变换. (2)设点 P(x,y)是平面直角坐标系中的任意一点,在变换 ������' = ������������(������ > 0), φ: 的作用下,点 P(x,y)对应到点 P'(x',y'),称 φ 为平面直 ������' = ������������(������ > 0) 角坐标系中的坐标伸缩变换,简称伸缩变换.

∵ 0 表示极点，而曲线 2acos 通过极点， ∴ 2acos 即为所求.
例 2．将极坐标方程2 a2cos2 化为直角坐标方程： 解： 2 a2(cos 2sin2), 4 a22(cos2sin2), 4 a2[(cos)2 (sin)2], (x2 y2)2 a2(x2 y2).
（三）极坐标系中曲线的对称性
（2）当 R, R 时，
M(, )
的量法 ：逆转为正，顺转为负. O
0
x
的量法 ： 0 时，则在角的 终边上取 M 点，使OM ；
0 时，则在角的 终边的反向延长线上取 M 点，
使 OM .
O
0
x
M(, )
M(, )
(, )
O
x
M1(, )
这样，一对实数(, ) 对应唯 一 点 M，
(, 2k) (, (2k
2．
椭圆
x2 a2
y2 b2
1
(ab0)
的参数方程：
xacost
ybsint
,
t[0, 2].
椭圆
(
x
x a2
)2
(
y
y b2
)2
1
(ab0)
的参数方程：
x y
x y
acost bsint
(a
b
0),
t[0, 2].
3．摆线的参数方程：
xa(t sint) y a(1cost )
(
y
)
2 3
1
，
aa
2 22
故普通方程为 x 3 y 3 a 3 .
（二）几种常见曲线的参数方程
1． 圆 x2 y2 a2 的参数方程：
x acost yasint

7、 , R
6
8、 sin 2 cos 1
4、 2sin 5、 2 cos 6、 2 2 cos 8 0
9、 sin( ) 2
42
10、 sin( ) 1
6
➢ 随堂演练----高考真题
【2018北京卷10】
在极坐标系中，直线cos sin a 与圆 2cos相切，则a _____.
当然，非标准形式下
x y
x0 y0
at 你能推的到吗？ bt
(t1 t2 )2 4t1t2
| AB | a2 b2 (t1 t2 )2 a2 b2 (t1 t2 )2 4t1t2
三种坐标系下的弦长问题----各具优势与特点
直线为参数方程标准形式、曲线为普通方程
非标准形式下弦长公式| AB | a2 b2 (t1 t2 )2 4t1t2
cos s in
(为参
数)，过点(0, 2)且倾斜角为的直线l与圆O交于A, B两点
(1)求的取值范围
(2)求AB中点P的轨迹的参数方程
近三年高考真题
【2017全国1卷22题】
在直角坐标系中，曲线C的参数方程为xy
3 c os s in
(为参
数)，直线l的参数方程为xy
a 4t(t为参数) 1t
近三年高考真题
【2018全国1卷22题】
在直角坐标系中，曲线C1的方程为y k | x | 2.以坐标 原点为极点，x轴正半轴为极轴建立极坐标系，曲线C2
的极坐标方程为 2 2cos 3 0
(1)求C2的直角坐标方程 (2)若C1与C2有且仅有三个公共点，求C1的方程
近三年高考真题
【2018全国2卷22题】
选修Байду номын сангаас-4极坐标及参数方程

详细描述
摆线的极坐标方程是ρ=a(1-cosθ)，其中ρ表示点到原点的距离，θ表示点与x轴的夹角，a表示摆线的 半径。通过这个方程，我们可以方便地计算摆线的长度和面积。
实例三：磁场线的参数方程
总结词
磁场线的参数方程表示
详细描述
磁场线的参数方程通常由两个参数构 成，例如时间和角度。参数方程可以 描述磁场线在任意时刻的位置和方向 ，从而方便地计算磁场线的长度和面 积。
极坐标与参数方程的转换关系
极坐标与直角坐标转换
极坐标系中的点可以用直角坐标系中的坐标表示，反之亦然。具体转换公式为 ：$x = rho cos theta, y = rho sin theta, x^2 + y^2 = rho^2$。
参数方程与直角坐标转换
参数方程中的点也可以用直角坐标系中的坐标表示，具体转换公式取决于参数 方程的形式。
05
极坐标与参数方程的习题及解析
习题一：求圆的极坐标方程
总结词
理解并掌握圆的极坐标方程的推 导方法
详细描述
通过给定的圆心和半径，利用极 坐标与直角坐标方程
80%
总结词
掌握参数方程转换为普通方程的 方法
100%
详细描述
通过消去参数，将参数方程转化 为普通方程，以便更好地理解曲 线的几何意义。
极坐标与直角坐标的关系
对于平面内任意一点P，其直角坐标为(x,y)，则其极坐标为(r,θ)， 其中r=√(x²+y²)，tanθ=y/x。
极坐标与直角坐标的转换
直角坐标转换为极坐标
已知点P的直角坐标为(x,y)，则其极 坐标为(r,θ)，其中r=√(x²+y²)， tanθ=y/x。
极坐标转换为直角坐标

x y
t t
1, t 1 t
(t为参数)
相交于
A、B
两点．求线段
AB
的
长．
3 ．（ 2008
年
广东
实验
中
学）
求
直
线
x y
1 1
4t 3t
（ t为参数）被曲线 2 cos( ) 所截的弦长
4
4.已知圆的极坐标方程为 2cos ，求该圆的圆 心到直线 sin 2 cos 1 的距离
到直线距离为 2，|PQ|的最小值为 2－1＝1
1．直接求解
例 1．在极坐标系中，过圆 =6cos 的圆心，且垂
直于极轴的直线的极坐标方程
分析：把极坐标方程化为普通方程求出直线， 再得到极坐标方程。
例 2．（08 广东卷理 13）已知曲线 C1，C2 的极坐标
方 程 分 别 为 cos 3 ，
五、考点预测
1．（江苏省启东中学 2009）在极坐标系中，从极点 O
作直线与另一直线 l : cos 4 相交于点 M，在 OM
上取一点 P，使 OM OP 12． （1）求点 P 的轨迹方程；（2）设 R 为 l 上任意一点，
试求 RP 的最小值
2．过点 P（－3，0）且倾斜角为 30°的直线和曲线
L
的参数方程为
x＝t＋3 y＝3－t
，（参数
t
R
），
圆
Ｃ
的
参
数
方
程
为
x＝2cos y＝2sin＋2
（
参
数
0，2 ），则圆Ｃ的圆心坐标为
，圆心
到直线 L 的距离为
。
例 9．（2008 江苏卷）在平面直角坐标系 xOy 中，点 P(x，y) 是 椭 圆 x2 y2 1 上 的 一 个 动 点 ， 求

当 θ1=θ2，|AB|＝/ρ1—-ρ2/
• 3．直线的极坐标方程：若直线过点M(ρ0，θ0)，且极 轴到此直线的角为α，则它的方程为：
• ρsin(θ－α)＝ρ0sin(θ0－α)． • 几个特殊位置的直线的极坐标方程 • (1)直线过极点：θ＝θ0和θ＝π+θ0； • (2)直线过点M(a,0)且垂直于极轴：ρcosθ＝a；
若 M1，M2 是 l 上的两点，其对应参数分别为 t1，t2，则 (1)M1，M2 两点的坐标分别是(x0＋t1cos α，y0＋t1sin α)，(x0 ＋t2cos α，y0＋t2sin α)． (2)|M1M2|＝|t1－t2|. (3)若线段 M1M2 的中点 M 所对应的参数为 t，则 t＝t1＋2 t2， 中点 M 到定点 M0 的距离|MM0|＝|t|＝t1＋2 t2. (4)若 M0 为线段 M1M2 的中点，则 t1＋t2＝0.
[解] (1)直线 l 的普通方程为 xsin α－ycos α＋cos α＝0. 曲线 C 的极坐标方程为 ρcos2θ＝4sin θ， 即 ρ2cos2θ＝4ρsin θ，∵ρcos θ＝x，ρsin θ＝y， ∴曲线 C 的直角坐标方程为 x2＝4y.
x＝tcos α， (2)将 l: y＝1＋tsin α 代入曲线 C∶x2＝4y 中， 得 t2cos2α－4tsin α－4＝0.
意判断点P所在的象限(即角θ的终边的位置)，以 便正确地求出角θ. • (2)注意“双坐标系”是直角坐标与极坐标互化的 前提．若要判断曲线的形状，通常是先将极坐标 方程化为直角坐标方程，再判断．
(3)极坐标系中两点间的距离公式：已知点 A(ρ1，θ1)，
B(ρ2，θ2)，那么|AB|＝ ρ12＋ρ22－2ρ1ρ2cosθ1－θ2.

解（1）直线的普通方程是y = 2（x+1），
令 y x 1 t ．选择 t 为参数， 25 5
y
P（x
5
5
,y） 直线的参数方程

x

1

5 t， 5
P0

y

25 5
t．
O x 若令 x t ．选择 t 为参数，
直线的参数方程

x y

t, 2t

2.
心之间的距离为 3 . （2）直线 l 的直角坐标方程是 x y 4 0 .
所以过 C1与 l 垂直的直线方程是 x y 1 0 . 化为极坐标方程为 r cosq r sinq 1 0 ,
即 r cos(q π ) 2 .
42
2019/9/11
15
破解难点：参数方程与普通方程互化
方程为 x 2y 0 ．因此点 P 到直线 l 的距离是
d | 2cosq 2sinq |
2 2 | sin(q π ) |

4 ，所 以 当
12 22
5
q kp p ， k Z 时 , 故 点 P 为 ( 2， 2 ) 或
4
2
( 2， 2 ) 时， d 取得最大值 2 5 ．
2019/9/11
39
思路分析
例 6 在极坐标系中，设圆 C：ρ= 3 上的点到直线
2019/9/11
13
思路分析
例 2 已知圆 C1 的极坐标方程为 ρ = 2cosθ，圆 C2 的极坐标方程为 ρ2－4ρcos ( θ－ p )－1 = 0，直线 l
3 的极坐标方程 ρcosθ－ρsinθ = 4． （1）求圆 C1、C2 圆心之间的距离；

∴直角坐标方程为 x2＋y2＝4ay. (2)把方程变形为 ρ2＝9(ρcos θ＋ρsin θ )， ∵ρ 2＝x2＋y2，ρ cos θ ＝x，ρ sin θ ＝y， ∴直角坐标方程为 x2＋y2＝9(x＋y)． 答案：(1)x2＋y2＝4ay (2)x2＋y2＝9(x＋y)
4．(1)直角坐标方程x＋y－2＝0化为极坐标方程是________；

2
（3）直线 l 过点 P a, 且与极轴平行，则直线 l 的极坐标方程为 sin 2
a
0
题型一 求简单的极坐标方程
解析：在圆上任取一点 P(ρ，θ )，那么，在△AOP 中，|OA|＝8， 解析：在圆上任取一点 P(ρ，θ)，那么，在△AOP 中，|OA|＝8， π π |AP|＝5，∠AOP＝ － θ 或 . θ － π π 3 p A － 3 . |AP|＝5，∠AOP＝ －θ 或θ 3 3 π 82＋ρ2－52 82＋ρ2－52 π 由余弦定理，得 cos －θ＝ . 由余弦定理，得 cos － . θ＝ 3 2 × 8 ρ 2×8ρ 3 π π ＋ 39 ＝ 为所求的极坐标方程． ＋ 即 ρ －16ρcosθ 39 ＝ 00为所求的极坐标方程． － － θ 33
2 2 即 ρ －16ρcos
＋ 39 ＝ 0 ＋ 答案：ρ －16ρcosθ－ 39 ＝ 0 3 3
π ，半径为 5 的圆的方程． 例 1 在极坐标平面上，求圆心A8， π 3 ，半径为 例 1 在极坐标平面上，求圆心 A8， 5 的圆的方程． 3
3π sin －θ 4
＝
. 7π sin 12
ρ

(t 为参数)．
极坐标、参数方程的综合应用
利用极坐标、参数方程与普通方程间的转化，把 点、线和曲线等问题转化为熟知内容，进而解决 有关问题．
例3 (2011 年盐城市高三调研)已知直线 l 的参数方 程xy＝＝1t ＋2t (t 为参数)和圆 C 的极坐标方程 ρ＝
2 2sin(θ＋π4)． (1)将直线 l 的参数方程化为普通方程，圆 C 的极 坐标方程化为直角坐标方程； (2)判断直线 l 和圆 C 的位置关系．
参数)，
所以曲线 C 的直线坐标方程为 y＝12x2(x∈[－
2,2])，
联立解方程组得xy＝＝00，，
或x＝2 3， y＝6.
根据 x 的范围应舍去x＝2 3， y＝6，
故 P 点的直角坐标为(0,0)．
考点探究·挑战高考
考点突破 极坐极系与直角坐标系的互化
1．极坐标的四要素：(1)极点；(2)极轴；(3)长 度单位；(4)角度单位和它的正方向，四者缺一 不可．
y)，极坐标是(ρ，θ)，可以得出它们之间的
关系：x＝_______，y＝_______.又可得到关
系 ρcosθ
ρsinθ
• 式：ρ2＝_______，tanθ＝ ___y_ (x≠0)．
x2＋y2
x
• 3．常见曲线的极坐标方程
• (1)直线的极坐标方程
• •
过 方 (2)点 程圆M为的(ρ_极ρs_0i_，n坐_(θ_θ标－_0)_方且α__)程倾＝__斜ρ_0_角s_in_为(_θ_α0_－的__α直_)_线_．l的极坐标
第三节 坐标系与参数方程
双基研习·面对高考 第 三 节
坐
标
考点探究·挑战高考
系
与