理论力学第二章

理论力学第二章习题答案理论力学是物理学中研究物体运动规律和相互作用的分支学科，它以牛顿运动定律为基础，通过数学方法来描述物体的运动和力的作用。

本章习题答案将帮助学生更好地理解和掌握理论力学的基本概念和计算方法。

习题1：考虑一个质量为m的物体在重力作用下自由下落。

忽略空气阻力，求物体下落过程中的速度和位移。

答案：物体自由下落时，受到的力只有重力，大小为mg，方向向下。

根据牛顿第二定律，F=ma，可以得到加速度a=g。

物体的速度v随时间t变化，可以使用公式v=gt计算。

物体的位移s随时间变化，可以使用公式s=1/2gt^2计算。

习题2：一个质量为m的物体在水平面上以初速度v0开始运动，受到一个大小为k的恒定摩擦力作用。

求物体停止前所经过的距离。

答案：物体在水平面上运动时，受到的摩擦力与物体的位移成正比，即F=-kx。

根据牛顿第二定律，F=ma，可以得到加速度a=-k/m。

物体的位移x随时间t变化，可以使用公式x=v0t - 1/2(k/m)t^2计算。

当物体速度减至0时，物体停止，此时t=2v0/k，代入公式得到x=2v0^2/k。

习题3：一个质量为m的物体在斜面上，斜面与水平面的夹角为θ。

物体受到一个向上的拉力F，使得物体沿斜面匀速上升。

求拉力F的大小。

答案：物体沿斜面匀速上升时，拉力F与重力分量mgsinθ和摩擦力μmgcosθ平衡。

根据平衡条件，F=mgsinθ + μmgcosθ。

如果摩擦系数为μ，可以进一步简化为F=mg(sinθ + μcosθ)。

习题4：考虑一个质量为m的物体在竖直平面内做圆周运动，圆心位于物体的正下方。

物体的运动由一个弹簧连接到圆心，弹簧的劲度系数为k。

求物体在圆周运动中的角速度。

答案：物体在圆周运动中，受到弹簧力和重力的作用。

根据牛顿第二定律，向心力Fc=mv^2/r=ma，其中r为圆的半径。

由于物体做圆周运动，向心力由弹簧力和重力的垂直分量提供。

因此，Fc=kx - mgcosθ，其中x为弹簧的伸长量，θ为物体与竖直方向的夹角。

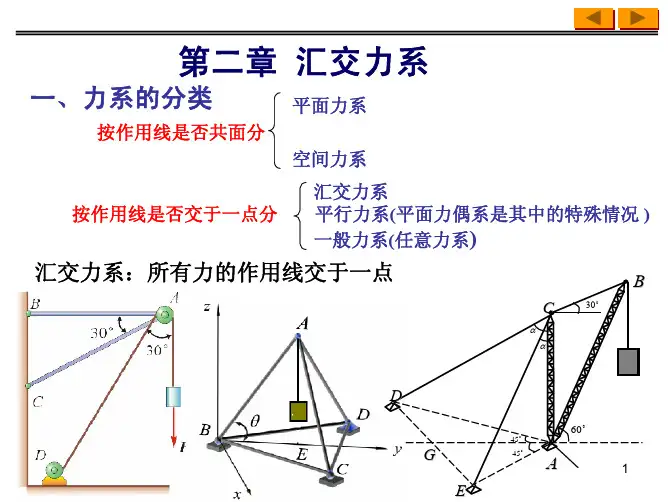
平面任意力系1第二章平面力系第二部分平面任意力系平面任意力系：各力的作用线在同一平面内，既不汇交于一点，又不相互平行的力系。

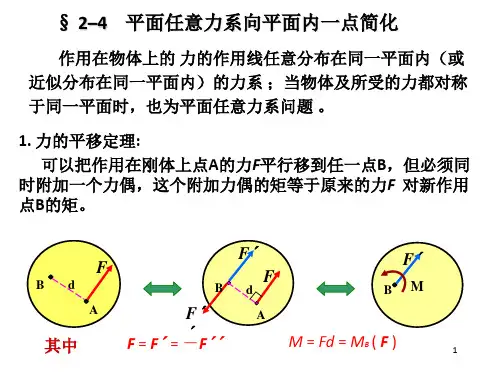
[例]第二章平面力系第二部分平面任意力系§2–5 力的平移定理§2–6 平面任意力系向一点简化§2–7 平面任意力系的简化结果• 合力矩定理§2–8 平面任意力系的平衡条件和平衡方程§2–9 平面平行力系的平衡方程§2–10 静定与超静定问题的概念•物体系统的平衡§2–11 平面简单桁架的内力分析平面任意力系习题课§2-5 力的平移定理力的平移定理：作用在刚体上点A的力可以平行移到任一点B，但必须同时附加一个力偶。

这个力偶的矩等于原来的力对新作用点B的矩。

FF[证] 力力系），力偶（力FFF''+'FFF''',,F说明：①力的平移定理揭示了力与力偶的关系：力力+力偶（例断丝锥）②力平移的条件是附加一个力偶M，且M与d有关，M=F•d③力的平移定理是力系简化的理论基础。

任意力系向一点简化汇交力系+力偶系未知力系）（已知力系）汇交力系力，F R '(主矢) ，(作用在简化中心)力偶系力偶，M O (主矩) ，(作用在该平面上)§2-6平面任意力系向一点简化大小：主矢方向：与简化中心的关系：'R F 123'R iF F F F F =+++=∑ 主矢12312 ()()()O O O O i M M M M M F M F M F =+++=++=∑主矩2222'''()()R Rx Ry x y F F F F F =+=+∑∑11tg tg xRyRx yF F F F α--==∑∑（移动效应）(与简化中心位置无关)[因主矢等于各力的矢量和]大小：主矩M O 方向：与简化中心的关系：()O O i M M F =∑（转动效应）固定端（插入端）约束在工程中常见的雨搭车刀方向规定+ —(与简化中心有关)[因主矩等于各力对简化中心取矩的代数和]固定端（插入端）约束说明①认为F i 这群力在同一平面内;②将F i 向A 点简化得一力和一力偶;③F RA 方向不定可用正交分力F Ay ,F Ax 表示;④F Ay ,F Ax , M A 为固定端约束力;⑤F Ay , F Ax 限制物体平动, M A 限制转动。

理论力学第二章习题答案理论力学第二章习题答案理论力学是物理学的基础学科之一，它研究物体的运动规律以及力的作用原理。

在理论力学的学习过程中，习题是检验学生理解和掌握程度的重要方式之一。

下面将为大家提供理论力学第二章的习题答案，希望对大家的学习有所帮助。

1. 一个质点在匀速直线运动中，它的加速度是多少？答：在匀速直线运动中，速度保持不变，所以加速度为0。

2. 一个质点的速度随时间的变化规律为v=3t+2，求它在t=2s时的速度。

答：将t=2s代入速度变化规律中，得到v=3*2+2=8m/s。

3. 一个质点做匀加速直线运动，它的初速度为2m/s，加速度为3m/s²，求它在t=4s时的位移。

答：根据匀加速直线运动的位移公式s=vt+1/2at²，将初速度v=2m/s，时间t=4s，加速度a=3m/s²代入，得到s=2*4+1/2*3*4²=8+24=32m。

4. 一个质点做匀加速直线运动，它的初速度为4m/s，位移为20m，加速度为2m/s²，求它的末速度。

答：根据匀加速直线运动的末速度公式v²=u²+2as，将初速度u=4m/s，位移s=20m，加速度a=2m/s²代入，得到v²=4²+2*2*20=16+80=96，所以末速度v=√96≈9.8m/s。

5. 一个质点做直线运动，它的速度随时间的变化规律为v=2t²+3t，求它在t=3s时的加速度。

答：加速度是速度对时间的导数，所以将速度变化规律v=2t²+3t对时间t求导，得到加速度a=dv/dt=4t+3。

将t=3s代入，得到a=4*3+3=15m/s²。

6. 一个质点做直线运动，它的速度随时间的变化规律为v=5t²+2t，求它在t=2s 时的加速度。

答：同样地，将速度变化规律v=5t²+2t对时间t求导，得到加速度a=dv/dt=10t+2。