【成才之路】2016高中数学 2.4.2二次函数的性质同步测试 北师大版必修1

2-4-2 二次函数的性质基础巩固一、选择题1．函数y＝－x2＋1在下列哪个区间上是增加的()A．[0，＋∞) B．(－∞，0]C．(0，＋∞) D．(－∞，＋∞)[答案] B[解析]y＝－x2＋1中二次项系数小于0，图像开口向下，易知递增区间为(－∞，0]．2．二次函数y＝－2(x＋1)2＋8的最值情况是()A．最小值是8，无最大值B．最大值是－2，无最小值C．最大值是8，无最小值D．最小值是－2，无最大值[答案] C[解析]因为二次函数开口向下，所以当x＝－1时，函数有最大值8，无最小值．3．二次函数f(x)＝ax2＋bx＋c的顶点为(4,0)，且过点(0,2)，则abc＝( )A ．－6B ．11C ．－14 D.14 [答案] C[解析] ∵f (x )图像过点(0,2)，∴c ＝2. 又顶点为(4,0)，∴－b2a ＝4，8a －b 24a ＝0. 解得：b ＝－1，a ＝18，∴abc ＝－14.4．若f (x )＝3x 2＋2(a －1)x ＋b 在区间(－∞，1]上是减函数，则a 的取值范围是( )A ．(－∞，－2]B ．[－2，＋∞)C ．(－∞，2]D ．[2，＋∞)[答案] A[解析] ∵对称轴x ＝1－a3，又开口向上，在(－∞，1]上是减函数．∴1－a3≥1，∴a ≤－2.5．二次函数y ＝f (x )的图像过原点，且顶点为(－2,8)，则f (x )＝( )A ．－2x 2－8xB ．2x 2－8xC ．2x 2＋8xD ．－2x 2＋8x[答案] A[解析] 由题意设二次函数的解析式为y ＝a (x ＋2)2＋8，又∵函数图像过原点，∴4a ＋8＝0，∴a ＝－2，∴y ＝－2x 2－8x .6．二次函数f (x )满足f (2＋x )＝f (2－x )，又f (x )在[0,2]上是增函数，且f (a )≥f (0)，那么实数a 的取值范围是( )A ．[0，＋∞)B ．(－∞，－0]C ．[0,4]D ．(－∞，0]∪[4，＋∞)[答案] C[解析] 此函数图像的对称轴为x ＝2＋x ＋2－x2＝2，在[0,2]上递增，如图所示，正确答案为C.二、填空题7．(2012·石家庄高一检测)已知函数f (x )＝4x 2－kx －8在[2,10]上具有单调性，则实数k 的取值范围是________．[答案] k ≤16或k ≥80[解析] 函数f (x )的对称轴为x ＝k 8， ∴k 8≤2或k8≥10， ∴k ≤16或k ≥80.8．已知抛物线y ＝ax 2与直线y ＝kx ＋1交于两点，其中一点的坐标为(1,4)，则另一交点的坐标为________．[答案] (－14，14)[解析] 把(1,4)的坐标代入y ＝ax 2与y ＝kx ＋1中得a ＝4，k ＝3.所以由⎩⎪⎨⎪⎧ y ＝4x 2，y ＝3x ＋1，解得⎩⎪⎨⎪⎧x ＝1，y ＝4，或⎩⎪⎨⎪⎧x ＝－14，y ＝14.三、解答题9．(2012·九江高一检测)已知二次函数y ＝－4x 2＋8x －3. (1)画出它的图像，并指出图像的开口方向、对称轴方程、顶点坐标；(2)求函数的最大值；(3)写出函数的单调区间．(不必证明)[解析] (1)图像如图所示，该图像开口向下；对称轴为直线x ＝1；顶点坐标为(1,1)．(2)y ＝－4(x －1)2＋1，故函数的最大值为1. (3)函数的单调增区间是(－∞，1]， 单调减区间是[1，＋∞).能 力 提 升一、选择题1．已知函数f (x )＝4x 2－mx ＋5在区间[－2，＋∞)上是增函数，则f (1)的取值范围是( )A ．f (1)≥25B ．f (1)＝25C ．f (1)≤25D ．f (1)>25[答案] A[解析] f (x )＝4x 2－mx ＋5在[m8，＋∞)上是增加的，故[－2，＋∞)⊆[m8，＋∞)，即－2≥m8，∴m ≤－16. ∴f (1)＝9－m ≥25.2．某种电热器的水箱盛水200升，加热到一定温度可浴用．浴用时，已知每分钟放水34升，在放水的同时按匀加速自动注水(即t 分钟自动注水2t 2升)，当水箱内的水量达到最小值时，放水自动停止．现假定每人洗浴用水量为65升，则该电热器一次至多可供________人洗浴．( )A ．3B ．4C ．5D ．6[答案] B[解析] 设t 分钟后水箱内的水量为y 升，则由题设，知y ＝200－34t ＋2t 2＝2⎝ ⎛⎭⎪⎫t －1722＋200－2892(t >0)，当t ＝172＝8.5分钟时，y 取最小值，此时共放浴用水34×8.5＝289升，而28965＝42965，故一次至多可供4人洗浴．二、填空题3．已知抛物线y ＝－2x 2＋8x －9顶点为A ，若二次函数y ＝ax 2＋bx ＋c 的图像经过点A ，且与x 轴交于B (0,0)、C (3,0)两点，则这个二次函数的解析式为________．[答案] y ＝12x 2－32x[解析] ∵y ＝－2x 2＋8x －9＝－2(x －2)2－1，∴A (2，－1)．设所求二次函数的解析式为y ＝ax (x －3)，则由题意知－1＝a ×2(2－3)，即a ＝12.∴所求解析式为y ＝12x 2－32x.4．已知二次函数y ＝－x 2＋2x ＋m 的部分图像如图所示，则关于x 的一元二次方程－x 2＋2x ＋m ＝0的根为________．[答案] 3或－1[解析] 由图像知f (3)＝0， ∴m ＝3.由－x 2＋2x ＋3＝0得x 2－2x －3＝0， ∴x ＝3或－1. 三、解答题5．根据下列条件，求二次函数的解析式． (1)图像过A (0,1)、B (1,2)、C (2，－1)三点； (2)图像顶点是(－2,3)，且过点(－1,5)；(3)图像与x 轴交于(－2,0)、(4,0)两点，且过点(1，－92)． [解析] (1)设二次函数的解析式为y ＝ax 2＋bx ＋c (a ≠0)，由已知函数的图像经过(0,1)、(1,2)、(2，－1)三点．得：⎩⎪⎨⎪⎧c ＝1a ＋b ＋c ＝24a ＋2b ＋c ＝－1，解之得：⎩⎪⎨⎪⎧a ＝－2b ＝3c ＝1，∴函数的解析式为y ＝－2x 2＋3x ＋1.(2)设二次函数的解析式为y ＝a (x －h )2＋k ，其顶点的坐标是(h ，k )，∵顶点的坐标是(－2,3)，∴y ＝a (x ＋2)2＋3. 又∵图像过点(－1,5)，∴5＝a (－1＋2)2＋3. ∴a ＝2，∴y ＝2(x ＋2)2＋3， ∴y ＝2x 2＋8x ＋11.即函数的解析式为y ＝2x 2＋8x ＋11.(3)设二次函数的解析式为y ＝a (x －x 1)(x －x 2)， 因为二次函数的图像交x 轴于(－2,0)、(4,0)两点， 且过点(1，－92)，设y ＝a (x ＋2)(x －4)， 则有－92＝a (1＋2)(1－4)，∴a ＝12. ∴所求的函数解析式为y ＝12(x ＋2)(x －4)， 即y ＝12x 2－x －4.6．已知关于x 的函数y ＝(m ＋6)x 2＋2(m －1)x ＋m ＋1的图像与x 轴总有交点．(1)求m 的取值范围；(2)若函数图像与x 轴的两个交点的横坐标的倒数和等于－4，求m 的值．[解析] (1)当 m ＋6＝0即m ＝－6时， 函数y ＝－14x －5与x 轴有一个交点； 当m ＋6≠0即m ≠－6时，有Δ＝4(m －1)2－4(m ＋6)(m ＋1)＝4(－9m －5)≥0，解得m ≤－59，即当m ≤－59且m ≠－6时，抛物线与x 轴有一个或两个交点， 综上可知，当m ≤－59时，此函数的图像与x 轴总有交点． (2)设x 1、x 2是方程(m ＋6)x 2＋2(m －1)x ＋m ＋1＝0的两个根， 则x 1＋x 2＝－2(m －1)m ＋6，x 1x 2＝m ＋1m ＋6.∵1x 1＋1x 2＝－4，即x 1＋x 2x 1x 2＝－4， ∴－2(m －1)m ＋1＝－4，解得m ＝－3，当m ＝－3时，m ＋6≠0，Δ>0，符合题意， ∴m 的值是－3.7．设f (x )＝x 2＋ax ＋3－a ，且f (x )在闭区间[－2,2]上恒取非负数，求a 的取值范围．[解析] f (x )＝⎝ ⎛⎭⎪⎫x ＋a 22＋3－a －a24，f (x )≥0在x ∈[－2,2]恒成立的充分条件是f (x )在x ∈[－2,2]上的最小值非负．(1)当－a2<－2，即a >4时，f (x )在[－2,2]上是增函数，最小值为f (－2)＝7－3a ，由7－3a ≥0，得a ≤73，这与a >4矛盾，此时a 不存在．(2)当－2≤－a2≤2，即－4≤a ≤4时，f (x )在[－2,2]上的最小值为f ⎝ ⎛⎭⎪⎫－a 2＝3－a －a 24，3－a －a 24≥0⇒a 2＋4a －12≤0，∴－6≤a ≤2. 结合－4≤a ≤4，可知此时－4≤a ≤2.(3)当－a2>2，即a <－4时，f (x )在[－2,2]上是减函数，最小值为f (2)＝7＋a ，由7＋a ≥0，得a ≥－7.∵a<－4，∴－7≤a<－4.由(1)(2)(3)可知，a的取值范围是[－7,2]．。

北师大版二次函数测试题及答案北师大版二次函数测试题一、选择题：1.下列关系式中，属于二次函数的是(x为自变量)()A. B. C.D.2. 函数y=x2-2x+3的图象的顶点坐标是()A. (1，-4)B.(-1，2)C. (1，2)D.(0，3)3. 抛物线y=2(x-3)2的顶点在()A. 第一象限B. 第二象限C. x轴上D. y轴上4. 抛物线的对称轴是()A. x=-2B.x=2C. x=-4D. x=45. 已知二次函数y=ax2+bx+c的图象如图所示，则下列结论中，正确的是()A. ab>0，c>0B. ab>0，c<0C. ab<0，c>0D. ab<0，c<0的点，P3(x3，y3)是直线上的点，且-1<x 1<x2，x3<-1，则y1，y2，y3的大小关系是()A. y1<y2<y3B. y2<y3<y1C. y3<y1<y2D. y2<y1<y310.把抛物线的图象向左平移2个单位，再向上平移3个单位，所得的抛物线的函数关系式是()A. B.C. D.二、填空题：11. 二次函数y=x2-2x+1的对称轴方程是______________.12. 若将二次函数y=x2-2x+3配方为y=(x-h)2+k 的形式，则y=________.13. 若抛物线y=x2-2x-3与x轴分别交于A、B 两点，则AB的长为_________.14. 抛物线y=x2+bx+c，经过A(-1，0)，B(3，0)两点，则这条抛物线的解析式为_____________.15. 已知二次函数y=ax2+bx+c的图象交x轴于A、B两点，交y轴于C点，且△ABC是直角三角形，请写出一个符合要求的二次函数解析式________________.16. 在距离地面2m高的某处把一物体以初速度v0(m/s)竖直向上抛物出，在不计空气阻力的情况下，其上升高度s(m)与抛出时间t(s)满足：(其中g是常数，通常取10m/s2).若v0=10m/s，则该物体在运动过程中最高点距地面_________m.17. 试写出一个开口方向向上，对称轴为直线x=2，且与y轴的交点坐标为(0，3)的抛物线的解析式为______________.18. 已知抛物线y=x2+x+b2经过点，则y1的值是_________.三、解答题：19. 若二次函数的图象的对称轴方程是，并且图象过A(0，-4)和B(4，0)，(1)求此二次函数图象上点A关于对称轴对称的点A′的坐标；(2)求此二次函数的解析式；20.在直角坐标平面内，点O为坐标原点，二次函数y=x2+(k-5)x-(k+4) 的图象交x轴于点A(x1，0)、B(x2，0)，且(x1+1)(x2+1)=-8. (1)求二次函数解析式；(2)将上述二次函数图象沿x轴向右平移2个单位，设平移后的图象与y轴的交点为C，顶点为P，求△POC的面积.21.已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为(-1，0)，点C(0，5)，另抛物线经过点(1，8)，M为它的顶点.(1)求抛物线的解析式；(2).求△MCB的面积S△MCB22.某商店销售一种商品，每件的进价为2.50元，根据市场调查，销售量与销售单价满足如下关系：在一段时间内，单价是13.50元时，销售量为500件，而单价每降低1元，就可以多售出200件.请你分析，销售单价多少时，可以获利最大.答案与解析：一、选择题1.考点：二次函数概念.选A.2.考点：求二次函数的顶点坐标.解析：法一，直接用二次函数顶点坐标公式求.法二，将二次函数解析式由一般形式转换为顶点式，即y=a(x-h)2+k的形式，顶点坐标即为(h，k)，y=x2-2x+3=(x-1)2+2，所以顶点坐标为(1，2)，答案选C.3.考点：二次函数的图象特点，顶点坐标.解析：可以直接由顶点式形式求出顶点坐标进行判断，函数y=2(x-3)2的顶点为(3，0)，所以顶点在x轴上，答案选C.4. 考点：数形结合，二次函数y=ax2+bx+c 的图象为抛物线，其对称轴为.解析：抛物线，直接利用公式，其对称轴所在直线为答案选B.5.考点：二次函数的图象特征.解析：由图象，抛物线开口方向向下，抛物线对称轴在y轴右侧，抛物线与y轴交点坐标为(0，c)点，由图知，该点在x轴上方，答案选C.6. 考点：数形结合，由抛物线的图象特征，确定二次函数解析式各项系数的符号特征.解析：由图象，抛物线开口方向向下，抛物线对称轴在y轴右侧，抛物线与y轴交点坐标为(0，c)点，由图知，该点在x轴上方，在第四象限，答案选D.7. 考点：二次函数的图象特征.解析：因为二次函数y=ax2+bx+c(a≠0)的图象的顶点P的横坐标是4，所以抛物线对称轴所在直线为x=4，交x轴于点D，所以A、B两点关于对称轴对称，因为点A(m，0)，且m>4，所以AB=2AD=2(m-4)=2m-8，答案选C.8.考点：数形结合，由函数图象确定函数解析式各项系数的性质符号，由函数解析式各项系数的性质符号画出函数图象的大致形状.解析：因为一次函数y=ax+b的图象经过第二、三、四象限，所以二次函数y=ax2+bx的图象开口方向向下，对称轴在y轴左侧，交坐标轴于(0，0)点.答案选C.9. 考点：一次函数、二次函数概念图象及性质.解析：因为抛物线的对称轴为直线x=-1，且-1<x1<x2，当x>-1时，由图象知，y随x的增大而减小，所以y2<y1；又因为x3<-1，此时点P3(x3，y3)在二次函数图象上方，所以y2<y1<y3.答案选D.10.考点：二次函数图象的变化.抛物线的图象向左平移2个单位得到，再向上平移3个单位得到.答案选C.二、填空题11.考点：二次函数性质.解析：二次函数y=x2-2x+1，所以对称轴所在直线方程.答案x=1.12.考点：利用配方法变形二次函数解析式.解析：y=x2-2x+3=(x2-2x+1)+2=(x-1)2+2.答案y=(x-1)2+2.13. 考点：二次函数与一元二次方程关系.解析：二次函数y=x2-2x-3与x轴交点A、B 的横坐标为一元二次方程x2-2x-3=0的两个根，求得x1=-1，x2=3，则AB=|x2-x1|=4.答案为4.14.考点：求二次函数解析式.解析：因为抛物线经过A(-1，0)，B(3，0)两点，解得b=-2，c=-3，答案为y=x2-2x-3.15.考点：此题是一道开放题，求解满足条件的二次函数解析式，答案不唯一.解析：需满足抛物线与x轴交于两点，与y 轴有交点，及△ABC是直角三角形，但没有确定哪个角为直角，答案不唯一，如：y=x2-1.16.考点：二次函数的性质，求最大值.解析：直接代入公式，答案：7.17.考点：此题是一道开放题，求解满足条件的二次函数解析式，答案不唯一.解析：如：y=x2-4x+3.18.考点：二次函数的概念性质，求值.答案：.三、解答题19. 考点：二次函数的概念、性质、图象，求解析式.解析：(1)A′(3，-4)(2)由题设知：∴y=x2-3x-4为所求(3)20. 考点：二次函数的概念、性质、图象，求解析式.解析：(1)由已知x1，x2是x2+(k-5)x-(k+4)=0的两根又∵(x1+1)(x2+1)=-8 ∴x1x2+(x1+x2)+9=0∴-(k+4)-(k-5)+9=0 ∴k=5 ∴y=x2-9为所求(2)由已知平移后的函数解析式为：y=(x-2)2-9且x=0时y=-5 ∴C(0，-5)，P(2，-9).21. 解：(1)依题意：(2)令y=0，得(x-5)(x+1)=0，x1=5，x2=-1∴B(5，0)由，得M(2，9)作ME⊥y轴于点E，则可得S△=15.MCB22.思路点拨：通过阅读，我们可以知道，商品的利润和售价、销售量有关系，它们之间呈现如下关系式：总利润=单个商品的利润×销售量.要想获得最大利润，并不是单独提高单个商品的利润或仅大幅提高销售量就可以的，这两个量之间应达到某种平衡，才能保证利润最大.因为已知中给出了商品降价与商品销售量之间的关系，所以，我们完全可以找出总利润与商品的价格之间的关系，利用这个等式寻找出所求的问题，这里我们不妨设每件商品降价x元，商品的售价就是(13.5-x)元了.单个的商品的利润是(13.5-x-2.5)这时商品的销售量是(500+200x)总利润可设为y元.利用上面的等量关式，可得到y与x的关系式了，若是二次函数，即可利用二次函数的知识，找到最大利润.解：设销售单价为降价x元.顶点坐标为(4.25，9112.5).即当每件商品降价 4.25元，即售价为13.5-4.25=9.25时，可取得最大利润9112.5元。

《2.4.1二次函数的图像》同步练习1.函数y ＝x2＋(a ＋2)x ＋3(a ≤x ≤b )的图象关于直线x ＝1对称，则b ＝ 2.设函数f (x )＝x 2＋bx ＋c ，若f (－4)＝f (0)，f (－2)＝－2，则f (x )＝________3.将二次函数y ＝－2x 2的顶点移到(－3,2)后，得到的函数的解析式为________4.二次函数y ＝x 2＋ax ＋b ，若a ＋b ＝0，则它的图象必经过点1.二次函数y ＝ax 2＋bx ＋c 的图象如图所示，则点(a ，c )在 ( )A .B .C .D . 2.如何平移抛物线y ＝2x 2可得到抛物线y ＝2(x －4)2－1 ( )A .4个单位，再向上平移1个单位 B .4个单位，再向下平移1个单位 C .4个单位，再向上平移1个单位 D .4个单位，再向下平移1个单位1.已知二次函数y ＝x 2＋bx ＋c 的图象向左平移2个单位，再向上平移3个单位，得到的二次函数为y ＝x 2－2x ＋1，求该二次函数的解析式。

答案与解析1.【解析】对称轴x＝－＝1，∴a＝－4.又a、b关于x＝1对称，∴＝1，b＝6【答案】62.【解析】∵f(－4)＝f(0)，f(－2)＝－2，∴解得b＝4，c＝2.∴f(x)＝x2＋4x＋2【答案】x2＋4x＋23.【解析】因为二次函数y＝－2x2的顶点为(0,0)，所以要将其顶点移到(－3,2)，只要把图像向左平移3个单位，向上平移2个单位即可，所以平移后的函数解析式为y＝－2(x＋3)2＋2【答案】y＝－2(x＋3)2＋24.【解析】∵a＋b＝0，∴当x＝1时，y＝1＋a＋b＝1，∴过点(1,1)【答案】(1,1)1.【解析】由图像可知，开口向上则a>0,与y轴的交点在y轴负半轴上则c<0，因此点（a，c）在第四象限。

【答案】D2.【解析】要得到y＝2(x－4)2－1的图象，只需将y＝2x2的图象向右平移4个单位，再向下平移1个单位。

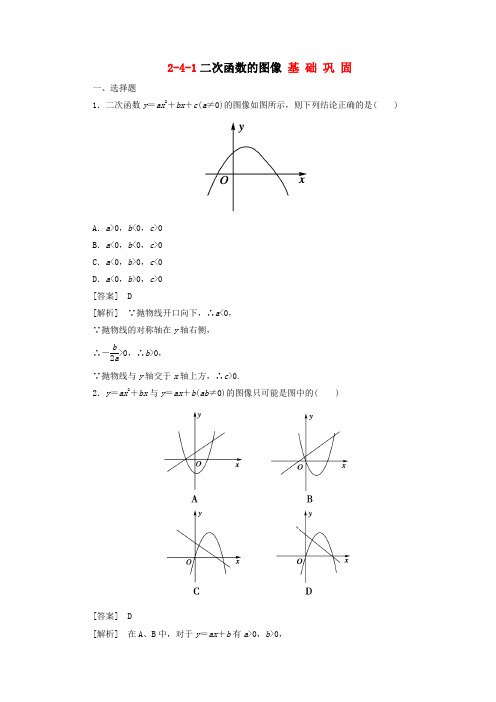
2-4-1二次函数的图像 基 础 巩 固一、选择题1．二次函数y ＝ax 2＋bx ＋c (a ≠0)的图像如图所示，则下列结论正确的是( )A ．a >0，b <0，c >0B ．a <0，b <0，c >0C ．a <0，b >0，c <0D ．a <0，b >0，c >0 [答案] D[解析] ∵抛物线开口向下，∴a <0， ∵抛物线的对称轴在y 轴右侧， ∴－b2a>0，∴b >0，∵抛物线与y 轴交于x 轴上方，∴c >0.2．y ＝ax 2＋bx 与y ＝ax ＋b (ab ≠0)的图像只可能是图中的( )[答案] D[解析] 在A 、B 中，对于y ＝ax ＋b 有a >0，b >0，∴－b2a<0，不符．在C 、D 中，y ＝ax ＋b ，有a <0，b >0，对于y ＝ax 2＋bx ＝x (ax ＋b )和y ＝ax ＋b 与x 轴有公共交点，故选D.3．不论m 取何值，二次函数y ＝x 2＋(2－m )x ＋m 的图像总过的点是( ) A ．(1,3) B ．(1,0) C ．(－1,3) D ．(－1,0) [答案] A[解析] 由题意知x 2＋2x －y ＋m (1－x )＝0恒成立，∴⎩⎪⎨⎪⎧x 2＋2x －y ＝01－x ＝0，解得⎩⎪⎨⎪⎧x ＝1y ＝3，∴图像总过点(1,3)．4．已知f (x )＝2(x －1)2和g (x )＝12(x －1)2，h (x )＝(x －1)2的图像都是开口向上的抛物线，在同一坐标系中，哪个开口最开阔( )A ．g (x )B ．f (x )C ．h (x )D ．不确定 [答案] A[解析] 因二次函数y ＝a (x －h )2＋k 的|a |越小，则二次函数开口越开阔．5．二次函数y ＝f (x )满足f (3＋x )＝f (3－x )，且f (x )＝0有两个实根x 1，x 2，则x 1＋x 2等于( )A ．0B ．3C ．6D ．不能确定 [答案] C[解析] 由f (3＋x )＝f (3－x )知函数y ＝f (x )的图像关于直线x ＝3对称，应有x 1＋x 22＝3⇒x 1＋x 2＝6.6．(2010·安徽文)设abc >0，二次函数f (x )＝ax 2＋bx ＋c 的图像可能是( )[答案] D[解析] 该题考查二次函数的图像和性质，采用排除法． 对A ：a <0.∵abc >0，∴bc <0.又∵轴－b2a <0.∴b <0，∴c >0，排除A ；对B ：a <0.∵abc >0，∴bc <0.又∵轴－b2a >0.∴b >0，∴c <0，排除B ；对C ：a >0.∵abc >0，∴bc >0.又∵轴－b2a <0.∴b >0，∴c >0，排除C ；对D ：a >0.∵abc >0，∴bc >0. 又∵轴－b2a >0.∴b <0，∴c <0，故选D.二、填空题7．抛物线y ＝－x 2－2x ＋3与x 轴的两交点为A 、B ，顶点为C ，则△ABC 的面积是________． [答案] 8[解析] y ＝－x 2－2x ＋3＝(－x ＋1)(x ＋3)＝－(x ＋1)2＋4， 由题意得A (－3,0)，B (1,0), C (－1,4)，∴S △ABC ＝12×4×4＝8.8．如果一条抛物线的形状与y ＝13x 2＋2的形状相同，且顶点是(4，－2)，则它的解析式是______________．[答案] y ＝13x 2－83x ＋103或y ＝－13x 2＋83x －223[解析] ∵顶点是(4，－2)，∴可设抛物线解析式为y ＝a (x －4)2－2. 又∵与y ＝13x 2＋2的形状相同，∴a ＝13或－13.∴y ＝13(x －4)2－2或y ＝－13(x －4)2－2.三、解答题9．已知二次函数f (x )＝－x 2＋bx ＋c 对于任意x 都满足f (1－x )＝f (1＋x )． (1)求实数b 的值；(2)比较f (－m 2－m －1)与f (14)的大小．[解析] (1)由于f (1－x )＝f (1＋x )，所以二次函数f (x )＝－x 2＋bx ＋c 的对称轴为x ＝1，所以x ＝－b－＝1，解得b ＝2.(2)因为－m 2－m －1＝－(m ＋12)2－34≤－34<14.又因为f (x )的对称轴为x ＝1，且开口向下， ∴f (－m 2－m －1)<f (14).能 力 提 升一、选择题1．如图所示的是二次函数y ＝ax 2＋bx ＋c (a ≠0)的图像，则|OA |·|OB |等于( ) A.c aB ．－c aC ．±c aD ．以上都不对[答案] B[解析] ∵f (x )＝ax 2＋bx ＋c ， ∴f (0)＝c >0，a <0，设ax 2＋bx ＋c ＝0的两根为x 1，x 2，则x 1·x 2＝c a， ∴|OA |＝－x 1，|OB |＝x 2， ∴|OA |·|OB |＝－c a. 故正确答案为B.2．已知二次函数y ＝ax 2＋bx ＋c 满足a >b >c ，且a ＋b ＋c ＝0，那么它的图像是下图中的( )[答案] A[解析] 因为a >b >c 且a ＋b ＋c ＝0，所以a >0，c <0.故排除B 、C ，又因为当x ＝1时，y ＝a ＋b ＋c ＝0，只有A 正确．二、填空题3．若函数y ＝x 2＋(a ＋2)x ＋3，x ∈[a ，b ]的图像关于直线x ＝1对称，则b ＝____________.[答案] 6[解析] 解法一：二次函数y ＝x 2＋(a ＋2)x ＋3的图像关于直线x ＝1对称，说明二次函数的对称轴为直线x ＝1，则－a ＋22＝1，∴a ＝－4.而该函数是定义在[a ，b ]上的，即a 、b 关于x ＝1也是对称的，则有a 到对称轴的距离与b 到对称轴的距离相等，∴1－a ＝b －1，∴b ＝6.解法二：∵二次函数y ＝x 2＋(a ＋2)x ＋3的图像的对称轴为直线x ＝1，∴该函数可表示为y ＝(x －1)2＋c ，与原二次函数的表达式比较同类项系数，可得a ＋2＝－2，∴a ＝－4.求b 同解法一．4．抛物线y ＝ax 2＋bx ＋c 与x 轴的两个交点的横坐标分别为－1、3，与y 轴交点的纵坐标为－32，则抛物线的解析式为________．[答案] y ＝12x 2－x －32[解析] 可设y ＝a (x ＋1)(x －3)，再把点(0，－32)代入上式可求得a ＝12，则y ＝12x 2－x－32. 三、解答题5．已知二次函数满足f (x －2)＝f (－x －2)，且其图像在y 轴上的截距为1，在x 轴上截得的线段长为22，求f (x )的表达式．[解析] 设f (x )＝ax 2＋bx ＋c (a ≠0)，由f (x －2)＝f (－x －2)得对称轴为x ＝－b2a ＝－2，∴b ＝4a .∵图像在y 轴上的截距为1，∴c ＝1，又|x 1－x 2|＝b 2－4ac|a |＝22，∴b ＝2或b ＝0(舍去)，a ＝12，∴f (x )＝12x 2＋2x ＋1.6．已知二次函数f (x )满足f (2)＝－1，f (－1)＝－1，且f (x )的最大值为8，试确定此二次函数的表达式．[解析] 解法一：设f (x )＝ax 2＋bx ＋c (a ≠0)． ∵f (2)＝f (－1)＝－1，f (x )最大值是8， ∴⎩⎪⎨⎪⎧4a ＋2b ＋c ＝－1，a －b ＋c ＝－1，4ac －b 24a ＝8.解得⎩⎪⎨⎪⎧a ＝－4，b ＝4，c ＝7.∴所求二次函数为f (x )＝－4x 2＋4x ＋7. 解法二：设f (x )＝a (x －m )2＋n . ∵f (2)＝f (－1)＝－1， ∴对称轴为x ＝2＋－2＝12，∴m ＝12. 又∵函数有最大值为8，∴n ＝8.∴f (x )＝a ⎝ ⎛⎭⎪⎫x －122＋8.∵f (2)＝－1，∴a ⎝ ⎛⎭⎪⎫2－122＋8＝－1，解之得a ＝－4. ∴f (x )＝－4⎝ ⎛⎭⎪⎫x －122＋8＝－4x 2＋4x ＋7.解法三：由已知f (x )＋1＝0的两根为x 1＝2，x 2＝－1， 故可设f (x )＋1＝a (x －2)(x ＋1)， 即f (x )＝ax 2－ax －2a －1. 且a ≠0，又函数有最大值8， ∴4a－2a －－a24a＝8，解之得a ＝－4，∴所求二次函数的表达式为f (x )＝－4x 2＋4x ＋7.7．已知抛物线y ＝ax 2＋bx ＋c (a ≠0)与x 轴有两个不同的交点A (x 1,0)、B (x 2,0)且x 21＋x 22＝269，试问该抛物线由y ＝－3(x －1)2的图像向上平移几个单位得到？ [解析] 由题意可设所求抛物线的解析式为y ＝－3(x －1)2＋k ，展开得y ＝－3x 2＋6x －3＋k ，由题意得x 1＋x 2＝2，x 1x 2＝3－k3， 所以x 21＋x 22＝(x 1＋x 2)2－2x 1x 2＝269，得4－－k 3＝269，解得k ＝43. 所以，该抛物线是由y ＝－3(x －1)2的图像向上平移43个单位得到的，它的解析式为y＝－3(x －1)2＋43，即y ＝－3x 2＋6x －53.。

温馨提示：此套题为Word版，请按住Ctrl,滑动鼠标滚轴，调节合适的观看比例，答案解析附后。

课时提能演练(十一) / 课后巩固作业(十一)(30分钟 50分)一、选择题（每小题4分，共16分）1.(2018·张掖高一检测)函数f(x)=x2+mx+1的图像关于直线x=1对称,则( )(A)m=-2 (B)m=2(C)m=-1 (D)m=12.二次函数y=4x2-mx+5的对称轴为x=-2,则当x=1时，y的值为( )（A）-7 （B）1 （C）17 （D）253.(2018·安溪高一检测）如果函数f(x)=x2+2(a-1)x+2在区间（-∞,4］上是减少的，那么实数a的取值范围是( )（A）a≤-3 （B）a≥-3 （C）a≤5 （D）a≥54.若函数f(x)=x2+ax+b的图像与x轴的交点为(1,0)和(3,0)，则函数f(x)( )(A)在(-∞,2］上是减少的，在［2,+∞)上是增加的(B)在(-∞,3)上是增加的(C)在［1,3］上是增加的(D)单调性不能确定二、填空题（每小题4分，共8分）5.(2018·蚌埠高一检测）函数y=x2+ax+3(0<a<2)在［-1，1］上的最大值是_____,最小值是______.6.已知关于x的函数f(x)=ax2+bx+c（a,b,c为常数），且ab≠0，若f(x1)=f(x2)(x1≠x2)，则f(x1+x2)的值等于______________.三、解答题（每小题8分，共16分）7.(2018·淮安高一检测）已知二次函数f(x)的最小值为1，且f(0)=f(2)=3.(1)求f(x)的解析式；(2)若f(x)在区间［2a,a+1］上不单调，求a的取值范围.8.（易错题）某商场以每件42元的价格购进一种服装,根据试营销量得知:这种服装每天的销售量t(t＞0,t∈N)件与每件的销售价x(x＞42,x∈N)元之间可看成是一次函数关系:t=-3x+204.(1)写出商场每天卖这种服装的销售利润y元与每件的销售价x元之间的函数关系式(每天的销售利润是指所卖出服装的总销售所得与购进这些服装所花费金额的差);(2)通过对所得函数关系式进行配方,指出:商场要想每天获得最大的销售利润,每件的销售价定为多少最合适?最大销售利润为多少?【挑战能力】[:（10分）已知二次函数f(x)=ax2+bx(a,b是常数且a≠0)满足条件:f(2)=0且方程f(x)=x有等根.(1)求f(x)的解析式;(2)问是否存在实数m、n（m＜n）使f(x)的定义域和值域分别为［m,n］和［2m,2n］？如果存在，求出m、n的值；如果不存在，请说明理由.答案解析1.【解析】选A.函数f(x)=x2+mx+1的图像的对称轴为x=-m2,于是-m2=1,得m=-2,故选A.2.【解析】选D.∵二次函数y=4x2-mx+5的对称轴为x=m24⨯,∴m8=-2,∴m=-16,∴f(1)=4×12+16×1+5=25.3.【解析】选A.函数f(x)的对称轴方程为x=-()2a121-⨯=1-a,要使函数f(x)在区间(-∞,4］上是减少的,必须1-a≥4,∴a≤-3.4.【解析】选A.由已知可得该函数的图像的对称轴为x=2,又二次项系数为1＞0,所以f(x)在（-∞,2］上是减少的，在［2,+∞)上是增加的,故选A.5.【解析】函数y=x2+ax+3的对称轴方程为x=-a2,∵0<a<2,∴-1<-a2<0,∴f(x)max=f(1)=4+a,f(x)min=f(-a2)=3-2a4.答案:4+a 3-2 a 46.【解析】∵x1+x2=-ba,∴f(x1+x2)=f(-ba)=a(-ba)2+b(-ba)+c=2ba-2ba+c=c.答案：c7.【解析】（1）∵f(x)为二次函数且f(0)=f(2),∴对称轴为x=1.又∵f(x)最小值为1，∴可设f(x)=a(x-1)2+1(a>0).∵f(0)=3,∴a=2,∴f(x)=2(x-1)2+1,即f(x)=2x2-4x+3.（2）由条件知2a<1<a+1,∴0<a<12.8.【解析】(1)由题意得,每天的销售利润y元与每件的销售价x元之间的函数关系式为y=(x-42)(-3x+204)=-3x2+330x-8 568(42＜x＜68,x∈N).(2)由(1)得y=-3(x-55)2+507(42＜x ＜68,x ∈N)，则当x=55时,y max =507.即当每件的销售价定为55元时,可获得最大的销售利润,每天的最大销售利润为507元.【误区警示】解答本题易漏掉函数的定义域而导致解析过程不完善.【挑战能力】【解题指南】本题是一道求函数解析式、定义域、值域的综合题，应从f(2)=0和f(x)=x 有等根着手，逐个击破.【解析】（1）∵方程ax 2+(b-1)x=0(a ≠0)有等根,∴Δ=(b-1)2-4a ×0=0,∴b=1.又f(2)=0,∴4a+2b=0,∴a=-12. ∴f(x)=-12x 2+x. （2）假设存在所求，∵f(x)=-12(x-1)2+12≤12, ∴2n ≤12,∴n ≤14. 又二次函数f(x)=-12(x-1)2+12的对称轴方程为x=1, ∴当n ≤14时,f(x)在［m,n ］上是增加的， 则()()f m 2m,f n 2n,=⎧⎪⎨=⎪⎩ 即221m m 0m 0m 2,21n n 0n 0n 2.2⎧--=⇒==-⎪⎪⎨⎪--=⇒==-⎪⎩或或 ∵m ＜n ≤14,∴m=-2,n=0. ∴存在实数m=-2,n=0使f(x)的定义域为［-2,0］,值域为［-4,0］.。

1.二次函数y=4x2-mx+5的对称轴为x=-2,则当x=1时,y的值为()A.-7B.1C.17D.25解析:由已知得-=-2,所以m=-16,这时y=4x2+16x+5.因此当x=1时,y=4×12+16×1+5=25.答案:D2f(x)=ax2+2(a-3)x+1在区间(-2,+∞)上是减少的,则a的取值范围是() A.[-3,0] B.(-∞,-3]C.[-3,0)D.[-2,0]解析:当a=0时,f(x)=-6x+1显然成立;当a≠0时,要使f(x)在(-2,+∞)上是减少的,需满足解得-3≤a<0.综上可知,a的取值范围是[-3,0].答案:A3.已知函数y=x2-2x+3在区间[0,m]上有最大值3,最小值2,则实数m的取值范围是()A.[1,+∞)B.[1,2)C.[1,2]D.(-∞,2]解析:由于y=x2-2x+3=(x-1)2+2,其图像如图所示,且f(0)=3,f(1)=2,f(2)=3.结合图像可知m的取值范围是[1,2].答案:C4.已知二次函数f(x)=ax2-6ax+1,其中a>0,则下列关系中正确的是()A.f()<f()B.f(2π)>f(π)C.f()<f(3)D.f(-1)<f(1)解析:函数f(x)=ax2-6ax+1的对称轴为x=3,其图像开口方向向上,离对称轴越近,对应的函数值越小.∵2π-3>π-3,∴f(2π)>f(π).故选B.答案:B5.(探究题)由于被墨水污染,一道数学题仅能见到下列文字:“已知二次函数y=x2+bx+c的图像过(1,0)……求证这个二次函数的图像关于直线x=2对称”.根据以上信息,题中的函数图像不具有的性质是()A.过点(3,0)B.顶点为(2,2)C.在x轴上截得的线段长为2D.与y轴交点为(0,3)解析:若顶点为(2,2),可设为y=a·(x-2)2+2,将点(1,0)代入得0=a+2,∴a=-2.即y=-2(x-2)2+2,与y=x2+bx+c中的a=1矛盾.答案:B6.某厂有许多形状为直角梯形的铁皮边角料,为了降低消耗,现要从这些边角料上截取矩形铁片(如图所示).当截取的矩形面积最大时,矩形两边的长x,y应为()A.x=15,y=12B.x=12,y=15C.x=14,y=10D.x=10,y=14解析:结合图形,可得,得y=24-,矩形面积S=xy=x=-+24x,所以当x=-=15时,S最大,此时y=24-×15=12,故选A.答案:A7.(2016江苏淮安高中联考)如果二次函数y=mx2+5x+4在区间(-∞,2]上是增函数,在区间[2,+∞)上是减函数,则m的值是.解析:由题意可知,-=2,则m=-.答案:-8.已知二次函数f(x)满足f(2+x)=f(2-x),又f(x)在[0,2]上是增加的,且f(a)≥f(0),那么实数a 的取值范围是.解析:此函数的对称轴为x==2,且f(x)在[0,2]上是增加的,如图所示,由f(0)=f(4),f(a)≥f(0),知0≤a≤4.答案:[0,4]9.将长度为1的铁丝分成两段,分别围成一个正方形和一个圆形.要使正方形与圆的面积之和最小,正方形的周长应为.解析:设正方形周长为x,则边长为,圆周长为(1-x),圆的半径为(0<x<1),依题意得,面积之和为+π,当x=时,有最小值,即正方形周长为.答案:10.求二次函数y=x2-6x+7在区间[-2,4]上的最大值和最小值.解法一:y=x2-6x+7=(x-3)2-2,故函数在区间[-2,3]上是减函数,在[3,4]上是增函数.①当-2≤x≤3时,y最大=23,y最小=-2;②当3≤x≤4时,y最大=-1,y最小=-2.综上可知,函数y=x2-6x+7的最小值为-2,最大值为23.解法二:(数形结合)令f(x)=y=x2-6x+7.对称轴:x=3,f(x)最大=f(-2)=23;f(x)最小=f(3)=-2.∴f(x)的最大值为23,最小值为-2.11f(x)的最小值为1,且f(0)=f(2)=3.(1)求f(x)的解析式;(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;(3)在区间[-1,1]上,y=f(x)的图像恒在y=2x+2m+1的图像上方,试确定实数m的取值范围.解:(1)由f(0)=f(2)知,二次函数f(x)的图像关于x=1对称.又f(x)的最小值为1,故可设f(x)=a(x-1)2+1,因为f(0)=3,得a=2,故f(x)=2x2-4x+3.(2)要使函数f(x)在区间[2a,a+1]上不单调,则2a<1<a+1,则0<a<.即实数a的取值范围是0<a<.(3)由已知,即2x2-4x+3>2x+2m+1,化简得x2-3x+1-m>0.设g(x)=x2-3x+1-m,则只要g(x)min>0,因为x∈[-1,1]时,g(x)是减少的,所以g(x)min=g(1)=-1-m,因此有-1-m>0,得m<-1.即实数m的取值范围是m<-1.。

［A基础达标]1．函数f（x）＝－x2＋4x＋5（0≤x〈5）的值域为（）A．（0，5］ B．［0，5］C．[5,9］D．（0,9］解析：选D。

f（x)＝－x2＋4x＋5＝－(x－2）2＋9(0≤x〈5）,当x＝2时，f(x)最大＝9；当x>0且x接近5时，f(x)接近0，故f（x）的值域为(0,9]．2．已知函数y＝x2－6x＋8在［1，a）上为减函数,则a的取值范围是( ）A．a≤3 B．0≤a≤3C．a≥3 D．1〈a≤3解析:选D。

函数y＝x2－6x＋8的对称轴为x＝3,故函数在（－∞,3］上为减函数，由题意［1，a）⊆（－∞，3]，所以1<a≤3.3．已知函数f（x）＝ax2－x＋a＋1在（－∞，2）上是递减的，则a的取值范围是（）A.错误!B。

错误!C。

错误!D。

错误!解析:选B。

当a＝0时，f（x)＝－x＋1在R上是递减的，符合题意；当a〈0时,不符合题意；当a〉0时,f（x)的对称轴为x＝错误!，在错误!上是递减的,由题意(－∞,2)⊆错误!，所以2≤错误!，即a≤错误!，综上,a的取值范围是错误!.4．如果函数f(x)＝x2＋bx＋c对任意的实数x，都有f(1＋x)＝f(－x),那么（）A．f(－2)＜f(0）＜f(2）B．f（0)＜f(－2）＜f（2）C．f(2)＜f（0)＜f（－2)D．f（0）＜f(2）＜f（－2)解析：选D.函数f(x）＝x2＋bx＋c对任意的实数x都有f（1＋x）＝f（－x）．可知函数f（x）图像的对称轴为x＝错误!,又函数图像开口向上,自变量离对称轴越远函数值越大，故选D。

5．设二次函数f（x）＝－x2＋x＋a(a<0），若f（m)>0,则f（m ＋1)的值为( ）A．正数B．负数C．非负数D．正数、负数或零都有可能解析：选B。

由题意可得,f（x）＝－x2＋x＋a的函数图像开口向下，对称轴为x＝错误!，又a<0，则函数f（x）的图像与y轴的交点在y轴负半轴上，如图所示．设使f(m）>0的m的取值范围为错误!－k〈m<错误!＋k错误!，所以1〈错误!－k〈m＋1〈错误!＋k，所以f（m＋1）<0，故选B。

4.2 二次函数的性质课后篇巩固提升1.已知二次函数y=4x 2-mx+5图像的对称轴为x=-2,则当x=1时,y 的值为( )A.-7 B .1 C .17 D .25 解析:由已知得--m 2×4=-2,所以m=-16,这时y=4x 2+16x+5.因此当x=1时,y=4×12+16×1+5=25. 答案:D2.已知函数f (x )=ax 2+2(a-3)x+1在区间(-2,+∞)上是减少的,则a 的取值范围是( )A.[-3,0]B.(-∞,-3]C.[-3,0)D.[-2,0]解析:当a=0时,f (x )=-6x+1显然成立;当a ≠0时,要使f (x )在(-2,+∞)上是减少的,需满足{a <0,-2(a -3)2a ≤-2,解得-3≤a<0. 综上可知,a 的取值范围是[-3,0].答案:A3.已知函数y=x 2-2x+3在区间[0,m ]上有最大值3,最小值2,则实数m 的取值范围是( )A.[1,+∞) B .[1,2)C .[1,2]D .(-∞,2]解析:由于y=x 2-2x+3=(x-1)2+2,其图像如图所示,且f (0)=3,f (1)=2,f (2)=3.结合图像可知m 的取值范围是[1,2].答案:C4.已知函数f (x )=x 2+bx+c 的图像的对称轴为直线x=1,则( )A .f (-1)<f (1)<f (2)B .f (1)<f (2)<f (-1)C .f (2)<f (-1)<f (1)D .f (1)<f (-1)<f (2)解析:∵函数f (x )=x 2+bx+c 的图像开口向上,且对称轴为x=1,∴f (x )在(-∞,1)内递减,在(1,+∞)内递增,∴f (1)<f (2)<f (-1).答案:B5.已知函数f (x )=-x 2+2x+4在区间[0,m ]上有最大值5,最小值-1,则m 的值等于( )A.-1B.1C.2D.3解析:因为函数f (x )=-x 2+2x+4=-(x-1)2+5,故函数在区间(-∞,1]上单调递增;在区间(1,+∞)上单调递减. 若m ≤1,则函数在区间[0,m ]上单调递增,其最小值为f (0)=-02+2×0+4=4>-1,显然不合题意. 若m>1,则函数在区间[0,1]上单调递增,在区间[1,m ]上单调递减,故函数的最大值为f (1)=5. 而f (0)=-02+2×0+4=4>-2.令f (m )=1,即-m 2+2m+4=1,也就是m 2-2m-3=0,解得m=-1或m=3. 又因为m>1,所以m=3.故选D .答案:D6.某厂有许多形状为直角梯形的铁皮边角料,为了降低消耗,现要从这些边角料上截取矩形铁片(如图所示).当截取的矩形面积最大时,矩形两边的长x ,y 应为( )A.x=15,y=12 B .x=12,y=15C .x=14,y=10D .x=10,y=14 解析:结合题中图形,可得x 20=24-y 24-8,得y=24-4x 5,矩形面积S=xy=x (24-4x 5)=-4x 25+24x ,所以当x=-242×(-45)=15时,S 最大,此时y=24-4×15=12,故选A . 答案:A7.若二次函数y=mx 2+5x+4在区间(-∞,2]上是增加的,在区间[2,+∞)上是减少的,则m 的值是 .解析:由题意可知,-52m =2,则m=-54.答案:-548.已知二次函数f (x )满足f (2+x )=f (2-x ),又f (x )在[0,2]上是增加的,且f (a )≥f (0),则实数a 的取值范围是 .解析:此函数图像的对称轴为x=2+x+2-x 2=2,且f (x )在[0,2]上是增加的,如图所示,由f (0)=f (4),f (a )≥f (0),知0≤a ≤4.答案:[0,4]9.导学号85104040将长度为1的铁丝分成两段,分别围成一个正方形和一个圆形.要使正方形与圆的面积之和最小,正方形的周长应为 .解析:设正方形周长为x ,则边长为x 4,圆周长为(1-x ),圆的半径为1-x 2π(0<x<1),依题意得,面积之和为x 216+π(1-x 2π)2=(4+π)x 2-8x+416π,当x=12·84+π=44+π时,有最小值,即正方形周长为44+π. 答案:44+π 10.求二次函数y=x 2-6x+7在区间[-2,4]上的最大值和最小值.解法一y=x 2-6x+7=(x-3)2-2,故函数在区间[-2,3]上是减少的,在[3,4]上是增加的.①当-2≤x ≤3时,y 最大=23,y 最小=-2;②当3≤x ≤4时,y 最大=-1,y 最小=-2.综上可知,函数y=x 2-6x+7的最小值为-2,最大值为23.解法二(数形结合)令y=f (x )=x 2-6x+7.对称轴:x=3,f (x )最大=f (-2)=23;f (x )最小=f (3)=-2.∴f (x )的最大值为23,最小值为-2.11.已知函数f (x )=x 2-2x+2.(1)求f (x )在区间[-2,3]上的最大值和最小值;(2)若g (x )=f (x )-mx 在[-1,2]上是单调递增函数,求m 的取值范围.解:(1)因为f (x )=x 2-2x+2=(x-1)2+1,而x ∈[-2,3],所以当x=1时,f (x )取得最小值,最小值为f (1)=1.又f (-2)=(-2-1)2+1=10,f (3)=(3-1)2+1=5,故f (-2)>f (3),所以函数f (x )在区间[-2,3]上的最大值为10.(2)因为g (x )=f (x )-mx=x 2-(m+2)x+2,其对称轴为x=m+22.由函数在区间[-1,2]上单调递增可得m+22≤-1,解得m ≤-4.故m的取值范围是(-∞,-4].由Ruize收集整理。