计算工具_kappa表

格式：xls
大小：34.50 KB
文档页数：2

下载文档原格式

MSA计数型(kappa)分析表

表单编号：QR-QA-50 版本：02
MSA计数型(Kappa)分析表
量具名称：量具编号：量具型号：零件名称：交叉表： A与基准 0 A 1 总计交叉表数量期望数量数量期望数量数量期望数量交叉表数量期望数量数量期望数量数量期望数量交叉表数量期望数量数量期望数量数量期望数量基准值 0 21 3.8 3 20.2 24 24.0 1 3 20.2 123 105.8 126 126.0 基准值 0 21 3.8 3 20.2 24 24.0 1 3 20.2 123 105.8 126 126.0 基准值 0 24 3.8 0 20.2 24 24.0 B 0 22 3.8 2 20.2 24 24.0 C 0 21 3.8 3 20.2 24 24.0 C 0 21 3.8 3 20.2 24 24.0 1 3 20.2 123 105.8 126 126.0 1 3 20.2 123 105.8 126 126.0 1 2 20.2 124 105.8 126 126.0 1 0 20.2 126 105.8 126 126.0 总计 24 24.0 126 126.0 150 150.0 总计 24 24.0 126 126.0 150 150.0 总计 24 24.0 126 126.0 150 150.0 总计 24 24.0 126 126.0 150 150.0 总计 24 24.0 126 126.0 150 150.0 总计 24 24.0 126 126.0 150 150.0 Po 0.96 Pe 0.73 评价人A：评价人B：评价人C：零件数量：分析人：评价时间：测量次数： 3次/人 50 pcs 评价人与基准值交叉数据： 0-0 0-1 1-0 A 21 3 3 B 21 3 3 C 24 0 0 Kappa程度： Kappa A A — B 90.08% C 85.12% 基准 85.12% 评价人有效性：项目 A 有效性 92.00% 漏检 12.50% 误判 2.38% 1-1 123 123 126

Kappa分析(自动生成)

评
确
价
认：
承认：
4/4
40 1 1 1 1 1 1 1 1 1
41 1 1 1 1 1 1 1 1 1
42 0 0 0 0 0 0 0 0 0
43 1 1 1 1 1 1 1 1 1
44 1 1 1 1 1 1 1 1 1
45 1 1 1 1 1 1 1 1 1
46 1 1 1 1 1 1 1 1 1
47 1 1 1 1 1 1 1 1 1
1/4
计数型测量系统分析报告
（评价人交叉分析）
A 与 B 交叉表
B
0.00
1.00
A
0.00
计算
29
1
期望的计算
6.4
23.6
1.00
计算
3
117
期望的计算
25.6
94.4
计算
32
118
总计
期望的计算
32.0
118.0
A 与 C 交叉表
C
0.00
1.00
A
0.00
计算
28
2
期望的计算
6.2
23.8
系统有效得分（所有评价人自己保持一致）
50 44 88.0%
系统有效得分与计数（所有评价人与基准一致）
50 44 88.0%
A B C
结论：
有效性 ≥90% 96.0%
96.0%
94.0%
漏发警报的比例 ≤2%
2.00%
误发警报的比例 ≤5%
2.00%
0.00%
4.00%
2.00%
4.00%
基于上述信息，判定该测量系统中，评价人ABC均接受，该测量系统符合要求

MSA计数型测量系统分析——假设试验分析法(Kappa)

6.136.13 计数型测量系统分析计数型测量系统分析——————假设试验分析法假设试验分析法假设试验分析法（（Kappa Kappa））说明：参照张智勇所著《ISO/TS16949五大工具最新版一本通》（机械工业出版社）编写。

计数型测量系统的分析是为了确定不同班次，不同生产线的检查人员是否能正确地区分合格品和不合格品，分析出测量结果与标准值的符合程度，以及他们自身和相互之间重复检查的一致程度。

假设试验分析—交叉表法是一种常用的计数型测量系统分析方法。

交叉表法可以在基准值（分析用样品称为基准，用计量型测量系统对样品进行测量，测量值称为基准值）已知的情况下进行，也可以在基准值未知的情况下进行。

在基准值未知的情况下进行，可以评价测量人之间的一致性，但不能评价测量系统区分好与不好的能力。

在基准值已知的情况下，即可评价测量人之间的一致性，又能评价测量人员与基准值的一致性，以及测量的有效性、漏判率和误判率，从而判断出测量人区分合格和不合格零件的能力。

6.136.13.1 .1 .1 未知基准值的一致性分析未知基准值的一致性分析1）随机选取g=50（一般选取g=30～50个样本）个能够覆盖过程范围的零件，对这些零件进行编号。

零件的编号不要让测量人知道，但分析人应该知道。

2）由3名评价人以随机盲测的方式测量所有零件各m=3次，每人测量次数为n=g×m=50×3=150次。

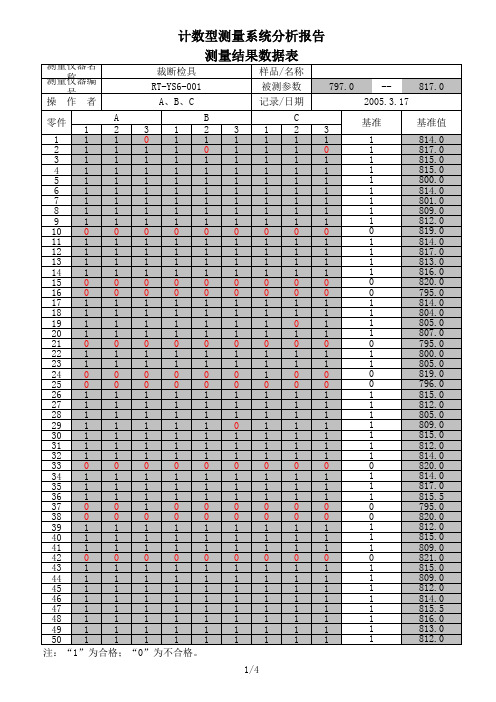
“接受”记为“1”，“拒绝”记为“0”，将三人所测150×3=450个数据记录于表6-21中。

测量时应按这样的规则进行：先让A 测量人以随机顺序对50个零件进行第1轮测量，然后让B 测量人、C 测量人以随机顺序进行第1轮测量，再让A 测量人进行第2轮测量，以此类推，完成测量工作。

表6-21 计数型测量系统分析数据表零件测量人A 测量人B 测量人C基准基准值代码A-1 A-2 A-3 B-1 B-2 B-3 C-1 C-2 C-31 1 1 1 1 1 1 1 1 1 1 0.476 901 +2 1 1 1 1 1 1 1 1 1 1 0.509015 +3 0 0 0 0 0 0 0 0 0 0 0.576459 －4 0 0 0 0 0 0 0 0 0 0 0.566152 －5 0 0 0 0 0 0 0 0 0 0 0.57036 －6 1 1 0 1 1 0 1 0 0 1 0.544 951 ×7 1 1 1 1 1 1 1 0 1 1 0.465454 ×8 1 1 1 1 1 1 1 1 1 1 0.502295 +9 0 0 0 0 0 0 0 0 0 0 0.437817 －10 1 1 1 1 1 1 1 1 1 1 0.515573 +11 1 1 1 1 1 1 1 1 1 1 0.488905 +12 0 0 0 0 0 0 0 10 0 0.559918 ×13 1 1 1 1 1 1 1 1 1 1 0.542704 +14 1 1 0 1 1 1 1 0 0 1 0.454518 ×15 1 1 1 1 1 1 1 1 1 1 0.517377 +16 1 1 1 1 1 1 1 1 1 1 0.531939 +17 1 1 1 1 1 1 1 1 1 1 0.519694 +18 1 1 1 1 1 1 1 1 1 1 0.484167 +19 1 1 1 1 1 1 1 1 1 1 0.520496 +20 1 1 1 1 1 1 1 1 1 1 0.477236 +21 1 1 0 1 0 1 0 1 0 1 0.452310 ×22 0 0 1 0 1 0 1 10 0 0.545604 ×23 1 1 1 1 1 1 1 1 1 1 0.529065 +24 1 1 1 1 1 1 1 1 1 1 0.514192 +25 0 0 0 0 0 0 0 0 0 0 0.599581 －26 0 1 0 0 0 0 0 0 1 0 0.547204 ×27 1 1 1 1 1 1 1 1 1 1 0.502436 +28 1 1 1 1 1 1 1 1 1 1 0.521642 +29 1 1 1 1 1 1 1 1 1 1 0.523754 +30 0 0 0 0 0 1 0 0 0 0 0.561457 ×31 1 1 1 1 1 1 1 1 1 1 0.503091 +32 1 1 1 1 1 1 1 1 1 1 0.505850 +33 1 1 1 1 1 1 1 1 1 1 0.487613 +34 0 0 1 0 0 1 0 1 1 0 0.449696 ×35 1 1 1 1 1 1 1 1 1 1 0.498698 +36 1 1 0 1 1 1 1 0 1 1 0.543077 ×37 0 0 0 0 0 0 0 0 0 0 0.409238 －38 1 1 1 1 1 1 1 1 1 1 0.488184 +39 0 0 0 0 0 0 0 0 0 0 0.427687 －40 1 1 1 1 1 1 1 1 1 1 0.501132 +41 1 1 1 1 1 1 1 1 1 1 0.513779 +42 0 0 0 0 0 0 0 0 0 0 0.566575 －43 1 0 1 1 1 1 1 1 0 1 0.462410 ×44 1 1 1 1 1 1 1 1 1 1 0.470832 +45 0 0 0 0 0 0 0 0 0 0 0.412453 －46 1 1 1 1 1 1 1 1 1 1 0.493441 +47 1 1 1 1 1 1 1 1 1 1 0.486379 +48 0 0 0 0 0 0 0 0 0 0 0.587893 －49 1 1 1 1 1 1 1 1 1 1 0.483803 +50 0 0 0 0 0 0 0 0 0 0 0.446697 －3）根据表6-21中的0和l 数据的结果将评价人A 和B、B 和C、A 和C 利用交叉表方法进行统计（见表6-22），A*B 栏中“0*0”代表A、B 两人均判拒绝的次数，统计有44个；“0*1”代表A 判拒绝而B 判接受的次数，统计有6个；“1*0”代表A 判接受而B 判拒绝的次数，统计有3个；“1*1”代表AB 两人同时判为接受的次数，统计有97个，将统计结果依次填入表6-22中。

KAPPA

KAPPA 测试流程
人员测试名单
配眼睛矫正视力测试 NG NG 淘汰 OK
重测
OK
培训/考核 OK NG KAPPA 测试 OK OK 合格检验员再进行考核3次 NG
淘汰
KAPPA 测试执行步骤
1. 测试点及人员确定（工站，名单）２．检验人员视力检查（矫正视力1.0上）３．产品检验标准培训（培训记录）４．测试样品收集５．Kappa测试（kappa表）６．Kappa值计算（交叉表）
第一格代表检验员A在第一次和第二次测量中判定为良品的次数
第二格代表检验员A在第一次测量中判定一个样品为次品，在第二次测量中判定为良品的次数
交叉表
Rater A First Measure Good Bad Rater A Second Measure Good Bad 10 1 11 2 7 9 12 8
下表代表上表的数据，其中每个单元格用总数的百分比来表示
Rater A First Measure Good Bad Rater A Second Measure
检验员A比例
代表10/20
Good Bad
0.5 0.05 0.55
0.1 0.35 0.45
0.6 0.4
由行和列的总和计算而得
计算检验员A的Kappa值
对Kappa的定义将有所不同，取决于我们是在定义检验员内部 Kappa，还是在定义检验员之间的Kappa
计算A的Kappa
Rater A First Measure Good Bad Rater A Second Measure Good Bad 0.5 0.1 0.6 0.4
0.05 0.35 P 0.55 Pchance 0.45 K observed 1 Pchance Pobserved 等于上表对角线上概率的总和： P observed =(0.500 + 0.350) = 0.850

MSA测量系统分析全套表格模板(全公式未加密)

1、2、3、4、5、线性GRR计数型Kappa分析MSA测量系统分析全套表格模板稳定性偏倚Excel原件可在本文档左侧回形针处取出再现性Kappa=(Po-Pe)/(1-Pe)A*参考交叉表A01总计Po:0.95Pe:0.51B*参考交叉表B01总计Po:0.97Pe:0.51C*参考交叉表C01总计Po:0.96Pe:0.5130期望的数量26.4636.5463数量38487期望的数量数量60363一致性好6666Kappa 一致性好判定误发期望的数量638728 4.76%可接受2.30%可接受 4.76%可接受3.45%可接受可接受5.75%可接受01参考总计62063871501C0.90有效性判定重复性检查总数匹配数漏发A A B 评价人评价人%B 93.33%可接受判定判定0.9383.33%2530 3.17%36.5450.4687数量638715090.00%可接受0.92A C 一致性好150期望的数量B 期望的数量36.9651.0488数量6387150期望的数量26.0435.9662数量38588期望的数量6387数量60248.7284150数量6387150期望的数量35.28数量28284总计01Kappa 判定A*B 0.89一致性好C 3027A*C 0.93一致性好参考B*C 参考总计可接受期望的数量27.7238.280.90一致性好数量615Page 11 of 11。

KAPPA 计算方法及理解

KAPPA 计算方法及理解
Kappa 统计量
是为了评价者之间比较的统计量,使用于标准和评价者之间的测量结果精确性或评价者之间测量结果的一致性判定.
P observed(Po):判定员一致同意的单元的比率=判定员一致判定为优良的比率+判定员一致判定为次劣的比率
P chance(Pe):预期偶然达成一致的比率=（判定员A判定为优良的比率判定员B判定为次劣的比率）+（判定员A判定为次劣的比率判定员B判定为优良的比率）
N 总检查人数
Kappa 中对样本的选择：样本数量50个，上公差限有争议的取25%，下公差限有争议的取25%，那么完全合格的及完全不合格的各取25%。

Ref参考值:1/0代表两个分类:比如正确/错误，良品/不良品等等
Kappa值: k=(Po-Pe)/(1-Pe)
Kappa取值在［-1，+1］之间, 其值的大小均有不同意义.
Kappa = +1 说明两次判断的结果完全一致
Kappa = -1 说明两次判断的结果完全不一致
Kappa = 0 说明两次判断的结果是机遇造成
Kappa < 0 说明一致程度比机遇造成的还差，两次检查结果很不一致，但在实际应用中无意义Kappa > 0 此时说明有意义，Kappa愈大，说明一致性愈好
Kappa：0~0.4 说明一致程度非常不理想
Kappa：0.4~0.75 说明一致程度仍不可接受
Kappa：0.75~0.9 说明一致程度已经可接受
Kappa：0.9~1说明一致程度已经非常优秀。

计数型MSA表格(Kappa模型)-公式可见-可编辑-无锁定

A
0.0
B
60
C
60.0
总计判定结论：
A — 0.000 0.000
B 0.000
— 0.000
C 0.000 0.000
—
B 0.00 数量
期望数量
1.00 数量
期望数量
60 60.0
0 0.0
0
60
0.0 60.0
0
0
0.0 0.0
总计 A与C交叉表
数量期望数量
A 总计
0.00 数量
期望数量
1.00 数量
期望数量数量期望数量
60 60.0
C 0.00
60 60.0
0 0.0
60 60.0
0 0.0
1.00 0
0.0 0
0.0 0
0.0
60 60.0 总计
60 60.0
0 0.0
60 60.0
注：Kapaa=(Po－Pe)/(1－Pe) Po=对角线单元中观测值的总和 Pe=对角线单元中期望值的总和有效性 = 正确判断的数量 / 判断的机会总数
计数型测量系统研究(Kappa模型)
零件 A-1
A-2
A-3
B-1
B-2
B-3
C-1
C-2
C-3
1
2
3
4
5
6
7

9
10
11
12
13
14
15
16
17
18
19
20
评价人
分析：
确认：
基准
基准值
代码－－－－－－－－－－－－－－－－－－－－

计数型-kappa

计数型研究数据表Data3503计数型研究数据表1*05120000*12150211*1129133129787677Selfagreeme nt/自评A BC 494449A*B 交叉表0.00 1.00总计Po:0.95A0.00计算14216期望的计 2.014.016Pe:0.791.00计算5129134期望的计17.0117.0134总计计算19131150期望的计19.0131.0150B*C 交叉0.00 1.00总计Po:0.95B0.00计算14519期望的计 2.017.019Pe:0.791.00计算2129131期望的计14.0117.0131总计计算16134150期望的计16.0134.0150A*C 交叉表0.00 1.00总计Po:0.99A0.00计算15116期望的计 1.714.316Pe:0.811.00计算1133134期望的计14.3119.7134总计计算16134150期望的计16.0134.0150Reprodu Kappa结论Kappa=(Po-Pe)/(1-Pe)A*B0.9300.774好好好B C C B*C0.774A*C3503计数型研究数据表A*基准交叉表0.00 1.00总计Po: 1.00A0.00计算12012期望的计 1.610.412.0Pe:0.771.00计算07878期望的计10.467.678.0总计计算127890期望的计12.078.090.0B*基准交叉表0.00 1.00总计Po:0.98B0.00计算12214期望的计 1.912.114.0Pe:0.751.00Count07676Expected 10.165.976.0Total Count 127890Expected12.078.090.0C*基准交叉表0.00 1.00总计Po:0.99C0.00计算12113期望的计 1.711.313.0Pe:0.761.00计算07777期望的计10.366.777.0总计计算127890期望的计12.078.090.0AB C一致性Kappa 1.000.910.95结论好好好重复和再AB C50505049444998%88%98%好差好A 可接受B 可接受C 可接受结论结论总受检数符合的Repeatability 符合率基准0%1%漏发误发0%3%0%0%可接受结论基准基准可接受可接受% 评价人。

excel灵敏度、特异度、Kappa值或系数计算模板

-
-
1070
48
女血清
-
-
1071
55
女血清
-
-
1072
79
男血清
-
-
1073
78
女血清
+
+
1074
86
男血清
+
+
1075
11
男血清
+
+
1076
50
女血清
+
+
1077
58
女血清
+
+
1078
45
男血清
+
+
1079
65
女血清
+
+
1080
70
男血清
-
-
1081
26
女血清
-
-
1082
excel灵敏度、特异度、Kappa值或系数计算模板
计算公式及结果如下：
参比方法+ 参比方法- 总
考核试剂+
59
4
63
考核方法-
4
总
63
33
37
37
100
计算结果
点估计p
置信区间下限
置信区间上限
灵敏度 93.65% 84.78% 97.50%
特异度 89.19% 75.29% 95.71%
总符合率 92.00% 85.00% 95.89%
62
男血清
+
+
1008
45
女血清

MSA计数测量系统分析KAPPA表

A*B交叉表
A 0.00 数量期望的数量
1.00 数量
总
期望的数量
计
数量
期望的数量
A*C交叉表
A 0.00
1.00 总计
A*参考交
数量期望的数量数量期望的数量数量期望的数量
A 0.00
1.00 总计
C*参考交
数量期望的数量数量期望的数量数量期望的数量
C 0.00
1.00 总计
0 0.0 150 150.0
参考 0.00
150 150.0
0 0.0 150 150.0
1.00 0
0.0 0
0.0 0
0.0
1.00 0
0.0 0
0.0 0
0.0
总计
150 150.0
0 0.0 150 150.0
kappa 结论：
B*参考交
总计
150 150.0
0 0.0 150 150.0
判断测量系统评价人可接受的条件件，评可价能人需不要可改接进受的条件，需要改进
有效性 ≥90% ≥80%
＜80%
错误率 ≤2%
≤5%
错误警报率
≤5%
≤10%
＞5%
＞10%
检测者 Op
制表者 Pe
可接受
□
日期 Date
批准 Ap
不可接受 □
日期 Date
日期 Date
第2页*共2页
GZCH-FM-QC-61-A1
*****************有限公司
MSA计数测量系统分析KAPPA表
量具名称
量具编号
评价人A
零件名称

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。