七级数学上册 3.3 有理数的乘方知识点解读素材 (新版)青岛版
- 格式:doc
- 大小:36.50 KB
- 文档页数:2

初中数学青岛版七年级上册高效课堂资料
3.3 有理数的乘方教学设计
第二课时
【教学目标】
1.让学生了解科学记数法的意义,会用科学记数法表示绝对值大于10的数.
2.让学生了解近似数,会按照要求取近似数并能说出一个近似数精确到哪一位.
3.培养学生在学习中养成认真、仔细的学习态度和学习习惯.
【教学重难点】
重点:会用科学记数法表示绝对值大于10的数.
难点:能说出一个用四舍五入得到的近似数,包括用科学记数法得到的近似数,精确到哪一位. 【评价任务】
1.通过对实例的观察与交流看学生能否正确用科学记数法表示数.
2.通过对训练题的交流与展示,评价学生对科学记数法、四舍五入法、有效数字是否真正掌握.
附:板书设计
3.3 有理数的乘方
1.科学记数法
2.近似数、四舍五入法【教学反思】。



初一上册数学青岛版第三章有理数的运算知识点归纳(史上最全面的总结)一、有理数的加法1.加法法则(1)同号两数相加,取相同的符号,并把绝对值相加。
(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大绝对值减较小绝对值。
(3)互为相反数的两个数相加得零。
(4)一个数与0相加仍得这个数。
2 . 加法运算律(1)加法交换律两个数相加,交换加数的位置,和不变。
a+b=b+a注意事项:对于三个或三个以上的数相加,加法交换律仍使用。
(2)加法结合律三个数相加,先把前两个数相加,或先把后两个数相加,和不变。
(a+b)+c=a+(b+c)注意事项:对于三个以上的数相加,加法结合律仍使用。
(3)常见结合方法a 把正数和负数分别结合。
b 把同分母分数或易通分的分数相结合。
C 把相加得零的几个数相结合。
d 把相加得整数的几个小数相结合。
e几个整数和分数相加,通常整数与分数分别结合。
3.重要结论(1)在有理数范围内,和不一定大于每一个加数。
(2)ba+≠a+b二、有理数的减法1.减法法则减去一个数等于加上它的相反数。
2.数轴上两点间的距离公式设点A表示有理数a,点B表示有理数b,则AB=ba-3.重要结论(1)在有理数范围内,差不一定小于被减数。
(2)任何数减去0仍得这个数。
(3)0减去一个数得这个数的相反数。
(4)ba-≠a-b(5)设a,b为任意有理数a>b ⟺ a-b>0a=b⟺ a-b=0a<b⟺a-b<0三、有理数的乘法1.乘法法则两数相乘,同号得正,异号得负。
并把绝对值相乘。
2.多个数相乘的乘法法则(1)几个不为0的数相乘,积的符号是由负因数的个数决定的,当负因数为偶数个时,积为正。
当负因数的个数为奇数时,积为负,并把绝对值相乘。
(2)几个数相乘,有一个因数为0,积为0.3.乘法运算律(1)乘法交换律两数相乘,交换因数的位置,积不变。
(2)乘法结合律三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变。

初中数学青岛版七年级上册高效课堂资料3.3有理数的乘方【学习目标】1.能运用有理数乘方的意义进行乘方运算;2.通过有理数乘方的探索过程,体会由特殊到一般的数学思想;3.养成严谨规范的学习习惯.【重点】有理数乘方的运算. 【难点】有理数乘方运算的符号法则.【使用方法与学法指导】1.先精读一遍教材P 66—P 68用红笔进行勾画;再针对预习案二次阅读教材,然后合上课本独立完成预习案,完成后再针对课本对自己的预习案进行初步修改;2.找出自己的疑惑和需要讨论的问题,随时记录在课本或导学案上,准备课上讨论质疑;预 习 案一、预习自学1.通过预习,(3)(3)(3)(3)(3)-⨯-⨯-⨯-⨯-可以记作__________,读作______________; 类似的)41()41()41()41(-⨯-⨯-⨯-可记作_____________,读作___________________.那么a a a a a a ⨯⨯⨯⨯⨯等于多少呢?通过上述例子,请概括出乘方以及与之相关的概念的含义.【思考】4)2(-与42-的底数和指数分别是什么?有什么区别?2.计算:(1) 221⎪⎭⎫ ⎝⎛ (2) 32 (3) ()33- (4)421⎪⎭⎫ ⎝⎛- (5)80你发现计算题中正数的幂的符号有什么规律?负数的幂的符号又有什么规律?请写出你得到的一般结论:二、预习自测:1.5(3)-表示的意义是( )A. -3乘5B. 3个5相乘C. 5个3-相加D. 5个3-相乘2.()62-中指数为 ,底数为 ,结果为 ;62-中指数为 ,底数为 ,结果为 。
62的相反数是______。
3.=771___;()=71-___;()=101-____;=32_____;=33_____;=34_____;=35_____. 4.分别比较下列各组数的大小:(1) 23- ()32-; (2)()22.0- ()42.0-; (3) ()23- 23- ; (4)33- ()33- .三、我的疑惑上节课知识链接:1.有理数除法法则:两数相除,同号得正,异号得负,并把绝对值相除;0除以任何一个不等于0的数,都得0;0不能作除数。
青岛版数学七年级上册3.3《有理数的乘方》教学设计1一. 教材分析《青岛版数学七年级上册3.3《有理数的乘方》》这一节主要讲述有理数的乘方概念和性质。
学生在学习了有理数的乘除法和幂的定义基础上,进一步掌握有理数的乘方,有助于加深对数的概念的理解,为后续的代数运算和函数学习打下基础。
二. 学情分析七年级的学生已经掌握了有理数的加减乘除和幂的基本概念,具备了一定的逻辑思维能力。
但乘方作为幂的进一步延伸,其概念和性质较为抽象,学生可能难以理解。
因此,在教学过程中,需要结合实例,让学生通过观察、操作、思考,自主探索乘方的规律。
三. 教学目标1.理解有理数的乘方概念,掌握有理数乘方的运算方法。
2.理解有理数乘方的性质,能运用乘方解决实际问题。
3.培养学生的逻辑思维能力和自主学习能力。
四. 教学重难点1.有理数的乘方概念和性质。
2.有理数乘方的运算方法。
五. 教学方法采用“问题驱动”的教学方法,通过实例引入,引导学生观察、操作、思考,发现乘方的规律。
利用多媒体辅助教学,形象直观地展示乘方的过程,提高学生的学习兴趣。
同时,注重师生互动,鼓励学生提问、交流,提高学生的参与度。
六. 教学准备1.多媒体教学设备。
2.PPT课件。
3.练习题。
七. 教学过程1.导入(5分钟)利用多媒体展示一个实际问题:某商品打八折优惠,即原价的80%,求原价。
引导学生思考如何用数学方法表示这个问题,引出有理数的乘方概念。
2.呈现(10分钟)讲解有理数的乘方定义,引导学生通过观察、操作,发现有理数乘方的规律。
如:23表示2乘以自己3次,即2×2×2=8。
同时,讲解有理数乘方的运算方法,如:a m×a n=a(m+n)。
3.操练(10分钟)让学生进行一些有理数乘方的练习,巩固所学知识。
教师巡回指导,解答学生的疑问。
4.巩固(10分钟)讲解有理数乘方的性质,如:a m÷a n=a(m-n);(a m)n=a(mn)。
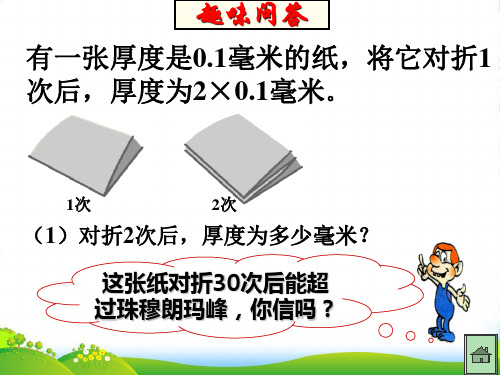
知识点解读:有理数的乘方
同学们,一张普通白纸的厚度只有0.01厘米,但是当你把这一张普通的白纸连续对折30次后,你知道有多厚吗?它的厚度竟然超过珠穆朗玛峰!你相信吗?通过对有理数乘方的学习,我们就会知道其中的奥妙了。
知识点一:有理数乘方的意义
一般地,n 个相同的因数a 相乘,即n a a a ⋅⋅⋅L 14
243个,记作a n
,读作a 的n 次方.求n 个相同因数的积的运算,叫做乘方,乘方的结果叫做幂。
在a n 中,a 叫做底数,n 叫做指数,当a n
看作a 的n 次方的结果时,也可读作a 的n 次幂。
知识点二:如何进行乘方运算 1.乘方和加、减、乘、除一样,也是一种运算,是乘法运算的特殊情况。
a n
就是表示n 个a 相乘,所以可以利用有理数的乘法运算来进行有理数的乘方运算;
2.幂的符号法则:负数的奇次幂是负的,负数的偶次幂是正的,即(-a )2n =a 2n ,(-
a )2n +1=-a 2n +1(n 是正整数),a 2n ≥0,即任何有理数的偶次幂是非负数;正数的任何次幂是正的; 0的任何次幂都是0;
3.一个数可以看作这个数本身的一次方,如5就是51,通常指数为1时可以省略不写。
4.有理数的混合运算时,应注意的运算顺序:
(1)先乘方,再乘除,最后加减;
(2)同级运算,从左到右进行;
(3)如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行. 例1 计算:(1)(-3)4;(2)(-8)3;(3)(-13
)4 分析:根据乘方的意义可直接用乘法来求出各乘方的值。
解:(1)(-3)4=(-3) (-3) (-3) (-3)=81.
(2)(-8)3=(-8) (-8) (-8)=-512.
(3)(-13)4=(-13)(-13)(-13)(-13)=181
. 说明:这里应特别注意“-”号问题,计算时也可以先根据符号法则确定其结果的符号,然后直接计算正数的乘方。
例2 计算(-0.125)12×813
的值.
分析:直接计算(-0.125)12与813
有一定的难度,但观察发现0.125×8=1,于是提醒我们利用乘方的意义和乘法的运算律就能比较容易地求值了。
解: (-0.125)12×813=(0.125)12×813
=(120.1250.1250.125⨯⨯⨯L 14444244443个)×(13888⨯⨯⨯L 14243个)
=(120.12580.12580.1258⨯⨯⨯⨯⨯⨯L 144444424444443个
)×8
=(12111⨯⨯⨯L 14243
个
)×8=8. 说明:当发现一个题目运算起来比较麻烦时,我们不妨认真地观察思考,寻求求解的突破口,使问题获解。
值得注意的几个问题
学习有理数的乘方,除了要能掌握乘方的意义,灵活运用乘方的知识解题外,还应注意以下几个问题:
1.要认清底数。
如-34是3的4次方的相反数,而(-3)4
则是-3的4次方,前者底数是3,后者底数是-3,不能等同。
不能把(-3)4写成-34,也不能把3
45⎛⎫ ⎪⎝⎭写成345。
2.进行乘方运算时,不能将底数与指数相乘。
如23与32看似相同,而实际上是不同的,切不可以犯23=32=2×3的错误。
3.进行乘方运算时,可以先要确定符号,再将底数的绝对值相乘。