变量-表格

excel单变量求解算法原理 -回复Excel是一种广泛使用的电子表格程序，具有强大的计算和数据处理功能。

在E x c e l中，单变量求解是通过已知一组数据和相关条件，推测未知因素的值。

本文将详细介绍Excel单变量求解算法的原理和步骤。

一、什么是单变量求解在Excel中，单变量求解是指根据已知数据和条件，计算出一个或多个未知变量的值。

具体而言，单变量求解适用于以下情况：1. 已知数据间存在函数关系，但其中某些数据缺失；2. 已知数据间存在数学关系，但其中某些因素未知；3. 通过修改一个或多个变量，使得某个目标变量达到预期值。

二、单变量求解的原理单变量求解的原理主要涉及数学方程求解和逼近方法。

Excel通过迭代计算的方式，不断更新未知变量的值，直到满足给定的条件或达到某种收敛状态。

具体而言，单变量求解主要采用以下两种方法：1. 手动求解：通过人工调整未知变量的值，观察目标变量的变化情况，逐步逼近预期结果。

2. 自动求解：通过Excel内置的求解器工具，根据给定的数据和条件，自动计算未知变量的值。

三、单变量求解的步骤下面将介绍Excel中使用单变量求解的步骤：1. 建立模型在求解之前，需要先建立一个数学模型来描述已知数据和未知变量之间的关系。

模型可以是简单的数学公式或复杂的函数关系，具体取决于问题的性质和要求。

2. 输入数据将已知数据输入Excel的工作表，包括已知变量的值和相应的条件。

在输入数据时，应确保数据的准确性和完整性，以获得可靠的求解结果。

3. 设置目标和约束确定需要求解的目标变量，并设置约束条件。

目标变量是我们希望计算出的未知变量，约束条件是对未知变量的限制，可以是数值范围、等式约束等。

4. 运行求解器在Excel中，点击“数据”选项卡中的“求解器”按钮，打开求解器对话框。

在对话框中，选择目标单元格和约束条件，并设置求解的精度和迭代次数。

5. 运行求解点击求解器对话框中的“求解”按钮，Excel 会自动计算未知变量的值，并更新工作表中的相应单元格。

变量分布的表达方法有
变量之间的关系”的三种表示方法
1、表格法：通过列表格可以得到变量之间的关系信息，进一步预测其变化趋势，从而作出科学的判断. 一般地，因变量随自变量的变化呈现一定的规律，依据此规律对结论作出预测.
2、关系式法：关系式是表示变量之间关系的另一种方法，它能准确地反应出因变量与自变量之间的数值对应关系. 也就是说，当自变量每一个确定的值，因变量就有惟一一个确定的值与它对应.
3、图象法：图象是表示变量之间关系的又一种方法，图象能非常直观形象地反映出因变量随自变量的变化的趋势.
分布函数必然单调不减,右连续,仅有第一类间断点,间断点可列.
分布函数（distribution function）是一个普遍的函数，正是通过它，人们能用数学分析的方法来研究随机变量。

分布函数的性质
(1)非负有界性0≤F(X)≤1
(2)单调不减性
证明：即对任意的X1<=F(X2)，有这是因为当X1<=x2时，，即。

从而证明F(x1)<=F(x2)
(3)右连续性F(x+0)=F(x)
按照数量标志分组形式的分布数列称为变量分布数列，简称变量数列。

根据分组变量在各组取值形式的不同，变量数列可分为单项式分布数列和组距式分布数列。

按照数量标志分组形式的分布数列称为变量分布数列，简称变量数列(Variable distribution series)。

变量数列根据变量标志的特征的不同分为离散变量数列和连续变量数列。

连续变量数列根据分组变量在各组取值形式的不同，变量数列可分为单项式分布数列和组距式分布数列。

竭诚为您提供优质文档/双击可除3个变量的表格篇一：3.3.1用表格表示两个变量之间的关系学案篇二：变量-表格一、填空题1．从圆的周长公式c=2r可以看出，圆的周长随半径的变化而变化，在这个变化过程中，自变量是____，因变量是____．2．某户每月的电费随该户每月的用电量的变化而变化，则自变量是,因变量是.3．下表是某市20xx年女学生各年龄组的平均身高：(1)由表可知，该市女学生11岁组的平均身高是_________．(2)上表反映了________和_________这两个变量间的关系；其中_________是自变量，__________是因变量．4．小亮帮母亲预算家庭4月份电费开支情况，下表是小亮家4月初连续8天每天早上电表显的读（1）表格中反映的变量是______，自变量是______，因变量是______．（2）估计小亮家4月份的用电量是______度，若每度电是0.49元，估计他家4月份应交的电费是___元。

5．小王到１０千米外的邮局寄包裹，他骑车的速度越快，所用的时间越短，在此变化过程中，自变量是。

二、简答题６．某公司决定投资新项目，通过考察，确定有6个项目可供选择，各项目所需资金及预计年利润如下表：（1）上表反映的两个变量是________和_________,其中自变量是__________,因变量是____________.（2）如果投资一个4亿元的项目，那么预计年利润有_______________.（3）如果预计获得0.9千万元的年利润,投资一个项目需要的资金是_____________.(4)写出表中两个变量之间的变化趋势：7．某兴趣小组通过在弹簧下挂物体，测得一个弹簧的长度与所挂物体的质量之间有如下一组数据：根据上表回答下列问题：(1)在没挂物体前弹簧的长度为cm（2）挂4.5kg的物体时，弹簧的长度为cm（3）当弹簧的长度是17cm时，估计所挂物体的质量为kg.8.下表是三发电器厂20xx年上半年每个月的产量：（1）根据表格中的数据，y随x的变化怎样变化？（2）根据表格你知道哪几个月的月产量保持不变？哪几个月的月产量在匀速增长？哪个月的产量最高？（3）求20xx年前半年的平均月产量。

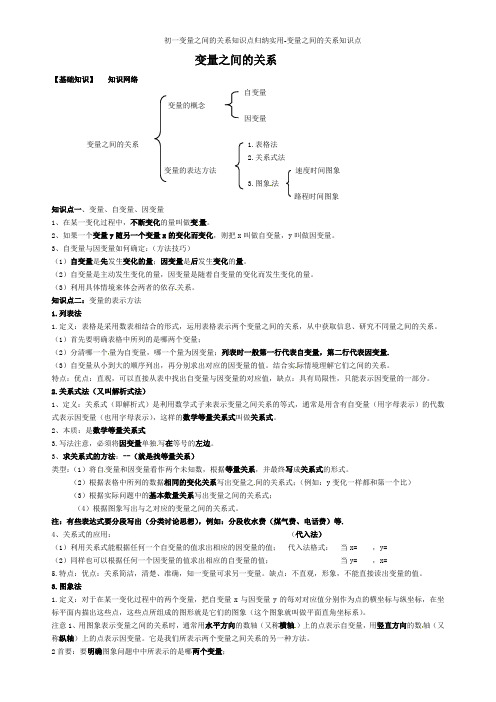
变量之间的关系【基础知识】知识网络自变量变量的概念因变量变量之间的关系 1.表格法2.关系式法变量的表达方法速度时间图象3.图象法路程时间图象知识点一、变量、自变量、因变量1、在某一变化过程中，不断变化的量叫做变量。

2、如果一个变量y随另一个变量x的变化而变化，则把x叫做自变量，y叫做因变量。

3、自变量与因变量如何确定：（方法技巧）（1）自变量是先发生变化的量；因变量是后发生变化的量。

（2）自变量是主动发生变化的量，因变量是随着自变量的变化而发生变化的量。

（3）利用具体情境来体会两者的依存关系。

知识点二：变量的表示方法1.列表法1.定义：表格是采用数表相结合的形式，运用表格表示两个变量之间的关系，从中获取信息、研究不同量之间的关系。

（1）首先要明确表格中所列的是哪两个变量；（2）分清哪一个量为自变量，哪一个量为因变量；列表时一般第一行代表自变量，第二行代表因变量.（3）自变量从小到大的顺序列出，再分别求出对应的因变量的值。

结合实际情境理解它们之间的关系。

特点：优点：直观，可以直接从表中找出自变量与因变量的对应值，缺点：具有局限性，只能表示因变量的一部分。

2.关系式法（又叫解析式法）1、定义：关系式（即解析式）是利用数学式子来表示变量之间关系的等式，通常是用含有自变量（用字母表示）的代数式表示因变量（也用字母表示），这样的数学等量关系式叫做关系式。

2、本质：是数学等量关系式3.写法注意，必须将因变量单独写在等号的左边。

3、求关系式的方法：--（就是找等量关系）类型：（1）将自变量和因变量看作两个未知数，根据等量关系，并最终写成关系式的形式。

（2）根据表格中所列的数据相同的变化关系写出变量之间的关系式；（例如：y变化一样都和第一个比）（3）根据实际问题中的基本数量关系写出变量之间的关系式；（4）根据图象写出与之对应的变量之间的关系式。

注：有些表达式要分段写出（分类讨论思想），例如：分段收水费（煤气费、电话费）等.4、关系式的应用：（代入法）（1）利用关系式能根据任何一个自变量的值求出相应的因变量的值；代入法格式：当x= ，y=（2）同样也可以根据任何一个因变量的值求出相应的自变量的值；当y= ，x=5.特点：优点：关系简洁，清楚、准确，知一变量可求另一变量。

《用表格表示的变量间关系》教案一、教学目标1. 让学生理解什么是变量，能够识别常量和变量。

2. 让学生掌握表格表示变量间关系的方法。

3. 培养学生运用表格解决实际问题的能力。

二、教学重点与难点1. 教学重点：识别变量和常量。

运用表格表示变量间的关系。

2. 教学难点：理解变量间关系的表达方式。

将实际问题转化为表格表示。

三、教学方法1. 采用问题驱动的教学方法，引导学生通过观察、思考、操作、交流等活动，发现变量间的关系。

2. 利用实例讲解，让学生在实际问题中体验变量间关系的表达方法。

3. 组织小组讨论，培养学生合作学习的能力。

四、教学准备1. 教学课件或黑板。

2. 实例材料。

3. 纸张、笔等学习用具。

五、教学过程1. 导入新课利用生活中的实例，如身高、体重等，引导学生认识变量。

讲解常量和变量的概念。

2. 讲解变量间关系通过实例，讲解变量间的关系，如身高与体重之间的关系。

引导学生观察、分析实例，发现变量间的规律。

3. 学习用表格表示变量间关系讲解如何用表格表示变量间的关系。

示例：以身高和体重为例，制作一个表格，展示身高和体重之间的对应关系。

4. 实践操作让学生分组，每组选择一个实际问题，如“某班级学生的身高和体重数据”，用表格表示变量间的关系。

学生分组讨论、操作，教师巡回指导。

5. 总结与拓展对学生进行总结，巩固所学知识。

提出拓展问题，激发学生思考，如“如何用表格表示复杂的多变量关系？”6. 布置作业让学生完成课后练习，运用表格表示变量间关系。

选择一个实际问题，制作表格，并分析变量间的关系。

六、教学评价1. 评价内容：学生对变量和常量的理解程度。

学生运用表格表示变量间关系的能力。

学生解决实际问题的能力。

2. 评价方法：课堂提问，检查学生对概念的理解。

作业批改，评估学生的实际操作能力。

小组讨论，观察学生的合作和问题解决能力。

七、教学反思1. 教师在课后应对本节课的教学效果进行反思，包括：学生对课堂内容的掌握情况。

初一数学常量与变量之间的关系易佰分教育培训学校教育从心开始一、结构梳理自变量丰富的现实情境变量因变量探索变量之间的关系变量及其关系变量之间的关系表格利用变量之间的关系解表示方法图象决问题进行预测关系式1(在某一变化过程中不断变化的数量叫，应该一个变量y随着另一个变量x 的变化而变化，那么把x叫，y叫2(在表达变量之间的关系时，、、是表达变量之间关系的重要方式( 知识点一:理解用表格来刻画变量之间的关系例1(圆周长C与圆的半径r之间的关系为C=2πr，其中变量是( )，常量是( )( 常量:在某一变化过程中,始终保持不变的量(变量:在某一变化过程中,可以取不同数值的量(包括自变量和因变量。

设在某一变化过程中有两个变量x和y，如果对于x的每一个值，y总有唯一的值与它对应，我们就说x是自变量，y是因变量。

例2 某公园决定投资开发新项目(通过考察确定有6个项目可供选择(各项目所需资金及预汁年利润如下表:所需资金(亿元) l 2 4 6 7 8预计利润(千万元) 0.2 0.35 0.55 O(7 0.9 l(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)如果投资一个4亿元的项目，那么其年利润预计有多少?(3)如果要预计获得O.9千万元的年利润(投资一个项目需要多少资金?(4)如果该公司可以拿出10亿元进行多个项目的投资(预计最大年利润是多少 ?变式:1. 表中反映了青春期男、女孩身高情况，从中你能获得哪些信息,年龄/岁 9 10 11 12 13 14男孩身高/厘米 126 129 134 140 145 153女孩身高/厘米 127 130 134 137 143 1522. 次实验中，小明把一根弹簧的上端固定，在其下端悬挂物体，下面是测得的弹簧的长度y与所挂物体质量1易佰分教育培训学校教育从心开始 x的一组对应值(所挂重量x/kg 0 1 2 3 4 5弹簧长度y/cm 18 20 22 24 26 28(1)上表反映了哪两个变量之间的关系,哪个是自变量,哪个是因变量,(2)当所挂物体重量为3kg时，弹簧多长,不挂重物呢,(3)若所挂重物为6kg时(在允许范围内)，你能说出此时的弹簧长度吗,3、声音在空气中传播的速度y(米/秒)(简称音速)与气温x(?)之间的关系如下从表中可知音速y随温度x的升高而( )(在气温为20?的一天召开运动会，某人看到发令枪的烟0.2秒后，听到了枪声，则由此可知，这个人距发令地点( )米( 气温(x/?) 0 5 10 15 20音速y(米/秒) 331 334 337 340 3434、下表中的数据是根据某地区入学儿童人数编制的:年份 2005 2006 2007 2008 2009入学儿童人数 2930 2720 2520 2330 2140(1)随着年份的变化，因变量入学儿童的人数变化的趋势是什么,答:( );(2)你认为入学儿童的人数会变成零吗,答:( )5、下表所列为某商店薄利多销的情况(某商品原价为560元，随着不同幅度的降价，日销量(单位为件)发生相应的变化(如表):降价(元) 5 10 15 20 25 30 35日销量(件) 780 810 840 870 900 930 960这个表反映了( )个变量之间的关系，( )是自变量，( )是因变量(从表中可以看出每降价5元，日销量增加( )件，从而可以估计降价之前的日销量为( )件，如果售价为500元时，日销量为( )件(6、重百大楼的销售量随商品价格的高低而变化，在这个变化过程中，自变量是( ) A(销售量 B(顾客 C(商品 D(商品的价格 7(用圆的半径r来表示圆的周长C，其式子为C=2πr(则其中的常量为( )A(r B(π C(2 D(2π28(在圆面积公式S=πR，R是半径，则变量是( )A(S，π B(π，R C(S，R，π D(S，R 9(从空中落下一个物体，它降落的速度随时间的变化而变化，即落地前速度随时间的增大而逐渐增大，这个问题中自变量是( )A(物体 B(速度 C(时间 D(空气知识点2:根据已知条件求关系式，利用关系式求值或者根据关系式做出相应的决策2易佰分教育培训学校教育从心开始 1、确定关系式的步骤:先找出题目中关于________与________的相等关系，再用________的代数式表示________2、半径为R的圆面积S=________，当R=3时，S=________例1、如图，ABC 底边BC上的高是6厘米，当三角形的顶点C沿底边所在直线向点B运动时，三角形的面积发生了变化((1)在这个变化过程中，自变量、因变量各是什么,2(2)如果三角形的底边长为(x厘米)，那么三角形的面积y(厘米)可以表示为_________2 (3)当底边长从12厘米变化到3厘米时，三角形的面积从____厘米变化到____厘米2变式1、如图，已知梯形的上底为x，下底为8，高为4((1)求梯形面积y与x的关系;(2)用表格表示，当x从3到7(每次增加1)时，y的相应值;(3)当x每增加1时，y如何变化,(4)当y=50时，x为多少,(5)当x=0时，y等于多少,此时它表示的是什么,例2、将若干张长为20cm、宽为10cm的长方形白纸，按下图所示的方法粘合起来，粘合部分的宽为2cm((1)求4张白纸粘合后的总长度;(2)设x张白纸粘合后的总长度为ycm，写出y与x之间的关系式;(3)并求当x=20时，y的值。

3.1用表格表示的变量间关系题型1：常量和变量的辨识1.一本笔记本5元，买x本共付y元，则5和x分别是（）A．常量，变量B．变量，变量C．常量，常量D．变量，常量【变式1-2】分析并指出下列关系中的变量与常量：（1）球的表面积S cm2与球的半径R cm的关系式是S＝4πR2；（2）以固定的速度v0米/秒向上抛一个小球，小球的高度h米与小球运动的时间t秒之间的关系式是h＝v0t﹣4.9t2；（3）一物体自高处自由落下，这个物体运动的距离h m与它下落的时间t s的关系式是h＝gt2（其中g取9.8m/s2）；（4）已知橙子每千克的售价是1.8元，则购买数量W千克与所付款x元之间的关系式是x＝1.8W．自变量和因变量一般地，在某个变化过程中，如果有两个变量x，y并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就说x是自变量，y是因变量.自变量与因变量的联系与区别（1）联系∶二者都是某一变化过程中的变量，因研究的侧重点或先后顺序不同可以互相转化，如当路程一定时，若时间随速度的变化而变化，这时速度是自变量，时间是因变量;当速度一定时，若路程随时间的变化而变化，这时时间是自变量，路程是因变量.（2）区别∶自变量是在一定范围内主动发生变化的量，因变量是随着自变量的变化而被动发生变化的量. 题型2：自变量和因变量的辨识2.正方形边长为5厘米，若边长减少x，则面积减少y．下列说法正确的是（）A．边长x是自变量，面积减少量y是因变量B．边长是自变量，面积是因变量C．上述关系式为y＝（5﹣x）2D．上述关系式为y＝52﹣（5﹣x）2【变式2-1】世纪花园居民小区收取电费的标准是0.6元/千瓦时，当用电量为x（单位：千瓦时）时，收取电费为y（单位：元）．在这个问题中，下列说法中正确的是（）A．x是自变量，0.6元/千瓦时是因变量B．0.6元/千瓦时是自变量，y是因变量C．y是自变量，x是因变量D．x是自变量，y是因变量，0.6元/千瓦时是常量【变式2-2】圆的周长公式C＝2πR中，下列说法正确的是（）A．π、R是自变量，2是常量B．C是因变量，R是自变量，2π为常量C．R为自变量，2π、C为常量D．C是自变量，R为因变量，2π为常量用表格表示变量间的关系1.借助表格，我们可以表示因变量随自变量的变化而变化的情况.2.用表格表示两个变量之间关系的步骤（1）确定各行、各列的栏目（一般有两行，第一行表示自变量，第二行表示因变量）;（2）写出栏目名称并根据问题内容写上单位;（3）在第一行列出自变量的各个变化取值，在第二行对应列出因变量的各个变化取值.一般情况下，自变量的取值从左到右应按由小到大的顺序排列，这样便于反映因变量随自变量变化的趋势. 3. 用表格表示两个变量之间关系的优缺点（1）优点∶直观，可以直接从表格中找出自变量和因变量的对应值;（2）缺点∶具有局限性，只能部分反映两个变量之间的关系，因此要从这部分数据中得出两个变量之间的关系时，需要对表格中的数据进行分析.题型3：利用表格获取变量的值3.对于气温，有的地方用摄氏温度表示，有的地方用华氏温度表示，从温度计上可以看出，摄氏温度x（℃）与华氏温度y（℉）有如下对应的关系．下列说法不正确的是（）x/℃…﹣100102030…Y/℉…1432506886…A．摄氏温度x（℃）与华氏温度y（℉）都是变量，且摄氏温度（℃）是自变量，华氏温度（℉）是因变量B．随着摄氏温度x的逐渐升高，华氏温度y也逐渐升高C．摄氏温度每升高10℃，华氏温度升高18℉D．当摄氏温度为40℃，华氏温度为102℉题型4：利用表格分析变量的关系4.研究表明，当每公顷钾肥和磷肥的施用量一定时，土豆的产量与氮肥的施用量有如下关系：上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？（2）当氮肥的施用量是101kg/hm2（hm2是单位“公顷”的符号）时，土豆的产量是多少？如果不施氮肥呢？（3）根据表格中的数据，你认为氮肥的施用量是多少时比较适宜？说说你的理由．（4）粗略说一说氮肥的施用量对土豆产量的影响．【变式4-1】植物呼吸作用受温度影响很大，观察如图，回答问题：（1）此图反映的自变量和因变量分别是什么？（2）温度在什么范围内时豌豆苗的呼吸强度逐渐变强？在什么范围内逐渐减弱？（3）要使豌豆呼吸作用最强，应控制在什么温度左右？要抑制豌豆的呼吸应控制在什么温度左右？．【变式4-2】已知某易拉罐厂设计一种易拉罐，在设计过程中发现符合要求的易拉罐的底面半径与铝用量有如下关系：上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？（2）当易拉罐底面半径为2.4cm时，易拉罐需要的用铝量是多少？（3）根据表格中的数据，你认为易拉罐的底面半径为多少时比较适宜？说说你的理由．（4）粗略说一说易拉罐底面半径对所需铝质量的影响．题型5：利用表格进行规律探究5.一种手持烟花，这种烟花每隔0.5秒发射一发花弹，每一发花弹的飞行路径，爆炸时的高度均相同．皮皮小朋友发射出的第一发花弹的飞行高度h（米）随飞行时间t（秒）变化的规律如下表所示．下列这一变化的过程说法正确的是（）A.飞行时间t每增加0.5秒，飞行高度h就增加5.5米B.飞行时间t每增加0.5秒，飞行高度h就减少5.5米C.估计飞行时间t为5秒时，飞行高度h为11.8米D.只要飞行时间t超过1.5秒后该花弹爆炸，就视为合格。

excel 单变量运算
Excel是一种功能强大的电子表格软件，可以进行各种数学运算，包括单变量运算。

单变量运算是指对一个变量进行操作，如求平均数、求标准差等。

以下是Excel中常用的单变量运算函数：
1. AVERAGE函数：求平均数
AVERAGE函数可以求出一组数的平均值。

例如：=AVERAGE(A1:A10)可以求出A1到A10单元格中的数的平均值。

2. SUM函数：求和
SUM函数可以对一组数进行求和操作。

例如：=SUM(A1:A10)可以求出A1到A10单元格中的数之和。

3. MAX函数：求最大值
MAX函数可以求出一组数中的最大值。

例如：=MAX(A1:A10)可以求出A1到A10单元格中的数中最大的那个数。

4. MIN函数：求最小值
MIN函数可以求出一组数中的最小值。

例如：=MIN(A1:A10)可以求出A1到A10单元格中的数中最小的那个数。

5. STDEV.S函数：求标准差
STDEV.S函数可以求出一组数的标准差。

例如：=STDEV.S(A1:A10)可以求出A1到A10单元格中的数的标准差。

6. VAR.S函数：求方差
VAR.S函数可以求出一组数的方差。

例如：=VAR.S(A1:A10)可以求出A1到A10单元格中的数的方差。

这些函数可以帮助我们在Excel中进行单变量运算，从而更好地分析数据。