2014~2015学年度 最新 吉林省长春市2015初中数学总复习试题(五)图形的变化

实用文档2015年吉林长春中考数学试卷解析版24分）小题，每小题3分，共一、选择题（本大题共8 ）3的绝对值是（（3分）（2015?长春）﹣1．DCB﹣33A．．．．绝对值．考点：分析：根据一个负数的绝对值等于它的相反数得出．﹣（﹣﹣3|=3解答：）=3．解：| 故选：A．考查绝对值的概念和求法．点评：绝对值规律总结：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．2m632000某工程队做了面积为“暖房子工程”?长春）在长春市实施过程中，2．（3分）（2015 ）的外墙保暖．632000这个数用科学记数法表示为（4566DBC A 10××××63.2106.32100.632100.632 ．．．．科学记数法—表示较大的数．考点：n a分析：≤1其中×10的形式，用科学记数法表示，科学记数法的表示形式为anna时，小数点移，10为整数．确定的值时，要看把原数变成＜||n1动了多少位，的绝对值与小数点移动的位数相同．当原数绝对值＞nn时，是正数；当原数的绝对值＜是负数．1时，5解答：632000=6.32解：×，10 B故选．a×此题主要考查了科学记数法的表示方法．科学记数法的表示形式为点评的形式，其1为整数，表示时关键要正确确1值以的值．实用文档23a））的结果是（20153．（3分）（?长春）计算（2563aaaa DBC A 3 ．．．．幂的乘方与积的乘方．考点：根据幂的乘方计算即可．分析：623aa解答：，解：（）= ．故选C 点评：此题考查幂的乘方，关键是根据法则进行计算．长春）图中的两个圆柱体底面半径相同而高度不同，关于这两个圆柱体（?（3分）20154．）的视图说法正确的是（A．主视图相同俯视图相同B．． C 左视图相同俯视D主视图、．图、左视图都相同考点：简单组合体的三视图．根据从正面看得到的视图是主视图，从左边看得到的图形是左视图，分析从上面看得到的图形是俯视图，可得答案错误解答解、主视图的宽不同，故实用文档BB正确；、俯视图是两个相等的圆，故CC错误；、主视图的宽不同，故DD错误；、俯视图是两个相等的圆，故B．故选：本题考查了简单组合体的三视图，从正面看得到的视图是主视图，从点评：左边看得到的图形是左视图，从上面看得到的图形是俯视图．2xx﹣2）+3=0的根的情况是（分）5．（3（2015?长春）方程只有一个实A有两个相等B数根．．的实数根有两个不相CD没有实数根等的实数根．．根的判别式．考点：2accbab分析：进行计算，然后根据计算结果判断﹣==1，4=﹣2，代入△把=3 方程根的情况．cab =32，解：∵，=1，=﹣解答：22acb 0，1×3=﹣8∴△=＜﹣4=（﹣2）﹣4×所以方程没有实数根．．故选C2cbaaxbxca点评：为常数）的根的，+=0（，≠0，本题考查了一元二次方程+2ab=00=4﹣时，方程有两个不相等的实数根；当△C．当△＞判别式△时，方程没有实数根．0时，方程有两个相等的实数根；当△＜BADABACAABC°，则∠1=70作∥．若∠C?（3．6（分）2015长春）如图，在△中，=，过点BAC）的大小为（实用文档°D7040°C50°30 A°B ．．．．平行线的性质．考点：BC∠分析：，根据等腰三角形的性质得出∠=根据平行线的性质求出∠C°，根据三角形内角和定理求出即可．=70ACAB =解答：解：∵，CB∠∴∠，=BCAD°，∵，∠∥1=70C 1=70∴∠°，=∠B =70∴∠°，CBACB =40°，°﹣70=180°﹣∠﹣∠°=180°﹣∴∠70 B．故选本题考查了三角形内角和定理，等腰三角形的性质，平行线的性质的点评：CBC三角形∠应用，解此题的关键是求出∠注意：的度数和得出∠，= °，两直线平行，内错角相等．内角和等于180 ABCOOABCD是平行四边形，则?长春）如图，四边形内接于⊙，若四边形37．（分）（2015ADC∠）的大小为（°75D°60C°50B°A 45．．．．考点：圆内接四边形的性质；平行四边形的性质；圆周角定理．分析ADAB 设的度的度由题意可，实用文档β即可解决问题．求出βαABCADC；的度数解答：解：设∠的度数==，∠OADC是平行四边形，∵四边形AOCADC；=∠∴∠βαβAOCαADC，∠+==180∵∠；而=°，∴，ADCβα=120°，=60=60°，∠解得：°，C．故选应牢固掌握该定理并能灵该题主要考查了圆周角定理及其应用问题；点评：活运用．xyAm上，=2）在直线3分）（2015?长春）如图，在平面直角坐标系中，点+3（﹣1，8．（bAOByxOAOA 则°，点的对应点上，恰好落在直线+连结将线段，=绕点﹣顺时针旋转90b的值为（）B21ACD﹣．．．．-考点：一次函数图象上点的坐标特征；坐标与图形变化旋转．BmxAy的坐标，再代，得出先把点坐标代入直线的值，然后得出点分析：=2+3byx入直线=﹣+解答即可．mAymx =，﹣解：把（﹣1，）代入直线=2+3，可得：2+3=1解答O°，所以因为线绕顺时针旋9的坐标为1代入直把，可得=1，实用文档．故选D 此题考查一次函数问题，关键是根据代入法解解析式进行分析．点评：分）6小题，每小题3分，共18二、填空题（本大题共）“1．长春）比较大小：（填“＞”、=”或“＜”＞?9．（3分）（2015实数大小比较．：考点分析：两个数的平方的大小故选，根据实数大小比较的方法，判断出即可判断出两个数的大小关系．解答：，解：1∵2＞，∴．故答案为：＞．此题主要考查了实数大小比较的方法，要熟练掌握，解答此题的关键点评：是判断出两个数的平方的大小关系．xx 4 的解集为．≥2015分）（?长春）不等式30﹣12≥（10．3解一元一次不等式．考点：即可求得1利用不等式的基本性质，把12分析：移到不等号的右边，系数化为原不等式的解集．x，≥解答：解：移项得，312x 4解得，≥x．故答案为≥4解答这类题学以及解简单不等式的能力，本题考查了解一元一次不等式，点评：生往往在解题时不注意移项要改变符号这一点而出错．解不等式要依据不等式的基本性质）不等式的两边同时加上或减去同一个数或整式不等号的方向不变）不等式的两边同时乘以或除以同一个正数不等号的方向不变2实用文档）不等式的两边同时乘以或除以同一个负数不等号的方向改变．（3OOP ABP AO的交点．若∠为切点，与⊙（3分）（2015?长春）如图，是为⊙的切线，11．ππPOA）（结果保留=20°，=3，则的长为切线的性质；弧长的计算．考点：POAOAP度数，根据弧长公式求出即根据切线性质得出∠分析：°，求出∠=90 可．AOP A于解答：解：∵，切⊙P AO∴∠°，=90P∵∠°，=20POA°，=70∴∠π=，∴π故答案为：．能正确运用弧长公式进行计本题考查了弧长公式，切线的性质的应用，点评：算是解此题的关键，注意：圆的切线垂直于过切点的半径．xyP过）0=（的图象上．＞长春）分）12．（3（2015?如图，在平面直角坐标系中，点在函数xCOBPCByPxA并延长交的中点、，取线段，连结点分别作轴、轴的垂线，垂足分别为APD．D 轴于点．则△的面积为6实用文档k的几何意义；全等三角形的判定与性质．反比例函数系数考点：kPBCDOC的几何意分析：≌△再根据反比例函数系数，根据已知条件证得△义即可得到结论．xyP APB轴，解答：解：∵轴，⊥⊥kS =|，|=6∴APBO矩形DOCPBC与△中，在△，DOCPBC≌△，∴△SS．∴=6=APBOAPD矩形△6．故答案为：k过双曲线上的任意一点分的几何意义，点评：本题考查了反比例函数系数k，全等|别向两条坐标轴作垂线，与坐标轴围成的矩形面积就等于|DOCPBC三角形的判定和性质，证明△≌△是解题的关键．CECDABEEABCD，8点，在正方形的边若△上．=3的面积为如图，?（3．13（分）2015长春）BE．则线段5 的长为正方形的性质；三角形的面积；勾股定理．：考点实用文档BCEMBCCDABAD，根据=，得出==4分析：根据正方形性质得出，根据面积求出= 勾股定理求出即可．解答：解：MABEME于⊥，过作ABCD是正方形，∵四边形ABBCCDAD =，=∴=CEADBMEM，，∴==ABE∵△，的面积为8EMAB =8×∴×，EM =4，解得：ABADDCBC ==4即=，=CE =3∵，BE ==由勾股定理得：=5，．故答案为：5解此题的关键是本题考查了三角形面积，点评：正方形性质，勾股定理的应用，BC的长，难度适中．求出2xAxy过在平面直角坐标系中，2015（14．3分）（?长春）如图，点+2在抛物线=2﹣上运动．BDACAxABCDCACBD 1 ．则对角线以点作⊥轴于点，为对角线作矩形，连结，的最小值为二次函数图象上点的坐标特征；垂线段最短；矩形的性质考：：专题计算题．实用文档，再根据矩形的性质得1）先利用配方法得到抛物线的顶点坐标为（1，分析：AACABDAC在抛物线的顶点时，的长等于点=的纵坐标，所以当点，由于BDxA 1，从而得到点到的最小值．轴的距离最小，最小值为22xxxy解答：+1（，﹣解：∵1=﹣2）+2= ，）∴抛物线的顶点坐标为（1，1ABCD∵四边形为矩形，ACBD =∴，xAC⊥而轴，AAC的长等于点∴的纵坐标，xAA到1当点轴的距离最小，最小值为在抛物线的顶点时，点，BD的最小值为1．∴对角线故答案为1．二次函数图象上点的坐标满足点评：本题考查了二次函数图象上点的坐标特征：其解析式．也考查了矩形的性质．小题，共78分）三、解答题（本大题共102xxxx 2=）（2015?长春）先化简，再求值：（+1）+，其中（．﹣615．（分）：整式的混合运算—化简求值．考点专题：计算题．第二项利用单项式乘以多项式法原式第一项利用完全平方公式化简，分析：x则计算，去括号合并得到最简结果，把的值代入计算即可求出值．222xxxxx解答：+1+﹣2，=2=解：原式+2+1x =．时，原式=6+1=7当熟练掌握运算法则是解本题点评：此题考查了整式的混合运算﹣化简求值，的关键．ba，，?（6．16（分）2015长春）一个不透明的盒子中有三张卡片，卡片上面分别标有字母c，每张卡片除字母不同外其他都相同，小玲先从盒子中随机抽出一张卡片，记下字母后放实用文档回并搅匀；再从盒子中随机抽出一张卡片并记下字母，用画树状图（或列表）的方法，求小玲两次抽出的卡片上的字母相同的概率．考点：列表法与树状图法．计算题．专题：先画树状图展示所有9种等可能的结果数，再找出两次抽出的卡片上的分析：字母相同的结果数，然后根据概率公式求解．解答：解：画树状图为：共有9种等可能的结果数，其中两次抽出的卡片上的字母相同的结果数为3种，所有小玲两次抽出的卡片上的字母相同的概率==．点评：本题考查了列表法或树状图法：通过列表法或树状图法展示所有等可能nABm，然后根据概或的结果求出的结果数目，再从中选出符合事件AB的概率．或率公式求出事件2km为的土地进行绿化．长春）为了美化环境，某地政府计划对辖区内60（17．6分）（2015?个月完成任务，倍．结果提前2了尽快完成任务．实际平均每月的绿化面积是原计划的1.5 求原计划平均每月的绿化面积．分式方程的应用．考点：2xkm分析：，实际平均每月的绿化面积是设原计划平均每月的绿化面积为2xkm 1.5，根据结果提前2个月完成任务列出方程解答即可．2xkm解答：实际平均每月的绿化面积是设原计划平均每月的绿化面积为解：，2xkm 1.5，由题意得=2﹣x=10解得：x=10是原方程的解，经检验实用文档2km．答：原计划平均每月的绿化面积为10找到原计划所用时间和实际所用时间的此题考查分是方程的实际运用，点评：等量关系是解决问题的关键．FGF AFCDCEABCCEACD，∥外角∠于点的平分线，718．（分）（2015?长春）如图，交是△ACGFCDACG∥．求证：四边形交于点是菱形．菱形的判定．考点：证明题．：专题，从而根据角平分线的性质得到32=∠首先根据平行线的性质得到∠分析：ACAF从而利用邻边相等的平行四边形是菱形证得结，得到，=3∠1=∠论．ACCDFGAF∥解答：证明：∵，∥，ACGF，∠3∴四边形是平行四边形，∠2=ACDCE，∵平分∠2，∴∠1=∠，1=∠3∴∠AF AC∴，=ACGF∴四边形是菱形．本题考查了菱形的判定，解题的关键是了解菱形的几种判定方法，点评：实用文档度不大．ACB岛的正东和正北方向．一艘、分）（2015?长春）如图，海面上两岛分别位于19．（7CBAC 岛在小时到达海里/时的速度向正北方向航行2船从岛，此时测得岛出发，以18BA海里）°．求（结果精确到、0.1两岛之间的距离．岛的南偏东43tancossin =0.93°=0.73，【参考数据：】43°=0.68，4343°-方向角问题．考点：解直角三角形的应用ABCACRt中，利2=36海里，在=根据路程速度×时间，可得△分析：=18×ACBACtanAB∠用正切函数的定义可得将数值代入计算即可求解．=，?ACBAC海里，∠°．解：由题意得，=43=18×2=36解答：AABCRt在°，△=90中，∵∠ACBtanABAC 33.5海里．=36∴×=0.93?∠≈BA 33.5、海里．故两岛之间的距离约为本题考查了解直角三角形的应用﹣方向角问题，正切函数的定义，路点评：程、速度与时间自己的关系，难度一般．理解方向角的定义，将实际问题转化为数学问题是解决问题的关键．n名本校学生，对长春）在“世界家庭日”前夕，某校团委随机抽取了20157分）（?（20．“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查．问卷中的家庭活动方式包括：．进行其他活动C．到公园游玩；D．在家里聚餐；A B．去影院看电影；该校团委收回全部问卷每位学生在问卷调查时都按要求只选择了其中一种喜欢的活动方式，解答下列问将收集到的数据整理并绘制成如图所示的统计图，根据统计图提供的信息，后，题：n）求（1的值；实用文档CABCD作答）、、、（2）四种方式中最受学生喜欢的方式为；选择该种方式的学生（用人数占被调查的学生人数的百分比为35% ．CB方式的学生多的人方式的学生比喜欢根据统计结果，估计该校1800名学生中喜欢（3）数．考点：条形统计图；用样本估计总体．ABCD的人数加起来，即可解答；，（1）根据条形图，把分析：，，CC的）的学生人数最多，即为四种方式中最受学生喜欢的方式；用（2人数÷总人数，即可得到百分比；CB方式的学生的人数，作）分别计算出喜欢方式的学生人数、喜欢（3差即可解答．n=30+40+70+60=200．解：（1）解答：C的学生人数最多，）∵（2C，∴四种方式中最受学生喜欢的方式为×100%=35%，C，35%．故答案为：（3）1800×=270（人），CB方式的学生多的人数名学生中喜欢方式的学生比喜欢1800答：该校为270人．点评：本题考查的是条形统计图和扇形统计图的综合运用．读懂统计图，从不的统计图中得到必要的信息是解决问题的关键条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．实用文档21．（8分）（2015?长春）甲、乙两台机器共同加工一批零件，在加工过程中两台机器均改变了一次工作效率．从工作开始到加工完这批零件两台机器恰好同时工作6小时．甲、乙两yxOAAB﹣台机器各自加工的零件个数（时）之间的函数图象分别为折线（个）与加工时间OCC D．如图所示．﹣与折线（1）求甲机器改变工作效率前每小时加工零件的个数．yx之间的函数关系式．与（2）求乙机器改变工作效率后（3）求这批零件的总个数．考点：一次函数的应用．（1分析：）甲改变工作效率前的工作效率为改变前加工的总件数，除以加工的总时间即可；（2）利用待定系数法求一次函数解析式即可；（3）利用函数解析式求出甲、乙两机器6小时加工的总件数，求其和即可．解答：解：（1）80÷4=20（件）；CD（5，110），），（2）∵图象过2（，80ykxbk≠0）（，∴设解析式为=+∴，解得：，yxx≤6）；=10 +60（2≤∴乙A过8）11ABymxnm≠0）=∴设的解析式为+（，甲实用文档∴，解得：，xyx）（4≤，≤∴=306﹣40甲yxy 6+60=12040=140，，=10当时，=6×=30×6﹣乙甲．∴这批零件的总个数是140+120=260根据题意得出函数关系式以及数形结此题主要考查了一次函数的应用，点评：合是解决问题的关键．ABEADAADAEABCD，连＞，使B中，已知．在边=上取点922．（分）（2015?长春）在矩形FEEFCEABCE作或其延长线交于点，过点⊥．，与边结DEAFDEAFF AB与的大小关系为猜想：如图①，当点．在边上时，线段=DEGAFF ABEFBC的大与探究：如图②，当点在边交于点的延长线上时，．与边判断线段小关系，并加以证明．BGADAB =5，利用探究得到的结论，求线段应用：如图②，若的长．=2，考点：四边形综合题．DCEAEF≌△①根据题意证明△分析：即可；②证明方法与①相同可以证明结论；③根据平行线分线段成比例定理列出比例式，计算得到答案．DEAF解答：=解：①；DEAF，②=DAFEC证明：∵∠°，=∠=∠=90DCEAEF∠=，∴DCAE中在和△实用文档，DCEAEF≌△，∴△DEAF =∴．DCEAEF≌△③∵△，ABDEFBF AAECDABAF，∴=1====2，，=﹣=3ADBG∵，∥∴=，BG∴．=本题考查的是矩形的性质、全等三角形的判定和性质、相似三角形的点评：性质和判定，灵活运用相关的定理和性质是解题的关键．ABBCP ABCABAD上于点D，．点⊥．23（10分）（2015?长春）如图，在等边△中，在边=6PEDFEDPEBCACEEDPEPEDFP?∥．，与边交于点为邻边作作，连结?，以、设运动，过点xABCyAPx与△．重叠部分图形的面积为＜，线段6的长为（0＜）xPE的代数式表示）（1）求线段（用含的长．xPEDF（2）当四边形为菱形时，求的值．xy与之间的函数关系式．（3）求ADABPEAA相交时，的对称点为点′，当线段的垂直平分线与直线′（4）设点关于直线xQQPBCBCQ上）时，直接写出同侧（不包括点在直线设其交点为，当点与点位于直线的取值范围．考点四边形综合题．：实用文档APE）证明△是等边三角形，即可求解；分析：（1ACECEDEPEDF AEDE是（2）四边形即可得到为菱形时，==，然后证明ABP的中点，则的中点，据此即可求解；是xBABPEBCFxP30=＜，则（3）当≤=3，即与是重合，当的中点时，PEDBxPEDF，6时，，当3＜重合部分是梯形≤时，重合部分就是平行四边形根据平行四边形和梯形的面积公式即可求解；xDAB 4）首先求得当时'的值，据此即可求解．的中垂线正好经过点（BCPE∥解：（1）∵，解答：ABCAPE∽△∴△，ABC又∵△是等边△，APE∴△是等边三角形，xPEAPx）0＜；∴＜==6（PEDF为菱形，（2）∵四边形xPEDE =，=∴PEAPEAE是等边三角形，则，=又∵△DEAE =∴，ADEDAC =∠，∴∠CDACADEEDC∠+∠°，=∠=90+又∵∠CEDC =∠∴∠，ECDE =∴，ABACDEECAE =3∴==．==x =3即；BFBCxP ABPE与的中点时，=重合．（3）当=3，即是，则PEDFx．时，重合部分就是平行四边形，如图1则当0＜≤3AP ABABCADsinAPEAM?==3=6等边△中，=?60°×，等边△中，xsin°60=，实用文档xDM =3﹣，则2xxxxyy（3+3﹣=﹣则；=），即PEDBx，如图2＜6时，重合部分是梯形3当＜．yxBDyPEDMx =﹣﹣），+3）?（则3=（+即）?；=（BCA所示，）情形一：当（4上方时，如图′在3BDADABD =，当时，′′的中垂线正好经过点=3AA．=3﹣3则′AAAM3′=则=3﹣），（APx ==3﹣∴=．xx﹣0＜．＜3则的取值范围是：ADPQABC，如图情形二：当4′在所示，上时，∥ABAAPPBP =6=3==．=′×BCA′在下方时，如图5情形三：当所示，BDADDAB =′=3当，′的中垂线正好经过点时，AA =3+3．则′AAAM3，+3）则=′=（APx．==3+∴=xx＜3+．＜3则的取值范围是：xxx﹣＜3或＜0的取值范围为综上所示，．3+ ＜＜3实用文档BF重合以本题是等边三角形的性质以及菱形的性质的综合应用，求得与点评：tABD及的值是关键．'时，两种情况下的中垂线正好经过点2xaxy轴交（与﹣=1）分）24．（12（2015?长春）如图，在平面直角坐标系中，抛物线+4PBAByC 在这条抛物线上，且不与的坐标为（3于点，、0两点，与）轴交于点，且点，点PQFPQyBCQRtPQFPBC°，轴的垂线与射线=90交于点，作以，为边作使∠、过点两点重合．△mPPQdQFFQ的长度为．，点=1．设线段点的横坐标为在点的下方，且1）求这条抛物线所对应的函数表达式．（md与之间的函数关系式．（2）求dRtPQFyPF（3）当△轴平分时，求的边被的值．OBDOBDOBFm的边上时304（）以为边作等腰直角三角形，当＜＜时，直接写出点落在△m的值．实用文档二次函数综合题．考点：2axBya分析：）+4=，求出（的值即可；﹣1（1）把点）代入抛物线（3，0PQQBC，即可的解析式，由点）先求出直线（2的纵坐标求出横坐标，求出得出结果；yQP关于（3）由题意得出点轴对称，得出方程，解方程即可；与点GOBFOBDQF，落在△交）分两种情况：①当点的直角边上时，延长于（4QFFGFGQGOFGOG，得出方程，解方，由﹣=证出△=是等腰直角三角形，得出程即可；QFOBDBQFBFF，证出△=是等腰直角三角形，得出②当点落在△=1的斜边上时，OF，得出方程，解方程即可．=22xyaB解答：+4，﹣）把点1（3，0）代入抛物线）=（解：（1a +4=0得：4，a，解得：=﹣122xxyx +3﹣1）+4=﹣+2∴抛物线的函数表达式为：=﹣（，2xxy +2；=﹣+3即抛物线解析式为：2xyx，+2（2）对于抛物线+3=﹣yx时，=3当；=0xyx当=3=0时，=﹣1，或，BAC，03，），∴0（，3），（﹣10），（bBCykx的解析式为：=，+设直线，根据题意得：bk =3，，﹣解得：=1xBCy﹣=∴直线的解析式为：+3，实用文档2mmPm +3的坐标为：（），﹣+2∵点，2mQm的纵坐标坐标为：﹣+3∴点+2，22mxmmxm +3=﹣，+2则﹣﹣+3，2=22mmmQm，﹣）+2的坐标为（，﹣2∴点+3m∴当﹣1≤，＜0时，如图122mmmmmd﹣2，﹣﹣=3=x时，如图20当＜，＜322mmmmdm）=2﹣=+3﹣（﹣dmd之间的函数关系式为：与=∴；yPPQFPFyQRt的边轴对称，被△轴平分时，点关于与点）当（3 ∴横坐标互为相反数，2mmm﹣2∴，+=0mm =1，或=0（不合题意，舍去）解得：，m =1∴，d 1=2；∴=3﹣）分四种情况：（4①情形一：如所示点的坐标为）实用文档2xxxyyx（舍去），=﹣，+2=2+3将得=3代入函数=021mP点的横坐标；=2∴NQFDDGCO点作与所示：过交⊥点，②情形二：如图522B）0，∵3（D）∴，（，2COQFQFCO =1，，，∵∥=3∴=，ND∴=，2Q，）1，∴2（2xxyyxx，，=1﹣+3得将=1+=2代入函数=﹣（舍去）+221m∴；=1+OBGDD点作所示：过⊥，②情形三：如图622B 3）∵0（，D，，）∴（2COQFQFBG∥，=，=1∵，∴，BF =1，∴Q，1∴（1，）2 xxxyyx，=1﹣+3得=1+（舍去），将=1代入函数=﹣+221m；∴=1+ 7④情形四：如图所示：CDQFCDBCQF∥，，=6∵，=1=3，且22，∴BQ，∴=Q点纵坐标为∴，即点纵坐标，实用文档2xxxxyy +3得，=，=将（舍去）=代入函数=﹣+221m∴=．mFmOBD，0＜＜3时，点落在△1+的边上时的值为：2，或综上所述：当或1+，或．本题是二次函数综合题目，考查了二次函数解析式的求法、轴对称的性质、点评：用待定系数法求一次函数解析式、等腰直角三角形的判定与性质、一元二次）中，需要进行分方程的解法等知识；本题难度较大，综合性强，特别是（4 类讨论，画出图形，证明等腰直角三角形和解一元二次方程才能得出结果．。

2014-2015学年吉林省长春市绿园区七年级（下）期末数学试卷一、选择题（共8小题，每小题3分，满分24分）1．下列四个方程中，有一个解为的是（）A．2x+5y=12 B．3x﹣y=1 C．x+y=1 D．6x+5y=142．已知关于x的方程2x﹣a﹣5=0的解是x=﹣2，则a的值为（）A．1 B．﹣1 C．9 D．﹣93．不等式2x﹣1≤5的解集在数轴上表示为（）A． B．C．D．4．若a＞b，则下列不等式一定成立的是（）A．a+1＞b+1 B．＜C．﹣2a＞﹣2b D．a+c＜b+c5．若一个正n边形的一个外角为36°，则n等于（）A．4 B．6 C．8 D．106．下列图形中，既是中心对称，又是轴对称图形的是（）A． B．C．D．7．只用下列图形不能镶嵌的是（）A．正三角形B．长方形C．正五边形D．正六边形8．如图，将△ABC沿BC方向平移2cm得到△DEF，若△ABC的周长为16cm，则四边形ABFD的周长为（）A．16cm B．18cm C．20cm D．22cm二、填空题（共6小题，每小题3分，满分18分）9．若a=1，b=2，则以a，b为边长的等腰三角形的周长为．10．若一个多边形内角和等于1260°，则该多边形边数是．11．如图，△ABC≌△BAD，A、C的对应点分别是B、D．若AB=9，BC=12，AC=7，则BD=．12．如图，平面上两个正方形与正五边形都有一条公共边，则∠α等于度．13．不等式2x﹣1≤3的非负整数解是．14．形如的式子叫做二阶行列式，它的运算法则用公式表示为=a×d﹣b×c，如=1×（﹣2）﹣0×2=﹣2，依此法则计算=﹣2中的x值为．三、解答题（共10小题，满分78分）15．．16．解方程组：．17．解不等式组，并把它的解集在数轴上表示出来．18．如图，四边形ABCD中，∠A+∠B=200°，∠ADC、∠DCB的平分线相交于点O，求∠COD的度数．19．如图，∠ABC=38°，∠ACB=100°，AD平分∠BAC，AE是BC边上的高，求∠DAE的度数．20．在长为10m，宽为8m的矩形空地中，沿平行于矩形各边的方向分割出三个全等的小矩形花圃，其示意图如图所示．求小矩形花圃的长和宽．21．如图1是3×3的正方形方格，将其中两个方格涂黑，并且使涂黑后的整个图案是轴对称图形，（要求：绕正方形ABCD的中心旋转能重合的图案都视为同一种图案，例如图2中的四幅图就视为同一种图案），请在图3中的四幅图中完成你的设计．22．如图的小方格都是边长为1个单位的正方形，按照下列要去作图，（不写作法，只作出图形即可）（1）作△ABC关于直线EF的轴对称图形△A1B1C1；（2）将△ABC向右平移4个单位得到△A2B2C2；（3）作△A3B3C3，使△A3B3C3和△ABC关于点O成中心对称．23．某移动公司开设了两种通讯业务：“全球通”使用者缴费50元月租费，然后每通话1min再付话费0.4元；“快捷通”不缴月租费，每通话1min付话费0.6元（本题的通话均指市内通话）．若一个月通话xmin，两种方式的费用分别为y1元和y2元．（1）用含x的式子分别表示y1和y2，则y1=，y2=；（2）某人估计一个月通话300min，选择哪种业务合算？（3）每个月通话多少分钟时，两种方式所付的费用一样多？24．如图，线段AB=20cm．（1）点P沿线段AB自A点向B点以2厘米/秒运动，同时点Q沿线段BA自B点向A点以3厘米/秒运动，几秒钟后，P、Q两点相遇？（2）如图，AO=PO=2cm，∠POQ=60°，现点P绕着点O以30°/s的速度顺时针旋转一周后停止，同时点Q沿直线BA自B点向A点运动，假若点P、Q两点也能相遇，求点Q运动的速度．2014-2015学年吉林省长春市绿园区七年级（下）期末数学试卷参考答案与试题解析一、选择题（共8小题，每小题3分，满分24分）1．下列四个方程中，有一个解为的是（）A．2x+5y=12 B．3x﹣y=1 C．x+y=1 D．6x+5y=14考点：二元一次方程的解．分析：把方程的解代入各个方程判定即可．解答：解：把分别代入各式中可得，x+y=1有一个解为，故选：C．点评：本题主要考查了二元一次方程的解，解题的关键是把方程的解代入各个方程．2．已知关于x的方程2x﹣a﹣5=0的解是x=﹣2，则a的值为（）A．1 B．﹣1 C．9 D．﹣9考点：一元一次方程的解．专题：计算题．分析：将x=﹣2代入方程即可求出a的值．解答：解：将x=﹣2代入方程得：﹣4﹣a﹣5=0，解得：a=﹣9．故选：D点评：此题考查了一元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值．3．不等式2x﹣1≤5的解集在数轴上表示为（）A． B．C．D．考点：在数轴上表示不等式的解集．专题：计算题．分析：先求此不等式的解集，再根据不等式的解集在数轴上表示方法画出图示即可求得．解答：解：解不等式得：x≤3，所以在数轴上表示为故选A．点评：不等式的解集在数轴上表示出来的方法：“＞”空心圆点向右画折线，“≥”实心圆点向右画折线，“＜”空心圆点向左画折线，“≤”实心圆点向左画折线．4．若a＞b，则下列不等式一定成立的是（）A．a+1＞b+1 B．＜C．﹣2a＞﹣2b D．a+c＜b+c考点：不等式的性质．分析：A、由不等式的性质1可判断A；B、由不等式的性质2可判断B；C、由不等式的性质3可判断C；D、由不等式的性质1可判断D．解答：解：A、a＞b，由不等式的性质1可知：a+1＞b+1，故A正确；B、a＞b，由不等式的性质2可知：＞，故B错误；C、a＞b，由不等式的性质3可知：﹣2a＜﹣2b，故C错误；D、a＞b，由不等式的性质1可知：a+c＞b+c，故D错误．故选：A．点评：本题主要考查的是不等式的性质，掌握不等式的基本性质是解题的关键．5．若一个正n边形的一个外角为36°，则n等于（）A．4 B．6 C．8 D．10考点：多边形内角与外角．分析：利用多边形的外角和即可解决问题．解答：解：n=360°÷36°=10．故选D．点评：本题主要考查了正n边形的外角特点．因为外角和是360度，所以当多边形是正多边形时，每个外角都相等．直接利用外角求多边形的边数是常用的方法．6．下列图形中，既是中心对称，又是轴对称图形的是（）A． B．C．D．考点：中心对称图形；轴对称图形．分析：根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形，以及轴对称图形的定义即可判断出．解答：解：A、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，也是轴对称图形，故此选项正确；B、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，不是轴对称图形，故此选项错误；C、此图形旋转180°后不能与原图形重合，此图形不是中心对称图形，是轴对称图形，故此选项错误；D、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，不是轴对称图形，故此选项错误．故选：A．点评：此题主要考查了中心对称图形与轴对称的定义，根据定义得出图形形状是解决问题的关键．7．只用下列图形不能镶嵌的是（）A．正三角形B．长方形C．正五边形D．正六边形考点：平面镶嵌（密铺）．分析：根据镶嵌的条件，判断一种正多边形能否镶嵌，要看周角360°能否被一个内角度数整除：若能整除，则能进行平面镶嵌；若不能整除，则不能进行平面镶嵌．解答：解：A、正三边形的每个内角是60°，能整除360°，能密铺；B、长方形每个内角都是90°，即能密铺；C、正五边形的每一个内角是180°﹣360°÷5=108°，不能整除360°，所以不能密铺；D、正六边形每个内角是120度，能整除360°，可以密铺．故选C．点评：本题考查了平面镶嵌，几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角．8．如图，将△ABC沿BC方向平移2cm得到△DEF，若△ABC的周长为16cm，则四边形ABFD的周长为（）A．16cm B．18cm C．20cm D．22cm考点：平移的性质．专题：几何图形问题．分析：根据平移的基本性质，得出四边形ABFD的周长=AD+AB+BF+DF=2+AB+BC+2+AC即可得出答案．解答：解：根据题意，将周长为16cm的△ABC沿BC向右平移2cm得到△DEF，∴AD=CF=2cm，BF=BC+CF=BC+2cm，DF=AC；又∵AB+BC+AC=16cm，∴四边形ABFD的周长=AD+AB+BF+DF=2+AB+BC+2+AC=20cm．故选：C．点评：本题考查平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．得到CF=AD，DF=AC是解题的关键．二、填空题（共6小题，每小题3分，满分18分）9．若a=1，b=2，则以a，b为边长的等腰三角形的周长为5．考点：等腰三角形的性质；三角形三边关系．分析：题目给出等腰三角形有两条边长a=1，b=2，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．解答：解：分两种情况考虑：（1）如果腰长为1，则三边是：1、1、2，不满足三角形两边之和大于第三边的性质，不成立；（2）如果腰长为2，则三边是：2、2、1，满足三角形两边之和大于第三边的性质，成立，故周长=2+2+1=5．所以以a，b为边长的等腰三角形的周长为5．故答案为：5．点评：本题考查了等腰三角形的性质及三角形三边关系；对于底和腰不等的等腰三角形，若条件中没有明确哪边是底哪边是腰时，应在符合三角形三边关系的前提下分类讨论．10．若一个多边形内角和等于1260°，则该多边形边数是9．考点：多边形内角与外角．专题：计算题．分析：根据多边形内角和定理及其公式，即可解答；解答：解：∵一个多边形内角和等于1260°，∴（n﹣2）×180°=1260°，解得，n=9．故答案为9．点评：本题考查了多边形的内角定理及其公式，关键是记住多边形内角和的计算公式．11．如图，△ABC≌△BAD，A、C的对应点分别是B、D．若AB=9，BC=12，AC=7，则BD=7．考点：全等三角形的性质．分析：根据全等三角形的性质得出BD=AC，即可得出答案．解答：解：∵△ABC≌△BAD，AC=7，∴BD=AC=7，故答案为：7．点评：本题考查了全等三角形的性质的应用，能理解全等三角形的性质是解此题的关键，注意：全等三角形的对应边相等，对应角相等．12．如图，平面上两个正方形与正五边形都有一条公共边，则∠α等于72度．考点：多边形内角与外角．分析：先分别求出正五边形的一个内角为108°，正方形的每个内角是90°，再根据圆周角是360度求解即可．解答：解：正五边形的一个内角为108°，正方形的每个内角是90°，所以∠α=360°﹣108°﹣90°﹣90°=72°．点评：主要考查了多边形的内角和．多边形内角和公式：（n﹣2）•180°．13．不等式2x﹣1≤3的非负整数解是0，1，2．考点：一元一次不等式的整数解．分析：首先利用不等式的基本性质解不等式，再从不等式的解集中找出适合条件的非负整数即可．解答：解：不等式的解集是x≤2，故不等式2x﹣1≤3的非负整数解为0，1，2．故答案为：0，1，2．点评：正确解不等式，求出解集是解答本题的关键．解不等式应根据不等式的基本性质．14．形如的式子叫做二阶行列式，它的运算法则用公式表示为=a×d﹣b×c，如=1×（﹣2）﹣0×2=﹣2，依此法则计算=﹣2中的x值为﹣2．考点：解一元一次方程．分析：根据已知得出4x﹣（﹣2）×3=﹣2，进而求出即可．解答：解：根据题意得：4x﹣（﹣2）×3=﹣2，4x+6=﹣2，4x=﹣8，x=﹣2．故答案为：﹣2．点评：此题主要考查了一元一次方程的解以及解一元一次方程，根据已知直接代入求出是解题关键．三、解答题（共10小题，满分78分）15．．考点：解一元一次方程．专题：计算题．分析：先去分母，再去括号，移项，合并，系数化1．解答：解：同分母可得：3（5﹣3x）=2（3﹣5x），移项可得：x+9=0，即x=﹣9．故原方程的解为x=﹣9．点评：对于带分母的方程：去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．16．解方程组：．考点：解二元一次方程组．专题：计算题．分析：方程组利用加减消元法求出解即可．解答：解：，①×3+②得：5x=0，即x=0，把x=0代入①得：y=5，则方程组的解为．点评：此题考查了解二元一次方程组，熟练掌握运算法则是解本题的关键．17．解不等式组，并把它的解集在数轴上表示出来．考点：解一元一次不等式组；在数轴上表示不等式的解集．专题：计算题．分析：首先把两条不等式的解集分别解出来，再根据大大取大、小小取小、比大的小比小的大取中间、比大的大比小的小无解的原则，把不等式的解集用一条式子表示出来．解答：解：解不等式2x﹣5≤3（x﹣1）得x≥﹣2，解不等式＞4x得x＜1，∴不等式组的解集为﹣2≤x＜1，在数轴上表示为：．点评：本题考查不等式组的解法和在数轴上的表示法，如果是表示大于或小于号的点要用空心，如果是表示大于等于或小于等于号的点用实心．18．如图，四边形ABCD中，∠A+∠B=200°，∠ADC、∠DCB的平分线相交于点O，求∠COD的度数．考点：多边形内角与外角；三角形内角和定理．分析：首先根据四边形内角和可得∠ADC+∠DCB=360°﹣200°=160°，再根据角平分线的性质可得∠ODC+∠OCD=×160°=80°，再进一步利用三角形内角和定理可得答案．解答：解：∵四边形ABCD中，∠A+∠B=200°，∴∠ADC+∠DCB=360°﹣200°=160°，∵∠ADC、∠DCB的平分线相交于点O，∴∠ODC=∠ADC，∠OCD=∠BCD，∴∠ODC+∠OCD=×160°=80°，∴∠COD=180°﹣80°=100°．点评：此题主要考查了多边形内角和定理，关键是掌握多边形内角和定理：（n﹣2）．180 （n≥3）且n为整数）．19．如图，∠ABC=38°，∠ACB=100°，AD平分∠BAC，AE是BC边上的高，求∠DAE的度数．考点：三角形内角和定理；三角形的外角性质．分析：先根据三角形内角和定理求出∠BAC的度数，由角平分线的定义得出∠BAD的度数，根据三角形外角的性质求出∠ADE的度数，由两角互补的性质即可得出结论．解答：解：∵∠ABC=38°，∠ACB=100°（己知）∴∠BAC=180°﹣38°﹣100°=42°（三角形内角和180°）．又∵AD平分∠BAC（己知），∴∠BAD=21°，∴∠ADE=∠ABC+∠BAD=59°（三角形的外角性质）．又∵AE是BC边上的高，即∠E=90°，∴∠DAE=90°﹣59°=31°．点评：此题考查的是三角形的内角和定理，熟知三角形内角和是180°是解答此题的关键．20．在长为10m，宽为8m的矩形空地中，沿平行于矩形各边的方向分割出三个全等的小矩形花圃，其示意图如图所示．求小矩形花圃的长和宽．考点：二元一次方程组的应用．专题：压轴题．分析：由图形可看出：小矩形的2个长+一个宽=10m，小矩形的2个宽+一个长=8m，设出长和宽，列出方程组即可得答案．解答：解：设小矩形的长为xm，宽为ym，由题意得：，解得：．答：小矩形的长为4m，宽为2m．点评：此题主要考查了二元一次方程组的应用，做题的关键是：弄懂题意，找出等量关系，列出方程组．21．如图1是3×3的正方形方格，将其中两个方格涂黑，并且使涂黑后的整个图案是轴对称图形，（要求：绕正方形ABCD的中心旋转能重合的图案都视为同一种图案，例如图2中的四幅图就视为同一种图案），请在图3中的四幅图中完成你的设计．考点：利用轴对称设计图案．分析：根据轴对称的性质画出图形即可．解答：解：如图所示．点评：本题考查的是利用轴对称设计图案，熟知轴对称的性质是解答此题的关键．22．如图的小方格都是边长为1个单位的正方形，按照下列要去作图，（不写作法，只作出图形即可）（1）作△ABC关于直线EF的轴对称图形△A1B1C1；（2）将△ABC向右平移4个单位得到△A2B2C2；（3）作△A3B3C3，使△A3B3C3和△ABC关于点O成中心对称．考点：作图-旋转变换；作图-轴对称变换；作图-平移变换．分析：（1）利用轴对称的性质分别作出点A、B、C的对称点A1、B1、C1即可；（2）利用平移的性质分别作出点A、B、C的对称点A2、B2、C2即可；（3）利用中心对称的性质分别作出点A、B、C的对称点A3、B3、C3即可．解答：解：（1）如图，△A1B1C1为所作；（2）如图，△A2B2C2为所作；（3）如图，△A3B3C3为所作．点评：本题考查了作图﹣旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了平移变换和轴对称变换．23．某移动公司开设了两种通讯业务：“全球通”使用者缴费50元月租费，然后每通话1min再付话费0.4元；“快捷通”不缴月租费，每通话1min付话费0.6元（本题的通话均指市内通话）．若一个月通话xmin，两种方式的费用分别为y1元和y2元．（1）用含x的式子分别表示y1和y2，则y1=50+0.4x，y2=0.6x；（2）某人估计一个月通话300min，选择哪种业务合算？（3）每个月通话多少分钟时，两种方式所付的费用一样多？考点：一元一次方程的应用；列代数式；代数式求值．分析：（1）因为移动通讯公司开设了两种通讯业务：“全球通”使用者先缴50元月租费，然后每通话1分钟，再付话费0.4元；“快捷通”不缴月租费，每通话1min付费0.6元．若一个月内通话xmin，两种方式的费用分别为y1元和y2元，则y1=50+0.4x，y2=0.6x；（2）令x=300，分别求出y1、y2的值，再做比较即可（3）令y1=y2，解方程即可．解答：解：（1）y1=50+0.4x；y2=0.6x；故答案为：50+0.4x，0.6x；（2）令x=300则y1=50+0.4×300=170；y2=0.6×300=180所以选择全球通合算．（3）令y1=y2，则50+0.4x=0.6x，解之，得x=250所以通话250分钟两种费用相同．点评：此题主要考查了一次函数的应用和一元一次方程的应用，本题需仔细分析题意，建立函数解析式，利用方程或简单计算即可解决问题．24．如图，线段AB=20cm．（1）点P沿线段AB自A点向B点以2厘米/秒运动，同时点Q沿线段BA自B点向A点以3厘米/秒运动，几秒钟后，P、Q两点相遇？（2）如图，AO=PO=2cm，∠POQ=60°，现点P绕着点O以30°/s的速度顺时针旋转一周后停止，同时点Q沿直线BA自B点向A点运动，假若点P、Q两点也能相遇，求点Q运动的速度．考点：一元一次方程的应用．专题：方程思想．分析：（1）根据相遇时，点P和点Q的运动的路程和等于AB的长列方程即可求解；（2）由于点P，Q只能在直线AB上相遇，而点P旋转到直线AB上的时间分两种情况，所以根据题意列出方程分别求解．解答：解：（1）设经过ts后，点P、Q相遇．依题意，有2t+3t=20，（2分）解得，t=分）答：经过4s后，点P、Q相遇；（4分）（2）点P，Q只能在直线AB上相遇，则点P旋转到直线AB上的时间为=2s，或s．（5分）设点Q的速度为ycm/s，则有2y=20﹣4，解得y=8；（7分）或8y=20，解得y=2.分）答：点Q的速度为8cm/s或2.5cm/s．（10分）点评：此题考查的知识点是一元一次方程的应用，关键是熟练掌握速度、路程、时间的关系．。

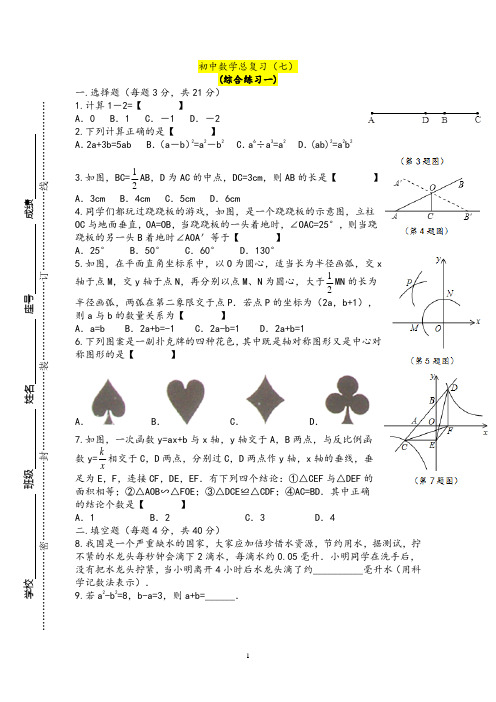
学校 班级 姓名 座号成绩 ……………………密……………………封……………………装……………………订……………………线…………………… 初中数学总复习（七）(综合练习一)一.选择题（每题3分，共21分） 1.计算1－2=【 】 A ．0 B ．1 C ．－1 D ．－2 2.下列计算正确的是【 】 A ．2a+3b=5ab B ．（a －b ）2=a 2－b 2 C ．a 6÷a 3=a 2 D ．(ab)2=a 2b 2 3.如图，BC=21AB ，D 为AC 的中点，DC=3cm ，则AB 的长是【 】 A ．3cm B ．4cm C ．5cm D ．6cm 4.同学们都玩过跷跷板的游戏，如图，是一个跷跷板的示意图，立柱OC 与地面垂直，OA=OB ，当跷跷板的一头着地时，∠OAC=25°，则当跷跷板的另一头B 着地时∠AOA ′等于【 】 A ．25° B ．50° C ．60° D ．130° 5.如图，在平面直角坐标系中，以O 为圆心，适当长为半径画弧，交x 轴于点M ，交y 轴于点N ，再分别以点M 、N 为圆心，大于21MN 的长为半径画弧，两弧在第二象限交于点P ．若点P 的坐标为（2a ，b+1），则a 与b 的数量关系为【 】 A ．a=b B ．2a+b=-1 C ．2a-b=1 D ．2a+b=1 6.下列图案是一副扑克牌的四种花色，其中既是轴对称图形又是中心对称图形的是【 】A ．B ．C ．D ．7.如图，一次函数y=ax+b 与x 轴，y 轴交于A ，B 两点，与反比例函数y=xk 相交于C ，D 两点，分别过C ，D 两点作y 轴，x 轴的垂线，垂足为E ，F ，连接CF ，DE ，EF ．有下列四个结论：①△CEF 与△DEF 的面积相等；②△AOB ∽△FOE ；③△DCE ≌△CDF ；④AC=BD ．其中正确的结论个数是【 】A ．1B ．2C ．3D ．4二.填空题（每题4分，共40分） 8.我国是一个严重缺水的国家，大家应加倍珍惜水资源，节约用水，据测试，拧不紧的水龙头每秒钟会滴下2滴水，每滴水约0.05毫升．小明同学在洗手后，没有把水龙头拧紧，当小明离开4小时后水龙头滴了约__________毫升水（用科学记数法表示）．9.若a 2-b 2=8，b-a=3，则a+b=______．10.若关于x 方程kx 2–6x+1=0有两个实数根，则k 的取值范围是 .11.如图，在△ABC 中，AB=AC ，∠B=50°，⊙A 与BC相切于点D ，与AB 相交于点E ，则∠AED=______°．12.如图，△ABC 中，CD ⊥AB 于D ，E 是AC 的中点．若AD=6，DE=5，则CD 的长等于 .13.如图，在8×4的矩形网格中，每个小正方形的边长都是1，若△ABC的三个顶点在图中相应的格点上，则tan∠ACB的值为．14.甲、乙、丙三台机床生产直径为60mm的螺丝，为了检验产品质量，从三台机床生产的螺丝中各抽取了20个测量其直径，进行数据处理后，发现三组数据的平均数都是60mm，它们的方差依次为S甲2=0.612，S乙2=0.058，S丙2=0.149，根据以上提供的信息，你认为生产螺丝的质量最好的是_____________机床.15.如图，矩形纸片ABCD中，AB=6cm，BC=10cm，点E在AB边上，将△EBC 沿EC所在直线折叠，使点B落在AD边上的点B′处，则AE的长为cm．16.五羊自行车厂组织78位劳动模范参观科普展览，为了节省经费，决定让其中10位劳模兼任司机.厂里有2种汽车：大车需1名司机，可坐11位乘客；小车需1名司机，可坐4名乘客.大车每辆出车费用为150元，小车每辆出车费用为70元.现备有大车7辆，小车8辆.为使费用最省，应安排开出大车________辆.17.如图，直线l1⊥x轴于点A（2，0），点B是直线l1上的动点．直线l2：y=x+1交l1于点C，过点B作直线l3垂直于l2，垂足为D，过点O，B的直线l4交l2于点E，当直线l1，l2，l3能围成三角形时，设该三角形面积为S1，当直线l2，l3，l4能围成三角形时，设该三角形面积为S2．（1）若点B在线段AC上，且S1=S2，则B点坐标为______；（2）若点B在直线l1上，且S2=3S1，则∠BOA的度数为_________．三.解答题（共89分）18.（9分）计算：12)21(30tan 320o 1+-+--.19.（9分）先化简，再求值：)131(442122--+÷-+--+x x x x x x x 其中x 满足0422=-+x x ．20.（9分）如图，把一个转盘分成四等份，依次标上数字：1，2，3，4，若连续自由转动转盘二次，指针指向的数字分别记作a ，b ，把a ，b 作为点A 的横、纵坐标．（1）用列表法或树状图表示出A （a ，b ）所有可能出现的结果；（2）求点A （a ，b ）在函数y=x 的图象上的概率．21．（9分）某中学开展“绿化家乡、植树造林”活动，为了解全校植树情况，对该校甲、乙、丙、丁四个班级植树的棵树和所占百分比情况进行了调查，将收集的数据整理并绘制成图1和图2两幅不完整的统计图，请根据图中的信息，完成下列问题：（1）这四个班共植树棵；（2）请补全两幅统计图；（3）若四个班级植树的平均成活率是95%，全校共植树2000棵，请你估计全校种植的树中成活的树大约有多少棵？（1）求证：AB=DF；（2）若AD=10，AB=6，求tan∠EDF的值.23．（9分）如图，在平面直角坐标系中，直线y 1=2x-2与反比例函数y 2=xk 的图象在第一象限交于点A （2，n ），在第三象限交于点B ，过B 作BD ⊥x 轴于D ，连接AD ．（1）求反比例函数的解析式；（2）求△ABD 的面积S △ABD ；（3）根据图象直接写出y 1＞y 2时自变量x 的取值范围．24．（9分）为了节约资源，科学指导居民改善居住条件，小王向房管部门提出了一个购买商品房的政策性方案．人均住房面积（平方米）单价（万元/平方米）不超过30（平方米）0.3超过30平方米不超过m（平方米）部分（45≤m≤60）0.5超过m平方米部分0.7根据这个购房方案：（1）若某三口之家欲购买120平方米的商品房，求其应缴纳的房款；（2）设该家庭购买商品房的人均面积为x平方米，缴纳房款y万元，请求出y 关于x的函数关系式；（3）若该家庭购买商品房的人均面积为50平方米，缴纳房款为y万元，且57＜y≤60 时，求m的取值范围．AC=BC，点A、C在x轴上，点B坐标为（3，m）（m＞0），线段AB与y轴相交于点D，以P（1，0）为顶点的抛物线过点B、D．（1）求点A的坐标（用m表示）；（2）求抛物线的解析式；（3）设点Q为抛物线上点P至点B之间的一动点，连接PQ并延长交BC于点E，连接BQ并延长交AC于点F，试证明：FC（AC+EC）为定值．26．（14分）如图，矩形ABCD的边AB=3cm，AD=4cm，点E从点A出发，沿射线AD移动，以CE为直径作圆O，点F为圆O与射线BD的公共点，连接EF、CF，过点E作EG⊥EF，EG与圆O相交于点G，连接CG．（1）试说明四边形EFCG是矩形；（2）当圆O与射线BD相切时，点E停止移动，在点E移动的过程中:①矩形EFCG的面积是否存在最大值或最小值？若存在，求出这个最大值或最小值；若不存在，说明理由；②求点G移动路线的长．初中数学总复习(七)参考答案一.选择题 题号 1 2 3 4 5 67答案 C D B B B C C二.填空题 三.解答题18.19.解：原式题号 8 9 10 1112 13 14 1516 17答案1.44×10338k ≤9且k ≠0 7831 乙 384 （2，0）；15°或75°∵∴∴原式20.解：（1）列表得：共有16种等可能的结果；（2）若点A 在y x =图象上，则a ＝b ，由（1）得点A 在y x =图象上的有4种，∴ ()41164a b P === 21.（1）200．（2）丁所占的百分比是：×100%=35%，丙所占的百分比是：1﹣30%﹣20%﹣35%=15%，丙植树的棵数是：200×15%=30（棵）． 补全两幅统计图如下：（3）根据题意得：2000×95%=1900（棵），答：全校种植的树中成活的树有1900棵．22.解：（1）证明：在矩形ABCD中，AD=BC，AD∥BC，∠B=90°，∵AD∥BC，∴∠BEA=∠FAD，∵DF⊥AE，∴∠DFA=90°，∴∠B=∠DFA，∵AE=BC，AD=BC，∴AE=AD，∴△AEB≌△DAF∴AB=DF；（2）由（1）可知：AF=AB=6，AE=AD=10，在Rt△AFD中，∠DFA=90°，∴，∴，在Rt△DFE中，∠DFE=90°，∴。

2014-2015学年长春市八年级下期末考试数学试题及答案2014-2015学年度第二学期期末教学质量跟踪测试八年级数学参考答案一、选择题（每小题2分，共16分）1.C2.D3.C4.D5.A6.C7.C8.B二、填空题（每小题3分，共21分）9.410.乙11.512.1313.22.514.2815.3三、解答题（本大题共9小题，共63分）16.(1) 12÷6=2.2) 23-27+3=23-33+3=-7.3) (5+1)(5-1)=(5)²-1²=25-1=24.17.因为四边形ABCD为矩形，所以AB=CD，∠A=∠D=90°。

因为AF=DE，所以AF-EF=DE-EF，所以AE=DF。

由于BE=CF，所以△ABE≌△DCF，因此BE=CF。

所以录用___，因为他的最终得分为81×30%+95×70%=90.8分，而___的最终得分为90×30%+82×70%=84.4分.18.(1) 这20位同学实验操作得分的中位数为9分.2) (10×5+9×8+8×4+7×3)/29=8.75分，因此这20位同学实验操作得分的平均分为8.75分.19.(1) 在菱形ABCD中，AC⊥BD，AD∥BC，因此AD∥CE.2) 四边形ACED是平行四边形，因此AC=DE=3，AD=CE。

又因为BD=4，BD⊥DE，所以由勾股定理得到BE=5.由于AD=BC=CD，所以BC=CE=BE/2=2.5，因此CD=2.5.所以△DCE的周长=DC+CE+DE=2.5+2.5+3=8.20.(1) 由于EF垂直平分BC，所以BF=CF，BE=CE.2) 因为CF=BE，所以BE=CE=CF=BF。

因此四边形BECF是菱形.3) ∠A=45°.21.(1) 由于EF垂直平分BC，所以BF=CF，BE=CE.2) 因为CF=BE，所以BE=CE=CF=BF。

2015年长春市初中毕业生学业考试数学试题（含答案全解全析）第Ⅰ卷(选择题,共24分)一、选择题(本大题共8小题,每小题3分,共24分)1.-3的绝对值是( )A.3B.-3C.D.-2.在长春市“暖房子工程”实施过程中,某工程队做了面积为632 000 m2的外墙保暖.632 000这个数用科学记数法表示为( )A.6 .2× 04B.6. 2× 05C.0.6 2× 06D.6. 2× 063.计算(a2)3的结果是( )A.3a2B.a5C.a6D.a84.图中的两个圆柱体底面半径相同而高度不同,关于这两个圆柱体的视图说法正确的是( )A.主视图相同B.俯视图相同C.左视图相同D.主视图、俯视图、左视图都相同5.方程x2-2x+3=0的根的情况是( )A.有两个相等的实数根B.只有一个实数根C.没有实数根D.有两个不相等的实数根6.如图,在△ABC中,AB=AC,过点A作AD∥BC.若∠ =70°,则∠BAC的大小为( )A. 0°B.40°C.50°D.70°7.如图,四边形ABCD内接于☉O,若四边形ABCO是平行四边形,则∠ADC的大小为( )A.45°B.50°C.60°D.75°8.如图,在平面直角坐标系中,点A(-1,m)在直线y=2x+3上.连结OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=-x+b上,则b的值为( )D.2A.-2B.1C.2第Ⅱ卷(非选择题,共96分)二、填空题(本大题共6小题,每小题3分,共18分)9.比较大小:2 1.(填“>”“=”或“<”)10.不等式3x- 2≥0的解集为.11.如图,PA为☉O的切线,A为切点,B是OP与☉O的交点.若∠P=20°,OA= ,则的长为(结果保留π).12.如图,在平面直角坐标系中,点P在函数y=6(x>0)的图象上,过点P分别作x轴、y轴的垂线,垂足分别为点A、B.取线段OB的中点C,连结PC并延长交x轴于点D,则△APD的面积为.13.如图,点E在正方形ABCD的边CD上.若△ABE的面积为8,CE=3,则线段BE的长为.14.如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD.则对角线BD的最小值为.三、解答题(本大题共10小题,共78分)15.(6分)先化简,再求值:(x+1)2+x(x-2),其中x=.16.(6分)一个不透明的盒子中有三张卡片,卡片上面分别标有字母a,b,c,每张卡片除字母不同外其他都相同.小玲先从盒子中随机抽出一张卡片,记下字母后放回并搅匀;再从盒子中随机抽出一张卡片记下字母.用画树状图(或列表)的方法,求小玲两次抽出的卡片上的字母相同的概率.17.(6分)为了美化环境,某地政府计划对辖区内60 km2的土地进行绿化.为了尽快完成任务,实际平均每月的绿化面积是原计划的1.5倍,结果提前2个月完成任务.求原计划平均每月的绿化面积.18.(7分)如图,CE是△ABC外角∠ACD的平分线.AF∥CD交CE于点F,FG∥AC交CD于点G.求证:四边形ACGF是菱形.19.(7分)如图,海面上B、C两岛分别位于A岛的正东和正北方向.一艘船从A岛出发,以18海里/时的速度向正北方向航行2小时到达C岛,此时测得B岛在C岛的南偏东4 °.求A、B两岛之间的距离.(结果精确到0.1海里)【参考数据:sin 4 °=0.68,cos 4 °=0.7 ,tan 4 °=0.9 】20.(7分)在“世界家庭日”前夕,某校团委随机抽取了n名本校学生,对“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查.问卷中的家庭活动方式包括:A.在家里聚餐;B.去影院看电影;C.到公园游玩;D.进行其他活动.每位学生在问卷调查时都按要求只选择了其中一种喜欢的活动方式.该校团委收回全部问卷后,将收集到的数据整理并绘制成如下的统计图.根据统计图提供的信息,解答下列问题:(1)求n的值;(2)四种方式中最受学生喜欢的方式为(用A、B、C、D作答);选择该种方式的学生人数占被调查的学生人数的百分比为;(3)根据统计结果,估计该校1 800名学生中喜欢C方式的学生比喜欢B方式的学生多的人数.21.(8分)甲、乙两台机器共同加工一批零件,在加工过程中两台机器均改变了一次工作效率.从工作开始到加工完这批零件两台机器恰好同时工作6小时.甲、乙两台机器各自加工的零件个数y(个)与加工时间x(时)之间的函数图象分别为折线OA—AB与折线OC—CD,如图所示.(1)求甲机器改变工作效率前每小时加工零件的个数;(2)求乙机器改变工作效率后y与x之间的函数关系式;(3)求这批零件的总个数.22.(9分)在矩形ABCD中,已知AD>AB.在边AD上取点E,使AE=AB,连结CE.过点E作EF⊥CE,与边AB或其延长线交于点F.猜想:如图①,当点F在边AB上时,线段AF与DE的大小关系为.探究:如图②,当点F在边AB的延长线上时,EF与边BC交于点G.判断线段AF与DE的大小关系,并加以证明.应用:如图②,若AB=2,AD=5,利用探究得到的结论,求线段BG的长.23.(10分)如图,在等边△ABC中,AB=6,AD⊥BC于点D.点P在边AB上运动,过点P作PE∥BC,与边AC交于点E,连结ED.以PE、ED为邻边作▱PEDF.设▱PEDF与△ABC重叠部分图形的面积为y,线段AP的长为x(0<x<6).(1)求线段PE的长;(用含x的代数式表示)(2)当四边形PEDF为菱形时,求x的值;(3)求y与x之间的函数关系式;(4)设点A关于直线PE的对称点为点A',当线段A'B的垂直平分线与直线AD相交时,设其交点为Q.当点P与点Q位于直线BC同侧(不包括点Q在直线BC上)时,直接写出x的取值范围.24.(12分)如图,在平面直角坐标系中,抛物线y=a(x-1)2+4与x轴交于A、B两点,与y轴交于点C,且点B的坐标为(3,0).点P在这条抛物线上,且不与B、C两点重合.过点P作y 轴的垂线与射线BC交于点Q.以PQ为边作Rt△PQF,使∠PQF=90°,点F在点Q的下方,且QF=1.设线段PQ的长度为d,点P的横坐标为m.(1)求这条抛物线所对应的函数表达式;(2)求d与m之间的函数关系式;(3)当Rt△PQF的边PF被y轴平分时,求d的值;(4)以OB为边作等腰直角三角形OBD.当0<m<3时,直接写出点F 落在△OBD的边上时m的值.答案全解全析：一、选择题1.A 因为|-3|=3,所以选项A 正确.故选A.2.B 因为6 2 000=6. 2× 05,所以选项B 正确.故选B.3.C (a 2)3=a 2× =a 6,所以选项C 正确.故选C.4.B 因为两个圆柱体底面半径相同而高度不同,所以这两个圆柱体的主视图、左视图不同,只有俯视图相同.选项B 符合.故选B.5.C 因为b 2-4ac=(-2)2-4× × =4-12<0,所以此方程没有实数根.选项C 正确.故选C. 6.B ∵AB=AC,∴∠B=∠C.∵AD∥BC,∴∠ =∠C=70°. ∴∠B=70°.∴∠BAC=40°.故选B.7.C 设∠ADC=x°,则∠AOC=2x°.∵四边形ABCO 是平行四边形,∴∠B=∠AOC.∵∠B+∠D= 80°,∴x+2x= 80.∴x=60.∴∠ADC=60°.故选C.8.D 把A(-1,m)代入y=2x+3,得m=2×(- )+ = ,,∴A 点坐标为(-1,1).将线段OA 绕点O 顺时针旋转90°,点A 的对应点B 的坐标是(1,1),把B(1,1)代入y=-x+b,得- +b= ,∴b=2.故选D.评析 本题考查了一次函数与旋转,需要通过旋转的性质准确求出对应点的坐标.属容易题.二、填空题 9.答案 >解析 因为2>1,所以 10.答案 x≥4解析 因为3x- 2≥0,所以 x≥ 2,所以x≥4.11.答案 7π6解析 ∵PA 是☉O 的切线,∴OA⊥AP.∵∠P=20°,∴∠AOP=70°.∴ 的长为70 π 80=7π6. 12.答案 6解析 ∵点P 在函数y=6(x>0)的图象上,∴S 矩形OAPB =6.∵点C 是OB 的中点,∴BC=OC.∵∠PBC=∠DOC,∠BCP=∠OCD,∴△COD≌△CBP.∴S △APD =S 矩形OAPB =6.评析 本题考查的是反比例函数的系数k 的几何意义,全等三角形的应用以及对中点的认识.本题中的点P 是不确定的,但是由点C 为BO 的中点,可以借助全等将要求的面积转化为易知的矩形面积.属中档题. 13.答案 5解析 ∵四边形ABCD 是正方形,∴AB=BC,∠C=90°.∵△ABE 的面积为8,∴ 2AB×BC=8,∴ 2AB 2=8.∴AB=4.∴BC=AB=4.∵CE= ,∴BE= 2 42=5.14.答案 1解析 ∵四边形ABCD 是矩形,∴AC=BD.当A 在抛物线的顶点处时,AC 最短,此时A(1,1),AC = ,∴BD= .即对角线BD 的最小值为1.三、解答题15.解析 原式=x 2+2x+1+x 2-2x =2x 2+1.(4分)当x= 时,原式=2×( )2+1=7.(6分)16.解析或(4分)∴P(字母相同)= 9=.(6分)17.解析 设原计划平均每月的绿化面积为x km 2. 根据题意,得60 -60.5=2.(3分) 解得x=10.(5分)经检验,x=10是原方程的解,且符合题意.答:原计划平均每月的绿化面积为10 km 2.(6分) 18.证明 ∵AF∥CD,FG∥AC,∴四边形ACGF 是平行四边形.(3分) ∵CE 平分∠ACD,∴∠ =∠2. ∵AF∥CD, ∴∠2=∠ . ∴∠ =∠ . ∴AF=AC.∴四边形ACGF 是菱形.(7分)19.解析 由题意,得AC= 8×2= 6.( 分) 在Rt△ABC 中,∠CAB=90°,∠ACB=4 °,tan∠ACB=,(3分)∴AB=AC·tan∠ACB= 6×tan 4 °= 6×0.9 = .48≈ .5(海里). 答:A 、B 两岛之间的距离约为33.5海里.(7分) 20.解析 (1)n=30+40+70+60=200, 所以n 的值为200.(2分) (2)C;35%.(4分)( ) 800×70200- 800×40200=270(人).所以喜欢C 方式的学生比喜欢B 方式的学生约多270人.(7分) 21.解析 ( )80÷4=20(个),所以甲机器改变工作效率前每小时加工零件20个.(2分)(2)设所求函数关系式为y=kx+b(k≠0). 将点(2,80),(5,110)代入,得 2 80,5 0.解得 0, 60.∴y= 0x+60(2≤x≤6).(5分)(3)设甲机器改变工作效率后y=mx+n(m≠0). 将点(4,80),(5,110)代入,得4 80,5 0.解得0, -40. ∴y= 0x -40(4≤x≤6).当x=6时,y 甲= 0×6-40=140,y 乙= 0×6+60= 20, ∴y 甲+y 乙=140+120=260.所以这批零件的总个数为260个.(8分) 22.解析 猜想:AF=DE.(2分) 探究:AF=DE.证明:∵EF⊥CE,∴∠CEF=90°. ∴∠ +∠2=90°.∵四边形ABCD 为矩形, ∴∠A=∠D=90°,AB=CD.∴∠2+∠ =90°. ∴∠ =∠ .∵AE=AB,∴AE=DC. ∴△AEF≌△DCE. ∴AF=DE.(6分)应用:∵AF=DE=AD -AE=5-2= ,∴BF=AF -AB=3-2=1. 在矩形ABCD 中,AD∥BC,∴△FBG∽△FAE. ∴ =,即 2=.∴BG=2.(9分)23.解析 ( )∵△ABC 为等边三角形, ∴∠BAC=∠B=∠C=60°. ∵PE∥BC,∴∠APE=∠B=60°,∠AEP=∠C=60°, ∴△APE 为等边三角形. ∴PE=AP=x(0<x<6).(2分) (2)∵四边形PEDF 为菱形, ∴PE=ED,∵PE=AE,∴ED=AE, ∴∠EAD=∠ADE.∵△ABC 为等边三角形,AD⊥BC 于点D, ∴∠EAD=∠ADE= 0°,∠ADC=90°, ∴∠CDE=∠C=60°,∴EC=ED=x. ∵AC=6,∴AE+EC=6. ∴x+x=6,∴x= .(5分)(3)当0<x≤ 时,如图①,y=x· 2·(6-x)=-2x 2+3 x; 当3<x<6时,如图②,y=2( +x)·2(6-x)=-4x 2+4x+92.(8分)图①图②(4)0<x<3- 或3<x<3+.(10分)【提示】如图③~⑤.24.解析( )∵抛物线y=a(x-1)2+4与x轴交于点B(3,0), ∴4a+4=0,解得a=-1.∴这条抛物线所对应的函数表达式为y=-(x-1)2+4,即y=-x2+2x+3.(2分)(2)∵抛物线y=-(x-1)2+4的对称轴为直线x=1,且B(3,0), ∴A(-1,0),当x=0时,y=-(0-1)2+4=3.∴C(0, ).∵B( ,0),C(0, ),∴射线BC所对应的函数表达式为y=-x+ (x≤ ).∵点P在抛物线y=-x2+2x+3上,∴P(m,-m2+2m+ ).∵PQ⊥y轴,∴Q(m2-2m,-m2+2m+3).当- ≤m<0时,如图①,图①d=m2-2m-m=m2-3m;当0<m<3时,如图②,d=m-(m2-2m)=-m2+3m.(6分)图②图③( )∵边PF被y轴平分,如图③,∴线段PQ被y轴平分,∴点P与点Q关于y轴对称.∴m+m2-2m=0,解得m1=0,m2=1.∵点P不与点C重合,∴m= .当m=1时,d=-12+ × =2.(8分)(4)2,1+,1+,2 4.(12分)2【提示】如图④~⑦.11。

2014-2015学年吉林省长春汽车开发区七年级（下）期末数学试卷一、选择题：每小题2分，共16分．1．（2分）9的算术平方根是（）A．±3 B．﹣3 C．3 D．92．（2分）方程2x﹣1=5的解是（）A．x=3 B．x=2 C．x=﹣3 D．x=﹣23．（2分）下列四个图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．4．（2分）下列多边形中，能够铺满地面的是（）A．正五边形B．正六边形C．正七边形D．正八边形5．（2分）把不等式组的解集表示在数轴上，正确的是（）A．B．C．D．6．（2分）设n为正整数，且n＜＜n+1，则n的值为（）A．2 B．3 C．4 D．57．（2分）已知，如图，△ABC中，∠B=∠DAC，则∠BAC和∠ADC的关系是（）A．∠BAC＜∠ADC B．∠BAC=∠ADC C．∠BAC＞∠ADC D．不能确定8．（2分）如图，将△ABC绕点A逆时针旋转一定角度，得到△ADE，且AD⊥BC．若∠CAE=65°，∠E=60°，则∠BAC的大小为（）A．60°B．75°C．85°D．95°二、填空题：每小题3分，共21分．9．（3分）﹣27的立方根是．10．（3分）当x=时，代数式2（x﹣2）﹣3的值等于﹣9．11．（3分）在一个直角三角形中，有一个锐角等于30°，则另一个锐角的大小为度．12．（3分）已知三角形的三边长分别为2、a、4，那么a的取值范围是．13．（3分）在五边形ABCDE中，如果∠A+∠B+∠C+∠D=430°，则∠E的大小为度．14．（3分）如图，在△ABC中，∠B=90°，AB=10．将△ABC沿着BC的方向平移至△DEF，若平移的距离是6，则图中阴影部分的面积为．15．（3分）如图，∠BAC=40°，直线l⊥AC，l与AB交于点D，将∠BAC沿直线l 翻折，点A落在AC边上点F处，则∠BDF的大小为度．三、解答题：共9小题，共63分．16．（6分）在数轴上画出表示下列各数的点：，，．17．（6分）如图，在8×8的正方形网格中，每个小正方形的边长为1，△ABC 的三个顶点均在格点上．（1）作△ABC关于直线MN的对称图形A′B′C′．（2）求△ABC的面积．18．（6分）课外活动中一些学生分组参加活动，原来每组6人，后来重新编组，每组10人，这样比原来减少4组．问这些学生共有多少人？19．（7分）已知方程组的解是方程3x+my=33的一个解．（1）求x，y的值．（2）求m的值．20．（7分）在一个正多边形中，一个内角是它相邻的一个外角的3倍．（1）求这个多边形的每一个外角的度数．（2）求这个多边形的边数．21．（7分）如图，在△ABC中，∠ACB=90°，D为AB边上一点，∠BCD=35°，∠BDC=80°．求∠A的度数．对于上述问题，在以下解答过程的空白处填上适当的内容（理由或数学式）．解：∵∠BCD+∠BDC+∠B=180°（）∴∠B=180°﹣∠BCD﹣∠BDC（等式性质）=180°﹣35°﹣=．∵在△ABC中，∠ACB=90°（已知）．∴∠A+ =90°（）∴∠A=90°﹣=．22．（7分）如图，CD⊥AB于点D，BE⊥AC于点E，△ABE≌△ACD，∠C=42°，AB=9，AD=6，G为AB延长线上一点．（1）求∠EBG的度数．（2）求CE的长．23．（8分）如图，长方形ABCD中，AB=CD=10cm，BC=AD=8侧面，动点P从点A出发，沿A→B→C→D路线运动到D停止，动点Q从点D出发，沿D→C→B→A 路线运动到A停止．若P、Q同时出发，点P速度为2cm/s，点Q速度为1cm/s，6s后点Q改变速度为2cm/s，点P速度不变．（1）求点P出发几秒后到达终点D．（2）求点Q出发几秒后到达终点A．（3）直接写出当点Q出发几秒时，点P、Q在运动路线上相距的路程为25cm．24．（9分）将一块直角三角板DEF放置在锐角△ABC上，使得该三角板的两条直角边DE、DF恰好分别经过点B、C．（1）如图①，若∠A=40°时，点D在△ABC内，则∠ABC+∠ACB=度，∠DBC+∠DCB=度，∠ABD+∠ACD=度；（2）如图②，改变直角三角板DEF的位置，使点D在△ABC内，请探究∠ABD+∠ACD与∠A之间存在怎样的数量关系，并验证你的结论．（3）如图③，改变直角三角板DEF的位置，使点D在△ABC外，且在AB边的左侧，直接写出∠ABD、∠ACD、∠A三者之间存在的数量关系．2014-2015学年吉林省长春汽车开发区七年级（下）期末数学试卷参考答案与试题解析一、选择题：每小题2分，共16分．1．（2分）9的算术平方根是（）A．±3 B．﹣3 C．3 D．9【解答】解：∵32=9，∴9的算术平方根是3．故选：C．2．（2分）方程2x﹣1=5的解是（）A．x=3 B．x=2 C．x=﹣3 D．x=﹣2【解答】解：方程2x﹣1=5，移项合并得：2x=6，解得：x=3，故选：A．3．（2分）下列四个图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．【解答】解：A、不是轴对称图形，是中心对称图形．故错误；B、不是轴对称图形，是中心对称图形．故错误；C、不是轴对称图形，是中心对称图形．故错误；D、是轴对称图形，也是中心对称图形．故正确．故选：D．4．（2分）下列多边形中，能够铺满地面的是（）A．正五边形B．正六边形C．正七边形D．正八边形【解答】解：正六边形的每个内角是120°，能整除360°，能密铺；正五边形，正七边形，正八边形的一个内角不能整除360°，所以都不能单独进行密铺．故选：B．5．（2分）把不等式组的解集表示在数轴上，正确的是（）A．B．C．D．【解答】解：，由①得，x＜1，由②得，x＞0.5，故不等式组的解集为：0.5＜x＜1．在数轴上表示为：．故选：C．6．（2分）设n为正整数，且n＜＜n+1，则n的值为（）A．2 B．3 C．4 D．5【解答】解：∵，∴3＜＜4，∵n＜＜n+1，∴n=3，故选：B．7．（2分）已知，如图，△ABC中，∠B=∠DAC，则∠BAC和∠ADC的关系是（）A．∠BAC＜∠ADC B．∠BAC=∠ADC C．∠BAC＞∠ADC D．不能确定【解答】解：由三角形的外角性质，∠ADC=∠B+∠BAD，∵∠BAC=∠BAD+∠DAC，∠B=∠DAC，∴∠BAC=∠ADC．故选：B．8．（2分）如图，将△ABC绕点A逆时针旋转一定角度，得到△ADE，且AD⊥BC．若∠CAE=65°，∠E=60°，则∠BAC的大小为（）A．60°B．75°C．85°D．95°【解答】解：∵△ABC绕点A逆时针旋转得到△ADE，∴∠C=∠E=60°，∠BAC=∠DAE，∵AD⊥BC，∴∠AFC=90°，∴∠CAF=90°﹣∠C=90°﹣60°=30°，∴∠DAE=∠CAF+∠EAC=30°+65°=95°，∴∠BAC=∠DAE=95°．故选：D．二、填空题：每小题3分，共21分．9．（3分）﹣27的立方根是﹣3．【解答】解：∵（﹣3）3=﹣27，∴=﹣3故答案为：﹣3．10．（3分）当x=﹣1时，代数式2（x﹣2）﹣3的值等于﹣9．【解答】解：根据题意得：2（x﹣2）﹣3=﹣9，去括号得：2x﹣4﹣3=﹣9，解得：x=﹣1，故答案为：﹣111．（3分）在一个直角三角形中，有一个锐角等于30°，则另一个锐角的大小为60度．【解答】解：∵三角形是直角三角形，一个锐角等于30°，∴另一个锐角为90°﹣30°=60°，故答案为：60．12．（3分）已知三角形的三边长分别为2、a、4，那么a的取值范围是2＜a ＜6．【解答】解：∵三角形的三边长分别为2、a、4，∴4﹣2＜a＜4+2，即2＜a＜6．13．（3分）在五边形ABCDE中，如果∠A+∠B+∠C+∠D=430°，则∠E的大小为110度．【解答】解：正五边形的内角和为（5﹣2）×180°=540°，∵∠A+∠B+∠C+∠D=430°，∴∠E=540°﹣430°=110°，故答案为：110．14．（3分）如图，在△ABC中，∠B=90°，AB=10．将△ABC沿着BC的方向平移至△DEF，若平移的距离是6，则图中阴影部分的面积为60．【解答】解：∵直角△ABC沿BC边平移6个单位得到直角△DEF，∴AC=DF，AD=CF=6，∴四边形ACFD为平行四边形，∴S=CF•AB=6×10=60，平行四边形ACFD即阴影部分的面积为60．故答案为60．15．（3分）如图，∠BAC=40°，直线l⊥AC，l与AB交于点D，将∠BAC沿直线l 翻折，点A落在AC边上点F处，则∠BDF的大小为80度．【解答】解：∵将∠BAC沿直线l翻折，点A落在AC边上点F处，∴∠DFA=∠A=40°，∴∠BDF=∠A+∠DFA=80°，故答案为：80．三、解答题：共9小题，共63分．16．（6分）在数轴上画出表示下列各数的点：，，．【解答】解：=2，=4，=3，如图，17．（6分）如图，在8×8的正方形网格中，每个小正方形的边长为1，△ABC 的三个顶点均在格点上．（1）作△ABC关于直线MN的对称图形A′B′C′．（2）求△ABC的面积．【解答】解：（1）如图；（2）S==3．△ABC18．（6分）课外活动中一些学生分组参加活动，原来每组6人，后来重新编组，每组10人，这样比原来减少4组．问这些学生共有多少人？【解答】解：设这些学生共有x人，根据题意，得﹣=4．解得x=60．答：这些学生共有60人．19．（7分）已知方程组的解是方程3x+my=33的一个解．（1）求x，y的值．（2）求m的值．【解答】解：（1），将①代入②，得5x﹣2x=9，解得x=3．把x=3代入①，得y=6．∴方程组的解；（2）把x=3，y=6代入3x+my=33，得3×3+6m=33．解得m=4．20．（7分）在一个正多边形中，一个内角是它相邻的一个外角的3倍．（1）求这个多边形的每一个外角的度数．（2）求这个多边形的边数．【解答】解：（1）设这个多边形的每一个外角的度数为x度．根据题意，得：3x+x=180，解得x=45．故这个多边形的每一个外角的度数为45°；（2）360°÷45°=8．故这个多边形的边数为8．21．（7分）如图，在△ABC中，∠ACB=90°，D为AB边上一点，∠BCD=35°，∠BDC=80°．求∠A的度数．对于上述问题，在以下解答过程的空白处填上适当的内容（理由或数学式）．解：∵∠BCD+∠BDC+∠B=180°（三角形的内角和等于180°）∴∠B=180°﹣∠BCD﹣∠BDC（等式性质）=180°﹣35°﹣80°=65°．∵在△ABC中，∠ACB=90°（已知）．∴∠A+ ∠B=90°（直角三角形的两个锐角互余）∴∠A=90°﹣65°=25°．【解答】解：∵∠BCD+∠BDC+∠B=180°（三角形的内角和等于180°），∴∠B=180°﹣∠BCD﹣∠BDC（等式的性质）=180°﹣35°﹣80°=65°．∵在△ABC中，∠ACB=90°（已知），∴∠A+∠B=90°（直角三角形的两个锐角互余）．∴∠A=90°﹣65°（或填∠B）=25°．22．（7分）如图，CD⊥AB于点D，BE⊥AC于点E，△ABE≌△ACD，∠C=42°，AB=9，AD=6，G为AB延长线上一点．（1）求∠EBG的度数．（2）求CE的长．【解答】解：（1）∵△ABE≌△ACD，∴∠EBA=∠C=42°，∴∠EBG=180°﹣42°=138°；（2）∵△ABE≌△ACD，∴AC=AB=9，AE=AD=6，∴CE=AC﹣AE=9﹣6=3．23．（8分）如图，长方形ABCD中，AB=CD=10cm，BC=AD=8侧面，动点P从点A出发，沿A→B→C→D路线运动到D停止，动点Q从点D出发，沿D→C→B→A 路线运动到A停止．若P、Q同时出发，点P速度为2cm/s，点Q速度为1cm/s，6s后点Q改变速度为2cm/s，点P速度不变．（1）求点P出发几秒后到达终点D．（2）求点Q出发几秒后到达终点A．（3）直接写出当点Q出发几秒时，点P、Q在运动路线上相距的路程为25cm．【解答】解：（1）∵（10+8+10）÷2=28÷2=14（秒）．∴点P出发14秒后到达终点D．（2）设点Q出发x秒后到达终点A，则1×6+2（x﹣6）=10+8+10，整理，可得2x﹣6=28，解得x=17，∴点Q出发17秒后到达终点A．（3）①如图1，，当点P、Q相遇前在运动路线上相距的路程为25cm时，即当点P到达点E，点Q到达点F时，∵（10+8+10﹣25）÷（2+1）=3÷3=1（秒）∴当点Q出发1秒时，点P、Q在运动路线上相距的路程为25cm．②如图2，，当点P、Q相遇后在运动路线上相距的路程为25cm时，由（1），可得点P出发14秒后到达终点D，由（2），可得点Q出发17秒后到达终点A，∴当点P到达终点D，点Q运动的路程是25cm时，即点Q到达点E，点P、Q 在运动路线上相距的路程为25cm，设点Q运动t秒后运动的路程是25cm，则1×6+2（t﹣6）=25，整理，可得2x﹣6=25，解得x=15.5，∴当点Q出发15.5秒时，点P、Q在运动路线上相距的路程为25cm．综上，可得当点Q出发1秒或15.5秒时，点P、Q在运动路线上相距的路程为25cm．24．（9分）将一块直角三角板DEF放置在锐角△ABC上，使得该三角板的两条直角边DE、DF恰好分别经过点B、C．（1）如图①，若∠A=40°时，点D在△ABC内，则∠ABC+∠ACB=140度，∠DBC+∠DCB=90度，∠ABD+∠ACD=50度；（2）如图②，改变直角三角板DEF的位置，使点D在△ABC内，请探究∠ABD+∠ACD与∠A之间存在怎样的数量关系，并验证你的结论．（3）如图③，改变直角三角板DEF的位置，使点D在△ABC外，且在AB边的左侧，直接写出∠ABD、∠ACD、∠A三者之间存在的数量关系．【解答】解：（1）在△ABC中，∵∠A=40°，∴∠ABC+∠ACB=180°﹣40°=140°，在△DBC中，∵∠BDC=90°，∴∠DBC+∠DCB=180°﹣90°=90°，∴∠ABD+∠ACD=140°﹣90°=50°；故答案为：140；90；50．（2）∠ABD+∠ACD与∠A之间的数量关系为：∠ABD+∠ACD=90°﹣∠A．证明如下：在△ABC中，∠ABC+∠ACB=180°﹣∠A．在△DBC中，∠DBC+∠DCB=90°．∴∠ABC+∠ACB﹣（∠DBC+∠DCB）=180°﹣∠A﹣90°．∴∠ABD+∠ACD=90°﹣∠A．（3）∠ACD﹣∠ABD=90°﹣∠A．初中数学几何模型【模型二】半角型：图形特征：45°4321A1FB正方形ABCD 中，∠EAF =45° ∠1=12∠BAD 推导说明：1.1在正方形ABCD 中，点E 、F 分别在BC 、CD 上，且∠FAE ＝45°，求证：EF ＝BE +DF45°DEa +b-a45°A1.2在正方形ABCD 中，点E 、F 分别在BC 、CD 上，且EF ＝BE +DF ，求证：∠FAE ＝45°DEa +b-aa45°ABE挖掘图形特征：a+bb x-aa 45°D Ba +b-a45°A运用举例：1．正方形ABCD 的边长为3，E 、F 分别是AB 、BC 边上的点,且∠EDF =45°.将△DAE 绕点D 逆时针旋转90°，得到△DCM . （1）求证：EF =FM（2）当AE =1时，求EF 的长．DE2.如图，△ABC 是边长为3的等边三角形，△BDC 是等腰三角形，且∠BDC =120°．以D 为顶点作一个60°角，使其两边分别交AB 于点M ，交AC 于点N ，连接MN ，求△AMN 的周长．ND CABM3．如图，梯形ABCD中，AD∥BC，∠C＝90°，BC＝CD＝2AD＝4，E为线段CD上一点，∠ABE＝45°.（1）求线段AB的长；（2）动点P从B出发，沿射线．．BE运动，速度为1单位/秒，设运动时间为t，则t为何值时，△ABP为等腰三角形；（3）求AE－CE的值.变式及结论：4.在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°．（1）将△ADF绕着点A顺时针旋转90°，得到△ABG（如图1），求证：△AEG≌△AEF；（2）若直线EF与AB，AD的延长线分别交于点M，N（如图2），求证：EF2=ME2+NF2；（3）将正方形改为长与宽不相等的矩形，若其余条件不变（如图3），请你直接写出线段EF ，BE ，DF 之间的数量关系．ABFEDCF。

吉林省长春汽车经济技术开发区2014-2015学年七年级数学下学期期末考试试题2014—2015学年度第二学期期末教学质量跟踪测试七年级数学参考答案一、选择题（每小题2分，共16分）1．B 2．A 3．B 4．A 5．C 6．B 7．B 8．D二、填空题（每小题3分，共21分）9．-3 10．-2 11．60 12．2<a <6 13．110 14．60 15．80三、解答题（本大题共9小题，共63分）16．（6分）（每个点2分，不写点上面对应的数字整体扣1分）17． （1）（4分）（每个对应点1分，所有对应字母1分） （2）△ABC 的面积为：.3232=⨯ （6分） 18.设这些学生共有x 人，根据题意，得 （1分）4106=-x x . （4分） 解得x =60. （6分）答：这些学生共有60人.19． （1）⎩⎨⎧=-=.95,2y x y x 将①代入②，得925=-x x ，解得3=x ． （2分）把3=x 代入①，得6=y ． （3分）∴⎩⎨⎧==.6,3y x （4分） （2）把3=x ，6=y 代入333=+my x ，得33633=+⨯m ． （6分）解得4=m ． （7分）20．（1）设这个多边形的每一个外角的度数为x 度.根据题意，得（1分）3x +x =180. （3分）解得x =45. （5分）∴这个多边形的每一个外角的度数为45°．（2）360°÷45°=8．∴这个多边形的边数为8． （7分）•••38169-A ′ B ′ C ′M A B C N② ①21．∵∠BCD +∠BDC +∠B=180°（三角形的内角和等于180° ），∴∠B=180°-∠BCD -∠BDC （等式的性质）=180°-35°- 80°= 65° ．∵在△ABC 中，∠ACB=90°（已知），∴∠A + ∠B =90°（直角三角形的两个锐角互余）．∴∠A=90°- 65° （或填∠B ） = 25° ．（每空1分）22．（1）∵△ABE ≌△ACD ，∴∠EBA=∠C=42°． （2分）∴∠EBG=180°-42°=138°． （4分）（2）∵△ABE ≌△ACD ，∴AC =AB=9，AE =AD=6． （6分）∴CE = AC - AE=9-6=3． （7分）23．（1）142)10810(=÷++（秒）．∴点P 出发14秒后到达终点D ． （3分）（2）设点Q 出发x 秒后到达终点A ，根据题意，得108102)6(61++=⨯-+⨯x ． （5分）解得x =17.∴点Q 出发17秒后到达终点A ． （6分）（3）1秒或15.5秒． （8分）24．（1）140；90；50． （3分）（每空1分）（2）∠ABD+∠ACD 与∠A 之间的数量关系为：∠ABD+∠ACD =90°-∠A ．证明如下：在△ABC 中，∠ABC+∠ACB=180°-∠A ． （4分）在△DBC 中，∠DBC +∠DCB =90°． （5分）∴∠ABC+∠ACB -（∠DBC +∠DCB ）=180°-∠A -90°．∴∠ABD+∠ACD =90°-∠A ． （7分）（3）∠ACD -∠ABD =90°-∠A ． （9分）。

学校 班级 姓名 座号 成绩 ……………………密……………………封……………………装……………………订……………………线……………………初中数学总复习（一)(数与式)一.选择题（每题3分，共21分） 1.-2的相反数是【 】 A ． B ．C ．D ．2.下列各式计算正确的是【 】A ．（a 2）2=a 4B ．a+a=a 2C ．3a 2+a 2=2a 2D ．a 4•a 2=a 83.第六次全国人口普查公布的数据表明，登记的全国人靠数量约为1 340 000 000人．这个数据用科学记数法表示为【 】A ．134×107人B ．13.4×108人C ．1.34×109人D ．1.34×1010人4.已知a 、b 在数轴上的位置如图，则a+b ，a-b ，b-a ，-a-b 中，最大的数是【 】（第4题图）A ．a+bB ．a-bC ．b-aD ．-a-b 5.若x<5，则的值为【】A ．-1B ．0C ．1D ．2 6.在化简时，甲、乙两位同学的解答如下： 【 】A.两人解法都对B.甲错乙对C.甲对乙错D.两人都错 7.已知a+=b+=c+，且a ≠b ≠c ，则a 2b 2c 2=【 】A. 5B. 3.5C. 1D. 0.5二.填空题（每题4分，共40分）8.数轴上点A表示－3，那么到点A的距离是4个单位长的点表示的数是__________.9.=___________．10.若x＋y＝3，xy＝1，则x2＋y2＝．11.有理数a，b，c在数轴上的位置如图所示，化简：|a-c|-|a-b|-|b-c|+|2a|=______．（第11题图）12.若分式的值为0，则x的值等于______________.13.已知，其中A，B，C，D为常数，则A=_________.14.写出一个大于3且小于4的无理数：___________．15.已知a为的整数部分，b为的小数部分，（0<b<1），则=___________．16.把数字按如图所示排列起来，从上开始，依次为第一行、第二行、第三行……，中间用虚线围的一列，从上至下依次为1、5、13、25、…，则第10个数为．17.勾股定理揭示了直角三角形三边之间的关系，其中蕴含着丰富的科学知识和人文价值，如图所示是一棵由正方形和含30°角的直角三角形按一定规律长成的勾股树，树主干自下而上第一个正方形和第一个直角三角形的面积之和为S1，第二个正方形和第二个直角三角形的面积之和为S2，…，第n个正方形和第n个直角三角形的面积之和为S n，设第一个正方形的边长为1。

２０１４长春初中毕业生试测试题数 学本试卷包括三道大题，共24小题.共6页．全卷满分120分．考试时间为120分钟．考试结束后，将本试卷和答题卡一并交回． 注意事项：1．答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形码区域内．2．答题时，考生务必按照考试要求在答题卡上的指定区域内作答，在草稿纸、试题卷上答题无效．一、选择题（每小题3分，共24分）1．下列各数0，1-，4，512-中，最小的数是 （A ）0. （B ）4. （C ）1-. （D ）512-.（A ）235a a a +=. （B ）54a a a -=. （C ）4520a a a ⋅=. （D ）1234a a a ÷=. 4．不等式3x ≥﹣6的解集在数轴上表示为（A ） （B ） （C ） （D ）5．如图，BD 平分∠ABC ，点E 在BC 上，EF ∥AB ．若∠ABD =50°，则∠BEF 的大小为 （A ）100°． （B ）90°． （C ）80°． （D ）70°（第5题） （第6题）6．如图，在ABC △中，6070B C ∠=︒∠=︒，．以AB 为直径的⊙O 交AC 于点D ，则BOD∠的大小为ADFBECCBODA（第14题）（A ）130°． （B ）120°． （C ）110°． （D ）100°． 7．如图，在□ABCD 中，点E 、F 分别为边AD 、BD 上的点，EF ∥AB ．若EA DE 21=，EF =4，则CD 的长为（A ）6． （B ）8． （C ）12． （D ）16．（第7题） （第8题）8．如图，在平面直角坐标系中，点P （12-，a ）在直线22y x =+与直线24y x =+之间，则a 的取值范围是（A ）2＜a ＜4． （B ）1＜a ＜3． （C ）1＜a ＜2． （D ）0＜a ＜2．二、填空题（每小题3分，共18分）9．分解因式：2218x -= .10．买单价为3元的笔记本m 本，付出n 元，应找回 元.（用含有m 、n 的代数式表示）11．如图，在⊙O 中，OC ⊥弦AB 于点C ．若AB =4，OC =1，则OB 的长是为 .（第11题） （第12题） （第13题）12．如图，在平面直角坐标系中，矩形ABCD 的对称轴与坐标轴重合，顶点A 的坐标为（3，2）.若反比例函数ky x=的图象经过点B ，则k 的值为_______． 13．如图，边长为6的大正方形中有两个小正方形，小正方形的各顶点均在大正方形的边或对角线上.若两个小正方形的面积分别为S 1、S 2，则S 1与S 2的和为 . 14．如图，在平面直角坐标系中，Rt △OAB 的顶点A （-2，4）在抛物线2y ax =上，直角顶点B 在x 轴上．将Rt △OAB 绕点O 顺时 针旋转90°得到△OCD ，边CD 与该抛物线交于点P ．则DP 的长为 .AD FE C2三、解答题（本大题共10小题，共78分）15．（6分）先化简，再求值: 2211()1121x x x x x x x +++÷---+，其中x = 16．（6分）把大小和形状完全相同的6张卡片分成两组，每组3张，卡片上分别标有数字1，2，3，将这两组卡片分别放入两个盒子中搅匀，再从每个盒中各随机抽取1张．用画树状图（或列表）的方法求抽出的2张卡片上数字之和为奇数的概率.17．（6分）春城服装店用4 500元购进一批某款式T 恤衫，由于深受顾客喜爱，很快售完，又用4 950元购进第二批该款式T 恤衫，所购数量与第一批相同，但每件进价比第一批多了9元，求第二批该款式T 恤衫每件进价.18．（7分）如图，D 为△ABC 边BC 延长线上一点，且CD ＝CA ，E 是AD 的中点，CF平分∠ACB 交AB 于点F ．求证：CE ⊥CF ．ADFBEC （第18题）19．（7分）某超市利用一个带斜坡的平台装卸货物，其纵断面ACFE 如图所示． AE 为台面，AC 垂直于地面，AB 表示平台前方的斜坡．斜坡的坡角∠ABC 为43°,坡长AB 为2m ．为保障安全，又便于装卸货物，决定减小斜坡AB 的坡角，AD 是改造后的斜坡（D 在直线BC 上），坡角∠ADC 为31°．求斜坡AD 底端D 与平台AC 的距离CD ．（结果精确到0.01m ）【参考数据：sin43°=0.682，cos43°=0.731，tan43°=0.933；sin31°=0.515，cos31°=0.857，tan31°=0.601】（第19题）20.（7分）某校就同学们对“长春历史文化”的了解程度进行随机抽样调查，将调查结果绘制成如下两幅统计图．被调查学生对“长春历史文化” 被调查学生对“长春历史文化” 了解程度情况条形统计图 了解程度情况扇形统计图(1)本次共凋查 名学生. (2)求条形统计图中m 的值.(3)若该校共有学生1 000名，按上述统计结果，估计该校不了解“长春历史文化”的学生人数.AD31°BEC43°F21．（8分）在一条笔直的公路上有A 、B 两地.甲、乙两人同时出发，甲骑电动车从A 地到B 地，中途出现故障后停车维修,修好车后以原速继续行驶到B 地；乙骑摩托车从B 地到A 地，到达A 地后立即按原路原速返回，结果两人同时到B 地.下图是甲、乙两人与B 地的距离y (km )与乙行驶时间x (h)之间的函数图象. (1) 求甲修车前的速度. (2)求甲、乙第一次相遇的时间.(3)若两人之间的距离不超过10km 时，能够用无线对讲机保持联系，请直接写出乙在行进中能用无线对讲机与甲保持联系的x 取值范围.（第21题）22．（9分）【感知】如图①，四边形ABCD 、CEFG 均为正方形.可知BE=DG .【拓展】如图②，四边形ABCD 、CEFG 均为菱形，且∠A=∠F .求证：BE=DG . 【应用】如图③，四边形ABCD 、CEFG 均为菱形，点E 在边AD 上,点G 在AD 延长线上.若AE =2ED ，∠A=∠F ，△EBC 的面积为8，则菱形CEFG 的面积为 .图① 图② 图③（第22题）甲 乙yABCDE FGA BCDE FGCDEFG A23．（10分）如图，在平面直角坐标系中，点A 在y 轴的正半轴上，点B 在第一象限，点C 的坐标为（3，0）．AB //x 轴，且OA =AB ，抛物线22y ax bx =++经过点A 、B 、C ．连 结BC ，过点B 作BD ⊥BC ，交OA 于点D ．将∠CBD 绕点B 按顺时针方向旋转得到∠EBF ，角的两边分别交x 轴的正半轴、y 轴的正半轴于E 、F ． （1）求a 、b 的值.（2）当直线BF 经过抛物线22y ax bx =++的顶点时，求CE 的长.（3）连结EF .设△BEF 与△BEC 的面积之差为S .当CE 为何值时S 最小，求出这个最小值．（第23题）24．（12分）将Rt △ABC 和Rt △DEF 按如图①摆放（点C 与点E 重合），点B 、C （E ）、F 在同一条直线上．△ABC 沿EF 所在直线以每秒1 个单位的速度向右匀速运动，AC 边与折线ED —DF 的交点为P ，如图②.当△ABC 的边AB 经过点D 时，停止运动．已知∠ACB = ∠EDF = 90°，∠DEF = 45°，AC = 4，BC =3 ，EF =6 ．设运动时间为t （秒）．（1）当点P 在ED 边上时，AP 的长为 （用含t 的代数式表示）． （2）当边AB 经过点D 时，求t 的值．（3）设△ABC 与△DEF 的重叠部分的面积为S ，求S 与t 的函数关系．（4）在△ABC 运动的同时，点Q 从△ABC 的顶点B 出发，沿B —A —B 以每秒2个单位的速度匀速运动，当△ABC 停止运动时，点Q 也随之停止. ①当PQ ⊥AB 时，求t 的值．②当以A 、P 、Q 为顶点的四边形APGQ 为菱形时，直接写出菱形APGQ 的周长．图① 图②（第24题）AFDADFP数学参考答案及评分标准一、选择题（本大题共8小题，每小题3分，共24分） 1．C 2．D 3．B 4．A 5．C 6．D 7．C 8．B 二、填空题（本大题共6小题，每小题3分，共18分）9．2（x +3）(x -3) 10．(3)n m - 11．5 12．– 6 13．17 14．2 三、解答题（本大题共10小题，共78分）15．原式=21(1)()111x x x x x -+⨯--+= 21(1)11x x x x +-⨯-+=1x -. （4分）当x =2时，原式=1x -=21-. （6分） 16．（4分）∴(49P 和为奇数）＝ （6分） 17．设第二批T 恤衫每件进价x 元． （1分）依题意，得450049509x x=-. （4分） 解得 99x =．经检验，99x =是原方程的解，且符合题意．答：第二批T 恤衫每件进价是99元． （6分） 18. ∵CD ＝CA ，E 是AD 的中点，∴∠ACE =∠DCE . （3分） ∵CF 平分∠ACB ， ∴∠ACF =∠BCF .∵∠ACE +∠DCE +∠ACF +∠BCF =180°， （5分）12312 3 4 2 3 4 5 3456一二和∴∠ACE +∠ACF =90°.即∠ECF =90°. （6分） ∴CE ⊥CF ． （7分） 19．在（4分）在 2.27≈. （7分）20．（1 （2分） （2）m =60-12-24-6=18. （4分） （3）60人中有12人不了解长春历史文化，估计全校1000人中不了解长春历史文化的占20%， 1000×20%=200.估计全校1 000人中不了解长春历史文化的人约为200人. （7分） 21.（1）130(2)202÷-=（km/h ）.∴甲修车前的速度为20km/h. (2分)（2）(3020)30x += ， 解得0.6x =.∴甲、乙第一次相遇是在出发后0.6小时. （5分） （3）257,2566x x ≤≤≤≤. （8分） 22．拓展：∵四边形ABCD 、四边形CEFG 均为正方形， ∴BC =CD ，CE =CG ，∠BCD =∠A ，∠ECG =∠F . ∵∠A =∠F ， ∴∠BCD =∠ECG .∴∠BCD -∠ECD =∠ECG -∠ECD ， 即∠BCE =∠DCG . ∴△BCE ≌△DCG .∴BE =DG . （6分） 应用：643. （9分） 23．（1）根据题意，B （2，2），C （3，0），则有4222,9320.a b a b ++=⎧⎨++=⎩解得2,34.3a b ⎧=-⎪⎪⎨⎪=⎪⎩（4分）（2）经过A 、B 、C 的抛物线为224233y x x =-++.顶点G 的坐标为（1，83）， 过点G 作GH ⊥AB 于点H ，则AH =BH =1，GH =82233-=. 过点B 作BM ⊥OC 于点M . 则四边形ABMO 为正方形. ∴BA =BM .∵∠ABM = ∠EBF =90°， ∴∠EBM =∠FBA . ∵∠BME =∠BAF =90°， ∴△EBM ≌△FBA . ∴EM = AF . ∵tan ∠ABF =AF HGAB HB=， ∴AF =43. ∴EM = A F = 43. 又∵C (3，0)，B （2，2），∴CM =1. ∴CE = CM + EM = 1+4733=． （7分）（3）设CE ＝m ，则EM ＝ m －1或1－ m ， ∴BE 2＝EM 2＋BM 2＝(m －1) 2＋2 2＝m 2－2m ＋5. 又∵△FBA ≌△EBM ，∴BF =BE . ∴S =S △BEF －S △BEC . 即211(2)22S m =-+. 当m = 2时，S 最小 = 12. （10分）24.（1）4－t . （2分）（2）如图，过点D 作DM ⊥EF 于点M ， ∵∠EDF = 90°，∠DEF = 45°， ∴∠DFE = 45°. ∴DE =DF.∵EF =6， ∴DM =EM=MF =3. ∵EC= t ， ∴EB= t －3.∴BM=6－t .当AB 经过点D 时，△DMB ∽△ACB ，∴3463=-t . ∴415=t . （5分）（3）当0≤t≤3时，221t S =当3≤t≤415时，2518272S t t =-+-. （9分）（4）①当PQ ⊥AB 时，△AQP ∽△ACB52445t t -=-或25445t t -=-或25425t t -=-， 解得32t =或4114t =或176t =（舍去）∴23=t ，1441=t .②12或4. （12分）。