机械原理典型例题(第五章凸轮)10-20
- 格式:ppt
- 大小:567.00 KB
- 文档页数:12

Harbin Institute of Technology机械原理大作业二作业名称:凸轮机构设计设计题目: 20 院系:机电工程学院班级:设计者:学号:指导教师:**设计时间: 2014年5月哈尔滨工业大学一、设计题目如图1所示直动从动件盘形凸轮机构,其原始参数见表1。
表1 凸轮机构参数升程/h mm 升程运动角 0/ϕ 升程运动规律 升程许用压力角[]/α 回程运动角 0/ϕ'回程运动规律 回城许用压力角[]/α'远休止角/s ϕ 近休止角/s ϕ' 110 120 正弦加速度 3590 正弦加速度 65 50 100二、运动方程式及运动线图本实验假设凸轮逆时针旋转。
1.确定凸轮机构推杆升程、回程运动方程(ϕ为凸轮转角,ω为凸轮角速度)。
推程(余弦加速度)(203ϕπ≤≤): 图1远休止段:当21738πϕπ≤≤时,110s h==,0v=,0a=回程(正弦加速度)(171389πϕπ≤≤):近休止段:当1329πϕπ≤≤时,0s=,0v=,0a=2.绘制推杆位移、速度、加速度线图图2三、绘制凸轮机构的ds s d ϕ-线图,并由此确定凸轮的基圆半径和偏距图3图4如图3、图4所示,在ds d ϕ轴正侧(对应于推程),以tan(90[])α-为斜率做ds s d ϕ-曲线的切线1L ,在ds d ϕ轴负侧(对应于回程),以tan(90[])α'+为斜率做ds s d ϕ-曲线的切线2L ,再过点(0,0)O 做斜率为tan(90[])α+的直线3L ,则直线1L 、2L 、3L 与s 轴的夹角分别为[]α、[]α'、[]α。
显然,1L 、2L 、3L 三条直线下方的公共部分即为满足推程压力角不超过[]α和回程压力角不超过[]α'时,凸轮回转中心的可取区域。
记直线1L 与2L 的交点为12P ,直线1L 与3L 的交点为13P ,则最小基圆半径013r OP ==45.79mm ,对应的偏距e =26.27mm (点13P 到s 轴的距离),2200s r e =-=37.51mm 。

凸轮机构设计 题目要求:试用计算机辅助设计完成下列偏置直动推杆盘形凸轮机构的设计,已知数据如下各表所示。
凸轮沿逆时针方向作匀速转动。
表一 偏置直动滚子推杆盘形凸轮机构的已知参数升程/mm 升程运动角/。
升程运动规律 升程许用压力角/。
回程运动角/。
回程运动规律 回程许用压力角/。
远休止角/。
近休止角/。
70 120 余弦加速度 35 90 正弦加速度65 60 90要求:1)确定凸轮推杆的升程、回程运动方程,并绘制推杆位移、速度、加速度线图。
2)绘制凸轮机构的sd ds -ϕ线图;3)确定凸轮基圆半径和偏距;4)确定滚子半径;5)绘制凸轮理论廓线和实际廓线。
推杆运动规律:(取32w π=) 1)推程运动规律:由余弦加速度运动公式可得⎥⎦⎤⎢⎣⎡-=)cos(1211θπψh s)sin(2hw v111θπϕθπ=)cos(2h 112122θπϕθπw a = 2)回程运动规律:正弦加速度运动公式可得⎥⎦⎤⎢⎣⎡+-=)2sin(211322T h s Tθππθ ⎥⎦⎤⎢⎣⎡--=)2cos(1v322T hw θπθ )2sin(2a32222T hw θπθπ-=试中:T=)(s θθϕ+1- 经带入计算可得:s1 = 0.035*(1 - cos(1.5*x));v1=0.105/2 * w * sin(1.5 * x);a1 = 0.1575/2 * w^2 .* cos(1.5*x);s3 = 0.070*(3 - 2*z/pi + 1/(2*pi).*sin (4*z - 4* pi));v3 = -0.140/pi * w .* (1 - cos(4*z - 4* pi));a3 = 0.56 * w^2/pi .*sin(4*z - 4* pi);三 计算程序(matlab )(1)推杆位移、速度、加速度线图编程;a.位移与转角曲线w = 2*pi/3x = 0:(pi/100):(2*pi/3);s1 = 0.035*(1 - cos(1.5*x));v1=0.105/2 * w * sin(1.5 * x);a1 = 0.1575/2 * w^2 .* cos(1.5*x);y = (2*pi/3):(pi/100):(pi);s2 = 0.070;v2=0;a2 = 0;z = (pi ):(pi/100):(3*pi/2);s3 = 0.070*(3 - 2*z/pi + 1/(2*pi).*sin (4*z - 4* pi)); v3 = -0.140/pi * w .* (1 - cos(4*z - 4* pi));a3 = 0.56 * w^2/pi .*sin(4*z - 4* pi);c = (3*pi/2):(pi/100):( 2*pi);s4 = 0;v4 = 0;a4 = 0;plot(x,s1,'b',y,s2,'b',z,s3,'b',c,s4,'b')xlabel('转角/rad')ylabel('位移/m/')title('位移与转角曲线')b.速度与转角曲线w = 2*pi/3x = 0:(pi/100):(2*pi/3);s1 = 0.035*(1 - cos(1.5*x));v1=0.105/2 * w * sin(1.5 * x);a1 = 0.1575/2 * w^2 .* cos(1.5*x);y = (2*pi/3):(pi/100):(pi);s2 = 0.070;v2=0;a2 = 0;z = (pi ):(pi/100):(3*pi/2);s3 = 0.07*(3 - 2*z/pi + 1/(2*pi).*sin (4*z - 4* pi)); v3 = -0.140/pi * w .* (1 - cos(4*z - 4* pi));a3 = 0.56 * w^2/pi .*sin(4*z - 4* pi);c = (3*pi/2):(pi/100):( 2*pi);s4 = 0;v4 = 0;a4 = 0;plot(x,v1,'g',y,v2,'g',z,v3,'g ',c,v4,'g')xlabel('转角/rad')ylabel('速度/(m/s)')title('速度与转角曲线')c.加速度与位移转角曲线w = 2*pi/3x = 0:(pi/100):(2*pi/3);s1 = 0.035*(1 - cos(1.5*x));v1=0.105/2 * w * sin(1.5 * x);a1 = 0.1575/2 * w^2 .* cos(1.5*x);y = (2*pi/3):(pi/100):(pi);s2 = 0.070;v2=0;a2 = 0;z = (pi):(pi/100):(3*pi/2);s3 = 0.070*(3 - 2*z/pi + 1/(2*pi).*sin (4*z - 4* pi)); v3 = -0.140/pi * w .* (1 - cos(4*z - 4* pi));a3 = 0.56 * w^2/pi .*sin(4*z - 4* pi);c = (3*pi/2):(pi/100):( 2*pi);s4 = 0;v4 = 0;a4 = 0;plot(x,a1,'r',y,a2,'r',z,a3,'r ',c,a4,'r')xlabel('转角/rad')ylabel('加速度/(m^2/s)')title('加速度与转角曲线')(2)凸轮机构的s d -ϕds 线图编程; w = 2*pi/3x = 0:(pi/100):(2*pi/3);s1 = 35*(1 - cos(1.5*x));news1 = 35*1.5*sin(1.5*x);y = (2*pi/3):(pi/100):(pi);s2 = 70;news2 = 0;z = (pi ):(pi/100):(3*pi/2);s3=70*(3 - 2*z/pi + 1/(2*pi).*sin (4*z - 4* pi));news3 =-140/pi * w .* (1 - cos(4*z - 4* pi));c = (3*pi/2):(pi/100):( 2*pi);s4 = 0;news4 = 0;plot(news1,s1,'b',news2,s2,'b',news3,s3,'b',news4,s4,'b')xlabel('ds/dp');ylabel('(位移s/mm)')title('ds/dp 与位移s 曲线') grid(3)确定基圆半径和偏距;(4)经过对凸轮机构的s d -ϕds 线图分析确定其偏距e=17,s=70,基圆半径r0=32,,得s0=50; a.先求凸轮理论轮廓曲线,程序如下:w = 2*pi/3;s0 = 50;s = 70;e = 17;x = 0:(pi/100):(2*pi/3);x1 = (s + s0)*cos(x)-e*sin(x);y1 = (s0 + s)*sin(x) - e*cos(x);y = (2*pi/3):(pi/100):(pi);x2 = (s + s0)*cos(y)-e*sin(y);y2 = (s0 + s)*sin(y) - e*cos(y);z = (pi):(pi/100):(3*pi/2);x3 = (s + s0)*cos(z)-e*sin(z);y3 = (s0 + s)*sin(z) - e*cos(z);c = (3*pi/2):(pi/100):( 2*pi);x4 = (s + s0)*cos(c)-e*sin(c);y4 = (s0 + s)*sin(c) - e*cos(c);plot(x1,y1,'b',x2,y2,'b',x3,y3,'b',x4,y4,'b');xlabel('x/mm')ylabel('y/mm')title('理轮轮曲线')b.再通过该廓线求其最小曲率半径,程序如下:v=[];syms x1 x2 x3 x4 x5s0 = 50;e = 20;s1 = 35*(1 - cos(1.5*x1));t1 = (s1 + s0)*cos(x1)-e*sin(x1);y1 = (s0 + s1)*sin(x1) - e*cos(x1);tx1=diff(t1,x1);txx1=diff(t1,x1,2);yx1=diff(y1,x1);yxx1=diff(y1,x1,2);for xx1= 0:(pi/100):(2*pi/3);k1=subs(abs((tx1*yxx1-txx1*yx1)/(tx1^2+yx1^2)^1.5),{x1},{xx1}); v=[v,1/k1];ends2 = 70;t2 = (s2 + s0)*cos(x2)-e*sin(x2);y2 = (s0 + s2)*sin(x2) - e*cos(x2);tx2=diff(t2,x2);txx2=diff(t2,x2,2);yx2=diff(y2,x2);yxx2=diff(y2,x2,2);for xx2=(2*pi/3):(pi/100):(pi);k2=subs(abs((tx2*yxx2-txx2*yx2)/(tx2^2+yx2^2)^1.5),{x2},{xx2}); v=[v,1/k2];ends3 = 110*(10/3- 2*x3/pi + 1/(2*pi).*sin (4*x3 - 14* pi/3));t3 = (s3 + s0)*cos(x3)-e*sin(x3);y3 = (s0 + s3)*sin(x3) - e*cos(x3);tx3=diff(t3,x3);txx3=diff(t3,x3,2);yx3=diff(y3,x3);yxx3=diff(y3,x3,2);for xx3=(pi):(pi/100):(3*pi/2);k3=subs(abs((tx3*yxx3-txx3*yx3)/(tx3^2+yx3^2)^1.5),{x3},{xx3}); v=[v,1/k3];ends4 = 0;t4 = (s4 + s0)*cos(x4)-e*sin(x4);y4 = (s0 + s4)*sin(x4) - e*cos(x4);tx4=diff(t4,x4);txx4=diff(t4,x4,2);yx4=diff(y4,x4);yxx4=diff(y4,x4,2);for xx4=(3*pi/2):(pi/100):( 2*pi);k4=subs(abs((tx4*yxx4-txx4*yx4)/(tx4^2+yx4^2)^1.5),{x4},{xx4}); v=[v,1/k4];endmin(v)(3)凸轮的理论廓线和其包络线;由基圆半径确定其滚子的半径为r=8mm,其他参数保持不变;a.凸轮的理论廓线w = 2*pi/3;s0 = 50;s = 70;e = 17;x = 0:(pi/100):(2*pi/3);x1 = (s + s0)*cos(x)-e*sin(x);y1 = (s0 + s)*sin(x) - e*cos(x);y = (2*pi/3):(pi/100):(pi);x2 = (s + s0)*cos(y)-e*sin(y);y2 = (s0 + s)*sin(y) - e*cos(y);z = (pi ):(pi/100):(3*pi/2);x3 = (s + s0)*cos(z)-e*sin(z);y3 = (s0 + s)*sin(z) - e*cos(z);c = (3*pi/2):(pi/100):( 2*pi);x4 = (s + s0)*cos(c)-e*sin(c);y4 = (s0 + s)*sin(c) - e*cos(c);plot(x1,y1,'b',x2,y2,'b',x3,y3,'b',x4,y4,'b');xlabel('x/mm')ylabel('y/mm')title('理轮轮曲线')b.凸轮的包络线w = 2*pi/3;s0 = 50;e = 17;r = 8;x = 0:(pi/100):(2*pi/3);s1 = 35*(1 - cos(1.5*x));x1 = (s1 + s0).*cos(x) - e*sin(x);y1 = (s0 + s1).*sin(x) - e*cos(x);n1 = -(35*1.5*sin(x) + s0).*sin(x) -e*cos(x);m1 = (s0 + 35*1.5*sin(x) ).*cos(x) + e*sin(x);xt1 = x1+(r*m1)./(sqrt(n1.^2+m1.^2));yt1 = y1 - (r*n1)./sqrt(m1.^2 +n1.^2);xw1 = x1 - (r*m1)./sqrt(m1.^2 +n1.^2);yw1 = y1 + (r*n1)./sqrt(m1.^2 +n1.^2);y = (2*pi/3):(pi/100):(pi);s2 = 70;x2 = (s2 + s0).*cos(y)-e*sin(y);y2 = (s0 + s2).*sin(y) - e*cos(y);n2 = -s0.*sin(y)-e*cos(y);m2 = s0 .*cos(y) + e*sin(y);xt2 = x2 + (r*m2)./sqrt(m2.^2+n2.^2);yt2 = y2 - (r*n2)./sqrt(m2.^2+n2.^2);xw2 = x2 - (r*m2)./sqrt(m2.^2+n2.^2);yw2 = y2 + (r*n2)./sqrt(m2.^2+n2.^2);z = (pi ):(pi/100):(3*pi/2);s3 = 70*(3- 2*z/pi + 1/(2*pi).*sin (4*z - 4* pi));x3 = (s3 + s0).*cos(z)-e*sin(z);y3 = (s0 + s3).*sin(z) - e*cos(z);n3 = -(140/pi *cos(4*z - 4*pi) + s0).*sin(z)-e*cos(z); m3 = (s0 + 140/pi *cos(4*z - 4*pi)).*cos(z) + e*sin(z);xt3= x3 + (r*m3)./sqrt(m3.^2+n3.^2);yt3 = y3 - (r*n3)./sqrt(m3.^2+n3.^2);xw3 = x3 -(r* m3)./sqrt(n3.^2+m3.^2);yw3 = y3 + (r*n3)./sqrt(n3.^2+m3.^2);c = (3*pi/2):(pi/100):( 2*pi);s4 = 0;x4 = (s4 + s0).*cos(c)-e*sin(c);y4 = s0 .*sin(c) - e*cos(c);n4 = - s0.*sin(c)-e*cos(c);m4 = s0 .*cos(c) + e*sin(c);xt4= x4 + (r*m4)./sqrt(m4.^2+n4.^2);yt4 = y4 - (r*n4)./sqrt(m4.^2+n4.^2);xw4 = x4 - (r*m4)./sqrt(n4.^2+m4.^2);yw4 = y4 + (r*n4)./sqrt(n4.^2+m4.^2);plot(xw1,yw1,'b',xw2,yw2,'b',xw3,yw3,'b',xw4,yw4,'b') xlabel('x/mm')ylabel('y/mm')title('凸轮的包络线')grid。

机械原理复习题05凸轮机构一、填空1.凸轮机构主要是由_凸轮_、__从动杆_和固定机架三个基本构件所组成。
2.按凸轮的外形,凸轮机构主要分为_盘行__凸轮和_圆柱_凸轮两种基本类型。
3.从动杆与凸轮轮廓的接触形式有_点__、_线__二种。
4.以凸轮的理论轮廓曲线的最小半径所做的圆称为凸轮的基园_。
5.凸轮理论轮廓曲线上的点的某点的法线方向(即从动杆的受力)与从动杆速度方向之间的夹角称为凸轮在该点的_压力角α__。
6.随着凸轮压力角α增大,有害分力F2将会_引起摩擦阻力过大_而使从动杆自锁“卡死”,通常对移动式从动杆,推程时限制压力角α_______。
7.凸轮机构从动杆等速运动的位移为一条_斜_线,从动杆等加速等减速运动的位移曲线为一条_抛物线。
8.等速运动凸轮在速度换接处从动杆将产生_刚性_冲击,引起机构强烈的振动。
9.凸轮机构的移动式从动杆能实现___c _。
(a 匀速、平稳的直线运动 b 简偕直线运动 c各种复杂形式的直线运动10.从动杆的端部形状有__尖顶、_滚子_和平底三种。
11.凸轮与从动件接触处的运动副属于___a____。
(a 高副 b 转动副 c 移动副)13.在要求_a_的凸轮机构中,宜使用滚子式从动件。
( a 传力较大 b 传动准确、灵敏 c 转速较高)14.使用滚子式从动杆的凸轮机构,为避免运动规律失真,滚子半径r与凸轮理论轮廓曲线外凸部分最小曲率半径ρ最小之间应满足__c___。
(a r >ρ最小 b r =ρ最小 c r <ρ最小)15.凸轮与移动式从动杆接触点的压力角在机构运动时是_ c ___。
( a 恒定的 b 变化的 c 时有时无变化的)16.当凸轮转角δ和从动杆行程H一定时,基圆半径r b与压力角α的关系是_b___。
(a r b愈小则愈小,b r b愈小则a愈大,c r b变化而α不变)17.下列凸轮机构中,图__b___所画的压力角是正确的。
18.在减小凸轮机构尺寸时,应首先考虑_a___。

机械原理凸轮机构习题与答案(五篇材料)第一篇:机械原理凸轮机构习题与答案解:曲柄的存在的必要条件是1)最短杆与追长杆的杆长之和应小于或等于其余两杆的长度之和;2)连架杆与机架必有最短杆1).杆件1为曲柄2).在各杆长度不变的情况下,选取c杆做为机架就可以实现双摇杆机构试以作图法设计一偏置尖底推杆盘形凸轮的轮廓曲线。
已知凸轮以等角速度顺时针回转,正偏距e=10,基园半径r0=30mm.推杆运动规律为:凸轮转角δ=0~150时,推杆00.凸轮转角δ=180~300时推杆等速上升16mm;.凸轮转角δ=150~180时推杆远休;等加速回程16mm;.凸轮转角δ=300~360时推杆近休。
解:解题步骤1)首先绘制位移S与转角δ的关系曲线S-δ曲线。
2)根据S-δ曲线、凸轮基园半径和正偏距,绘制凸轮的轮廓曲线。
000000凸轮仅用了0度,90度,150度,180度,300度几个点绘制轮廓曲线,同学们绘制时英多用些点(一般取12个点,再勾画轮廓曲线)第二篇:机械原理_凸轮机构设计机械原理课程设计——凸轮机构设计(一)目录 (1)_________________________(一)、题目及原始数据 (2)(二)、推杆运动规律及凸轮廓线方程 (3)(三)、(四)、(五)、(六)、(七)、(八)、计算程序方框图..........................5 计算源程序..............................6 程序计算结果及分析......................10 凸轮机构图..............................15 心得体会................................16 参考书. (16)(一)、题目及原始数据试用计算机辅助设计完成偏置直动滚子推杆盘形凸轮机构的设计,凸轮以1rad/s的角速度沿逆时针方向转动。
要求:(1)、推程运动规律为等加速等减速运动,回程运动规律为五次多项式运动规律;(2)、打印出原始数据;(3)、打印出理论轮廓和实际轮廓的坐标值;(4)、打印出推程和回程的最大压力角,以及出现最大压力角时凸轮的相应转角;(5)、打印出凸轮实际轮廓曲线的最小曲率半径,以及相应的凸轮转角;(6)、打印出凸轮运动的位移;(7)、打印最后所确定的凸轮的基圆半径。

此文档下载后即可编辑五、(12分)图示为一偏心圆盘凸轮机构,凸轮的回转方向如图所示。
要求:(1)说明该机构的详细名称;(2)在图上画出凸轮的基圆,并标明图示位置的凸轮机构压力角和从动件2的位移;(3)在图上标出从动件的行程h及该机构的最小压力角的位置。
五、总分12分。
(1)2 分;(2)6 分;(3)4 分(1) 偏置直动滚子从动件盘形凸轮机构。
(2) r0,α,s如图所示。
(3) h及αmin发生位置如图示。
五、(10分)试在图示凸轮机构中,(1)标出从动件与凸轮从接触点C到接触点D时,该凸轮转过的转角ϕ;(2)标出从动件与凸轮在D点接触的压力角α;(3)标出在D点接触时的从动件的位移s。
五、总分10分。
(1)4 分;(2)3 分;(3)3 分(1)ϕ如图示。
(2)α如图示。
(3) s如图示。
-5、图示为一偏置直动滚子从动件盘形凸轮机构。
试在图上:(1)画出并标明基圆r0;(2)作出并标明凸轮按ω方向转过60︒后,从动件与凸轮廓线接触处的压力角α;(3)作出并标明滚子从图示位置反转到B处与凸轮接触时,对应的凸轮转角ϕ。
1.在图示的凸轮机构中,画出凸轮从图示位置转过60 时从动件的位置及从动件的位移s。
1.总分5分。
(1)3 分;(2)2 分(1) 找出转过60 的位置。
(2) 标出位移s。
1.四、(10分)在图示凸轮机构中,已知:20AO mm,ο60=BO=∠AOB,=且A B(为圆弧;CO=DO=40mm,ο60∠COD,CD(为圆弧;滚子半径=r r=10mm,从动件的推程和回程运动规律均为等速运动规律。
(1)求凸轮的基圆半径;(2)画出从动件的位移线图。
四、总分10分。
(1)2分;(2)8分(1) r0=AO+r r=20+10=30 mm(2) s-ϕ线图如图示。
五、(10分)在图示直动平底从动件盘形凸轮机构中,请指出:(1 )图示位置时凸轮机构的压力角 。
(2 )图示位置从动件的位移。
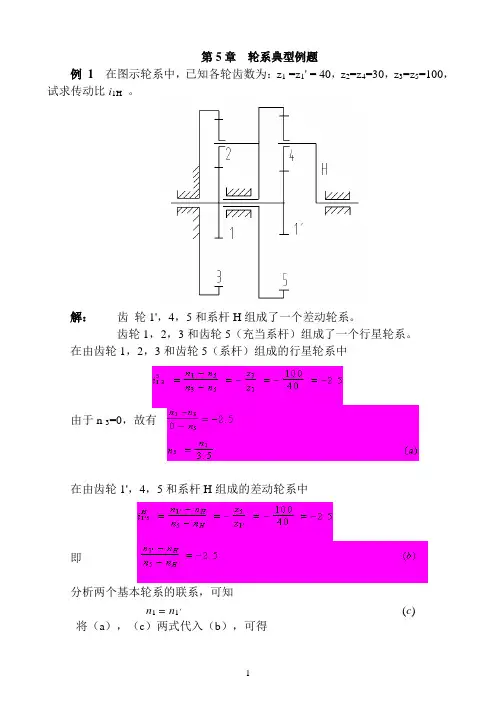
第5章轮系典型例题例1在图示轮系中,已知各轮齿数为:z1 =z1' = 40,z2=z4=30,z3=z5=100,试求传动比i1H。
解:齿轮1',4,5和系杆H组成了一个差动轮系。
齿轮1,2,3和齿轮5(充当系杆)组成了一个行星轮系。
在由齿轮1,2,3和齿轮5(系杆)组成的行星轮系中由于n 3=0,故有在由齿轮1',4,5和系杆H组成的差动轮系中即分析两个基本轮系的联系,可知n1= n1'(c)将(a),(c)两式代入(b),可得计算结果为正,表明从动系杆H和主动齿轮1的转向相同。
例2 在图示轮系中,已知各轮齿数为:z 1 = 90,z 2 = 60,z 2' = 30,z 3 =30,z 3' = 24,z 4 = 18,z 5 = 60,z 5' = 36,z 6 = 32。
运动从A,B两轴输入,由构件H输出。
已知n A=100r/min,n B=900r/min,转向如图所示。
试求输出轴H的转速n H的大小和方向。
解:齿轮3',4,5和系杆H组成了一个差动轮系齿轮1,2,2',3组成了一个定轴轮系,齿轮5',6组成了另一个定轴轮系。
对于齿轮3',4,5和系杆H组成的差动轮系,有即对于齿轮1,2,2',3组成的定轴轮系,有即对于齿轮5,6组成的定轴轮系,有即分析三个轮系之间的基本联系,有将该结果带入(a)式,可得化简整理后得计算结果为负,说明n H转向与n 5 相同,即n A,n B转向相反。
例3 在图示轮系中,已知齿轮1的转速为n 1 =1650 r/min,齿轮4的转速n4=1000r/min,所有齿轮都是标准齿轮,且z 2=z 5=z 6=20。
求各个齿轮中未知的齿轮齿数。
解:由齿轮1与齿轮3和齿轮6与齿轮4的同轴条件得齿轮1,2,3及系杆H1组成差动轮系;齿轮4,5,6及系杆H2组成行星轮系。

华科机械原理凸轮习题答案华科机械原理凸轮习题答案凸轮是机械原理中一个重要的概念,它在机械运动中起到了关键的作用。
华科机械原理课程中,凸轮也是一个需要重点掌握的内容。
下面将为大家提供一些华科机械原理凸轮习题的答案,希望能够对大家的学习有所帮助。
1. 一个凸轮有一个半径为50mm的基圆,凸轮的最大半径为100mm,凸轮的转角为120度。
求凸轮的凸度。
解答:凸度是指凸轮曲线上一点的曲率半径的倒数。
根据题目中给出的凸轮的基圆半径和最大半径,可以得出凸轮的凸度为1/50mm。
2. 一个凸轮的凸度为1/100mm,基圆半径为50mm,转角为120度。
求凸轮的最大半径。
解答:凸度是凸轮曲线上一点的曲率半径的倒数。
根据题目中给出的凸度和基圆半径,可以得出凸轮的最大半径为150mm。
3. 一个凸轮的凸度为1/80mm,基圆半径为60mm,最大半径为120mm。
求凸轮的转角。
解答:凸度是凸轮曲线上一点的曲率半径的倒数。
根据题目中给出的凸度和基圆半径,可以得出凸轮的最大转角为96度。
以上是华科机械原理凸轮习题的答案,通过这些题目的解答,我们可以更好地理解凸轮的相关概念和计算方法。
凸轮在机械运动中的应用非常广泛,掌握凸轮的原理和计算方法对于我们的学习和工作都非常重要。
除了凸轮的基本概念和计算方法,我们还需要了解凸轮的运动规律和应用。
凸轮的运动规律可以通过凸轮曲线来描述,凸轮曲线是凸轮上一点的运动轨迹。
凸轮的应用包括凸轮与从动件的配合、凸轮的运动速度和加速度分析等。
在机械设计中,凸轮的应用非常广泛。
凸轮可以用来控制机械装置的运动轨迹和运动速度,可以实现复杂的运动功能。
凸轮还可以用来传递动力和变换运动形式,提高机械装置的工作效率和性能。
总之,凸轮是机械原理中一个重要的概念,掌握凸轮的原理和计算方法对于我们的学习和工作都非常重要。
通过对华科机械原理凸轮习题的解答,我们可以更好地理解凸轮的相关概念和应用。
希望以上内容对大家有所帮助,祝大家学习进步!。


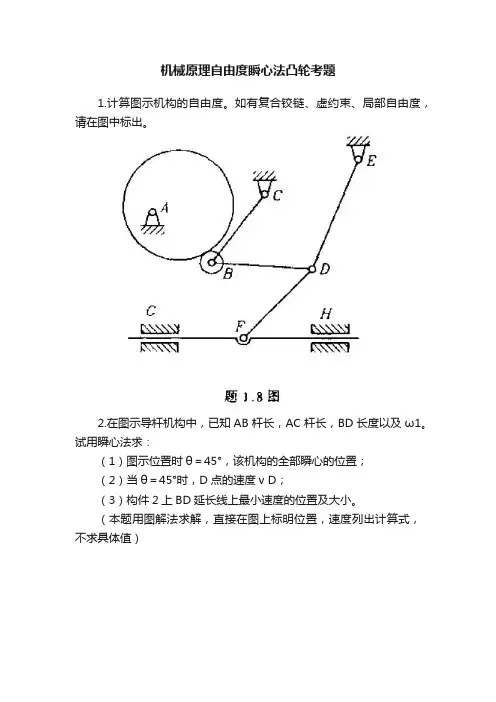
机械原理自由度瞬心法凸轮考题1.计算图示机构的自由度。
如有复合铰链、虚约束、局部自由度,请在图中标出。
2.在图示导杆机构中,已知AB杆长,AC杆长,BD长度以及ω1。
试用瞬心法求:(1)图示位置时θ=45°,该机构的全部瞬心的位置;(2)当θ=45°时,D点的速度v D;(3)构件2上BD延长线上最小速度的位置及大小。
(本题用图解法求解,直接在图上标明位置,速度列出计算式,不求具体值)3.图示为一偏置式滚子推杆盘状凸轮机构,凸轮为一偏心圆,逆时针回转,其直径D=32mm,滚子半径为r=5mm,偏距e=6mm,试根据图示位置1)画出凸轮的理论廓线、偏距圆;2)求出基圆半径rb、最大行程h、升程角δ0;3)画出图示位置时凸轮的压力角。
答案:1.2.(1)共有6个瞬心,如图所示;(2)vD=ω1·DF(3)最小速度点位置为E点,如图所示vE=ω1·EF3.1.计算下图机构自由度(若机构中存在复合铰链、局部自由度或虚约束,请明确指出)。
2.图示机构运动简图中,设已知各构件的尺寸及原动件1的速度v1和加速度a1,现要求:(1)确定图示位置时该机构全部瞬心的位置;(2)用瞬心法求构件2及构件3的瞬时角速度ω2、ω3(列出计算式,不求具体值);(3)求构件2上瞬时速度为零的点的位置(在图上标出)。
G A B E FC D3.图示为一偏心圆凸轮机构,O 为偏心圆的转动中心,C 为几何中心。
(1)画出凸轮的理论廓线并求出凸轮的基圆半径r b ;(2)用作图法求从动件2的最大升程h 和推程运动角δ1;(3)在图中标出凸轮从图示位置转过90时从动件的位移s 与机构的压力角α。
答案:1.6,8,1L h n P P ===(2′)机构自由度:323628111L h F n P P =--=?-?-?=(1′)2.3.。

第1章平面机构的结构分析解释下列概念1.运动副;2.机构自由度;3.机构运动简图;4.机构结构分析;5.高副低代。
验算下列机构能否运动,如果能运动,看运动是否具有确定性,并给出具有确定运动的修改办法。
题图题图绘出下列机构的运动简图,并计算其自由度(其中构件9为机架)。
计算下列机构自由度,并说明注意事项。
计算下列机构的自由度,并确定杆组及机构的级别(图a所示机构分别以构件2、4、8为原动件)。
题图题图第2章平面机构的运动分析试求图示各机构在图示位置时全部瞬心。
题图在图示机构中,已知各构件尺寸为l AB=180mm , l BC=280mm , l BD=450mm ,l CD=250mm ,l AE=120mm ,φ=30º, 构件AB上点E的速度为v E=150 mm /s ,试求该位置时C、D两点的速度及连杆2的角速度ω2。
在图示的摆动导杆机构中,已知l AB=30mm , l AC=100mm , l BD=50mm ,l DE=40mm ,φ1=45º,曲柄1以等角速度ω1=10 rad/s沿逆时针方向回转。
求D点和E点的速度和加速度及构件3的角速度和角加速度(用相对运动图解法)。
题图题图在图示机构中,已知l AB=50mm , l BC=200mm , x D=120mm , 原动件的位置φ1=30º, 角速度ω1=10 rad/s,角加速度α1=0,试求机构在该位置时构件5的速度和加速度,以及构件2的角速度和角加速度。
题图图示为机构的运动简图及相应的速度图和加速度图。
(1)在图示的速度、加速度多边形中注明各矢量所表示的相应的速度、加速度矢量。
(2)以给出的速度和加速度矢量为已知条件,用相对运动矢量法写出求构件上D点的速度和加速度矢量方程。
(3)在给出的速度和加速度图中,给出构件2上D点的速度矢量和加速度矢量。
题图在图示机构中,已知机构尺寸l AB=50mm,l BC=100mm, l CD=20mm , 原动件的位置φ1=30º, 角速度ω1=ωrad/s,试用相对运动矢量方程图解法求图示位置时构件2的角速度ω2和角加速度α2的大小和方向。
五、(12分)图示为一偏心圆盘凸轮机构,凸轮的回转方向如图所示。
要求:(1)说明该机构的详细名称;(2)在图上画出凸轮的基圆,并标明图示位置的凸轮机构压力角和从动件2的位移;(3)在图上标出从动件的行程h及该机构的最小压力角的位置。
五、总分12分。
(1)2 分;(2)6 分;(3)4 分(1) 偏置直动滚子从动件盘形凸轮机构。
(2) r0,α,s如图所示。
(3) h及αmin发生位置如图示。
五、(10分)试在图示凸轮机构中,(1)标出从动件与凸轮从接触点C到接触点D时,该凸轮转过的转角ϕ;(2)标出从动件与凸轮在D点接触的压力角α;(3)标出在D点接触时的从动件的位移s。
五、总分10分。
(1)4 分;(2)3 分;(3)3 分(1)ϕ如图示。
(2)α如图示。
(3) s如图示。
-5、图示为一偏置直动滚子从动件盘形凸轮机构。
试在图上:(1)画出并标明基圆r0;(2)作出并标明凸轮按ω方向转过60︒后,从动件与凸轮廓线接触处的压力角α;(3)作出并标明滚子从图示位置反转到B处与凸轮接触时,对应的凸轮转角ϕ。
1.在图示的凸轮机构中,画出凸轮从图示位置转过60 时从动件的位置及从动件的位移s。
1.总分5分。
(1)3 分;(2)2 分(1) 找出转过60 的位置。
(2) 标出位移s。
1.四、(10分)在图示凸轮机构中,已知:20==BO AO mm , 60 =∠AOB ,且A B (为圆弧;CO =DO =40mm ,60=∠COD ,CD (为圆弧;滚子半径r r =10mm ,从动件的推程和回程运动规律均为等速运动规律。
(1)求凸轮的基圆半径;(2)画出从动件的位移线图。
四、总分10分。
(1)2分;(2)8分(1) r0=AO+r r=20+10=30 mm(2) s-ϕ线图如图示。
五、(10分)在图示直动平底从动件盘形凸轮机构中,请指出:(1 )图示位置时凸轮机构的压力角 。
(2 )图示位置从动件的位移。
00901、凸轮机构中的压力角是和所夹的锐角。
00902、凸轮机构中,使凸轮与从动件保持接触的方法有和两种。
00903、在回程过程中,对凸轮机构的压力角加以限制的原因是。
00904、在推程过程中,对凸轮机构的压力角加以限制的原因是。
00905、在直动滚子从动件盘形凸轮机构中,凸轮的理论廓线与实际廓线间的关系是。
00906、凸轮机构中,从动件根据其端部结构型式,一般有、、等三种型式。
00907、设计滚子从动件盘形凸轮机构时,滚子中心的轨迹称为凸轮的廓线;与滚子相包络的凸轮廓线称为廓线。
00908、盘形凸轮的基圆半径是上距凸轮转动中心的最小向径。
00909、根据图示的dd2sϕϕ2-运动线图,可判断从动件的推程运动是_________________________________,从动件的回程运动是____________________________________________。
00910、从动件作等速运动的凸轮机构中,其位移线图是线,速度线图是线。
00911、当初步设计直动尖顶从动件盘形凸轮机构中发现有自锁现象时,可采用、、等办法来解决。
00912、在设计滚子从动件盘形凸轮轮廓曲线中,若出现时,会发生从动件运动失真现象。
此时,可采用方法避免从动件的运动失真。
00913、用图解法设计滚子从动件盘形凸轮轮廓时,在由理论轮廓曲线求实际轮廓曲线的过程中,若实际轮廓曲线出现尖点或交叉现象,则与的选择有关。
00914、在设计滚子从动件盘形凸轮机构时,选择滚子半径的条件是。
00915、在偏置直动从动件盘形凸轮机构中,当凸轮逆时针方向转动时,为减小机构压力角,应使从动件导路位置偏置于凸轮回转中心的侧。
00916、平底从动件盘形凸轮机构中,凸轮基圆半径应由来决定。
00917、凸轮的基圆半径越小,则凸轮机构的压力角越,而凸轮机构的尺寸越。
00918、凸轮基圆半径的选择,需考虑到、,以及凸轮的实际廓线是否出现变尖和失真等因素。
机械原理大作业说明书课程名称:机械原理设计题目:凸轮机构设计院系:班级:设计者:学号:指导教师:设计时间:2014年6月哈尔滨工业大学一、设计题目如右图所示直动从动件盘形凸轮机构,选择一组凸轮机构的原始参数,据此设计该凸轮机构。
序号行程(mm)推程运动角推程运动规律推程许用压力角15 90 150 正弦加速度30°回程运动规律回程许用压力角远休止角近休止角回程运动角100°余弦加速度60°55°55°二. 凸轮推杆升程、回程运动方程及推杆位移、速度、加速度线图凸轮推杆推程运动方程:凸轮推杆回程运动方程% t表示转角,s表示位移t=0:0.01:5*pi/6;%升程阶段s=90*[(6*t)/(5*pi)-1/(2*pi)*sin(12*t/5)];hold onplot(t,s);t= 5*pi/6:0.01:41*pi/36;%远休止阶段s=90;hold onplot(t,s);t=41*pi/36:0.01:61*pi/36;%回程阶段s=45*[1+cos((9*t/5)-(41*pi/20))]; hold onplot(t,s);t=61*pi/36:0.01:2*pi;%近休止阶段s=0;hold onplot(t,s);grid onhold off% t表示转角,令ω1=1t=0:0.01:5*pi/6;%升程阶段v=108*1*[1-cos(12*t/5)]/pihold onplot(t,v);t= 5*pi/6:0.01:41*pi/36;%远休止阶段v=0hold onplot(t,v);t=41*pi/36:0.01:61*pi/36;%回程阶段v=-81*1*sin((9*t/5)-(41*pi/20)) hold onplot(t,v);t=61*pi/36:0.01:2*pi;%近休止阶段v=0 hold on0123456-100-80-60-40-20020406080t=0:0.001:5*pi/6;a=259.2*sin(12*t/5)/pi; hold on plot(t,a);t=5*pi/6:0.01:41*pi/36; a=0; hold on plot(t,a);t=41*pi/36:0.001:61*pi/36;a=-145.8*cos((9*t/5)-(41*pi/20)); hold on plot(t,a);t=61*pi/36:0.001:2*pi; a=0; hold on0123456-150-100-5050100150三. 绘制凸轮机构的sd ds -ϕ线图% t 表示转角,x(横坐标)表示速度ds/d φ,y (纵坐标)表示位移s t=0:0.001:5*pi/6; % 升程阶段x= 108*1*(1-cos(12*t/5))/pi;y= 90*((6*t)/(5*pi)-1/(2*pi)*sin(12*t/5)); hold on plot(x,y,'-r');t= 5*pi/6:0.01:41*pi/36; %远休止阶段 x=0; y=90; hold on plot(x,y,'-r');t=41*pi/36:0.001:61*pi/36; % 回程阶段x=-81*1*sin ((9*t/5)-(41*pi/20)); y=45*(1+cos((9*t/5)-(41*pi/20))); hold on plot(x,y,'-r');t=61*pi/36:0.01:2*pi; %近休止阶段 x=0; y=0;hold on plot(x,y,'-r'); grid on hold off-100-80-60-40-200204060800102030405060708090四.按许用压力角确定凸轮基圆半径和偏距 1. 求切点转角(1)在图-4中,右侧曲线为升程阶段的类速度-位移图,作直线D t d t 与其相切,且位移轴正方向呈夹角[ 1]=300,则切点处的斜率与直线D t d t 的斜率相等,因为k Dtdt =tan300,右侧曲线斜率可以表示为 ,所以,,通过编程求其角度。
05凸轮机构及其设计1.凸轮机构中的压力角是和所夹的锐角。
2.凸轮机构中�使凸轮与从动件保持接触的方法有和两种。
3.在回程过程中�对凸轮机构的压力角加以限制的原因是。
4.在推程过程中�对凸轮机构的压力角加以限制的原因是。
5.在直动滚子从动件盘形凸轮机构中�凸轮的理论廓线与实际廓线间的关系是。
6.凸轮机构中�从动件根据其端部结构型式�一般有、、等三种型式。
7.设计滚子从动件盘形凸轮机构时�滚子中心的轨迹称为凸轮的廓线�与滚子相包络的凸轮廓线称为廓线。
8.盘形凸轮的基圆半径是上距凸轮转动中心的最小向径。
9.根据图示的dd 2 s��2�运动线图�可判断从动件的推程运动是_________________________________�从动件的回程运动是____________________________________________。
10.从动件作等速运动的凸轮机构中�其位移线图是线�速度线图是线。
11.当初步设计直动尖顶从动件盘形凸轮机构中发现有自锁现象时�可采用、、等办法来解决。
12.在设计滚子从动件盘形凸轮轮廓曲线中�若出现时�会发生从动件运动失真现象。
此时�可采用方法避免从动件的运动失真。
13.用图解法设计滚子从动件盘形凸轮轮廓时�在由理论轮廓曲线求实际轮廓曲线的过程中�若实际轮廓曲线出现尖点或交叉现象�则与的选择有关。
14.在设计滚子从动件盘形凸轮机构时�选择滚子半径的条件是。
15.在偏置直动从动件盘形凸轮机构中�当凸轮逆时针方向转动时�为减小机构压力角�应使从动件导路位置偏置于凸轮回转中心的侧。
16.平底从动件盘形凸轮机构中�凸轮基圆半径应由来决定。
17.凸轮的基圆半径越小�则凸轮机构的压力角越�而凸轮机构的尺寸越。
18.凸轮基圆半径的选择�需考虑到、�以及凸轮的实际廓线是否出现变尖和失真等因素。
19.当发现直动从动件盘形凸轮机构的压力角过大时�可采取��等措施加以改进�当采用滚子从动件时�如发现凸轮实际廓线造成从动件运动规律失真�则应采取�等措施加以避免。