最新人教版七年级上册教案2.1 第3课时 多项式2

2.1整式第 3课时多项式学习内容：课本p58 例 3 及课本 p64 提到的一个内容学习目的和要求：1、经过用整式来表示事物间的关系，逐渐掌握数学建模思想；2、理解多项式的升(降 )幂摆列的观点，会进行多项式的升(降 )幂摆列。

3、经过试试和沟通，领会多项式升(降 )幂摆列的可行性和必需性。

4、初步体验摆列组合思想与数学美感，培育审雅观。

学习要点和难点：要点：会进行多项式的升(降 )幂摆列，体验此中包含的数学美。

难点：会进行多项式的升(降 )幂摆列，体验此中包含的数学美。

一、自主学习：1、教材 p58 例 3：我们知道船在河流中行驶时，船的速度需要分两种状况议论：（ 1）顺流行驶：船的速度=；（ 2）逆水行驶：船的速度=；在上边两个关系式中若用字母V 表示静水速度则船的顺流速度为船的逆水速度为当 V=20 时则甲船顺流速度甲船逆水速度乙船顺流速度乙船逆水速度2..请运用加法互换律，随意互换多项式x 2＋ x＋ 1 中各项的地点，能够获得几种不一样的摆列方式？在众多的摆列方式中，你以为那几种比较齐整？【提示】有六种不一样的摆列方式，像 x2＋ x＋1 与 1＋x＋ x2这样的摆列比较齐整。

这两种摆列有一个共同点，那就是 x 的指数是渐渐变小 (或变大 )的。

我们把这类摆列叫做升幂摆列与降幂摆列。

比如：把多项式5x2＋ 3x－2x3－ 1 按 x 的指数从大到小的次序摆列，能够写成－2x3＋ 5x 2＋ 3x－1，这叫做这个多项式按字母x 的降幂摆列。

若按 x 的指数从小到大的次序摆列，则写成－ 1＋ 3x＋ 5x2－ 2x3，这叫做这个多项式按字母 x 的升幂摆列。

二、合作研究1、请把卡片＋ 3x2 y2－ 7xy 3＋ 2y－ 11x7 y5－ 35x3按 x 降幂摆列3 2 2按 r 升幂摆列。

2、把多项式 － π2πr－1＋ 3πr r【提示】：π是数字，不是字母，题目中一次项、二次项、三次项系数分别为3π。

2.1.3 多项式及整式教学设计一、教学目标通过本节课的学习，学生将能够：1.了解多项式的概念；2.能够识别多项式的各个术语，如系数、次数；3.掌握多项式的加减运算并能够进行简单的化简；4.能够将算式转化为整式。

二、教学重点1.多项式的概念；2.多项式的运算规则。

三、教学内容本节课将重点介绍多项式及整式的概念和运算规则。

3.1 多项式的概念多项式是由若干单项式相加或相减而得到的代数式，通常用字母表示未知数。

例如，3x + 5y - 2z 就是一个多项式，其中3x、5y和-2z都是单项式。

在多项式中，系数表示数字的乘法因子，常用字母表示未知数，乘法因子与未知数的乘积称为单项式。

例如，在3x中，3是系数，x是未知数。

多项式的次数是指其中各单项式中未知数的指数最大的值。

例如，在4x^2 + 2x + 7中，4x^2的次数是2，2x的次数是1，7的次数是0。

多项式的形式可以是一元多项式（只有一个未知数），也可以是多元多项式（有多个未知数）。

3.2 多项式的运算多项式的运算包括加法和减法。

对于一元多项式，将同类项相加或相减即可，不同类项不能进行运算。

同类项是指具有相同未知数次数的项。

例如，对于多项式2x^2 + 3x + 2 和 4x^2 - 5x - 1，将其相加的步骤如下：1.将同类项相加：(2x^2 + 4x^2) + (3x - 5x) + (2 - 1)；2.化简得到：6x^2 - 2x + 1。

对于多项式的减法，可以通过将减数变为相反数，然后进行加法运算来得到结果。

3.3 算式与整式算式是由数字符号和运算符号组成的代数式，可以进行运算。

例如，2x + 3y - 5 是一个算式。

整式是由常数项、单项式或多项式组成，也可以进行运算。

例如，2 + 3x -5y、4x^2 + 2x + 7 都是整式。

四、教学方法1.案例引入：通过实际生活中的例子引入多项式的概念，增加学生的兴趣和理解；2.讲解与示范：通过课堂讲解和示范演示，逐步介绍多项式的定义和运算规则；3.互动讨论：组织学生进行小组讨论和问题解答，拉近师生之间的距离，激发学生的思考；4.练习与应用：布置多项式的练习题，培养学生的实际操作能力，巩固所学知识。

第二章 整式的加减2.1 整式第3课时 多项式...._____与_____）相乘组成的代数式叫做单项式.单独的一个___.叫做这个单项式的系数. 叫做这个单项式的次数.__________，次数是______________.都叫做这个多项式的项，多项式含有几项，这个多项式叫.的次数，叫做这个多项式的次数,多项式的次数是几，这个多. _____项，它们分别是______ _.其中常数项是______，它是.－b 3的项数为_______，次数为_______. ________，常数项为_________.四、我的疑惑______________________________________________________________________________________________________________________________________________________一、要点探究探究点1：多项式的相关概念 问题1：列式表示下列数量（1）温度由t ℃下降5℃后是______℃.（2）买一个篮球需要x 元，买一个排球需要y 元，买一个足球需要z 元，买3个篮球、5个排球、2个足球共需要___________元.（3）如图三角尺的面积为___________.（4）如图是一所住宅区的建筑平面图，这所住宅的建筑面积是___________.问题2：上述几个式子都是单项式吗？这些式子有什么共同特点？与单项式有什么关系？要点归纳：1.几个单项式的和叫做多项式2.在多项式中，每个单项式叫做多项式的项3.不含字母的项叫做常数项4.多项式里次数最高项的次数就是多项式的次数5.单项式与多项式统称为整式例1 下列整式中哪些是单项式？哪些是多项式？是单项式的指出系数和次数，是多项式的指出项和次数：4222232341π,,1,,32,,31,2.273－－＋3－m n a b x y x t x y xy x x y +-+-要点归纳：(1)多项式的各项应包括它前面的符号；(2)多项式没有系数的概念，但其每一项均有系数，每一项的系数也包括前面的符号； (3)要确定一个多项式的次数，先要确定此多项式中各项(单项式)的次数，然后找次数最高的；(4)一个多项式的最高次项可以不唯一.课堂探究教学备注 配套PPT 讲授1.情景引入 （见幻灯片3）2.探究点1新知讲授（见幻灯片4-13）例2：已知－5x m ＋104x m －4x m y 2是关于x 、y 的六次多项式，求m 的值，并写出该多项式.【归纳总结】 解题的关键是弄清多项式次数是多项式中次数最高的项的次数.然后根据题意，列出方程，求出m 的值.探究点2：多项式的应用例3 如图所示，用式子表示圆环的面积．当r=15 cm ，r=10cm 时，求圆环的面积（π取3.14 ）．例4 某公园的门票价格是：成人10元/张；学生5元/张.（1）一个旅游团有成人x 人、学生y 人，那么该旅游团应付多少门票费？ （2）如果该旅游团有37个成人、15个学生，那么他们应付多少门票费？ 针对训练1.将代数式①3，②x 1，③b a -3，④π，⑤π1，⑥21x 2，⑦3a ＋1，⑧712-a ，⑨－31x 2＋yz ，⑩14+x x填入适当的空格中（填序号）： 单项式：___________________________________________________； 多项式：___________________________________________________； 整式：_____________________________________________________.2.多项式3m 3-2m-5+m 2的常数项是______，一次项是_____，二次项的系数是_____.3.（1）a ，b 分别表示长方形的长和宽，则长方形的周长l ＝______，面积S ＝___，当a ＝2 cm ，b ＝3 cm 时，l ＝______ cm ，S ＝______cm 2 ；（2）a ，b 分别表示梯形的上底和下底，h 表示梯形的高，则梯形面积S ＝_______，当a ＝2 cm ，b ＝4 cm ， h ＝5 cm 时， S ＝______cm 2 ． 4.如果x n －(m －1)x ＋2为三次二项式，求m 2＋n 的值．教学备注 配套PPT 讲授3.探究点2新知讲授（见幻灯片14-17）4.若)3(3)2(2+---axxa是关于x的一次式,则a =______,若它是关于x的二次二项式,则a =______.5.多项式521)3(2-++abbax y是关于a、b的四次三项式，且最高次项的系数为－2，则x=______,y=______.6.已知多项式:621653222+-+-+xxyyx m是六次四项式,单项式zyx mn-4332的次数与这个多项式的次数相同,求n的值.。

人教版数学七年级上册2.1 第3课时《多项式》精品教学设计1一. 教材分析人教版数学七年级上册第2章《多项式》是学生在小学阶段学习基础上，进一步深化对数学概念的理解和运用的关键内容。

本节课主要介绍多项式的定义、多项式的项、次数和系数等基本概念。

通过本节课的学习，使学生掌握多项式的基本知识，能够正确理解并运用多项式进行简单的计算和问题解决。

二. 学情分析七年级的学生已经具备了一定的数学基础，对于数学概念的理解和运用有一定的掌握。

但同时，学生对于较为抽象的数学概念的理解还存在一定的困难，需要通过具体实例和实际操作来加深理解。

此外，学生的学习习惯和方法还需要进一步指导和培养。

三. 教学目标1.知识与技能目标：理解多项式的定义、多项式的项、次数和系数等基本概念，能够正确运用多项式进行简单的计算和问题解决。

2.过程与方法目标：通过观察、操作、交流等活动，培养学生的数学思维能力和问题解决能力。

3.情感态度与价值观目标：激发学生学习数学的兴趣，培养学生的自主学习能力和团队合作精神。

四. 教学重难点1.重点：多项式的定义、多项式的项、次数和系数等基本概念。

2.难点：对于多项式概念的理解和运用。

五. 教学方法1.情境教学法：通过生活实例和实际问题，引发学生的兴趣和思考，引导学生理解和掌握多项式的概念。

2.启发式教学法：通过提问和讨论，激发学生的思维，引导学生主动探索和发现问题的解决方法。

3.合作学习法：学生进行小组讨论和合作，培养学生的团队合作精神和交流沟通能力。

六. 教学准备1.教学PPT：制作多媒体教学PPT，包括多项式的定义、多项式的项、次数和系数等基本概念的介绍，以及相关的例题和练习。

2.教学素材：准备相关的数学题目和实际问题，用于引导学生进行观察和操作。

3.教学工具：准备黑板、粉笔等教学工具，用于板书和演示。

七. 教学过程1.导入（5分钟）通过一个实际问题引入本节课的主题——多项式。

例如：已知一个数的平方减去这个数等于3，求这个数。

2.1 整式第3课时多项式教学目标1.通过本节课的学习,使学生掌握整式、多项式的项及其次数、常数项的概念.2.初步体会类比和逆向思维的数学思想.教学重点掌握整式及多项式的有关概念,掌握多项式的定义、多项式的项和次数以及常数项等概念.教学难点准确指出多项式的次数.教学过程一、复习引入1.列代数式(1)长方形的长与宽分别为a、b,则长方形的周长是;(2)某班有男生人,女生21人,则这个班共有学生人;(3)图中阴影部分的面积为;(4)鸡兔同笼,鸡a只,兔b只,则共有头个,脚只.2.观察以上所得出的四个代数式与上节课所学单项式有何区别.(1)2(a+b); (2)21+; (3)ab-π()2;(4)2a+4b.二、讲授新课1.多项式板书由学生自己归纳得出的多项式概念.上面这些代数式都是由几个单项式相加而成的.像这样,几个单项式的和叫做多项式.在多项式中,每个单项式叫做多项式的项.其中,不含字母的项,叫做常数项.例如,多项32-2+5有三项,它们是32,-2,5,其中5是常数项.一个多项式含有几项,就叫几项式.多项式里,次数最高项的次数,就是这个多项式的次数.例如,多项式32-2+5是一个二次三项式.注意(1)多项式的次数不是所有项的次数之和.(2)多项式的每一项都包括它前面的符号.2.例题【例1】判断①多项式a3-a2b+ab2-b3的项为a3、a2b、ab2、b3,次数为12;②多项式3n4-2n2+1的次数为4,常数项为1.【例2】指出下列多项式的项和次数(1)3-1+32; (2)43+2-2y2.【例3】指出下列多项式是几次几项式.(1)3-+1; (2)3-22y2+3y2.【例4】已知代数式3n-(m-1)+1是关于的三次二项式,求m、n的值.注意多项式的项包括前面的符号,多项式的次数应为最高次项的次数.在例3讲完后插入整式的定义单项式与多项式统称整式.分析例4时要紧扣多项式的定义,培养学生的逆向思维,使学生透彻理解多项式的有关概念,培养他们应用新知识解决问题的能力.【例5】一条河流的水流速度为2.5千米/时,如果已知船在静水中的速度,那么船在这条河流中顺水行驶和逆水行驶的速度分别怎样表示?如果甲、乙两船在静水中的速度分别是20千米/时和35千米/时,则它们在这条河流中顺水行驶和逆水行驶的速度各是多少?3.课堂练习课本P58练习第1、2题.填空-a2b-ab+1是次项式,其中三次项系数是,二次项为,常数项为,写出所有的项.三、课时小结1.理解多项式的定义,能说出一个多项式是几次几项式,最高次数是几,分别由哪几项组成,各项的系数分别为多少,常数项为几.2.这堂课学习了多项式,与前一节所学的单项式合起统称为整式,使知识形成了系统.(让学生小结,师生进行补充.)四、课堂作业课本P59习题2.1的第3、4题.。

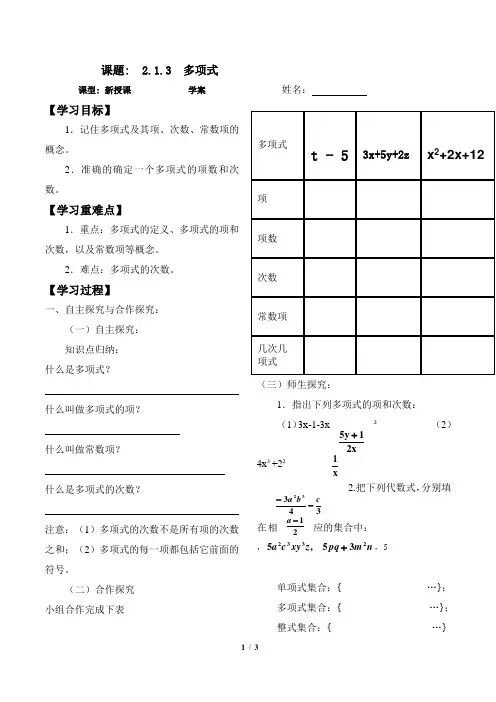
34332cb a --课题: 2.1.3 多项式课型: 新授课 学案【学习目标】1．记住多项式及其项、次数、常数项的概念。

2．准确的确定一个多项式的项数和次数。

【学习重难点】1．重点：多项式的定义、多项式的项和次数，以及常数项等概念。

2．难点：多项式的次数。

【学习过程】一、自主探究与合作探究：（一）自主探究： 知识点归纳： 什么是多项式？什么叫做多项式的项？什么叫做常数项？什么是多项式的次数？注意：（1）多项式的次数不是所有项的次数之和；（2）多项式的每一项都包括它前面的符号。

（二）合作探究 小组合作完成下表姓名：（三）师生探究：1．指出下列多项式的项和次数：（1）3x-1-3x ² （2）4x ³+2²2.把下列代数式，分别填在相应的集合中：， ,5332z xy c a n m pq 235+，5单项式集合：{…}；多项式集合：{…}；整式集合：{…}21-a x 1x 21y 5+3．下列多项式二次三项式的是（ ） A ．a+b+1 B ．a ²b+a+b C ．ab+a+b D ．ab+b+π+1【当堂达标】1．指出下列多项式的项和次数，并说明它是几次几项式？（1）a 3-a 2b+ab 2-b 3；（2）3n 4-2n 2+1。

2．指出下列整式的次数：（1）3xy-1； （2）2x ²-3x+1；（3）4x ²y-5xy ³+2xy ²+1； （4）32ba +。

3. 填空题：（1）多项式x+y-z 是单项式___ , ___ ,___的和,它是___次___项式.（2）多项式z+y-x 是单项式，，的和，它是___次___项式。

（3）多项式3m 3-2m-5+m 2的常数项是____,一次项是_____, 二次项的系数是_____.（3）－254143a b ab 是 次项式，其中三次项系数是 二次项为，常数项为，写出所有的项 。

人教版初中数学重点知识精选掌握知识点，多做练习题，基础知识很重要！人教版初中数学和你一起共同进步学业有成！2.1 整式第3课时　多项式教学目标:1.通过本节课的学习,使学生掌握整式、多项式的项及其次数、常数项的概念.2.初步体会类比和逆向思维的数学思想.教学重点:掌握整式及多项式的有关概念,掌握多项式的定义、多项式的项和次数以及常数项等概念.教学难点:准确指出多项式的次数.教学过程一、复习引入1.列代数式:(1)长方形的长与宽分别为a、b,则长方形的周长是 ;(2)某班有男生x人,女生21人,则这个班共有学生 人;(3)图中阴影部分的面积为 ;(4)鸡兔同笼,鸡a只,兔b只,则共有头 个,脚 只.2.观察以上所得出的四个代数式与上节课所学单项式有何区别.(1)2(a+b);　(2)21+x;　(3)ab-π()2;(4)2a+4b.二、讲授新课1.多项式:板书由学生自己归纳得出的多项式概念.上面这些代数式都是由几个单项式相加而成的.像这样,几个单项式的和叫做多项式.在多项式中,每个单项式叫做多项式的项.其中,不含字母的项,叫做常数项.例如,多项3x2-2x+5有三项,它们是3x2,-2x,5,其中5是常数项.一个多项式含有几项,就叫几项式.多项式里,次数最高项的次数,就是这个多项式的次数.例如,多项式3x2-2x+5是一个二次三项式.注意:(1)多项式的次数不是所有项的次数之和.(2)多项式的每一项都包括它前面的符号.2.例题:【例1】判断:①多项式a3-a2b+ab2-b3的项为a3、a2b、ab2、b3,次数为12;②多项式3n4-2n2+1的次数为4,常数项为1.【例2】指出下列多项式的项和次数:(1)3x-1+3x2; (2)4x3+2x-2y2.【例3】指出下列多项式是几次几项式.(1)x3-x+1; (2)x3-2x2y2+3y2.【例4】已知代数式3x n-(m-1)x+1是关于x的三次二项式,求m、n的值.注意:多项式的项包括前面的符号,多项式的次数应为最高次项的次数.在例3讲完后插入整式的定义:单项式与多项式统称整式.分析例4时要紧扣多项式的定义,培养学生的逆向思维,使学生透彻理解多项式的有关概念,培养他们应用新知识解决问题的能力.【例5】一条河流的水流速度为2.5千米/时,如果已知船在静水中的速度,那么船在这条河流中顺水行驶和逆水行驶的速度分别怎样表示?如果甲、乙两船在静水中的速度分别是20千米/时和35千米/时,则它们在这条河流中顺水行驶和逆水行驶的速度各是多少?3.课堂练习:课本P58练习第1、2题.填空:-a2b-ab+1是 次 项式,其中三次项系数是 ,二次项为 ,常数项为 ,写出所有的项 .三、课时小结1.理解多项式的定义,能说出一个多项式是几次几项式,最高次数是几,分别由哪几项组成,各项的系数分别为多少,常数项为几.2.这堂课学习了多项式,与前一节所学的单项式合起来统称为整式,使知识形成了系统.(让学生小结,师生进行补充.)四、课堂作业课本P59习题2.1的第3、4题.相信自己，就能走向成功的第一步教师不光要传授知识，还要告诉学生学会生活。

2.1 整式（第3课时）教学设计一、内容和内容解析1.内容本节课是人教版《义务教育教科书•数学》七年级上册（以下统称“教材”）第二章“整式的加减”2.1整式第3课时，内容包括多项式的概念，多项式的项数和次数的概念.2.内容解析多项式是在学生学习了单项式的基础上进一步学习的．通过本节课的学习让学生理解多项式的概念，并使学生能准确地确定一个多项式的次数和项数．通过多项式的学习加深对整式的认识．多项式既是学生学过单项式后的延续和拓展，又是后续研究整式的加减运算的基础．此外也可以用来表示数学关系以及解决相关的实际问题，它是整个初中数学中起着承上启下作用的核心知识之一．基于以上分析，确定本节课的教学重点为：多项式以及有关概念．二、目标和目标解析1.目标（1）理解多项式、多项式的项和次数、整式的概念；（2）会用多项式表示简单的数量关系，并根据多项式中字母的值求多项式的值；（3）会用整式解决简单的实际问题，体会用整式表示数量关系的简洁性和一般性．2.目标解析达成目标（1）的标志是：会根据概念判断多项式，能确定多项式的项、项数和次数，并能说出判断的依据，能举例说明．达成目标（2）的标志是：会分析简单实际问题中的数量关系，并能够正确地用多项式表示数量关系．目标（3）是“内容所蕴含的思想方法”，学生需要在分析多项式结构特征过程中，经历由特殊（具体）到一般（抽象）的认识过程，感受多项式是一种重要的数学式子，从中提高观察、分析、归纳、概括能力．学生需要从列多项式的过程中，进一步感受整式中的字母表示数，整式可以表示实际问题中的数量关系，整式更具有简洁性和一般性．三、教学问题诊断分析七年级的学生注意力易分散，学习新的知识需要较长的理解过程，就本节课知识而言，容易将单项式与多项式的相关概念混淆，所以教学中教师应予以简单明了、深入浅出地分析，带着学生去发现和探究新知识，以问题的提出、问题的解决为主线，同时要创造条件和机会，让学生发表见解，发挥学生学习的主动性，提高学习的积极性．基于以上分析，确定本节课的教学难点为：准确确定多项式的次数和项，并且掌握单项式和多项式次数之间的联系和区别.四、教学过程设计（一）复习巩固，引入新课问题1：什么叫单项式？单项式的系数和次数？由数与字母的乘积组成的代数式叫做单项式.单项式中的数字因数，叫作单项式的系数一个单项式中，所有字母的指数的和，叫做这个单项式的次数．问题2：填空：1. 单项式－5y 的系数是_____，次数是_____.2. 单项式a 3b 的系数是_____，次数是_____.3. 单项式32ab 的系数是_____，次数是____. 4. 5x 2yz 与－15xzy n 是同次单项式，则n = .答案：1. －5；1；2. 1；43. 32；2 4. 2.师生活动：学生讨论，学生代表回答，教师根据学生回答进行评价【设计意图】巩固单项式的相关知识，为形成多项式的概念打下基础，形成对比．（二）新知探究问题3：观察这些式子：v +2.5， v －2.5，3x +5y +2z ，212ab r π-， x 2+2x +18？ 它们有什么共同特点？与单项式有什么联系？师生活动：学生小组讨论交流，自由发言回答上面的问题．教师参与小组讨论，并有针对性地进行指导．教师进一步提出问题，以上各式显然不是单项式，它们与单项式有联系吗？教师给出定义：这些式子都可以看作是几个单项式的和．多项式中，次数最高项的次数，叫做这个多项式的次数．多项式中，每个单项式叫做多项式的项．不含字母的项叫做常数项．一个多项式由几个单项式组成，就把它叫做几项式，如2x －3可以叫做二项多项式，3x +5y +2z 可以叫做三项多项式．教师进一步引导学生探究多项式次数的概念．学生可以发挥自己的想象去探究给多项式的次数命名的方法．教师不必苛求学生怎样想，让学生大胆发言，只要能发挥他们的想象力即可．教师在这一过程中教师可以引导，多项式的次数是不是也可以将所有字母的指数加在一块呢？如果字母多的话是不是有点太乱呢?如果这样的话我们是不是派个代表就行了，派谁当代表呢？引导学生说出，以次数最高的项的次数作为代表．教师总结：多项式中次数最高的项的次数叫做多项式的次数．同单项式一样，一个多项式的次数是几，我们就称它为几次式．如2x －3可以叫做一次二项式，3x +5y +2z 可以叫做一次三项式．【设计意图】通过问题引出多项式的概念，进而通过教师的导与学生的学很自然地得出多项式的项数、次数的概念.针对训练：1．判断下列各式哪些是多项式？（1）a ； （2）213x y ； （3）2x －1； （4）x 2+xy +y 2． 解：多项式有（3）和（4）．（1）和（2）是单项式．2．多项式x 2+y －z 是单项式___，___，___的和，它是___次___项式．（x 2；y ；－z ；）3．多项式3m 3－2m －5+m 2的常数项是____，二次项是_____，一次项的系数是_____．（－5；m 2；－2；）4. 一个多项式的次数是3，则这个多项式的各项次数（ D ）A ．都等于3B ．都小于3C ．都不小于3D ．都不大于3师生活动：在总结前面知识的基础上，进一步归纳，至此我们学习了单项式和多项式，单项式和多项式统称为整式．教师进一步提问，你能说一说单项式、多项式和整式三者之间的关系吗?学生讨论后回答．教师根据学生回答情况予以点拨、强调．教师点拨：①多项式的项，要包括它前面的性质符号；②对多项式的每一项来讲来，有系数．但对常数项不说系数，对整个多项式来说，没有系数的概念；③多项式的次数是多项式中次数最高的项的次数．【设计意图】通过自主观察、小组讨论交流，分析式子的结构特征，发现共同特点，并通过特征描述，抽象概括出多项式的概念．通过观察、分析每个单项式的结构特征，发现不同点，在此基础上定义多项式的项、项数和次数的概念及整式的概念．在讨论中激发学生参与学习的热情，培养观察、比较、分析、抽象概括的能力．（三）典例分析例1：用多项式填空：（1）温度由t℃下降5℃后是℃；（2）甲数x的13与乙数y的12的差可以表示为_________．解：（1）（t－5）；（2）1132x y．例2：如图所示，用式子表示圆环的面积．当R=15 cm，r=10cm时，求圆环的面积（π取3.14 ）．解：外圆的面积减去内圆的面积就是圆环的面积，所以圆环的面积是πR2－πr2．当R=15 cm，r=10cm时，圆环的面积（单位：cm2）是：3.14×152－3.14×102=392.5．这个圆环的面积是392.5cm2．针对训练：一个花坛的形状如图所示，这的两端是半径相等的半圆，求：（1）花坛的周长L；（2）花坛的面积S．解：（1）L＝2a+2πr．（2）花坛的面积是一个长方形的面积与两个半圆的面积之和，即S=2ar+ πr2．师生活动：学生独立完成例1，例2由教师板书示范.此环节教师应关注学生书写的规范性．【设计意图】从实际问题出发,再次体验多项式的次数、项数的概念,教师从中及时反馈学生的掌握情况,进一步巩固多项式的有关概念,同时体会用字母表示数的意义和学习求多项式的值的方法．（四）当堂巩固1．指出下列多项式的项和次数a 5－a 2b +ab －b 3．解：多项式的项：a 5，－a 2b ，ab ，－b 3；多项式的次数： 5．2．式子3x a+1+4x –2b 是四次二项式，试求a ，b 的值．解：因为式子的次数是四次，所以a +1=4，所以a =3．又因为式子是二项式，所以2b =0，即b =0．所以a =3，b =0．3．下列整式中哪些是单项式？哪些是多项式？是单项式的指出系数和次数，是多项式的指出项和次数：212a b -，427m n ，x 2+y 2－1，x ，32t 3，3π，3x 2－y +3xy 3+x 4－1，2x －y ．【设计意图】进一步巩固多项式、多项式的项、项数和次数的概念.（五）能力提升1．多项式112134634n n n n x x x x -++-+-是几次几项式？其中最高次项是哪项？最高次项的系数是多少？ 解：n ＋2次多项式，最高次项是234n x +-， 最高次项系数是34-． 2．多项式－a ＋2a 2－3a 3＋4a 4－5a 5＋……第99项是 ，第2022项是 ，第n 项是 ． （－99a 99；2022a 2022；(－1)n •n •a n ．）3．某公园的门票价格是：成人10元/张；学生5元/张．（1）一个旅游团有成人x 人、学生y 人，那么该旅游团应付多少门票费？（2）如果该旅游团有37个成人、15个学生，那么他们应付多少门票费？解：（1）该旅游团应付的门票费是（10x＋5y）元．（2）把x＝37，y＝15代入代数式，得10x＋5y =10×37＋5×15 ＝445．因此，他们应付445元门票费．【设计意图】提升学生灵活应用多项式及相关的概念解决问题的能力.（六）感受中考1．（3分）（2021•青海2/25）一个两位数，它的十位数字是x，个位数字是y，那么这个两位数是（）A．x+y B．10xy C．10（x+y）D．10x+y【解答】解：一个两位数，它的十位数字是x，个位数字是y，这个两位数10x+y．故选：D．2．（8分）（2021•河北20/26）某书店新进了一批图书，甲、乙两种书的进价分别为4元/本、10元/本．现购进m本甲种书和n本乙种书，共付款Q元．（1）用含m，n的代数式表示Q；（2）若共购进5×104本甲种书及3×103本乙种书，用科学记数法表示Q的值．【解答】（1）由题意可得：Q＝4m+10n；（2）将m＝5×104，n＝3×103代入（1）式得：Q＝4×5×104+10×3×103＝2.3×105．【设计意图】通过对最近几年的中考试题的训练，使学生提前感受到中考考什么，进一步了解考点.（七）课堂小结1．说一说单项式、多项式、整式各有什么特点？2．它们三者之间的关系是怎样的？【设计意图】通过小结，使学生梳理本节课所学内容，掌握本节课的核心——多项式、多项式的项、项数和次数的概念及整式的概念，体会多项式在实际中的应用，感受由“数”到“式”，由特殊（具体）到一般（抽象）的数学思想.（八）布置作业1．P59：习题2.1：第3、4题；2．P60：习题2.1：第6、7题．五、教学反思在此之前学生已经学习了单项式及单项式的系数、次数的概念，这为过渡到本节的学习起着铺垫的作用．教材遵循“由特殊到一般”的学习规律，先是引进背景比较熟悉的实际问题，从实际问题中抽象出多项式的概念，并且让学生体会到多项式概念的产生源于实际的需要．在本节课中，多项式概念的学习是在单项式的基础上引出来的，着重指出多项式是几个单项式的和．因此，本节课的教学设计是通过比较单项式与多项式之间的异同点，掌握两个概念之间的区别和联系来突出多项式概念的本质，帮助学生理解多项式的概念，以及多项式的项和次数的概念．因而，观察分析、抽象概括、练习巩固成为本节课学习的主要方式．。

第3课时 多项式1．理解多项式的概念；(重点)2．能准确迅速地确定一个多项式的项数和次数；3．能正确区分单项式和多项式．(重点)一、情境导入列代数式：(1)长方形的长与宽分别为a 、b ，则长方形的周长是________；(2)图中阴影部分的面积为________；(3)某班有男生x 人，女生21人，则这个班的学生一共有________人．观察我们所列出的代数式，是我们所学过的单项式吗？若不是，它又是什么代数式？二、合作探究探究点一：多项式的相关概念【类型一】 单项式、多项式与整式的识别指出下列各式中哪些是单项式？哪些是多项式？哪些是整式？x 2＋y 2，－x ，a ＋b3，10，6xy ＋1，1x ，17m 2n ，2x 2－x －5，2x 2＋x，a 7. 解析：根据整式、单项式、多项式的概念和区别来进行判断．解：2x 2＋x ，1x 的分母中含有字母，既不是单项式，也不是多项式，更不是整式． 单项式有：－x ，10，17m 2n ，a 7； 多项式有：x 2＋y 2，a ＋b 3，6xy ＋1，2x 2－x －5； 整式有：x 2＋y 2，－x ，a ＋b3，10，6xy ＋1，17m 2n ，2x 2－x －5，a 7. 方法总结：(1)分母中含有字母(π除外)的式子不是整式；(2)单项式和多项式都是整式；(3)单项式不含加、减运算，多项式必含加、减运算．【类型二】 确定多项式的项数和次数写出下列各多项式的项数和次数，并指出是几次几项式．(1)23x 2－3x ＋5； (2)a ＋b ＋c －d ；(3)－a 2＋a 2b ＋2a 2b 2.解析：根据多项式的项数是多项式中单项式的个数，多项式的次数是多项式中次数最高的单项式的次数，可得答案．解：(1)23x 2－3x ＋5的项数为3，次数为2，二次三项式； (2)a ＋b ＋c －d 的项数为4，次数为1，一次四项式；(3)－a 2＋a 2b ＋2a 2b 2的项数为3，次数为4，四次三项式．方法总结：(1)多项式的项一定包括它的符号；(2)多项式的次数是多项式里次数最高项的次数，而不是各项次数的和；(3)几次项是指多项式中次数是几的项．【类型三】 根据多项式的概念求字母的取值已知－5x ＋10x －4x y 是关于x 、y 的六次多项式，求m 的值，并写出该多项式．解析：根据多项式中次数最高的项的次数叫做多项式的次数可得m ＋2＝6，解得m ＝4，进而可得此多项式．解：由题意得m ＋2＝6，解得m ＝4，此多项式是－5x 4＋104x 4－4x 4y 2.方法总结：此题考查了多项式，解题的关键是弄清多项式次数是多项式中次数最高的项的次数．【类型四】 与多项式有关的探究性问题若关于x 的多项式－5x －mx ＋(n －1)x －1不含二次项和一次项，求m 、n 的值．解析：多项式不含二次项和一次项，则二次项和一次项系数为0.解：∵关于x 的多项式－5x 3－mx 2＋(n －1)x －1不含二次项和一次项，∴m ＝0，n －1＝0，则m ＝0，n ＝1.方法总结：多项式不含哪一项，则哪一项的系数为0.探究点二：多项式的应用如图，某居民小区有一块宽为2a 米，长为b 米的长方形空地，为了美化环境，准备在此空地的四个顶点处各修建一个半径为a 米的扇形花台，在花台内种花，其余种草．如果建造花台及种花费用每平方米为100元，种草费用每平方米为50元．那么美化这块空地共需多少元？解析：四个角围成一个半径为a 米的圆，阴影部分面积是长方形面积减去一个圆面积．解：花台面积和为πa 2平方米，草地面积为(2ab －πa 2)平方米．所以需资金为[100πa 2＋50(2ab －πa 2)]元．方法总结：用式子表示实际问题的数量关系时，首先要分清语言叙述中关键词的含义，理清它们之间的数量关系和运算顺序．三、板书设计多项式：几个单项式的和叫做多项式．多项式的项：多项式中的每个单项式叫做多项式的项．常数项：不含字母的项叫做常数项．多项式的次数：多项式里次数最高项的次数叫做多项式的次数．整式：单项式与多项式统称整式．这节课的教学内容并不难，如果采用讲授的方式，很快90%以上的学生都可以理解、掌握．虽然单纯地从学生接受知识的角度，讲授法应该效果更好，但同时学生的自主学习的习惯和能力也不知不觉地被忽略了．事实证明，学生没有养成一个良好的自主学习的习惯，不会自己阅读、分析题意，他们今后的学习会受到很大的制约．。

第二章整式的加减2.1 整式课时3 多项式【知识与技能】理解并掌握多项式及多项式的项和次数的概念，能准确地找出多项式的项和次数.【过程与方法】通过观察、讨论、自主探究，提高学生的概括能力.【情感态度与价值观】培养学生自主探索知识和合作交流的能力.多项式、多项式的项和次数、整式的概念.求多项式的次数.多媒体课件出示问题：观察一列数1，4，9，16，25，…，第6个数是多少？第n个数呢？你能用含n的式子表示第n个数吗？观察一列数2，5，10，17，26，…，第6个数是多少？第n个数呢？你能用含n的式子表示第n个数吗？学生思考得出答案，第一列第6个数是36，第n个数是n2；第二列第6个数是37，第n个数是n2+1.我们知道，n2是一个单项式，而n2+1不是单项式，那么它属于哪一类式子呢？这就是我们今天要解决的问题.（引入新课，板书课题）一、思考探究，获取新知活动1：说一说.（1）若一个长方形的长与宽分别为a，b，则此长方形的周长是；（2）若某班有男生x人，女生21人，则这个班共有学生人；（3）鸡兔同笼，若鸡有a只，兔有b只，则共有头个，脚只.答案：（1）2（a+b）（2）（21+x）（3）（a+b）（2a+4b）活动2：观察以上所得出的四个式子与上节课所学的单项式有何区别.小组讨论后，派代表回答，师生共同归纳多项式的相关概念：多项式：几个单项式的和叫作多项式.多项式的项和次数：每个单项式叫作多项式的项，不含字母的项叫作常数项.例如，多项式3x2-2x+5有三项，它们是3x2，-2x，5，其中5是常数项.一个多项式含有几项，就叫几项式.多项式里，次数最高项的次数，叫作这个多项式的次数.例如，多项式3x2-2x+5是一个二次三项式.二、典例精析，掌握新知例2一条河流的水流速度为2.5千米/时，如果船在静水中的速度为x千米/时，那么船在这条河流中顺水行驶和逆水行驶的速度分别怎样表示？如果甲、乙两条船在静水中的速度分别是20千米/时和35千米/时，那么它们在这条河流中顺水行驶和逆水行驶的速度分别是多少？【解】船在这条河流中顺水行驶的速度为（x+2.5）千米/时，逆水行驶的速度为（x-2.5）千米/时.甲船顺水行驶的速度为20+2.5=22.5（千米/时），逆水行驶的速度为20-2.5=17.5（千米/时）.乙船顺水行驶的速度为35+2.5=37.5（千米/时），逆水行驶的速度为35-2.5=32.5（千米/时）.点拨：先用多项式表示实际问题中的数量关系，再将多项式中的字母表示的数代入计算，即可求出相应的值.整式：单项式与多项式统称整式.1.多项式及多项式的项、次数的概念.2.对比单项式和多项式，总结出单项式与多项式统称整式.教材P59习题2.1第2，3，4，5题。

2.1整式第 3课时多项式教课目的 :1.经过本节课的学习,使学生掌握整式、多项式的项及其次数、常数项的观点.2.初步领会类比和逆向思想的数学思想.教课要点 :掌握整式及多项式的相关观点,掌握多项式的定义、多项式的项和次数以及常数项等概念 .教课难点 :正确指出多项式的次数.教课过程一、复习引入1.列代数式 :(1)长方形的长与宽分别为a、 b,则长方形的周长是;(2)某班有男生 x人 ,女生 21人 ,则这个班共有学生人 ;(3)图中暗影部分的面积为;(4) 鸡兔同笼 ,鸡 a只 ,兔 b只 ,则共有头个,脚只.2.察看以上所得出的四个代数式与上节课所学单项式有何差别.(1)2(a+b); (2)21+x;(3)ab- π() 2;(4)2a+4b.二、讲解新课1.多项式 :板书由学生自己概括得出的多项式观点.上边这些代数式都是由几个单项式相加而成的.像这样 ,几个单项式的和叫做多项式 .在多项式中 ,每个单项式叫做多项式的项 .此中 ,不含字母的项 ,叫做常数项 .比如 ,多项 3x 2-2x+5 有三项 ,它们是 3x2 ,-2x,5, 此中 5是常数项 .一个多项式含有几项,就叫几项式 .多项式里 ,次数最高项的次数,就是这个多项式的次数.比如 ,多项式 3x2-2x+5 是一个二次三项式.注意 :(1) 多项式的次数不是全部项的次数之和.(2) 多项式的每一项都包含它前方的符号.2.例题 :【例 1】判断 :①多项式 a3 -a2 b+ab2-b 3的项为 a3、 a2 b、 ab2、 b3 ,次数为 12;②多项式 3n4-2n 2+1的次数为 4,常数项为 1.【例2】指出以下多项式的项和次数:(1)3 x-1+3x 2 ;(2)4x 3+2x-2y 2 .【例3】指出以下多项式是几次几项式.(1)x 3-x+1;(2)x 3 -2x 2y2+3y 2.【例4】已知代数式3x n-(m-1)x+1 是对于 x的三次二项式 ,求 m、n的值 .注意:多项式的项包含前方的符号,多项式的次数应为最高次项的次数.在例 3讲完后插入整式的定义 :单项式与多项式统称整式.剖析例 4时重要扣多项式的定义,培育学生的逆向思想,使学生透辟理解多项式的相关观点,培育他们应用新知识解决问题的能力.【例 5】一条河流的水流速度为 2.5 千米 /时 ,假如已知船在静水中的速度,那么船在这条河流中顺流行驶和逆水行驶的速度分别如何表示?假如甲、乙两船在静水中的速度分别是20千米 /时和 35?千米 /时 ,则它们在这条河流中顺流行驶和逆水行驶的速度各是多少3.讲堂练习 :课本 P58练习第 1、 2题 .填空 :-a2b-ab+1 是次项式 ,此中三次项系数是,二次项为,常数项为,写出全部的项.三、课时小结1.理解多项式的定义,能说出一个多项式是几次几项式,最高次数是几,分别由哪几项构成,各项的系数分别为多少,常数项为几.2.这堂课学习了多项式,与前一节所学的单项式合起来统称为整式,使知识形成了系统.(让学生小结 ,师生进行增补.)四、讲堂作业课本 P59习题 2.1的第 3、 4题 .。

整式第3课时 多项式学习内容：课本p58例3及课本p64提到的一个内容学习目的和要求：1、通过用整式来表示事物间的关系，逐步掌握数学建模思想；2、理解多项式的升(降)幂排列的概念，会进展多项式的升(降)幂排列。

3、通过尝试和交流，体会多项式升(降)幂排列的可行性和必要性。

4、初步体验排列组合思想与数学美感，培养审美观。

学习重点和难点：重点：会进展多项式的升(降)幂排列，体验其中蕴含的数学美。

难点：会进展多项式的升(降)幂排列，体验其中蕴含的数学美。

一、自主学习：1、教材p58例3：我们知道船在河流中行驶时，船的速度需要分两种情况讨论： 〔1〕顺水行驶：船的速度= ；〔2〕逆水行驶：船的速度= ；在上面两个关系式中假设用字母V 表示静水速度那么船的顺水速度为 船的逆水速度为当V=20时那么甲船顺水速度 甲船逆水速度乙船顺水速度 乙船逆水速度2..请运用加法交换律，任意交换多项式x 2＋x ＋1中各项的位置，可以得到几种不同的排列方式？在众多的排列方式中，你认为那几种比拟整齐？【提示】有六种不同的排列方式，像x 2＋x ＋1与1＋x ＋x 2这样的排列比拟整齐。

这两种排列有一个共同点，那就是x 的指数是逐渐变小(或变大)的。

我们把这种排列叫做升幂排列与降幂排列。

例如：把多项式5x 2＋3x －2x 3－1按x 的指数从大到小的顺序排列，可以写成－2x 3＋5x 2＋3x －1，这叫做这个多项式按字母x 的降幂排列。

假设按x 的指数从小到大的顺序排列，那么写成－1＋3x ＋5x 2－2x 3，这叫做这个多项式按字母x 的升幂排列。

二、合作探究1、请把卡片按x 降幂排列2、把多项式2πr－1＋3πr3－π2r2按r升幂排列。

【提示】：π是数字，不是字母，题目中一次项、二次项、三次项系数分别为2π、－π2、3π。

3、把多项式a3－b3－3a2b＋3a b2重新排列。

(1)按a升幂排列；(2)按a降幂排列。