下载文档原格式
第四章
第四章
无约束优化问题标准形式：
无约束优化问题标准形式：
§
§
§
§
§
§
图最速下降法的收敛过程
αα
2
2
例4－1 求目标函数
取初始点
[2,2]
=
x
例4－2 求目标函数解取初始点[2,2]
=x
算出一维搜索最佳步长
§
例4－3 用梯度法求下面无约束优化问题：
例4－3 用梯度法求下面无约束优化问题：
例4－3 用梯度法求下面无约束优化问题：
例4－3 用梯度法求下面无约束优化问题：
例4－3 用梯度法求下面无约束优化问题：
梯度法的特点
x
给定0,ε
一般迭代式：
§4.3
§4.3
§4.3
§4.3
α0
d 0
x
x 1
x*
1
α1d 1
1()
f −∇x d 1
4-4 共轭方向法
假设目标函数f (x ) 在极值点附近的二次近似函数为
沿某个下降方向
如果能够选定这样的搜索方向，那么对于二
α
0d0
x0x1x*
1
α
1
d1
1
()
f
−∇x d
1。
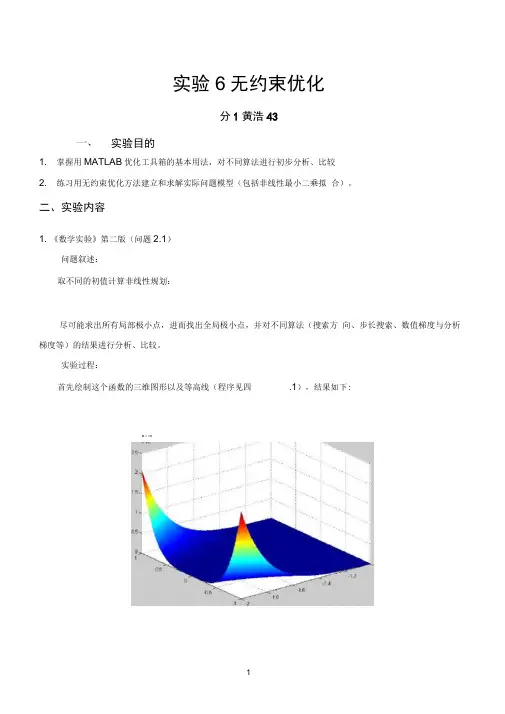
实验6无约束优化分1黄浩43实验目的1. 掌握用MATLAB优化工具箱的基本用法，对不同算法进行初步分析、比较2. 练习用无约束优化方法建立和求解实际问题模型（包括非线性最小二乘拟合）。
二、实验内容1. 《数学实验》第二版（问题2.1）问题叙述：取不同的初值计算非线性规划：尽可能求出所有局部极小点，进而找出全局极小点，并对不同算法（搜索方向、步长搜索、数值梯度与分析梯度等）的结果进行分析、比较。
实验过程：首先绘制这个函数的三维图形以及等高线（程序见四.1），结果如下:s M tn0-”19 A8 A1G \ 5 -14 -13 \ 2 A1通过观察这两幅图，可以得到，x2确定时，x1越负，函数值越大，x1确定时，x2绝对值越大，函数值越大。
但对于x1正向偏离0的情况，并没有很好的反映，于是扩大绘图范围，做出下图（程序见四.2）：-1 -10由上面两幅图可见，方程像是一个四角被捏起的花布，而且z的最小值为0< 因此只要求解该方程的零点，即得到了方程的局部极小点，且若将原方程变形为:我们容易发现，该方程的零点为：x2=0或x1=0或x1=1或在求解零点之前，先针对一个零点，不妨用x1=1, x2=1，分析不同算法的优劣。
在matlab的无约束优化中，可以使用fminumc和fminsearch两种函数，搜索方向的算法有BFGS 公式、DFP公式和最速下降法三种（书中还提到的Gill-Murray 公式在matlab中已经不再使用），步长的一维搜索有混合二次三次多项式插值和三次多项式插值两种方法，另外，在求解函数梯度是也有数值方法和分析方法两种。
在对上述四类算法因素进行分析时，我们采用控制变量法，每次只保持一种或两种算法因素改变，分析它的精度及效率。
（一）分析fminumc与fminsearch两种方法的精度及效率选择初值为x1=0.8,x2=0.8，使用fminunc和fminsearch的默认算法及控制参数，输出结果如下（程序见四.3、四.4）：因为精确解为x1=1, z=0,我们便可以比较出不同算法的精度。
数学建模案例之多变量无约束最优化多变量无约束最优化问题是指在变量间没有限制条件的情况下，求解目标函数的最优值。
这类问题在数学建模中非常常见，实际应用非常广泛。
下面以一个实际案例说明多变量无约束最优化的建模过程。
假设地有几个旅游景点，现在需要制定一个旅游路线，使得游客的游玩时间最长，同时经济成本最低。
已知每个旅游景点之间的距离和游玩时间，以及游客每次游玩每公里所需的成本。
目标是找到一条旅游路线，使得游客在游览所有景点后，花费的经济成本最少。
首先，我们需要定义问题的数学模型。
假设有n个旅游景点，用x1, x2, ..., xn表示每个景点的游玩时间（单位：小时），用dij表示第i个景点和第j个景点之间的距离（单位：公里），用c表示游客游玩每公里所需的成本。
为了定义问题的数学模型，我们需要明确如下几个关键部分：1. 决策变量：定义一个n维向量X，其中每一个分量xi表示游客在第i个景点的游玩时间。
2. 目标函数：定义一个目标函数f(X)，表示游客花费的经济成本。
在本例中，目标函数可以定义为：f(X) = ∑dij * xi * c。
3.约束条件：由于是无约束最优化问题，这里没有额外的约束条件。
有了以上几个关键部分，我们可以将问题的数学模型表达为如下形式：最小化：f(X) = ∑dij * xi * c其中，i=1,2,...,n下一步是求解这个最优化问题。
可以使用各种数值优化算法，比如梯度下降法、牛顿法、遗传算法等。
具体的求解过程会涉及到算法的具体细节，这里不再详述。
最后，根据求解结果，我们可以得到游玩时间最长且经济成本最低的旅游路线。
这条路线就是我们需要制定的旅游路线。
总结起来，多变量无约束最优化问题在数学建模中的应用非常广泛。
通过定义合适的决策变量、目标函数和约束条件，可以将实际问题转化为数学模型，并通过数值优化算法求解这个模型，得到最优解。
在实际应用中，对于复杂的问题，可能需要结合多种算法和技巧来求解。
实验五：无约束优化班级 姓名 学号一、实验目的：学会用matlab 软件求解单变量和多变量无约束优化问题。
二、实验要求：1. 熟悉一维搜索的方法：进退法、黄金分割法、抛物线插值法、Armijo 准则；2. 熟悉求解多变量无约束问题的方法：变量轮换法、最速下降法、牛顿法、共轭梯度法；3. 会用matlab 软件求解无约束优化问题。
三、实验内容：1、试用matlab 优化工具箱中的fmincon 函数求解下列非线性规划问题：2221232212323123212223123m in ()8020..2023,,0f x x x x x x x x x x s t x x x x x x x =+++⎧-+≥⎪++≤⎪⎪--+=⎨⎪+=⎪⎪≥⎩(1)给出matlab 源代码； (2)求解结果粘贴.2、(精确一维搜索) 用0.618法求函数2()sin f x x x =-在[]0,1上的极小点，取自变量的允许误差为410δ-=，函数变量的允许误差为510ε-=。
3、(不精确一维搜索) Armijo 准则是许多非线性规划算法求步长时都必须执行的步骤。
Armijo 准则是指给定()0,1,(0,0.5),βσ∈∈令步长因子km k αβ=，其中km 是满足下列不等式的最小非负整数()()()mmTk k k k k f x d f x g d βσβ+≤+*这里k g 是函数()f x 在当前迭代点k x 处的梯度函数，k d 是当前迭代点k x 处的搜索方向. 可以证明()f x 若是连续可微的且满足0T k k g d <，则准则是有限终止的，即存在正数σ，使得对于充分大的正整数m ，()*成立.为了程序实现的方便，我们把Armijo 准则描述成下列详细的算法步骤： 算法1（Armijo 准则）步0：给定()0,1,(0,0.5),βσ∈∈令:0m =；步1：若不等式()()m m T k k k k k f x d f x g d βσβ+≤+成立， 置:,k m m = 1:km k k k x x d β+=+，停止.否则,转步2；步2：令:1m m =+，转步1.（1）试将上述的Armijo 准则编制成可重复利用的matlab 程序模块。
