下载文档原格式
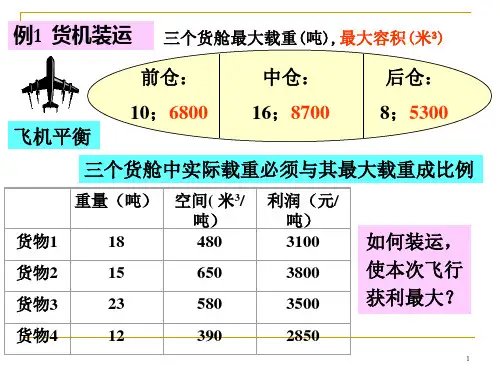
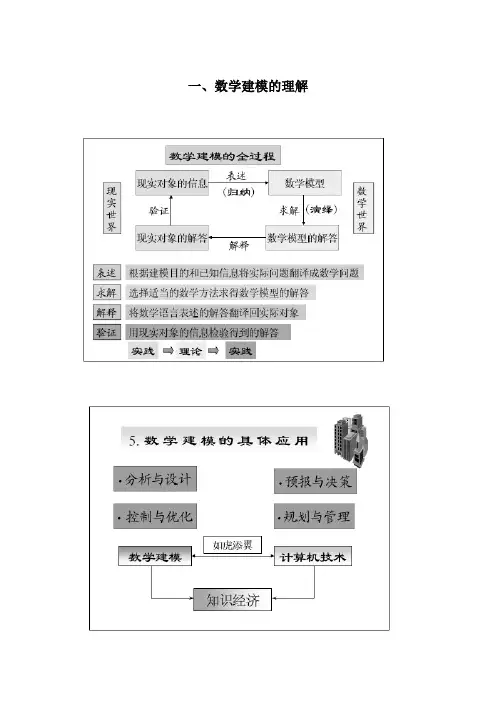
一、数学建模的理解例子：二、经典最优化方法1、微分与极值2、无约束极值问题3、约束极值问题三、无约束优化问题数值解法（向量）1、最优梯度法（梯度下降法）2、牛顿法3、共轭梯度法4、阻尼牛顿法5、变尺度法1.1 无约束优化的一般形式无约束非线性规划问题为其最优解通常都是局部最优解，寻找全局最优解需要对局部最优解进行比较以后得到（如果能够求出所有局部最优解的话）。
1.2 最优性条件是最优解的必要条件为；充分条件为，且正定。
1.3 下降法的基本思想在迭代的第k步，确定一个搜索方向和一个步长，使沿此方向、按此步长走一步到达下一点时，函数值下降。
其基本步骤为1）选初始解；2）对于第次迭代解，确定搜索方向并在此方向确定搜索步长令，使<；3）若符合给定的迭代终止原则，停止迭代，最优解；否则，转2。
搜索方向的选择（不同方向产生不同的算法）：1）最速下降法（梯度法）2）牛顿法3）拟牛顿法：利用第和步得到的，用BFGS公式，DFP公式，GM公式等迭代公式构造正定矩阵近似代替，或直接构造近似代替，从而由，或得到下降方向d k+1。
搜索步长的确定——线性搜索：用二分法、黄金分割法（即0.618法）、Fibonacci 法，牛顿切线法和割线法，插值方法等近似方法求一维优化问题：来确定步长。
2.1 非线性最小二乘拟合问题有一组数据要拟合一个已知函数y=f(x, t), x=(x1,x2,…,xm),, x为待定系数。
记误差，，拟合误差定义为的平方和，于是问题表示为如下的优化模型：当对（的某些分量）是非线性函数时，称非线性最小二乘拟合。
四线性规划1、线性规划的数学模型某工厂安排生产1、2两种产品，2、线性规划的图解法单纯形及其求解法1.1 线性规划的图解法线性规划的图解法只能用于求解两个决策变量（2维）的情形。
由于线性规划的约束条件和目标函数均为线性函数，所以对于2维情形，可以在平面坐标系下画出可行域和目标函数的等值线。
1 用MATLAB优化工具箱解无约束优化问题用MATLAB优化工具包求解无约束非线性规划时必须先化为如下形式：Min f(x) (NLP)求解程序名为fminunc，其最简单的调用格式为：x = fminuncn('fun',x0)其最复杂的调用格式为：[x,fval,exitflag,output,grad,hessian] =fminunc(@f,x0,options,P1,P2,...)输出参数输入参数注意事项1.4.1 程序fminunc输出变量其中输出变量的含义为：1） x ：最优解2） fval ：最优解处的函数值3） exitflag ：程序结束时的状态指示：· >0：收敛· 0：函数调用次数或迭代次数达到最大值（该值在options中指定）· <0：不收敛4) Output: 包含以下数据的一个结构变量· funcCount 函数调用次数· iterations 实际迭代次数· cgiterations 实际PCG迭代次数（大规模计算用）· algorithm 实际使用的算法· stepsize 最后迭代步长（中等规模计算用）5) grad: 目标函数梯度6) hessian: 目标函数的hessian矩阵1.4.2 程序fminunc输入参数其中输入变量的含义为：· x0为初始解（缺省时程序自动取x0=0）· fun.m给出目标函数，当GradObj='on时必须给出其梯度，当Hessian='on 时还必须给出其Jacobi矩阵，一般形式为· function [f,g,H] = fun(x)· f = ... % objective function value· if nargout > 1· g = ... % gradient of the function· if nargout > 2· H = ... % Hessian of the function· end· options：包含算法控制参数的结构设定（或显示）控制参数的命令为Optimset，有以下一些用法：Optimset //显示控制参数optimset optfun //显示程序'optfun的控制参数opt=optimset //控制参数设为[]（即缺省值opt=optimset(optfun)// 设定为程序'optfun的控制参数缺省值Opt=optimset('par1',val1,'par2',val2,...)Opt=optimset(oldopts,'par1',val1,...)opt=optimset(oldopts,newopts)可以设定的参数比较多，对fminunc，常用的有以下一些参数：Diagnostics 是否显示诊断信息（ 'on' 或'off）Display 显示信息的级别（'off' ， 'iter' ， 'final，'notify）LargeScale 是否采用大规模算法（ 'on' 或'off）缺省值为onMaxIter 最大迭代次数TolFun 函数计算的误差限TolX 决策变量的误差限GradObj 目标函数是否采用分析梯度（'on' ，'off）Hessian 目标函数是否采用分析Hess矩阵（'on' ，'off）MaxFunEvals 目标函数最大调用次数HessUpdate 拟牛顿法修改方法（’bfgs’(缺省值)，’dfp’,’gillmurray’,’steepdesc’）LineSearchType 线搜索方法(‘cubicpoly’,’quadcubic’(缺省值))1.4.3 注意事项· fminunc中输出变量、输入参数不一定写全，可以缺省。
采用缺省值效果一般会很好。
· 当中间某个输入参数缺省时，需用[]占据其位置。
· 当函数高度非线性或严重不连续时，用程序fminsearch代替fminunc。
2用MATLAB优化工具箱解非线性最小二乘拟合问题l 非线性最小二乘问题mins.t. v1x v2求解程序名为lsqnonlin，其最简单的调用格式为：x=lsqnonlin(@F,x0, v1,v2)其最复杂的调用格式为：[x,norm,res,ef,out,lam,jac] = lsqnonlin(@F,x0,v1,v2,opt,P1,P2, ... ) l 非线性拟合问题mins.t. v1x v2求解程序名为lsqcurvefit，其最简单的调用格式为：x=lsqcurvefit(@F, x0,t,y,v1,v2)其最复杂的调用格式为：[x,norm,res,ef,out,lam,jac] =lsqcurvefit(@F,x0,t,y,v1,v2,opt,P1,P2,...)输出参数输入参数注意事项2.3.1 程序lsqnonlin和lsqcurvefit的输出参数其中输出变量的含义为：1） x ：最优解2） norm ：误差的平方和3）res: 误差向量4） ef ：程序结束时的状态指示：· >0：收敛· 0：函数调用次数或迭代次数达到最大值（该值在options中指定）· <0：不收敛5) out: 包含以下数据的一个结构变量· funcCount 函数调用次数· iterations 实际迭代次数· cgiterations 实际PCG迭代次数（大规模计算用）· algorithm 实际使用的算法· stepsize 最后迭代步长（中等规模计算用）· firstorderopt 一阶最优条件满足的情况（大规模计算用）6) lam：上下界所对应的Lagrange乘子7) jac：结果（x点）处的雅可比矩阵2.3.2程序lsqnonlin和lsqcurvefit的输入参数其中输入变量的含义为：· x0为初始解（缺省时程序自动取x0=0）· F给出目标函数的M文件，当Jacobian='on时必须给出其Jacobi矩阵，一般形式为：function [F,J] = Fun(x)(对程序lsqcurvefit为Fun(x,t))F = ... % objective function values at xif nargout > 1 % two output argumentsJ = ... % Jacobian of the function evaluated at xend· t,y: 拟合数据· v1,v2: 上下界· options：包含算法控制参数的结构设定（或显示）控制参数的命令为Optimset，有以下一些用法：Optimset //显示控制参数optimset optfun //显示程序'optfun的控制参数opt=optimset //控制参数设为[]（即缺省值opt=optimset(optfun)// 设定为程序'optfun的控制参数缺省值Opt=optimset('par1',val1,'par2',val2,...)Opt=optimset(oldopts,'par1',val1,...)opt=optimset(oldopts,newopts)可以设定的参数比较多，对lsqnonlin和lsqcurvefit，常用的有以下一些参数：Diagnostics 是否显示诊断信息（ 'on' 或'off）Display 显示信息的级别（'off' ， 'iter' ， 'final，'notify）LargeScale 是否采用大规模算法（ 'on' 或'off）缺省值为onMaxIter 最大迭代次数TolFun 函数计算的误差限TolX 决策变量的误差限Jacobian 目标函数是否采用分析Jacobi矩阵（'on' ，'off）MaxFunEvals 目标函数最大调用次数LevenbergMarquardt 搜索方向选用LM法(‘on’), GN法(‘off’,缺省值) LineSearchType 线搜索方法(‘cubicpoly’,’quadcubic’(缺省值))2.3.3 注意事项· fminunc中输出变量、输入参数不一定写全，可以缺省。
· 当中间某个输入参数缺省时，需用[]占据其位置。
3 用MATLAB优化工具包解线性规划用MATLAB优化工具包求解线性规划时必须先化为如下形式：（LP）求解程序名为linprog，其最简单的调用格式为：x = linprog(c,A1,b1) （用于不含有等式约束和上下解约束的问题）其最复杂的调用格式为：[x,fval,exitflag,output,lambda] =linprog(c,A1,b1,A2,b2,v1,v2,x0,options)4 用MATLAB优化工具包解二次规划用MATLAB优化工具包求解二次规划时必须先化为如下形式：(QP)求解程序名为quadprog，其最简单的调用格式为：x = quadprog(H,c,A1,b1) （用于不含有等式约束和上下解约束的问题）其最复杂的调用格式为：[x,fval,exitflag,output,lambda] =quadprog(H,c,A1,b1,A2,b2,v1,v2,x0,options)5插值方法的Matlab实现a．对于Lagrange插值必须自编程序b．低次插值的Matlab命令分段线性插值：y=inter1(x0, y0, x)，其中输入离散数据x0、y0、x，输出对应x的插值y。
三次样条插值：y=inter1(x0, y0, 'spline')或y=spline(x0, y0, x)其中，x0、y0、x和y的意义同上。
6数值积分的Matlab实现trapz(x)用梯形公式计算(h=1)，输入数组x为各区间端点的函数值。
