量子力学课件(7)( 一维线性谐振子)
- 格式:ppt
- 大小:362.50 KB
- 文档页数:19

一维线性谐振子波函数及概率分布的可视演示一维线性谐振子是量子力学中重要的模型系统之一,它被广泛应用于许多领域,包括原子物理、分子物理和固体物理等。
在本文中,我们将会进行一维线性谐振子的波函数及概率分布的可视演示,通过图像和数学方程式的结合,来帮助读者更直观地理解这一重要模型系统。
一维线性谐振子的哈密顿量可以写成如下形式:\[ \hat{H} = -\frac{\hbar}{2m} \frac{\partial^2}{\partial x^2} +\frac{1}{2}m\omega^2x^2 \]m为谐振子的质量,ω为谐振频率,ħ为普朗克常量。
谐振子的能量本征态满足薛定谔方程:\[ \hat{H}\psi(x) = E\psi(x) \]E为能量本征值,ψ(x)为波函数。
下面,我们将通过数学方程式和图像的结合,来展示一维线性谐振子的波函数及概率分布。
我们首先绘制一维线性谐振子的前几个能级的波函数图像。
通过数值计算和图像化技术,我们可以得到一维线性谐振子在不同能级下的波函数的形状。
在这些波函数图像中,我们可以看到波函数在空间中的分布情况,以及不同能级下波函数的节点、振荡等特性。
这样一来,读者可以更直观地理解一维线性谐振子的波函数在空间中的分布规律。
接下来,我们将展示一维线性谐振子的概率分布。
一维线性谐振子的概率分布可以通过波函数的模长的平方来表示:\[ P(x) = |\psi(x)|^2 \]通过绘制一维线性谐振子在不同能级下的概率分布图像,我们可以直观地展示谐振子在空间中的概率分布情况。
这可以帮助读者更加清晰地了解一维线性谐振子的概率分布规律。
通过波函数及概率分布的可视演示,读者可以更加深入地理解一维线性谐振子模型系统的性质。
通过图像和数学方程式的结合,我们可以直观地看到一维线性谐振子的波函数在空间中的分布情况,以及概率分布的特性。
这样一来,读者可以更加深入地理解一维线性谐振子系统的物理本质。


一维线性谐振子波函数及概率分布的可视演示一维线性谐振子是量子力学中的经典问题之一,它是描述原子、分子和晶格振动的重要模型。
一维线性谐振子的波函数及概率分布对于理解量子力学的基本原理具有重要意义。
本文将针对一维线性谐振子的波函数及概率分布进行可视化演示,帮助读者更直观地理解这一重要问题。
一维线性谐振子的哈密顿量可表示为:\[ \hat{H} = -\frac{\hbar^2}{2m} \frac{d^2}{dx^2} + \frac{1}{2}m\omega^2x^2 \]\( \hbar \)为约化普朗克常数,m为谐振子的质量,\( \omega \)为振动频率,x为位置算符。
谐振子的定态波函数可表示为:\[ \psi_n(x) = \left( \frac{m\omega}{\pi\hbar} \right)^{1/4}\frac{1}{\sqrt{2^n n!}} H_n\left( \sqrt{\frac{m\omega}{\hbar}}x \right)e^{-\frac{m\omega x^2}{2\hbar}} \]\( \psi_n(x) \)为第n个能级的波函数,Hn(x)为厄米多项式。
接下来,我们将通过数值计算的方法,对谐振子的波函数及概率分布进行可视化演示。
我们将选择一个合适的谐振子势能函数,并设定谐振子的质量m和振动频率ω的数值。
假设我们选择的谐振子势能函数为:\[ V(x) = \frac{1}{2}m\omega^2x^2 \]并且选择谐振子的质量m为1kg,振动频率为\( \omega = 2\pi \)rad/s。
通过这些设定,我们可以计算出谐振子的波函数及概率分布。
接下来,我们将利用数值计算的方法,求解谐振子的波函数。
我们可以利用数值方法(如数值积分、微分方程求解等)来求解Schrodinger方程,并得到谐振子的波函数。
一般来说,我们可以利用数值计算软件(如MATLAB、Python等)来进行计算。

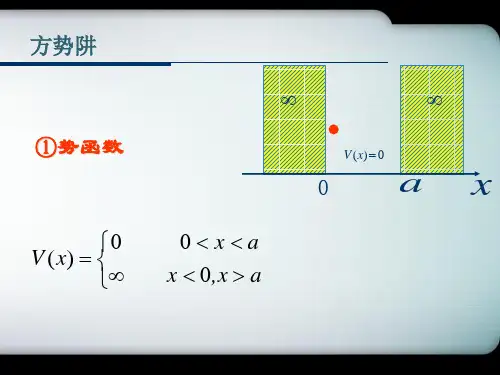
一维线性谐振子势能为2221)(x x U μω= 能量本征值 ωη)21(+=n E n),2,1,0( Λ=n 能量本征函数 2212( ) ,x n n n N eH x αψα-=22()(1)e e ,n n n nd H d ξξξξ-=- 2301231, H =2, H =4-2 , H =8-12 ,H ξξξξ=n N α==( 递推公式1111()2()2()0()2()2()0n n n n n n H H nH H x xH x nH x ξξξξαααα+-+--+=⇒-+=求导公式11()()2()2()n n n n dH dH x nH n H x d dxξαξααξ--=⇒=2.1 利用Hermite 多项式的递推公式,证明谐振子波函数满足下列递推关系:111()()()n n n x x x x a ψ-+⎤=+⎥⎦22221()()(21)()()2n n n n x x x n x x aψψ-+⎤=+++⎦并由此证明,在n ψ态下,0x =,2nE V =。
证:利用 11()2()2()0n n n H x xH x nH x αααα+--+= []2222222222221222112211211( )2xH (x)2=2()()21= nH (x)+H (x)21=()1+x x n n n n n x n n n x x n n x n x N e xH x N e Ne nH x H x eeH xααααααψααααααααααααα----+---+--⋅=⋅=⋅+⋅⋅⋅⎤⎥⎥⎦2221()x n H x αα-+⎤⎥⎥⎦111()()n n x x a -+⎤=+⎥⎦2112221()()()1()()()()n n n n n n n x x x x x x a x x x x ψψψα-+-+⎤=+⎥⎦⎫⎤⎤⎪=+++⎬⎥⎥⎪⎦⎦⎭2221()(21)()()2n n n x n x x aψ-+⎤=+++⎦**1110nnn n x x dx dx ψψψα∞-+-∞⎤==⋅+=⎥⎦⎰⎰,*22*222111(21)2221()112().222nn n n n V m x dx m n dxn E n x m ψωψψωψαωω∞∞-∞-∞=⋅⋅=⋅⋅++=+==⎰⎰hh L L L L 或者 2.2 利用Hermite 多项式的求导公式,证明谐振子波函数满足下列关系:11()()()n n n d x x x dx ψα-+⎤=-⎥⎦22222()()(21)()()2n n n n d x x n x x dx αψψ-+⎤=-++⎦证明:Hermite 多项式的求导公式11()()2()2()n n n n dH dH x nH n H x d dxξαξααξ--=⇒=, 所以222222212111111()[()()2()]()()()()()()()x x n n n n n n n n n n n d x N x e H x en H x dxx x x x x x x x ααψαααααψααα-----+--+=-+⋅=-+⎤=-++⎥⎦⎤=-⎥⎦2222222()(21)2n n n n n n n n d x dx n ψααψ-+-+=-⎤⎤=-⎥⎥⎦⎦⎤=-++⎦**11()()0nn n n n d p i dx i dx dx ψψψα-+⎤=-=-⋅-=⎥⎦⎰⎰h h222*22222*2211(21)(21)()224222n n nn n p d T dx m m dxE n dx n n m m ψψααψψω==-=+=+=+=⎰⎰h h h h 2.3 计算一维谐振子122()x x x ⎡⎤∆=-==⎣⎦122()p p p ⎡⎤∆=-==⎣⎦ 1()2x p n ∆⋅∆=+h , 对于基态, 2x p ∆⋅∆=h。

6-4-7 定态薛定谔方程的应用(三)线性谐振子其能量是振幅的连续函数一、经典线性谐振子在势场中运动的质量为的微观粒子2221)(x m x U m 二、量子线性谐振子xU 当时,势能谐振子的势能曲线亦为无限深势阱,只不过不是方势阱而已,所以粒子只能作有限的运动,即处于束缚态。
221E m A 2 谐振子在运动中能量守恒定态薛定谔方程1.谐振子的能量, )21()21( h n n E n n = 0, 1, 2, (22)222()1()()22d x m x x E x m dx (1) 能量量子化经典:能量连续(2) 最低能级01E h 2经典:的态对应00 E 0p x 零点能零点能不等于零是量子效应,是微观粒子波粒二相性的表现。
不可能静止E n nh 普朗克谐振子的能量:n = 1, 2, …(3) 能级间隔均匀E h假想存在许多虚构的粒子,其每个的能量为h 这种粒子叫做量子(Quantum )在晶体中,这种量子叫做声子phonon(4) 当n 时,符合玻尔对应原理。
能量量子化 能量连续, 0Δ nE E(1)在E <U 区,概率密度不为0——隧道效应2. 概率密度例如基态位置概率分布在x =0处最大,经典振子在x = 0处概率最小。
(3) n 小时,概率分布与经典谐振子完全不同xn 很大E n E 1E 2E 00U (x )21 2n 22 20 (2) 波函数有n 个零点,在零点处概率为零。
n 为奇数时,x =0处,概率为零。
经典:无零点。
当n 时,符合玻尔对应原理。
量子概率分布 经典概率分布,简谐振子n =11 时的概率密度分布:211 11n x虚线是经典结果(4)只有在n 较大的情况下,有与经典相似。
谐振子的定态薛定谔方程谐振子的能量量子化线性谐振子势函数2221)(x m x U 小结22222()1()()22d x m x x E x m dx , )21()21( h n n E n ,2,1,0 n。


一维线性谐振子波函数及概率分布的可视演示1. 引言1.1 介绍一维线性谐振子概念一维线性谐振子是量子力学中常见的模型之一,它是一种简单但非常重要的系统。
在一维线性谐振子中,质点受到一个与位移成正比的恢复力作用,该系统的势能函数可以表示为一个二次函数。
谐振子是一种能永远保持振动的系统,其运动的频率只取决于系统的质量和弹性常数,而与振幅和初相位无关。
一维线性谐振子在物理学和工程学中有着广泛的应用,例如在分子振动、固体声子、原子力显微镜等领域都有着重要作用。
谐振子模型的基本方程是薛定谔方程,通过求解薛定谔方程可以得到谐振子的波函数和能量本征值。
波函数描述了谐振子在不同位置处的可能性振动状态,它可以用来计算系统的物理量,如位置、动量、能量等。
概率分布是描述粒子在不同位置或状态的可能性的函数,对于一维线性谐振子而言,概率分布可以帮助我们了解系统的稳定性和振动行为。
在量子力学中,概率分布是一个非常重要的概念,它反映了粒子在不同态中的出现可能性,是描述微观粒子行为的关键工具。
通过研究一维线性谐振子的波函数和概率分布,我们可以深入理解量子系统的性质和行为,为进一步的物理研究提供基础和指导。
1.2 谐振子波函数的意义谐振子波函数是描述谐振子系统状态的数学函数。
在量子力学中,波函数是描述微观粒子运动及性质的基本工具,而谐振子波函数则是描述谐振子系统可能状态的函数。
谐振子波函数的意义在于通过波函数的数学表达,我们可以揭示谐振子系统的量子性质,如能级结构、态的叠加等。
波函数的意义还在于它可以用来计算系统的物理量,比如位置、动量、能量等的期望值。
谐振子波函数的意义还体现在其具有很强的几何意义。
波函数的模的平方代表了在空间中找到粒子的概率密度,而相位则含有波函数的相对相位信息。
通过波函数的几何意义,我们可以直观理解谐振子系统的量子态分布规律,如波函数的振幅大小和位置分布的关系等。
谐振子波函数的意义在于提供了描述谐振子系统状态的数学工具,揭示了系统的量子性质和几何结构。


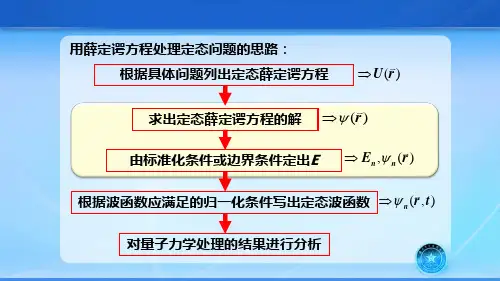
一维线性谐振子一维线性谐振子势能为2221)(x x U μω= 能量本征值 ω )21(+=n E n),2,1,0( =n 能量本征函数 2212( ) ,x n n n N eH x αψα-=22()(1)e e ,n n n nd H d ξξξξ-=- 2301231, H =2, H =4-2 , H =8-12 ,H ξξξξ=, 2!n nm N n ωααπ==()递推公式1111()2()2()0()2()2()0n n n n n n H H nH H x xH x nH x ξξξξαααα+-+--+=⇒-+=求导公式11()()2()2()n n n n dH dH x nH n H x d dxξαξααξ--=⇒=2.1 利用Hermite 多项式的递推公式,证明谐振子波函数满足下列递推关系:1111()()()22n n n n n x x x x a ψψψ-+⎤+=+⎥⎦22221()(1)()(21)()(1)(2)()2n n n n x x n n x n x n n x aψψψψ-+⎤=-+++++⎦并由此证明,在n ψ态下,0x =,2nE V =。
证:利用 11()2()2()0n n n H x xH x nH x αααα+--+= []222222222222122211221121111( )2xH (x)2=2()()211= nH (x)+H (x)22!2!1=()22(1)!1(1)+22(x x n n n n n x n n n x x n n nnx n n n x N e xH x N e N e nH x H x een n n e H x n n n ααααααψαααααααααααααππαααπααπ----+---+---+⋅=⋅=⋅+⋅⋅⋅⋅⋅⋅⋅⎤⎥⋅⋅-⎥⎦+⋅+2221()1)!x n e H x αα-+⎤⎥⎥⎦1111()()22n n n n x x a ψψ-+⎤+=+⎥⎦21122211()()()2211112()()()()222222n n n n n n n n n x x x x x x a n n n n n n x x x x ψψψψψψψα-+-+⎡⎤+=+⎢⎥⎣⎦⎫⎤⎤-+++⎪=+++⎬⎥⎥⎪⎦⎦⎭2221(1)()(21)()(1)(2)()2n n n n n x n x n n x aψψψ-+⎡⎤=-+++++⎣⎦**1111022nnn n n n x x dx dx ψψψψψα∞-+-∞⎡⎤+==⋅+=⎢⎥⎣⎦⎰⎰,*22*222111(21)2221()112().222nn n n n V m x dx m n dxn E n x m ψωψψωψαωω∞∞-∞-∞=⋅⋅=⋅⋅++=+==⎰⎰或者 2.2 利用Hermite 多项式的求导公式,证明谐振子波函数满足下列关系:111()()()22n n n d n n x x x dx ψαψψ-+⎡⎤+=-⎢⎥⎣⎦22222()(1)()(21)()(1)(2)()2n n n n d x n n x n x n n x dx αψψψψ-+⎡⎤=--++++⎣⎦证明:Hermite 多项式的求导公式11()()2()2()n n n n dH dH x nH n H x d dxξαξααξ--=⇒=, 所以222222212111111()[()()2()]()2()1()()2()221()()22x x n n n n n n n n n n n d x N x e H x en H x dxx x n x n n x x n x n n x x ααψαααααψαψαψψαψαψψ-----+--+=-+⋅=-+⎡⎤+=-++⎢⎥⎣⎦⎤+=-⎥⎦2112222221()221112222222(1)(21)(1)(2)2n n n n n n n n n n d d d n n x dx dx dxn n n n n n n n n n n ψψψααψψαψψαψψψ-+-+-++=-⎡⎤⎤-+++=---⎢⎥⎥⎣⎦⎦⎡⎤=--++++⎣⎦**111()()022nn n n n d n n p i dx i dx dx ψψψαψψ-+⎡⎤+=-=-⋅-=⎢⎥⎣⎦⎰⎰222*22222*2211(21)(21)()224222n n n nn p d T dx m m dxE n dx n n mm ψψααψψω==-=+=+=+=⎰⎰2.3 计算一维谐振子122221()()2x x x x x n m ω⎡⎤∆=-=-=+⎣⎦ 122221()()2p p p p p n m ω⎡⎤∆=-=-=+⎣⎦ 1()2x p n ∆⋅∆=+, 对于基态, 2x p ∆⋅∆=。
一维线性谐振子波函数及概率分布的可视演示
一维线性谐振子是量子力学中的经典问题之一,它的波函数和概率分布在物理学中有着重要的意义。
在本文中,我们将通过可视演示的方式,来展示一维线性谐振子的波函数及其概率分布。
一维线性谐振子是指在一维空间中,受到线性回复力作用的质点。
它的势能函数可以表示为V(x) = 0.5 * k * x^2,其中k为弹簧的弹性系数,x为质点与平衡位置的位移。
让我们来看一维线性谐振子的波函数是怎样的。
根据量子力学的定态方程,一维线性谐振子的波函数可以表示为:
Ψ(x) = A * exp(-0.5 * (m * ω * x^2 / ℏ)) * Hn(m * ω / ℏ)^0.5(x),
其中A为归一化系数,m为质点的质量,ω为振子的频率,ℏ为普朗克常数,Hn为厄米多项式。
通过对波函数的可视化,我们可以看到谐振子波函数在位移x方向上的变化规律,以及不同能级的波函数形态。
P(x) = |Ψ(x)|^2,
通过对概率分布的可视化,我们可以看到不同能级的概率分布形态,以及在不同位置上质点的出现概率。
这有助于我们更直观地理解一维线性谐振子在空间中的分布规律。
除了波函数和概率分布的可视化演示,我们还可以通过改变谐振子的参数(如弹簧的弹性系数、质点的质量、振子的频率等),来观察波函数和概率分布的变化规律。
这有助于我们更深入地理解一维线性谐振子的量子特性。
通过可视演示一维线性谐振子的波函数及其概率分布,我们可以更直观地理解量子力学中的经典问题,有助于我们在学习和研究中更好地理解和运用相关概念。
希望本文能对读者有所帮助,激发对量子力学的兴趣和深入探索。
一维线性谐振子波函数及概率分布的可视演示一维线性谐振子是最简单的量子系统之一,在量子力学中具有重要的地位。
它的波函数和概率分布可以通过可视演示来展示,下面是一维线性谐振子波函数及概率分布的可视演示。
我们先来了解一维线性谐振子模型。
一维线性谐振子是一个粒子在一个势能为V(x) = \frac{1}{2}m\omega^2x^2的势场中运动的模型,其中m是粒子的质量,\omega是谐振子的频率。
波函数是描述量子系统的最基本的物理量,一维线性谐振子的波函数可以用一个简单的数学函数来表示。
一维线性谐振子的波函数为:\psi(x) = A e^{-\frac{1}{2}\alpha x^2}e^{ipx/\hbar}其中A是归一化常数,\alpha = \sqrt{\frac{m\omega}{\hbar}},p是粒子的动量。
概率分布是表示在不同位置上找到粒子的概率的函数。
根据量子力学的原理,概率分布可以通过波函数的模方计算得到。
一维线性谐振子的概率分布为:现在我们来进行可视演示。
我们先设定一维线性谐振子的参数。
假定m=1、\omega=1、\hbar=1。
然后,我们可以选择一个合适的归一化常数A,使得波函数满足归一化条件:\int_{-\infty}^{\infty}|\psi(x)|^2dx = 1接下来,我们可以使用计算机程序来计算和绘制一维线性谐振子的波函数和概率分布。
可以使用Python语言编写一个程序,使用数值计算的方法来计算波函数和概率分布,并使用数据可视化库来绘制图形。
我们可以使用高斯函数来表示波函数的振幅部分。
高斯函数可以用numpy库中的函数来计算:```pythonimport numpy as npdef gaussian(x, A, alpha):return A * np.exp(-alpha * x**2)```然后,我们可以使用波函数的振幅部分来计算概率分布:我们可以使用matplotlib库来绘制波函数和概率分布的图形:x = np.linspace(-5, 5, 1000) # 选择一个合适的范围和精度A = 1.0 # 选择一个合适的归一化常数alpha = np.sqrt(1) # 计算alpha# 绘制波函数的图形plt.plot(x, gaussian(x, A, alpha), label='\psi(x)')plt.xlabel('x')plt.ylabel('\psi(x)')plt.legend()plt.show()通过运行这段程序,我们可以得到一维线性谐振子的波函数和概率分布的图形。