九年级BBF答案 卷二十三

2023-2024学年九年级数学上册《第二十三章旋转》单元测试卷有答案(人教版)学校:___________班级：___________姓名：___________考号：___________一、单选题1．下列图形既是轴对称图形又是中心对称图形的是（）A．B．C．D．2．已知点A(−2，3)经变换后到点B，下面的说法正确的是（）A．点A与点B关于x轴对称，则点B的坐标为B(2，3)B．点A绕原点按顺时针方向旋转90°后到点B，则点B的坐标为B(2，3)C．点A与点B关于原点中心对称，则点B的坐标为B(3，−2)D．点A先向上平移3个单位，再向右平移4个单位到点B，则点B的坐标为B(2，6)3．如图，将一个含30°角的直角三角尺AOB放在平面直角坐标系中，两条直角边分别与坐标轴重叠．已知∠OAB=30°，AB=16，点D为斜边AB的中点，现将三角尺AOB绕点O顺时针旋转90°，则点D的对应点D′的坐标为（）A．(4√3，4)B．(8√3，−8)C．(4，−4√3)D．(4√3，−4)4．如图，直角三角板ABC的斜边AB=12㎝，∠A=30°，将三角板ABC绕C顺时针旋转90°至三角板A′B′C′的位置后，再沿CB方向向左平移，使点落在原三角板ABC的斜边AB上，则三角板平移的距离为（）A．6㎝B．4㎝C．（6－2√3）㎝D．（4√3−6）㎝5．如图，△ABC中，∠C=70°，∠B=30°，将△ABC绕点A顺时针旋转后，得到△AB´C´，且C´在边BC上，则∠B´C´B的度数为（）A．30°B．40°C．46°D．60°6．已知A（4，1），B（5，4），将线段AB绕点A逆时针旋转90°得线段AC，则点C的坐标为（）A．（1，2）B．（2，1）C．（7，0）D．（1，3）7．如图，在平面直角坐标系中，若△ABC与△A1B1C1关于E点成中心对称，点A，B，C的对应点分别为A1，B1，C1，则对称中心E点的坐标是（）A．（3，-1）B．（0，0）C．（2，-1）D．（-1，3）8．如图，在△ABC中，AB＝AC，∠BAC＝50°，将△ABC绕着点A顺时针方向旋转得△ADE，AB，CE相交于点F，若AD∥CE时，则∠BAE的大小是（）A．20°B．25°C．30°D．35°二、填空题9．如图，矩形ABCD中，AB=5，BD=13，Rt△EFG的直角边GE在CB的延长线上，E点与矩的B点重，∠FGE=90°，FG=3．将矩形ABCD固定，把Rt△EFG沿着射线BC方向运动，当点F恰好经过BD时，将△EFG绕点F逆时针旋转α°（0°＜α°＜90°），记旋转中的△EFG为△E′F′G′，在旋转过程中，设直线E′G′与直线BC交于N，与直线BD交于M点，当△BMN为以MN为底边的等腰三角形时，FM的长为．10．如图，△ABC是边长为12的等边三角形，D是BC的中点，E是直线AD上的一个动点，连接EC，将线段EC绕点C逆时针旋转60°得到FC，连接DF．则在点E的运动过程中，DF的最小值是．11．有一种电脑软件叫做“画图”，它有个功能，可以复制已经出现在窗口的所有图形或部分图形，粘贴的图形又可以进行任意的平移.如图，在画图窗口中已有一个正方形.从窗口中已有图形开始，复制、粘贴已有图形或部分图形一次，且通过平移后与原图形拼接，叫做一次操作.则要出现一个4×6的网格，至少需要操作次.12．如图，在正方形方格中，阴影部分是涂黑7个小正方形所形成的图案，再将方格内空白的一个小正方形涂黑，使得到的新图案成为一个轴对称图形的涂法有种．13．如图，在Rt△ABC中，AB=AC，D，E是斜边BC上两点，且∠DAE=45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连结EF．则∠EAF=三、解答题14．在边长为1的小正方形网格中，△AOB的顶点均在格点上．（1）将△AOB向左平移3个单位长度，再向上平移1个单位长度得到△A1O1B1，请画出△A1O1B1，并写出点A1的坐标；（2）将△AOB绕点O沿顺时针方向旋转90°得到△A2OB2，请画出△A2OB2，并写出点A2的坐标．x+4与x轴、y轴分别交于A，B两点，将线段AB绕点A顺时针旋转90°15．如图，直线y=−43后得到线段AB1．求点B1的坐标．16．如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90º，∠B=∠E=30º.（1）操作发现如图2，固定△ABC，使△DEC绕点C顺时针旋转．当点D恰好落在AB边上时，填空：线段DE与AC的位置关系是；设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是，证明你的结论；猜想论证当△DEC绕点C旋转到图3所示的位置时，小明猜想（1）中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AE中BC，CE边上的高，请你证明小明的猜想．17．长方形OABC绕顶点C（0，5）逆时针方向旋转，当旋转到CO′A′B′位置时，边O′A′交边AB于D，且A′D=2，AD=4．（1）求BC长；（2）求阴影部分的面积．18．如图，将△ABC绕点A按顺时针方向旋转90°，得到△ADE，点B的对应点为点D，点C的对应点E落在BC边上，连接BD．（1）求证：DE⊥BC；（2）若AC=3√2，BC=7，求线段BD的长．19．如图1，在△ ABC中，CA＝CB，∠ACB＝90°，D是△ ABC内部一点，∠ADC＝135°，将线段CD绕点C逆时针旋转90°，得到线段CE，连接DE．（1）求∠CDE的度数，并说明A、D、E三点是否共线；（2）在（1）的条件下，连接BE，如图2，过点C作CM⊥DE于点M，请判断线段AE，CM和BE之间的数量关系，并说明理由．参考答案1．B2．D3．D4．C5．B6．A7．A8．C9．3 √2610．311．512．313．45°14．（1）解：如图所示，由平移之后的图形可知A1(−2，4)（2）解：如图所示，由旋转之后的图形可知A2(3，−1)15．解：如图，当y=0时x=3；当x=0时∴A(3，0)，B(0，4)∴OA=3，OB=4过点B1作B1C⊥x轴于C∴∠ACB1=AOB=90°由题AB=AB1，∠BAB1=90°∴∠OAB+∠CAB1=90°又∵∠OAB+∠ABO=90°∴∠ABO=∠CAB1∴ΔAOB≌ΔB1CA∴OB=AC=4，OA=B1C=3∴OC=OA+AC=7∴B 1(7，3)16．解：（1）①线段DE 与AC 的位置关系是平行．②S 1与S 2的数量关系是相等．证明：如图2，过D 作DN ⊥AC 交AC 于点N ，过E 作EM ⊥AC 交AC 延长线于M ，过C 作CF ⊥AB 交AB 于点F ．由①可知△ADC 是等边三角形，DE ∥AC∴DN=CF ，DN=EM ．∴CF=EM ．∵∠ACB=90º，∠B=30º∴AB=2AC ．又∵AD=AC∴BD=AC ．∵S 1=12CF ·BD ，S 2=12AC ·EM∴S 1=S 2．证明：如图3，作DG ⊥BC 于点G ，AH ⊥CE 交EC 延长线于点H.∵∠DCE=∠ACB=90º∴∠DCG+∠ACE=180º．又∵∠ACH+∠ACE=180º，∴∠ACH=∠DCG ．又∵∠CHA=∠CGD=90º，AC=CD∴△AHC ≌△DGC ．∴AH=DG ．又∵CE=CB17．（1）解：∵长方形OABC 绕顶点C （0，5）逆时针方向旋转得到矩形CO ′A ′B ′∴BC=AO=O ′A ′，AB=CO=CO'=5，∠B=∠O'=90°∵AD=4，AB=5∴BD=5﹣4=1设BC=x，则DO'=O'A'﹣A'D=x﹣2连接CD，则BC2+BD2=CD2=CO'2+DO'2即x2+12=52+（x﹣2）2解得：x=7∴BC=7；（2）解：∵BC=7，BD=1，CO'=5，DO'=7﹣2=5，∠B=∠O'=90°∴阴影部分的面积=△BCD面积+△O'CD面积= 12×7×1+ 12×5×5=16．18．（1）证明：∵将△ABC绕点A按顺时针方向旋转90°∴AC=AE，∠CAE=90°，∠AED=∠ACE∴∠ACE=∠AEC=45°=∠AED∴∠DEC=90°∴DE⊥BC；（2）解：∵AE=AC=3√2，∠EAC=90°∴EC=6∴BE=BC﹣EC=1．∵将△ABC绕点A按顺时针方向旋转90°∴DE=BC=7∴DB=√BE2+DE2=√49+1=5√2．19．（1）解：∵将线段CD绕点C逆时针旋转90°∴CD＝CE，∠DCE＝90°∴∠CDE＝45°∵∠ADC＝135°∴∠ADC+∠CDE＝180°∴A、D、E三点共线；（2）解：AE＝BE+2CM，理由如下：∵∠ACB＝∠DCE＝90°∴∠ACD＝∠BCE在△ACD和△BCE中{AC=BC∠ACD=∠BCE CD=CE∴△ACD≌△BCE（SAS）∴BE＝AD∵CD＝CE，∠DCE＝90°，CM⊥DE ∴DE＝2CM∴AE＝AD+DE＝BE+2CM。

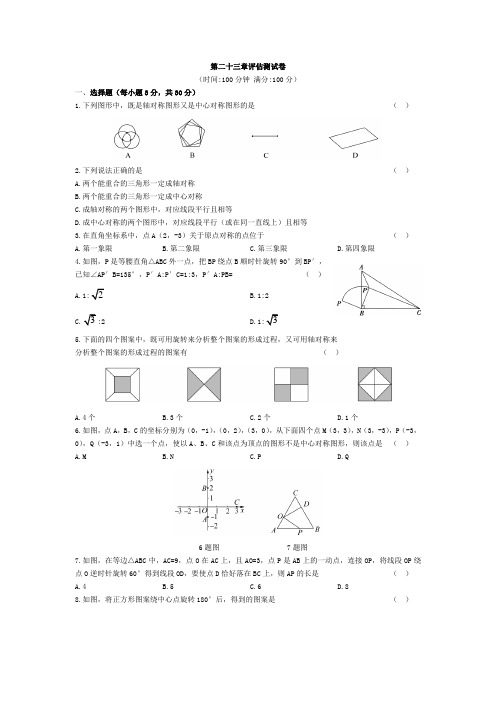
第二十三章评估测试卷（时间:100分钟满分:100分）一、选择题（每小题3分，共30分）1.下列图形中，既是轴对称图形又是中心对称图形的是（）2.下列说法正确的是（）A.两个能重合的三角形一定成轴对称B.两个能重合的三角形一定成中心对称C.成轴对称的两个图形中，对应线段平行且相等D.成中心对称的两个图形中，对应线段平行（或在同一直线上）且相等3.在直角坐标系中，点A（2，-3）关于原点对称的点位于（）A.第一象限B.第二象限C.第三象限D.第四象限4.如图，P是等腰直角△ABC外一点，把BP绕点B顺时针旋转90°到BP′，已知∠AP′B=135°，P′A:P′C=1:3，P′A:PB= （）B.1:25.下面的四个图案中，既可用旋转来分析整个图案的形成过程，又可用轴对称来分析整个图案的形成过程的图案有（）A.4个B.3个C.2个D.1个6.如图，点A，B，C的坐标分别为（0，-1），（0，2），（3，0），从下面四个点M（3，3），N（3，-3），P（-3，0），Q（-3，1）中选一个点，使以A、B、C和该点为顶点的图形不是中心对称图形，则该点是（）A.MB.NC.PD.Q6题图 7题图7.如图，在等边△ABC中，AC=9，点O在AC上，且AO=3，点P是AB上的一动点，连接OP，将线段OP绕点O逆时针旋转60°得到线段OD，要使点D恰好落在BC上，则AP的长是（）A.4B.5C.6D.88.如图，将正方形图案绕中心点旋转180°后，得到的图案是（）9.若点P（-1-2a，2a-4）关于原点对称的点是第一象限内的点，则a的整数解有（）A.1个B.2个C.3个D.4个10.在如图所示的方格纸上，两条对称轴EF，MN相交于中心点O，对△ABC分别作下列变换:①先以点A为中心顺时针方向旋转90°，再向右平移4格、向上平移4格;②先以点O为中心旋转180°，再以点A的对应点为中心逆时针方向旋转90°;③先以直线MN为轴作轴对称图形，再向上平移4格，再以点A的对应点为中心顺时针方向旋转90°，其中，能将△ABC变换成△PQR的是（）A.①②B.①③C.②③D.①②③二、填空题（每小题3分，共24分）11.如图，在矩形ABCD中，AB=1，AD=2，AD绕着点A顺时针旋转，当点D落在BC上点D′时，则AD′= ，∠AD′B= .12.如图，在△ABC中，∠CAB=70°，在同一平面内，将△ABC绕点A旋转到△AB′C′的位置使得CC′∥AB，则∠BAB′= .11题图 12题图 14题图 15题图13.已知A（-3，x），B（y，-5）是关于原点O的对称点，则x+y的值是 .14.如图，在 Rt△ABC中，∠ACB=90°，∠ABC=30°，AC=1，将△ABC绕点C逆时针旋转至△A′B′C，使得点A′恰好落在AB上，连接BB′，则BB′的长度为 .15.如图，△ABC是等腰直角三角形，BC是斜边，点P是△ABC内的一点，将△ABP绕点A逆时针旋转后与△ACP′重合.如果AP=3，那么线段PP′的长是 .16.如图，在直角坐标系中，已知点A（-3，0），B（0，4），对△OAB连续作旋转变换，依次得到三角形①，②，③，④，…，则三角形⑩的直角顶点的坐标为 .16题图 17题图 18题图17.如图，将放置于平面直角坐标系中的三角板AOB绕点O顺时针旋转90°得△A′OB′.已知∠AOB=30°，∠B=90°，AB=1，则点B′的坐标是 .18.如图所示，EF过平行四边形的对角线的交点O，若四边形ABFE绕O点旋转一定的角度后能与四边形EFCD 重合，且AB=3，BC=4，OE=1.5，则四边形EFCD的周长是 .三、解答题（共46分）19.（6分）小芳家有一块菜地，其形状如图所示，经测量AB=AD，∠A=∠C=90°，点A到BC的长度为6 m,请你帮忙计算下小芳家菜地的面积.20.（6分）如图，在平面直角坐标系中，△ABC和△A1B1C1关于点E成中心对称.（1）画出对称中心E，并写出点E、A、C的坐标;（2）P（a，b）是△ABC的边AC上一点，△ABC经平移后点P的对应点为P2（a+6，b+2），请画出上述平移后的△A2B2C2，并写出点A2、C2的坐标;（3）判断△A2B2C2和△A1B1C1的位置关系（直接写出结果）.21. （6分）如图，已知四边形ABCD和点O，作四边形EFGH，使四边形EFGH和四边形ABCD关于点O成中心对称.22.（9分）四边形ABCD是正方形，△ADF旋转一定角度后得到△ABE，如图所示，如果AF=4，AB=7. （1）指出旋转中心和旋转角度;（2）求DE的长度;（3）BE与DF的位置关系如何?23.（9分）如图，将一个钝角△ABC（其中∠ABC=120°）绕点B顺时针旋转得△A1BC1，使得点C落在AB 的延长线上的点C1处，连接AA1.（1）写出旋转角的度数.（2）（2）求证:∠A1AC=∠C1.24.（10分）如图①，在 Rt △ABC 中，∠BAC=90°，D 、E 两点分别在AC 、BC 上，且DE ∥AB ，将△CDE 绕点C 顺时针旋转，得到△CD ′E ′（如图②，点D ′、E ′分别与点D 、E 对应），点E ′在AB 上，D ′E ′与AC 相交于点M. （1）求∠ACE ′的度数; （2）求AD ′的长.答案1. C A 项是轴对称图形，不是中心对称图形，B 项既不是轴对称图形也不是中心对称图形;C 项是轴对称图形也是中心对称图形;D 项是中心对称图形，但不是轴对称图形.2. D A 项两个能重合的三角形不一定成轴对称;B 项两个能重合的三角形不一定成中心对称;C 项成轴对称的两个图形中，对应线段相等但不一定平行.3. B 根据关于原点对称的点纵、横坐标均互为相反数，可得点A （2，-3）关于原点对称的点为（-2，3），在第二象限.4. B 连接AP ，PP ′，如图，由SAS 可知 APB ≌△CP ′B ， ∴P ′C=PA.∵P ′A: P ′C=1:3，∴P ′A:AP=1:3，设P ′A =x ，则AP=3x ，由旋转可知△PBP ′是等腰直角三角形， ∴∠PP ′B =45°，又∠APB=135°，∴△APP ′是直角三角形， ∴PP ′， BP=2x ，∴P ′A:PB=1:2.5. A 图形1和图形4可以旋转90°碍到，也可以经过轴对称，沿一条直线对折，能够完全重合;图形2和图形3可以旋转180°得到，也可以经过轴对称，沿一条直线对折，能够完全重合.故既可用旋转来分析整个图案的形成过程，又可用轴对称来分析整个图案的形成过程的图案有4个.6. C 当第四个点为M ，N 或Q 时都可以判定该四边形是平行四边形，而平行四边形是中心对称图形.7. C 线段OP 绕点O 逆时针旋转60°得到线段OD ，若连接DP ，则△OPD 为等边三角形，当点D 落在BC 上时，不难得出△OAP ≌△DCO （ ASA 或AAS ），所以AP=OC=9-3=6.8. C 根据绕中心点旋转180°是中心对称可得 C 项正确.9. B 点P 关于原点的对称点P ′的坐标为（1+2a ，4- 2a ）.又∵点P ′在第一象限，∴ 12a 042a 0+>⎧⎨->⎩，，解得-12<a<2.∴满足条件的a 的整数解为0，1. 10. D 通过这三种变换方式，都能将△ABC 变换成△PQR. 11. 2 30°因为AD 绕着点A 旋转，得到AD ′，则AD ′=AD=2.又AB=1，△ABD ′是直角三角形，则∠AD ′B=30°. 12. 40°∵∠CAB=70°，CC ′∥AB ，∴∠C ′CA=∠CAB= 70°，AC=AC ′，∴∠AC ′C=70°，∴∠C ′AC=40°，∴ ∠BAB ′=40°. 13. 8根据关于原点对称的坐标特征可得x=5，y=3，x+y=3+5=8.14.在 Rt △ABC 中，∠ACB=90°，∠ABC=30°，∴∠A= 60°.又A ′C=AC ，∴∠ACA ′=60°.∴∠A ′CB =30°，∵∠A ′CB ′=90°，∴∠BCB ′=60°，又BC= B ′C ，∴BB ′=BC.∵AC=1，∴BB ′.由旋转的性质，知∠PAP ′等于旋转角的度数90°，AP ′=AP=3，所以PP ′16.（36，0）由原图到图③，相当于向右平移了12个单位长度，像这样平移三次直角顶点是（36，0），再旋转一次到三角形⑩，直角顶点仍然是（36，0），则三角形⑩的直角顶点的坐标为（36，0）.17.32）在 Rt △AOB 中，∵∠AOB=30°，∴OA=2AB=2.过点B 作BD ⊥OA 于点D ，在 Rt △ABD 中，AD=12，∴OD=2-12=32，所以点B 的坐标是（-32，2）.将△AOB 绕着原点顺时针旋转90°，点B 也绕着原点顺时针旋转90°，与点B ′重合，所以点B ′的坐标是（2，32）.18. 10∵四边形ABFE 旋转后与四边形EFCD 重合，∴四边 形ABFE ≌四边形CDEF ，OE=OF=1.5，∴AB=CD ，AE=CF ，BF=DE.∴四边形EFCD 的周长为EF+FC+CD+ED=OE+OF+FC+AB+BF=1.5+1.5+3+4=10. 19.如图，过点A 作AG ⊥BC ，垂足为G ，将△ABG 绕点A 逆时针旋转90°得到△ADF ， 由旋转的性质，可得AF=AG=6（ m ）， ∠FAD=∠GAB ，∵∠DAB=90°， ∴∠FAG=90°，∴四边形FAGC 为 正方形. ∴S 四边形ABCD =S 正方形FAGC =36 m 220.（1）图略，E （-3，-1），A （-3，2）C （-2，0） （2）略 A 2（3， 4）C 2（4，2）（3）△A 2B 2C 2与△A 1B 1C 1关于原点O 成中心对称.21.图略22.（1）旋转中心:点A，旋转角度:90°（2）DE=3 （3）垂直关系23.（1）旋转角的度数为60°.（2）∵点A，B，C1在一条直线上，∴∠ABC1=180°.由旋转知∠A1BC1=∠ABC=120°，∴∠ABA1=∠CBC1=60°，∴∠A1BC= 60°.又∵AB=A1B，∴△ABA，是等边三角形，∴∠AA1B=∠A1BC=60°，∴AA1∥BC，∴∠A1AC=∠C.∵△ABC≌△A1BC1，∴∠C=∠C1，∴∠A1AC=∠C1.24.（1）在图①中，∵∠BAC=90°，AB=AC，∴∠B=∠ACB =45°，∵DE∥AB，∴∠DEC=∠DCE=45°，∠EDC=90°，∴DE=CD=2∴CE=4.在图②的 Rt△ACE′中，∠E′AC=90°，，CE′=CE=4，∴AE′=2，∴∠ACE′=30°.分别过点A、D′作AF⊥BC于点F，D′N⊥BC于点N，可得∴AD′。

冀教版九年级数学上册第二十三章达标检测卷一、选择题(1～10题每题3分，11～16题每题2分，共42分)1．一组数据3，6，9，4，12，5，3的中位数是()A．6 B．5 C．4 D．32．数据－1，0，3，4，4的平均数是()A．4 B．3C．2.5 D．23．在一次数学测试中，小明的成绩是72分，超过班级半数同学的成绩，分析得出这个结论所用的统计量是()A．中位数B．众数C．平均数D．方差4．某市6月份某周气温(单位：℃)为23，25，28，25，28，31，28，则这组数据的众数和中位数分别是()A．25 ℃，25 ℃B．28 ℃，28 ℃C．25 ℃，28 ℃D．28 ℃，31 ℃5．某中学规定学生的学期体育成绩满分为100分，其中课外体育占20%，期中考试成绩占30%，期末考试成绩占50%.小彤的这三项成绩(百分制)分别为95分，90分，88分，则小彤这学期的体育成绩为()A．89分B．90分C．92分D．93分6．制鞋厂准备生产一批男皮鞋，经抽样(120名中年男子)，得知所需鞋号和人数如下表所示：并求出鞋号的中位数是24 cm，众数是25 cm，平均数约是24 cm，下列说法正确的是()A．因为需要鞋号为27 cm的人数太少，所以鞋号为27 cm的鞋可以不生产B．因为平均数约是24 cm，所以这批鞋可以一律按24 cm的鞋生产C．因为中位数是24 cm，所以24 cm的鞋的生产量应占首位D．因为众数是25 cm，所以25 cm的鞋的生产量应占首位7．已知一组数据2，3，4，x，1，4，3有唯一的众数4，则这组数据的平均数、中位数分别是()A．4，4 B．3，4C．4，3 D．3，38．济南某中学足球队的18名队员的年龄如下表所示：这18名队员年龄的众数和中位数分别是()A．13岁，14岁B．14岁，14岁C．14岁，13岁D．14岁，15岁9．对于一组数据5，9，7，5，4，下列说法正确的是()A．中位数是7 B．众数是9C．平均数是6 D．方差是310．小华所在的九年级一班共有50名学生，一次体检测量了全班学生的身高，由此求得该班学生的平均身高是1.65米，而小华的身高是1.66米，下列说法错误的是()A．1.65米是该班学生身高的平均水平B．班上比小华高的学生人数不会超过25人C．这组身高数据的中位数不一定是1.65米D．这组身高数据的众数不一定是1.65米11．如图是甲、乙两同学五次数学测试成绩的折线统计图．比较甲、乙的成绩，下列说法正确的是()A．甲平均分高，成绩稳定B．甲平均分高，成绩不稳定C．乙平均分高，成绩稳定D．乙平均分高，成绩不稳定12．某公司生产的一种产品按照质量由高到低分为A，B，C，D四级，为了增加产量、提高质量，该公司改进了一次生产工艺，使得生产总量增加了一倍．为了解新生产工艺的效果，对改进生产工艺前、后的四级产品的占比情况进行了统计，绘制了如下扇形统计图：根据以上信息，下列推断合理的是()A．改进生产工艺后，A级产品的数量没有变化B．改进生产工艺后，B级产品的数量增加了不到一倍C．改进生产工艺后，C级产品的数量减少D．改进生产工艺后，D级产品的数量减少13．去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵，每棵产量的平均数x(单位：千克)及方差s2(单位：千克2)如下表所示：今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植，应选的品种是()A．甲B．乙C．丙D．丁14．一组数据的方差为s2，将这组数据中的每个数据都乘2，所得到的一组新数据的方差是()A.s22B．s2C．2s2D．4s215．已知某校女子田径队23人年龄的平均数和中位数都是13岁，但是后来发现其中有一名同学的年龄登记错误，将14岁写成了15岁．经重新计算后，正确的平均数为a岁，中位数为b岁，则下列结论中正确的是()A．a<13，b＝13 B．a<13，b<13C．a>13，b<13 D．a>13，b＝1316．某校在开展“节约每一滴水”的活动中，从九年级的100名同学中任选20名同学汇总了各自家庭一个月的节水情况，将有关数据(每人上报的节水量都是整数)整理如下表所示：请你估计这100名同学的家庭一个月节约用水的总量大约是()A．180 t B．230 tC．250 t D．300 t二、填空题(每题3分，共9分)17．某中学举行歌咏比赛，六名评委对某歌手打分(单位：分)如下：77，82，78，95，83，75，去掉一个最高分和一个最低分后的平均分是________．18．为监测某河道水质，进行了6次水质检测，绘制了如图的氨氮含量的折线统计图．若这6次水质检测氨氮含量的平均数为1.5 mg/L，则第3次检测得到的氨氮含量是________mg/L.19．甲、乙两地9月上旬的日平均气温如图所示，则甲、乙两地这10天日平均气温方差大小关系为s2甲__________s2乙(填“＞”或“＜”)．三、解答题(20～22题每题10分，23，24题每题12分，25题15分，共69分) 20．九年级(1)班组织了一次经典诵读比赛，甲、乙两队各有10人，他们的比赛成绩如下表所示(10分制)：甲7 8 9 7 10 10 9 10 10 10乙10 8 7 9 8 10 10 9 10 9(1)甲队成绩的中位数是________分，乙队成绩的众数是________分．(2)计算乙队的平均成绩和方差．21．某校招聘学生会干部一名，对A，B，C三名候选人进行了四项素质测试，他们的各项测试成绩如下表所示：根据实际需要，学校将语言、综合知识、创新、处理问题能力按20%，30%，30%，20%的比例计算成绩，此时谁将被录用？22．在某市开展的“好书伴我成长”读书活动中，某中学为了解九年级300名学生读书情况，随机调查了九年级50名学生读书的册数，统计数据如下表所示：册数0 1 2 3 4人数 3 13 16 17 1(1)求这50个样本数据的平均数、众数和中位数．(2)根据样本数据，估计该校九年级300名学生在本次活动中读书多于2册的人数．23．某工厂甲、乙两名工人参加操作技能培训．现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次，记录如下表所示：(1)请你计算这两组数据的平均数．(2)现要从中选派一人参加操作技能比赛，从稳定性的角度考虑，你认为选派谁参加比较合适？请说明理由．24．某市需调查该市九年级男生的体能状况，为此抽取了50名九年级男生进行引体向上个数测试，测试情况绘制成如下表格：(1)求这次抽样测试数据的平均数、众数和中位数．(2)在平均数、众数和中位数中，你认为用哪一个统计量作为该市九年级男生引体向上项目测试的合格标准个数较为合适？简要说明理由．(3)如果该市今年有3万名九年级男生，根据(2)中你认为合格的标准，试估计该市九年级男生引体向上项目测试的合格人数是多少．25．为了解学生掌握垃圾分类知识的情况，增强学生环保意识．某学校举行了“垃圾分类人人有责”的知识测试活动，现从该校八、九年级中各随机抽取20名学生的测试成绩(满分为10分，6分及6分以上为合格)进行整理、描述和分析，下面给出了部分信息．八年级20名学生的测试成绩(单位：分)为7，8，7，9，7，6，5，9，10，9，8，5，8，7，6，7，9，7，10，6.九年级20名学生的测试成绩条形统计图如图．八、九年级抽取的学生的测试成绩的平均数、众数、中位数、8分及以上人数所占百分比如下表所示：年级平均数众数中位数8分及以上人数所占百分比八年级7.5 a 7 45%九年级7.5 8 b c根据以上信息，解答下列问题：(1)直接写出上述表中的a，b，c的值．(2)根据上述数据，你认为该校八、九年级中哪个年级学生掌握垃圾分类知识较好？请说明理由(写出一条理由即可)．(3)该校八、九年级共1 200名学生参加了此次测试活动，估计参加此次测试活动成绩合格的学生人数有多少．答案一、 1. B 2. D 3. A 4. B 5. B 6. D 7. D 8. B 9. C 10. B 11. D 12. C 13. B 14. D 15. A16. C 【点拨】1×6＋2×2＋3×8＋4×420＝2.5(t)，2．5×100＝250(t)．故选C.二、 17. 80分 18. 1 19. ＞ 三、 20. 解：(1)9.5；10(2)乙队的平均成绩是110×(10×4＋8×2＋7＋9×3)＝9(分)．则乙队的方差是110×[4×(10－9)2＋2×(8－9)2＋(7－9)2＋3×(9－9)2]＝1(分2)． 21. 解：A 的测试成绩为85×20 % ＋90×30 % ＋95×30 % ＋95×20 % ＝91.5； B 的测试成绩为95×20 % ＋85×30 % ＋95×30 % ＋90×20 % ＝91； C 的测试成绩为90×20 % ＋95×30 % ＋85×30 % ＋95×20 % ＝91； 因此A 将被录用．22. 解：(1)观察表格，可知这组样本数据的平均数是 0×3＋1×13＋2×16＋3×17＋4×150＝2(册)，∴这组样本数据的平均数为2册．∵在这组样本数据中，3出现了17次，出现的次数最多， ∴这组样本数据的众数为3册．∵将这组样本数据按从小到大的顺序排列，其中处于中间的两个数都是2，有2＋22＝2，∴这组样本数据的中位数为2册．(2)∵在50名学生中，读书多于2册的学生有18名， ∴300×1850＝108(名)．∴根据样本数据，可以估计该校九年级300名学生在本次活动中读书多于2册的约有108名．23. 解：(1)x 甲＝18×(95＋82＋88＋81＋93＋79＋84＋78)＝85；x 乙＝18×(83＋92＋80＋95＋90＋80＋85＋75)＝85.(2)选派甲参加比较合适．理由如下：由(1)知x 甲＝x 乙＝85，则s 2甲＝18×[(78－85)2＋(79－85)2＋(81－85)2＋(82－85)2＋(84－85)2＋(88－85)2＋(93－85)2＋(95－85)2]＝35.5，s 2乙＝18×[(75－85)2＋(80－85)2＋(80－85)2＋(83－85)2＋(85－85)2＋(90－85)2＋(92－85)2＋(95－85)2]＝41，∴s 2甲<s 2乙，∴甲的成绩较稳定， ∴选派甲参加比较合适．24. 解：(1)平均数为(1×1＋1×2＋6×3＋18×4＋10×5＋6×6＋2×7＋2×8＋1×9＋1×10＋2×11)÷50＝5(个)． 众数为4个，中位数为4个．(2)用中位数或众数(4个)作为合格标准个数较为合适，因为大部分同学都能达到4个．(3)30 000×4250＝25 200(人)．所以估计该市九年级男生引体向上项目测试的合格人数是25 200人． 25. 解：(1)a ＝7，b ＝7.5，c ＝50 % . (2)九年级学生掌握垃圾分类知识较好．理由：九年级8分及以上人数所占百分比大于八年级，故九年级学生掌握垃圾分类知识较好．(3)∵从调查的数据看，八年级2人的成绩不合格，九年级2人的成绩不合格， ∴估计参加此次测试活动成绩合格的学生有1 200×（20－2）＋（20－2）20＋20＝1 080(人)．。

九年级数学第二十三章试卷一、单选题（共10题；共20分）1.下列图形中，既是轴对称图形，又是中心对称图形的是( )A. 线段B. 直角三角形C. 等边二角形D. 平行四边形2.如图的四个图形中，由基础图形通过平移、旋转或轴对称这三种变换都能得到的是（）A. B. C. D.3.在平面直角坐标系内，点(-1，2)关于原点对称的点的坐标是（）A. （2，-1）B. （1,2）C. （1，-2）D. （-1，-2）4.在平面直角坐标系中，点的坐标为，以原点为中心，将点顺时针旋转得到点，则点的坐标为（）A. B. C. D.5.如图，的斜边在轴上，，含角的顶点与原点重合，直角顶点在第二象限，将绕原点顺时针旋转后得到,则点的对应点的坐标是（）A. B. C. D.6.图中阴影部分是由4个完全相同的正方形拼接而成，若要在①，②，③，④四个区域中的某个区域处添加一个同样的正方形，使它与阴影部分组成的新图形是中心对称图形，则这个正方形应该添加在（）A. 区域①处B. 区域②处C. 区域③处D. 区域④处7.如图，把△ABC绕点C逆时针旋转90°得到△DCE，若BE=17，AD=7，则BC为( )A. 3B. 4C. 5D. 68.在平面直角坐标系中，点G的坐标是，连接，将线段绕原点O旋转，得到对应线段，则点的坐标为（）A. B. C. D.9.若点P（a+1，a﹣2）关于原点对称的点位于第二象限，则a的取值范围表示正确的是（）A. B. C. D.10.如图所示，A1（1，），A2（，），A3（2，），A4（3，0）.作折线A1A2A3A4关于点A4的中心对称图形，再做出新的折线关于与x轴的下一个交点的中心对称图形……以此类推，得到一个大的折线.现有一动点P从原点O出发，沿着折线一每秒1个单位的速度移动，设运动时间为t.当t＝2020时，点P的坐标为（）A. （1010，）B. （2020，）C. （2016，0）D. （1010，）二、填空题（共7题；共7分）11.如图，正方形ABCD的边长为4，点E是CD的中点，AF平分∠BAE交BC于点F，将△ADE绕点A顺时针旋转90°得△ABG，则CF的长为________.12.如图，正方形ABCD可以看作由什么“基本图形”经过怎样的变化形成的？________．13.如图，△ABC中，∠ACB=90°，∠ABC=32°，以点C为旋转中心顺时针旋转后得到△A′B′C，且点A在边A′B′上，则旋转角的度数为________．14.如图，平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上，∠AOB＝∠B＝30°，OA＝2，将△AOB绕点O逆时针旋转90°，点B的对应点B'的坐标是________15.如图，在中，，．将绕点A按顺时针方向旋转至的位置，点恰好落在边的中点处，则的长为________．16.如图，将含有45°角的直角三角板ABC（∠C=90°）绕点A顺时针旋转30°得到△AB′C′，连接BB′，已知AC=2，则阴影部分面积为________．17.如图，在等腰直角三角形ABC中，，，把绕点C顺时针旋转得到，边、分别交AB于E、F，则的长为________.三、解答题（共2题；共10分）18.如图，在等边中，点是边上一点，连接，将线段绕点按顺时针方向旋转后得到，连接.求证: .19.如图，在△ABC中，AB=AC，△ABC与△DEC关于点C成中心对称，连接AE、BD．（1）线段AE、BD具有怎样的位置关系和大小关系？说明你的理由．（2）如果△ABC的面积为5cm2，求四边形ABDE的面积．（3）当∠ACB为多少度时，四边形ABDE为矩形？说明你的理由．四、作图题（共4题；共35分）20.如图，4×6的正方形网格中，每个小正方形的顶点称为格点，A，B，C均为格点。

人教版九年级上册第二十三章旋转单元测试（含答案）(4)一、单项选择题1．如图，△ABC是等边三角形， D 是BC的中点，以 D 为旋转中心，把△ABC顺时针旋转 60 后，所成的图形是（）．A．B．C．D．2．如图，点 E 是正方形ABCD的边 DC 上一点，把△ ADE绕点 A 顺时针旋转到△ ABF 的地点，若四边形AECF的面积为25， DE=2，则 AE 的长为（）A．7B．29C． 6D． 53．如图，将木条a， b 与 c 钉在一同，∠1=70 °，∠ 2=50 °，要使木条 a 与b 平行，木条 a 旋转的度数起码是（）A．10°B． 20°C． 50°D． 70°4．如右图，将 Rt△ ABC（此中∠ B=35°，∠ C=90°）绕点 A 按顺时针方向旋转到△ AB1C1的位置，使得点 C、A、B1在同一条直线上，那么旋转角等于（）A．105 °B． 70°C． 115 °D． 125 °5．以下图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．6．点（ -1，2）对于原点的对称点坐标是（）A．（-1， -2）B．（1，-2）C．（ 1， 2）D．（ 2， -1）7．以下图形中，即是轴对称图形又是中心对称图形的是（）A．B．C．D．8．若点 A（ 3，2）与 B（ -3， m）对于原点对称，则 m 的值是（）A．3B． -3C． 2D． -29．在平面直角坐标系中，若点与点对于原点对称，则点在 () A.第一象限 B.第二象限 C.第三象限 D.第四象限10．如图，在正方形方格中，暗影部分是涂黑7 个小正方形所形成的图案，再将方格内空白的一个小正方形涂黑，使获得的新图案成为一个轴对称图形的涂法有()A.1 种B.2 种C.3 种D.4 种11．以下每个图中都有一对全等三角形,此中的一个三角形只经过一次旋转运动即可和另一个三角形重合的是()A．B．C．D．12．由基本图案 1 获得图案 2 的方法是()A．旋转和平移C．平移和轴对称B．中心对称和轴对称D．中心对称二、填空题13．如图，点 E 是正方形 ABCD的边 DC 上一点，把△ ADE绕点 A 顺时针旋转 90°到△ ABF 的地点，若四边形 AECF的面积为 25， DE＝ 2，则 AE 的长为 ________．14．若点A a, 1与点B3，b对于原点对称，则a b_______________.15．如图，将△ ABC 的绕点 A 顺时针旋转获得△ AED，点D 正好落在BC边上．已知∠C=80°，则∠ EAB=°．16．有以下平面图形：①线段；②等腰直角三角形；③平行四边形；④矩形；⑤正八边形；⑥圆．此中既是轴对称图形，又是中心对称图形的有 _____．（填序号）三、解答题17．如图，ABC 在平面直角坐标系内，极点的坐标分别为 A 4,4 ，B 2,5 、C 2,1 .（1）平移ABC，使点C12, 4，画出平移后的A1B1C1，并写出点 A1的坐移到点C标.（2）将ABC 绕点0,3旋转 180，获得A2 B2C 2，画出旋转后的A2 B2C2，并写出点A2的坐标.（3）求（2）中的点 C 旋转到点C2时，点C 经过的路径长（结果保存） .18．已知点A(a，－ 4)， B(3， b)，依据以下条件求a、b的值．(1)A、 B 对于x 轴对称；(2)A、 B 对于 y 轴对称；(3)A、 B 对于原点对称．19．如图，在△ABC中，ABC 75 ，在同一平面内，将△ABC绕点B旋转到DBE 的地点，使得 DA BC ，求EBC 的度数．20．（课题研究）旋转图形中对应线段所在直线的夹角（小于等于90 的角）与旋转角的关系．（问题初探）线段AB绕点O 顺时针旋转得线段CD，此中点A与点C 对应，点 B 与点D 对应，旋转角的度数为，且0180．（1）如图（ 1）当90时，线段 AB 、CD所在直线夹角为______．（2）如图（ 2）当60人教版九年级数学上册第23 章旋转单元练习卷含答案(1)一、选择题1.以下几个图形是国际通用的交通标记，此中不是中心对称图形的是（）A. B. C. D.2．在平面内，将一个图形绕一个定点沿某个方向转动一个角度，这样的图形运动称为旋转．下列图形中不可以由一个图形经过旋转而构成的是( )A B C D3．以下运动形式属于旋转的是（）A．在空中上涨的氢气球B．飞奔的火车C．时钟上钟摆的摇动D．运动员掷出的标枪4．如图是扬州“三菱”电梯的标记，它能够看作是由菱形经过旋转获得的，每次旋转了（）A． 60°B． 90°C．120 °5. 若点 P(－ m，m－ 3)对于原点对称的点是第二象限内的点，则m 知足 (A. m＞ 3B. 0 ＜m≤3C. m＜ 0D. m＜ 0 或 m＞ 3D． 150 °)6．如图，是用围棋子摆出的图案(围棋子的地点用有序数对表示，如点 A 在 (5， 1)) ，假如再摆一黑一白两枚棋子，使9 枚棋子构成的图案既是轴对称图形又是中心对称图形，则以下摆放正确的选项是()A ．黑 (3，3)，白 (3， 1)B．黑 (3， 1)，白(3， 3)C．黑 (1， 5)，白 (5， 5)D．黑 (3， 2)，白(3， 3)7．如图，△DEF是由△ ABC绕着某点旋转获得的，则这点的坐标是（）A．（1， 1）8. 如图，△ACDB．（2， 0）和△AEB 都是等腰直角三角形，∠C．（ 0，1）D．（ 3， 1）CAD＝∠ EAB＝90°.四边形 ABCD是平行四边形，以下结论中错误的选项是()A. △ACE以点 A 为旋转中心，逆时针旋转90°后与△ADB重合B.△ACB以点 A 为旋转中心，顺时针旋转270 °后与△DAC重合C.沿 AE 所在直线折叠后，△ACE 与△ADE 重合D.沿 AD 所在直线折叠后，△ADB 与△ADE 重合9．如图，点 E 是正方形ABCD的边DC 上一点，把△ADE 绕点A 顺时针旋转到ABF 的地点，若四边形AECF的面积为25， DE=2，则AE 的长为（）A．7B． 6C．D． 510．已知等边△获得△ ACQ，点ABC 的边长为 4，点 P 是边 BC 上的动点，将△ABP 绕点 A 逆时针旋转D 是 AC边的中点，连结DQ，则 DQ 的最小值是（）60°A．B．C． 2D．不可以确立二、填空题11. 钟表分针的运动能够看作是一种旋转现象，经过40 分钟分针旋转了°.12．如图，在△ABC 中，∠ C＝ 90°，∠ BAC＝70°，将△ABC 绕点 A 顺时针旋转70°，点B， C旋转后的对应点分别是点 D 和E，连结BD，则∠BDE的度数是．13．如图，线段AB 的端点A、 B 分别在x 轴和y 轴上，且A（ 2，0）， B（ 0， 4），将线段AB 绕坐标原点O 逆时针旋转90°得线段A'B'，设线段AB'的中点为C，则点C的坐标是．14．如图，大圆的面积为4π，大圆的两条直径相互垂直，则图中暗影部分的面积的和为____．15.如图，△ABC 绕点 A 逆时针旋转 30°后到△A′B′C′的地点，若∠ B′＝ 45°，∠ C′＝ 60°，则∠B′AC＝.16．如图，在直角坐标系中，已知点P0的坐标为（ 1，0），将线段 OP0依据逆时针方向旋转45°，再将其长度伸长为OP0的 2 倍，获得线段 OP1；又将线段 OP1依据逆时针方向旋转 45°，长度伸长为 OP1的 2 倍，获得线段OP2；这样下去，获得线段OP3， OP4，， OP n（ n 为正整数），则点 P8的坐标为．17.如图，在△ABC 中、∠ C＝ 90°， AC ＝ 3， BC＝ 4，点 O 是 BC 的中点，将△ABC 绕点 O 旋转得△A' B' C' ,则在旋转过程中点 A ，C' 两点间的最大距离是 __________.18．如图，正方形ABCD，将正方形AEFG绕点 A 旋转，连结DF，点 M 是 DF 的中点，连结CM，若 AB＝ 4， AE＝1 ，则线段 CM 的最大值为．三、解答题19．如图，△ ABC为等边三角形，△AP′B 旋转后能与△APC重合，那么：（ 1）指出旋转中心；（2）求旋转角的度数；（3）求∠ PAP′的度数．20．在平面直角坐标系中，△ ABC的地点如下图（每个小方格都是边长方形）．（ 1）将△ ABC沿 x 轴方向向左平移 6 个单位，画出平移后获得的△1 个单位长度的正A1B1 C1；（ 2）将△ ABC绕着点 A 顺时针旋转90°，画出旋转后获得的△AB2C2；直接写出点B2的坐标；（ 3）作出△ABC对于原点O 成中心对称的△A3B3C3，并直接写出B3的坐标．21.如图，在平面直角坐标系中，O 为坐标原点，每个小方格的边长为 1 个单位长度，在第二象限内有横、纵坐标均为整数的A， B 两点，点B(－ 2， 3)，点 A 的横坐标为－ 2，且 OA ＝ 5.(1)直接写出 A 点的坐标，并连结AB， AO， BO；(2)画出△OAB 对于点 O 成中心对称的图形△OA1B1，并写出点 A1， B1的坐标 (点 A1， B1的对应点分别为 A， B)；(3)将△OAB 逆时针旋转90°获得△O1A2B2，画出△O1A2B2.22．如图，在正方形ABCD 中，E 为 CD 上一点， F 为 BC 延伸线上一点，CE＝CF.(1)△ DCF 能够当作是△ BCE 绕点 C 旋转某个角度获得的吗？(2)若∠ CEB ＝ 60°，求∠ EFD 的度数．23．如图①，△ ABC 和△ AEF 都为等腰直角三角形，∠ACB＝∠ AEF ＝90°，连结 EC、BF ，点 D 为 BF 的中点，连结 CD ．(1) 如图①，当点 E 落在 AB 边上时，请判断线段EC 与 DC 的数目关系，并证明你的结论；(2)将△ AEF 绕点 A 顺时针旋转 n°（ n＜180），如图②，请判断线段 EC 与 DC 的数目关系，并证明你的结论；(3) 若 AC＝ 2，点P为BC中点，动点Q 知足 PQ＝，如图③，将线段AQ 绕点 A 逆时针旋转 90°到线段AM ，连PM，则线段PM 的最小值为.图①图②人教版九年级上册第二十三章旋转单元测试卷一、单项选择题1.以下电视台的台标中，是中心对称图形的是（）A. B. C. D.2.如图的四个图形中，由基础图形经过平移、旋转或轴对称这三种变换都能获得的是（）A. B. C. D.3.以下图形中，既是轴对称图形，又是中心对称图形的是( )A. 线段B直.角三角形C等.边二角形D平.行四边形4.在平面直角坐标系内，点(-1，2)对于原点对称的点的坐标是（）A. （2， -1）B（. 1,2）C（. 1， -2）D（. -1， -2）5.在平面直角坐标系中，点的坐标为，以原点为中心，将点顺时针旋转获得点，则点的坐标为（）A. B. C. D.6.如图，的斜边在轴上，，含角的极点与原点重合，直角顶点在第二象限，将绕原点顺时针旋转后获得,则点的对应点的坐标是（）A. B.C. D.二、填空题7.如图，正方形 ABCD的边长为 4，点 E 是 CD 的中点， AF 均分∠ BAE 交 BC于点 F，将△ADE 绕点 A 顺时针旋转 90°得△ ABG，则 CF的长为 ________.8.如下图的图案是由全等的图形拼成的，此中AD=0.5cm，BC=1cm，则 AF=________cm．9.如图，正方形ABCD能够看作由什么“基本图形”经过如何的变化形成的？________．三、作图题10.如图， 4×6的正方形网格中，每个小正方形的极点称为格点，A，B，C 均为格点。

加油！有志者事竟成答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！第二十三章综合测试一、选择题（30分）1.下列图形中，既是轴对称图形又是中心对称图形的是（ ）ABCD2.如图，在方格纸中，ABC △经过变换得到DEF △，正确的变换是（ ） A .把ABC △绕点C 逆时针方向旋转90︒，再向下平移2格 B .把ABC △绕点C 顺时针方向旋转90︒，再向下平移5格 C .把ABC △向下平移4格，再绕点C 逆时针方向旋转180︒ D .把ABC △向下平移5格，再绕点C 顺时针方向旋转180︒3.如图，将ABC △绕点B 逆时针旋转α，得到EBD △，若点A 恰好在ED 的延长线上，则CAD ∠的度数为（ ） A .90α︒-B .αC .180α︒-D .2α4.同学们曾玩过万花筒，它是由三块等宽等长的玻璃片围成的。

人教版数学9年级上册第23单元·时间：120分钟满分：120分班级__________姓名__________得分__________一、选择题（共10小题，满分30分，每小题3分）1．（3分）下列所给图形中，既是中心对称图形又是轴对称图形的是（ ）A．B．C．D．2．（3分）如图五幅图案中，②、③、④、⑤哪一个图案可以通过平移图案①得到？（ ）A．②B．③C．④D．⑤3．（3分）如图，△ABC与△A′B′C′关于点O成中心对称，则下列结论不成立的是（ ）A．点A与点A′是对称点B．BO＝B′OC．∠ACB＝∠C′A′B′D．△ABC≌△A′B′C′4．（3分）观察下列图案，其中旋转角最大的是（ ）A．B．C．D．5．（3分）下列图形都是由两个全等三角形组合而成，其中是轴对称图形的是（ ）A．B．C．D．6．（3分）下列图形中，不能通过其中一个四边形平移得到的是（ ）A．B．C．D．7．（3分）已知点P（m﹣3，m﹣1）关于原点的对称点P′在第四象限，则m的取值范围在数轴上表示正确的是（ ）A．B．C．D．8．（3分）如图，△ABC是等腰直角三角形，DE是过点C的直线，BD⊥DE，AE⊥DE，则△BDC通过下列变换能与△ACE重合的是（ ）A．绕点C逆时针旋转90度B．沿AB的垂直平分线翻折C．绕AB的中点M顺时针旋转90度D．沿DE方向平移9．（3分）有下列说法：①平行四边形既是中心对称图形，又是轴对称图形②正方形有四条对称轴③平行四边形相邻两个内角的和等于180°④菱形的面积计算公式，除了“S菱形＝底×高”之外，还有“S菱形＝两对角线之积”⑤矩形和菱形均是特殊的平行四边形，因此具有平行四边形的所有性质其中正确的结论的个数有（ ）A．1B．2C．3D．410．（3分）如图，将等边三角形OAB放在平面直角坐标系中，A点坐标（1，0），将△OAB绕点O逆时针旋转60°，则旋转后点B的对应点B′的坐标为（ ）A．（―12，2）B．（﹣1，12）C．（―32，2）D．（，12）二、填空题（共5小题，满分15分，每小题3分）11．（3分）已知，点A（a，1）和点B（3，b）关于点（5，0）成中心对称，则a+b的值为 ．12．（3分）如图，在△ABC中，∠BAC＝108°，将△ABC绕点A按逆时针方向旋转得到△AB'C'．若点B'恰好落在BC边上，且AB'＝CB'，则∠C'的度数为 ．13．（3分）一个图形无论经过平移变换还是旋转变换，下列结论一定正确的是 （把所有你认为正确的序号都写上）①对应线段平行；②对应线段相等；③对应角相等；④图形的形状和大小都不变．14．（3分）如图，在△ABC中，AB=AC BAC＝30°，将△ABC绕点A 逆时针旋转60°得到△AB1C1，连接BC1，则BC1的长为 ．15．（3分）在平面直角坐标系中，O为原点，点A在第一象限，B（0），OA＝AB，∠AOB＝30°，把△OAB绕点B顺时针旋转60°得到△MPB，点O，A的对应点分别为M（a，b），P（p，q），则b﹣q的值为 ．三、解答题（共10小题，满分75分）16．（7分）如图，在平面直角坐标系内，△ABC三个顶点的坐标分别为A（1，﹣2），B（4，﹣1），C（3，﹣3）（正方形网格中，每个小正方形的边长都是1个单位长度）．（1）若△A1B1C1与△ABC关于原点O成中心对称，则点A1的坐标为 ；（2）以坐标原点O为旋转中心，将△ABC逆时针旋转90°，得到△A2B2C2，则点A2的坐标为 ；（3）求出（2）中线段AC扫过的面积．17．（7分）△ABC在平面直角坐标系中如图：（1）画出将△ABC绕点O逆时针旋转90°所得到的△A1B1C1，并写出A1点的坐标；（2）画出△A1B1C1关于原点成中心对称的△A2B2C2，并直接写出△AA1A2的面积．18．（7分）P为等边△ABC内的一点，PA＝10，PB＝6，PC＝8，将△ABP绕点B顺时针旋转60°到△CBP′位置．（1）判断△BPP′的形状，并说明理由；（2）求∠BPC的度数．19．（7分）如图，△ABC中，∠BAC＝120°，以BC为边向外作等边△BCD，把△ABD 绕着D点按顺时针方向旋转60°后到△ECD的位置，且点A、C、E在同一直线上．若AB＝6，AC＝4，求∠BAD的度数和AD的长．20．（7分）如图所示，△ABC的∠BAC＝120°，以BC为边向形外作等边△BCD，把△ABD绕着D点按顺时针方向旋转60°到△ECD的位置，若AB＝3，AC＝2，求∠BAD的度数和线段AD的长．21．（7分）在△ABC中，∠B+∠ACB＝30°，AB＝4，△ABC逆时针旋转一定角度后与△ADE重合，且点C恰好成为AD中点，如图（1）指出旋转中心，并求出旋转角的度数．（2）求出∠BAE的度数和AE的长．22．（7分）如图，已知△ABC和点，求作△ABC关于点C成中心对称的△A1B1C1，保留作图痕迹，不要求写过程．23．（8分）如图，在正方形网格中，△ABC的顶点均在格点上，请在所给的直角坐标系中解答下列问题：（1）作出△ABC关于原点O成中心对称的△A1B1C1，写出B1的坐标；（2）直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标 ．24．（9分）如图网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2）、B（1，3）．（1）点A关于点O中心对称点的坐标为 ；（2）△AOB绕点O顺时针旋转90°后得到△A1OB1，在方格纸中画出△A1OB1，并写出点B1的坐标（ ， ）；（3）在y轴上找一点P，使得PA+PB最小，请在图中标出点P的位置，并求出这个最小值．25．（9分）在平面直角坐标系中，O为原点，点A（2，0），点B（0，2），把△ABO绕点B逆时针旋转，得△A′BO′，点A，O旋转后的对应点为A′，O′．记旋转角为α．（1）如图①，当点O′落在边AB上时，求点O′的坐标；（2）如图②，当α＝60°时，求AA′的长及点A′的坐标．参考答案一、选择题（共10小题，满分30分，每小题3分）1．D；2．D；3．C；4．A；5．B；6．D；7．D；8．C；9．C；10．A；二、填空题（共5小题，满分15分，每小题3分）11．612．24°13．②③④14．315．1三、解答题（共10小题，满分75分）16．解：（1）∵△A1B1C1与△ABC关于原点O成中心对称，A（1，﹣2），∴点A1的坐标为（﹣1，2）．故答案为：（﹣1，2）；（2）如图，△A2B2C2即为所求，点A2的坐标为（2，1）．故答案为：（2，1）；（3）∵OA=OC=∴线段AC扫过的面积＝扇形OCC2的面积﹣扇形OAA2的面积90π2360=9π2―5π4=13π4．17．解：（1）如图，△A1B1C1为所作，A1点的坐标为（﹣3，2）；（2）如图，△A 2B 2C 2为所作；△AA 1A 2的面积=12×2＝13．18．解：（1）△BPP ′是等边三角形；理由如下：∵△ABP 绕点B 顺时针旋转60°到△CBP ′位置，∴BP ＝BP ′，∠PBP ′＝60°，AP ＝CP ′＝10，∴△BPP ′是等边三角形；（2）∵△BPP ’是等边三角形，∴∠BPP ’＝60°，PP ′＝PB ＝6，∵62+82＝102，∴PP ′2+PC 2＝P ′C 2，∴△PCP ′是直角三角形，∠P ′PC ＝90°，∴∠BPC ＝∠BPP ′+∠P ′PC ＝60°+90°＝150°．19．解：∵把△ABD 绕点D 按顺时针方向旋转60°后到△ECD 的位置，∴AD ＝DE ，∠ADE ＝60°，AB ＝CE ，∵∠BDC +∠BAC ＝60°+120°＝180°，∴∠ABD +∠ACD ＝180°，∵∠ABD ＝∠DCE ，∴∠ACD +∠DCE ＝180°，∴A ，C ，E 在一条直线上，∴△ADE 是等边三角形，∴∠DAE ＝60°，∴∠BAD ＝120°﹣60°＝60°；∴AE ＝AD ＝AC +EC ＝AC +AB ＝10．20．解：法1：∵△ABC的∠BAC＝120°，以BC为边向形外作等边△BCD，∴∠BAC+∠BDC＝120°+60°＝180°，∴A，B，D，C四点共圆，∴∠BAD＝∠BCD＝60°，∠ACD+∠ABD＝180°，又∵∠ABD＝∠ECD，∴∠ACD+∠ECD＝180°，∴∠ACE＝180°，即A、C、E共线，∵把△ABD绕着D点按顺时针方向旋转60°到△ECD的位置，AB＝3，∴AB＝CE＝3，∴AD＝AE＝AC+AB＝3+2＝5；21．解：（1）在△ABC中，∵∠B+∠ACB＝30°，∴∠BAC＝150°，当△ABC逆时针旋转一定角度后与△ADE重合，∴旋转中心为点A，∠BAD等于旋转角，即旋转角为150°；（2）∵△ABC绕点A逆时针旋转150°后与△ADE重合，∴∠DAE＝∠BAC＝150°，AB＝AD＝4，AC＝AE，∴∠BAE＝360°﹣150°﹣150°＝60°，∵点C为AD中点，∴AC=12AD＝2，∴AE＝2．22．解：如图，△A1B1C1即为所求作．23．解：（1）如图，△A1B1C1即为所求；B1（4，﹣1）（2）顶点D 的坐标为：（1，1）或（﹣3，﹣1）或（﹣5，3）．故答案为：（1，1）或（﹣3，﹣1）或（﹣5，3）．24．解：（1）点A 关于点O 中心对称点的坐标为（﹣3，﹣2），故答案为：（﹣3，﹣2）．（2）如图，△A 1OB 1即为所求作，并写出点B 1的坐标（3，﹣1），故答案为：3，﹣1．（3）如图，点P 即为所求作，最小值为==25．解：（1）如图①，∵点A （2，0），点B （0，2），∴OA ＝OB ＝2，△ABO 是等腰直角三角形，∴AB ＝当点O ′落在边AB 上时，α＝45°，∴点O ′的横坐标为12AB 2―∴点O 2―；（2）如图②，当α＝60°时，∴∠ABA ′＝60°，AB ＝A ′B ，∴△ABA ′为等边三角形，∴AA′＝A′B＝AB＝连接OA′，在△OBA′和△OAA′中，OB=OAOA′=OA′，A′B=A′A∴△OBA′≌△OAA′（SSS），∴∠BOA′＝∠AOA′，∠BA′O＝∠AA′O，∴直线OA′的函数解析式为y＝x，∴OA′⊥AB，∴＝2×2，即OM=A′M==∴OA′＝OM+A′M=∴点A′的坐标为（1+1．。

人教版九年级数学上册第二十三章测试卷一、选择题(每题3分，共30分)1．下列图形中是中心对称图形的是()2．点(－1，2)关于原点的对称点坐标是()A．(－1，－2) B．(1，－2) C．(1，2) D．(2，－1) 3．如图，该图形围绕圆心按下列角度旋转后，不能．．与其自身重合的是() A．72°B．108°C．144°D．216°(第3题)(第4题)(第5题)(第6题)4．如图，在△ABC中，∠CAB＝65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为()A．35°B．40°C．50°D．65°5．如图，点O是▱ABCD的对称中心，EF是过点O的任意一条直线，它将平行四边形分成两部分，四边形ABOE和四边形CDOF的面积分别记为S1，S2，那么S1，S2之间的关系为()A. S1>S2B. S1<S2C．S1＝S2 D. 无法确定6．如图，四边形ABCD为正方形，O为对角线AC，BD的交点，则△COD绕点O经过下列哪种旋转可以得到△DOA()A．顺时针旋转90°B．顺时针旋转45°C．逆时针旋转90°D．逆时针旋转45°7．如图，四边形ABCD是边长为5的正方形，E是DC上一点，DE＝1，将△ADE 绕着点A顺时针旋转到与△ABF重合，则EF＝()A.41B.42 C．5 2 D．213(第7题) (第8题) (第9题)8．如图，在平面直角坐标系中，将点P (2，3)绕原点O 顺时针旋转90°得到点P ′，则点P ′的坐标为( ) A ．(3，2)B ．(3，－1)C ．(2，－3)D ．(3，－2)9．如图，点P 是等腰直角三角形ABC 外一点，把BP 绕点B 顺时针旋转90°到BP ′，已知∠AP ′B ＝135°，P ′A ∶P ′C ＝1∶3，则P ′A ∶PB 等于( ) A ．1∶ 2B ．1∶2C.3∶2D ．1∶ 310．如图，在平面直角坐标系中，将边长为1的正方形OABC 绕点O 顺时针旋转45°后得到正方形OA 1B 1C 1；依此方式，绕点O 连续旋转2 022次得到正方形OA 2 022B 2 022C 2 022，那么点A 2 022的坐标是( )A.⎝ ⎛⎭⎪⎫22，－22 B ．(－1，0)C.⎝ ⎛⎭⎪⎫－22，－22 D ．(0，－1)二、填空题(每题3分，共24分)11．将如图所示的图案绕其中心旋转n °时与原图案完全重合，那么n 的最小值是________．(第11题) (第12题) (第13题) (第14题) 12．如图，大圆的面积为4π，大圆的两条直径互相垂直，则图中阴影部分的面积的和为________．13．如图，将△ABC绕点A逆时针旋转得到△ADE，点C和点E是对应点，若∠CAE＝90°，AB＝1，则BD＝________.14．如图，阴影部分组成的图案既是关于x轴成轴对称的图形又是关于坐标原点O成中心对称的图形，若点A的坐标是(1，3)，则点M的坐标是__________，点N的坐标是__________．15．如图，点A，B，C的坐标分别为(0，－1)，(0，2)，(3，0)．从点M(3，3)，N(3，－3)，P(－3，0)，Q(－3，1)中选择一个点，以点A，B，C与该点为顶点的四边形不是．．中心对称图形，则该点是________．(第15题)(第16题)(第17题)(第18题) 16．如图，在Rt△OAB中，∠OAB＝90°，OA＝AB＝6，将△OAB绕点O逆时针方向旋转90°得到△OA1B1.连接AA1，则四边形OAA1B1的面积为________．17．如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α(0°＜α＜90°)．若∠1＝110°，则α＝________．18．如图，将一个45°角的顶点与正方形ABCD的顶点A重合，在正方形的内部绕着点A旋转，角的两边分别与CD，CB边相交于F，E两点，与对角线BD交于N，M两点，连接EF，则下列结论：①AE＝AF；②EF＝BE＋DF；③△CEF的周长等于正方形ABCD周长的一半；④S△AEF ＝S△ABE＋S△ADF.其中正确的结论有____________(填序号)．三、解答题(19～22题每题8分，23题10分，其余每题12分，共66分) 19．如图，在△ABC中，∠B＝10°，∠ACB＝20°，AB＝4，△ABC逆时针旋转一定角度后与△ADE重合，且点C恰好成为AD的中点．(1)指出旋转中心，并求出旋转角的度数；(2)求∠BAE的度数和AE的长．20．在平面直角坐标系中，△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形)．(1)将△ABC沿x轴方向向左平移6个单位长度，画出平移后得到的△A1B1C1；(2)将△ABC绕着点A顺时针旋转90°，画出旋转后得到的△AB2C2，并直接写出点B2，C2的坐标．21．平面直角坐标系第二象限内的点P(x2＋2x，3)与另一点Q(x＋2，y)关于原点对称，试求x＋2y的值．22．图①、图②都是由边长为1的小等边三角形构成的网格，每个网格图中有5个小等边三角形已涂上阴影，请在余下的空白小等边三角形中，按下列要求选取一个涂上阴影．(1)使得6个阴影小等边三角形组成一个轴对称图形；(2)使得6个阴影小等边三角形组成一个中心对称图形．(请将两个小题依次作答在图①、图②中，均只需画出符合条件的一种情形)23．如图，△BAD是由△BEC在平面内绕点B旋转60°得到的，且AB⊥BC，BE＝CE，连接DE.(1)求证：△BDE≌△BCE；(2)试判断四边形ABED的形状，并说明理由．24．已知△ABC与△DEC是两个大小不同的等腰直角三角形．(1)如图①，连接AE，DB，试判断线段AE和DB的数量和位置关系，并说明理由；(2)如图②，连接DB，将线段DB绕D点顺时针旋转90°到DF，连接AF，试判断线段DE和AF的数量和位置关系，并说明理由．25．在△ABC中，AB＝AC，∠BAC＝α(0°＜α＜60°)，将线段BC绕点B逆时针旋转60°得到线段BD.(1)如图①，直接写出∠ABD的大小(用含α的式子表示)；(2)如图②，∠BCE＝150°，∠ABE＝60°，试判断△ABE的形状并加以证明；(3)在(2)的条件下，连接DE，若∠DEC＝45°，求α.答案一、1.B 2.B 3.B 4.C 5.C 6.C 7．D8.D9.B10.B二、11.12012.π13. 214．(－1，－3)；(1，－3)15. P16. 3617.20°18. ②③④三、19.解：(1)旋转中心是点A.∵∠CAB＝180°－∠B－∠ACB＝150°，∴旋转角是150°.(2)∠BAE＝360°－150°×2＝60°.由旋转的性质得△ABC≌△ADE，∴AB＝AD，AC＝AE.又∵点C是AD的中点，∴AC＝12AD＝12AB＝12×4＝2.∴AE＝2.20．解：(1)如图，△A1B1C1即为所求．(2)如图，△AB2C2即为所求．点B2的坐标为(4，－2)，点C2的坐标为(1，－3)．21．解：根据题意，得(x2＋2x)＋(x＋2)＝0，y＝－3.解得x1＝－1，x2＝－2.∵点P在第二象限，∴x2＋2x＜0.∴x＝－1.∴x＋2y＝－7.22．解：(1)如图①所示．(答案不唯一)(2)如图②所示．(答案不唯一)23．(1)证明：∵△BAD 是由△BEC 在平面内绕点B 旋转60°得到的，∴DB ＝CB ，∠ABE ＝∠DBC ＝60°. ∵AB ⊥BC ， ∴∠ABC ＝90°. ∴∠CBE ＝30°. ∴∠DBE ＝30°. ∴∠DBE ＝∠CBE . 在△BDE 和△BCE 中，⎩⎨⎧DB ＝CB ，∠DBE ＝∠CBE ，BE ＝BE ，∴△BDE ≌△BCE (SAS)． (2)解：四边形ABED 为菱形． 理由：由(1)得△BDE ≌△BCE ， ∴EC ＝ED .∵△BAD 是由△BEC 旋转得到的， ∴△BAD ≌△BEC . ∴BA ＝BE ，AD ＝EC ＝ED . 又∵BE ＝CE ， ∴BA ＝BE ＝AD ＝ED . ∴四边形ABED 为菱形． 24．解：(1)AE ＝DB ，AE ⊥DB .理由：由题意可知，CA ＝CB ，CE ＝CD ，∠ACE ＝∠BCD ＝90°， ∴Rt △ACE ≌Rt △BCD (SAS)． ∴AE ＝DB .如图①，延长DB 交AE 于点M . ∵Rt △ACE ≌Rt △BCD ，∴∠AEC＝∠BDC.又∵∠AEC＋∠EAC＝90°，∴∠BDC＋∠EAC＝90°.∴在△AMD中，∠AMD＝180°－90°＝90°.∴AE⊥DB.(2)DE＝AF，DE⊥AF.理由：如图②，设ED与AF相交于点N，由题意易知BE＝AD.∵∠EBD＝∠C＋∠BDC＝90°＋∠BDC，∠ADF＝∠BDF＋∠BDC＝90°＋∠BDC，∴∠EBD＝∠ADF.又∵DB＝DF，∴△EBD≌△ADF(SAS)．∴∠E＝∠F AD，DE＝AF.∵∠E＝45°，∴∠F AD＝45°.又∵∠EDC＝45°，∴∠AND＝90°.∴DE⊥AF.25．解：(1)∠ABD＝30°－1 2α.(2)△ABE为等边三角形．证明如下：连接AD，CD.∵线段BC绕点B逆时针旋转60°得到线段BD，∴BC＝BD，∠DBC＝60°.∴△BCD是等边三角形．∴BD＝CD.又∵∠ABE＝60°，∴∠ABD＝60°－∠DBE＝∠EBC＝30°－1 2α.在△ABD 和△ACD 中，⎩⎨⎧AB ＝AC ，AD ＝AD ，BD ＝CD ，∴ △ABD ≌△ACD (SSS)． ∴∠BAD ＝∠CAD ＝12∠BAC ＝12α. ∵∠BCE ＝150°，∴∠BEC ＝180°－⎝ ⎛⎭⎪⎫30°－12α－150°＝12α. ∴∠BAD ＝∠BEC . 在△ABD 和△EBC 中，⎩⎨⎧∠BAD ＝∠BEC ，∠ABD ＝∠EBC ，BD ＝BC ，∴△ABD ≌△EBC (AAS)． ∴AB ＝BE . 又∵∠ABE ＝60°， ∴△ABE 为等边三角形．(3)由(2)可知△BCD 为等边三角形，∴∠BCD ＝60°. ∵∠BCE ＝150°，∴∠DCE ＝150°－60°＝90°. ∵∠DEC ＝45°，∴ △DCE 为等腰直角三角形， ∴DC ＝CE ＝BC . ∴∠CBE ＝∠BEC . ∵∠BCE ＝150°，∴∠EBC ＝180°－150°2＝15°. 而由(2)知∠EBC ＝30°－12α，∴30°－12α＝15°. ∴α＝30°.。