第11章机械波
- 格式:ppt
- 大小:2.00 MB
- 文档页数:81







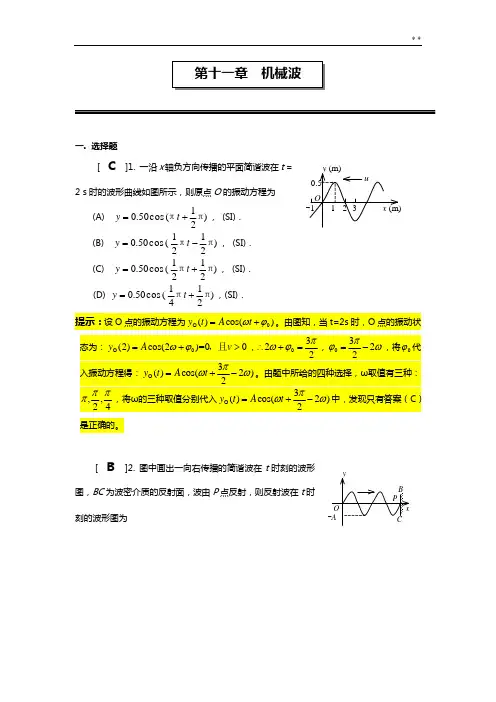
一. 选择题[ C ]1. 一沿x 轴负方向传播的平面简谐波在t = 2 s 时的波形曲线如图所示,则原点O 的振动方程为(A) )21(cos 50.0ππ+=t y , (SI).(B) )2121(cos 50.0ππ-=t y , (SI).(C) )2121(cos 50.0ππ+=t y , (SI).(D) )2141(cos 50.0ππ+=t y ,(SI).提示:设O 点的振动方程为O 0()cos()y t A t ωϕ=+。
由图知,当t=2s 时,O 点的振动状是正确的。
[ B ]2. 图中画出一向右传播的简谐波在t 时刻的波形图,BC 为波密介质的反射面,波由P 点反射,则反射波在t 时刻的波形图为提示:由题中所给波形图可知,入射波在P 点的振动方向向下;而BC 为波密介质反射面,故在P 点反射波存在“半波损失”,即反射波与入射波反相,所以,反射波在P 点的振动方向向上,又P 点为波节,因而得答案B 。
[ A ]3. 一平面简谐波沿x 轴正方向传播,t = 0 时刻的波形图如图所示,则P 处质点的振动在t = 0时刻的旋转矢量图是ωSAϖO ′ωSA ϖO ′ωϖO ′ωSAϖO ′(A)(B)(C)(D)S[ B ]4. 一平面简谐波在弹性媒质中传播时,某一时刻媒质中某质元在负的最大位移处,则它的能量是(A) 动能为零,势能最大.(B) 动能为零,势能为零.(C) 动能最大,势能最大.(D) 动能最大,势能为零.提示:动能=势能,在负的最大位移处时,速度=0,所以动能为零,势能也为零。
[ B ]5. 在驻波中,两个相邻波节间各质点的振动(A) 振幅相同,相位相同.(B) 振幅不同,相位相同.(C) 振幅相同,相位不同.(D) 振幅不同,相位不同.提示:根据驻波的特点判断。
[ C ]6. 在同一媒质中两列相干的平面简谐波的强度之比是I1 / I2 = 4,则两列波的振幅之比是(A) A1 / A2 = 16.(B) A1 / A2 = 4.(C) A1 / A2 = 2.(D) A1 / A2 = 1 /4.二.填空题1. 一平面简谐机械波在媒质中传播时,若一媒质质元在t时刻的总机械能是10 J,则(t+在2. 一列强度为I 的平面简谐波通过一面积为S 的平面,波速u ϖ与该平面的法线0n v的夹角为θ,则通过该平面的能流是cos IS θ。

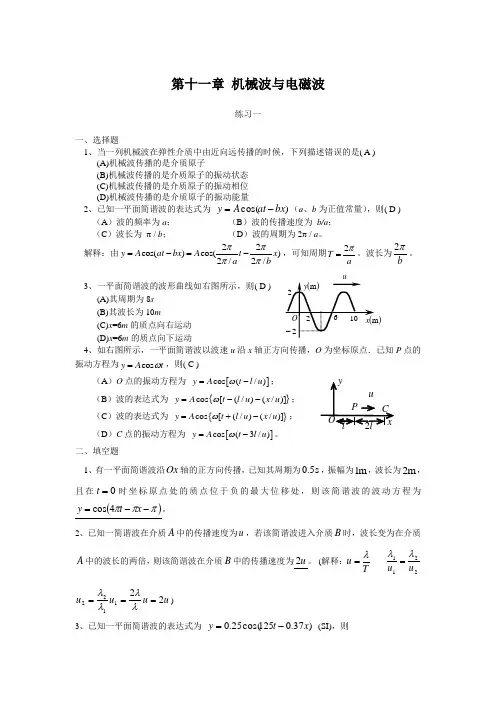
第十一章 机械波与电磁波练习一一、选择题1、当一列机械波在弹性介质中由近向远传播的时候,下列描述错误的是( A ) (A)机械波传播的是介质原子(B)机械波传播的是介质原子的振动状态 (C)机械波传播的是介质原子的振动相位 (D)机械波传播的是介质原子的振动能量2、已知一平面简谐波的表达式为 )cos(bx at A y -=(a 、b 为正值常量),则( D ) (A )波的频率为a ; (B )波的传播速度为 b/a ; (C )波长为 π / b ; (D )波的周期为2π / a 。
解释:由22cos()cos()2/2/y A at bx A t x a b ππππ=-=-,可知周期2T a π=。
波长为bπ2。
3、一平面简谐波的波形曲线如右图所示,则( D )(A)其周期为8s (B)其波长为10m(C)x =6m 的质点向右运动(D)x =6m 的质点向下运动4、如右图所示,一平面简谐波以波速u 沿x 轴正方向传播,O 为坐标原点.已知P 点的振动方程为cos y A t ω=,则( C )(A )O 点的振动方程为 []cos (/)y A t l u ω=-; (B )波的表达式为 {}cos [(/)(/)]y A t l u x u ω=--; (C )波的表达式为 {}cos [(/)(/)]y A t l u x u ω=+-; (D )C 点的振动方程为 []cos (3/)y A t l u ω=-。
二、填空题1、有一平面简谐波沿Ox 轴的正方向传播,已知其周期为s 5.0,振幅为m 1,波长为m 2,且在0=t 时坐标原点处的质点位于负的最大位移处,则该简谐波的波动方程为()πππ--=x t y 4cos 。
2、已知一简谐波在介质A 中的传播速度为u ,若该简谐波进入介质B 时,波长变为在介质A 中的波长的两倍,则该简谐波在介质B 中的传播速度为2u 。
![第十一章+波动答案[1]..](https://uimg.taocdn.com/c246b14369eae009581bec4a.webp)
一. 选择题[D] 1.(基础训练2)一平面简谐波,沿x 轴负方向传播.角频率为ω ,波速为u .设 t = T /4 时刻的波形如图14-11所示,则该波的表达式为:(A) )(cos xu t A y -=ω.(B)]21)/(cos[π+-=u x t A y ω.(C) )]/(cos[u x t A y +=ω.(D)])/(cos[π++=u x t A y ω. 【提示】}])4[(cos{ϕω++-=uxT t A y 。
ϕ为0=x 处初相。
[C] 2.(基础训练4) 一平面简谐波在弹性媒质中传播,在某一瞬时,媒质中某质元正处于平衡位置,此时它的能量是 (A) 动能为零,势能最大. (B) 动能为零,势能为零.(C) 动能最大,势能最大. (D) 动能最大,势能为零. 【提示】波的能量特点。
[B] 3.(基础训练5)在驻波中,两个相邻波节间各质点的振动 (A) 振幅相同,相位相同. (B) 振幅不同,相位相同.(C) 振幅相同,相位不同. (D) 振幅不同,相位不同. 【提示】驻波特点。
[C] 4.(基础训练8)如图14-15所示两相干波源S 1和S 2相距λ /4,(λ 为波长),S 1的相位比S 2的相位超前π21,在S 1,S 2的连线上,S 1外侧各点(例如P 点)两波引起的两谐振动的相位差是:(A) 0. (B) π21. (C) π. (D) π23. 【提示】21212()r r πϕϕϕπλ-∆=--=-[D] 5.(自测提高6)如图14-25所示,S 1和S 2为两相干波源,它们的振动方向均垂直于图面,发出波长为λ 的简谐波,P 点是两列波相遇区域中的一点,已知 λ21=P S ,λ2.22=P S ,两列波在P 点发生相消干涉.若S 1的振动方程为 )212cos(1π+π=t A y ,则S 2的振动方程为图14-25(A) )212cos(2π-π=t A y . (B) )2cos(2π-π=t A y . (C) )212cos(2π+π=t A y . (D) )1.02cos(22π-π=t A y【提示】21212()r r πϕϕϕλ∆=---22(2.2 2.0)(21)2k ππϕλλπλ=---=+[C] 6.(自测提高7)在弦线上有一简谐波,其表达式是 ]3)2002.0(2cos[100.221π+-π⨯=-x t y (SI) 为了在此弦线上形成驻波,并且在x = 0处为一波节,此弦线上还应有一简谐波,其表达式为:(A) ]3)2002.0(2cos[100.222π++π⨯=-x t y (SI). (B) ]32)2002.0(2cos[100.222π++π⨯=-x t y (SI).(C) ]34)2002.0(2cos[100.222π++π⨯=-x t y (SI).(D) ]3)2002.0(2cos[100.222π-+π⨯=-x t y (SI).【提示】两沿反方向传播的波在0x =处振动合成为零。
第十一章机械波一、是非题1.机械波的强度与振幅的平方、频率的平方成正比,与媒质的密度无关··················()2.机械波的强度与媒质的密度成正比,与振幅无关。
··································()3.声强30dB的声音听起来一定比20dB的声音响。
···································()4.声波在空气中只能以横波的形式传播············································()5.波动方程表示在沿波的传播方向上各个不同质点在不同时刻的位移··················()6.机械波的强度既与振幅和频率有关,还与媒质的密度和波速有关·····················()7.机械波传播过程中,任意时刻,体元中动能与势能相等。