模糊控制位置跟踪的SIMULINK仿真
- 格式:doc
- 大小:561.50 KB
- 文档页数:7

simulink轨迹跟踪方法Simulink是一种基于模型的设计和仿真工具,广泛应用于自动控制系统的开发和测试中。
轨迹跟踪是自动控制系统中的一个重要问题,通过控制对象在给定轨迹上的运动,实现对系统的精确控制。
Simulink提供了多种方法来实现轨迹跟踪,本文将介绍其中几种常用的方法。
1. 基于PID控制器的轨迹跟踪方法:PID控制器是一种常见的控制器,通过比较实际输出与期望输出的偏差,调整控制信号来实现对系统的控制。
在Simulink中,可以使用PID控制器模块来实现轨迹跟踪。
通过调整PID控制器的参数,可以实现对系统的精确控制。
例如,可以调整比例系数来增强系统的响应速度,调整积分系数来消除系统的稳态误差,调整微分系数来抑制系统的震荡。
2. 基于模型预测控制(MPC)的轨迹跟踪方法:模型预测控制是一种基于系统数学模型的控制方法,通过预测系统的未来状态,优化控制信号来实现对系统的控制。
Simulink提供了MPC工具箱,可以方便地进行模型预测控制。
在轨迹跟踪问题中,可以使用MPC来预测系统在给定轨迹上的运动,并根据预测结果来调整控制信号,使系统实现轨迹跟踪。
MPC可以考虑系统的约束条件,例如输入和输出的限制,从而实现对系统的更加精确的控制。
3. 基于模糊控制的轨迹跟踪方法:模糊控制是一种通过模糊推理来实现对系统的控制的方法。
在Simulink中,可以使用模糊控制器模块来实现模糊控制。
在轨迹跟踪问题中,可以使用模糊控制器来根据系统的当前状态和轨迹的要求,输出相应的控制信号,使系统实现轨迹跟踪。
模糊控制器可以考虑系统的非线性和不确定性,适用于复杂系统的控制。
4. 基于神经网络的轨迹跟踪方法:神经网络是一种模拟人脑神经网络结构和工作原理的计算模型。
在Simulink中,可以使用神经网络模块来实现神经网络控制。
在轨迹跟踪问题中,可以使用神经网络来学习系统的输入和输出之间的映射关系,并根据学习到的映射关系来生成控制信号,使系统实现轨迹跟踪。



模糊控制系统的仿真实验实验目的:现有被控对象一:G(s)=1/(s2+2s+1)被控对象二:G(s)=K /【(T1s+1)(T2s+1) 】试设计一个模糊控制系统来实现对它的控制,并完成以下任务:任务一:通过仿真分析模糊控制器的参数的变化(主要讨论控制器解模方法和量化因子的变化)对系统性能的影响。
任务二:在控制器参数一定的情况下改变被控对象的参数,分析对象参数变化时fuzzy controller的适应能力。
任务三:在控制器参数一定的情况下改变被控对象的结构,分析对象结构变化时fuzzy controller的适应能力。
实验分析:要完成以上任务应分两个步骤:一设计模糊控制器,二用matlab的模糊逻辑工具箱建立模糊推理系统,并在simulink中实现对模糊系统的仿真。
接下来就以对象一为例说明模糊控制系统的仿真。
一、模糊控制器的设计模糊控制器的设计步骤为:1、选择控制器的输入输出:选择误差e及误差变化量ec为输入,u作为输出用于控制对象,这样模糊控制器具有二输入一输出的结构。
2、模糊集及论域的定义:z输入e的模糊子集为{NB NM NS NO PO PS PM PB}z输入ec和输出u的模糊子集均为{NB NM NS ZO PS PM PB}z e的论域为{-6 -5 -4 -3 -2 -1 -0 +0 1 2 3 4 5 6 }z ec的论域为{-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 }z u的论域为{-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 }我们选择三角形作为隶属度函数的形状,e的隶属度函数如下图所示:图1-1 ec的隶属度函数如下图所示:图1-2 u的隶属度函数如下图所示图1-3表1-14、选择输入输出变量的量化因子:这里暂时选定输入输出的量化因子Ke=Kc=Ku=1,接下来的仿真过程还可以调整。
5、择模糊规则前提交的方法为min,模糊推理方法为min,而反模糊化方法可以在仿真过程中设置。

模糊控制simulink实例一、模糊控制概述模糊控制是一种基于人工智能的控制方法,它模拟人类的思维方式进行控制决策。
模糊控制的核心思想是将模糊语言和模糊推理应用于控制系统中,通过建立模糊规则和模糊集合来实现对系统的控制。
模糊控制具有适应性强、处理非线性和复杂系统能力强等优点,在工业控制领域得到了广泛应用。
二、Simulink简介Simulink是MathWorks公司开发的一款基于MATLAB的通用仿真平台。
Simulink提供了一个直观的图形化界面,可以用于设计、模拟和实现各种系统模型。
Simulink 支持多领域的仿真,包括控制系统、信号处理、通信系统等,同时也提供了丰富的库函数和工具箱,方便用户进行系统建模与仿真。
三、模糊控制在Simulink中的应用模糊控制在Simulink中的应用可以通过Fuzzy Logic Toolbox来实现,该工具箱提供了一系列用于模糊控制设计和仿真的函数和模块。
下面介绍一个简单的模糊控制实例来说明模糊控制在Simulink中的应用。
3.1 系统建模首先,我们需要确定模糊控制系统的输入、输出和控制规则。
假设我们要设计一个小型的温度控制系统,系统的输入是环境温度(T),输出是加热器的电压(V)。
根据经验,我们可以定义几个模糊集合来描述温度和电压的状态,例如”冷”、“适中”和”热”。
然后,我们可以根据这些模糊集合定义一些模糊规则,例如”当温度冷时,增加电压”等。
3.2 模糊控制器设计在Simulink中,我们可以使用Fuzzy Logic Controller模块来设计模糊控制器。
该模块提供了一种快速且简单的方法来创建模糊控制器。
首先,我们需要定义输入和输出的模糊集合,以及模糊规则。
然后,我们可以将这些参数传递给Fuzzy Logic Controller模块,并设置输入输出的信号传递方式。
3.3 系统仿真在完成模糊控制器的设计后,我们可以进行系统的仿真。
在Simulink中,我们可以通过连接输入信号和模拟环境来模拟系统的行为。


1模糊P1D用命令FUZZy翻开模糊控制工具箱。
AnfiSedit翻开自适应神经模糊控制器,它用给定的输入输出数据建个一个模糊推理系统,并用一个反向传播或者与最小二乘法结合的来完成隶属函数的调节。
SUrfVieW(newfis)可以翻开外表视图窗口8.1模糊PID串联型新建一个SimUIink模型同时拖入一个fuzzy1ogiccontro11er模块,双击输入已经保存的fis模糊控制器的名字。
由于这个控制模块只有一个输入端口,需要用到I I1UX模块。
模糊结合PID,当输出误差较大时,用模糊校正,当较小时,用PID校正。
8.2模糊自适应PID[1)PID参数模糊自整定的原那么PID调节器的控制规律为:u(k)=Kpe(k)+Ki∑e(i)+Kdec(k)其中:KP为比例系数;Ki为积分系数;Kd为微分系数;e(k)、ec(k)分别为偏差和偏差变化率.模糊自整定P1D参数的目的是使参数Kp、Ki、Kd随着e和ec的变化而自行调整,故应首先建立它们间的关系.根据实际经验,参数KP、Ki、Kd在不同的e和ec下的自调整要满足如下调整原那么:(1)当e较大时,为加快系统的响应速度,防止因开始时e的瞬间变大可能会引起的微分溢出,应取较大的Kp和较小的Kd,同时由于积分作用太强会使系统超调加大,因而要对积分作用加以限制,通常取较小的Ki值;(2)当e中等大小时,为减小系统的超调量,保证一定的响应速度,Kp应适当减小;同时Kd 和Ki的取值大小要适中;(3)当e较小时,为了减小稳态误差,Kp与Ki应取得大些,为了防止输出响应在设定值附近振荡,同时考虑系统的抗干扰性能,Kd值的选择根据IeC1值较大时,Kd取较小值,通常Kd为中等大小。
同时按照需要,将输入语言变量E和EC分为7个模糊子集,分别用语言值正大(PB)、正中(PM)、正小(PS)、零(Z)、负小(NS)、负中(NM)、负大(NB)来表示,它们的隶属函数为高斯型(gaussmf),输出语言变量Kp/、Ki,、Ker用语言值小正大(PB)、正中(PM)、正小(PS)、零(Z)、负小(NS)、负中(NM)、负大(NB)来表示隶属函数为三角型(trimf),方法二:图-1模糊自适应Simu1ink模型根据各模糊子集的隶属度赋值表和各参数模糊控制模型,应用模糊合成推理设计分数阶PID参数的模糊矩阵表,算出参数代入下式计算:Kp=KpO+(E,EOpjKi=KiO+(E,EC)I;Kd=KdO+(E,EC)d式中:KpO.KiO.KdO为P1D参数的初始设计值,由传统的PID控制器的参数整定方法设计。
智能控制作业二“模糊控制位置跟踪的SIMULINK 仿真一、题目 设被控对象的传递函数为s s s G 252500)(2+=,输入信号为方波,周期为1秒,幅值为1,(可以用Pulse Generator 模块来产生)。
1)试设计两输入单输出模糊控制器,输入为偏差E 和偏差变化率EC ,输出为控制量U ,使系统输出能实时跟踪输入信号。
2)通过仿真理解并分析E 和EC 的参数选择对系统稳态误差和动态性能的影响,这些参数包括模糊子集的个数,论域的范围等。
作业中最好把不同参数下的仿真结果附上。
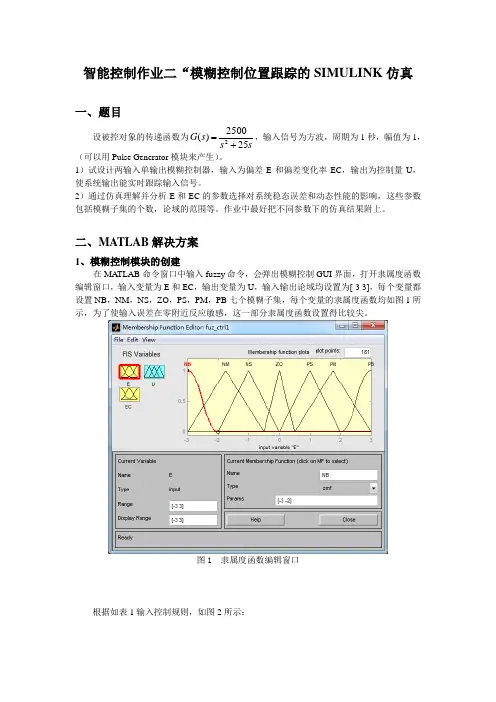
二、MATLAB 解决方案1、模糊控制模块的创建在MA TLAB 命令窗口中输入fuzzy 命令,会弹出模糊控制GUI 界面,打开隶属度函数编辑窗口,输入变量为E 和EC ,输出变量为U ,输入输出论域均设置为[-3 3],每个变量都设置NB ,NM ,NS ,ZO ,PS ,PM ,PB 七个模糊子集,每个变量的隶属度函数均如图1所示,为了使输入误差在零附近反应敏感,这一部分隶属度函数设置得比较尖。
图1 隶属度函数编辑窗口根据如表1输入控制规则,如图2所示:表1 控制规则编辑完成后可以看到如图3所示的模糊输入与输出的三维示意图:图2 控制规则输入窗口图3 输出三维示意图2、simulink的仿真新建一个model,搭建如图4所示的控制框图,保存为fuc2文件夹中的fuz_ctrl.mdl。
其中增益模块用来控制将输入或输出与模糊控制器的论域相匹配。
图4 simulink控制框图3、调试后的仿真结果经过调试优化,最终得到的仿真波形如图5所示。
其中Ke=3,Kec=0.06,Ku=1.图5 最终运行结果三、控制参数对控制结果的影响1、论域对控制结果的影响这里采用Ke和Kec来起到控制输入变量的论域的作用,当增大量化因子,相当于缩小了输入变量的论域,当减小量化因子时,相当于增大了输入变量的论域。
在原来的基础上改变Ke,Kec的值,通过观察跟踪效果来说明论域对控制结果的影响。
下面用一个简单的例子作介绍:(本例不是特别针对实现什么功能,只是为了介绍方便)第一部分创建一个模糊逻辑(.fis文件)第一步:打开模糊推理系统编辑器步骤:在Commond Window 键入fuzzy回车打开如下窗口,既模糊推理系统编辑器第二步:使用模糊推理系统编辑器本例用到两个输入,两个输出,但默认是一个输人,一个输出步骤:1、添加一个输入添加一个输出得如下图2、选择Input、output(选中为红框),在Name框里修改各输入的名称并将And method 改为prod,将Or method 改为 probor提示:在命名时’_’在显示时为下标,可从上图看出。
第三步:使用隶属函数编辑器该编辑器提供一个友好的人机图形交互环境,用来设计和修改模糊推理系中各语言变量对应的隶属度函数的相关参数,如隶属度函数的形状、范围、论域大小等,系统提供的隶属度函数有三角、梯形、高斯形、钟形等,也可用户自行定义。
步骤:1、双击任何一个输入量(In_x、In_y)或输出量打开隶属度函数编辑器。
2、在左下处Range和Display Range处添加取值范围,本例中In_x和In_y的取值范围均为[0 10], Out_x和Out_y的取值范围均为[0 1]3、默认每个输入输出参数中都只有3个隶属度函数,本例中每个输入输出参数都需要用到五个,其余几个需要自己添加:选中其中一个输入输出参数点击Edit菜单,选Add MFS…打开下列对话框将MF type设置为trimf(三角形隶属度函数曲线,当然你也需要选择其他类型) 将Number of MFs 设置为2点击OK按钮同样给其他三个加入隶属度函数4、选中任何一个隶属度函数(选中为红色),在Name 中键入名称,在Type中选择形状,在Params中键入范围,然后回车如下图:5、关闭隶属函数编辑器第四步:使用规则编辑器通过隶规则编辑器来设计和修改“IF...THEN”形式的模糊控制规则。

模糊控制实例及simulink仿真实验报告
一、背景介绍
模糊控制是一种基于模糊逻辑的控制方法,其优点在于可以很好地处理复杂的非线性和不确定性系统,而且不需要精确的数学模型和计算,能够快速实现控制的优化。
二、实例介绍
本次实例采用一个双轮小车为对象,实现小车在平面上向指定位置运动的控制。
通过小车的速度和转向角两个输入变量,输出一个模糊控制信号,控制小车前进和转向。
三、实验过程
1. 建立模糊控制系统模型
打开Simulink软件,建立一个新模型,模型中包括输入变量、输出变量和控制器。
2. 设计输入变量和输出变量
(1)设计输入变量
本实例选择小车速度和转向角两个输入变量,每个变量包含三个模糊集合,速度变量分别为“慢速”、“中速”、“快速”,转向角变量分别为“左转”、“直行”、“右转”。
(2)设计输出变量
模糊控制信号输出变量选择小车的前进和转向,每个变量包含三个模糊集合,分别为“慢行”、“中行”、“快行”、“左转”、“直行”、“右转”。
3. 建立控制器
建立模糊控制器,包含输入变量和输出变量的关系,建立控制规则库和模糊关系。
4. 仿真实验
在Simulink下进行仿真实验,调整控制器参数,观察小车运动状态,对比试验。
四、实验结果
经过多次试验和调整,得到最优的小车模糊控制参数,可以实现小车的平滑运动
和准确转向。
五、实验结论
本实验通过建立一个小车的模糊控制系统,可以有效实现小车的平滑运动和准确转向,控制效果优于传统的PID控制方法。
模糊控制可以很好地处理非线性、不确定性和模糊性的系统,适合许多需要快速优化控制的场合。

课程名称:智能控制理论与技术授课老师:徐华中学院:自动化学院专业名称:控制科学与控制工程姓名:廖桂潘学号:班级:自研0902班导师姓名:刘教瑜2010年9月1.一个三阶系统201232123b b ba a as ss s s+++++,其中a,b的值由自己设定,该系统具有非线性环节,如下图所示:依据上述条件设计一个模糊控制器:①用MATLAB仿真,得出仿真结果,②并通过改变a、b值对仿真结果的影响;③改变隶属度函数,从仿真结果图分析隶属度函数,模糊化对系统的影响;解:①(1)取b0=0,b1=0,b2=1.5,a1=4,a2=2,a3=0,在SIMULINK里建模如下图所示(2)用GUI建立FISE和EC分别为系统输出误差和误差的变化量,U为控制输出,编辑其隶属度函数如下编辑模糊推理规则如下(3)仿真结果如下2自己选定一个对象,设计一个神经网络控制系统。
解:被控对象为y(k)=0.3y(k-1)+0.2y(k-2)+0.1u(k-1)+0.6u(k-2),采用单神经元PID 控制,控制结构如下图所示:采用有监督的Hebb 学习规则,控制算法及学习算法如下:3131111222333()(1)()()()()/()()(1)()()()()(1)()()()()(1)()()()i i i i i i i I P D u k u k K w k x k w k w k w k w k w k z k u k x k w k w k z k u k x k w k w k z k u k x k ηηη=='=-+'==-+=-+=-+∑∑式中,2123()();()()(1);()()()2(1)(2);x k e k x k e k e k x k e k e k e k e k ==--=∆=--+-K K>0I P D ηηη﹑﹑分别为积分﹑比例﹑微分的学习速率,为神经元比例系数,。
64 | 电子制作 2021年02月热能,当电流流过电阻材料时,电能转换成热能,产生热量,再通过热的传导、对流、辐射,能有效地用来加热特定的试验件,并保持高的效率,此种加热方式称为辐射加温。
辐射加热具有热转换率高、加热温度高等优点,因此是试验车台上使用最广泛的一种加热方式。
温度是试验任务中一项很重要的监控指标,很多试验任务要求在特定的温度下才能进行,实际温度值和控制的精度、准确度决定了试验能否进行下去,因此研究温度控制工作原理,寻找合适的控制算法具有重要意义。
辐射加温控制系统是典型的一阶纯滞后环节,可用一阶惯性环节加滞后环节表示,具有升温单向性、大惯性、纯滞后、非线性和时变性等特点,用传统控制方式易导致超调大、调节时间长、控制精度低。
其升温、保温是依靠电阻丝加热,当其温度一旦超调就无法用控制手段使其降温。
理论和经验表明,传统的PID 控制对温度控制系统无法达到理想效果[1-2]。
模糊控制是目前十分成熟的一种智能控制方法,其采用模糊逻辑把人的控制经验归纳为定性描述的一组条件语言,利用模糊集理论,将其定量化,使控制器模仿人的操作策略,模糊控制具有很强的鲁棒性和稳定性,大量的理论研究和实践也充分证明了用模糊控制理论控制电阻炉温度是一种非常好的方法策略[3]。
PLC 具有通用性好、性能可靠、编程灵活、扩展方便等优点,在工业控制中广泛使用,PLC 指令越来越强大,能够实现许多复杂的控制算法,利用PLC 实现模糊控制,结合二者的长处,在工业控制中大有前景。
基于上述,本文提出在PLC 平台上将模糊控制方法和常规PID 控制结合的控制策略。
1 控制策略当实际温度值和给定温度值偏差较大时,采用模糊控制合式控制策略,既可以保证系统动态响应效果,又能改善稳态控制精度,系统控制框图如图1所示。
其中S 为转换开关,其设定值一般取最大误差的10%,本文取20,即给定值和实际值偏差在20℃以内采用PID 控制,超过20℃采用模糊[4]模糊控制器能在线对PID 参数进行修改,进一步完善了传统PID 控制器的性能,更好的适应控制系统参数变化和工作条件,如图1所示,模糊控制器由模糊化,模糊推理和解模糊三个环节构成,将工程上的精确量转换为模糊输入信息,利用模糊规则进行模糊推理,经解模糊后转换为精确值,送到被控对象。
下面用一个简单的例子作介绍:(本例不是特别针对实现什么功能,只是为了介绍方便)第一部分创建一个模糊逻辑(.fis文件)第一步:打开模糊推理系统编辑器步骤:在Commond Window 键入fuzzy回车打开如下窗口,既模糊推理系统编辑器第二步:使用模糊推理系统编辑器本例用到两个输入,两个输出,但默认是一个输人,一个输出步骤:1、添加一个输入添加一个输出得如下图2、选择Input、output(选中为红框),在Name框里修改各输入的名称并将And method 改为prod,将Or method 改为probor提示:在命名时’_’在显示时为下标,可从上图看出。
第三步:使用隶属函数编辑器该编辑器提供一个友好的人机图形交互环境,用来设计和修改模糊推理系中各语言变量对应的隶属度函数的相关参数,如隶属度函数的形状、范围、论域大小等,系统提供的隶属度函数有三角、梯形、高斯形、钟形等,也可用户自行定义。
步骤:1、双击任何一个输入量(In_x、In_y)或输出量打开隶属度函数编辑器。
2、在左下处Range和Display Range处添加取值范围,本例中In_x和In_y的取值范围均为[0 10], Out_x和Out_y的取值范围均为[0 1]3、默认每个输入输出参数中都只有3个隶属度函数,本例中每个输入输出参数都需要用到五个,其余几个需要自己添加:选中其中一个输入输出参数点击Edit菜单,选Add MFS…打开下列对话框将MF type设置为trimf(三角形隶属度函数曲线,当然你也需要选择其他类型) 将Number of MFs设置为2点击OK按钮同样给其他三个加入隶属度函数4、选中任何一个隶属度函数(选中为红色),在Name中键入名称,在Type 中选择形状,在Params中键入范围,然后回车如下图:5、关闭隶属函数编辑器第四步:使用规则编辑器通过隶规则编辑器来设计和修改“IF...THEN”形式的模糊控制规则。
模糊控制simulink实例模糊控制是一种基于人类智能的控制方法,其能够克服传统控制方法中的困难和不足,使得控制系统能够更加稳定和灵活地进行控制。
在模糊控制中,模糊规则和模糊推理是非常关键的,而Simulink正是一款非常适合模拟和控制系统的MATLAB工具箱。
现在,我们就来看一个基于Simulink的模糊控制实例。
假设我们有一个小车可以沿着一条直线上下运动,并且需要通过模糊控制来控制小车的运动。
我们将小车的速度和位置分别作为系统的输入和输出,其中小车的速度可以在0-10m/s之间变化,而小车的位置则可以在0-50m之间变化。
需要注意的是,在这个系统中,小车的速度和位置都是模糊的,我们需要通过模糊规则和推理来确定小车应该如何移动。
首先,我们需要确定一组模糊规则来描述小车的运动。
这里我们设定了三个模糊规则,分别是:1. 如果小车位置很靠近上限,那么小车速度应该减缓。
2. 如果小车位置中间,那么小车速度应该保持不变。
3. 如果小车位置很靠近下限,那么小车速度应该加速。
然后,我们需要建立一组模糊推理机制来根据当前状态来确定小车的下一个状态。
这里我们选择了三个模糊推理机制:模糊最小性、模糊加法和模糊乘法。
其中,模糊最小性是用来确定模糊集合之间的交集,模糊加法是用来确定两个模糊集合之间的并集,而模糊乘法则是用来确定两个模糊集合之间的乘积。
最后,我们需要使用Simulink建立一个模糊控制系统,并将上述规则和推理机制应用到这个系统中。
在Simulink中,我们可以使用Fuzzy Logic Controller来实现这个过程。
首先,我们需要将输入和输出变量添加到Fuzzy Logic Controller中。
然后,我们需要为每个变量设置一个模糊集合,以便能够将当前状态转换为模糊状态。
接下来,我们需要将模糊规则添加到Fuzzy Logic Controller中,并为每个规则设置一些权重,以便能够决定规则的优先级。
实验一 模糊控制器设计与实现实验名称:模糊控制器设计与实现实验教学的指导思想和教学目的:本实验是在学生掌握模糊控制器基本工作原理和设计方法基础上,阅读有关参考书利用MATLAB 中Fuzzy toolboxes 设计模糊控制器,并建立模糊控制系统。
实验教学的基本要求:要求学生通过上机实习,熟悉MATLAB 的基本操作命令、simulink 和模糊控制工具箱的使用,掌握利用MATLAB 设计模糊控制器的基本方法,为以后利用计算机进行模糊控制系统分析与设计打下良好的基础。
实验步骤:模糊控制位置跟踪被控对象为首先运行模糊控制器程序chap4_2.m ,并将模糊控制系统保存在a2之中。
然后运行模糊控制的Simulink 仿真程序,位置指令取正弦信号,仿真结果如图4-10所示。
模糊控制位置跟踪的Simulink 仿真程序见chap4_3.mdl 。
图4-10 正弦位置跟踪s 50s 400)(2+=s G实验二 洗衣机模糊控制器的设计与仿真实验名称:洗衣机模糊控制器的设计与仿真实验目的:掌握洗衣机模糊控制器的设计步骤以及MATLAB 仿真实现实验步骤:(1)模糊控制器的结构选用单变量二维模糊控制器。
控制器的输入为衣物的污泥和油脂,输出为洗涤时间。
(2)定义输入输出模糊集将污泥分为三个模糊集:SD (污泥少),MD (污泥中),LD (污泥多),取值范围为[0,100]。
(3)定义隶属函数选用如下隶属函数:采用三角形隶属函数实现污泥的模糊化,如图4-11所示。
采用Matlab 仿真,可实现污泥隶属函数的设计,仿真程序为chap4_4.m将油脂分为三个模糊集:NG (无油脂),MG (油脂中),LG (油脂多),取值范围为[0,100]。
选用如下隶属函数:采用三角形隶属函数实现污泥的模糊化,如下图4-12所示。
仿真程序同污泥隶属函数。
⎪⎪⎩⎪⎪⎨⎧≤<-=⎩⎨⎧≤<-≤≤=≤≤-==1005050/)50()(1005050/)100(50050/)(50050/)50()(x x x x x x x x x x x LD MD SD μμμμ污泥⎪⎪⎩⎪⎪⎨⎧≤≤-=⎩⎨⎧≤<-≤≤=≤≤-==1005050/)50()(1005050/)100(50050/)(50050/)50()(y y y y y y y y y y y LG MG NG μμμμ油脂图4-12 油脂隶属函数将洗涤时间分为三个模糊集:VS (很短),S (短),M (中等),L (长),VL (很长),取值范围为[0,60]。
如何使⽤Simulink模糊控制在⽤这个控制器之前,需要⽤readfis指令将fuzzy1.fis加载到matlab的⼯作空间,⽐如我们⽤这样的指令:fis1=readfis(‘fis1.fis’);就创建了⼀个叫myFLC的结构体到⼯作空间,并在fuzzy logic controller中参数设为:fis1。
可以看到,在模糊控制器的输⼊和输出均有⼀个⽐例系数,我们叫它量化因⼦,它反映的是模糊论域范围与实际范围之间的⽐例关系,例如,模糊控制器输⼊输出的论域范围均为[-3,3],⽽实际误差的范围是[-10,10],误差变化率范围是[-100,100],控制量的范围是[-24,24],那么我们就可以算出量化因⼦分别为0.3,0.03,8。
量化因⼦的选取对于模糊控制器的控制效果有很⼤的影响,因此要根据实际情况认真选取哦。
好,现在我们可以设定仿真步长,⽐如定步长的10ms,就可以运⾏了。
运⾏后,产⽣这样⼀个错误:MinMax blocks do not accept 'boolean' signals. The input signal(s) of block 'test_fuzzy/Fuzzy Logic Controller/FISWizard/Defuzzification1/Max (COA)' must be one of the MATLAB 'uint8', 'uint16', 'uint32', 'int8', 'int16', 'int32', 'single', or 'double' data types 我想很多朋友做模糊控制的时候都会遇到这个情况。
没关系,这⾥提供两个解决办法:1.直接在Defuzzification1这个模块中的那个⽐较环节后加⼊数据类型转换模块,将boolean转化为double型,或者双击那个⽐较模块,选中show additional parameters,将输出数据类型改为specify via dialog,然后选uint(8)即可;但是在仿真之后,⼜会发现很多地⽅都存在这个问题,因此你不得不⼀个⼀个去修改,如果你不怕累的话。
智能控制作业二“模糊控制位置跟踪的SIMULINK 仿真
一、题目 设被控对象的传递函数为s s s G 252500)(2+=,输入信号为方波,周期为1秒,幅值为1,(可以用Pulse Generator 模块来产生)。
1)试设计两输入单输出模糊控制器,输入为偏差E 和偏差变化率EC ,输出为控制量U ,使系统输出能实时跟踪输入信号。
2)通过仿真理解并分析E 和EC 的参数选择对系统稳态误差和动态性能的影响,这些参数包括模糊子集的个数,论域的范围等。
作业中最好把不同参数下的仿真结果附上。
二、MATLAB 解决方案
1、模糊控制模块的创建
在MA TLAB 命令窗口中输入fuzzy 命令,会弹出模糊控制GUI 界面,打开隶属度函数编辑窗口,输入变量为E 和EC ,输出变量为U ,输入输出论域均设置为[-3 3],每个变量都设置NB ,NM ,NS ,ZO ,PS ,PM ,PB 七个模糊子集,每个变量的隶属度函数均如图1所示,为了使输入误差在零附近反应敏感,这一部分隶属度函数设置得比较尖。
图1 隶属度函数编辑窗口
根据如表1输入控制规则,如图2所示:
表1 控制规则
编辑完成后可以看到如图3所示的模糊输入与输出的三维示意图:
图2 控制规则输入窗口图3 输出三维示意图
2、simulink的仿真
新建一个model,搭建如图4所示的控制框图,保存为fuc2文件夹中的fuz_ctrl.mdl。
其中增益模块用来控制将输入或输出与模糊控制器的论域相匹配。
图4 simulink控制框图
3、调试后的仿真结果
经过调试优化,最终得到的仿真波形如图5所示。
其中Ke=3,Kec=0.06,Ku=1.
图5 最终运行结果
三、控制参数对控制结果的影响
1、论域对控制结果的影响
这里采用Ke和Kec来起到控制输入变量的论域的作用,当增大量化因子,相当于缩小了输入变量的论域,当减小量化因子时,相当于增大了输入变量的论域。
在原来的基础上改变Ke,Kec的值,通过观察跟踪效果来说明论域对控制结果的影响。
首先讨论偏差E的论域对控制结果的影响:保持Kec=0.06,当Ke=4时,运行结果如图6所示:
图6 Ke=4时的运行结果
当Ke=1时的运行结果如图7所示:
图7 Ke=1时运行结果
从以上两幅图的对比可以看出,当偏差E的论域过大时,响应速度回变慢,超调会减小,当论域过小时,响应速度回变快,但会出现超调。
下面讨论偏差的变化率对控制结果的影响:保持Ke=3,当Kec=0.4时的运行结果如图8所示:
图8 Kec=0.04时的运行结果
当Kec=0.12时的运行结果如图9所示:
图9 Kec=0.12时的运行结果
从以上两图的对比可以看出,偏差的变化率的论域增大有利于提高响应时间,但会引起过大的超调,论域减小有利于减小超调,但会减慢响应速度,在实际控制中应该综合考虑以上两点。
2、模糊子集个数对控制结果的影响
本示例中设置了七个模糊子集,在同样的控制参数下,模糊子集个数为5和3时的控制结果图:其中模糊子集数为5时的仿真模型保存为文件夹fuc2_1中的fuz_ctrl2.mdl,模糊子集数为3的仿真模型保存为文件夹fuc2_2中fuz_ctrl3.mdl。
图10 模糊子集为5个是响应波形
图11 模糊子集为7个和5个时局部放大比较
图12 模糊子集个数为3时的响应波形
从上述几幅波形对比可以看到,模糊子集个数越少,其控制就越不精确,引起的误差也越大,但当模糊子集个数太大时,每一步计算花费的时间会变长,在实际设计中应综合考虑这两个因素。
四、讨论与心得
此次大作业主要利用了模糊控制的GUI 界面为simulink 创建一个论域连续的模糊控制模型,然后将其运用到实际的控制过程当中去。
在刚开始时,隶属度函数和控制规则就采用常用的函数和控制规则。
最初遇到的问题就是论域我都选择了[-3 3],然后仿真出来的波形根本不对,于是我查阅了相关的文献,在输入和输出的环节中都加入了一个量化因子,用示波器观察了偏差和偏差的变化率的变化范围以后,按照课本中的公式2e H L m K e e =-,2ec H L
n K ec ec =-,初步选择了Ke 和Kec ,Ku 初步选择为1,然后再调整各个量化因子,
观察各个参数对结果的影响,最后得到一个比较理想的结果。
由于修改论域比较麻烦,我就采用了这种量化因子的方式对论域进行了讨论,因为这两者的效果是一样的。
经过调整后得到图形后,发现在误差快为零的那一段变化不是很敏感,因此我又对隶属度函数进行了适当的修改,使得误差较小时的隶属度函数变得尖一点,使得系统对误差较小时的响应变得比较敏感,分辨率提高。
总体来说,这个跟踪效果还是比较理想的。