第五篇-单因素实验设计及实验因素水平确定方法解读
- 格式:ppt
- 大小:916.50 KB
- 文档页数:66



单因素实验设计及结果分析实验设计是科学研究中至关重要的一部分,它帮助研究者确定实验的目的、方法和结果的解释。
在本文中,我们将探讨单因素实验设计及其结果分析方法。
单因素实验设计在科学研究和统计分析中被广泛应用,它可以帮助我们了解一个因素对实验结果的影响。
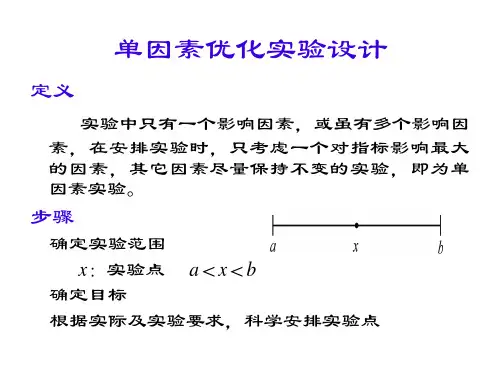
单因素实验设计是指在一个实验中,研究者只改变一个因素(独立变量),并观察这个因素对实验结果(依赖变量)的影响。
这种实验设计有助于我们分析变量之间的因果关系。
下面将介绍一些常见的单因素实验设计及其结果分析方法。
1. 随机分组设计:这是一种常见的单因素实验设计方法。
研究者通过随机将被试分为实验组和对照组,实验组接受独立变量的处理,而对照组则不接受处理。
比较两组的实验结果,可以得出独立变量对实验结果的影响。
2. 重复测量设计:这种设计方法适用于需要连续观察同一组被试的实验。
研究者在不同时间点对被试进行多次测量,比较测量结果的差异,以确定独立变量对实验结果的影响。
3. 配对设计:配对设计适用于需要考虑个体差异的实验。
在这种设计中,被试会与其他被试进行配对,以使每对配对中的两个被试在某些重要特征上相似。
然后,每对配对中的一名被试接受独立变量的处理,而另一名被试作为对照。
结果的分析是单因素实验中不可或缺的一部分。
下面将介绍一些常见的对实验结果进行分析的统计方法。
1. 描述统计分析:描述统计分析是对数据进行总结和描述的方法。
通过计算均值、标准差、百分位数等参数,我们可以对实验结果的整体特征进行描述。
2. 方差分析:方差分析是一种用于比较不同组之间差异的方法。
通过计算组间方差和组内方差之间的比值,我们可以确定独立变量对实验结果是否有显著影响。
3. T检验:T检验是一种用于比较两组均值差异是否显著的方法。
在单因素实验中,可以使用独立样本T检验(用于比较不同组)或配对样本T检验(用于比较同一组在不同条件下的均值)。
4. 相关分析:当我们需要研究两个变量之间的关系时,可以使用相关分析。




单因素实验设计单因素实验设计是指在实验中只有一个研究因素,即研究者只分析一个因素对效应指标的作用,但单因素实验设计并不是意味着该实验中只有一个因素与效应指标有关联。
单因素实验设计的主要目标之一就是如何控制混杂因素对研究结果的影响。
常用的控制混杂因素的方法有完全随机设计、随机区组设计和拉丁方设计等。
一、完全随机设计1.概念与特点又称单因素设计或成组设计,是医学科研中最常用的一种研究设计方法,它是将同质的受试对象随机地分配到各处理组进行实验观察,或从不同总体中随机抽样进行对比研究。
该设计适用面广,不受组数的限制,且各组的样本含量可以相等,也可以不相等,但在总体样本量不变的情况下,各组样本量相同时的设计效率最高。
例如:为了研究煤矿粉尘作业环境对尘肺的影响,将18只大鼠随机分到甲、乙、丙3组,每组6只,分别在地面办公楼、煤炭仓库和矿井下染尘,12周后测量大鼠全肺湿重(g),通过评价不同环境下大鼠全肺平均湿重推断煤矿粉尘对作用尘肺的影响,具体的随机分组可以如下实施:第一步:将18只大鼠编号:1,2,3, (18)第二步:可任意设置种子数,但应作为实验档案记录保存(本例设置spss11.0软件的种子数为200);第三步:用计算机软件一次产生18个随机数,每个随意数对应一只老鼠(本例用spss11.0软件采用均匀分布最大值为18时产成的18个随机数);第四步:最小的6个随机数对应编号的大鼠为甲组,排序后的第7个至第12个随机数随因编号为乙组,最大的6个随机数对应编号的大鼠为丙组(结果见表1)。
表1 分配结果编号 1 2 3 4 5 6 7 8 93.75 8.75 16.29 11.12 5.49 3.98 13.64 16.71 1.69随机数组别甲乙丙乙乙甲丙丙甲编号10 11 12 13 14 15 16 17 1813.62 16.36 2.12 4.74 11.54 3.98 0.13 17.35 16.38 随机数组别丙丙甲乙乙甲甲丙丙2.随机数的产生方法(1)随机数字表:如附表13(马斌荣,医学统计学,第4版),这是一个由0~9十个数字组成60行25列的数字表。



单因素实验讨论总结单因素实验是一种常用的实验设计方法,用于研究一个因素对实验结果的影响。
本文将对单因素实验进行讨论,并总结其相关内容。
一、简介单因素实验是指在一个实验中只改变一个因素,其他所有因素保持不变。
通过改变这个因素的不同水平,观察和测量其对实验结果的影响,从而得出结论。
二、实验设计1. 因素选择:在进行单因素实验前,需要确定研究的目标和所要研究的因素。
选择一个具有重要影响且容易控制的因素进行研究。
2. 水平设置:确定该因素的不同水平,通常选取3个或以上水平进行比较。
3. 随机分组:将被试随机分为各个处理组,每组接受不同水平的处理。
4. 实施处理:按照设计好的处理方案进行处理。
5. 数据收集:记录每组数据,并进行测量和观察。
6. 数据分析:通过统计方法对数据进行分析。
三、数据分析方法1. 描述性统计:对数据进行描述性统计分析,包括均值、标准差、频数等指标。
2. 方差分析(ANOVA):用于比较不同水平之间的差异是否显著。
3. 多重比较:当方差分析结果显著时,进行多重比较以确定不同水平之间的具体差异。
4. 效应量分析:通过计算效应量,评估因素对实验结果的实际影响程度。
四、实验结果解读1. 方差分析结果:根据方差分析结果,判断不同水平之间是否存在显著差异。
2. 多重比较结果:通过多重比较,确定不同水平之间的具体差异。
3. 效应量分析结果:根据效应量分析结果,评估因素对实验结果的实际影响程度。
五、讨论与总结1. 结果解释:根据数据分析结果,解释因素对实验结果的影响。
讨论可能的原因和机制。
2. 结果验证:将实验结果与已有研究或理论进行比较和验证,探讨其一致性或不一致性。
3. 实验局限性:指出实验设计和方法上可能存在的局限性,并提出改进建议。
4. 结论总结:总结单因素实验研究的主要发现和结论,并对未来研究方向提出建议。
六、参考文献列出本文参考的相关文献,包括经典实验设计教材、研究论文等。
单因素实验是一种常用的实验设计方法,通过改变一个因素的不同水平,观察和测量其对实验结果的影响。
单因素实验设计报告单因素实验设计报告:因素实验报告设计单因素实验设计举例正交实验单因素实验设计方案篇一:实验报告单因素方差分析5.1、实验步骤: 1(建立数据文件。
定义2个变量:PWK和DCGJSL,分别表示排污口和大肠杆菌数量。
2. 选择菜单“分析?比较均值?单因素”,弹出“单因素方差分析”对话框。
在对话框左侧的变量列表中,选择变量“DCGJSL”进入“因变量”列表框,选择变量“PWK”进入“因子”列表框。
3(单击“确定”按钮,得到输出结果。
结果解读:由以上结果可以看到,观测变量大肠杆菌数量的总离差平方和为460.438;如果仅考虑“排污口”单个因素的影响,则大肠杆菌数量总变差中,排污口可解释的变差为308.188,抽样误差引起的变差为152.250,它们的方差(平均变差)分别为102.729和12.688,相除所得的F统计量的观测值为8.097,对应的概率P值为0.003。
在显著性水平α为0.05的情况下。
由于概率P值小于显著性水平α,则应拒绝零假设,认为不同的排污口对大肠杆菌数量产生了显著影响,它对大肠杆菌数量的影响效应不全为0。
因此,可判断各个排污口的大肠杆菌数量是有差别的。
5.2、实验步骤: 1(建立数据文件。
定义2个变量:Branch和Turnover,分别表示分店和日营业额。
将Branch的值定义为1=第一分店,2=第二分店,3=第三分店,4=第四分店,5=第五分店。
2. 选择菜单“分析?比较均值?单因素”,弹出“单因素方差分析”对话框。
在对话框左侧的变量列表中,选择变量“Turnover”进入“因变量”列表框,选择变量“Branch”进入“因子”列表框。
3(单击“确定”按钮,得到输出结果。
结果解读:由以上结果可以看到,观测变量日营业额的总离差平方和为1187668.733;如果仅考虑“分店”单个因素的影响,则日营业额总变差中,分店可解释的变差为366120.900,抽样误差引起的变差为821547.833,它们的方差(平均变差)分别为91530.225和14937.233,相除所得的F统计量的观测值为6.128,对应的概率P 值近似为0。
单因素实验设计单因素实验设计是指在实验中只有一个研究因素,即研究者只分析一个因素对效应指标的作用,但单因素实验设计并不是意味着该实验中只有一个因素与效应指标有关联。
单因素实验设计的主要目标之一就是如何控制混杂因素对研究结果的影响。
常用的控制混杂因素的方法有完全随机设计、随机区组设计和拉丁方设计等。
一、完全随机设计1.概念与特点又称单因素设计或成组设计,是医学科研中最常用的一种研究设计方法,它是将同质的受试对象随机地分配到各处理组进行实验观察,或从不同总体中随机抽样进行对比研究。
该设计适用面广,不受组数的限制,且各组的样本含量可以相等,也可以不相等,但在总体样本量不变的情况下,各组样本量相同时的设计效率最高。
例如:为了研究煤矿粉尘作业环境对尘肺的影响,将18只大鼠随机分到甲、乙、丙3组,每组6只,分别在地面办公楼、煤炭仓库和矿井下染尘,12周后测量大鼠全肺湿重(g),通过评价不同环境下大鼠全肺平均湿重推断煤矿粉尘对作用尘肺的影响,具体的随机分组可以如下实施:第一步:将18只大鼠编号:1,2,3, (18)第二步:可任意设置种子数,但应作为实验档案记录保存(本例设置spss11.0软件的种子数为200);第三步:用计算机软件一次产生18个随机数,每个随意数对应一只老鼠(本例用spss11.0软件采用均匀分布最大值为18时产成的18个随机数);第四步:最小的6个随机数对应编号的大鼠为甲组,排序后的第7个至第12个随机数随因编号为乙组,最大的6个随机数对应编号的大鼠为丙组(结果见表1)。
表1 分配结果编号1234567893.758.7516.2911.12 5.49 3.9813.6416.71 1.69随机数组别甲乙丙乙乙甲丙丙甲编号101112131415161718113.6216.36 2.12 4.7411.54 3.980.1317.3516.38随机数组别丙丙甲乙乙甲甲丙丙2.随机数的产生方法(1)随机数字表:如附表13(马斌荣,医学统计学,第4版),这是一个由0~9十个数字组成60行25列的数字表。
第1篇一、实验背景随着科学技术的不断发展,实验研究在各个领域都发挥着越来越重要的作用。
为了提高实验研究的效果,研究者们常常采用单因素实验设计,通过控制其他变量不变,研究某一特定因素对实验结果的影响。
本实验旨在探讨单一因素对实验结果的影响,并总结实验过程中的关键步骤和结果。
二、实验目的1. 研究单一因素对实验结果的影响。
2. 掌握单因素实验设计的基本方法。
3. 提高实验操作技能和数据分析能力。
三、实验原理单因素实验设计是指在实验过程中,只改变一个自变量,保持其他自变量和因变量不变,观察和记录因变量的变化。
通过对比实验结果,可以得出单一因素对实验结果的影响。
四、实验材料与仪器1. 实验材料:实验对象、实验试剂、实验仪器等。
2. 实验仪器:天平、量筒、试管、滴定管、pH计等。
五、实验步骤1. 实验分组:将实验对象分为若干组,每组包含相同数量的样本。
2. 实验变量设置:根据实验目的,设置单一自变量,如温度、压力、光照等。
3. 实验操作:按照实验设计,对各组实验对象进行相应处理,如加热、加压、光照等。
4. 数据记录:记录实验过程中各组的因变量数据,如颜色、沉淀、pH值等。
5. 数据分析:对实验数据进行统计分析,得出单一因素对实验结果的影响。
六、实验结果根据实验结果,可以得出以下结论:1. 单一因素对实验结果具有显著影响。
2. 实验过程中,控制其他变量不变,有助于研究单一因素对实验结果的影响。
3. 实验结果具有一定的可靠性和可重复性。
七、实验讨论1. 实验过程中,单一因素对实验结果的影响具有显著性和一致性。
2. 实验结果表明,单一因素在不同条件下对实验结果的影响存在差异。
3. 实验结果与理论预测基本相符,验证了实验设计的合理性。
八、实验总结1. 本实验成功研究了单一因素对实验结果的影响,达到了实验目的。
2. 通过单因素实验设计,可以有效地研究单一因素对实验结果的影响。
3. 实验过程中,应注意控制其他变量不变,以保证实验结果的可靠性。