下载文档原格式
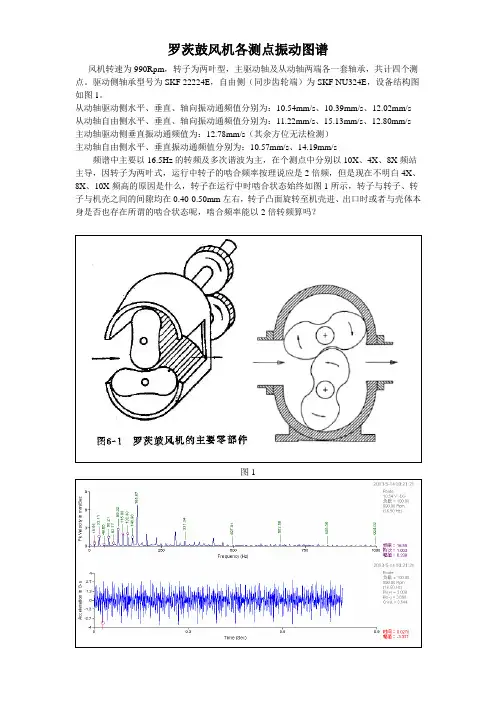
罗茨鼓风机各测点振动图谱
风机转速为990Rpm，转子为两叶型，主驱动轴及从动轴两端各一套轴承，共计四个测点。
驱动侧轴承型号为SKF 22224E，自由侧（同步齿轮端）为SKF NU324E，设备结构图如图1。
从动轴驱动侧水平、垂直、轴向振动通频值分别为：10.54mm/s、10.39mm/s、12.02mm/s 从动轴自由侧水平、垂直、轴向振动通频值分别为：11.22mm/s、15.13mm/s、12.80mm/s 主动轴驱动侧垂直振动通频值为：12.78mm/s（其余方位无法检测）
主动轴自由侧水平、垂直振动通频值分别为：10.57mm/s、14.19mm/s
频谱中主要以16.5Hz的转频及多次谐波为主，在个测点中分别以10X、4X、8X频站主导，因转子为两叶式，运行中转子的啮合频率按理说应是2倍频，但是现在不明白4X、8X、10X频高的原因是什么，转子在运行中时啮合状态始终如图1所示，转子与转子、转子与机壳之间的间隙均在0.40-0.50mm左右，转子凸面旋转至机壳进、出口时或者与壳体本身是否也存在所谓的啮合状态呢，啮合频率能以2倍转频算吗？
图1
图2：驱动侧从动轴水平方向（3H）
图3：驱动侧从动轴垂直方向（3V）
图4：驱动侧从动轴轴向（3A）
图5：驱动侧主动轴垂直方向（4V）
图6：自由侧从动轴水平方向（5H）
图7：自由侧从动轴垂直方向（5V）
图8：自由侧从动轴轴向（5A）
图9：自由侧主动轴水平方向（6H）
图10：自由侧主动轴垂直方向（6V）。
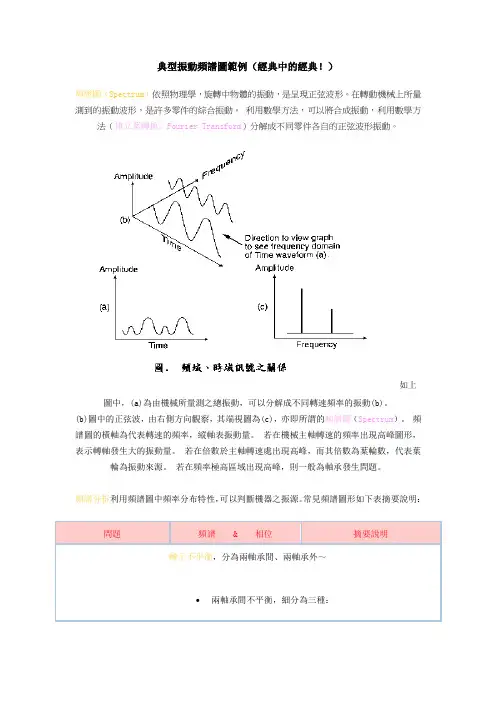
典型振動頻譜圖範例（經典中的經典！）頻譜圖（Spectrum）依照物理學，旋轉中物體的振動，是呈現正弦波形。
在轉動機械上所量測到的振動波形，是許多零件的綜合振動。
利用數學方法，可以將合成振動，利用數學方法（傅立葉轉換，Fourier Transform）分解成不同零件各自的正弦波形振動。
如上圖中，(a)為由機械所量測之總振動，可以分解成不同轉速頻率的振動(b)。
(b)圖中的正弦波，由右側方向觀察，其端視圖為(c)，亦即所謂的頻譜圖（Spectrum）。
頻譜圖的橫軸為代表轉速的頻率，縱軸表振動量。
若在機械主軸轉速的頻率出現高峰圖形，表示轉軸發生大的振動量。
若在倍數於主軸轉速處出現高峰，而其倍數為葉輪數，代表葉輪為振動來源。
若在頻率極高區域出現高峰，則一般為軸承發生問題。
頻譜分析利用頻譜圖中頻率分布特性，可以判斷機器之振源。
常見頻譜圖形如下表摘要說明：問題頻譜& 相位摘要說明轉子不平衡，分為兩軸承間、兩軸承外～•兩軸承間不平衡，細分為三種：1.靜不平衡 StaticUnblance •振動頻率為 1倍轉速（1×RPM）。
•徑向振動大，軸向小。
•兩軸承徑向呈同相（In Phase）運動，兩相角相差0°，同軸承垂直與水平相位差90°。
2.偶不平衡 CoupleUnblance •徑向振動大，軸向有可能大。
•振動頻率為 1倍轉速（1×RPM）。
•兩軸承徑向呈反相（Out of Phase）運動，兩相角相差180°，同軸承垂直與水平相位差90°。
3.動不平衡同上•徑向振動大，軸向有可能大。
•振動頻率為 1倍轉速（1×RPM）。
•兩軸承徑向呈不同相運動。
•兩軸承外不平衡OverhungRotorUnblance •軸向及徑向振動大。
•振動頻率為 1倍轉速（1×RPM）。
•兩軸承徑向呈同相（In Phase）運動，徑向相位不穩定。
类型A频谱是机器地脚，底板或基础的结构松动/减弱引起的，或者由基础上恶化的水泥浆，松动的地脚螺栓、或者框架或者基础变形（即软脚）引起的。
相位分析可以揭示在螺栓、机器地脚、基础底板或者基础本身垂直方向测量之间的相位差约90度到180度。
类型B频谱通常是由螺栓松动引、框架结构或轴承座裂纹引起的。
类型C频谱通常是由零部件之间配合不良引起的，由于松动的零部件对转子的动态力产生非线性的响应，所以，将产生许多谐波频率。
引起时域波形截断和在频谱中提高噪声地平。
类型C往往是由轴承衬套在其盖内松动、轴承松动和在轴上旋转。
滑动轴承或滚动轴承间隙过大，叶轮在轴上松动等引起的。
类型C的振动相位往往是不稳定的，这一次测量到下一次测量可能变化很大，尤其是如果转子在轴上的位置从这一次到下一次起动漂移的话。
机械松动往往是非常定向的，在一个轴承座的径向方向每隔30度测量的振动值完全不同。
而且，松动往往引起精确的1/2倍或1/3倍转速频率的亚谐波频率（0.5、1.5、2.5等等）
类型A 类型B 类型C
案例分析：
对数谱
设备：电机－联轴器－水泵（多级泵、两端支撑）
现状：电机轴承频繁损坏（运转一周左右），设备不能正常备用。
根据奇数倍频及其谐波高于偶数倍频及现场情况，诊断为基础故障。
现场检查情况：水泵侧地脚螺栓没有正常栽在水泥基础里，而是焊接在基础之上的铁板上。
重新制作基础及地脚螺栓后，设备运行正常。
振动数据的特征分析由于振动是动态参数，为表示振动特性，通常采用各种图形方式来进行描述。
振动特征分析就是将振动信号时域分析和频域分析的结果用一定的图形或曲线表示出来。
主要有以下几种图形及其特点：1、波形图（waveform plot）：包含的信息量大，具有直观、易于理解等特点，但不太容易看出所包含信息与故障的联系2、频谱图(Frequency Spectrogram)：频谱分析是机械故障诊断中用得最广泛的信号处理方法之一，在振动分析和故障诊断中起着提取特征和压缩数据的作用3、轴心轨迹图(Orbit Plot)：轴心轨迹的形状及其方向对于旋转机械故障的诊断也是很重要的4、轴心位置图（Shaft Center Position）：轴的中心位置变化趋势，从而可以了解轴承的磨损程度5、波特图(Bode Plot)：波德图是最常使用的振动分析工具之一，其用来确定机器的临界转速及其过临界转速时的振幅和相位，从2X分量的波德图可以看出转子的副临界转速。
波德图常用作设备的验收试验。
6、极坐标图(Polar Plot,Nyquist Plot)：在极坐标图中很容易得到原始晃矢量，即与低转速所对应的矢量。
7、级联图(Cascade Plot)：可以更清楚地看出各种频率成分随转速的变化情况，这对于故障分析是十分有用的。
这类最典型的故障是油膜涡动和油膜振荡8、瀑布图(Waterfall Plot)：可以清楚地看出各种频率的振幅随时间是如何变化的，对分析定转速下出现的动静碰摩、热弯曲、电磁激振、汽流激振等故障是很有用的9、相关趋势图(Rative Vibration Trend Plot)：这种曲线非常直观，对运行人员监视机组状况很有用下面将对分析振动原因极其有用的有关图形作一详述：1、波形图(Waveform Plot)波形图是转子响应随时间的变化曲线，其横坐标为时间，通常表示为周期数，纵坐标为振动实时值，通常它近似为正波，是最原始的信号，所以包含的信息量大，具有直观、易于理解等特点，但不太容易看出所包含信息与故障的联系。
类型A频谱是机器地脚，底板或基础的结构松动/减弱引起的，或者由基础上恶化的水泥浆，松动的地脚螺栓、或者框架或者基础变形（即软脚）引起的。
相位分析可以揭示在螺栓、机器地脚、基础底板或者基础本身垂直方向测量之间的相位差约90度到180度。
类型B频谱通常是由螺栓松动引、框架结构或轴承座裂纹引起的。
类型C频谱通常是由零部件之间配合不良引起的，由于松动的零部件对转子的动态力产生非线性的响应，所以，将产生许多谐波频率。
引起时域波形截断和在频谱中提高噪声地平。
类型C往往是由轴承衬套在其盖内松动、轴承松动和在轴上旋转。
滑动轴承或滚动轴承间隙过大，叶轮在轴上松动等引起的。
类型C的振动相位往往是不稳定的，这一次测量到下一次测量可能变化很大，尤其是如果转子在轴上的位置从这一次到下一次起动漂移的话。
机械松动往往是非常定向的，在一个轴承座的径向方向每隔30度测量的振动值完全不同。
而且，松动往往引起精确的1/2倍或1/3倍转速频率的亚谐波频率（0.5、1.5、2.5等等）
类型A 类型B 类型C
案例分析：
对数谱
设备：电机－联轴器－水泵（多级泵、两端支撑）
现状：电机轴承频繁损坏（运转一周左右），设备不能正常备用。
根据奇数倍频及其谐波高于偶数倍频及现场情况，诊断为基础故障。
现场检查情况：水泵侧地脚螺栓没有正常栽在水泥基础里，而是焊接在基础之上的铁板上。
重新制作基础及地脚螺栓后，设备运行正常。
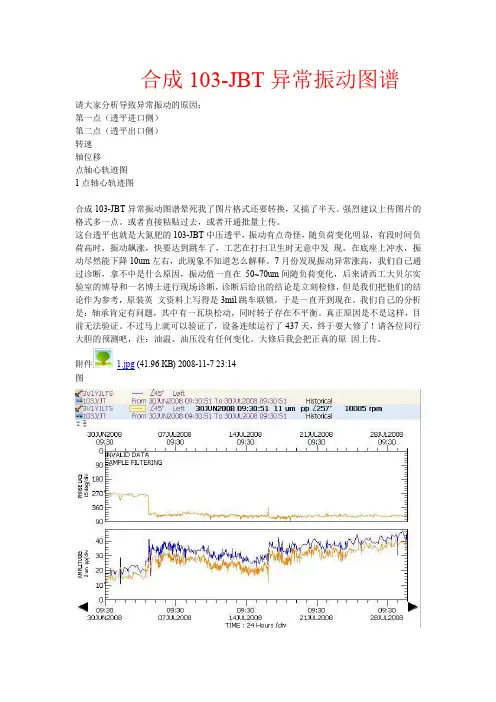
合成103-JBT异常振动图谱请大家分析导致异常振动的原因：第一点（透平进口侧）第二点（透平出口侧）转速轴位移点轴心轨迹图1点轴心轨迹图合成103-JBT异常振动图谱晕死我了图片格式还要转换，又搞了半天。
强烈建议上传图片的格式多一点。
或者直接粘贴过去，或者开通批量上传。
这台透平也就是大氮肥的103-JBT中压透平，振动有点奇怪，随负荷变化明显，有段时间负荷高时，振动飙涨，快要达到跳车了，工艺在打扫卫生时无意中发现，在底座上冲水，振动尽然能下降10um左右，此现象不知道怎么解释。
7月份发现振动异常涨高，我们自己通过诊断，拿不中是什么原因，振动值一直在50~70um间随负荷变化，后来请西工大贝尔实验室的博导和一名博士进行现场诊断，诊断后给出的结论是立刻检修，但是我们把他们的结论作为参考，原装英文资料上写得是3mil跳车联锁，于是一直开到现在。
我们自己的分析是：轴承肯定有问题，其中有一瓦块松动，同时转子存在不平衡。
真正原因是不是这样，目前无法验证。
不过马上就可以验证了，设备连续运行了437天，终于要大修了！请各位同行大胆的预测吧，注：油温、油压没有任何变化。
大修后我会把正真的原因上传。
附件 1.jpg(41.96 KB) 2008-11-7 23:14图2.jpg(41.79 KB) 2008-11-7 23:14 图3.jpg(41.85 KB) 2008-11-7 23:14 图4.jpg(40.68 KB) 2008-11-7 23:14 图5.jpg(29.96 KB) 2008-11-7 23:14 图6.jpg(29.22 KB) 2008-11-7 23:14 图7.jpg(48.2 KB) 2008-11-7 23:14 图8.jpg(58.41 KB) 2008-11-7 23:14 图9.jpg(44.08 KB) 2008-11-7 23:14 图合成103-JBT异常振动图谱轴位移有变化并且相当大，主要是在负荷发生变化时。
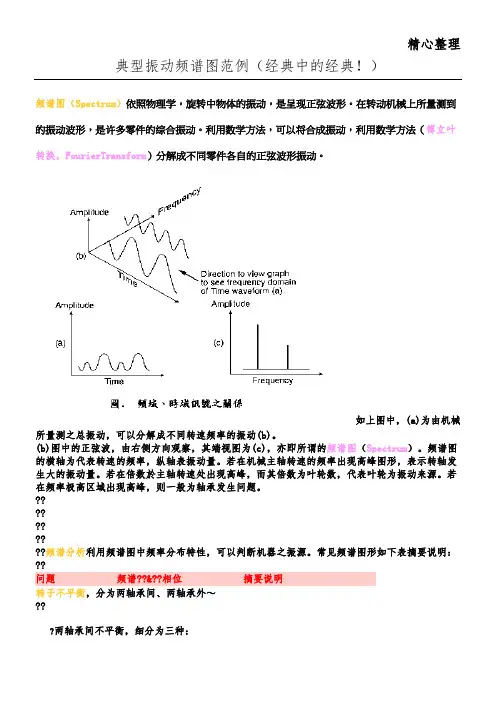
精心整理典型振动频谱图范例（经典中的经典！）频谱图（Spectrum）依照物理学，旋转中物体的振动，是呈现正弦波形。
在转动机械上所量测到的振动波形，是许多零件的综合振动。
利用数学方法，可以将合成振动，利用数学方法（傅立叶转换，FourierTransform）分解成不同零件各自的正弦波形振动。
(b)??????????频谱分析利用频谱图中频率分布特性，可以判断机器之振源。
常见频谱图形如下表摘要说明：转子不平衡，分为两轴承间、两轴承外～??两轴承间不平衡，细分为三种：1.静不平衡StaticUnblance ?振动频率为1倍转速（1×RPM）。
?径向振动大，轴向小。
?两轴承径向呈同相（InPhase）运动，两相角相差0°，同轴承垂直与水平相位差90°。
2.∙径向振动大，轴向有可能大。
3.∙∙∙∙偏心转子(EccentricRotor ) ∙之直线振动。
∙振动频率出现在1倍转速（1×RPM）。
∙同轴承垂直或水平相位差180°或90°。
轴弯曲?会产生大的轴向振动。
?两轴承间之相位相差180°。
转子对心不良，分为联轴器、轴承两类～??∙联轴器两端，再细分为角度与平行两种：1.角度不对心∙会产生大的轴向振动。
∙频率出现在1×、2×、3×...等，严重时会出现更高频之谐波。
∙在联轴器两端之相位差180°反向。
2.1.2.3.平轴承1.油漩2.轴承间隙过大?振频出现於1×、2×、3×...等，甚至有更高频之谐波。
传动皮带1.皮带松动、损坏∙皮带振动频率低於轴转速，通常会有1、2、3...倍之皮带振动频率出现。
∙2倍之皮带振动频率通常为主振动频率。
2.皮带对心不良?会导致很高之轴向振动。
?振频出现於1倍之主动轮或从动轮之转速。
转子摩擦RotorRub ∙与机械松动之频谱类似。
振动分析常见图谱
一、跟踪轴心轨迹
轴心轨迹是轴心相对于轴承座的运动轨迹，它反映了转子瞬时的涡动状况。
对轴心轨迹的观察有利于了解和掌握转子的运动状况。
跟踪轴心轨迹是在一组瞬态信号中，相隔一定的时间间隔（实际上是相隔一定的转速）对转子的轴心轨迹进行观察的一种方法。
这种方法是近年来随着在线监测技术的普及而逐步被认可的，它具有简单、直观，判断故障简便等优点。
图4-20是某压缩机高压缸轴承处轴心轨迹随转速升高的变化情况，在能过临界转速及升速结束之后，轨迹在轮廓上接近椭圆，说明这时基频为主要振动成分，如果振幅值不高，应该说机组是稳定的。
如果达到正运行工况时机组振幅值仍比较高，应重点怀疑不平衡，转子弯曲一类的故障。
二、波德（Bode）图
波德图是描述某一频带下振幅和相位随过程的变化而变化的两组曲线。
频带可以是1×、2×或其他谐波；这些谐波的幅、相位既可以用FFT法计算，也可以用滤波法得到。
当过程的变化参数为转速时，例如启、停机期间，波德图实际上又是机组随激振频率（转速）不同而幅值和相位变化的幅频响应和相频响应曲线。
当过程参数为速度时，比较关心的是转子接近和通过临界转速时的幅值响应和相位响应情况，从中可以辨识系统的临界转速以及系统
的阻尼状况。
图4-21 某压缩机高压缸波德图
图4-21是某转子在升速过程中的波德图。
从图中可以看出，系统在通过临界转速时幅值响应有明显的共振峰，而相位在临界前后转了近180。
除了随转速变化的响应外，波德图实际上还可以做机组随其他参数变化时的响应曲线，比如时间，不过这时的横坐标应是时间，这对诊断转子缺损故障非常有效。
也可以针对工况，当工况条件改变时做波德图，这时的幅频响应和相频响应如果不是两条直线，说明工况变化对振动的大小和相位有影响，利用这一特点可以甄别或确认其他症兆相近的故障。
三、极坐标图
极坐标图实质上就是振动向量图，和波德图一样，振动向量可以是1×、2
×或其他谐波的振动分量。
极坐标图有时也被称为振型圆和奈奎特图（Nyquist图），但严格说来，二者是有差别的，因为极坐标图是按实际响应的幅值相位来绘制的，而Nyquist图一般理解为是按机械导纳来绘制的。
极坐标图可以看成是波德图在极坐标上的综合曲线，它对于说明不平衡质量的部位，判断临界转速以及进行故障分析是十分有用的。
和波德图相比，极坐标图在表现旋转机械的动态特征性方面更为清楚和方便，所以其应用也越来越广。
极坐标图除了记录转子在升速或降速过程中系统幅值与相位的变化规律外，也可以描述在定速情况下，由于工作条件或负荷变化而导致的基频或其他谐波幅值与相位的变化规律。
例如转子局部腐蚀、掉块，转子部件脱落而使转子不平衡质量发生变化，导致基频幅值与相位变化。
又如轴上某一局部温升所导致轴的不均匀热变形，这相当于给转子增添不平衡质量而使基频幅值与相位发生变化。
利用极坐标图诊断这类故障非常有效。
图4-22 某机组升速过程的极坐标图
图4-22为某压缩机高压缸自由端轴承处轴的水平振动的极坐标图，其工作转速为12400r/min,借助图上所示的变化趋势，有助于诊断、甄别一些症兆相近的故障。
四、三维谱阵图
转子的转速或其他过程参数在变化过程中，转子的振动呈动态变化，许多情
况下需要连续观察并对比这种变化，因此将转子振动信号的频谱随转速或其他过程参数的变化过程表示在一个谱阵中，称为三维谱阵图。
常用的三维谱阵图有三维转速谱阵图和三维时间谱阵图。
1.三维转速谱阵图
以机组启、停机为例，当转子升（降）速时，各转速下都对应有反映转子频域特性的频谱图。
将这些谱图按转速大小顺序排列，在转速一频率平面上定义了一个三维谱阵图，又称“级联图“、”“瀑布图”，它的水平轴为频率ƒ(或
ω)，垂直转为转速，铅直轴为谱值。
如图4-23所示，它描述了频谱随转速变化。
在图上可以看到，谱阵上有的峰值形成汇交于一点的斜线，它们是与转速成正比的频率成分。
有的峰值形成与频率垂直的直线，这此频率成分与转速无关，它他代表系统的固有频率。
如果将三维转速谱阵图的水平轴单位改为无量纲参数阶比，则为转速阶比谱阵图。
图4-24是某设备每转采样128个点，最大阶比为64的振动噪声转速阶比谱阵图
2.三维时间谱阵
机组正常运行时，不同时刻的振动信号也对应有反映转子频域特性的频谱图，如果将这些谱图按时间顺序排列，同样可以在时间-频率平面上定义一个三维谱阵图。
此时它的水平轴为频率f(或w)，垂直轴为时间，铅直轴为谱值，如图4-25所示，它描述的是频谱随时间的变化，这在故障诊断过程中也非常有用。
图4-25 三维时间谱阵
三维谱阵图与波德图以及坐标图的不同在于它不是对某一频带幅值的描述，而是对全频带的响应进行描述，这样便可以在速度或其他参量变化的过程中，观察到转子许多频率分量下转子的动态响应过程。
比如利用瀑布可以更清楚地看出各种频率成分随转速的变化情况，这对于故障分析是十分有用的。
五、坎贝尔图(Campber)
坎贝尔图和三维谱阵图属同一种特征分析，包含有相同的信息，
只是他们表达的形式不同。
在坎贝尔图中，横坐标表示转速（r/min），纵坐标表示频率f,与转速有关的频率成分（或阶比成分）用圆圈来表示，圆圈的直径表示信号的幅值大小，阶次由原点引出的射线表示，如图4-26所示。
图4-26 坎贝尔图实例。
