2021-2021学年第二学期初三年级质量检测(27校联考) 数学答案(2021-7月)
- 格式:docx
- 大小:328.34 KB
- 文档页数:1


初三数学第二学期第二次质量检测本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分;共8页;满分120分;考试时间为120分钟.第Ⅰ卷(选择题 共48分)一、选择题(共12个小题;每小题4分;共48分) 在每个小题给出的四个备选答案中;只有一个是符合题目要求的;请将你认为符合题目要求的答案选出来.1.-5的绝对值是( )A .5B .-5C .±5D .51 2.据测算;我国每年因沙漠化造成的直接经济损失超过5400000万元;用科学记数法表示这个数;应记为( )A .51054⨯万元B .6104.5⨯万元C .5104.5⨯万元D .71054.0⨯万元 3.下列二次根式中属于最简二次根式的是( ) A .2xB .8C .2xD .12+x 4.甲、乙两人在相同的情况下;各射靶10次;两人命中环数的平均数7==乙甲x x ;方差32=甲S ,22=乙S ;则射击成绩较稳定的是( ) A .甲 B .乙 C .一样 D .不能确定 5.若∠A 是锐角;且sinA =cosA ;则∠A 的度数是( )A .30°B .45°C .60°D .90° 6.如图;到△ABC 的三个顶点距离相等的点是△ABC 的( )A .三条中线的交点B .三条角平分线的交点C .三条高线的交点D .三条边的垂直平分线的交点7.已知AB 、CD 是⊙O 的两条直径;则四边形ABCD 一定是( )A .等腰梯形B .菱形C .矩形D .正方形8.函数211--+=x x y 中;自变量x 的取值范围是( ) A .x ≥-1 B .x >-1且x ≠2 C .x ≠2 D .x ≥-1且x ≠29.如图;在△ABC 中;若∠AED =∠B ;DE =6;AB =10;AE =8;则BC 的长为( ) A .415 B .7 C .215 D .52410.下列说法:①如果两个三角形的周长之比是2:3;那么这两个三角形的面积之比是3∶4; ②平行四边形是中心对称图形; ③经过三点有且只有一个圆; ④化简a 1-的结果是aa -. 其中正确命题的个数是( )A .4B .3C .2D .111.如图;P (x ;y )是以坐标原点为圆心;5为半径的圆周上的点;若x 、y 都是整数;则这样的点共有( )A .4个B .8个C .12个D .16个12.一家三人(父亲、母亲、女儿)准备参加旅行团外出旅游;甲旅行社告知:“父母买全票价;女儿按半价优惠”;乙方旅行社告知:“家庭旅游可按团体票计价;即每人均按全票价的54收费”;若这两家旅行社每人的全票价相同;则优惠条件是( ) A .甲比乙更优惠 B .乙比甲更优惠 C .甲与乙优惠条件相同 D .与原票价有关第Ⅱ卷(非选择题 共72分)二、填空题(共4个小题;每小题4分;共16分) 13.化简:=-+11x x__________________. 14.若点(m ;-m)在反比例函数xky =的图象上;则k_______0(填“>”或“<”) 15.已知两圆的半径分别是一元二次方程01272=+-x x 的两个根;若两圆的圆心距为5;则这两个圆的位置关系是__________.16.己知两个任意正数a 和b ;有下列命题:(1)若a +b =2;则1≤ab ; (2)若21=+b a ;则41≤ab ; (3)若2=+b a ;则22≤ab . 根据以上三个命题所提供的规律;试猜想出a +b 与ab 应满足的最佳关系式:______________________;三、解答题(共7个小题;共56分) 17.(本题满分9分)(1)(5分)计算:()12200432212101----+⎪⎭⎫ ⎝⎛-(2)(4分)分解因式:y x y x x +--23 18.(本题满分8分)解不等式组:()()⎪⎩⎪⎨⎧<+-+--≤+,121331,341082x x x x 并求出其整数解.19.(本题满分7分)已知:如图;四边形ABCD 是等腰梯形;AB =DC ;AD ∥BC ;点E 在AD 上;且EB =EC ;试问点E 是AD 的中点吗?若是;请给出证明;若不是;请说明理由.20.(本题满分8分)已知;如图;折叠矩形ABCD 的一边AD ;使点D 落在BC 边的点F 处;若折痕cm AE 55=;且43tan =∠EFC . (1)证明:△AFB ∽△FEC ; (2)求矩形ABCD 的周长.21.(本题满分8分)对于上抛物体;在不计空气阻力的情况下;有如下关系式:2021gt t v h -=;其中h(米)是上抛物体上升的高度;0v (米/秒)是上抛物体的初速度;g (2/秒米)是重力加速度;t (秒)是物体抛出后所经过的时间;如图是h 与t 的函数关系图.(1)求:0v 和g ;(2)几秒后;物体在离抛出点25米高的地方?22.(本题满分8分)如图;⊙O '经过⊙O 的圆心;E 、F 是两圆的交点;直线OO '交⊙O '于点P ;交EF 于点C ;交⊙O 于点Q ;且152=EF ;41sin =∠P . (1)求证:PE 是⊙O 的切线;(2)求⊙O 和⊙O '的半径的长; (3)若点A 在劣弧上运动(与点Q 、F 不重合);连结PA 交劣弧于点B ;连结BC并延长交⊙O 于点G ;设CG =x ;PA =y ;求y 关于x 的函数关系式;并写出自变量x 的取值范围.23.(本题满分8分)如图;直线l 与x 轴、y 轴的正半轴分别交于A 、B 两点;OA 、OB 的长分别是关于x 的方程0)2(4142=++-AB x x 的两个根(OB >OA );P 是直线l 上A 、B 两点之间的一动点(不与A 、B 重合);PQ ∥OB 交OA 于点Q .(1)求tan ∠BAO 的值;(2)若OQPB PAQ S S 四边形31=∆时;请确定点P 在AB 上的位置;并求出线段PQ 的长;(3)当点P 在线段AB 上运动时;在y 轴上是否存在点M ;使△MPQ 为等腰直角三角形;若存在;请直接写出点M 的坐标;若不存在;请说明理由.参考答案题号 1 2 3 4 5 6 7 8 9 10 11 12 答案ABDBBDCDCDCB二、填空题(共4个小题;每个小题4分;共16分)13.11+-x ; 14.<; 15.相交; 16.ab 2b a ≥+(或ab b a ≥+2)三、解答题(共7个小题;共56分) 17.(本题满分9分) (1)(5分)计算:()12200432212101----+⎪⎭⎫ ⎝⎛-解:原式=()13223210-+-+ …………………………………………… 4分=5.…………………………………………………………………… 5分(2)(4分)分解因式:y x y x x +--23解法1:原式=()()y x y x x ---23 …………………………………………… 1分=()()y x y x x ---2 …………………………………………… 2分 =()()12--x y x ………………………………………………… 3分 =(x -y )(x +y )(x -1) …………………………………… 4分解法2:原式=()()y y x x x ---23 …………………………………………… 1分=()()1122---x y x x …………………………………………… 2分 =()()y x x --12 ………………………………………………… 3分=(x -1)(x +1)(x -y). …………………………………… 4分 18.(本题满分8分)解:解不等式2(x +8)≤10-4(x -3);得x ≤1. ……………………………………………………………………… 2分解不等式121331<+-+x x ;得 x >-1 ……………………………………………………………………… 4分∴ 这个不等式组的解集为-1<x ≤1. …………………………………………… 6分 ∴ 这个不等式组的整数解为0;1. ……………………………………………… 8分 19.(本题满分7分)解:点E 是AD 的中点. …………………………………………………………… 1分 证明:∵ AD ∥BC ;AB =CD ;∴ ∠ABC =∠DCB …………………………………………………………………… 2分 ∵ EB =EC ;∴ ∠EBC =∠ECB …………………………………………………………………… 3分 ∴ ∠ABE =∠DCE …………………………………………………………………… 4分 ∴ △ABE ≌△DCE . ………………………………………………………………… 6分 ∴ AE =DE ;即点E 是AD 的中点. ……………………………………………… 7分20.(本题满分8分)解(1)∵四边形ABCD 是矩形;∴ ∠B =∠C =∠D =90°. ………………………………………………………… 1分 由题意;得Rt △ADE ≌Rt △AFE ;∴ ∠AFE =∠D =90°. ……………………………………………………………… 2分 ∴ ∠AFB +∠EFC =90°; 又∵ ∠EFC +∠FEC =90°;∴ ∠AFB =∠FEC . …………………………………………………………………… 3分 ∴ △AFB ∽△FEC . …………………………………………………………………… 4分 (2)由43tan =∠EFC ;可设EC =3k (k >0〕;则FC =4k .在Rt △ECF 中;EF =5k . ∴ DE =5k .∴ DC =AB =8k . ……………………………………………………………………… 5分 又∵ △ABF ∽△FCE ;∴CE BF FC AB =;即k BFk k 348=; ∴ BF =6k .∴ AF =10k . ………………………………………………………………………… 6分 在Rt △AFE 中;222AE EF AF =+; ∴ ()()()22255510=+k k ;∴ k =1(cm )(取正值). …………………………………………………………… 7分 ∴ 四边形ABCD 的周长=2(AB +BC )=2(8+10)=36(cm ) ………………… 8分 21.(本题满分8分) 解:(1)由图可知;2021gt t v h -=的图像经过(6;0)、(3;45)点; … 1分 ∴ ⎪⎩⎪⎨⎧-=-=.29345,186000g v g v …………………………………………………………………… 3分解这个方程组;得300=v ;g =10.∴ 300=v (米/秒);g =10(2/秒米). ………………………………………… 4分 (2)由(1)得;函数关系式是2530t t h -=. …………………………………… 5分 当h =25时;则255302=-t t . …………………………………………………… 6分 解这个方程;得11=t ;52=t . …………………………………………………… 7分 ∴ 经过1秒或5秒的物体在离抛出点25米高的地方. ………………………… 8分 22.(本题满分8分) 解:(1)连结OE . ∵ OP 是⊙O '的直径;∴ ∠OEP =90°;∴ PE 是⊙O 的切线. ………………………………………………………………… 2分 (2)设⊙O 、⊙O '的半径分别为r ;r '. ∵ ⊙O 与⊙O '交于E 、F ;∴ EF ⊥OO ';1521==EF EC . ∴ 在Rt △EOC 、Rt △POE 中;∠OEC =∠OPE . ∴ sin ∠OEC =sin ∠OPE =41. ∴ 41sin ===∠r OC OE OC OEC . 即r OC 41=; …………………………………………………………………………… 3分 ∴ 1516122=-r r ;解得r =4. Rt △OPE 中;r rOP OE OPE '==∠2sin . ∴ r '=8. …………………………………………………………………………… 4分 (3)连结OA .∵ ∠OEP =90°;CE ⊥OP ; ∴ PO PC PE ·2=. 又∵ PE 是⊙O 的切线; ∴ PA PB PE ·2=; ∴ PC ·PO =PB ·PA .即 POPBPA PC =………………………………………………………………………… 5分 又∵ ∠CPB =∠APO ; ∴ △CPB ∽△APO ; ∴PAPCOA BC =; ∴ PABC 60=. 由相交弦定理;得BC ·CG =CF ·CE ; ∴ CGBC 15=. ……………………………………………………………………… 7分 ∴ PA =4CG ; 即y =4x (515<<x ). …………………………………………………………… 8分 23.(本题满分8分)解:(1)由已知可得⎩⎨⎧+==+),2(4·,14AB OB OA OB OA又∵ 222AB OB OA =+;∴ ()222AB OB OA OB OA =⋅-+;即()222814AB AB =+-. ∴ 018082=-+AB AB .∴ AB =10或AB =-18(不合题意;舍去).∴ AB =10; …………………………………………………………………………… 2分 ∴ 048142=+-x x . 解得 61=x ;82=x .∵ OB >OA ; ∴ OA =6;OB =8. ∴ 34tan ==∠OA OB BAO ……………………………………………………………… 4分 (2)∵ OQPB PAQ S S 四边形31=∆;∴ AOB PAQ S S ∆∆=41. ∵ PQ ∥BO ;∴ △PQA ∽△BOA . ∴41S S BO PQ AB AP BOA PQA 22==⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛∆∆. 5分 ∴21=AB AP . ∵ AB =10; ∴ AP =5. 又∵ 34tan =∠BAO ; ∴ 54sin =∠BAO . ∴ PQ =PA ·sin ∠BAO 4545=⨯=. …………………………………………………………………… 6分 (3)存在M 点的坐标分别为1M (0;0)、⎪⎭⎫ ⎝⎛724,02M 、⎪⎭⎫⎝⎛512,03M . ……………………… 8分。

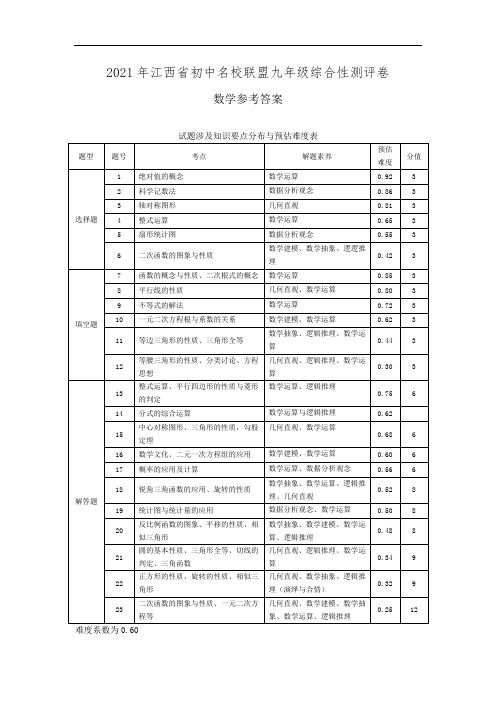
2021年江西省初中名校联盟九年级综合性测评卷数学参考答案试题涉及知识要点分布与预估难度表难度系数为0.60一、选择题(本大题共6小题,每小题3分,共18分) 1.B【解析】|-2|=2. 2.C【解析】1.3亿=130 000 000=1.3×108. 3.B【解析】只有第1个和第4个是轴对称图形. 4.D【解析】734m m m -=,故A 错误;236(2)8m m -=- ,故B 错误;2(2)(3)56m m m m --=-+,故C 错误;2510)5(22++=+m m m ,故D 正确.5.A【解析】∵A 款品牌汽车共销售了132辆,占20%,∴该店的销售总量是132÷20%=660(辆).∴D 款品牌汽车的销售量为660×(1-20%-144÷360-10%)=198(辆). 6.B【解析】∵二次函数y=ax 2+bx +1(a ≠0)图象的顶点在第一象限,且过点(﹣1,0), ∴01=+-b a ,0<a ,0>b .由1-=b a 得10<<b ,由1+=a b 得01<<-a , ∴11<+<-b a ,∴210<++<b a ,即20<<m 二、填空题(本大题共6小题,每小题3分,共18分) 7.2-≥x【解析】被开方数+20≥x ,∴ x ≥-2. 8.65°【解析】∵ l 1∥l 2,∴ ∠4=∠1=40°.∵ ∠4+∠5+∠3=180°,∠2=∠5, ∴ 40°+75°+∠3=180°,得∠3=65°.9.1<x ≤32【解析】不等式组可化为1,3,2x x >⎧⎪⎨≤⎪⎩∴ 不等式组的解集为1<x ≤32. 10.24【解析】∵126x x +=,122x x =,∴2212121212222()22624x x x x x x x x +=+=⨯⨯=. 11.72【解析】如图,连接OB 和OC ,∵△ABC 是等边三角形,点O 为三条中线的交点, ∴ OB =OC ,∠DBO =∠ECO =30°,∠BOC =120°.∵∠DOE =120°,∴∠DOB =∠EOC .∴△BDO ≌△CEO .∴OD =OE . ∵∠DOE =120°,∴DE.∴当OE 最小时,DE 最小. ∵当OE ⊥BC 时,OE 最小,此时△BDE 是等边三角形, ∴DE 的最小值为BC 的一半,即72.B12.2或32或131+(每个答案1分,答对几个给几分) 【解析】①如图1,当点P 在BC 上时,116 2.33==⨯=CP BC ②如图2,当点P 在AB 上,且PC ⊥BC 时,BP=2CP,tan 306===CP BC ③如图3,当点P 在AC 上时,设CP =x ,则BP =2x .作PD ⊥BC 交BC 的延长线于点D ,则CD =12CP =12x,PD=x .在Rt △PBD 中,BD 2+PD 2=BP 2,即2221(6)()(2)22x x x ++=,解得1x =(负值舍去).∴CP=1CP 可以为2或32或131+.PABBAAB图1 图2 图3三、(本大题共5小题,每小题6分,共30分)13.解:(1)原式=99622+-++x x x …………………………………………………2分 =6x +18.………………………………………………………………3分(2)证明:∵四边形ABCD 是平行四边形,∴AD =BC ,AD ∥BC .…………………………………………………………………………4分 ∵AE ∥CF ,∴四边形AECF 是平行四边形. ………………………………………………5分 ∵BE+AE=AD ,∴BE+AE=AD=BC=BE+EC .∴AE=EC .∴四边形AECF 是菱形. ……………………………………………………………………6分 14.解:原式=1])1()1()1)(1()12[2+÷----++x xx x x x x x x (=x x x x x x 1)112(+⋅--- =1111-+=+⋅-x x x x x x .…………………………………………………………4分当5-=x 时,原式=3264151511=--=--+-=-+x x .……………………………………………6分15.(1)如图1,ED 即为所求.………………………………………………………………3分 (2)如图2,∠EAF 即为所求. ……………………………………………………………6分 (其他合理答案也给分)16.解:设上、下禾每束之实各为x 升和y 升.……………………………………………1分 依题意,得61810,1555,x y y x -=⎧⎨-=⎩………………………………………………………………4分解得8,3.x y =⎧⎨=⎩答:上禾每束之实8升,下禾每束之实3升. ……………………………………………6分 17.解:(1)322个生 ………………………………………………………2分 (2)根据题意,列出树状图如下:………………………………………………4分由树状图可知,共有6种等可能的结果,其中正好是两个熟鸡蛋的共有2种. 所以P (两个熟鸡蛋)=3162= . …………………………………………………………6分 四、(本大题共3小题,每小题8分,共24分)18.解:(1)100° …………………………………………………………………………1分 (60-20cos 20°)m ……………………………………………………………………3分 (2)如图,当风车的三个叶片顺时针旋转90°后, ∠AOM =130°,∠BOM =110°,∠COM =10°,∴此时点A 最高. ……………………………………………………………………………4分 过点A 作AD ⊥MO ,交MO 的延长线于点D ,则∠AOD =180°-∠AOM =50°. ……5分 在Rt △AOD 中,cos ODAOD OA∠=,即20cos5012.86(m).OD ︒=⨯≈………………7分 ∴DM =12.86+60≈72.9 (m ),∴风车最高点到地面的距离为72.9 m . …………… 8分D ACBOM成绩分组210≤x≤229230≤x≤249 250≤x≤269 270≤x≤289 290≤x≤309 310≤x ≤329 等级 A B C D E F 人数355124…………………………………………………………………………………3分(平均数 众数 满分率 265.826230%…………………………………………………………………………………5分(1)C ………………………………………………………………………………………6分 (2)∵所抽取的20人中,有12人达标,∴.1803002012(人)=⨯ 答:估计九年级300学生中测试“1分钟阅读数学字符数”达标的人数为180人.……8分 20.解:(1)∵点B (3,4)在反比例函数y (0)kx x=>上, ∴k =3×4=12. ……………………………………………………………………………1分 ∴反比例函数为12(0).y x x =>∵点C (3a ,a )也在比例函数12(0)y x x=>上, ∴3a ·a =12,得a =±2(负值舍去),即a =2.………………………………………3分 (2)如图,过点C 作CD ⊥x 轴于点D ,∵∠CDO ′=∠BAO =90°,∠CO ′D =∠BOA , ∴△CDO ′∽△BAO .………………………4分∴'=CD BA O D OA ,即246'3OO =-,得OO ′=92. ∴△OAB 沿x 轴向右平移的距离为92个单位.………………………………………………5分∵点B (3,4),BA ⊥x 轴于点A , ∴在△OAB 中,OA =3,AB =4, OB =5.∵点C (6,2),OD =6,CD =2,∴OC =由B (3,4),C (6,2),可得13)24()63(22=-+-=BC . ………………7分∵402=OC ,132=BC ,252=OB ,∴2OC >2BC +2OB ,即△OBC 是钝角三角形.……………………………………………………………………8分五、(本大题共2小题,每小题9分,共18分)21.(1)证明:如图,连接OC , ∵OP ∥AC ,∴∠COP =∠OCA . ………………………………………………………………………1分 ∵△ABC 内接于⊙O ,OA ⊥BC ,∴∠OCA =∠OAC =∠COP ,∠OAC +∠ACB =90º. ……………………………………2分 ∵∠ACB =∠OPC ,∴∠COP +∠CPO =90º,即OC ⊥CP .∴PC 是⊙O 的切线. …………………………………………………………………………3分 (2)解:方法一:如图,延长AO 交⊙O 于点M ,连接PM . ………………………………………4分 ∵ OP ∥AC ,∴∠MOP =∠OAC ,∠COP =∠OCA . ∵∠OAC =∠OCA ,∴∠MOP =∠COP . 又由OC =OM ,OP =OP ,可得△OMP ≌△OCP .∴∠OMP =∠OCP =90˚. ……………………………………………………………6分 ∵tan∠OCA =34=tan∠COP ,∠OCP =90˚,∴sin∠COP =54,cos∠COP =53.∵OP =10,∴OC =OM =OA =OP ·cos∠COP =6,PC =PM =OP ·sin∠COP =8.……7分 ∴在Rt △AMP 中,AM =2OM =12,MP =8. ∴13422=+=PM AM AP .…………………………………………………………9分12KHG'F'E'C DBA方法二:∵OA =OC ,OP ∥AC ,∴∠OAC =∠OCA =∠COP . …………………………………4分 ∴tan∠COP =OC PC = tan∠OCA =34. 设PC =4x ,OC =3x ,在Rt△OCP 中,OC 2+PC 2=OP 2,即(3x )2+(4x )2=102, 得x =2.∴OC =6,PC =8. ………………………………………………………………………5分 ∵∠OAC =∠OCA , ∴tan∠OAC =AF CF = tan∠OCA =34. 设CF =4y ,AF =3y ,则OF =OA -AF =6-3y ,AC =5y .在Rt△OCF 中,OF 2+CF 2=OC 2,即(6-3y )2+(4y )2=62,得y =2536,AC =5y =536. …………………………………………………………………6分 ∵OP ∥AC ,∴△A CE ∽△POE .∴PEAEOE CE PO AC ==. ∴CE CE -=610536,得CE =43108. …………………………………………………………7分 在Rt△PCE 中,PE =13431008)43108(2222=+=+PC CE . ∵PE AE PO AC =,即134310010536AE =,得AE =134372,…………………………………8分 ∴AP =AE +PE =1341343100134372=+.…………………………………………9分22.解:(1)2CG DF = 45° ……………………………………………………2分(2)'2'CG DF =,DF ′与CG ′所在直线所夹锐角的度数为45°,结论仍然成立.…………………………3分 理由:如图,连接AC ,AG ′,延长DF ′交AC 于点K ,交CG ′的延长线于点H .……………………………4分在正方形ABCD 中,ACAD =CAD =45°,在正方形AE ′G ′F ′中,''AG AF =G ′AF ′=45°.∴''AC AG AD AF =.……………………………………………………………………………5分 ∵∠CAD -∠CAF ′=∠G ′AF ′-∠CAF ′,即∠DAF ′=∠CAG ′,∴△ACG ′∽△ADF ′.………………………………………………………………………6分∴''CG ACDF AD==,∠1=∠2.∴''CG =. ……………………………………………………………………7分∵在△ADK 中,∠KAD +∠2+∠DKA =180°,在△HCK 中,∠H +∠1+∠CKH =180°, 且∠DKA =∠CKH , ∴∠H =∠KAD =45°.∴''CG =,DF ′与CG ′所在直线所夹锐角的度数为45°.………………9分六、(本大题共12分)23.解:(1)当点P ′在x 轴上时,点P 的纵坐标为2 , 解方程 -x 2+4x +5=2, 得 72±=x .∴此时点P 的坐标为(72+,2)或(72-,2). ………………………………1分 当点P ′在y 轴上时,点P 的横坐标为0,则点P 的纵坐标为5,∴此时点P 的坐标为(0,5).………………………………………2分 综上所述,点P 的坐标为(72+,2)或(72-,2)或(0,5). ………………3分 (2)①点P ′构成的曲线是二次函数的图象,设点P 的坐标为(a ,-a 2+4a +5), ∵点A 坐标为(0,-2),∴中点P ′的坐标为(2a ,2342++-a a ). …………………………………………5分设2a x =, 2342++-=a a y ,消去a ,得P ′所在二次函数图象的解析式为23422++-=x x y .……………………6分 作出该函数的图象如下: ……………………………………………………………………7分y=m②存在B 3B 4-B 1B 2=2. ……………………………………………………………………8分 设点B 1,B 2的横坐标分别为b 1,b 2,∵抛物线y =-x 2+4x +5的对称轴为直线x =2, 抛物线23422++-=x x y 的对称轴为直线x =1, ∴点B 3,B 4的横坐标分别为2-b 2,4-b 1. ……………………………………………10分 ∴B 3B 4-B 1B 2=[(4-b 1)-(2-b 2)]-(b 2-b 1)=2. ………………………………12分。


2021-2022学年下学期初三27校联考数学试卷(22.03)参考答案一、选择题:(本大题共10小题,每小题3分)题号12345678910选项BCACBDBDCD三、解答题:(本大题共7小题,其中第16题6分,第17题6分,第18题8分,第19题8分,第20题8分,第21题9分,第22题10分,共55分)16.212(3)3(1)x x x x +-=-+ 原式2=1x +----------4分;1x -当时,原式----------6分;17.解:(1)m =360﹣(48+96+72)=144;----------2分;(2)补全频数分布直方图如下:----------4分;(3)该年级一分钟跳绳次数在160次以上的学生数占该年级全部学生数的百分比为216360×100%=60%.----------6分;18.解:(1)过点(2,0)作x轴垂线,过点(5,3)作与BC垂直的线,两线的交点即为D点坐标,∴D(2,0),故答案为:(2,0);----------2分;(2)连接AC,∵A(0,4),B(4,4),C(6,2),∴AD=2,CD=2,AC=2,∵AC2=AD2+CD2,∴∠ADC=90°,∴的长=×2π×2=π,∵扇形DAC是一个圆锥的侧面展开图,∴π=2πr,∴r=,故答案为:;----------5分;(3)设AB的中点为E,∴E(2,4),∴DE=4,∴S=π×(A D2﹣DE2)=4π,∴线段AB扫过的面积是4π.----------8分;19.(1)证明:连接OD,∵OB=OD,∴∠3=∠B,∵∠B=∠1,∴∠1=∠3,在Rt△ACD中,∠1+∠2=90°,∴∠2+∠3=90°,∴∠4=180°﹣(∠2+∠3)=90°,∴OD⊥AD,则AD为圆O的切线;----------4分;(2)解:设圆O的半径为r,在Rt△ABC中,AC=BC tan B=4,根据勾股定理得:AB=∴OA=﹣r,在Rt△ACD中,tan∠1=tan B=1 3,∴CD=AC tan∠1=4 3,根据勾股定理得:AD2=AC2+CD2=16160 1699+=,在Rt△ADO中,OA2=OD2+AD2,即(﹣r)2=r2+160 9,解得:r,∴⊙O.----------8分;20.解:(1)设每台乙型平板的进价为x 元,则每台甲型平板的进价为(x+600)元,依题意,得:6000045000600x x=+,解得:x =1800,----------2分;经检验,x =1800是原方程的解,且符合题意,∴x+600=2400.答:每台甲型平板的进价为2400元,每台乙型平板的进价为1800元.----------3分;(2)设最大利润是W 元,∵购进m 台甲型平板,∴购进(80﹣m )台乙型平板,依题意,得:W =(2800﹣2400)m+(2400﹣1800)(80﹣m )=﹣200m+48000.∵购买资金不超过17.76万元.甲型平板不少于乙型平板的2倍,∴2400m +1800(80-m )177600, m 2(80-m ).ìïïíïï解得:160563m #,----------5分;∵m 是整数,∴m =54,55,56∴有3种种进货方案:1购进54台甲型平板,26台乙型平板;2购进55台甲型平板,25台乙型平板;3购进56台甲型平板,24台乙型平板;----------7分;由W =﹣200m +48000,∵k=﹣200<0,∴W 随m 值的增大而减小,∴方案①,即购进54台甲型平板,26台乙型平板时利润W 取得最大,最大值为:﹣200×54+48000=37200(元).答:购进54台甲型平板,26台乙型平板时利润W 取得最大,最大利润为37200元.----------8分;21.(1)如图1,连接AE ,PF ,延长EF 、AP 交于点Q ,当α=60°时,△ABC和△PDC都是等边三角形,∴∠PCD=∠ACB=60°,PC=CD,AC=CB,∵F、E分别是CD、BC的中点,∴,,∴,∵∠PCD=∠ACB∴∠PCD-∠ACD=∠ACB-∠ACD∴∠ACP=∠ECF,∴△ACP∽△ECF,∴,∠CEF=∠CAP,∴∠Q=β=∠ACB=60°,当α=90°时,△ABC和△PDC都是等腰直角三角形,∴∠PCD=∠ACB=45°,PC=CD,AC =CB,∵F、E分别是CD、BC的中点,∴,,∴,∵∠PCD=∠ACB∴∠PCD-∠ACD=∠ACB-∠ACD∴∠ACP=∠ECF,∴△ACP∽△ECF,∴,∠CEF=∠CAP,∴∠Q=β=∠ACB=45°,由此,可归纳出22yEF CE yAP AC x x===,β=∠ACB=;故第(1)答案是:,60°,,45°,2yx,,----------6分(填对一空给1分);(2)当α=120°,连接AE,PF,延长EF、AP交于点Q,∵AB=AC,E为BC的中点,∴AE⊥BC,∠CAE=60°,∠ACB=30°∴sin60°=,同理可得:,∴,∴,∵∠PCD=∠ACB∴∠PCD+∠ACD=∠ACB+∠ACD∴∠ACP=∠ECF,又∵∠ECF=∠ACP,∴△PCA∽△FCE,∴,∠CEF=∠CAP,∴∠Q=β=∠ACB=30°.----------9分(没有解题过程只有答案不得分);22.解:(1)∵抛物线y=x2+bx+c经过点A(0,﹣4)和点B(4,0),∴41640cb c=-⎧⎨++=⎩,解得:34bc=-⎧⎨=-⎩,∴b,c的值分别为﹣3,﹣4----------2分;(2)①设直线AB 的解析式为y =kx +t,(k ≠0),把A (0,﹣4),B (4,0)的坐标分别代入表达式,得440t k t =-⎧⎨+=⎩,解得14k t =⎧⎨=-⎩,∴直线AB 的函数表达式为y =x ﹣4----------3分;由(1)得,抛物线C 的对称轴是直线x =32,当x =32时,y =x ﹣4=32﹣4=52-,∴点M 的坐标是35(,)22-;----------4分;②设抛物线C 1的表达式为y =(x ﹣32+m )2﹣254,∵MN ∥y 轴,∴点N 的坐标是2325(,m )24-,且M 、N 不能重合∵点P 的横坐标为﹣1,∴P 点的坐标是(﹣1,m 2﹣5m ),----------5分;设PE 交抛物线C 1于另一点Q ,∵抛物线C 1的对称轴是直线x =32﹣m ,PE ∥x 轴,∴根据抛物线的对称性,点Q 的坐标是(4﹣2m ,m 2﹣5m ),----------6分;(Ⅰ)如图1,当点N 在点M 下方,即0<m <152时,∴PQ =4﹣2m ﹣(﹣1)=5﹣2m ,MN =52-﹣(m 2﹣254)=154﹣m 2,由平移的性质得,QE =m ,∴PE =5﹣2m +m =5﹣m ,∵PE +MN =274,∴5﹣m +154﹣m 2=274,解得,m 1=﹣2(舍去),m 2=1,----------7分;(Ⅱ)如图2,当点N 在点M 上方,点Q 在点P 右侧,即2<m<52时,PE=5﹣m,MN=m2﹣15 4,∵PE+MN=27 4,∴5﹣m+m2﹣154=274,解得,m1=2(舍去),m2=2(舍去).----------8分;(Ⅲ)如图3,当点N在M上方,点Q在点P左侧,即m>52时,PE=m,MN=m2﹣154,∵PE+MN=27 4,∴m+m2﹣154=274,解得,m1=1432--(舍去),m2=1432-+,----------9分;综合以上可得m的值是1或12-+.----------10分;。
九年级数学试卷答卷时间:120分钟 满分值:150分一、选择题(每题3分,共24分) 1.-12的绝对值是( ▲ )A .2B .12C .-2D .-122.下列计算正确的是( ▲ )A.284x x x -÷=B.22a a a ⋅= C.()623a a = D.()3393a a =3.下列计算中错误的是( ▲ ) A.020181= B.224-= C.24= D.1133-=4.x =1是关于x 的方程2x -a =0的解,则a 的值是( ▲ ) A .-2 B .2 C .-1 D .15.在函数y =34x x --中,自变量x 的取值范围是( ▲ )A .x >3B .x ≥3C .x >4 D.x ≥3且x ≠46.不等式组2x 12x 40->⎧⎨+≥⎩的解集,在数轴上表示正确的是( ▲ )A .B .C .D .7.如图,在四边形ABCD 中,DC ∥AB ,CB ⊥AB ,AB=AD ,CD= AB ,点E 、F 分别为AB 、AD 的中点,则△AEF 与多边形BCDFE 的面积之比为( ▲ )A.B.C.D.8.二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,顶点坐标为(-2,-9a),下列结论:①abc>0;②4a+2b+c<0;③9a-b+c=0;④若方程a(x+5)(x-1)=-1有两个根x1和x2,且x1<x2,则-5<x1<x2<1;⑤若方程|ax2+bx+c|=1有四个根,则这四个根的和为-8,其中正确的结论有( ▲)个.A.2B.3C.4D.5(第7题图)(第8题图)二、填空题(每题3分,共24分)9.首都大兴国际机场占地面积1 400 000平方米,是世界上规模最大的单体航站楼,于2016年被英国媒体评选为“新世界七大奇迹”之首.其中1 400 000用科学记数法表示为▲。
10.因式分解2x2-8y2 =▲。
11.在某次七年级期末测试中,甲、乙两个班的数学平均成绩都是89.5分,且方差分别为20.15S=甲,20.2S=乙,则成绩比较稳定的是▲班。
【九年级】2021届九年级数学质量检测试题(带答案)2021年利川市九年级质量检测数学试题卷本试卷共6页,三个大题24个小题。
全卷满分120分。
考试用时120分钟。
注意事项:1.考生答题全部在答题卷上,答在试题卷上无效.2.请认真核对监考教师在答题卷上所粘贴条形码的姓名.准考证号是否与本人相符合,再将自己的姓名.准考证号用0.5毫米的黑色墨水签字笔填写在答题卷及试题卷上.3.选择题作答必须用2B铅笔将答题卷上对应的答案标号涂黑.如需要改动,请用橡皮擦干净后,再选涂其他答案.非选择题作答必须用0.5毫米黑色墨水签字笔写在答题卷上指定位置,在其他位置答题一律无效.4.作图必须用2B铅笔作答,并请加黑加粗,描写清楚.5. 考生不得折叠答题卷,保持答题卷的整洁.考试结束后,请将试题卷和答题卷一并上交.一、选择题(本大题共有12个小题,每小题3分,共36分.在每小题给出的四个选项中,恰有一项是符合题目要求的,请将正确选择项前的字母代号填涂在答题卷相应位置上)。
1、-3的绝对值等于A、3 B、 C、D、-32、PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物。
其中2.5微米=0.0000025米,将0.0000025用科学计数法表示正确的是A、2.5×B、0.25×C、2.5× D、0.25×3、下列图形中,是中心对称图形但不是轴对称图形的是A、正三角形B、平行四边形C、正方形 D、菱形4、若代数式有意义,则x的取值范围是A、且B、且C、且D、且5、已知是非零实数,则下列计算正确的是A、 B、C、 D、6、投掷一枚均匀的硬币,落地时正面或反面向上的可能性相同。
有甲、乙、丙三人做“投硬币”实验,他们分别投100次,结果正面向上的次数为:甲60次、乙40次、丙50次。
则下列说法正确的是A、甲第101次投出正面向上的概率最大B、乙第101次投出正面向上的概率最大C、只有丙第101次投出正面向上的概率为0.5D、甲、乙、丙三人第101次投出正面向上的概率相等7、如图,直线m∥n,将含有45°角的三角板ABC的一个锐角顶点C放在直线n上,则∠1+∠2等于A、30°B、45°C、60° D、90°8、分解因式的结果是A、 B、 C 、 D、9、若一元二次方程的一个根为,则该方程的另一个根是A、 B、 C、 D、10、随机抽取九年级某班10位同学的年龄情况为:17岁1人,16岁5人,15岁2人,14岁2人。
人教版九年级数学《图形的相似》单元测试(附答案)(时间:120分钟 满分:120分)一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知△ABC ∽△DEF ,若△ABC 与△DEF 的相似比为34,则△ABC 与△DEF 对应中线的比为( )A.34B.43C.916D.169 2.已知b a =513,则a -b a +b的值是( )A.23B.32C.94D.493.如图,在四边形ABCD 中,AD ∥BC ,对角线AC ,BD 相交于点O.若AD =1,BC =3,则AOCO的值为( ) A.12 B.13 C.14 D.194.如图,在△ABC 中,DE ∥BC ,DE 分别与AB ,AC 相交于点D ,E.若AD =12,DB =4,则DE ∶BC 的值为( )A.23B.12C.34D.355.如图,不能判定△AOB和△DOC相似的条件是( )A.AO·CO=BO·DO B.AODO=ABCDC.∠A=∠D D.∠B=∠C6.如图,矩形ABCD∽矩形ADFE,AE=1,AB=4,则AD=( )A.2 B.2.4 C.2.5 D.37.已知如图①,②中各有两个三角形,其边长和角的度数如图上标注,则对图①,②中的两个三角形,下列说法正确的是( )A.只有①相似B.只有②相似C.都不相似D.都相似8.如图,在8×4的矩形网格中,每个小正方形的边长都是1.若△ABC的三个顶点在图中相应的格点上,图中点D,E,F也都在格点上,则下列与△ABC相似的三角形是( ) A.△ACD B.△ADF C.△BDF D.△CDE9.如图,点M 在BC 上,点N 在AM 上,CM =CN ,AM AN =BMCM,下列结论正确的是( )A .△ABM ∽△ACB B .△ANC ∽△AMB C .△ANC ∽△ACM D .△CMN ∽△BCA10.如图,在△ABC 中,DE ∥BC ,DF ∥AC ,EG ∥AB ,且AE ∶EC =3∶2.若BC =10,则FG 的长为( )A .1B .2C .3D .411.阳光通过窗口AB 照射到室内,在地面上留下2.7米的亮区DE(如图所示),已知亮区到窗口下的墙角的距离EC =8.7米,窗口高AB =1.8米,则窗口底边离地面的高BC 为( )A .4米B .3.8米C .3.6米D .3.4米12.在Rt △ABC 和Rt △DEF 中,已知∠C =∠F =90°,在下列条件中:①∠A =30°,∠E =60°;②AC =5,BC =4,DF =15,EF =12;③AB =5,AC =3,DE =10,DF =6;④AC ∶AB =1∶3,DF =a ,DE =3a.能够判断Rt △ABC ∽Rt △DEF 的有( )A .1个B .2个C .3个D .4个13.如图,将矩形纸片ABCD 沿EF 折叠,使点B 与CD 的中点重合.若AB =2,BC =3,则△FCB ′与△DGB ′的面积之比为( )A .9∶4B .16∶9C .4∶3D .3∶214.如图,将△ABC的高AD四等分,过每一个分点作底边的平行线,把三角形的面积分成四部分S1,S2,S3,S4,则S1∶S2∶S3∶S4等于( )A.1∶2∶3∶4 B.2∶3∶4∶5 C.1∶3∶5∶7 D.3∶5∶7∶915.如图,在△ABC中,AC=BC,CD是边AB上的高线,且有2CD=3AB=6,CE=EF =DF,则下列判断中不正确的是( )A.∠AFB=90°B.BE= 5C.△EFB∽△BFC D.∠ACB+∠AEB=45°16.如图1,在Rt△ABC中,∠ACB=90°,点P以每秒1 cm的速度从点A出发,沿折线AC—CB运动,到点B停止,过点P作PD⊥AB,垂足为D,PD的长y(cm)与点P的运动时间x(秒)的函数图像如图2所示.当点P运动5秒时,PD的长是( ) A.1.5 cm B.1.2 cm C.1.8 cm D.2 cm二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有2个空,每空3分.把答案写在题中横线上)17.如图,已知AD∥BE∥CF,且AB=4,BC=5 ,EF=4,则DE=.18.如图,已知△OAB与△OA′B′是位似比为1∶2的位似图形,点O为位似中心.若△OAB 内一点P(x,y)与△OA′B′内一点P′是一对对应点,则点P′的坐标是.19.如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E.则当BD=4时,CE=;当∠AED=90°时,BD=.三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤) 20.(本小题满分8分)如图,矩形ABCD中,AB=3,BC=6,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于点F,求CFCD的值.21.(本小题满分9分)如图,△ABC的顶点坐标分别为A(1,1),B(2,3),C(3,0).(1)以点O为位似中心画△DEF,使它与△ABC位似,且位似比为2;(2)在(1)的条件下,若M(a,b)为△ABC边上的任意一点,则△DEF的边上与点M对应的点M′的坐标为.22.(本小题满分9分)已知:如图,在△ABC中,BC=10,BC边上的高h=5,点E在边AB上,过点E作EF∥BC,交AC边于点F,点D为BC上一点,连接DE,DF,△DEF的面积为4,求点E到BC的距离.23.(本小题满分9分)如图,CD是Rt△ABC斜边AB上的中线,过点D垂直于AB的直线交BC于点E,交AC延长线于点F.求证:(1)△ADF∽△EDB;(2)CD2=DE·DF.24.(本小题满分10分)小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2 m,CE=0.8 m,CA=30 m(点A,E,C在同一直线上).已知小明的身高EF是1.7 m,请你帮小明求出楼高AB.(结果精确到0.1 m)25.(本小题满分10分)如图,在△ABC 中,BC =8 cm ,AC =6 cm ,点P 从B 出发,沿BC 方向以2 cm/s 的速度移动,点Q 从C 出发,沿CA 方向以1 cm/s 的速度移动,若P ,Q 分别从B ,C 同时出发,设运动的时间为t s ,则△CPQ 能否与△CBA 相似?若能,求出t 的值;若不能,请说明理由.26.(本小题满分11分)如图,四边形ABCD 中,AC 平分∠DAB ,∠ADC =∠ACB =90°,E 为AB 的中点.(1)求证:AC 2=AB ·AD ; (2)求证:CE ∥AD ;(3)若AD =4,AB =6,求ACAF的值.答案一、选择题二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有2个空,每空3分.把答案写在题中横线上) 17.165.18.(-2x ,-2y).19.CE =4.8;当∠AED =90°时,BD =8. 三、解答题20.解:∵四边形ABCD 是矩形,∴∠BAD =90°. 又∵AB =3,AD =BC =6,∴BD =AB 2+AD 2=3.∵BE =1.8,∴DE =3-1.8=1.2.∵AB ∥CD ,∴DFAB =DE BE ,即DF 3=1.21.8.解得DF =233.∴CF=CD-DF=33.∴CFCD=333=13.21.点M′的坐标为(2a,2b)或(-2a,-2b).解:如图,△DEF和△D′E′F′为所作.22.解:设点E到BC的距离为x.∵EF∥BC,∴△AEF∽△ABC. ∴EFBC=5-x5.∴EF=10-2x.∴S△DEF=12(10-2x)·x=4.解得x1=4,x2=1.∴点E到BC的距离为4或1.23.证明:(1)在Rt△ABC中,∠B+∠A=90°.∵DF⊥AB,∴∠BDE=∠ADF=90°.∴∠A+∠F=90°.∴∠B=∠F.∴△ADF ∽△EDB.(2)由(1)可知∠B =∠F ,∵CD 是Rt △ABC 斜边AB 上的中线,∴CD =AD =DB. ∴∠DCE =∠B.∴∠DCE =∠F.又∵∠CDE =∠FDC ,∴△CDE ∽△FDC. ∴CD DF =DE CD,即CD 2=DE ·DF. 24.解:过点D 作DG ⊥AB ,分别交AB ,EF 于点G ,H ,则EH =AG =CD =1.2 m ,DH =CE =0.8 m ,DG =CA =30 m.∵EF ∥AB ,∴FHBG =DH DG . 由题意,知FH =EF -EH =1.7-1.2=0.5(m).∴0.5BG =0.830,解得BG =18.75. ∴AB =BG +AG =18.75+1.2=19.95(m)≈20.0 m.答:楼高AB 约为20.0 m.25.解:设经过t s 时△CPQ 与△CBA 相似,此时BP =2t ,CQ =t ,CP =8-2t ,①当△CPQ ∽△CBA 时,CP CB =CQ CA ,即8-2t 8=t 6,解得t =2.4;②当△CPQ ∽△CAB 时,CP CA =CQ CB ,即8-2t 6=t 8,解得t =3211. 综上可知,经过2.4 s 或3211s 时,△CPQ 与△CBA 相似.26.解:(1)证明:∵AC 平分∠DAB ,∴∠DAC =∠CAB.又∵∠ADC =∠ACB =90°,∴△ADC ∽△ACB.∴AD AC =AC AB,即AC 2=AB ·AD. (2)证明:∵E 为AB 的中点,∴CE =12AB =AE.∴∠EAC =∠ECA. 由(1)知∠DAC =∠CAB.∴∠DAC =∠ECA.∴CE ∥AD.(3)∵CE ∥AD ,∴△AFD ∽△CFE.∴AD CE =AF CF. ∵CE =12AB ,∴CE =12×6=3. ∴43=AF CF. ∴AF AC =47,即AC AF =74.。