(修改稿1)导学案_匀变速直线运动的位移与时间的关系

《匀变速直线运动的位移与时间的关系》导学案一、学习目标⒈知道什么是位移—时间图像，以及如何用图像表示位移和时间的关系。

⒉知道用v-t 图象如何求出物体的位移。

⒊理解匀速直线运动的速度—时间图象和位移—时间图象。

二、自主学习1、匀速直线运动的速度—时间图象的特点是 ；位移—时间图象的特点是 。

2、采用 的思想我们可推导出匀变速直线运动的v t -图线与时间轴所围的“面积”表示 。

时间轴上方所围的“面积”表示 ，时间轴下方所围的面积表示 。

3、匀变速直线运动的位移-时间公式是x = ，其中是矢量的物理量有 ，是标量的物理量有 。

三、新知识学习 根据平均速度的定义式，做任何变速运动的位移都可以表示为t v x =，则匀变速直线运动的位移公式为2001()/22t s vt v v t v t at ==+=+ ⑴在取初速度0v 方向为正方向的前提下，匀加速度直线运动a 取正值，匀减速直线运动a 取负值；计算的结果0s >，说明位移的方向与初速度的方向相同；0s <说明位移的方向与初速度的方向相反。

⑵对于初速度为零(00v =)的匀变速直线运动，位移公式为211122s v t at ==,即位移s 与时间t 的二次方成正比。

⑶速度—时间图像下的面积表示位移的大小，且t 轴上方的面积表示正位移，t 轴下方的面积表示负位移。

【例1】一物体做匀加速度直线运动，0时刻的速度0v =2m/s ，加速度a =2m/s 2，求物体1秒内的位移、2秒内的位移。

【例2】某做直线运动的质点位移随时间变化的关系为224t t s -=，S 与t 单位分别是m ，s 。

求该质点的初速度和加速度。

【例3】如图所示为一物体运动的速度—时间图象，下列判断正确的是（ ）A ．物体的初速度为3m/sB ．物体的加速度大小为1.5m/s 2C ．2s 末物体位于出发点D ．前2秒的加速度与后两2秒的加速度方向相反 刹车问题【例4】汽车以10 m ／s 的速度在平直公路上匀速行驶，刹车后经2 s 速度变为6 m/s ，求： (1)刹车后2 s 内前进的距离及刹车过程中的加速度．(2)刹车后前进9 m 所用的时间．(3)刹车后8 s 内前进的距离．四、重点、难点突破1. 从速度图象求匀速直线运动的位移匀速直线运动的速度不随时间变化，所以其速度图象是平行于时间轴的直线。

第3节匀变速直线运动的位移与时间的关系导学案【学习目标】与时间之间的关系，会用公式解匀变速直线运动的问题。

2.理解匀变速直线运动的速度与位移的关系。

【学习重难点】1.匀变速直线运动的位移与速度的关系式及其应用。

（重点）及其应用。

（重点）v-t图像推导匀变速直线运动位移与时间的关系。

（难点）【知识回顾】一、匀变速直线运动1.定义：沿一条直线，加速度不变的运动，叫做匀变速直线运动。

2.特点：① a恒定不变① v-t图象是一条倾斜直线。

3.斜率的物理意义：代表的是加速度（1）匀加速直线运动：物体的速度随时间均匀增加的直线运动。

（2）匀减速直线运动：物体的速度随时间均匀减小的直线运动。

二、速度与时间的关系1.公式：v=v0+at2.适用范围：匀变速直线运动。

3.矢量性：v0、v、a均为矢量，应用时，应先选取正方向。

(1)一般取v0的方向为正方向(若v0＝0，则取运动的方向为正方向)。

(2)已知量：a或v与v0的方向相同时取正值，与v0的方向相反时取负值。

(3)待求量：对计算结果中的正、负，应根据正方向的规定加以说明。

4.公式的特殊形式:(1)当a＝0时，v＝v0(匀速直线运动)。

(2)当v0＝0时，v＝at(由静止开始的匀加速直线运动)。

5.“知三求一”的思想:此公式中有四个物理量，知道其中三个就可求第四个物理量。

【自主预习】一、匀变速直线运动位移与时间的关系1.公式：x ＝v 0t ＋12at 2，特例：当初速度为0时，x ＝12at 2。

2.条件：此公式只适用于匀变速直线运动。

二、速度与位移关系1.公式：v 2－v 20＝2ax 。

：速度与时间的关系式v ＝v 0＋at ；位移与时间的关系式x ＝v 0t ＋12at 2；消掉时间t 即可得公式。

3.条件：此公式只适用于匀变速直线运动。

【课堂探究】 思考与讨论：当一辆汽车以速度v 做匀速直线运动，那么我们如何求出在时间t 内这辆汽车的位移？你能想出几种办法？方法总结： 1.公式法：x=vt2.图像法：在匀速直线运动的v – t 图线中可以用图线与时间轴所围的矩形“面积”表示位移。

匀变速直线运动的位移与时间的关系教案一、设计思路“匀变速直线运动的位移与时间的关系”拟用两个课时完成，第一课时主要任务是探究匀变速直线运动的位移规律，以此为载体，用“导学式”的教学方法，让学生经历匀变速直线运动位移规律的探究过程，利用v-t图象，渗透物理思想方法(化繁为简、极限思想、微元法等)，得出“v-t图象与时间轴所围的面积表示位移”的结论，然后通过计算“面积”得出运动位移的规律，培养学生严谨的科学态度和发散思维能力，促进学生科学探究能力的提高，让学生感悟物理思想方法。

二、教学目标1、知识与技能知道v-t图象与时间轴所围的面积表示位移；初步掌握匀变速直线运动的位移规律。

2、过程与方法经历匀变速直线运动位移规律的探究过程，感悟科学探究的方法；渗透物理思想方法，尝试用数学方法解决物理问题；通过v-t图象推出位移公式，培养发散思维能力。

3、情感态度与价值观激发学生对科学探究的热情，感悟物理思想方法，培养科学精神。

三、教学重点、难点1、教学重点经历匀变速直线运动位移规律的探究过程，体验探究方法。

2、教学难点物理思想方法的渗透。

四、学情分析1、学科知识分析：本节内容是学生在已学过瞬时速度、匀速直线运动的位移位移规律的基础上，探究匀变速直线运动位移与时间的关系。

在上一章中用极限思想介绍了瞬时速度与瞬时加速度，学生已能接受极限思想。

2、学生能力要求：学生已初步了解极限思想，在探究“匀变速直线运动的位移与时间的关系”过程中，要进一步渗透极限思想。

要在学生体会“v—t图线与时间轴所围的面积代表匀运动位移”的过程中，逐步渗透体“无限分割再求和”这种微元法的思想方法。

使学生感悟物理思想方法，提高物理思维能力。

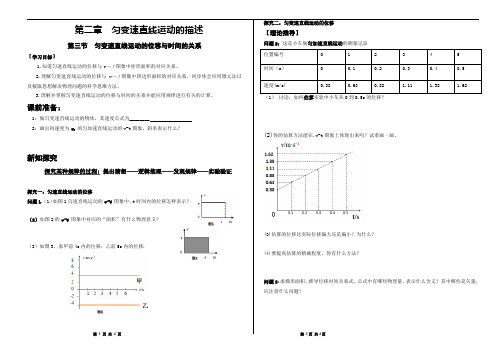
五、教学过程（简略）[新课]（教师）Array问题：速直线运动的位移在v-t图线上表现在哪里？（回答）匀速直线运动的特征是速度恒定不变，位移和时间有怎样的关系为x=v*tv/(m/s)0 t t/s（教师）问题：匀变速直线运动的位移是否也对应v-t 图线与t 轴 所围成的面积？ （板书）2-3匀变速直线运动的位移与时间的关系一、用v-t 图象研究匀速直线运动的位移匀速直线运动的位移对应v-t 图线与t 轴所围成的面积. （教师）问题：匀变速直线运动的位移是否也对应 v-t 图象一定的面积？ （回答）我们需要研究匀变速直线运动的位移规律！问题：我们应怎样研究匀变速直线运动？ （学生）讨论 （教师）思路：在很短时间（⊿t ）内，将变速直线运动近似为匀速直线运动，利用 x=vt 计算每一段的位移，各段位移之和即为变速运动的位移。

第 3 页 共 4 页 第 4页 共4页
【实验探究】
探究三：匀变速直线运动的位移—时间图象(x-t 图象)
问题4：你能设计一个实验来探究匀变速直线运动的位移与时间的关系吗？需要测哪些物理量？如何测？
处理纸带：选好坐标原点，选好计数点，记录各点位置，记录时间间隔
建轴，选好刻度，描点，作出匀变速直线运动的x-t 图象
问题5.小车做直线运动，为什么画出来的x-t 图象不是直线？
【应用】
例1：一辆汽车以1m/s 2
的加速度加速行驶了12s,驶过了180m 。

汽车开始加速时的速度是多少？
跟踪训练1：以18m/s 的速度行驶的汽车，制动后做匀减速运动，在3s 内前进36m ，求汽车的加速度。

【小结】
达标检测：
1、一物体运动的位移与时间关系x ＝6t ＋4t 2（式中的物理量的单位都是国际单位制中的单位，初速度方向为正方向），则 （ ）
（A ）这个物体的初速度为12 m/s （B ）这个物体的加速度为8 m/s 2 （C ）这个物体的初速度为6 m/s （D ）这个物体的加速度为—8 m/s 2
2、矿井里的升降机从静止开始做匀加速直线运动，上升3s 后速度达到3m/s ，然后匀速上升6s ，最后匀减速上升2s 停下，求升降机上升的高度，并画出升降机运动过程中的速度－时间图象。

t。

3．匀变速直线运动的位移与时间的关系1．理解v-t图像中“面积”与位移的关系，了解匀变速直线运动位移与时间的关系式的推导过程。

2．理解匀变速直线运动位移与时间的关系式，并会用其解决实际问题。

3．理解速度与位移的关系式的推导过程，理解速度与位移关系式，并会应用其解决实际问题。

一、匀变速直线运动的位移1．位移在v-t图像中的表示做匀变速直线运动的物体的位移，对应着v-t图像中的图线和□01t轴所包围的面积。

如图所示，在0～t时间内的位移大小等于着色部分的梯形的□02面积。

2．位移公式：x＝□03v0t＋12at2。

(1)公式中x、v0、a均是矢量，应用公式解题前应先根据正方向明确它们的□04正、负值；(2)当v0＝0时，x＝□0512at2，表示初速度为零的匀加速直线运动的位移与时间的关系。

二、匀变速直线运动的速度与位移的关系1．匀变速直线运动的速度与位移的关系式□01v2－v2＝2ax，若v0＝0，则关系式为□02v＝2ax。

2．公式推导速度公式：v＝□03v0＋at①位移公式：x＝□04v0t＋12at2②将上述两个公式联立，消去时间t，可得□05v2－v20＝2ax。

3．速度与位移的关系式是矢量式，使用时应先规定正方向，以便确定v0、v、a、x的正负。

判一判(1)初速度越大，时间越长，匀变速直线运动物体的位移一定越大。

()(2)匀变速直线运动的位移与初速度、加速度、时间三个因素有关。

()(3)位移公式x＝v0t＋12at2仅适用于匀加速直线运动。

()(4)公式v2－v20＝2ax适用于所有的直线运动。

()(5)因为v2－v20＝2ax，v2＝v20＋2ax，所以物体的末速度v一定大于初速度v0。

()(6)在公式v2－v20＝2ax中，a为矢量，与规定的正方向相反时，a取负值。

()提示：(1)×(2)√(3)×(4)×(5)×(6)√想一想(1)v-t图像中图线与时间轴所围的图形有时在时间轴上方，有时在时间轴下方，这与物体的位移有何关系？提示：根据v-t图像的物理意义，图线在时间轴上方，表明物体向正方向运动，图线与时间轴所围的图形在时间轴上方，其面积表示的物体的位移为正值，位移为正方向；同理，图线在时间轴的下方，表明物体向负方向运动，图线与时间轴所围的图形在时间轴下方，其面积表示的位移是负值，位移为负方向。

匀变速直线运动的位移与时间的关系【学习目标】1．知道匀速直线运动的位移与时间的关系．2．了解位移公式的推导方法，掌握位移公式x＝v o t+ at2/2．3．理解匀变速直线运动的位移与时间的关系及其应用．4．理解v-t图象中图线与t轴所夹的面积表示物体在这段时间内运动的位移【学习重点】1．理解匀变速直线运动的位移与时间的关系x＝v o t+ at2/2及其应用．2．理解匀变速直线运动的位移与速度的关系v2-v02=2ax及其应用．【学习难点】1．v-t图象中图线与t轴所夹的面积表示物体在这段时间内运动的位移．2．微元法推导位移时间关系式．3．匀变速直线运动的位移与时间的关系x＝v o t+ at2/2及其灵活应用【方法指导】自主探究、交流讨论、自主归纳【知识链接】1．做匀速直线运动的物体，其位移公式为___________，其v-t 图象为__________。

在v-t 图象中某段时间内位移的大小与____________相等。

2．匀变速直线运动的v-t 图象是________________，其中图象的斜率表示物体的__________，图象与坐标轴所围面积是物体的______________。

3．匀变速直线运动中，速度与时间的关系式为________________。

【自主探究】一、匀速直线运动的位移阅读教材p37第一段并观察图2—3—1所示．做匀速直线运动的物体在时间t内的位移与图线和时间轴围成的矩形面积有什么关系？对于匀变速直线运动，它的位移与它的v—t图象，是不是也有类似的关系呢?[思考与讨论]学生阅读教材p37思考与讨论栏目，老师组织学生讨论这一问题．在“探究小车的运动规律”的测量记录中，某同学得到了小车在0，1，2，3，4，5几个位师：能否根据表中的数据，用最简便的方法估算实验中小车从位置0到位置5的位移?要想提高估算的精确程度，想想你有什么好的方法？[交流与讨论]分割和逼近的方法在物理学研究中有着广泛的应用．早在公元263年，魏晋时的数学家刘徽首创了“割圆术”请同学们观察下面两个图并体会圆内正多边形的边数越多，其周长和面积就越接近圆的周长和面积．下面我们采用这种思想方法研究匀加速直线运动的速度一时间图象．一物体做匀变速直线运动的速度一时间图象，如图甲所示．我们模仿刘徽的“割圆术”做法，来“分割”图象中图线与初、末时刻线和时间轴图线所围成的面积．请大家讨论．探究1：我们先把物体的运动分成5个小段，例如t/5算一个小段，在v—t图象中，每小段起始时刻物体的瞬时速度由相应的纵坐标表示(如图乙)．各小段中物体的位移可以近似地怎么表示？整个过程中的位移可以近似地怎么表示？探究2：我们是把物体的运动分成了10个小段结果这怎样呢？探究3：请大家想想当它们分成的小段数目越长条矩形与倾斜直线间所夹的小三角形面积越小．这说明什么?为了精确一些，我们可以怎么做？可以想象，如果把整个运动过程划分得非常非常细，很多很多小矩形的面积之和，就能准确地代表物体的位移了．这时，“很多很多”小矩形顶端的“锯齿形”就看不出来了，这些小矩形合在一起组成了一个梯形OABC，梯形OABC的面积就代表做匀变速直线运动物体在0(此时速度是v0)到t(此时速度是v)这段时间内的位移．在图丁中，v—t图象中直线下面的梯形OABC的面积怎么计算？你能推导出x＝v o t+at2/2吗？在匀变速直线运动中平均速度v平＝（v0＋v）/2，你也能推导出来吗？课堂检测1、一辆汽车以1 m／s2的加速度行驶了12s，驶过了180m．汽车开始加速时的速度是多少?认真审题，弄清题意后你能用自己的语言将题目所给的物理情景描述出来吗？你能确定研究的对象和研究的过程吗？你能画物理过程示意图，并把已知待求量在图上标出来吗？试着自己写出这题的解体题过程？2、在平直公路上，一汽车以15m／s的速度做匀速直线运动，从某时刻开始刹车，在阻力作用下，汽车以2 m／s2的加速度做匀减速直线运动，问刹车后5s末、10s末车离开始刹车点各为多远?【达标检测】(A级) 1．某质点的位移随时间的变化关系式为x=4t+2t2，x与t的单位分别是米与秒，则质点的初速度与加速度分别是（）A ．4m/s 与2m/s 2B ．0与4m/s 2C ．4m/s 与4m/s 2D ．4m/s 与0(B 级)2．根据匀变速运动的位移公式2/20at t v x +=和t v x =，则做匀加速直线运动的物体，在 t 秒内的位移说法正确的是（ ）A ．加速度大的物体位移大B ．初速度大的物体位移大C ．末速度大的物体位移大D ．平均速度大的物体位移大 (C 级)3、做初速度为零的匀加速直线运动的物体，前一秒、前二秒、前三秒的位移之比是（ ） 第一秒、第二秒、第三秒的位移之比又是（ ）A. 1：2：4B. 1：4：9C. 1：3：5D. 1：2：3 (B 级) 4、一火车以2 m/s 的初速度，0.5 m/s 2的加速度做匀加速直线运动，求： （1）火车在第3 s 末的速度是多少？ （2）在前4 s 的平均速度是多少？ （3）在第5 s 内的位移是多少？ （4）在第2个4 s 内的位移是多少？(B 级)5．以10m/s 的速度行驶的汽车关闭油门后后做匀减速运动，经过6s 停下来，求汽车刹车后的位移大小。

2.3匀变速直线运动的位移与时间的关系导学案年级：班级：使用人：学习目标1.知道匀速直线运动的位移与v-t图像中矩形面积的对应关系；2.知道匀变速直线运动的位移与v-t图像中四边形面积的对应关系；3.理解位移公式的意义和导出过程；4.能运用位移公式、匀变速直线运动的v-t图像解决有关问题，掌握匀变速直线运动x-t图像的特点，会用它解决简单的问题；5. 会用atvv+=0和2021atvx+=推导位移和速度的关系公式222tv v ax-=.学习重难点重点：微元法推导位移时间关系式，以及会用2021atvx+=及图像解决简单问题.难点：用atvv+=0和2021atvx+=推导位移和速度的关系公式222tv v ax-=.导学流程“导”知识要点一：匀变速直线运动的位移.对于匀速直线运动，其速度大小为v，经历时间t，位移大小为多少？在x-t图中，如何表示他的位移x？“思”“议”“展”x=vt1．做匀速直线运动的物体，其位移公式为___________，其v-t 图象为__________.在v-t 图象中某段时间内位移的大小与____________相等.2．匀变速直线运动的v-t 图象是________________，其中图象的斜率表示物体的__________，图象与坐标轴所围面积是物体的______________.“导”怎样利用v-t图求解匀变速直线运动的位移？将运动进行分割，在很短时间（Δt ）内，将变速直线运动近似为匀速直线运动，利用x=vt 计算每一段的位移，各段位移之和即为变速运动的位移.将复杂问题抽象成一个我们熟悉的简单模型，利用这个模型的规律进行近似研究,能得到接近真实值的研究结果.这是物理思想方法之一.“思”“议”“展”02t v v x t += 将运动分成等时的段， 即Δt 取得很小进行研究。

且取Δt 的初速度研究。

1.位移公式2. 对位移公式的理解:（1）反映了位移随时间的变化规律.（2）因为v0、a、x均为矢量，使用公式时应先规定.（一般以v0的方向为正方向）若物体做匀加速运动,a取,若物体做匀减速运动,则a取. （3）若v0=0,则x= .（4）特别提醒:t是指物体运动的实际时间,要将位移与发生这段位移的时间对应起来. （5）代入数据时,各物理量的单位要统一.(用国际单位制中的主单位).“导”知识要点二：速度与位移的关系“思”“议”“展”1.反映了位移速度之间的关系.2.因为v0、a、x均为矢量，使用公式时应先规定.（一般以v0的方向为正方向）若物体做匀加速运动,a取,若物体做匀减速运动,则a取.“讲”针对知识要点一、二知识点做相应讲解.。

匀变速直线运动地位移与时间关系教案课题匀变速直线运动地位移与时间关系课时2课时（第1课时）课型探究型教具PPT课件、坐标纸、铅笔教材普通高中课程标准实验教科书《物理》必修第一章第三节教学目标一、知识目标：1.知道匀速直线运动地位移和时间关系.2.理解匀变速直线运动地位移与时间关系及其应用.3.理解v-t图象中图线与t轴所夹地面积.二、能力目标1.通过近似推导位移地过程体验微元法地特点和技巧.2.应用s-t图分析物理现象，培养学生分析解决实际问题地能力、一些数学方法地应用.三、情感目标经历观察、实验、合作探究等学习活动，培养尊重客观事实，实事求是地科学态度和团结协作地科学精神.教学手段教学重难点采用探究式教学方法：根据生活经验提出问题进行，实例分析、类比、讨论、验证猜想与假设，归纳总结得出科学结论.教学重点：理解匀变速直线运动地位移与时间关系及其应用教学难点：1.v-t图象中图线与t轴所夹地面积2.微元法地特点和技巧教学过程教学内容及教师活动学生活动引入新课新课①取运动初始时刻地位置为坐标原点，写出t时间内位移与时间地关系及匀速直线运动地v-t图像.②匀变速直线运动地位移可以用v-t图中所夹地面积来表示，那么匀变速直线运动是否也有类似情况呢？接下来就来讨论.一、匀变速直线运动地位移讨论课本地“思考与讨论”思考讨论x=vt学生参与动手在做标纸上画出图像.学生思考讨论回答：学生A计算中时间间隔越小计算出地误差就越小越接近真值微元法：先微分后累加无限分割逐渐逼近学生在纸上画出初速度V地匀变速直线运动地v-t图，分析图线与时间轴所夹面积是否它地位移.老师分析讲解（无限分割逐渐逼近）1.定义：V-t图像中图像与t轴所夹面积表示t时间内物体匀变速直线运动地位移二、匀变速直线运动地位移与时间公式根据图2.3-2d图试着推导出位移与时间关系适用范围i.仅适用匀变速直线运动；ii、x、v、a都是矢量，用事要选取统一正方向学生：作图分组讨论（也可参照图2.3-2）学生：推导讨论，梯形面积公式X=vt+1/2at²时间与位移地图像叫s-t图运用初中二次函数，可以画出X=vt+1/2at²地s-t图其中v,a是常数.三、匀变速直线运动位移时间公式应用学生阅读书p42地例题，运用位移公式对它进行分析（先不看解析，独立思考）一辆汽车以1m/s地加速度加速行驶了12s，驶过了180M.汽车开始加速时地速度是多少？老师引导解答……实例探究火车沿平直轨道匀加速前进通过某一路标时v=10.8m/s,一分钟后变成火车地54km/h.再经一段时间，火车地速度达到64.8km/h.求所述过程中火车地位移是多少？画图是抛物线在纸上计算V.=9m/s学生自我练习检测发现问题板书设计1.3匀变速直线运动地位移与时间一、匀变速直线运动地位移1、定义：V-t图像中图像与t轴所夹面积表示t时间内物体匀变速直线运动地位移二、匀变速直线运动地位移与时间公式X=vt+1/2at²I．仅适用匀变速直线运动；Ii、 x、v、a都是矢量，用事要选取；三、匀变速直线运动位移时间公式应用---实例探究教学反思通过本课地学习，学生能独自主解释许多物理现象及知识.可以解决本节课地重点、难点问题.有利于培养学生学习物理地兴趣，有利于培养学生地物理思维能力.版权申明本文部分内容，包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some parts, including text, pictures,and design. Copyright is personal ownership.b5E2R。

贺龙中学高一物理导学案编制时间：2013-10-14 编制人：陈守文审定人：编号：005§2.3《匀变速直线运动的位移与时间的关系》（2课时）班级：___________组名：___________姓名：___________【学习目标】1、知道匀速直线运动的位移与v t-图像中矩形面积的对应关系。

2、知道匀变速直线运动的位移与v t-图像中的面积的对应关系。

3、了解匀变速直线运动的位移公式的推导方法,理解匀变速直线运动的位移与时间的关系,会应用此关系分析和计算。

【重点难点】1、正确理解匀变速直线运动的位移与v t-图像中的面积的对应关系。

2、探究匀变速直线运动的位移与时间的关系。

【学法指导】1、精读教材，并用红色笔标注重点，完成学案，时间不得少于30分钟。

2、根据完成学案中存在的问题进行教材的二次阅读。

3、记下自学中的发现和疑惑，便于在课堂中分享和讨论解决。

【自主学习】一、知识链接二、基础知识梳理1、匀速直线运动的位移（1）公式：；（2）图象表达：v—t图象与时间轴围成的图形。

2、匀变速直线运动的位移（1）公式：。

其中，v0为时刻的速度，t为运动时间。

若v0=0,则公式为.在v－t图象中，位移对应．任何直线运动(包括非匀变速直线运动)的位移都可以在其v－t图象中用图线与时间轴所围成的面积表示．【合作探究】（小组讨论全班交流）探究一：匀速直线运动的位移∆，建立怎样坐标系时能将t∆变为t、x∆问题1、做匀速直线运动的物体在时间t∆内的位移为x变为x？问题2、下图像中的的v×t数学意义是什么？物理意义呢？匀速直线运动的位移与它的v t-图像有什么关系？猜想一下：匀变速直线运动是否也有类似的位移与面积的对应关系？探究二：匀变速直线运动的位移问题1、教材第37页的“思考与讨论”中学生A估算实验中小车从位置0到位置5的位移比实际值小。

一个同学c仿照图2.3-1的方法画出了v t-图像且指出各矩形面积之和即为小车从位置00.3 0.63 1.11 0.88 1.38 1.62 v /(m.s -1)0.1 0.4 0.5 0.2 t /s0.38 到位置5的位移，这样的计算结果还是比实际值小，你能找出比实际值小的部分是图像中的那一部分吗？你认为怎样选取时间间隔才能减小误差？问题2、物体以初速度0v 做匀加速运动直线运动的v t -图像如下，从图像上怎样求物体在时间t 内的位移？写出关系式。