简单迭代法

简单迭代法解方程例题
简单迭代法是一种求解方程的数值方法，它通过逐步逼近的方式求得方程的近似解。

本文将介绍一个具体的例题，并使用简单迭代法来解决。

假设我们要解如下方程：
x = e^(-x)
我们的目标是找到方程的解x。

首先，我们可以将方程改写成迭代格式：
x_{n+1} = e^(-x_n)
其中，x_n表示第n次迭代的近似解，x_{n+1}表示下一次迭代的近似解。

现在，我们需要选择一个初始值x_0作为起始点。

通常情况下，可以选择一个离方程解比较接近的初始值，这样可以加快收敛速度。

在本例中，我们选择x_0 = 0作为初始值。

接下来，我们按照迭代格式进行迭代计算，直到满足收敛条件。

在本例中，我们可以选择迭代次数达到一定的值，或者判断两次迭代之间的差值是否小于一个给定的容差。

具体的迭代计算如下：
x_1 = e^(-x_0)
x_2 = e^(-x_1)
...
x_n = e^(-x_{n-1})
在每一次迭代中，我们将得到一个新的近似解x_n。

我们可以继续进行迭代计算，直到满足收敛条件。

需要注意的是，简单迭代法并不保证能够得到方程的解。

有些方程可能不满足迭代过程的收敛条件，或者方程可能有多个解，而简单迭代法只能找到其中一个解。

总而言之，简单迭代法是一种简单但有效的数值方法，可以用于求解一些方程的近似解。

通过选择合适的初始值和收敛条件，我们可以得到方程的一个近似解。

然而，需要注意的是并不是所有方程都适合使用简单迭代法进行求解，有些方程可能需要使用其他更复杂的方法。

c语言迭代法自洽计算简单举例迭代法是一种常用的数值计算方法，特别适用于需要反复迭代求解的问题。

在C语言中，我们可以通过循环来实现迭代计算。

下面我将列举10个简单的例子，来说明如何使用C语言迭代法进行自洽计算。

1. 求解平方根：假设我们需要计算一个数的平方根，可以使用迭代法来逼近平方根的值。

我们可以从一个初始值开始，通过不断迭代计算来逼近平方根的真实值。

2. 求解方程的根：对于一元方程 f(x) = 0，我们可以使用迭代法来求解方程的根。

通过不断迭代计算，我们可以逼近方程的根的值。

3. 计算圆周率：圆周率是一个无理数，它的值可以使用迭代法进行计算。

通过不断迭代计算，我们可以逼近圆周率的真实值。

4. 计算斐波那契数列：斐波那契数列是一个经典的数列，可以使用迭代法来计算。

通过不断迭代计算，我们可以得到斐波那契数列的前n个数。

5. 计算阶乘：阶乘是一个常见的数学运算，可以使用迭代法来计算。

通过不断迭代计算，我们可以得到给定数的阶乘值。

6. 求解最大公约数：最大公约数是两个数的公共因子中最大的一个，可以使用迭代法来求解。

通过不断迭代计算，我们可以得到两个数的最大公约数。

7. 求解矩阵乘法：矩阵乘法是一种常见的数学运算，可以使用迭代法来计算。

通过不断迭代计算，我们可以得到两个矩阵的乘积。

8. 求解线性方程组：线性方程组是一组线性方程的集合，可以使用迭代法来求解。

通过不断迭代计算，我们可以得到线性方程组的解。

9. 进行排序算法：排序算法是一种常见的算法，可以使用迭代法来实现。

通过不断迭代计算，我们可以将一组数据按照一定的规则进行排序。

10. 进行图像处理：图像处理是一种常见的应用领域，可以使用迭代法来实现。

通过不断迭代计算，我们可以对图像进行增强、滤波等操作。

以上是我列举的10个使用C语言迭代法进行自洽计算的简单例子。

通过这些例子，我们可以看到迭代法在数值计算中的广泛应用。

希望这些例子能够帮助你更好地理解和应用迭代法。

简单迭代法求方程的根1. 引言简单迭代法是一种常用的求解非线性方程根的方法。

它基于方程的连续性和局部斜率连续的性质，通过迭代逼近方程的根。

在本文中，我们将详细介绍简单迭代法的原理和步骤，并使用MATLAB编写代码来解决方程求根问题。

2. 简单迭代法原理简单迭代法的基本思想是，将非线性方程转化为迭代形式，通过不断迭代逼近方程的根。

其原理基于不动点定理，即给定一个函数f(x)，若存在一个不动点x∗，满足x∗=f(x∗)，则迭代过程x k+1=f(x k)中的序列x k将收敛到x∗。

对于求解方程f(x)=0的问题，我们可以将其转化为x=g(x)的形式，其中g(x)= x−f(x)，且f′(x)不等于0。

这样，我们可以通过迭代逼近x=g(x)的根，从而得f′(x)到原方程的解。

3. 简单迭代法步骤简单迭代法的步骤如下：3.1 选择初始点选择一个合适的初始点x0作为迭代的起点。

3.2 迭代计算根据迭代公式x k+1=g(x k)，计算序列x k的下一个值。

3.3 判断终止条件根据预设的终止条件，判断是否满足终止条件。

常用的终止条件包括： - 迭代次数达到预设的最大值。

- 迭代过程中下一个值与当前值之差小于预设的精度。

3.4 输出结果当满足终止条件时，输出最终的逼近根的值。

4. 简单迭代法在MATLAB中的实现以下是简单迭代法在MATLAB中的实现代码：function root = simple_iter_method(f, g, x0, max_iter, precision) % f: 原方程% g: 迭代函数% x0: 初始点% max_iter: 最大迭代次数% precision: 精度x = x0;iter = 0;while iter < max_iterx_next = feval(g, x); % 使用feval函数计算迭代值if abs(x_next - x) < precisionroot = x_next;return;endx = x_next;iter = iter + 1;enderror('达到最大迭代次数，未找到合适的解');end5. 示例与应用5.1 示例：求解方程x2−3x+2=0。

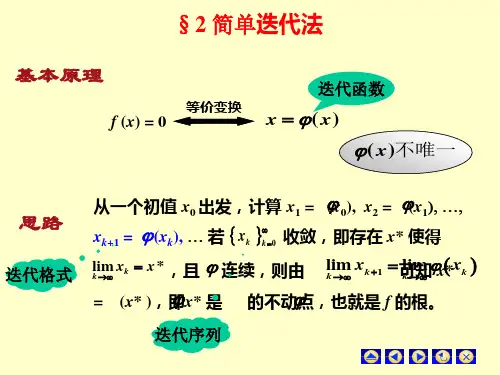
§2简单迭代法——不动点迭代(iterate)迭代法是数值计算中的一类典型方法，被用于数值计算的各方面中。

一、简单迭代法设方程f(x)=0 (3)在[a,b]区间内有一个根*x ，把(3)式写成一个等价的隐式方程x=g(x) (4)方程的根*x 代入(4)中，则有)(**=x g x (5)称*x 为ｇ的不动点（在映射ｇ下，象保持不变的点），方程求根的问题就转化为求(5)式的不动点的问题。

由于方程(4)是隐式的，无法直接得出它的根。

可采用一种逐步显式化的过程来逐次逼近，即从某个[a,b]内的猜测值0x 出发，将其代入(4)式右端，可求得)(01x g x =再以1x 为猜测值，进一步得到)(12x g x =重复上述过程，用递推关系——简单迭代公式求得序列}{k x 。

如果当k →∞时*→x x k ,}{k x 就是逼近不动点的近似解序列，称为迭代序列。

称(6)式为迭代格式，g(x)为迭代函数，而用迭代格式(6)求得方程不动点的方法，称为简单迭代法，当*∞→=x x k k lim 时，称为迭代收敛。

构造迭代函数g(x)的方法：(1)=x a x x -+2，或更一般地，对某个)(,02a x c x x c -+=≠；(2)x a x /=； (3))(21xa x x +=。

取a=3,0x =2及根*x =1.732051，给出三种情形的数值计算结果见表表 032=-x 的迭代例子问题：如何构造g(x)，才能使迭代序列}{k x 一定收敛于不动点？误差怎样估计？通常通过对迭代序列}{k x 的收敛性进行分析，找出g(x)应满足的条件，从而建立一个一般理论，可解决上述问题。

二、迭代法的收敛性设迭代格式为),2,1,0()(1 ==+k x g x k k而且序列}{k x 收敛于不动点*x ，即∞→→-*k x x k (0时）因而有)3,2,1(1 =-≤-*-*k xx x x k k (7)由于),(),)((11*-*-*∈-'=-x x x x g x x k k k ξξ当g(x)满足中值定理条件时有),(),)((11*-*-*∈-'=-x x x x g x x k k k ξξ (8)注意到(8)式中只要1)(<<'L g ξ时，(7)式成立.经过上述分析知道,迭代序列的收敛性与g(x)的构造相关,只要再保证迭代值全落在[a,b]内，便得：假定迭代函数g(x)满足条件(1) 映内性：对任意x ∈[a,b]时，有a ≤g(x) ≤b ；(2) 压缩性：g(x)在[a,b]上可导，且存在正数Ｌ<1，使对任意 x ∈[a,b]，有L x g <')( （9）则迭代格式)(1k k x g x =+对于任意初值0x ∈[a,b]均收敛于方程x=g(x)的根，并有误差估计式011x x LL x x kk --≤-*（10）证明 ：收敛性是显然的。

一、引言在数学建模和计算机编程中，简单迭代法是一种常用的求解方程近似解的方法。

其原理是通过不断迭代计算，逼近实际的解。

在Matlab 编程中，简单迭代法也是一种常见的应用。

本文将介绍简单迭代法的原理，并给出在Matlab中实现简单迭代法的例题程序。

二、简单迭代法原理1. 简单迭代法的基本思想是将需要求解的方程转化为迭代形式，即 x = g(x)，然后通过不断迭代计算得到方程的近似解。

2. 简单迭代法的收敛条件是 |g'(x)| < 1，即迭代函数的导数的绝对值小于1时，迭代过程才能收敛。

3. 简单迭代法的收敛速度取决于迭代函数的选择，通常可以通过调整迭代函数来提高收敛速度。

三、Matlab中的简单迭代法实现在Matlab中，可以通过编写脚本文件来实现简单迭代法。

下面给出一个简单的例题：求解方程 x^2 - 3x + 2 = 0 的近似解。

4. 以下是Matlab中实现简单迭代法的脚本文件示例：```matlab定义迭代函数g = (x) 3*x - x^2;设置迭代初值和迭代次数x0 = 0.5;N = 100;迭代计算for k = 1:Nx = g(x0);fprintf('第d次迭代，近似解为：.10f\n', k, x);if abs(x - x0) < 1e-8 判断迭代是否收敛break;endx0 = x;end```5. 通过运行上述脚本文件，即可得到方程 x^2 - 3x + 2 = 0 的近似解。

四、实例分析通过上述例题程序的运行结果可以看出，简单迭代法在Matlab中的实现比较简单直观。

但是需要注意的是，迭代函数的选择和迭代初值的设定对最终的近似解都会产生影响，需要经过一定的调试和优化。

五、总结简单迭代法是一种常用的求解方程近似解的方法，在Matlab编程中也有着广泛的应用。

通过本文的介绍和示例程序，相信读者已经对简单迭代法在Matlab中的实现有了更深入的了解。

x=e^x用简单迭代法matlab篇一：在MATLAB中,我们可以使用简单迭代法来求解函数`f(x) = e^x`的导数`f"(x)`,即`f"(x) = e^x - 1`.下面是一个简单的迭代公式:```x0 = 0;for i = 1:1000x = x0 + (x - x0) / (i - 1);end```这个迭代公式使用了一个递归算法,每次将当前`x`值减去上一个`x`值,并除以迭代次数`i - 1`,直到迭代次数达到1000为止。

在每次迭代中,`x`值都会增加`e^x`的值,因此`f"(x)`的值也会增加`e^x - 1`的值。

我们可以通过计算`f"(x)`的值来得到`e^x`在`x`处的导数。

下面是MATLAB代码来求解`f"(x)`:```x = 0:0.1:10;f = e^x;f" = f";```在这个例子中,我们使用一个长度为10的`x`列表来求解`f"(x)`,并将结果保存到变量`f"`中。

使用这个迭代公式和`f"`的值,我们可以计算`e^x`在`x`处的导数,即`f(x)`的斜率。

这个斜率可以用来进行加速收敛的迭代计算,例如在优化问题中。

下面是MATLAB代码来计算`e^x`在`x`处的导数:```x = 0:0.1:10;f = e^x;f" = @(x) f"(x);```这个代码定义了一个函数`f"`,它使用迭代公式和`f`的值来计算`f"(x)`的值。

这个函数会使用一个循环来迭代`x`的值,并计算`f"(x)`的值。

这样,我们就可以使用这个函数来加速收敛,并得到更快的迭代结果。

总的来说,简单迭代法是一种常用的方法来求解函数的导数,特别是在数值计算中。

它简单易行,但收敛速度可能较慢,需要根据具体情况进行调整。

篇二：在本文中,我们将介绍如何使用简单迭代法在 MATLAB 中计算圆周率的近似值。

简单迭代法
简单迭代法是一种常用的数值计算方法，通常用于求解方程的近似解。

它是一种基于迭代的算法，通过不断逼近方程的解来得到一个足够精确的近似解。

在实际应用中，简单迭代法的可靠性、效率和实用性都得到了广泛的认可和应用。

简单迭代法最常用的形式是不动点迭代法，其基本思路是通过将方程的解表示为函数的不动点来进行迭代。

具体实现方法是，从一个起始点开始，将该点代入函数计算，得到一个新的点，然后将新的点再代入函数中计算，这样不断进行下去，直到得到一个满足要求的近似解为止。

在实际应用中，简单迭代法的使用需要一定的条件限制，如函数必须具有连续性和单调性等等。

此外，迭代过程的收敛性也是需要关注的一个重要问题。

一般而言，只有当函数的导数小于1时，才能保证迭代的收敛性。

因此，在使用简单迭代法求解方程时，需要对函数的特性进行仔细的分析和评估，以确保迭代过程的有效性和准确性。

简单迭代法在实际应用中具有广泛的用途和应用场景。

例如，在工程设计中，可以利用简单迭代法对复杂的函数进行求解，以确定合适的参数和方案。

此外，在金融领域、物流领域和医疗领域等领域，简单迭代法也被广泛应用于问题求解和决策分析中。

总之，简单迭代法作为一种常用的数值计算方法，为我们解决实际问题和提高工作效率提供了有力的支持和保障。

在今后的工作中，
我们应注重加强对简单迭代法的学习和应用，进一步挖掘其潜力和价值，为推动科技进步和社会发展做出更大的贡献。

简单迭代法求方程的根matlab一、简介简单迭代法，又称为逐次逼近法或枚举法，是求解非线性方程的一种重要方法。

其基本思想是将原方程转化为等价的形式，然后通过不断迭代逼近方程的根。

在MATLAB中，可以通过编写程序来实现简单迭代法求解方程的根。

二、算法原理设非线性方程f(x)=0有一个实根α，将f(x)在α处进行泰勒展开，则有：f(x)=f(α)+(x-α)f'(α)+O((x-α)^2)其中O((x-α)^2)表示高阶无穷小。

由于f(α)=0，因此上式可化为：f(x)=(x-α)f'(α)+O((x-α)^2)移项得到：x=α-f(x)/f'(a)这就是简单迭代法的基本公式。

显然，如果从一个初始值x0开始，不断使用公式进行迭代，则可以逐步逼近方程的根。

三、MATLAB程序设计1. 设定初始值和误差限制我们首先需要确定初始值x0和误差限制epsilon。

其中epsilon通常取较小的值（如10^-6），用于控制计算精度。

在MATLAB中可以编写如下代码：clc;format long; % 设置输出精度% 设定初始值和误差限制x0 = 1; % 初始值epsilon = 1e-6; % 误差限制2. 编写迭代公式根据简单迭代法的基本公式，我们可以编写一个函数来进行迭代计算。

假设要求解方程x^2-3=0的根，可以编写如下代码：function y = f(x)y = x^2 - 3;endfunction y = g(x)y = 2*x;end% 简单迭代法求解方程x^2-3=0的根x0 = 1; % 初始值epsilon = 1e-6; % 误差限制nmax = 100; % 最大迭代次数for n = 1:nmaxx1 = x0 - f(x0)/g(x0);if abs(x1-x0) < epsilon % 判断是否满足精度要求break;x0 = x1;endfprintf('方程的根为：%f\n', x1);在上面的代码中，我们使用了两个函数f和g来分别表示原方程和其导数。

迭代法简单举例
嘿，朋友们！今天咱来唠唠迭代法，这可真是个超有趣的东西呢！
比如说，咱就想想减肥这件事儿吧。

你瞧，一开始你给自己定了个目标，要减掉多少斤。

那第一步，你可能就会试着少吃一点，多运动一点，就像在黑暗中摸索着前进。

然后你看看效果，哎呀，可能没减多少。

但这时候你不会放弃呀，你会根据这个情况调整策略，比如再少吃点其他的，或者增加一些运动的种类。

这就好像迭代法一样，一次次地尝试，一点点地改进。

这不就是在不断地迭代嘛！
再比如学一门新语言，你一开始可能只会说几个简单的单词和句子，但随着你不断地学习、练习，和别人交流，你会发现自己越来越熟练，能表达的东西越来越多。

每次的进步都能让你更有信心，更愿意去继续提升。

这就是迭代的魔力啊！
你想想，生活中好多事情不都是这样嘛！就像搭积木，一开始可能搭得歪歪扭扭，但你不断调整，一块一块地加，最后就能搭出漂亮的城堡呀！
迭代法就像是人生的指南针，指引着我们不断前进，变得更好。

每次的尝试虽然不一定完美，但都是向成功迈进的一步啊！不要害怕失败，因为每
一次失败都是下一次成功的开始。

咱们要勇敢地去尝试，不断地去迭代，让自己的生活变得丰富多彩，超级精彩！这不就是迭代法的魅力所在嘛！所以呀，大家都行动起来，在生活的各个方面运用迭代法，迈向更美好的未来吧！。