数值分析第三章 线性方程组的迭代法

数值分析第三章线性方程组解法在数值分析中，线性方程组解法是一个重要的主题。

线性方程组是由一组线性方程组成的方程组，其中未知数的次数只为一次。

线性方程组的解法包括直接解法和迭代解法两种方法。

一、直接解法1.1矩阵消元法矩阵消元法是求解线性方程组的一种常用方法。

这种方法将方程组转化为上三角矩阵，然后通过回代求解得到方程组的解。

1.2LU分解法LU分解法是将系数矩阵A分解为一个下三角矩阵L和一个上三角矩阵U的乘积，然后通过解两个三角方程组求解线性方程组。

这种方法可以减少计算量，提高计算效率。

1.3 Cholesky分解法Cholesky分解法是对称正定矩阵进行分解的一种方法。

它将系数矩阵A分解为一个下三角矩阵L和它的转置的乘积，然后通过解两个三角方程组求解线性方程组。

Cholesky分解法适用于对称正定矩阵的求解，具有较高的精度和稳定性。

二、迭代解法2.1 Jacobi迭代法Jacobi迭代法是一种迭代求解线性方程组的方法。

它通过分解系数矩阵A为一个对角矩阵D和一个余项矩阵R，然后通过迭代更新未知数的值，直至达到一定精度要求为止。

Jacobi迭代法简单易懂，容易实现，但收敛速度较慢。

2.2 Gauss-Seidel迭代法Gauss-Seidel迭代法是一种改进的Jacobi迭代法。

它通过使用新计算出的未知数值代替旧的未知数值，达到加快收敛速度的目的。

Gauss-Seidel迭代法是一种逐步逼近法，每次更新的未知数值都会被用于下一次的计算，因此收敛速度较快。

2.3SOR迭代法SOR迭代法是一种相对于Jacobi和Gauss-Seidel迭代法更加快速的方法。

它引入了一个松弛因子，可以根据迭代的结果动态地调整未知数的值。

SOR迭代法在理论上可以收敛到线性方程组的解，而且收敛速度相对较快。

三、总结线性方程组解法是数值分析中的一个重要内容。

直接解法包括矩阵消元法、LU分解法和Cholesky分解法，可以得到线性方程组的精确解。

数值分析第三章线性方程组迭代法线性方程组是数值分析中的重要问题之一，涉及求解线性方程组的迭代法也是该领域的研究重点之一、本文将对线性方程组迭代法进行深入探讨。

线性方程组的一般形式为AX=b，其中A是一个n×n的系数矩阵，x和b是n维向量。

许多实际问题，如电路分析、结构力学、物理模拟等，都可以归结为求解线性方程组的问题。

然而，当n很大时，直接求解线性方程组的方法计算量很大，效率低下。

因此，我们需要寻找一种更高效的方法来求解线性方程组。

线性方程组迭代法是一种基于迭代思想的求解线性方程组的方法。

其基本思想是通过构造一个序列{xn}，使得序列中的每一项都逼近解向量x。

通过不断迭代，可以最终得到解向量x的一个近似解。

常用的线性方程组迭代法有雅可比迭代法、高斯-赛德尔迭代法和逐次超松弛迭代法等。

雅可比迭代法是其中的一种较为简单的迭代法。

其基本思想是通过分解系数矩阵A，将线性方程组AX=b转化为x=Tx+c的形式，其中T是一个与A有关的矩阵，c是一个常向量。

然后，通过不断迭代，生成序列xn，并使序列中的每一项都逼近解向量x。

高斯-赛德尔迭代法是雅可比迭代法的改进方法。

其核心思想是利用当前迭代步骤中已经求得的近似解向量的信息。

具体而言，每次迭代时，将前一次迭代得到的近似解向量中已经计算过的分量纳入计算，以加速收敛速度。

相比于雅可比迭代法，高斯-赛德尔迭代法的收敛速度更快。

逐次超松弛迭代法是高斯-赛德尔迭代法的改进方法。

其核心思想在于通过引入一个松弛因子ω，将高斯-赛德尔迭代法中的每次迭代变为x[k+1]=x[k]+ω(d[k+1]-x[k])的形式，其中d[k+1]是每次迭代计算得到的近似解向量的一个更新。

逐次超松弛迭代法可以根据问题的特点调整松弛因子的值，以获得更好的收敛性。

除了以上提到的三种迭代法，还有一些其他的线性方程组迭代法，如SOR迭代法、共轭梯度法等。

这些方法都具有不同的特点和适用范围，可以根据问题的具体情况选择合适的迭代法。

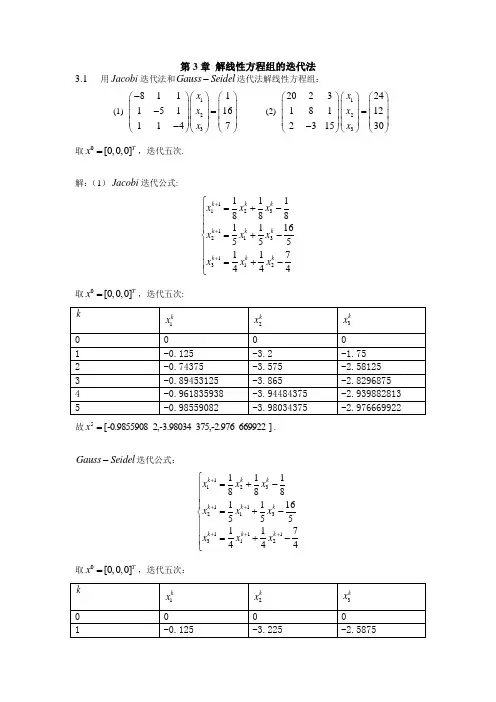
第3章 解线性方程组的迭代法3.1 用Jacobi 迭代法和Gauss Seidel -迭代法解线性方程组：(1)1238111151161147x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭(2)12320232418112231530x x x ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭取0[0,0,0]Tx =，迭代五次.解：（1）Jacobi 迭代公式:⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=-+=-+=+++4741415165151818181211331123211k k k k k k k k k x x x x x x x x x取0[0,0,0]Tx =，迭代五次:kk x 1k x 2 kx 30 01 -0.125 -3.2 -1.75 2 -0.74375 -3.575 -2.581253 -0.89453125 -3.865-2.8296875 4 -0.961835938 -3.94484375 -2.939882813 5 -0.98559082-3.98034375 -2.976669922故]669922375,-2.9762,-3.98034-0.9855908[5=x .Gauss Seidel -迭代公式：⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=-+=-+=++++++4741415165151818181121113311123211k k k k k k k k k x x x x x x x x x 取0[0,0,0]Tx =，迭代五次：kk x 1 k x 2 kx 31 -0.125-3.225 -2.58752 -0.8515625 -3.8878125 -2.934843753 -0.977832031 -3.982535156 -2.9900917974 -0.996578369 -3.997334033 -2.998478101 5-0.999476517 -3.999590923 -2.99976686故]997668690923,-2.917,-3.9995-0.9994765[5=x（2）Jacobi 迭代公式:⎪⎪⎪⎩⎪⎪⎪⎨⎧++-=+--=+--=+++25115223818156203101211331123211k k k k k k k k k x x x x x x x x x 取0[0,0,0]Tx =，迭代五次:kk x 1 k x 2 kx 30 0 1 1.2 1.5 2 2 0.75 1.12.14 3 0.769 1.13875 2.124 0.768125 1.138875 2.125216667 5 0.767331.1383322922.125358333故]32.12535833138332292,0.76733,1.[5=x .Gauss Seidel -迭代公式：⎪⎪⎪⎩⎪⎪⎪⎨⎧++-=+--=+--=++++++25115223818156203101121113311123211k k k k k k k k k x x x x x x x x x 取0[0,0,0]Tx =，迭代五次：kk x 1 k x 2 kx 30 0 1 1.2 1.352.112 0.74851.14268752.12873753 0.766420625 1.138105234 2.12543163 4 0.767374732 1.138399205 2.12536321 50.767355598 1.138410149 2.12536795故]6795149,2.12538,1.1384100.76735559[5=x3.2 用Jacobi 迭代法解线性方程组123101091102702108x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪--= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭， 取初值向量0[0,0,0]Tx =，要求13||||10k k x x --∞-≤，并讨论方差的收敛性.解：Jacobi 迭代公式：⎪⎪⎪⎩⎪⎪⎪⎨⎧+=++=+=+++1081021071021011091012133112211k k k k k k k x x x x x x x取初值向量0[0,0,0]Tx =kk x 1 k x 2 kx 30 0 0 1 0.9 0.7 0.8 2 0.97 0.95 0.94 3 0.995 0.985 0.99 4 0.9985 0.9975 0.997 5 0.99975 0.99925 0.9995 6 0.9999250.999875 0.9998535610000625.0||-≤=-x x ，迭代6次后可以得到满足误差要求的解； ]99985.999875,0.0.999925,0[6=x ，Jacobi 迭代法收敛.3.3 社线性方程12311112211x x ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭讨论解该线性方程的Jacobi 迭代法和Gauss Seidel -迭代法的收敛性. 解：按Jacobi 迭代法展开：⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛=--=⎪⎪⎪⎭⎫ ⎝⎛-=010220022010111122111221U L D A(1) 对于Jacobi 迭代法，其迭代矩阵为：⎪⎪⎪⎭⎫⎝⎛-----=⎪⎪⎪⎭⎫ ⎝⎛-----⎪⎪⎪⎭⎫⎝⎛=+=--022101220022101220111)(11L U D B J J B 的特征矩阵为：3221122||λλλλλ=⎪⎪⎪⎭⎫⎝⎛-=-J B I 解得03,2,1=λ10)(<=J B ρ，故Jacobi 迭代法收敛.(2) 对Gauss Seidel -迭代法，其迭代矩阵为：⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫⎝⎛------=-=--200320220010220122111)(11U L D B G G B 的特征矩阵为：2)2(20032022||-=⎪⎪⎪⎭⎫⎝⎛---=-λλλλλλG B I 解得：01=λ，23,2=λ12)(>=G B ρ，故Gauss Seidel -迭代法发散.3.4 设线性方程组1122332313a x b a x b ⎢⎥⎢⎥⎢⎥-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦其中a 为参数，且0a ≠，试求a 的取值范围，使得解该线性方程组的Jacobi 迭代法收敛.解：按Jacobi 迭代法展开：⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛=--=⎪⎪⎪⎭⎫ ⎝⎛---=030120031020313212a a a U L D a a a AJacobi 迭代法，其迭代矩阵为：⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=+=-031302120313********)(1aaa a a a a aaU L D B J J B 的特征矩阵为：)14(313212||2a aaa a a aB I J +=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛---=-λλλλλλ 解得01=λ，i a 142=λ，当1|14||14|)(<==ai a B J ρ，即14||>a 时，Jacobi 迭代法收敛.3.5 用Gauss Seidel -迭代法解线性方程组123142*********x x x --⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 是否收敛？若不收敛，则能否改写成线性方程组，使得Gauss Seidel -迭代法收敛.解：（1）按Gauss Seidel -迭代法展开：⎪⎪⎪⎭⎫⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛-=--=⎪⎪⎪⎭⎫ ⎝⎛--=000240020040411420014241U L D A 对Gauss Seidel -迭代法，其迭代矩阵为⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛-=-=--480816024000024025.05.02014000000240420141)(11U L D B G G B 的特征矩阵为：)20(480816024||2-=⎪⎪⎪⎭⎫⎝⎛---=-λλλλλλG B I 120)(>=G B ρ,Gauss Seidel -迭代法发散.（2）将A 改写成严格对角占优矩阵，则Gauss Seidel -迭代法必收敛，比如：⎪⎪⎪⎭⎫ ⎝⎛=120014241C对Gauss Seidel -迭代法，其迭代矩阵为：⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫⎝⎛=-=--163208160240000240128014001000240120141)(11U L D B G G B 的特征矩阵为：316320816024||λλλλλ=⎪⎪⎪⎭⎫⎝⎛+--=-G B I 10)(<=G B ρ,Gauss Seidel -迭代法收敛.3.7 设迭代法f Bx x k k +=+1，,...)2,1,0(=k ，的迭代矩阵B 的谱半径()0B ρ=，试证明该迭代法最多迭代n 次便可得到方程组x Bx f =+的解*x ，即*n x x =.解：n 阶矩阵B 一定相似于它的若当标准型J ，即存在可逆矩阵P 使得1P BP J -=，因为()0B ρ=，故B 的特征值全为0，于是得：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=000 J 由此可知0n J =.x Bx f =+显然有唯一解*x ，即**x Bx f =+，又1**()k k x x B x x +-=-，于是()*2(2)*(0)*()()n n n x x B x x B x x --=-==-又因为1110n n P BP J B P JP B P J P ---=⇒=⇒==所以()*0n xx -=，即*n x x =.3.8 给定线性方程组Ax b =，其中323,121A b ⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦若用迭代法,...)1,0)((1=-+=+k b Ax x x k k k α，求解，问：（1） 实数取何值时该迭代法收敛；（2） 实数取何值时该迭代法收敛最快. 解：该迭代公式可改写为b x A I x k k αα-+=+)(1，其对应的迭代矩阵为：⎪⎪⎭⎫⎝⎛+++=+=ααααα21231A I B ， B 的特征矩阵为：)]1()][41([)21()2()31(||αλαλαλαααλλ+-+-=⎪⎪⎭⎫ ⎝⎛+--+-+-=-B I ， 解得αλ411+=，αλ+=12，41,0.4()max{|14|,|1|}1,0.4014,0,B ααραααααα--<-⎧⎪=++=+-<<⎨⎪+>⎩（1）1)(<B ρ，即⎩⎨⎧<+<+1|1|1|41|αα，解得021<<-α，该迭代法收敛.（2）在021<<-α上，当4.0-=α时，)(B ρ达到最小，该迭代法收敛最快.3.9 用SOR 迭代法解线性方程1233.21141 3.71 4.511 4.25x x x ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 取初始向量0[0,0,0]Tx =， 1.25ω=，迭代三次，并讨论其收敛性. 解：SOR 迭代公式：⎪⎪⎪⎩⎪⎪⎪⎨⎧--+-=--+-=--+-=++++++)5(2.4)1()5.4(7.3)1()4(2.3)1()1(2)1(1)(3)1(3)(3)1(1)(2)1(2)(3)(2)(1)1(1k k k k k k k k k k k k x x x x x x x x x x x x ϖϖϖϖϖϖ 取初始向量0[0,0,0]Tx =， 1.25ω=，迭代三次，kk x 1k x 2 kx 31 1.56250.992398649 0.727708736 2 0.499958053 0.857418315 0.902186992 3 0.7501646640.747688781 0.816758774]58774781,0.81674,0.7476880.75016466[)3(=x因A 为对称正定矩阵，10)(<=A ρ，SOR 迭代法必收敛.3.11 用SOR 迭代法解线性方程组123410114140143x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪--= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭其精确解*11[,1,]22Tx =-，分别取 1.03ω=，1ω=， 1.1ω=，要求当*5||||10kx x -∞-≤时迭代终止，并且对每一个ω值确定迭代次数. 解：用SOR 迭代公式：(1)()()112(1)()(1)()2213(1)()(1)332(1)[1]4(1)[4]4(1)[3]4k k k k k k k k k k x x x x x x x x x x ϖωϖωϖω+++++⎧=-++⎪⎪⎪=-+++⎨⎪⎪=-+-+⎪⎩(1) 取初值向量0[0,0,0]Tx =，当 1.03ω=时k错误!1kx2k x 3k x0 01 0.25751.09630625 -0.490201141 2 0.532073859 1.007893038 -0.498261509 3 0.501070241 1.000486458 -0.499926892 4 0.500093156 1.000028219 -0.499994927 5 0.500004472 1.000001611 -0.499999737 60.500000281 1.000000092 -0.4999999846*5||||0.00000028110x x -∞-=≤，迭代6次后得到满足精度要求的根：]999984092,-0.4991,1.0000000.50000028[6=x(2) 取初值向量0[0,0,0]Tx =，当1ω=时k错误!1kx2k x 3k x0 0 01 0.251.0625 -0.484375 2 0.515625 1.0078125 -0.498046875 3 0.501953125 1.000976563 -0.499755859 4 0.500244141 1.00012207 -0.499969482 5 0.500030518 1.000015259 -0.499996185 6 0.500003815 1.000001907 -0.499999523 70.500000477 1.000000238 -0.499999947*5||||0.00000047710x x -∞-=≤，迭代7次后得到满足精度要求的根：]99994238,-0.4997,1.0000000.50000047[7=x(3) 取初值向量0[0,0,0]Tx =，当 1.1ω=时k错误!1kx2k x 3k x0 010.275 1.175625 -0.5017031252 0.570796875 1.001438281 -0.499434163 0.49331584 0.998173634 -0.500558835 4 0.500166165 1.000074653 -0.499923587 5 0.500003913 1.000014624 -0.500003626 0.50000363 0.999998541 -0.5000000397 0.499999236 0.999999925 -0.5000000177*5||||0.00000076436110x x -∞-=≤，迭代7次后满足精度要求.3.12 考虑迭代法,...)1,0(1=+=+k f Bx x k k其中⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-=021212102121210B ，⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=21121f 证明：该迭代法收敛，取初始向量0[0,0,0]Tx =，计算4x . 证：B 的特征矩阵为3212121212121||λλλλλ=⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-----=-B I 0)(=B ρ，该迭代法收敛.该迭代法的迭代公式为：⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=++=--=+++21212112121212121211331123211k k k kk k k k k x x x x x x x x x 取初始向量0[0,0,0]Tx =，迭代四次：k错误!1kx2k x 3k x0 0 0 0 1 -0.5 1 -0.5 2 0.353553391 0.5 -0.353553391 3 0 1 0 40 1 0 故]0,1,0[)4( x。

数值分析课程实验报告实验名称 线性方程组的迭代解法Ax b =的系数矩阵对角线元素容许误差。

雅可比（Jacobi ）迭代法解方程组的算法描述如下：任取初始向量(0)(0)1(xx =1+，并且 1,2,...,n ，计算 11(ni j ii j ib a a =≠-∑()k x ，结束；否则执行④，则不收敛，终止程序；否则转② 迭代法的算法描述）迭代法中，如果当新的分量求出后，马上用它来代替旧的分量，则可能会更快地接近方程组的准确解。

基于这种设想构造的迭代公式,n ，k = （2）算法可相应地从雅可比（Jacobi ）迭代法改造得到(Gauss-Seidel)迭代得到的值进一()()()1((1k i ii k k i i x b a x x ωω==+-1,2,,n ，2,k =（3）为松弛因子（显然当1ω=塞德尔迭代公式） ()k ix 通常优于旧值(1)k ix -，在将两者加工成松弛值时，自然要求松弛因子1ω>，以尽量发挥新值的优势，这类迭代就称为逐次超松弛迭代法。

SOR 迭代的关键在于选取合适的松弛因子，松弛因子的取值对收敛速度影响很大，但如何选取最佳松弛因子的问题，至今仍未有效解决，在实际计算时，通常依据系数矩阵的特点，并结合以往的经验选取合适的松弛因子。

练习与思考题分析解答(0)(1,1,1,1)x =[ -0.999976, -0.999976, -0.999976, -0.999976]x =[ -0.99999, -0.999991, -0.999992, -0.999993]x =塞德尔迭代算法的收敛速度要比雅可比迭代算法的收敛速度快SOR 迭代实质上是高斯原理和基本方法相同。

如果选择合适的松弛因子，它能够加快收敛速度。

SOR 迭代算法更加普通，当选取一个合适的松弛因子后收敛速度明显加快。

迭代算法将前一步的结果[ -0.99999, -0.999991, -0.999992, -0.999993]x =[ -0.999992, -0.999993, -0.999994, -0.999995]x =[ -0.999993, -0.999994, -0.999995, -0.999995]x =[ -0.999992, -0.999993, -0.999994, -0.999995]x =[ -0.999999, -1.0, -1.0, -1.0]x =[ -0.999999, -1.0, -1.0, -1.0]x =因为为了保证迭代过程收敛，松弛因子1.3左右。

数值分析--第三章--迭代法迭代⼀般⽅程：本⽂实例⽅程组：⼀.jacobi迭代法从第i个⽅程组解出xi。

线性⽅程组Ax=b，先给定⼀组x的初始值，如[0,0,0]，第⼀次迭代，⽤x2=0，x3=0带⼊第⼀个式⼦得到x1的第⼀次迭代结果，⽤x1=0,x3=0,带⼊第⼆个式⼦得到x2的第⼀次迭代结果，⽤x1=0,x2=0带⼊第三个式⼦得到x3的第⼀次迭代结果。

得到第⼀次的x后，重复第⼀次的运算。

转化成⼀般的形式：（其中L是A的下三⾓部分，D是A的对⾓元素部分，U 是上三⾓部分）得到迭代公式：其中的矩阵B和向量f如何求得呢？其实，矩阵B的计算也很简单，就是每⾏的元素/该⾏上的对⾓元素⼆.Gauss-Seidel迭代法【收敛速度更快】这个可以和jacobi法对⽐进⾏理解，我们以第⼆次迭代为例（这⾥的第⼀次迭代结果都⽤⼀样的，懒得去换）从上表对⽐结果可以看出，Jacobi⽅法的第⼆次迭代的时候，都是从第⼀次迭代结果中，获取输⼊值。

上⼀次迭代结果[2.5,3.0,3.0]，将这个结果带⼊上⾯式⼦1，得到x1=2.88，；将[2.5,3.0,3.0]替换成[2.88,3.0,3.0]带⼊第⼆个式⼦的运算，这⾥得到x2=1.95，所以把[2.88,3.0,3.0]替换成[2.88,1.95,3.0]输⼊第三个式⼦计算X3=1.0.这就完成了这⼀次的迭代，得到迭代结果[2.88,1.95,1.0],基于这个结果，开始下⼀次迭代。

特点：jacobi迭代法，需要存储，上⼀次的迭代结果，也要存储这⼀次的迭代结果，所以需要两组存储单元。

⽽Gauss-Seidel迭代法，每⼀次迭代得到的每⼀个式⼦得到的值，替换上⼀次迭代结果中的值即可。

所以只需要⼀组存储单元。

转化成⼀般式：注意：第⼆个式⼦中的是k+1次迭代的第⼀个式⼦的值，不是第k次迭代得值。

计算过程同jacobi迭代法的类似三.逐次超松弛法SOR法上⾯仅仅通过实例说明，Jacobi和Seidel迭代的运算过程。

【关键字】分析数值分析实验报告（3）学院：信息学院班级：计算机0903班姓名：王明强学号：课题三线性方程组的迭代法一、问题提出1、设线性方程组=x= ( 1, -1, 0, 1, 2, 0, 3, 1, -1, 2 )2、设对称正定阵系数阵线方程组=x = ( 1, -1, 0, 2, 1, -1, 0, 2 )3、三对角形线性方程组=x= ( 2, 1, -3, 0, 1, -2, 3, 0, 1, -1 )试分别选用Jacobi 迭代法，Gauss-Seidol迭代法和SOR方法计算其解。

二、要求1、体会迭代法求解线性方程组，并能与消去法做以比较；2、分别对不同精度要求，如由迭代次数体会该迭代法的收敛快慢；3、对方程组2，3使用SOR方法时，选取松弛因子=0.8，0.9，1，1.1，1.2等，试看对算法收敛性的影响，并能找出你所选用的松弛因子的最佳者；4、给出各种算法的设计程序和计算结果。

三、目的和意义1、通过上机计算体会迭代法求解线性方程组的特点，并能和消去法比较；gauss消去法是一种规则化的加减消元法。

它的基本思想是：通过逐次消元计算把需要求求解的线性方程转化成上三角形方程组，也就是把线性方程组的系数矩阵转化为上三角矩阵，从而使一般线性方程组求解转化为等价（同解）的上三角方程组的求解。

消去法是直接方法的一种。

优点：对于简单的方程组可以很快得出结果，计算中如果没有舍入误差，在稳定的方程组中容易得到精确解，理论上可以求解任何可以求出解得方程组。

缺点：数值有的时候不稳定（可采用列主元gauss消去法），既要消去，又要回代，算法实现起来比较复杂，不适用于大规模方程组。

迭代法是从某一取定的初始向量x(0)出发，按照一个适当的迭代公式，逐次计算出向量x(1)，x(2)，......，使得向量序列{ x(k)}收敛于方程组的精确解，这样，对于适当大的k，可取x(k)作为方程组的近似解。

优点：算法简单，程序易于实现，特别适用求解庞大稀疏线性方程组。

第3章 解线性方程组的迭代法§1 Jacobi 迭代法和Gauss-Seidel 迭代法（I ）迭代概念（1） A x b = ， n n A R ⨯∈， nb R ∈A M N =- ， n n M R ⨯∈ ， n n N R ⨯∈ ，M 非奇异M x N x b-= Mx Nx b =+11x M Nx M b --=+如果令 11,B M N f M b --==，那么上式写成（2） x B x f =+ 此方程组等价于A x b= 任给(0)n xR ∈，(1)(0)x B x f =+(2)(1)xB x f =+（3） (1)()k k xBx f +=+由（3）可以确定{}()k x ，当()*k n xx R →∈，即()*0k x x -→ 时，有**x Bx f =+*x 同样满足 *Ax b =定义 式（3） (1)()k k xBx f +=+称为求解 （1）Ax b = 的简单形式迭代法，B 称为迭代矩阵。

（II ）Jacobi 迭代法Ax b =写成分量形式有1,1,2,,nij ji j a xb i n ===∑111,1,2,,i nii i ij j ijji j j i a x a x a xb i n -==+++==∑∑假定 0ii a ≠ ，那么有1111(),1,2,,i ni i ij j ij j j j i ii x b a x a x i n a -==+=--=∑∑迭代法为任给 (0)(0)(0)(0)12(,,,)T n n x x x x R =∈1(1)()()111(),1,2,,;0,1,i nk k k ii ij j ij j j j i ii xb a x a x i n k a -+==+=--==∑∑即：{}{}{}(1)()()()11122133111(1)()()()22211233222(1)()()()1122,111(1(1(k k k k n n k k k k n n k k k k n n n n n n n nnx b a x a x a x a x b a x a x a x a x b a x a x a x a +++--⎧=----⎪⎪⎪=----⎪⎨⎪⎪⎪=----⎪⎩上式迭代方法称为Jacobi 迭代 例1.1用Jacobi 迭代法解方程组123123123522142241x x x x x x x x x +-=⎧⎪++=⎨⎪-+=-⎩解 Jacobi 迭代方法为(1)()()()()123231(122)0.20.40.45k k k k k x x x x x +=-+=-+ (1)()()()()213131(2)0.50.250.254k k k k k x x x x x +=--=-- (1)()()()()312121(12)0.250.250.54k k k k k x x x x x +=--+=--+取 (0)3(0,0,0)T xR =∈()()()123000010.20.50.2520.10.51250.05110.0000080.4998820.000039120.0000340.4999880.000025130.0000150.5000020.000003k k k k x x x ------方程组 Ax b =的准确解为*3(0,0.5,0)Tx R =∈。

实验报告
一、实验目的
体会求解线性方程组的Jacobi 迭代法和Gauss-Seidel 迭代法的收敛速度。

二、实验题目
用迭代法分别对200,20==n n 解方程组b Ax =，其中
n
n A ⨯⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------------------=431513143151513143151513143151513143151314
（1）选取不同的初值0x 和不同的右端向量b ，给定迭代误差，用Jacobi 迭代法和Gauss-Seidel 迭代法计算,观测得到的迭代向量并分析计算结果给出结论；
(2）取定初值0x 和右端向量b ，给定迭代误差，将A 的主对角元成倍放大，其余元素不变，用Jacobi 迭代法计算多次，比较收敛速度，分析计算结果并给出结论。

三、实验原理
求解线性方程组的Jacobi 迭代法和Gauss —Seidel 迭代法
四、实验内容及结果
1.Jacobi 迭代法：
4。

设取定的初值x0=ones(n,1），b=2*ones（n,1）；改变A的主对角线元素成倍放大，只需要将第二步中的
五、实验结果分析
（1）前面四个程序输出的结果,都有迭代次数和x的值，说明矩阵是收敛的。

Gauss-seidel的迭代速度比Jacobi的迭代速度快。

(2）观察k值发现迭代次数是减少的,再根据已学的知识，可以推断出随着A的主对角元值的成倍放大收敛的速度加快。