频域性能指标和时域性能指标的关系

一、简答题1. 被控对象、被控量、干扰各是什么？答：对象：需进行控制的设备或装置的工作进程。

被控量：被控对此昂输出需按控制要求变化的物理量。

干扰：对生产过程产生扰动，使被控量偏离给定值的变量。

2. 按给定信号分类，控制系统可分为哪些类型？答：恒值控制系统、随动控制系统、程序控制系统。

3. 什么是系统的静态？答：被控量不随时间改变的平衡状态。

4. 什么是系统的动态？答：被控量随时间变化的不平衡状态。

5. 什么是系统的静态特性？答：系统再平衡状态下输出信号与输入信号的关系。

6. 什么是系统的动态特性？答：以时间为自变量，动态系统中各变量变化的大小、趋势以及相互依赖的关系。

7. 控制系统分析中，常用的输入信号有哪些？答：阶跃、斜坡、抛物线、脉冲。

8. （3次）传递函数是如何定义的？答：线性定常系统在零初始条件下输出响应量的拉氏变换与输入激励量的拉氏变换之比。

9. 系统稳定的基本条件是什么？答：系统的所有特征根必须具有负的实部的实部小于零。

10. 以过渡过程形式表示的质量指标有哪些？答：峰值时间t p 、超调量δ%、衰减比n d 、调节时间t s 、稳态误差e ss 。

11. 简述典型输入信号的选用原因。

答：①易于产生；②方便利用线性叠加原理；③形式简单。

12. 什么是系统的数学模型？答：系统的输出参数对输入参数的响应的数学表达式。

13. 信号流图中，支路、闭通路各是什么？答：支路：连接两节点的定向线段，其中的箭头表示信号的传送方向。

闭通路：通路的终点就是通路的起点，且与其他节点相交不多于一次。

14. 误差性能指标有哪些？答：IAE ，ITAE ，ISE ，ITSE二、填空题1. 反馈系统又称偏差控制，起控制作用是通过给定值与反馈量的差值进行的。

2. 复合控制有两种基本形式，即按参考输入的前馈复合控制和按扰动输入的前馈复合控制。

3. 某系统的单位脉冲响应为g(t)=10e -0.2t +5e -0.5t ，则该系统的传递函数G(s)为ss s s 5.052.010+++。

自动控制原理填空题复习（一）1. 对于一个自动控制的性能要求可以概括为三个方面： 稳定性 、 快速性 、 准确性 。

2. 反馈控制系统的工作原理是按 偏差 进行控制，控制作用使 偏差 消除或减小，保证系统的输出量按给定输入的要求变化。

3. 系统的传递函数只与系统 本身 有关，而与系统的输入无关。

4. 自动控制系统按控制方式分，基本控制方式有：开环控制系统 、 闭环控制系统 、混合控制系统 三种。

5. 传递函数G(S)的拉氏反变换是系统的单位 阶跃 响应。

6. 线性连续系统的数学模型有 电机转速自动控制系统。

7. ★系统开环频率特性的低频段，主要是由 惯性 环节和 一阶微分 环节来确定。

8. 稳定系统的开环幅相频率特性靠近（-1，j0）点的程度表征了系统的相对稳定性，它距离（-1，j0）点越 远 ，闭环系统相对稳定性就越高。

9. 频域的相对稳定性常用 相角裕度 和 幅值裕度 表示，工程上常用这里两个量来估算系统的时域性能指标。

10. 某单位反馈系统的开环传递函数2()(5)G S s s =+，则其开环频率特性是 2-2.0tan -)(1πωωϕ-= ，开环幅频特性是424252)(A ωωω+=，开环对数频率特性曲线的转折频率为 。

11. 单位负反馈系统开环传递函数为2()(5)G S s s =+，在输入信号r(t)=sint 作用下，，系统的稳态输出c ss (t)= , 系统的稳态误差e ss (t)= .12. 开环系统的频率特性与闭环系统的时间响应有关。

开环系统的低频段表征闭环系统的 稳定性 ；开环系统的中频段表征闭环系统的 动态性能 ；开环系统的高频段表征闭环系统的 抗干扰能力 。

自动控制原理填空题复习（二）1、反馈控制又称偏差控制，其控制作用是通过 输入量 与反馈量的差值进行的。

2、复合控制有两种基本形式：即按 参考输入 的前馈复合控制和按 扰动 的前馈复合控制。

3、两个传递函数分别为G 1(s)与G 2(s)的环节，以并联方式连接，其等效传递函数为()G s ，则G(s)为 G 1(s)+G 2(s) （用G 1(s)与G 2(s) 表示）。

5.7 频域性能指标和时域性能指标的关系频率响应法是通过系统的开环频率特性和闭环频率特性的一些特征量间接地表征系统的瞬(暂)态响应的性能，因而这些特征量又被称为频域性能指标。

常用的频域性能指标有幅值裕度、相位裕度、谐振峰值、谐振频率和频带宽度等。

虽然这些指标没有时域性能指标那样直观，但在二阶系统中，它们与时域性能指标有着确定的对应关系，对于高阶系统，也有近似的关系。

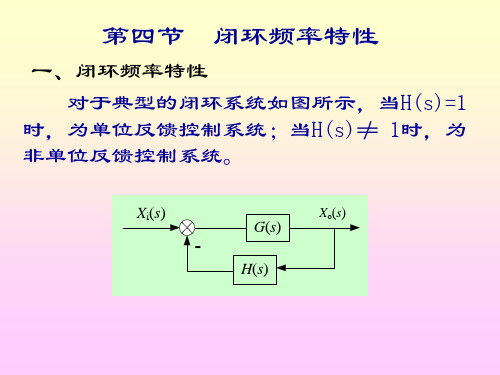
5.7.1频域指标和二阶系统的过渡过程指标设二阶单位反馈系统的方框图如图5-80所示。

图 5-80 二阶单位反馈系统的方框图此系统的闭环传递函数为2222)()(nn n s s s X s Y ωξωω++= 其中ξ为阻尼比，n ω为无阻尼自然振荡频率。

令s j =ω代入上式，可得系统的闭环频率响应为:ja n nM j j X j Y e 2)1(1)()(22=+-=ωωξωωωω式中 M nn =-+1122222()()ωωξωω2212a r c t a n nn ωωωωξα--= 根据式(5-67)可知，当00707≤≤ξ.时，在谐振频率ωr 处，M 出现峰值ωωξr n =-122M r =-1212ξξ二阶系统的闭环频率特性如图5-81所示。

图 5-81 图5-80所示系统的闭环频率特性对于二阶系统，在012≤<ξ时，频率特性的谐振峰值M r 可以反映系统的阻尼系数ξ，而其谐振频率ωr 可以反映给定ξ对应的自然频率ωn ,从而也能反映响应速度。

这样就可把二阶系统闭环频率特性的M r 和ωr 当作性能指标用。

系统的频带宽度(带宽)由图5-81可见，当ωω>r 时，闭环频率特性的幅值M 单调下降。

当闭环频率特性的幅值下降到707.021==M 时，或者说，当闭环频率特性的分贝值下降到零频率时分贝值以下3分贝时，对应的频率ωb 称为截止频率，又称带宽频率。

此时有b j M j M ωωω>-<3)0(lg 20)(lg 20对于0)0(lg 20=j M ，有b j M ωωω>-<3)(lg 20系统对频率高于ωb 的输入衰减很大，只允许频率低于ωb 的输入通过。

自动控制理论B一、填空题：(每空1分，共15分)1、2、自动控制系统有两种基本控制方式，当控制装置与受控对象之间只有顺向作3、稳定是对控制系统最基本的要求，若一个控制系统的响应曲线为衰减振荡，。

判断一个闭环线性控制系统是否稳定，在时域分析中采用劳斯判据 ；在频域分析中采用4、之比。

5、设系统的开环传递函数为2(1)(1)K s s Ts τ++，6、频域性能指标与时域性能指标有着对应关系，开环频域性能指标中的幅值穿越频率c ω二、选择题（每题2分，共20分） 1、关于传递函数，错误的说法是 ( B )B 传递函数不仅取决于系统的结构参数，给定输入和扰动对传递函数也有影响； 2、下列哪种措施对改善系统的精度没有效果 (C )。

C 、增加微分环节4、已知系统的开环传递函数为50(21)(5)s s ++，则该系统的开环增益为 ( C )。

C 、105、若某系统的根轨迹有两个起点位于原点，则说明该系统( B ) 。

B 、含两个积分环节6、开环频域性能指标中的相角裕度γ对应时域性能指标( A ) 。

A 、超调%σ7、已知某些系统的开环传递函数如下，属于最小相位系统的是( B8、若系统增加合适的开环零点，则下列说法不正确的是 ( B ) B 、会增加系统的信噪比；9、开环对数幅频特性的低频段决定了系统的( A )。

A 、稳态精度10、下列系统中属于不稳定的系统是( D )。

D 、脉冲响应为0.4()8t h t e =的系统三、（共24分）设系统闭环传递函数22()1()()21C s s R s T s Ts ξΦ==++，试求：1、0.2ξ=；s T 08.0=； 0.8ξ=；s T 08.0=时单位阶跃响应的超调量%σ、调节时间s t 及峰值时间p t 。

（9分） 解：系统的闭环传函的标准形式为：222221()212n n n s T s Ts s s ωξξωωΦ==++++，其中1nTω=当 0.20.08T s ξ=⎧⎨=⎩ 时，0.2%52.7%4440.08 1.60.20.26s n p d ee T t s t s πξπσξωξπω--⎧⎪===⎪⎪⨯⎪====⎨⎪⎪=====⎪⎪⎩当0.80.08T sξ=⎧⎨=⎩时，0.8% 1.5%4440.080.40.80.42snpde eTt st sπξπσξωξπω--⎧⎪===⎪⎪⨯⎪====⎨⎪⎪=====⎪⎪⎩2、4.0=ξ；sT04.0=和4.0=ξ；sT16.0=时单位阶跃响应的超调量%σ、调节时间st和峰值时间p t。

1.凡是输入输出关系符合_______和齐次性的系统称之为线性系统。

2.叠加原理是线性系统的基本性质之一，对于非线性系统，叠加原理_____成立。

3.线性系统与非线性系统的本质区别是是否满足_______。

4.输入输出模型是对系统的外部描述，_______是这种描述的是最基本的形式，传递函数、框图、信号流图均是由它导出。

5.根轨迹法与频域法都是建立在_______基础上的，需用要根据其画出相应的图，进而进行分析。

6.控制理论有四个重要概念：动态、模型、互联和______，这四个概念是系统分析和设计的关键。

7.计算机网络IP协议采用开环控制，TCP协议则采用______控制。

8.自动控制系统主要由对象、检测单元、执行单元和________等四个基本部分构成。

9.控制理论把系统满足物理约束条件下的负载扰动抑制、测量噪声衰减、指令跟踪、系统结构及参数变化的不确定性问题，归结为求解反馈系统的稳定性、快速性、准确性和_______。

10.反馈是处理不确定性的工具，采用反馈控制，要使系统达到稳定性、_______、准确性、鲁棒性的要求。

11.________是处理不确定性的工具，采用反馈控制，要使系统达到稳定性、快速性、准确性、鲁棒性的要求。

12.灵敏度函数不但可以描述系统对于过程参数变化的鲁棒性，同时也刻画了闭环系统对于______的抑制性能。

13.灵敏度函数不但可以描述系统对于过程_______的鲁棒性，同时也刻画了闭环系统对于扰动的抑制性能。

)14.对于物理系统，由于系统的因果性，传递函数分母的阶次n总是_________分子的阶次m。

15.传递函数2(3)ss++的极点是________。

16.传递函数23(2)(3)ss++的零点是________。

17.传递函数5(3)ss s++的有限零点是________。

18.传递函数23ss++的有限极点是________。

19.线性系统渐近稳定的充要条件是其特征方程的所有根均位于_______。

控制系统时域与频域性能指标的联系经典控制理论中,系统分析与校正方法一般有时域法、复域法、频域法.时域响应法是一种直接法，它以传递函数为系统的数学模型,以拉氏变换为数学工具，直接可以求出变量的解析解.这种方法虽然直观，分析时域性能十分有用，但是方法的应用需要两个前提,一是必须已知控制系统的闭环传递函数,另外系统的阶次不能很高。

如果系统的开环传递函数未知，或者系统的阶次较高,就需采用频域分析法。

频域分析法不仅是一种通过开环传递函数研究系统闭环传递函数性能的分析方法,而且当系统的数学模型未知时，还可以通过实验的方法建立。

此外，大量丰富的图形方法使得频域分析法分析高阶系统时，分析的复杂性并不随阶次的增加而显著增加。

在进行控制系统分析时，可以根据实际情况，针对不同数学模型选用最简洁、最合适的方法,从而使用相应的分析方法，达到预期的实验目的.系统的时域性能指标与频域性能指标有着很大的关系，研究其内在联系在工程中有着很大的意义.一、系统的时域性能指标延迟时间t d阶跃响应第一次达到终值h （∞）的50％所需的时间上升时间t r阶跃响应从终值的10%上升到终值的90%所需的时间;对有振荡的系统，也可定义为从0到第一次达到终值所需的时间峰值时间tp阶跃响应越过终值h （∞)达到第一个峰值所需的时间调节时间ts阶跃响应到达并保持在终值h （∞)的±5％误差带内所需的最短时间超调量%σ 峰值h(tp）超出终值h(∞）的百分比，即%σ=()()()∞∞-h h h t p ⨯100%二、系统频率特性的性能指标采用频域方法进行线性控制系统设计时,时域内采用的诸如超调量,调整时间等描述系统性能的指标不能直接使用，需要在频域内定义频域性能指标。

1、零频振幅比M （0)：即ω为0时闭环幅频特性值。

它反映了系统 的稳态精度， M(0）越接近于1，系统的精度越高.M(0）≠1时，表明系统有稳态误差。

2、谐振峰值Mr ：为幅频特性曲线的A （ω）的最大值.一般说来，Mr 的大小表明闭环控制系统相对稳定性的好坏。

A.阶跃函数 斜坡函数 抛物线函数 脉冲函数 正弦函数B.典型环节的传递函数 比例环节 惯性环节(非周期环节) 积分环节微分环节 二阶振荡环节(二阶惯性环节) 延迟环节 C.环节间的连接串联并联反馈 开环传递函数=前向通道传递函数=负反馈闭环传递函数正反馈闭环传递函数D.梅逊增益公式E.劳斯判据 劳斯表中第一列所有元素均大于零 s n a 0 a 2 a 4 a 6 …… s n-1 a 1 a 3 a 5 a 7 ……s n-2 b 1 b 2 b 3 b 4 …… s n-3c 1 c 2 c 3 c 4 …… … … …s 2 f 1 f 2s 1 g 1 s 0 h 1,,,,,,141713131512121311171603151402131201b b b a a c b b b a a c b b b a a c a a a a a b a a a a a b a a a a a b -=-=-=-=-=-=劳斯表中某一行的第一个元素为零而该行其它元素不为零，ε→0； 劳斯表中某一行的元素全为零。

P(s)=2s 4+6s 2-8。

F.赫尔维茨判据 特征方程式的所有系数均大于零。

⎩⎨⎧≥<=00)(t A t t r ⎩⎨⎧≥<=000)(t At t t r ⎪⎩⎪⎨⎧≥<=02100)(2t At t t r ⎪⎩⎪⎨⎧>≤≤<=εεt t z At t r 0000)(⎩⎨⎧≥<=0sin 00)(t t A t t r ωKs R s C s G ==)()()(1)()()(+==Ts K s R s C s G s T s R s C s G i 1)()()(==sT s R s C s G d ==)()()(2222)(n n ns s K s G ωζωω++=se s R s C s G τ-==)()()()()()( )()()()()()()()()(211121s G s G s G s X s C s X s X s R s X s R s C s G n n =⋅==-)()()( )()()()()()()(2121s G s G s G s R s C s C s C s R s C s G n n +++=+++== )()()()(s H s G s E s B =)()()(s G s E s C =)()(1)()()()(s H s G s G s R s C s +==Φ)()(1)()()()(s H s G s G s R s C s -==Φ∆∆=∑kk P TG.误差传递函数扰动信号的误差传递函数I.二阶系统的时域响应： 其闭环传递函数为 或 系统的特征方程为2)(22=++=nn s s s D ωζω特征根为1,221`-±-=ζωζωn n s上升时间t r其中 峰值时间t p最大超调量M p调整时间t sa.误差带范围为 ±5%b.误差带范围为± 2%振荡次数NJ.频率特性：还可表示为：G (jω)=p (ω)+jθ(ω) 为G (jω)的实部，称为实频特性； 为G (jω)的虚部，称为虚频特性。

控制系统时域和频域性能指标的联系首先，稳态误差与系统的频率响应特性有直接的关系。

稳态误差是指系统在稳态下的输出与期望输出之间的差异。

对于一个给定的输入信号，系统的稳态误差取决于系统的静态增益以及输入信号的频率。

频域分析可以帮助我们理解系统的静态增益以及系统对不同频率信号的响应。

在频域中，系统的增益可以用频率响应函数（Bode图）表示。

通过分析频率响应函数，可以了解系统在不同频率上对输入信号的衰减或放大程度，进而得出稳态误差的大小。

其次，超调量、上升时间和调整时间与系统的带宽有关。

超调量是指系统在达到稳态之前超过期望值的最大幅度，上升时间是指系统从初始状态到达稳态的时间，调整时间是指系统在超调量和上升时间基础上调整到稳态的时间。

这些性能指标反映了系统的动态响应特性。

在频域中，带宽可以用系统的频率响应曲线上的3dB截止频率表示。

带宽越大，系统对输入信号的高频成分的放大程度越高，超调量越小，上升时间和调整时间也越短。

另外，增益裕度和相位裕度与系统的稳定性有关。

增益裕度是指系统在保持稳定性的前提下，可以承受的最大增益变化。

相位裕度是指系统在保持稳定性的前提下，可以承受的最大相位变化。

在频域中，增益裕度和相位裕度可以通过系统的频率响应曲线来确定。

如果增益裕度或相位裕度较小，则可能导致系统的不稳定性。

一、概述在控制系统工程中，频域指标和时域指标是评价系统性能的重要标准。

二阶系统是一类简单且常见的动态系统，其频域指标和时域指标之间存在一定的对应关系。

本文将探讨二阶系统频域指标与动态时域指标之间的对应关系，以及在实际工程中的应用。

二、二阶系统概述1. 二阶系统的数学描述二阶系统是指具有两个传递函数零点和两个传递函数极点的动态系统。

其数学模型可以用如下的传递函数形式表示：$$ G(s) = \frac{K}{s^2 + 2ζω_ns + ω_n^2} $$其中，K为系统的增益，ζ为阻尼比，ω_n为自然频率。

2. 二阶系统的特性二阶系统在频域和时域上有着特定的性能指标，包括频域指标如增益裕度、相位裕度、共振峰值等，以及时域指标如上升时间、峰值时间、定时时间等。

三、频域指标与动态时域指标的对应关系1. 增益裕度与峰值时间的关系在频域分析中，增益裕度是指系统在开环增益相对于临界增益时的增益范围。

而峰值时间是指系统的输出响应中出现的最大过渡过程时间。

二者之间存在如下的关系：$$MG = \frac{1}{\sqrt{1 - ζ^2}}$$$$Tp = \frac{π}{ω_n\sqrt{1 - ζ^2}}$$其中，MG为增益裕度，Tp为峰值时间。

2. 相位裕度与上升时间的关系相位裕度是指系统在开环相位相对于-180°时的相位范围。

上升时间是指系统输出响应从初始稳态值上升到峰值的时间。

二者之间的关系可以表示为：$$PM = \frac{1}{2ζ\sqrt{1 - ζ^2}}$$$$Tr = \frac{π}{ω_n\sqrt{1 - ζ^2}}$$其中，PM为相位裕度，Tr为上升时间。

3. 共振峰值与峰值时间的关系共振峰值描述了系统在共振频率处的增益倍数。

而峰值时间则是描述了系统输出响应中的最大过渡过程时间。

二者的关系如下：$$M_p = \frac{1}{2ζ\sqrt{1 - ζ^2}}$$$$Tp = \frac{π}{ω_n\sqrt{1 - ζ^2}}$$其中，M_p为共振峰值，Tp为峰值时间。