一典型数字控制器设计数字PID控制器全

数字PID控制系统设计方案如下：一、引言PID控制器是一种常用的闭环控制算法，用于调节系统的输出以使系统稳定在设定值附近。

数字PID控制系统通过数字信号处理器（DSP）或单片机实现PID控制算法，具有灵活性高、易实现和调试等优点。

本文将介绍数字PID控制系统的设计方案，包括硬件连接、软件算法设计和系统调试等内容。

二、硬件设计1. 控制对象：确定待控制的物理对象或过程，例如电机转速、温度、液位等。

2. 传感器：选择合适的传感器获取待控量的反馈信号，如编码器、温度传感器、压力传感器等。

3. 执行器：选择合适的执行器，如电机、阀门等，用于调节系统输出。

4. 控制器：采用DSP或单片机作为数字PID控制器，负责计算PID 控制算法输出并控制执行器。

三、软件算法设计1. PID算法：根据系统特性和需求设计PID控制算法，包括比例项、积分项和微分项的权重和计算方法。

2. 离散化：将连续时间的PID算法离散化，适应数字控制器的运算方式。

3. 反馈控制：读取传感器反馈信号，计算PID输出，并控制执行器实现闭环控制。

四、系统调试1. 参数整定：通过实验和调试确定PID控制器中的比例系数、积分时间和微分时间等参数。

2. 稳定性测试：观察系统响应和稳定性，调整PID参数以提高系统性能。

3. 实时监测：实时监测系统输入、输出和误差信号，确保PID控制器正常工作。

五、性能优化1. 自适应控制：根据系统动态特性调整PID参数，实现自适应控制。

2. 鲁棒性设计：考虑系统模型不确定性和外部扰动，设计鲁棒性PID 控制算法。

3. 高级控制：结合模糊控制、神经网络等高级控制方法，优化系统性能。

六、总结数字PID控制系统设计是一项重要的控制工程任务，通过合理的硬件设计和软件算法实现，可以实现对各种控制对象的精确控制。

希望通过本文的介绍，读者能够了解数字PID控制系统的设计原理和实现方法，并在实践中不断提升控制系统设计和调试的能力。

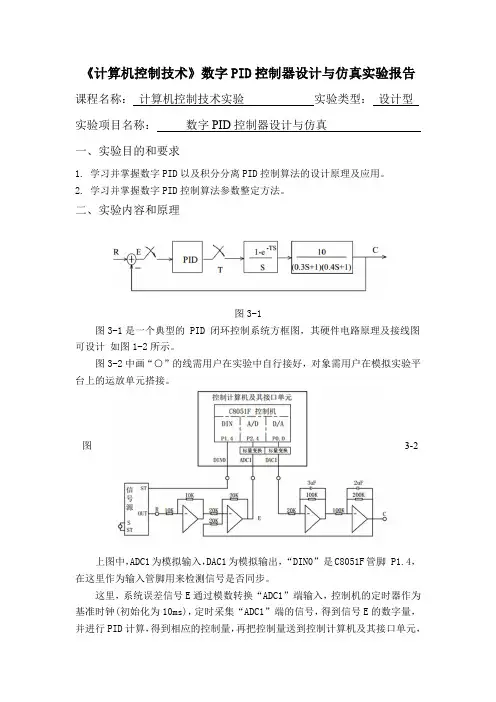
《计算机控制技术》数字PID控制器设计与仿真实验报告课程名称：计算机控制技术实验实验类型：设计型实验项目名称：数字PID控制器设计与仿真一、实验目的和要求1. 学习并掌握数字PID以及积分分离PID控制算法的设计原理及应用。

2. 学习并掌握数字PID控制算法参数整定方法。

二、实验内容和原理图3-1图3-1是一个典型的 PID 闭环控制系统方框图，其硬件电路原理及接线图可设计如图1-2所示。

图3-2中画“○”的线需用户在实验中自行接好，对象需用户在模拟实验平台上的运放单元搭接。

图3-2上图中，ADC1为模拟输入，DAC1为模拟输出，“DIN0”是C8051F管脚 P1.4，在这里作为输入管脚用来检测信号是否同步。

这里，系统误差信号E通过模数转换“ADC1”端输入，控制机的定时器作为基准时钟(初始化为10ms)，定时采集“ADC1”端的信号，得到信号E的数字量，并进行PID计算，得到相应的控制量，再把控制量送到控制计算机及其接口单元，由“DAC1”端输出相应的模拟信号，来控制对象系统。

本实验中，采用位置式PID算式。

在一般的PID控制中，当有较大的扰动或大幅度改变给定值时，会有较大的误差，以及系统有惯性和滞后，因此在积分项的作用下，往往会使系统超调变大、过渡时间变长。

为此，可采用积分分离法PID控制算法，即：当误差e(k)较大时，取消积分作用；当误差e(k)较小时才将积分作用加入。

图3-3是积分分离法PID控制实验的参考程序流程图。

图3-3三、主要仪器设备计算机、模拟电气实验箱四、操作方法与实验步骤1.按照图3-2搭建实验仿真平台。

2.确定系统的采样周期以及积分分离值。

3.参考给出的流程图编写实验程序，将积分分离值设为最大值0x7F，编译、链接。

4.点击，使系统进入调试模式，点击，使系统开始运行，用示波器分别观测输入端R以及输出端C。

5.如果系统性能不满意，用凑试法修改PID参数，再重复步骤3和4，直到响应曲线满意，并记录响应曲线的超调量和过渡时间。

PI控制器的设计
PID是一个经典的控制律，被广泛应用于各种控制系统中。

PID控制器可以用模拟电路来实现，也可以用数字算法来实现。

实际应用中，PI控制相对于PD 或PID控制用的更多一些。

下图为一个采用运放来实现的PI控制器电路：
U1A部分是比例为1的差分电路，此电路输入为反馈值和设定值输出为它们之间的偏差。

U1B部分是一个比例电路，比例系数为R2/R1 。

U1C部分是一个积分电路，积分系数为1/(R4 * C1) 。

U2A与U2B部分是一个加法电路，输出为控制值。

比例控制可以实现对偏差的快速响应，积分控制可以消除静差。

将比例与积分控制结合起来可以在消除静差的同时加快对偏差的响应。

采用上述电路设计了一个电流控制器，实现电流输出值对电流设定值的跟踪。

当仅采用积分控制时，波形如下（红色为设定值，橙色为输出值）：
X轴单位为1ms
X轴单位为10us
当采用比例积分控制时，波形如下：
X轴单位为1ms
X轴单位为1ms
X轴单位为10us
由上可见，两种方法都可以消除静差，实现输出值对设定值的跟踪，不过相比于纯积分控制，比例积分控制的效果更好一些，超调量小，稳定时间短。

频域下基于参数调整的PID控制器设计与实现PID控制器是一种常见的控制器，它在工业自动化系统中广泛应用。

为了提高控制系统的性能，研究人员一直在努力改进PID控制器的设计方法。

本文将重点介绍频域下基于参数调整的PID控制器设计与实现。

1. 简介PID控制器是基于目标系统的反馈信息进行控制的一种控制器。

它包括比例、积分和微分三个部分，通过调节这三个部分的参数来实现对控制系统的稳定性、快速响应和抑制干扰等目标的实现。

2. 频域分析频域分析是将系统的输入和输出信号转换到频率域上进行分析的方法。

在频域下，我们可以通过系统的频率响应来了解系统的特性，并根据这些特性来设计控制器。

3. 参数调整方法PID控制器的参数调整一直是控制领域的研究热点。

常用的参数调整方法包括试错法、Ziegler-Nichols方法和频域分析方法等。

3.1 试错法试错法是一种基于经验的参数调整方法。

根据系统的响应特性，通过改变PID 控制器的参数来改善系统的性能。

试错法常见的调整规则包括增大比例增益提高系统响应速度、增大积分时间消除系统稳态误差、增大微分时间抑制系统振荡等。

3.2 Ziegler-Nichols方法Ziegler-Nichols方法是一种经典的PID参数调整方法。

它通过试验得到系统的临界增益和临界周期，根据这些参数来计算出P、I和D的合适取值。

例如，根据临界增益和临界周期可以计算出比例增益、积分时间和微分时间的取值。

3.3 频域分析方法频域分析方法是一种相对较精确的PID参数调整方法。

它通过分析系统的频率响应来得到合适的PID参数。

具体方法包括根轨迹法、奈奎斯特曲线法和频率曲线法等。

这些方法可以通过计算系统的开环传递函数和频率响应曲线，然后根据要求设计合适的PID参数。

4. PID控制器的实现PID控制器可以通过硬件和软件两种方式实现。

在硬件实现中，我们可以使用模拟电路或数字电路来搭建PID控制器。

在软件实现中，我们可以使用编程语言来实现PID算法，并在微控制器上运行。

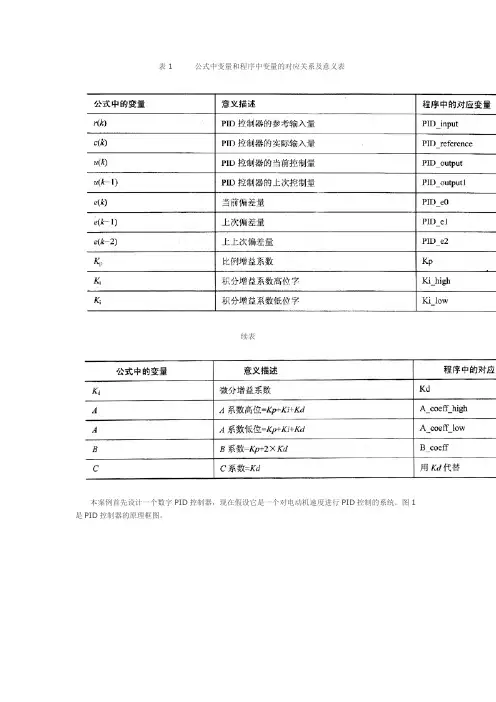
表1 公式中变量和程序中变量的对应关系及意义表续表本案例首先设计一个数字PID控制器，现在假设它是一个对电动机速度进行PID控制的系统。

图1是PID控制器的原理框图。

图1 PID控制器的原理框图图1中，r(t)是电机速度设定值，c(t)是电机转速的实际测量值，e(t)是输入控制器的偏差信号，勿⑺是控制器输出的控制量，则PID控制算式如式4－1所示。

在式4-1中，Kp是比例系数，起比例调整作用。

Ti是积分时间常数，它决定了积分作用的强弱。

Td 是微分时间常数，它决定了微分作用的强弱。

在PID控制的3种作用中，比例作用可对系统的偏差做出及时响应；积分作用主要用来消除系统静差，改善系统的静态特性，体现了系统的静态性能指标；微分作用主要用来减少动态超调，克服系统振荡，加快系统的动态响应，改善系统的动态特性。

，PID控制的3种作用（比例、积分、微分）是各自独立的，可以分别使用，也可以结合徒用，但是积分控制和微分控制不能单独使用，必须和比例控制结合起来，形成Pl控制器或者PD控制器。

式4－1是模拟形式的PID控制算式，现在采用LF2407实现数字PID控制，则对式4-1离散化，得到PID控制的离散形式，如式4－2所示。

其中Ts为采样周期。

这是位置式PID控制算式，为了增加控制系统的可靠性，采用增量式PID控制算式，即让LF2407只输出控制量u(k)的增量ΔU(k)。

式4-2是第k次PID控制器的输出量，那么第k －1次PID控制器的输出量如式4－3所示。

方程式4-5就是本控制程序中用到的增量式PID控制算式。

增量式PID控制与位置式ΠD控制相比仅是算法上有所改变，但是它只输出增量，减少了DSP误操作时对控制系统的影响，而且不会产生积分失控。

本案例基于LF2407的PID控制器的实现框图如图2所示。

图2 基于LF24O7的PID控制器的实现框图从图2可以看出被控电机的速度设定量由DSP给出，经过DSP计算出控制量u（k），对它进行DA 转换，产生模拟控制量u（t），从而实现对被控电机速度的控制，而电机实际转速c（t）通过AD转换器送入DSP，使整个系统构成一个闭环系统。

数字PID控制器设计实验报告学院电子信息学院专业电气工程及其自动化学号姓名指导教师杨奕飞数字PID控制器设计报告一．设计目的采用增量算法实现该PID控制器。

二．设计要求掌握PID设计方法及MATLAB设计仿真。

三．设计任务设单位反馈系统的开环传递函数为：设计数字PID控制器，使系统的稳态误差不大于0.1，超调量不大于20%，调节时间不大于0.5s。

采用增量算法实现该PID控制器。

四．设计原理数字PID原理结构图PID控制器的数学描述为：式中，Kp为比例系数；T1为积分时间常数；T D为微分时间常数。

设u(k)为第K次采样时刻控制器的输出值，可得离散的PID表达式为:使用模拟控制器离散化的方法,将理想模拟PID控制器D(s)转化为响应的理想数字PID控制器D(z).采用后向差分法,得到数字控制器的脉冲传递函数。

2.增量式PID控制算法u(k)=u(k-1)+Δu(k)增量式PID控制系统框图五．Matlab仿真选择数字PID参数利用扩充临界比例带法选择数字PID参数，扩充临界比例带法是以模拟PID调节器中使用的临界比例带法为基础的一种数字PID参数的整定方法。

其整定步骤如下1)选择合适的采样周期T：，因为Tmin<1/10 T,选择采样周期为0.003s；2)在纯比例的作用下,给定输入阶跃变化时,逐渐加大比例作用Kp(即减小比例带δ),直至系统出现等幅震荡,记录比例增益Kr,及振荡周期Tr 。

Kr成为临界振荡比例增益(对应的临界比例带δ),Tr成为临界振荡周期。

在Matlab中输入如下程序G=tf(1,[1/150,36/150,185/150,1]);p=[35:2:45];for i=1:length(p)Gc=feedback(p(i)*G,1);step(Gc),hold onend;axis([0,3,0,2.3])得到如下所示图形：改变其中的参数P=[35:2:45]为p=[40:1:45]得到下图曲线，得Kr约为43，Tr 约为0.5.在smulink中建立如下模型，可得Kr=43.4,Tr=0.45。

13个基于PID控制器的设计实例
PID 控制器(比例-积分-微分控制器)是一个在工业控制应用中常见的反馈回路部件，由比例单元比例P(proportion)、积分单元I(integration)和微分单元D(differentiation)组成。

PID 控制器作为最早实用化的控制器已有近百年历史，现在仍然是应用最广泛的工业控制器。

PID 控制器简单易懂，使用中不需精确
的系统模型等先决条件，因而成为应用最为广泛的控制器。

PID 控制的原理及常用口诀总结
基于AT89S51 单片机的PID 温度控制系统设计
本文对系统进行硬件和软件的设计，在建立温度控制系统数学模型的基
础之上，通过对PID 控制的分析设计了系统控制器，完成了系统的软、硬件调试工作。

算法简单、可靠性高、鲁棒性好，而且PID 控制器参数直接影响控制效果。

基于ARM 与PID 算法的开关电源控制系统
本文将SAMSUNC 公司的嵌入式ARM 处理器S3C4480 芯片，应用到开关电源的控制系统的设计中，采用C 语言和少量汇编语言，就可以实现一种以嵌入式ARM 处理器为核心、具有智能PID 控制器以及触摸屏、液晶显示器等
功能的开关电源控制系统。

基于DSP 的电子负载：模糊自适应整定PID 控制策略
本系统引入模糊控制理论设计一个模糊PID 控制器，根据实时监测的电压或电流值的变化，利用模糊控制规则自动调整PID 控制器的参数。

基于FPGA 的高速PID 控制器设计与仿真
本设计使用Altera 公司的Cyclone 系列FPGA 器件EP1C3 作为硬件开发平台，对运动控制中常用的增量式数字PID 控制算法进行优化处理，提高了运。

实验三 PID 控制器设计及其参数整定一、实验目的1) 通过本实验，掌握使用Simulink 仿真设计连续和离散PID 控制器的方法。

2) 掌握对给定控制系统进行PID 控制器参数在线实验工程整定的方法。

二、实验原理PID 控制是最经典、应用最广泛的控制方法，是单回路控制系统主要的控制方法，是其他控制思想的基础。

本实验针对被控对象，选定控制器的调节规律，在控制器的调节规律已经确定的情况下，控制系统的品质主要决定于控制器参数的整定。

1. 连续PID 控制器本实验采用的PID 控制器传递函数为：111()(1)(1)C p d d i i G s K T S T S T S T Sδ=++=++ 或写成：()iC p d K G s K K S S=++ 有,p i d p d iK K K K T T ==其中K p 、K i 、K d 分别为比例系数、积分系数和微分系数；T i 、T d 分别为积分时间常数和微分时间常数；δ为比例度。

控制系统的Simulink 仿真图如图1所示。

连续PID 控制器如图2所示。

根据不同的参数设置，可以得到单纯的比例控制、比例积分控制、比例微分控制以及比例积分微分控制等不同的控制系统。

控制器参数的工程整定实验法，是通过对典型输入响应曲线所得到的特征量，按照动态特性参数法、衰减曲线法、临界比例度法、或经验法中的某一种方法，求得控制器的各个参数，进行工程整定，使系统的性能达到最佳。

图1 控制系统Simulink 仿真图图2 连续PID 控制器Simulink 仿真图2. 离散PID 控制器将描述模拟PID 控制器的微分方程式化为差分方程，即为数字PID 控制算法。

1()(1)()()()kp i di e k e k u k K e k K T e i K T=--=++∑因为上式包含的数字积分项，需要存储过去全部偏差量，而且累加运算编程不太方便，计算量也较大，所以在应用中，通常都是将上式改为增量算法。

基于MATLAB的数字PID控制器设计及仿真分析摘要PID控制作为历史最为悠久，生命力最强的控制方式一直在生产过程自动化控制中发挥着巨大的作用。

PID控制是最早发展起来的控制策略之一，由于其算法简单、鲁棒性好和可靠性高，被广泛用于过程控制和运动控制中。

数字PID控制算法是将模拟PID离散化而得到的，各参数有着明显的物理意义，而且调整方便，所以PID控制器很受工程技术人员的喜爱。

本论文主要实现基于MATLAB的数字PID控制器设计及仿真。

首先介绍了传统的模拟PID控制方法，包括比例控制方法、比例积分控制方法、比例积分微分控制方法等。

接下来，介绍了数字PID控制。

随着时代的发展，科技的进步，传统的模拟PID控制方法不能满足人们的需求，数字PID控制的改进算法也便随之而来。

本文最后，应用MATLAB软件，在实验的环境下实现了其设计及仿真。

本次毕业设计用来完成数字PID控制器的设计，并通过MATLAB实现其仿真同时加以分析。

通过查阅文献得知，与传统模拟PID控制器相比较，该控制器具有良好的灵活性，而且可得到精确的数学模型。

另外，基于MATLAB的数字PID 控制器设计及仿真，充分的利用了MATLAB的实验环境，整个设计验证了数字PID的广泛可实现性及准确性。

关键词：PID控制；模拟PID控制器；数字PID控制器；MATLAB仿真；Design and simulation analysis of Digital PID ControllerMATLAB-basedAbstractAs the most age-old and powerful control mode, PID control always has had a great effect on the automatic control of the production process. PID control is one of the first developed control strategy, because of thesimple algorithm，great robust and high reliability, it is widely used in process control and motor control. Digital PID control algorithm is gotten by discreting the analog PID control, and the parameters have obvious physical meaning and facility adjustment, so PID controller is popular with engineering and technical personnel.In the paper, the main idea is to accomplish MATLAB-based digital PID controller design and simulation analysis. In the first place, the traditional analog PID control methods is introduced, including proportional control methods, proportional integral control and proportional integral differential control. In the second place, the digital PID control methods are offered. With the development of the times, the advancement of technology, traditional analog PID control method cannot make a satisfaction, then digital PID control is followed. At last，the application of MATLAB software to achieve their design and simulation is easy to accomplish.The graduation project is to complete the digital PID controller design and simulation through MATLAB simulation and analysis. It is known that through the literature, compare with traditional PID controller, the controller has good flexibility and precision of the mathematical models available. In addition, in the number of MATLAB-based PID controller design and simulation, the MATLAB experiment environment is used comprehensively. The entire design is confirmed the wide range and accuracy of digital PID controller.Key words：PID control；analog PID controller；digital PID controller；MATLAB simulatio目录摘要 (I)ABSTRACT...................................................................... I I 第1章绪论.. (1)1.1课题目的及意义 (1)1.2数字PID控制器的研究现状 (2)第2章 PID控制器 (3)2.1传统PID控制器概述 (3)2.2PID控制器的基本原理 (5)2.2.1 比例(P)调节 (6)2.2.2 比例积分(PI)调节 (7)2.2.3 比例积分微分(PID)调节 (9)第3章数字PID控制器 (13)3.1数字PID控制系统 (13)3.2数字PID控制的基本算法 (14)3.2.1 位置式PID控制算法 (14)3.2.2 增量式PID控制算法 (16)3.2.3 位置算式与增量算式的比较 (17)第4章数字PID的改进算法 (19)4.1积分算法的改进 (20)4.1.1 积分分离法 (21)4.1.2 变速积分法 (24)4.1.3 遇限消弱积分法 (25)4.1.4 梯形积分法 (26)4.2微分算法的改进 (27)4.2.1 不完全微分PID控制算法 (27)4.2.2 微分先行PID控制算法 (30)4.3带死区的PID控制算法 (32)第5章基于MATLAB的数字PID控制器设计及仿真 (34)5.1位置式PID控制算法仿真实例 (34)5.2增量式PID控制算法仿真实例 (35)参考文献 (37)谢辞 (37)第1章绪论1.1 课题目的及意义PID控制器又称为PID调节器，是按偏差的比例P、积分I、微分进行控制的调节器的简称，它主要针对控制对象来进行参数调节。

数字PID控制系统设计I(一)数字PID控制系统设计I数字PID控制系统是一种闭环控制系统，根据反馈信号控制输出信号，以使被控对象的状态达到期望值。

本文将探讨数字PID控制系统的设计。

1. 确定系统动态特性要设计一个优秀的数字PID控制系统，首先需要了解被控对象的动态特性。

这些特性可以通过实验或模拟获得。

在获得这些数据之后，我们可以确定被控对象的传递函数，并使用MATLAB等工具进行分析和设计。

2. 确定控制框架控制框架决定数字PID控制系统中PID控制器的配置方式。

常见的控制框架有并行控制、串联控制和嵌套控制等。

- 并行控制是指PID控制器的三个参数分别作用于误差、误差之积和误差变化值（即Kp、Ki、Kd）。

它们的输出信号相加后，作为控制器的输出。

- 串联控制是指一个PID控制器的输出作为另一个PID控制器的输入。

其中，外层PID控制器通常用于控制被控对象的位置，而内层PID控制器用于控制被控对象的速度或加速度。

- 嵌套控制是指用一个PID控制器控制一个相似或小规模的被控对象，该被控对象是另一个PID控制器的输入，该控制器控制着整个系统。

这样，就可以分层控制对象，使整个系统更加稳定和可靠。

3. 设计控制器当确定了控制框架后，需要确定PID控制器的参数。

对于一个数字PID 控制器，Kp、Ki和Kd参数应根据被控对象的特性逐渐调整和优化。

- Kp参数代表比例放大系数，它根据误差量进行比例放大。

较大的Kp值会增加控制器的响应速度，但可能出现过调，引起振荡。

- Ki参数代表积分放大系数，它根据误差的历史值进行比例放大。

Ki 较大的值能够抑制系统的静态误差，但如果设置得过大，可能会使系统失去稳定性。

- Kd参数代表微分放大系数，它对误差的变化率进行比例放大。

调节Kd参数可以提高系统的稳定性，但太大的Kd值可能会增加系统噪声。

4. 模拟和实现控制系统在设计好数字PID控制器后，需要对数字PID控制系统进行仿真和实现。

实验三数字PID控制一、实验目的1．研究PID控制器的参数对系统稳定性及过渡过程的影响。

2．研究采样周期T对系统特性的影响。

3．研究I型系统及系统的稳定误差。

二、实验仪器1．EL-AT-III型计算机控制系统实验箱一台2．PC计算机一台三、实验容1．系统结构图如3-1图。

图3-1 系统结构图图中 Gc（s）=Kp（1+Ki/s+Kds）Gh（s）=（1－e-TS）/sGp1（s）=5/（（0.5s+1）（0.1s+1））Gp2（s）=1/（s（0.1s+1））2．开环系统（被控制对象）的模拟电路图如图3-2和图3-3，其中图3-2对应GP1（s）,图3-3对应Gp2（s）。

图3-2 开环系统结构图1 图3-3开环系统结构图2 3．被控对象GP1（s）为“0型”系统，采用PI控制或PID控制，可系统变为“I型”系统，被控对象Gp2（s）为“I型”系统，采用PI控制或PID控制可使系统变成“II型”系统。

4．当r（t）=1（t）时（实际是方波），研究其过渡过程。

5．PI调节器及PID调节器的增益Gc（s）=Kp（1+K1/s）=KpK1(（1/k1）s+1) /s=K(Tis+1)/s式中 K=KpKi , Ti=（1/K1）不难看出PI调节器的增益K=KpKi，因此在改变Ki时，同时改变了闭环增益K，如果不想改变K,则应相应改变Kp。

采用PID调节器相同。

6．“II型”系统要注意稳定性。

对于Gp2（s）,若采用PI调节器控制，其开环传递函数为G（s）=Gc（s）·Gp2（s）=K（Tis+1）/s·1/s（0.1s+1）为使用环系统稳定，应满足Ti>0.1，即K1<107．PID递推算法如果PID调节器输入信号为e（t），其输送信号为u（t）,则离散的递推算法如下：u（k）=u（k-1）+q0e（k）+q1e（k-1）+q2e（k-2）其中 q0=Kp（1+KiT+（Kd/T））q1=－Kp（1+（2Kd/T））q2=Kp（Kd/T）T--采样周期四、实验步骤1.连接被测量典型环节的模拟电路(图3-2)。

第四章１．设计一个ＰＩＤ控制器，实现对下例被控对象的控制，并观察选择不同的ＰＩＤ系数对控制效果的影响：210()10G s s s =++其中系数输入信号和正弦信号（绘制simulink 方块图，设置ＰＩＤ参数）．２．采用Simulink 建立一个系统，该系统方程为．式中，Ｘ为输入，Ｙ为输出．Ａ．Ｂ．Ｃ为常数．对该系统进行封装，要求能通过对话框修改Ａ．Ｂ．Ｃ的值．３．创建下面一个非线性环节的Ｓ函数和Ｍ函数模型，Ｋ１，Ｋ２，Ｋ３为各线段的斜，均大于零．创建子系统并封装，要求Ｋ１，Ｋ２，Ｋ３可调．K3K24.在ＭＡＴＬＡ下键入sltank,观察水箱模糊控制系统的Simulink 框图的设计及动态仿真结果．（１）注意ＰＩＤ控制器，模糊控制器及Ｓ函数所起的作用．（２）通过ＥＤＩＴ下的ＬＯＯＫ ＵＮＤＥＲ ＭＡＳＫ的功能观看封装模块ＰＩＤ，ＶＡＬＶＥ和ＷＡＴＥＲ ＴＡＮＫ各自的构成．５．已知ＡＰＯＬＬＯ运动轨迹（Ｘ，Ｙ）满足下面的方程***......33331111()()2,2x x yyx y x y x y r r r r μμμμμμ+-=+--=-+--其中*22221/82.45,1,1(),2()r x y r x y μμμμμ==-=++=-+初始条件：X(0)=1.2,y(0)=0,..(0)0,(0) 1.049x y ==-试求：（１）用ＸＤＯＴ命令进行仿真，绘制ＡＰＯＬＬＯ的位置（Ｘ，Ｙ）的轨迹曲线．（２）用Simulink 方块图进行仿真，所有参数用Ｍ文件输入．６．建立下面框图给定系统的Simulink 模型，其中的非线性块用Ｍ函数实现．选择合适的仿真参数进行仿真．。