若干非线性算子的性质及应用

耦合 不动 点． （ｉ） 如 果 面∈Ｄ满 足 ＝ 面 ）则 称 是 Ａ的不 动点 ． ｉ ｉ Ａ（ ， ，
１ 主 要 结 果
定理 ２ １ 设存 在 。 ∈Ｅ使 Ｉ ≤ 。算 子 Ａ， ［。 ］×［。 ］ ． ， ｔ ， ０ Ｂ．Ｍ ， Ｘ Ｉ ， 一Ｅ满足 下列 条件 ：
（ｖ ｉ） （） Ａ ， ， ｏ ＝ ； ｚ ， ） （ ） Ｖｕ ｓＭ三 三 ０ ≤
％；
（ Ⅱ ＋Ｑ（ 一“） （ ， ）Ａ ，。 。 （） ｕ ）其 中 Ｑ， Ｖ） ｏ 。 ≤ 。 ， （。 ） 。 一Ｇ ｔ 。 ， 。一 Ｇ为正有 界线 性算 子．
：
’
（ ＋ ［ （ ， ， ） Ａ “ ）一Ｂ ｕ ， ）＋ｒ ｖ 一ｕ）＋Ｑ 一ｕ ）＋Ｇ 一１ ） ． （ （ （ （ ２ ］ ，
＋Ｑ（ 一ｕ ）一Ｂ 一， １ （ ｌ 一）一Ｔ ｌ＋Ｑ（ Ｉ一 一） ｕ一 一 １ ］
类 似上 面的证 明易证 得 ＋ ＋ ０ 一 ． Ｍ＋ １一Ｍ ： （ ）１ 曰 ｕ ， ）＋ ，＋ Ｉ［ （
一
（ ）１Ａ （ ｌ 一）＋ 一 ＋Ｇ 一 一）一Ｂ（ ｌ １ ，＋ ＿［ （ 一， １ ｌ （ １一 １ ｕ一， ）一Ｔ ｌ＋ｑ（ ｌ—ｕ一） 一 ｕ一 ｖ一 １ ］ ［ ，＋ ） ＋Ｑ＋Ｇ＋ ） （０一ｕ） （ 一（ ］ ０． （． ） ２ ３
一“ ，
第３ ６卷
第 ４期
２１ ０ ０年 ｌ ０月
曲 阜 师 范 大 学 Ｊｕ ａ ｏ Ｑ ｆ Ｎ ｒ ａ ｏｒ ｌ ｆ ｕｕ ｏｍ ｌ ｎ
Ｖｏ ． ６ Ｎｏ． １３ ４ Ｏｃ ．２ ０ ｔ ０１
非线性算子方程组解的存在唯一性及其应 用
邱 忠华
（ 齐鲁 师范学 院数学 系，５０ ３ 山东省济南市） ２０１ ，

非线性定理非线性定理是数学分析中的一个重要定理，它描述了线性空间中非线性映射的存在性及特性。

非线性定理的研究在数学和物理学等领域有着广泛的应用。

首先，我们来回顾一下线性空间的概念。

线性空间是指满足线性运算法则的向量集合。

在线性空间中，任意两个向量的线性组合仍然是该空间中的向量。

而非线性定理是指对于某些非线性映射，它们无法表示成线性映射的线性组合。

非线性定理最早由法国数学家皮埃尔-隆佩尔特于1912年提出。

他证明了在某些无限维线性空间中，存在一个非线性映射，无法通过线性组合的方式来表示。

这一定理被称为“隆佩尔特非线性定理”。

隆佩尔特非线性定理的证明是基于一个构造方法。

首先，我们定义一个非线性函数f(x)，它在单位正方体上的值为1，而在正方体外的值为0。

然后，我们将这个函数无限次地缩放和平移，分布在整个线性空间中。

通过这个方法，我们构造出了一个非线性映射，无法通过线性组合的方式来表示。

隆佩尔特非线性定理的证明为非线性映射的存在性提供了一个数学依据。

它告诉我们，在某些情况下，我们无法使用线性组合的方法来表示一个非线性映射。

这在实际问题中有着重要的意义。

非线性定理在数学和物理学中有着广泛的应用。

在数学领域，非线性定理为非线性方程的解的存在性提供了一个基础。

在物理学中，非线性定理则被用于描述一些复杂的物理现象，例如流体力学中的湍流现象。

除了隆佩尔特非线性定理之外，还有许多其他非线性定理在数学和物理学中得到了研究。

其中一些定理是通过构造出一些特殊的非线性映射来证明的，而另一些定理则是通过使用数学分析中的其他方法来证明的。

非线性定理的研究在不断深入发展。

随着计算机技术和数值计算方法的进步，我们可以更好地理解非线性定理的特性和应用。

非线性定理在计算机图形学、计算机模拟、优化算法等领域中都得到了广泛的应用。

总结起来，非线性定理是数学分析中的一个重要定理，它描述了线性空间中非线性映射的存在性及特性。

隆佩尔特非线性定理是其中的一个经典结果，它证明了在某些无限维线性空间中存在一个无法通过线性组合表示的非线性映射。

《几类内部具有不连续性的微分算子耗散性及特征值关于问题依赖性的研究》篇一一、引言在数学物理中，微分算子及其耗散性是理解复杂系统动态行为的关键工具。

本文着重研究几类内部具有不连续性的微分算子，尤其是其耗散性及特征值与问题依赖性的关系。

不连续性在物理系统中广泛存在，如相变、材料界面等，因此，对这类微分算子的研究具有重要的理论和实践意义。

二、不连续性微分算子的基本概念不连续性微分算子指的是在定义域内存在不连续点的微分算子。

这类算子在描述某些物理现象时尤为关键，如量子力学中的波函数、流体力学中的边界层等。

其特点在于其导数在某一点或某一片区域内可能不存在或突然改变。

三、几类具有不连续性的微分算子（一）具有跳跃不连续性的微分算子这类算子的导数在某一点发生跳跃，如Dirac delta函数。

这类算子在描述冲击波等物理现象时有着广泛应用。

（二）具有振荡不连续性的微分算子此类算子在不连续点处呈现振荡特性，常见于某些波传播过程中，如波动方程中的周期性波包。

（三）其他类型的微分算子包括含有不规则几何边界或介质属性的不连续性微分算子等，如流体通过不同介质的界面时所形成的复杂流动模型。

四、耗散性的研究耗散性是描述系统能量随时间逐渐减少的性质。

对于具有不连续性的微分算子，其耗散性更为复杂。

一方面，不连续性可能使能量在某些点上突然释放或累积；另一方面，它也可能导致能量传递路径的改变。

本文通过理论推导和数值模拟两种方法，研究了这几类微分算子的耗散性，揭示了其与系统稳定性及能量转移的关系。

五、特征值与问题依赖性的研究特征值是描述微分算子性质的重要参数，与系统的稳定性、响应速度等密切相关。

对于具有不连续性的微分算子，其特征值与问题的具体形式密切相关。

本文通过分析不同问题背景下的特征值变化规律，探讨了其与问题依赖性的关系，为解决实际问题提供了理论依据。

六、结论与展望本文研究了几类内部具有不连续性的微分算子的耗散性和特征值与问题依赖性的关系。

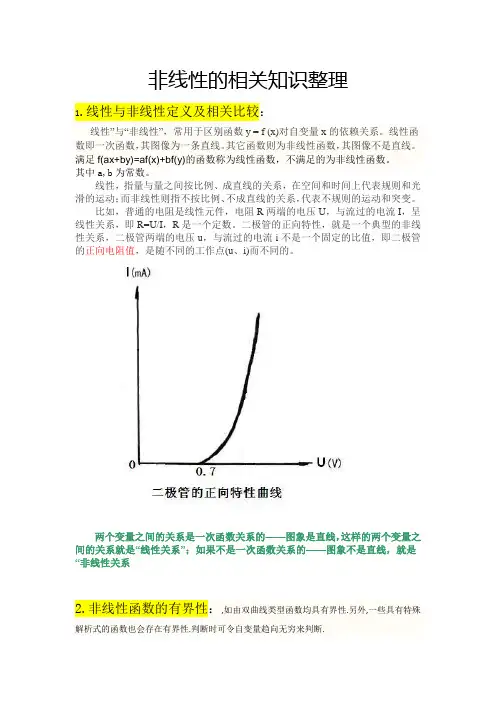
非线性的相关知识整理1.线性与非线性定义及相关比较：线性”与“非线性”，常用于区别函数y = f (x)对自变量x的依赖关系。

线性函数即一次函数，其图像为一条直线。

其它函数则为非线性函数，其图像不是直线。

满足f(ax+by)=af(x)+bf(y)的函数称为线性函数，不满足的为非线性函数。

其中a,b为常数。

线性，指量与量之间按比例、成直线的关系，在空间和时间上代表规则和光滑的运动；而非线性则指不按比例、不成直线的关系，代表不规则的运动和突变。

比如，普通的电阻是线性元件，电阻R两端的电压U，与流过的电流I，呈线性关系，即R=U/I，R是一个定数。

二极管的正向特性，就是一个典型的非线性关系，二极管两端的电压u，与流过的电流i不是一个固定的比值，即二极管的正向电阻值，是随不同的工作点(u、i)而不同的。

两个变量之间的关系是一次函数关系的——图象是直线，这样的两个变量之间的关系就是“线性关系”；如果不是一次函数关系的——图象不是直线，就是“非线性关系2.非线性函数的有界性：,如由双曲线类型函数均具有界性.另外,一些具有特殊解析式的函数也会存在有界性.判断时可令自变量趋向无穷来判断.3.非线性方程：就是因变量与自变量之间的关系不是线性的关系，这类方程很多，例如平方关系、对数关系、指数关系、三角函数关系等等。

求解此类方程往往很难得到精确解，经常需要求近似解问题。

而非线性方程组：就是几个非线性方程组合在一起成为一个方程组4.非线性规划的求解很灵活：不像解线性规划问题有单纯形法表这一通用方法，每种方法都有自己特定的适用范围。

算法概述无约束非线性规划算法确定搜索方向有如下方法：(1)最速下降法；(2)牛顿法；(3)拟牛顿法；在实际应用中，真正无约束的情况是很少的。

5.约束非线性规划算法：（1）可行方向法；（2）罚函数法；（3）梯度投影法；（4）逐步二次规划法（SQP）（MATLAB软件中常用SQP算法。

）6.非线性规划的数学模型为：(1) minf(X)(2)Hi(X)=0, i=1,2,…,m(3)Gj(X)≥0,j=1,2…l7.非线性方程组的解法例题：（1.）已知某非线性方程组如下：ff(1)=(3-5*x(1))*x(1)+1-2*x(2)＝0for k=2:9ff(k)=(3-5*x(k))*x(k)+1-x(k-1)-2*x(k+1)＝0endff(10)=(3-5*x(10))*x(10)+1-x(9)＝0试求该方程组的解。

非线性电路学习报告电路是由电气、电子器件按某种特定的目的而相互连接所形成的系统的总称。

当电路中至少存在一个非线性电路元件时（例如非线性电阻、非线性电感元件等），其运动规律要由非线性微分方程或非线性算子来描述，我们称之为非线性电路或非线性系统。

一、非线性电路的特点：1、非线性电路不满足叠加定理是否满足叠加定理是线性系统与非线性系统之间的最主要区别。

2、非线性电路的解不一定唯一存在对于仅由非线性电阻元件组成的电阻性电路，或考察非线性动态电路的稳态性质时，其电路的特性有一组非线性代数方程来描述。

这组方程可能有唯一解，也可能有多个解，甚至可能根本无解。

因此，在求解之前，应该对系统的解得性质进行判断。

3、非线性系统平衡状态的稳定性问题线性系统一般存在一个平衡状态，并且很容易判断系统的平衡状态是否稳定。

而非线性系统往往存在多个平衡状态，其中有些平衡状态是稳定的，有些平衡状态则是不稳定的。

4、非线性电路中的一些特殊现象在非线性电路中常常会发生一些奇特的现象，这些奇特的现象在过去和现在一直都是非线性电路理论的重要研究课题，促进了非线性理论的研究和发展。

例如，非线性电路在周期激励作用下的次谐波振荡和超次谐波振荡；系统解的形式因为参数的微小变化而发生本质性改变的分叉现象；对于某些非线性电路和系统，还会出现一种貌似随机的混沌现象。

分叉和混沌现象的研究大大丰富了非线性系统科学的理论，促进了系统科学的发展。

二、非线性电阻电路非线性电阻电路研究的内容大体可分为理论定性分析和定量分析两大部分。

理论定性分析主要研究非线性电阻电路解得存在性和唯一性问题。

对于由无源电阻网络组成的网络，其无增益性质也是研究的重要内容之一。

定量分析大体包含四个方面：一是图解分析法和小信号分析法，二是数值分析方法，三是分段线性化方法，四是友网络法。

1、图解分析方法图解分析法用来解决简单非线性电阻电路的工作点分析、DP图和TC图分析等问题。

(1)曲线相交法：将其中一些非线性元件用串并联方法等效为一个非线性电阻元件，将其余不含非线性电阻的部分等效一个戴维南电路，画出这两部分电路的伏女關线，它们的交点为电路的丄作点，或称为静态丄作点Q(U Q,I Q)O图1曲线相交法(2)DP图法：若某非线性一端口网络的端口伏安矢系也称为驱动点特性曲线DP确定，则已知端口的激励波形，通过图解法可求得响应的波形。

n n
T 是线性算子。 {Tn }是基本列 0, N , 当 n, m N 时，Tn Tm Tn Tm Tn 为基本数列 Tn 有界，设 Tn M , ( n 1, 2,3, ) Tn x Tn x M x Tx M x（n ） T 是有界算子 T B ( X , Y )
注：1）定义中，D为算子T的定义域; M是算子T的界值；T(D)={Tx|xD}称
为算子T的值域 2）有界算子与有界函数不同。例如 f(x)=x 无界函数 有界算子: |f(x)|=|x|<2|x|
3) T是连续算子 T在D上处处连续
2. 有界线性算子的性质 定理1 设X、Y是线性赋范空间，DX是线性子空间，T: DY 是线性算子，则
x X
定理2 设X、Y是线性赋范空间，DX是线性子空间，T: DY是 有界线性算子，则T的范数具有下列性质： (1) ||Tx||||T|| ||x||, xD (2)
T sup Tx Y sup Tx Y
x 1 xD x 1 xD
(即||T||是有界线性算子T的最小界值） （可作为范数定义）
x 1 x D
则B (X,Y)成为线性赋范空间，称之为（有界）线性算子空间。
2. 线性算子空间中的极限理论 定义4 （算子序列的一致收敛与强收敛）设X、Y是两个线性赋范 空间，Tn, TB(X,Y), n=1,2,…
(1) 如果||Tn-T||0, 则称算子序列{Tn}按范数收敛于T, 或称{Tn}一致收敛于T. (2) 如果xX,||Tnx -Tx||0, 则称算子序列{Tn}强收敛 于T, 或称{Tn}按点收敛于T.
T su p T x T x 0 m ax

2000年10月16日
2-5
第6页/共93页
收敛
Newton-Raphson 法需要一个收敛的度量以决定何时结束迭代。给 定外部载荷（Fa），内部载荷（ Fnr ）（由单元应力产生并作用于 节点），在一个体中，外部载荷必须与内力相平衡。
Fa - Fnr = 0
收敛是平衡的度量。
2000年10月16日
样将易于绘制载荷－位移曲线。
2000年10月16日
2-18
第19页/共93页
自动时间步
• 子步中的载荷增量大小 (F) 由时间 步的大小t决定。
• 时间步大小可由用户设定或由 ANSYS自动预测与控制。
载荷
F2 F
• 自动时间步 算法可在载荷步内为所有
子步预测与控制时间步长的大小（载 荷增量）。
F1
CRITERION= 2.113
DISP CONVERGENCE VALUE = 0.1024E-01 CRITERION= 0.9406
<<< CONVERGED
EQUIL ITER 3 COMPLETED. NEW TRIANG MATRIX. MAX DOF INC= 0.3165E-02
FORCE CONVERGENCE VALUE = 2.179
CRITERION= 2.108
<<< CONVERGED
>>> SOLUTION CONVERGED AFTER EQUILIBRIUM ITERATION 4
*** LOAD STEP
1 SUBSTEP 15 COMPLETED. CUM ITER =
31
*** TIME = 59.1250

《非线性算子不动点问题的迭代算法及其应用》读书笔记1. 非线性算子不动点问题的背景和意义在数学的众多分支中，非线性分析是一个极具挑战性和实用性的领域。

非线性算子不动点问题作为非线性分析的重要组成部分，一直是数学研究中的热点和难点。

该问题广泛存在于数学理论、物理研究、工程技术和经济金融等多个领域，具有非常丰富的实际背景和研究意义。

随着科学技术的飞速发展，各个领域中所遇到的实际问题越来越多地呈现出非线性特征。

在物理学的许多领域，如量子力学、场论、相对论等，很多物理现象的本质是非线性的。

在工程领域，许多实际问题如结构优化、控制系统、信号处理等也涉及大量的非线性问题。

这些问题往往可以通过转化为非线性算子不动点问题进行研究。

研究非线性算子不动点问题具有重要的理论价值和实践意义。

首先，对于非线性算子不动点问题的研究有助于推动非线性分析及相关领域的发展。

通过对非线性算子性质、迭代算法及其应用的研究，可以丰富和发展非线性分析的理论体系。

非线性算子不动点问题在实际应用中具有广泛的价值，在求解复杂系统的平衡态、优化问题、控制理论、图像处理等领域，非线性算子不动点问题的研究方法和技术都发挥着重要作用。

随着计算机科学的快速发展，非线性算子的迭代算法在数值计算、机器学习等领域的应用也日益广泛。

非线性算子不动点问题作为数学和其他领域交叉研究的重要课题，不仅具有深厚的理论背景，而且在实际应用中具有广泛的价值和深远的意义。

通过对该问题的深入研究，不仅可以推动数学理论的发展，还可以为其他领域的实际问题提供有效的解决方法和工具。

1.1 非线性算子的基本概念其中X是一个线性赋范空间。

这类问题的主要挑战在于，由于非线性算子可能不具备解析解，因此需要寻求数值解法。

非线性算子不动点问题的核心在于寻找一个序列{x_n}，使得x_{n+1} f(x_n)，并且这个序列的极限满足某个条件。

我们需要找到一个近似解x，使得f(x) approx 0。

则称 为 ＺＰ Ｓ空 间． ——
在 ＺＰＳ空 间 Ｅ 中， －— 记 ： ： ： ， 中 ∈Ｅ， 兰：： 其 几为 自然数．
礼
易证 下面 引理 成立．
引理 １３ 当 ｔ ０１， ． ∈（，）佗∈Ⅳ ， ≥１ 下列不等式成立 ： 十 ，
（ 一ｔ ～ｔ ） ≤
那 么 ｚ＝Ｘ在 Ｄ 中必有解．
（ ） Ｇ３
证明 不妨设 ≠ ｚ∈Ｏ 否则定理得证） 令 （） —ｔｘ ｔ ０１ ∈ ． ， Ｄ（ ． Ｘ ＝Ｘ Ａ ， ∈［ 】 下面证 明 ，，
ｋ（Ｊ）ｔ∈［，］ ［ ， ０１．事实上 ， ） 假设 ∈ｈ（Ｄ）则存 在 ｔ ［ １， ｏ∈Ｏ 使得 ＝ ｔ Ｏ ， ｏ∈ ０ ］Ｘ ， Ｄ， ０一ｔＡ ０ ｏ ｘ， 则 ｔ ０否则， ｔ ０ ＝ ｏ≠ （ 若 ｏ＝ ，由 ０一ｔＡ ｏ得 到 Ｘ ｏｘ Ｏ＝ ｐ∈ Ｄ， Ｘ ＿Ｄ 矛 盾） ｔ １否 与 ｏ∈Ｏ 且 ０≠ （
第 １ 卷 第 ２期 ３
２ １ 年 ６月 ０１
应用泛函分析学报
ＡＣＴＡ ＡＮＡＬｙＳ Ｓ ＦＵＮＣＴ１ Ｉ ０ＮＡＬ Ｓ ＡＰＰＬＩ Ｉ ＣＡＴＡ
、ｏ１１ ， ．３．Ｎ Ｏ． ２
Ｊ ｎｅ ２ １ ｕ ， ０１
ＤＯ ｉ． ２／ＰＪ １０ ０１ ０６ Ｉ： ０ ７４Ｓ ．． ６． １． １８ ３ １ ２ ０ 文章编号： ０ ９１２ （ １）２０６—４ １０—３７２ １０—１８ ０ ０
１ 厶 （） ； ） ０ ＝０
下列条 件：
２ （） ） ｓ ：日（）Ｖ ｓ， ８∈Ｒ 当且仅 当 Ｘ：０（ 中 ０表 Ｅ 中零元） 其 ； ３ 对 任意 实数 。≠ ０ ， ｓ ＝ （ ） ） ， ｎ（） ； ４ 对任意 的， １８ ∈Ｒ， ） ８，２ 如果 ８） １ ｆ（２ ＝１ 则 ＋ （１ ２ ＝ １ １ ＝ ，￣８） ， ｓ ＋ｓ） ； ５ 对 任意 的 ＸＹ∈Ｅ 以及 一切 ８，２ ） ， １８ ∈Ｒ＋ 有 ＋ （１ ２ ≥Ａ（ｘ８）凡（２） ， ｓ ＋８） ｆ （１， ｓ）．

山东大学博士学位论文非线性算子方程的多重解与变号解及其应用姓名：***申请学位级别：博士专业：基础数学指导教师：***2002.3.18非线性算子方程的多重解与变号解及其应用张克梅（山东大学数学院，济南，２５０１００）摘要ｌ对来自于数学，物理，化学，生物学，控制论等中的非线性闻题，已日益引起人们的广泛重视．目前，非线性分析已成为现代数学中最重要的研究方向之一．锥理论和拓扑度理论作为研究非线性算子的基本工具，已成为非线性分析的最重要的组成部分．在七十年代Ａｍａｎｎ将锥理论与拓扑度理论结合，建立了锥映射的不动点指数理论．许多著名的数学家，如Ｈ．Ａｍａｎｎ，Ｋ．Ｄｅｉｍｌｉｎｇ，Ｖ．Ｌａｋｓｈｍｉｋａｎｔｈａｍ，郭大钧，孙经先等利用这些理论作过许多很深刻的工作／本文利用拓扑度理论和、不动点指数理论，研究非线性算子方程的多重解和变号解的存在性．多解性结果对著名的Ａｍａｎｎ三解定理作了本质上的改进，而有关变号解的存在性结果是一个崭新的工作，到目前为止，这方面的结论还很少见．ｆ在非线性算子方程的多重解的研究中，已有许多好的结果，其中最著名的当属Ａｍａｎｎ在１９７６年得到的Ａｍａｎｎ三解定理（见【１］）．此结论利用两对上下解得到三个非零解，其中两对上下解丑，矾（ｉ＝１，２）满足下列序关系：ｚｌ＜掣ｌ＜Ｘ２＜Ｙ２Ｓｈｉｖａｊｉ［４】将上述序关系放宽为下列形式Ｘｌ＜Ｙｌ＜Ｙ２，，Ｔ１＜Ｘ２＜Ｙ２，Ｘ２垡Ｙｌ事实上，上述序关系可以放宽为下列更广的形式ｚｉ＜Ｙｌ，Ｘ２＜Ｙ２，ｚｌ＜抛，奶ｇＹｌ山东大学博士学位论文＝＝＝＝：：：＝！＝：＝＝＝＝：：！：＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝Ｉ＿－但上述三种情况都要求ｚｌ＜Ｙｌ，ｚ２＜耽，ｚ１＜Ｙ２，鉴于此种原因，我们在本文的第一章和第二章作了下面两方面的推广：（ｉｏ）ｚ１ｇＹｌ，。

２≤Ｙ２，ｚ１＜ｙ２；（２０）ｚｌ＜Ｙｌ，Ｘ２＜Ｙ２，Ｘｌ茗Ｙ２，Ｘ２ｇＹ１．情形（１０）称为两对反向上下解，情形（２０）称为两对平行上下解（见注１·２·２和注１．３１）．反向上下解的最初想法是由郭大钧教授在二十世纪八十年代中期提出的，后来孙经先教授在文献ｆ１７］中首次提出了反向上下解这一概念，并且在ｆ７】中利用一对反向上下解得到了正解的存在性，平行上下解是本文提出的一个新定义．本文第一章在假定线性算子Ｋ满足一致正条件（见定义１．２．１）的前提下，证明了若Ａ＝Ｋｆ有两对反向上下解，则算子方程ｚ＝Ａｘ至少有三个不同的解；若Ａ＝Ｋｆ有两对平行上下解，则Ｘ＝Ａｘ至少有六个不同的解，并且对本章的关键性条件一一致正条件作了讨论，证明了一类Ｈａｍｍｅｒｓｔｅｉｎ型线性积分算子满足一致正条件．作为应用，我们考虑了非线性Ｓｔｕｒｍ—Ｌｉｏｕｖｉｌｌｅ两点边值问题和微分方程组，证明了Ｓｔｕｒｍ．Ｌｉｏｕｖｉｌｌｅ问题和微分方程组分别有三个和六个不同的连续解．第二章是第一章的继续．本章在假设算子Ａ存在两对平行上下解的前提下，讨论了算予方程ｚ＝Ａｚ的多解的存在性，得到了一个六解定理．第一章使用的关键＿条件一一致正条件是一个比较强的条件，本章结果中没有使用这一条件，而是用另外一个条件一（日）一条件来代替．（Ｈ）一条件是孙经先教授在文献［６】中首次提出的。

几类非线性偏微分方程精确解的研究几类非线性偏微分方程精确解的研究摘要：非线性偏微分方程在数学和物理领域中有着广泛的应用，其求解是一个重要的研究方向。

精确解研究涉及到方法和技术，大大提高了求解的速度和精度。

本论文针对几类非线性偏微分方程进行研究，探讨其精确解。

首先，本文介绍了这些非线性偏微分方程的基本概念和性质，包括一些应用领域和模型的描述。

然后，我们提出了精确解研究的一般思路和流程，并阐述了具体实现方法。

接着，我们选择了几种典型的非线性偏微分方程，分别介绍其数学特性、求解方法、解的性质等方面，并通过实例进行验证和说明。

最后，我们评估了精确解研究的优缺点，探讨其未来发展方向。

关键词：非线性偏微分方程、精确解、方法、技术、数学特性。

正文：第一章绪论1.1 非线性偏微分方程的基本概念偏微分方程（Partial differential equation）是描述自然界中物理学、工程学、化学、社会学等学科中的数量关系的数学方法之一。

偏微分方程的解法往往是比较困难的，因此近年来许多研究者将精力集中在非线性偏微分方程的求解上。

非线性偏微分方程是指，未知函数出现在方程的高次项、积、除法、指数函数等时，即同一方程中出现有关函数和其偏导数的非线性项。

1.2 非线性偏微分方程的应用领域非线性偏微分方程的求解方法及其精度和速度在科学和工程应用中具有广泛的应用。

例如，在流体力学中，非线性偏微分方程可用于描述涡旋流、湍流、振荡流、波浪等。

在分子生物学中，非线性偏微分方程可用于描述分子扩散、蛋白质演化等。

在量子力学中，非线性偏微分方程可用于描述玻色、费米子体系等。

在统计学中，非线性偏微分方程可用于描述随机微分方程、布朗运动等。

1.3 非线性偏微分方程的模型如果要用非线性偏微分方程来描述一个现象，我们需要构造出一个非线性偏微分方程模型。

偏微分方程模型一般包含几个要素，例如：基本方程、边界条件、初始条件、材料参数等。

第二章精确解研究的一般思路和流程2.1 精确解的定义和种类精确解是指以公式的形式表示的解。

１２
ｋ
并称Δ为一分布，对任意 ｘ ∈ Ｕ，有Δ（ｘ）
为由ｆ （ｘ），ｆ （ｘ），…，ｆ （ｘ）所张成的一个Ｒｎ空
１
２
ｋ
间。
由此有对非线性系统：
（３）
式（３）中 ｕ ∈ Ｕ，ｘ ∈ Ｘ，Ｕ 为输入子集，通 常为 ｍ 维的 Ｌｅｂｅｓｇｕｅ 可积函数组成的线性子 空间，Ｘ 为状态流形，通常理解为 Ｒｎ 中的一个 开集。从而对非线性系统在状态 ｘ 的特性的分 析，便转换为其分布Δ（ｘ）的分析。
由于微分几何中的一些病态问题的发现， 导致了微分代数的发展，其基本思想与微分几 何雷同。微分几何与微分代数的方法，从某种 意义上说是将非线性的问题通过空间的变换 转换为线性的问题，并照搬线性处理中相关理 论的方法， 具有数学的抽象性， 理论上的局限 性及计算上的困难性。
摄动法： 摄动法将非线性系统的解按小参数ε的 幂次展开的近似计算方法，称为摄动法或小参 数法［２］。在弱非线性的情形下，设非线性方程 为：
信号分析中，为了能有效的分析非平稳信 号 Ｗｉｇｎｅｒ［３］和 Ｖｉｌｌｅ［４］率先引入了 Ｗｉｇｎｅｒ－ Ｖｉｌｌｅ分布，进行信号的非线性变换，设复信号 为的时域表示 ｚ（ｔ）则有其时域 Ｗｉｇｎｅｒ－Ｖｉｌｌｅ 变换：
这种非线性的信号变换在非平稳信号的 分析与处理中起着极为重要的作用，而且在此 基础之上也发展起了各种形式的变形和改进。
学 术 论 坛
魏敏 （１．长沙航空职业技术学院 湖南长沙 ４１０１２４； ２．湖南师范大学 湖南长沙 ４１００８１）
摘 要：被动句是俄汉语基本句型之一，文章以符号学为基础，以符号标记理论为出发点，分析了俄、汉语被动句的识别方式并讨论了俄、
汉语中被动句的对应情况。通过对比，我们可以更清楚地认识到在俄汉语被动句的识别中除了根据形态标记外还要重视句子的意义和词

非线性动力学理论及其在机械系统中应用的若干进展陈予恕1, 2曹登庆1吴志强21哈尔滨工业大学航天学院，137信箱，哈尔滨1500012天津大学机械工程学院，天津市 300072摘要：非线性动力学的理论及其工程应用是非线性科学研究的前沿和热点，应用非线性动力学的理论揭示事物动态过程现象的本质和机理，进行自主性原始创新，具有十分重大的理论和应用价值，在科学与工程中具有广阔的应用前景。

本文综述非线性动力学基础理论方面的近期研究成果及其在机械系统中应用的研究进展。

理论研究方面主要涉及揭示非线性动力系统周期分岔解与系统结构参数之间关系的C-L方法、高余维分岔的普适分类、高余维非对称分岔的普适开折、约束分岔的分类、计算非线性自治系统正规形的直接方法、计算非线性非自治系统正规形的复内积平均法以及高维非线性系统的降维方法等。

应用方面主要涉及大型旋转机械非线性转子系统的失稳机理、分岔解与混沌运动、故障诊断及其综合治理技术；冲击振动机械的稳定性、Hopf分岔、亚谐分岔、余维二分岔和混沌运动；大型共振筛的非线性振动及其动力学设计方法等。

关键词：非线性动力学，C-L理论方法，非线性转子动力学，故障治理技术，复杂分岔与混沌非线性动力学的基础理论与数学或应用数学有着非常紧密的联系，同时又是机械、土木、航空航天、水陆运输、兵器等工程学科的重要基础。

它与技术学科结合推动了现代工程技术的蓬勃发展，具有应用性很强的鲜明特色。

在国民经济、国防工业和工程技术中，有大量的重要实际问题迫切需要用非线性动力学理论和方法加以处理，动力学理论的工程应用在带来巨大经济效益的同时，也为推动高维复杂非线性动力学系统的基础理论研究提供更广的发展空间，其意义十分重大。

复杂高维非线性动力学系统的降维、全局分岔、周期解分岔理论及通向混沌的道路，是当前科学研究的重大前沿课题之一，是各科技工程领域进行自主创新的重要理论基础，同时也是具有挑战性的国际前沿领域。

发展新的分析方法、揭示新的现象及其产生机理一直是非线性动力学理论研究的主题，解决工程动力学疑难问题、探索基于非线性动力学的设计方法，越来越受到各国科学家与工程师们的高度重视。

关于具有凸性的非线性算子及其应用【摘要】：本文的研究内容主要有两部分．第一部分：讨论了α(1)-凸算子，具有凹凸性的序压缩算子及φ凸-ψ凹混合单调算子等三类非线性算子．第二部分：用非线性算子理论，特别是用我们得到的结论讨论了一类泛函微分方程奇异边值问题和一类脉冲积分-微分方程初值问题的求解．深入研究带有凸性的非线性算子无论在理论上还是在应用上都具有重要意义．比如，在工程问题中，核问题中及经济问题中往往涉及到带有凸性的非线性算子．但遗憾的是对这类算子的研究尚未能深入，因而对解决有关问题尚无有力工具．脉冲微分方程理论兴起于上世纪六十年代末．脉冲现象在现代科技各领域的实际问题中是普遍存在的，其数学模型往往可归结为脉冲微分系统．脉冲微分系统能够更深刻，更精确地反映事物的变化规律．近年来，这类系统已重要应用于航天技术，信息科学，控制系统，通讯，生命科学，医学，经济等领域．但对它的理论及应用研究仍处于初级阶段．讨论这类问题有十分重要的意义．本文的讨论主要采用了半序方法．与一般文献相比，本文的不同之处在于，不是对单值的像用半序，而是对集值的原像用半序．本文主要的研究结果有：在§2．1中，讨论了一类α(1)-凸算子；在较弱的条件下得到了α(1)-凸算子不动点的存在性和唯一性，具体结果见定理2．1．1，定理2．1．4，定理2．1．6，定理2．1．8，定理2．1．11，定理2．1．12，定理2．1．21等；并应用于一类偏微分方程的求解，见定理2．1．23．在§2．2中，讨论了一类具有凹凸性的序压缩算子；得到了其不动点的存在唯一性条件，具体结果见定理2．2．15，定理2．2．16，定理2．2．18，定理2．2．21，定理2．2．24-2．2．27等；并应用于讨论一类减算子，见定理2．2．17，定理2．2．20．在§2．3中，引入了本质上是讨论凸性问题的φ凸-ψ凹混合单调算子的概念，在较宽松的条件下获得了这类算子正不动点的存在性和唯一性条件，具体结果见定理2．3．2-2．3．20；并应用于一类积分方程的求解，见例2．3．21．在§3．1中，讨论了Banach 空间中泛函微分方程奇异边值问题其中y~t(s)=y(t+s)，(?)s∈(-r，a]．利用Avery和Henderson的一个不动点定理，得到了(1)至少有两个正解的充分条件，见定理3．1．4；又利用α(∈(0，1))0凹算子的不动点定理得到了(1)有唯一正解的条件，见定理3．1．6．在§3．2中，讨论了如下Banach空间中一阶和二阶脉冲积分0微分方程初值问题(2)和(3)：其中f∈C(J×P×P,P)，I_k∈C(P,P)(k=1，2，…)，x_0θ，△x|_(t=t_k)=x(t_k~+)-x(t_k)，x(t_k~+)表示x(t)在t=t_k处的右极限；Tx(t)=∫_(t0)~tK(t，s)x(s)ds((?)t∈J)，K∈C(D，R~+)，D={(t，s)∈J×J|t≥s}，(R~+=[0，+∞))；其中f∈C(J×P×P×P,P)，I_k，I_k∈C(P,P)(k=1，2，…,)，x_0θ，x’_0≥θ，△x|_(t=t_k)=x(t_k~+)-x(t_k)，△x’|_(t=t_k)=x’(t_k~+)-x’(t_k~-)，x’(t_k~-)和x’(t_k~+)分别表示x’(t)在t=t_k处的左极限和右极限；Tx(t)=∫_(t0)~tK(t，s)x(s)ds((?)t∈J)，K∈C(D，R~+)，D={(t，s)∈J×J|t≥s}，(R~+=[0，+∞))；Sx(t)=∫_(t0)~(+∞)H(t，s)x(s)ds((?)t∈J)，H∈C(J×J,R~+)；利用我们在文[58]中的结论，得到了(2)及(3)的正解的存在性和唯一性，并给出了求解的迭代式及解的误差估计式，见定理3．2．5，定理3．2．10，定理3．2．14，定理3．2．16，定理3．2．18，定理3．2．22，定理3．2．26，定理3．2．28，定理3．2．30．【关键词】：锥Banach空间凸算子脉冲积分-微分方程【学位授予单位】：山西大学【学位级别】：博士【学位授予年份】：2008【分类号】：O177.91【目录】：中文摘要6-8英文摘要8-11第一章概述11-19§1.1关于第二章的介绍11-16§1.2关于第三章的介绍16-19第二章具有凸性的几类非线性算子19-69§2.1一类α(>1)-凸算子19-36§2.2具有凹凸性的序压缩算子36-50§2.3φ凸-(ψ)凹混合单调算子50-69第三章具有凹性凸性的若干非线性算子在微分方程中的应用69-99§3.1一类奇异边值问题69-75§3.2一类脉冲积分-微分方程初值问题75-99参考文献99-108发表文章目录108-109致谢109-110 本论文购买请联系页眉网站。

单参数变换群中L算子的性质和应用作者：杨在春来源：《科技创新导报》 2014年第3期杨在春(山东科技大学信息系山东泰安 271019)摘要：通过无穷小变换引入单参数变换群(OPG)中的L算子，介绍并证明L算子的几个重要性质，在此基础上给出了其性质的一个应用。

关键词：无穷小变换单参数变换群 L算子中图分类号：O177 文献标识码：A 文章编号：1674-098X(2014)01(c)-0219-0221世纪60年代中期以来，非线性波动的研究取得了惊人的进展，非线性科学在许多科学研究领域得到了广泛的应用[1]。

近年来，各种由非线性发展方程描述的非线性问题在一定程度上都取得了较好的解决方法，如反散射方法、李变换群方法、齐次平衡法、双曲正切函数展开法、试探函数法、非线性变换法、s i n e — c o s i n e方法和Ja c obi椭圆函数展开法等，并用这些方法求解了很多非线性发展方程。

但是非线性方程的求解仍然难以把握，特别是当非线性方程带有高维、高阶或高次项时求解更是难上加难，所以寻求非线性发展方程的解析解仍是一个长期而艰巨的任务[2]。

算子是现代科学技术中广泛使用的一个概念，是函数、映射等概念的进一步推广。

常用的算子有哈密尔顿算子、拉普拉斯算子、遗传算子等，许多学科分支是在一些基本算子的基础之上构建起来的。

算子也称为算符，在数学上，常把无限维空间到无限维空间的变换叫做算子。

从更广泛的意义上来讲，算子通常用来表示一个或一组作用，对一个算子的应用，我们必须研究其整体性质。

1 L算子的定义李变换群方法是由挪威数学家M.S.L i e发展起来的一种求解微分方程的方法。

该方法涉及到的单参数变换群(OPG)是一种连续群[3]，给出x-y平面上的变换：如果( 1 ) 式满足以下三个条件，1 ：表示恒等变换；2：表示逆变换；3：两个变换的乘积仍为(1)式对应的群中的元素，则称(1)式对应的群为单参数变换群，又称L i e点变换群。

(H3)算子B∶P2→P1是线性的,当x≠θ时有Bx>θ.存在e∈P1+和实数ε0>0使Bx≥ε0‖x‖e,(V)x∈P2+(3.2.1)
(H4)算子A=BF是全连续算子.则A存在正不动点.定理3.2.2设E是实Banach空间,P是E中的正规锥,A∶P→P是-α凹的全连续算子(α>0),且
sup{||Ax‖∶||x|=1}<∞,inf{||Ax‖∶||x=1}>0则A在P中至少有一个正不动点.
全文分四章。在第一章中,主要介绍了半序Banaeh空间非线性算子的研究历史背景、现状以及半序Banach空间中的预备知识;在第二章中,利用半序方法研究了Banach乘积空间中严格集压缩减算子不动点存在唯一性问题,在弱连续的条件下,得到了不动点的存在唯一性和迭代收敛性,同时,给出了它们的一些应用;在第三章中,建立了拟弱连续减算子的正不动点定理,并证明了算子C=A+B,C=D-A的正不动点存在唯一性定理;在第四章中,得到了半序Banach空间中混合单调算子的不动点存在性及唯一性定理。
4.学位论文孙单单半序Banach空间中非线性算子的若干问题的研究2007
非线性泛函分析已成为现代数学中的重要研究方向之一,而非线性算子理论又是非线性泛函分析的重要内容。自二十世纪八十年代初以来,郭大钧、孙经先、杜一宏、刘兆理、朱传喜、李福义等利用半序方法研究了缺乏紧性或缺乏连续性条件的非线性问题,并获得一系列新的结果。本文分别对半序Banach空间中非线性算子一些问题进行了研究。
1),(n=1,2…),且对任给的δ,inf{|λ|∶λ∈σ(I+T)}<δ<1存在n0,当n≥n0时,有下面的误差估计‖xn-u*‖≤Nδn‖x0-u0‖+1Nδnδ‖u1-

非线性优化算法研究及其应用一、引言非线性优化是一类重要的数学问题，应用广泛于科学、工程、经济等领域。

目前，该领域已经发展出多种非线性优化算法，本文将介绍其中常用的几种算法及其应用。

二、常见非线性优化算法1. 梯度法梯度法也称作最速下降法，是求解无约束问题的常用方法。

该算法的基本思想是：从某一初始点出发，在每一步中沿着当前位置的求导方向下降最快的方向走向下一个点，直到达到最优解。

梯度法的优点是简单易用，但由于其收敛速度较慢，在复杂问题中应用受到限制。

2. 共轭梯度法共轭梯度法是用于求解对称正定问题的一种方法。

在每一步中，该算法找到和前一步方向不同的下降方向，从而加快了收敛速度。

如果函数能够准确地表示为二次函数，则共轭梯度法能够在有限步数内找到最优解。

3. 牛顿法牛顿法是使用二阶导数信息来求解无约束问题的一种加速方法。

该算法在每一步中使用当前位置的一阶导数和二阶导数信息来进行迭代。

由于牛顿法需要计算二阶导数，因此它可能会受到数值不稳定性的影响。

此外，在复杂问题中它的收敛速度也较慢。

4. 拟牛顿法拟牛顿法是一种非常流行的无约束问题求解方法。

与牛顿法不同的是，拟牛顿法使用一阶导数信息来逼近二阶导数信息。

通常情况下，它会使用BFGS或DFP方法进行逼近。

拟牛顿法的优点是在需要求解大型问题时，它能够处理复杂的变量空间，且比梯度法更快。

三、应用案例1.工程中的优化问题在工程中，优化问题常常用于设计产品、制造工艺和材料的选择等领域。

利用非线性优化算法，工程师可以对设计和生产流程进行优化，提高产品的质量和降低成本。

例如，一家航空公司可能会使用拟牛顿法来优化旅客飞行过程中的飞机燃油消耗问题。

借助该算法，他们可以计算出最佳飞行路线以及在飞机使用的燃料和航速之间进行最优权衡。

2.金融中的优化问题金融中的优化问题也非常关键。

例如，一家投资组合管理公司可能需要在市场上进行投资，并考虑一些限制因素。

非线性优化算法可以帮助他们优化投资策略，达到最佳风险/收益比。