部分线性变系数模型的一种新的轮廓_Profile_最小二乘估计_张波
- 格式:pdf
- 大小:853.89 KB
- 文档页数:9

随机丢失响应的半参数变系数部分非线性模型的估计张文佳【摘要】通过研究随机缺失响应变量的半参数变系数部分非线性模型,对模型中的各个参数进行估计;通过将线性近似方法与随机缺失响应变量的变系数部分非线性模型的样条估计方程相结合来估计模型中的未知参数,并验证了所得估计量的渐近性质;最后,通过进行两组模拟来验证估计过程的合理性,评估所提出的估计方法的性能,并根据不同的数据量做出估计精确度的对比;结果表明,两个步骤在有限样本中表现良好,随着样本数据量的增加及缺失率的降低,估计的精确性提高.【期刊名称】《重庆工商大学学报(自然科学版)》【年(卷),期】2018(035)004【总页数】6页(P7-12)【关键词】变系数部分非线性模型;样条估计;线性近似;数据缺失【作者】张文佳【作者单位】南京理工大学理学院,南京210094【正文语种】中文【中图分类】O152.50 引言作为非参数回归模型的演化版本,许多学者已经对其进行过研究。
为了充分利用已知数据中的有效信息,考虑半参数变系数部分非线性模型,它可以定义为Y=XTα(U)+g(Z,β)+ε(1)其中α(·)=(α1(·),α2(·),…,αp(·))T是一个p维未知变系数函数,β=(β1,β2,…,βr)T是一个r维未知向量。
Y是响应变量,(X,Z)∈Rp×Rq及U∈R是协变量。
为了避免维数祸根,一般简单假设U是单变量。
ε是模型的随机误差且与协变量(X,Z,U)独立,其期望和方差分别满足E(ε|X,Z,U)=0,E(ε2|X,Z,U)=σ2。
g(Z,β)是已知的非线性函数,且Z和β不需要具有相同的维度。
变系数部分线性模型是最常见的半参数模型,被广泛研究。
ZHOU X和YOU JH[1],ZHAO P和XUE L G[2]及AHMAD I等[3]阐述了这种模型的许多经典方法、例子和应用。
但在该模型中响应变量Y和协变量Z之间的关系是线性的,这可能会增加模型估计过程中的误差。

最小二乘拟合的概念-概述说明以及解释1.引言1.1 概述最小二乘拟合是一种常用的数据分析方法,通过最小化观测值与拟合值之间的残差平方和来求取最优拟合曲线或平面,从而描述数据的模式和趋势。
该方法被广泛应用于统计建模、机器学习、信号处理、金融分析等领域。
最小二乘法的核心思想是寻找一条曲线或平面,使得该曲线或平面与数据点的残差之和最小。
通过最小二乘法,我们可以得到最佳拟合曲线或平面,从而对数据进行更准确的描述和预测。
因此,最小二乘拟合在数据分析中具有重要的意义。
本文将详细介绍最小二乘拟合的定义、原理和应用,从而帮助读者更好地理解和运用这一重要的数据分析方法。
1.2 文章结构文章结构部分的内容如下:文章结构部分将介绍整篇文章的组织结构和主要内容安排,以便读者对文章的整体框架有一个清晰的认识。
在本文中,主要分为引言、正文和结论三个部分。
- 引言部分包括对最小二乘拟合的概念进行简要介绍,阐述本文撰写的目的和重要性。
- 正文部分将详细讨论最小二乘拟合的定义、原理和应用,以便读者全面了解这一重要的数据分析方法。
- 结论部分将对最小二乘拟合的重要性进行总结,探讨最小二乘法在数据分析中的价值,并展望最小二乘拟合在未来的发展趋势。
通过这样的结构安排,读者可以清晰地了解本文的主要内容和章节布局,有助于他们更好地理解和掌握最小二乘拟合的相关知识。
1.3 目的本文的主要目的是介绍最小二乘拟合这一重要的数学方法。
通过对最小二乘拟合的定义、原理和应用进行详细讨论,希望读者能够深入了解这一方法在数据分析和模型拟合中的重要性。
此外,本文还将探讨最小二乘法在实际问题中的应用,以及展望未来最小二乘拟合在数据分析领域的发展趋势。
通过阐述这些内容,旨在让读者更加深入地理解和应用最小二乘拟合方法,为其在数据分析和模型拟合中提供有效的工具和思路。
2.正文2.1 最小二乘拟合的定义最小二乘拟合是一种常用的数学方法,用于通过调整参数来拟合一个数学模型以最小化观测数据和模型之间的残差平方和。

线性回归模型是统计学中用于分析预测变量(自变量)和响应变量(因变量)之间线性关系的一种方法。
它是预测分析和因果推断中应用最广泛的技术之一。
在这篇文章中,我们将探讨线性回归模型如何评估自变量对因变量的影响力度,并将讨论分为三个部分。
线性回归模型的基本原理与参数估计线性回归模型以简单直观的方式量化自变量和因变量之间的关系。
在最基本的单变量线性回归中,模型预设因变量Y与自变量X之间存在线性关系,其数学表达式通常写作 Y = β0 + β1X + ε,其中,β0是截距项,β1是斜率系数,ε代表误差项。
模型的核心目标是估计这些参数,以便准确描述这两个变量之间的线性关系。
使用最小二乘法是线性回归中最普遍的参数估计方法。
它通过最小化实际观测值和回归直线之间距离的平方和来寻找合适的β0和β1。
结果得到的参数估计值能够提供每个自变量单位变化时因变量变动的平均量。
回归系数β1是衡量自变量对因变量影响力度的直接指标。
如果β1的估计值为正,表明自变量增加会导致因变量增加;如果为负,则表示自变量的增加会导致因变量减少。
β1的绝对值大小反映了自变量对因变量的影响强度。
为了确保参数估计的准确性,回归分析要满足几个关键假设,如线性关系、独立性、同方差性和误差项的正态性。
这些假设保证了模型参数估计的无偏性和最小方差性,是评估自变量影响力度的基础。
统计检验与回归系数的显著性评估回归参数的具体影响力度还需要进行统计检验。
这一过程能帮助我们判断自变量的影响是否具有统计学上的显著性,以及模型对数据拟合的好坏。
统计检验大多依赖于构建一个假设检验框架,包括零假设(通常为自变量系数等于零,即没有影响)和备择假设(自变量系数不等于零,即有实际影响)。
t检验被广泛应用于单个回归系数的显著性检验。
通过计算t 统计量及相应的p值,我们能够决定是否拒绝零假设。
若p值低于事先选择的显著性水平(例如0.05),则认为自变量对因变量的影响是显著的。
对于模型的整体评估,F检验提供了一种方法,用以判断模型中自变量对预测因变量是否整体上有显著的解释能力。
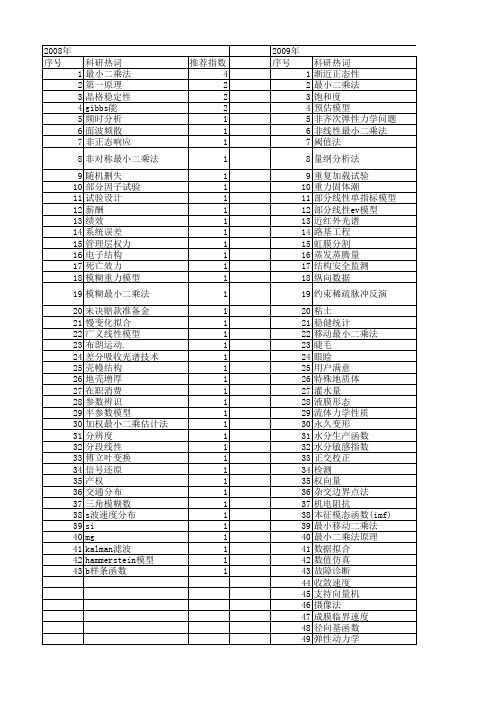
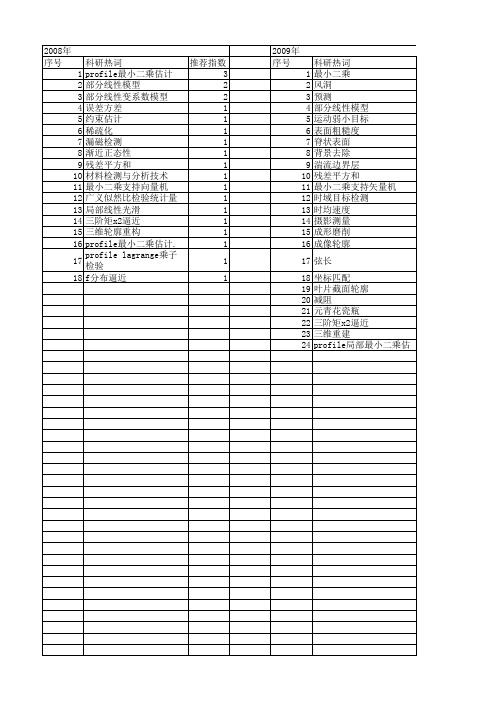

基于支持向量机分位数回归的部分r变系数动态模型的估计刘征;陈爽【摘要】本文研究部分变系数动态模型,一些参数的值可以成为协变量的函数,并提出了参数和非参数函数系数的估计.本文提出一个基于支持向量机分位数回归的部分变系数动态模型,及它的三步估计法和迭代加权最小二乘法估计模型的参数和非参数函数,提出的方法能被简单有效地应用到线性和非线性分位数回归光滑变量的高维情况.同时,本文也提出模型的惩罚参数、核参数的选择方法——交叉验证方法.【期刊名称】《统计与管理》【年(卷),期】2016(000)012【总页数】2页(P31-32)【关键词】部分变系数模型;分位数回归;支持向量机分位数回归;迭代加权最小二乘;超参数选择【作者】刘征;陈爽【作者单位】河北工业大学;北京石油化工学院【正文语种】中文分位数回归方法最早是由Koenker和Bassett在1978年提出,在各种行业有广泛的应用,包括金融、经济、机械和生物行业。
例如,条件分位数的估计是风险管理中的常用方法。
它是一种在因变量的条件分布的不同分位点上量化自变量的回归技术,分位数回归有弱条件性、渐进优良性和稳健性等优势。
在回归分析中,为了处理“维数祸根”问题, Hastie和Tibshirani在1993年提出了变系数模型。
最近,Cai and Xu (2008)研究了时间序列上的变系数分位数回归模型;Cai and Xiao (2012)讨论了部分线性变系数分位数回归模型,他们用局部多项式拟合的方法估计系数。
Shim, Hwang and Seok在2015年提出了变系数支持向量机分位数回归及两种估计方法。
作为传统的统计学的重要补充和发展,支持向量机方法展现出优秀的学习性能,支持向量机一改传统方法的经验风险最小原则,根据结构风险最小化原则提出的,这使其能够达到更好的泛化能力。
本文研究的主要目的在于提出了一种新的基于支持向量机分位数回归的半参数部分变系数模型,在该模型中,一些外生变量和滞后变量或离散变量的系数可以是线性的,也可以是非线性的。
最小二乘法和theil-sen趋势估计方法概述说明以及解释1. 引言1.1 概述引言部分将总体介绍本篇文章的研究主题和方法。
本文将探讨最小二乘法和Theil-Sen趋势估计方法,这两种方法旨在通过拟合数据来寻找变量间的关系,并用于预测和估计未来的趋势。
最小二乘法是一种常见且广泛应用的回归分析方法,而Theil-Sen趋势估计方法是一种鲁棒性更强的非参数统计方法。
1.2 文章结构引言部分还需要简要描述整篇文章的结构以供读者参考。
本文包含以下几个主要部分:引言、最小二乘法、Theil-Sen趋势估计方法、对比与对比分析、结论与展望。
每个部分将详细说明相关概念、原理及其在实际应用中的特点。
1.3 目的引言部分还需明确指出本文的目的。
本文旨在比较和对比最小二乘法和Theil-Sen趋势估计方法,评估它们在不同场景下的优缺点,并为读者提供选择适当方法进行数据拟合和趋势预测的依据。
此外,我们也会展望未来这两种方法的改进和应用领域扩展的可能性。
以上为“1. 引言”部分的详细清晰撰写内容。
2. 最小二乘法:2.1 原理介绍:最小二乘法是一种常用的回归分析方法,用于寻找一个函数(通常是线性函数)来逼近已知数据点的集合。
其基本原理是通过最小化实际观测值与模型预测值之间的残差平方和,寻找到使得残差最小化的系数,并将其作为估计值。
利用最小二乘法可以得到拟合直线、曲线或者更复杂的函数来描述数据点之间的关系。
2.2 应用场景:最小二乘法广泛应用于各种领域和行业,包括经济学、社会科学、物理学等。
例如,在经济学中,最小二乘法可以用于研究变量之间的关系以及预测未来趋势。
在工程领域,它可以用于建立模型并进行参数估计。
2.3 优缺点分析:最小二乘法具有以下优点:- 算法简单易行:只需要对数据进行简单处理即可求解出最佳拟合曲线。
- 表示能力强:可以适应不同类型函数的拟合。
- 结果一致性较好:针对相同数据集,得到的结果通常是一致的。
然而,最小二乘法也存在一些缺点:- 对异常值敏感:在数据集中存在离群值时,会对拟合曲线产生较大影响。
参数估计中的常用公式总结参数估计是统计学中重要的一部分,用于通过样本数据对总体参数进行估计。
在参数估计中,有一些常用的公式被广泛应用。
本文将总结这些常用的参数估计公式,帮助读者更好地理解和应用这些公式。
一、最大似然估计(Maximum Likelihood Estimation)最大似然估计是一种常见的参数估计方法,用于通过最大化似然函数来估计参数。
在最大似然估计中,常用的参数估计公式如下:1. 似然函数(Likelihood Function):似然函数L(θ)定义为给定参数θ下的样本观测值的联合概率密度函数或概率质量函数。
在连续型分布的情况下,似然函数可以表示为:L(θ) = f(x₁; θ) * f(x₂; θ) * ... * f(xₙ; θ)其中x₁, x₂, ..., xₙ为样本观测值。
2. 对数似然函数(Log-Likelihood Function):对数似然函数l(θ)定义为似然函数的对数:l(θ) = log(L(θ))3. 最大似然估计(Maximum Likelihood Estimation):最大似然估计通过最大化对数似然函数l(θ)来估计参数θ,常用的公式为:θ̂= argmaxₐ l(θ)其中θ̂表示参数的最大似然估计值。
二、最小二乘估计(Least Squares Estimation)最小二乘估计是一种常见的参数估计方法,用于对线性回归模型中的参数进行估计。
在最小二乘估计中,常用的参数估计公式如下:1. 残差平方和(Sum of Squares of Residuals):残差平方和定义为观测值与回归直线(或曲线)之间的差异的平方和。
最小二乘法通过最小化残差平方和来估计参数。
2. 最小二乘估计(Least Squares Estimation):最小二乘估计通过最小化残差平方和来估计参数。
对于简单线性回归模型,估计参数b₀和b₁的公式分别为:b₁ = Σ((xᵢ - x)(yᵢ - ȳ)) / Σ((xᵢ - x)²)b₀ = ȳ - b₁x其中xᵢ为自变量的观测值,yᵢ为因变量的观测值,x和ȳ分别为自变量和因变量的样本均值。