线性方程组解的情况及其判别准则
- 格式:doc
- 大小:453.50 KB
- 文档页数:12




摘要:近年来,线性代数在自然科学和工程技术中的应用日益广泛,而线性方程组求解问题是线性代数的基本研究内容之一,同时它也是贯穿线性代数知识的主线。
本文探究了线性方程组一般理论的发展,用向量空间和矩阵原理分析了线性方程组解的情况及其判别准则。
介绍了线性方程组理论在解决解析几何问题中的作用,举例说明了线性方程组解的结构理论在判断空间几何图形间位置关系时的便利之处。
关键字:线性方程组;解空间;基础解系;矩阵的秩Abstract:In recent years, linear algebra in science and engineering application, and wide linear equations solving problems is the basic content of linear algebra, at the same time, it is one of the main knowledge of linear algebra.This article has researched the development of system of linear equations theory,discussed the general theory of linear equations, vector space with the development and matrix theory to analyze the linear equations and the criterion of the situation. Introduces the theory of linear equations in solving the problem of analytic geometry, illustrates the role of linear equations of structure theory in judgment space relation between the geometry of the convenience of position. space geometric figure between time the position relations with theory of the system of linear equation with examples.Key words: linear equations, The solution space, Basic solution, Matrix rank一、线性方程组理论的发展进程早在初等代数的学习中,我们就讨论过一元二次方程和二元一次方程组,他们是线性方程组中最简单的两种形式。

线性方程组解的判定
线性方程组解的判定是一个重要的数学问题,它涉及到对一组未知量的求解。
解的判定问题的主要内容如下:
1. 系数矩阵存在不等式:在求解线性方程组时,首先要判断系数矩阵是否存在不等式,即是否存在元素值为负的情况:若存在,则解不存在;如果全部元素值都不为负,则判定解存在。
2. 是否存在无穷解:通常情况下,一个线性方程组只有唯一解,即只有一组解。
但也有可能存在无穷多解,即系数矩阵存在元素值全为0,此时解可以是任意一组数,因此可以判定存在无穷解。
3. 闭解的确定:当系数矩阵存在不等式或存在元素值全为0时,可以判定存在无穷解;当系数矩阵存在唯一解时,需要通过计算、符号识别和几何意义的结合,来确定具体的闭解。
4. 压缩可行性:压缩可行性判定法是指将求解所求出来的解,压缩在基本解所构成的空间上,以便表达出更复杂的结果。
5. 方程式系数:也可以通过方程式系数的分析,来判定方程组的解的存在与否,这是一种常用的判定方法。
从上述内容可以看到,线性方程组解的判定是一个复杂的数学问题,要想判断线性方程组的解的存在性,需要结合不等式判定、无穷解判定、压缩可行性判定以及方程式系数等步骤,一步步进行判断,才能正确地确定某个线性方程组的解的存在性。





第二节 线性方程组解的情况判定教学目的:掌握线性方程组解的存在性的判别方法。
教学重点:线性方程组有解判别定理及其推论。
教学过程:下面我们来说明如何利用初等变换来解一般的线性方程组。
第一步 对于方程组(9.1),如果1x 的系数不全为零,那么利用初等变换1,可以设110a ≠;第二步 利用初等变换2,分别把第一个方程的111i a a -倍加到第i 个方程(2,,)i s = ,于是方程组(9.1)变成111122112222222n n n n s sn n s a x a x a x b a x a x b a x a x b +++=⎧⎪'''++=⎪⎨⎪⎪'''++=⎩(9.2) 其中1111(2,,;2,,)i ij ij j a a a a i s j n a '=-⋅== 。
这样,解方程组(9.1)就归结为解方程组2222222n n s sn n s a x a x b a x a x b ⎧'''++=⎪⎪⎨⎪'''++=⎪⎩ (9.3)方程组(9.1)有解的充分必要条件为方程组(9.3)有解;第三步 对(9.2)上面的类似变换,最后得到一个阶梯形方程组111122*********100000r r n n r r n n rr r rn n r r c x c x c x c x d c x c x c x d c x c x d d ++++++=⎧⎪+++=⎪⎪⎪++=⎪⎨=⎪⎪=⎪⎪⎪=⎩(9.4) 其中0(1,2,,)ii c i r ≠= 。
方程组(9.4)中的“00=”这样一些恒等式可能不出现,也可能出现,去掉它们不影响(9.4)的解。
方程组(9.1)与方程组(9.4)是同解的。
下面讨论方程组(9.4)解的情况,即方程组(9.1)解的情况。
1.如(9.4)中有方程10r d +=,而10r d +≠,这是不管1,,n x x 取什么值都不能使它成为等式,所以(9.4)无解,从而(9.1)无解。
摘要:近年来,线性代数在自然科学和工程技术中的应用日益广泛,而线性方程组求解问题是线性代数的基本研究内容之一,同时它也是贯穿线性代数知识的主线。
本文探究了线性方程组一般理论的发展,用向量空间和矩阵原理分析了线性方程组解的情况及其判别准则。
介绍了线性方程组理论在解决解析几何问题中的作用,举例说明了线性方程组解的结构理论在判断空间几何图形间位置关系时的便利之处。
关键字:线性方程组;解空间;基础解系;矩阵的秩Abstract:In recent years, linear algebra in science and engineering application, and wide linear equations solving problems is the basic content of linear algebra, at the same time, it is one of the main knowledge of linear algebra.This article has researched the development of system of linear equations theory,discussed the general theory of linear equations, vector space with the development and matrix theory to analyze the linear equations and the criterion of the situation. Introduces the theory of linear equations in solving the problem of analytic geometry, illustrates the role of linear equations of structure theory in judgment space relation between the geometry of the convenience of position. space geometric figure between time the position relations with theory of the system of linear equation with examples.Key words: linear equations, The solution space, Basic solution, Matrix rank一、线性方程组理论的发展进程早在初等代数的学习中,我们就讨论过一元二次方程和二元一次方程组,他们是线性方程组中最简单的两种形式。
近年来,线性代数被广泛的应用在自然科学和工程技术中,在实际问题中常常需要处理几十个、几百个甚至成千上万个未知量的线性方程组,且方程组中方程的个数与未知数的个数也不一定相等,所以就需要对一般线性方程组的求解情况进行讨论分析。
下面就具体讨论线性方程组解的情况及其判别准则。
线性方程组的解法,早在中国古代的数学著作《九章算术》方程章中就作了比较完整的论述,其所述方法实质上相当于现代的高斯消元法。
在西方,线性方程组的研究是在17世纪后期由莱布尼茨开创的,他曾研究含两个未知量的三个线性方程组成的方程组。
1693年4月,莱布尼茨在写给洛比达的一封信中使用并给出了行列式,并给出方程组的系数行列式为零的条件。
同时代的日本数学家关孝和在其著作《解伏题元法》中也提出了行列式的概念与算法。
1750年克莱姆在他的《线性代数分析导言》中发表了求解线性系统方程的重要基本公式,既人们熟悉的克莱姆法则。
1764年,数学家贝祖把确定行列式每一项的符号的手续系统化了。
对给定了含n个未知量的n个齐次线性方程,贝祖证明了系数行列式等于零是这方程组有非零解的条件。
大约在1800年,高斯提出了高斯消元法并用它解决了天体计算和后来的地球表面测量计算中的最小二乘法问题。
19世纪,英国数学家史密斯和道奇森继续研究线性方程组理论,前者引进了线性方程组的系数矩阵和增广矩阵的概念,后者证明了线性方程组相容的充要条件是系数矩阵和增广矩阵的秩相等,这是现代方程组理论中的重要结果之一。
现在我们解线性方程组正是通过对增广矩阵施行初等行变换进行的。
此后的一百多年间,线性方程组的一般理论已逐渐趋于成熟,而人们对线性方程组的研究也从理论转移到应用上来了。
线性方程组在实践中应用的非常广,如天气预报、运输调度、安排生产、飞机飞行所涉及的空气动力学等等……在当代,人们正在努力研究出一下适合特殊情况下的大型线性方程组的求解方法。
例如,徐成贤、孔麦英在《大型稀疏矩阵线性方程组的一种稳定解法》中研究了如何恰当地把这种方法嵌入到高斯消去法中,得到的算法使得高斯消去法总是能稳定有效地求解。
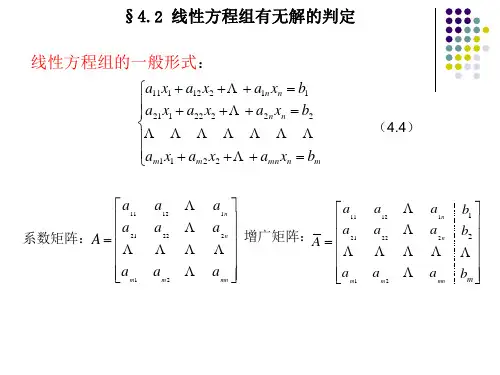
二、一般线性方程组的理论定义1 用12,,,n x x x 表示未知量在数域F 上一般线性方程组的模型为,11112211n n a x a x a x b +++=21122222n n a x a x a x b +++=1122m m mn n m a x a x a x b +++= 其中每个方程左端是未知量12,,,n x x x 的一次齐次式,左端是常数(称为常数项)。
与未知量相乘的数称为系数,ij a F ∈是第i 个方程中j x 的系数1,2,,;1,2,,.i m j n ==方程组(1)称为含有m 个未知量,n 个方程的线性方程组(,m n m n m n ><=或都可能)1111n m mn a a A a a ⎛⎫ ⎪= ⎪ ⎪⎝⎭称为方程组(1)的系数阵;而矩阵11111n m mn m a a b B a a b ⎛⎫ ⎪= ⎪ ⎪⎝⎭称为方程组(1)的增广阵。
(一)线性方程组解的判别准则在向量理论和矩阵理论的基础上,我们可以得出以下关于线性方程组解的情况的判定定理1(线性方程组有解判别定理)线性方程组(1)有解的充分必要条件是其系数矩阵A 和增广矩阵B 的秩相等,即()()r A r B =。
下面再来讨论方程组(1)有解的情况下解的结构问题。
定理2 在()()r A r B =的条件下,有Ⅰ 如果()r A n =,则方程组(1)有唯一解;Ⅱ 如果()r A n <,则方程组(1)有无穷多组解。
(1)证明参见【5】(二)线性方程组解的结构在方程组有唯一解的时候当然没有什么解的结构,在无穷多个解的时候才有条件讨论解的结构,所谓线性方程组解的结构是指解与解之间的关系。
在讨论一般线性方程组解的结构之前,我们先来研究齐次线性方程组解的结构。
1、 齐次线性方程组解的结构定义2 称形如11112210n n a x a x a x +++= 21122220n n a x a x a x +++=11220m m mn n a x a x a x +++= 的线性方程组为齐次方程组。
其系数阵为A ,令12(,,,),00,0,,0n X x x x ''==()则有 AX=0。
定义3 把(2)的一个解12,,,n x x x 看成一个n 维列向量12(,,,)T n x x x ,称为齐次线性方程组的一个解向量,记做12(,,,)T n V x x x =。
齐次线性方程组一定有无穷多个解空间(都是n 维向量),这无穷多个解向量的全体构成一个向量空间,叫做齐次线性方程组的解空间W 。
当然,这无穷多个n 为解向量是线性相关的,因此只要找出它的一个极大无关解向量组,就可以用它的线性组合来表示齐次线性方程组的全部解向量。
定义4 如果12,,,n V V V 是齐次线性程组(2)的解向量组的一个极大无关组,则称12,,,n V V V 是齐次线性方程组(2)的一个基础解系。
定理3 如果齐次线性方程组(2)的系数矩阵A 的秩()r A r n =<,则齐次线性方程组必定存在基础解系,且每一个基础解系中所含的解向量的个数为n r -个。
证明:由于()r A r n =<,说明独立的方程的个数少于未知量的个数。
假如对增广矩阵B 作初等行变换化成了如下的形状:(2)1112121100001000010000000r n r n rr rn k k k k B k k +++⎛⎫ ⎪ ⎪ ⎪→ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭这说明齐次线性方程组(2)与下列方程组同解:11111r r n n x k x k x ++=--- 22112r r n n x k x k x ++=---11r rr r rn n x k x k x ++=--- 其中的1r x +,,n x 为自由未知量,他们是可以任意取值的,现对他们分别取为12100010,,,001r r n x x x ++⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ 就可以得到齐次线性方程组(2)的n r -个非零解向量为11121212221212,,,100010001r r n r r n rr rr rn n r k k k k k k k k k V V V ++++++----⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪--- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--- ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 他们就是齐次线性方程组(2)的一个基础解系。
显然12,,,n r V V V -线性无关,因为设12(,,,)n V d d d '=是(2)的任一个解向量,故11111221r r r r n n d k d k d k d ++++=----22112222r r r r n n d k d k d k d ++++=----1122r rr r rr r rn n d k d k d k d ++++=----用向量表示为1122r r n n r V d V d V d V ++-=+++,因此12,,,n r V V V -线性相关。
这就是说,基础解系12,,,n r V V V -构成了齐次线性方程组的解向量空间的一组基,任何一个解向量都可以有这组基线性表示。
所以齐次线性方程组的全部解向量为12,,,n r V V V -的线性组合:1122n r n r V c V c V c V --=+++ 由此得出了求齐次线性方程组(2)的基础解系方法:第一步 对其系数矩阵机型初等行变换,判别是否有非零解。
第二步 若有非零解,写出与原方程组同解的方程组,给自由未知量赋值,找出其一个基础解系。