8-2安培环路定理

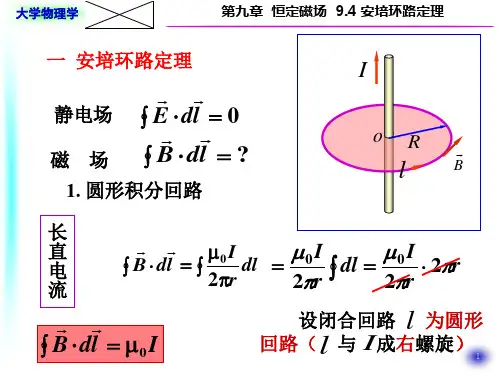
安培环路定理安培环路定理的严格证明(缩略图)在稳恒磁场中，磁场强度H沿任何闭合路径的线积分，等于这闭合路径所包围的各个电流之代数和。

这个结论称为安培环路定理（Ampere circuital theorem）。

安培环路定理可以由毕奥－萨伐尔定律导出。

它反映了稳恒磁场的磁感应线和载流导线相互套连的性质。

目录按照安培环路定理，环路所包围电流之正负应服从右手螺旋法则。

安培环路定理应用如果闭合路径l包围着两个流向相反的电流I1和I2（如左图所示），这在下式中，按图中选定的闭合路径l 的绕行方向，B矢量沿此闭合路径的环流为如果闭合路径l包围的电流等值反向（如右图所示），或者环路中并没有包围电流，则：安培环路定理的证明(严格证明,大图见参考资料的链接)编辑本段安培环路定理的证明（不完全证明）以长直载流导线产生的磁场为例，证明安培环路定理的正确性。

安培环路定理应用在长直载流导线的周围作三个不同位置，且不同形状的环路，可以证明对磁场中这三个环路，安培环路定理均成立。

取对称环路包围电流在垂直于长直载流导线的平面内，以载流导线为圆心作一条半径为r 的圆形环路l，则在这圆周上任一点的磁感强度H的大小为其方向与圆周相切．取环路的绕行方向为逆时针方向，取线元矢量dl，则H与dl间的夹角，H沿这一环路 l 的环流为式中积分是环路的周长。

于是上式可写成为从上式看到，H沿此圆形环路的环流只与闭合环路所包围的电流I 有关，而与环路的大小、形状无关。

取任意环路包围电流在垂直于长直载流导线的平面内，环绕载流直导线作一条如下图所示的任意环路l，取环路的绕行方向为逆时针方向。

在环路上任取一段线元dl，载流直导线在线元dl处的磁感强度B大小为H与dl的夹角为，则H对dl的线积分为直导线中心向线元的张角为，则有，所以有可见，H对dl的线积分与到直导线的距离无关。

那么B对整个环路的环流值为上述计算再次说明H的环流值与环路的大小、形状无关。

取任意环路不包围电流在垂直于长直载流导线的平面内，在载流直导线的外侧作一条如下图所示的任安培环路定理应用意环路l，取环路的绕行方向为逆时针方向。

安培环路定理例题
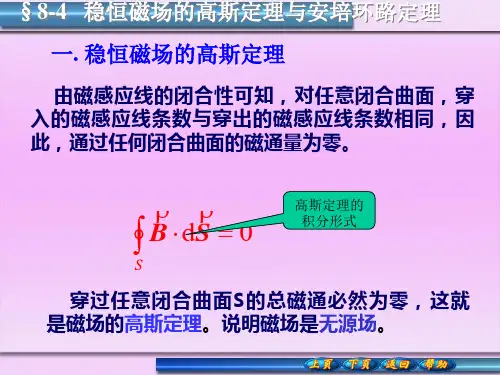
一、安培环路定理简介
安培环路定理是电磁学中的一个重要定理，它是由德国物理学家安培（Ampère）提出的。

该定理描述了电流与磁场之间的关系，为我们研究电磁现象提供了有力的理论依据。

二、安培环路定理的数学表达式
安培环路定理的数学表达式为：
∮μJ·dλ = με∮φdλ
其中，μ为真空磁导率，J为电流密度，λ为路径，ε为真空介电常数，φ为磁感应强度。

三、安培环路定理的应用
1.计算磁场强度：利用安培环路定理，我们可以通过测量电流和磁场路径上的磁场强度来计算磁感应强度。

2.分析电磁感应现象：在电磁感应现象中，安培环路定理可以帮助我们理解磁场变化产生的电动势，从而分析电路中的电流分布。

3.求解电磁场问题：安培环路定理在求解电磁场问题时具有重要意义，例如在电磁波传播、电磁感应等领域。

四、安培环路定理的拓展
1.非均匀磁场中的安培环路定理：在非均匀磁场中，安培环路定理仍然适用，但需要对磁场进行积分运算。

2.多维空间中的安培环路定理：在多维空间中，安培环路定理可以扩展为
更高维度的公式，以描述不同维度下的电磁现象。

3.其他相关定理：与安培环路定理密切相关的还有法拉第电磁感应定律、楞次定律等，它们共同构成了电磁学的理论基础。

通过掌握安培环路定理，我们可以更好地理解和分析电磁现象，为实际应用提供理论支持。

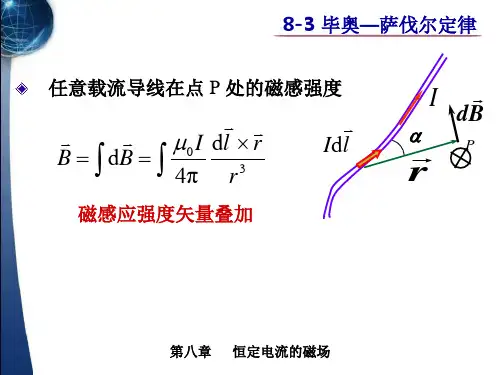
第19讲 安培环路定理毕奥-萨伐尔定律的应用 毕奥 萨伐尔定律的应用 安培环路定理及其应用毕奥－萨伐尔定律毕奥—萨伐尔定律 一 毕奥 萨伐尔定律(给出了电流元在空间产生的磁场) 给出了电流元在空间产生的磁场 给出了电流元在空间产生的磁场v Idlv dBdB =µ0 Idl sin θ4π r2v dBP *v rθv IdlIv v v µ0 Idl × r dB = 3 4π rv r任意载流导线在点 P 处的磁感强度 磁感强度叠加原理v v v v µ0 I dl × r B = ∫ dB = ∫ 3 4π rA. 无限长载流长直导线的磁场B=µ0I2π rI BIXBB.半无限长载流长直导线的磁场 半无限长载流长直导线的磁场 半无限长BP =µ0I4π rIor* P圆形载流导线的磁场. 例2 圆形载流导线的磁场 真空中 , 半径为R 的载流导线 , 通有电流I , 称圆 电流. 的磁感强度的方向和大小. 电流 求其轴线上一点 p 的磁感强度的方向和大小v Idlrv Bv dBp *oRϕv BI 解 根据对称性分析4π r B = Bx = ∫ dB sin ϕdB =µ 0 Id l2xv IdlRrxoϕr 2 2 2 ϕ r =R +x α µ 0 I cos αdl *p x B= 4 π ∫l r 2v dBcosα = R4π r µ 0 I cos αdl dB x = 2 4π rdB =µ 0 Id l2B=B=µ0 IR4π r 2 µ0 IR2 23 0∫2π Rdl3（x + R ）2 2IR o x *v BxB=B=µ0 IR22 2 3讨 论（x + R ）2 2 v v 2）x < 0 B 的方向不变 I 和 B 成右螺旋关系） 的方向不变( 右螺旋关系 关系） ） µ 0I B = 3）x = 0 ） 2R 2 µ 0 IR µ 0 IS 4）x >> R ） B= ， B= 3 3 2x 2π x2 21）若线圈有 N 匝 ）（x + R ）2 2 2 N µ 0 IR3（1） ）I （2 ）v R B x 0 µ0I o B0 = 2RI R o+（4） ）BA =d *AR1µ0 I4π dB0 =µ0 I4R（5） ） IR2（3） I ） R o*oB0 =µ0 I8RB0 =µ0 I4 R2−µ0 I4 R1−µ0 I4π R1磁偶极矩（磁矩） 二 磁偶极矩（磁矩）v v m = IS e n圆电流磁感强度公式也可写成I Sv env mB=µ 0 IR2x32v µ0m v B= e 3 n 2π xv v µ0m B= 3 2π xv mv enI S说明：只有当圆形电流的面积S很小，或场点距 说明：只有当圆形电流的面积 很小， 很小 圆电流很远时，才能把圆电流叫做磁偶极子 磁偶极子. 圆电流很远时，才能把圆电流叫做磁偶极子三. 载流直螺线管的磁场 如图所示，有一长为l 半径为R的载流密绕直螺线 例 如图所示，有一长为 , 半径为 的载流密绕直螺线 管，螺线管的总匝数为N，通有电流I. 设把螺线管放 螺线管的总匝数为 ，通有电流 在真空中，求管内轴线上一点处的磁感强度. 在真空中，求管内轴线上一点处的磁感强度Ro* p xdxx++ ++++++ +++ ++ +解 由圆形电流磁场公式B=µ 0 IR22 2 3/ 2（x + R ） 2β1βx1o pβ2x2++ + + + + + + + + + + + + +xdB =µ02B = ∫ dB =µ 0 nI2(RR In d x22+xx2 x12 3/2)∫ (R3R 2 dx2x = R cot β 2 dx = − R csc βdβ+x22 3/ 2)R + x = R csc β2 2 2 2B=−µ 0 nI2∫ββ21R csc β d β µ0 nI β 2 =− 3 3 ∫β1 sin β d β 2 R csc β d β讨 论B=µ0 nI2(cos β 2 − cos β1 )β1 = π − β 2l/2点位于管内轴线中点 （1）P点位于管内轴线中点 ） 点位于管内cos β1 = − cos β 2B = µ0 nI cos β 2 =若cos β2 =(l / 2)l2+ R2µ0 nI2(l2/4+ R2 1/ 2)l >> RB = µ 0 nI(2) 无限长的螺线管 无限长的螺线管（3）半无限长螺线管 ）半无限长螺线管B = µ 0 nI或由 β1 = π , β 2 = 0 代入π β1 = , β 2 = 0 21 B = µ 0 nI 2µ0nIxL/2B=µ0nI2(cos β2 − cos β1 )B1 µ 0 nI 2O-L/2安培环路定理一 安培环路定理 载流长直导线的磁感强度为 流长直导线的磁感强度为B=µ0IIov BR2π Rv dlv v µ0 I ∫l B ⋅ dl = ∫ 2π R dl v v µ0I ∫l B ⋅ dl = 2π R ∫l dl v v ∫ B ⋅ dl = µ0 Ill设闭合回路 l 为圆形 螺旋） 回路（ 回路（ l 与 I 成右螺旋）Iov BR若回路绕向化为逆时针时，则 回路绕向化为逆时针时，v dllv v µ0 I 2π ∫l B ⋅ d l = − 2π ∫0 dφ = −µ0 I对任意形状的回路dφv vB dlIrll与 I 成右螺旋v v µ0 I µ0 I B ⋅ dl = rdφ = dφ 2π r 2π v v B ⋅ dl = µ 0 I ∫l电流在回路之外dφv B1Ir1v ， B2 = B1 = B2 2π r1 2π r2 v v v v v µ0 I v dl B1 ⋅ dl1 = −B2 ⋅ dl2 = − dφ 2 dl1 2π r2 v v v v B1 ⋅ dl1 + B2 ⋅ dl2 = 0 l v v ∫ B ⋅d l = 0lµ0 Iµ0 I多电流情况I1I2I3v v v v B = B1 + B2 + B3 v v ∫ B ⋅ d l = µ0 ( I 2 − I 3 )ll以上结果对任意形状 以上结果对任意形状 任意 的闭合电流（ 的闭合电流（伸向无限远 的电流）均成立. 的电流）均成立n v v ∫ B ⋅ dl = µ 0 ∑ I i i =1安培环路定理安培环路定理n v v ∫ B ⋅ dl = µ 0 ∑ I i i =1一闭合路径的积分的值， 一闭合路径的积分的值，等于 所包围的各电流的代数和. 所包围的各电流的代数和 注意v 即在真空的稳恒磁场中， 即在真空的稳恒磁场中，磁感应强度 B 沿任µ 0 乘以该闭合路径I正负的规定 电流 I 正负的规定 ：I 与 之为负 为正；反之为负.螺旋时， L 成右螺旋时，v v B⋅dl = µ0 (−I1 + I1 − I1 − I2 ) ∫LI1 I1LI2 I 3 I1= −µ0 I1 + I2） （问v 1） B 是否与回路 L 外电流有关？ 外电流有关？ ） v v v 2）若 ∫ B ⋅ d l = 0 ，是否回路 L上各处 B = 0？ ） L 内无电流穿过？ 是否回路 L 内无电流穿过？二 安培环路定理的应用举例 例1 求长直密绕螺线管内磁场解 1 ) 对称性分析螺旋管内为均匀场 , 方向沿 轴向, 轴向 外部磁感强度趋于零 ，即 B ≅ 0 .2 ) 选回路 电流L.M N +++ + + + ++++++ L O PNO OP PMv 磁场 B 的方向与右螺旋. I 成右螺旋v Bv v v v v v v v v v ∫ B ⋅ d l = ∫ B ⋅ d l + ∫ B ⋅ d l + ∫ B ⋅ d l +∫ B ⋅ d ll MNB ⋅ MN = µ 0 n MN IB = µ 0 nI无限长载流螺线管内部磁场处处相等 , 外部磁场 为零. 为零v 解 1） 对称性分析；环内 B ） 对称性分析； v 线为同心圆，环外 B 为零. 线为同心圆， 为零例2 求载流螺绕环内的磁场v v ∫l B ⋅ d l = 2π RB = µ0 NI µ0 NI B= 2π R令 当2）选回路 . ）dRL = 2 πRB = µ0 NI L2R >> d 时，螺绕环内可视为均匀场 .例3 无限长均匀载流圆柱体的磁场 解 1）对称性分析 2）选取回路 ） ）Ir>R2π rB = µ0 Iv v ∫ B ⋅ d l = µ0 IlR RLr2π r 2 v v πr 0 < r < R ∫ B ⋅ d l = µ0 2 I l πR 2 µ0r µ0 Ir 2π rB = 2 I B= 2 R 2π RB=µ0 II.v Bv dBdIv Bv B 的方向与 I 成右螺旋 µ 0 Ir B= 2 0 < r < R, 2π R µ0I r > R, B= 2π rIµ0I2π RBRo Rr例4 无限长载流圆柱面的磁场L1rRµ0 I2π RBIL2解ro R rB=0 µ0I2π rv v 0 < r < R, ∫ B ⋅ d l = 0lv v r > R, ∫ B ⋅ d l = µ 0 IlB=作业 作业：练习 作业：练习16。

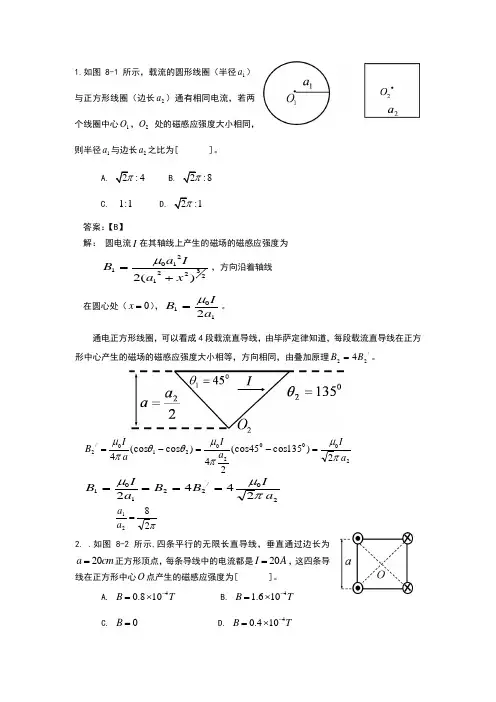
1.如图8-1所示，载流的圆形线圈（半径1a ）与正方形线圈（边长2a ）通有相同电流，若两个线圈中心1O ，2O 处的磁感应强度大小相同，则半径1a 与边长2a 之比为[ ]。

A. 2:4πB. 2:8πC. 1:1D. 2:1π答案：【B 】解： 圆电流I 在其轴线上产生的磁场的磁感应强度为232212101)(2x a Ia B +=μ，方向沿着轴线 在圆心处（0=x ），1012a IB μ=。

通电正方形线圈，可以看成4段载流直导线，由毕萨定律知道，每段载流直导线在正方形中心产生的磁场的磁感应强度大小相等，方向相同，由叠加原理/224B B =。

200020210/22)135cos 45(cos 24)cos (cos 4a I a I a I B πμπμθθπμ=-=-= 20/221012442a I B B a IB πμμ====π2821=a a 2. .如图8-2所示,四条平行的无限长直导线，垂直通过边长为20a cm =正方形顶点，每条导线中的电流都是20I A =，这四条导线在正方形中心O 点产生的磁感应强度为[ ]。

A. 40.810B T -=⨯B. 41.610B T -=⨯C. 0B =D. 40.410B T -=⨯答案：【A 】解：建立直角坐标系，则4根无限长载流直导线在正方形中心产生的磁感应强度为i a I B 45cos 201πμ=，j a I B 45cos 202πμ= i a IB 45cos 203πμ=，j a I B45cos 204πμ= )(45cos 2204321j i a I B B B B B+=+++=πμ T B 5108-⨯= 3.一根无限长直导线abcde 弯成图8-3所示的形状，中部bcd 是半径为R 、对圆心O 张角为0120的圆弧，当通以电流I 时，O 处磁感应强度的大小B = ，方向为 。

a 答案：)32(2600-=RI R IB πμμ＋， 方向垂直纸面向里解：将整个载流导线分为三段：直线ab 、圆弧bcd 、直线de 。

《大学物理》作业 No.6 磁场的安培环路定理班级 ___________ 学号 __________ 姓名 ____________ 成绩 __________说明：字母为黑体者表示矢量内容提要：安培环路定理 ∑⎰=⋅I l d B L0μ1. 安培环路定理的理解：①B是环路上各点的磁感应强度，是环路内外所有电流共同激发的磁场。

②∑I 只是被环路包围的电流的代数和。

③不被环路包围的电流在环路上激发的磁场在环路的线积分中抵消掉了。

④环路上各点0=B 时，必有0=∑I ；但0=∑I 时，未必环路上各点的B 一定都为零。

⑤对于电流的正负的规定：当电流的方向与环路积分的方向符合右手螺旋关系时，电流为正，否则为负。

⑥安培环路定理中的电流应该是闭合（或无限长）恒定电流，对于一段恒定电流的磁场，安培环路定理不成立。

2. 安培环路定理的应用：①只有在磁场具有较好的对称性时才能用安培环路定理求解B ，但安培环路定理是普遍成立的，不具有较好对称性的磁场不能用安培环路定理求解B ，但定理依然成立。

②利用安培环路定理求磁场分布一般包含两步：首先依据电流的对称性分析磁场分布的对称性，然后再利用安培环路定理计算磁感应强度的数值和方向。

此过程中决定性的技巧是选取合适的闭合路径L （环路），以便⎰⋅Ll d B 中的B 能以标量形式从积分号内提出来。

基本要求：1.掌握安培环路定理：2.掌握安培环路定理分析计算磁感应强度的条件和方法，并能熟练运用。

一、选择题1.如图6.1所示,有两根无限长直载流导线平行放置,电流分别为I 1和I 2, LI 1在L 内,I 2在L 外,P 是L 上的一点,今将I 2 在L 外向I 1移近时,则有 [ ] (A)l B d ⋅⎰L与B P同时改变. (B) l B d ⋅⎰L与B P都不改变. (C) l B d ⋅⎰L不变,B P改变.(D)l B d ⋅⎰L改变,BP不变.2.对于某一回路l ，积分l B d ⋅⎰l等于零，则可以断定I 图6.1[ ] (A) 回路l 内一定有电流. (B) 回路l 内可能有电流.(C) 回路l 内一定无电流. (D) 回路l 内可能有电流，但代数和为零.3. 如图6.2所示，两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上，稳恒电流I 从a 端流入而从d 端流出，则磁感应强度B 沿图中闭合路径L 的积分l B d ⋅⎰l等于[ ] (A) I u 0(B) I u 031(C)I u 041(D) I u 0324. 用相同细导线分别均匀密绕成两个单位长度匝数相等的半径为R 和r 的长直螺线管(R =2r )，螺线管长度远大于半径.今让两螺线管载有电流均为I ，则两螺线管中的磁感强度大小B R 和B r 应满足：[ ] (A) B R = 2B r . (B) B R = B r . (C) 2B R = B r . (D) B R = 4B r .二、填空题1.在安培环路定理中iLI∑=⋅⎰0d μl B , 其中∑I i 是指 ;B 是由 的电流产生的.2. 两根长直导线通有电流I ,图6.3所示有三种环路,对于环路a ,=⋅⎰a L l B d ;对于环路b , =⋅⎰b L l B d 。

安培环路定理的推导与应用安培环路定理是电磁学中的重要定律之一，它描述了电流在闭合回路中所围成的磁通量与电路中的总电流的关系。

本文将对安培环路定理的推导进行讲解，并介绍一些其在实际应用中的例子。

一、安培环路定理的推导安培环路定理是由法国物理学家安培在19世纪初提出的。

它的数学表达形式是：∮B·dl = μ0·I其中，∮B·dl表示磁场B在闭合回路上的环路积分，μ0为真空中的磁导率，I为该回路中的总电流。

推导安培环路定理的基本思路是利用法拉第电磁感应定律和高斯定理。

我们知道，根据法拉第电磁感应定律，磁感应强度B的变化率与电场强度E的闭合回路积分之比等于贯穿该回路的总电流I：∮(B·dl)/(dt) = -∫E·ds = -dΦE/dt其中，ΦE表示电场的通量。

再根据高斯定理，可以将闭合回路上的磁场积分转化为磁通量的二重积分：∮B·dl = ∬(∇×B)·dS结合以上两个式子，可得到安培环路定理的数学表达式：∬(∇×B)·dS = -μ0·dΦE/dt = -μ0·d/dt(∬E·dS)经过进一步的推导和化简，可以得到安培环路定理的最终形式。

二、安培环路定理的应用安培环路定理可以应用于各种电磁场问题的求解中，下面将介绍几个实际应用的例子。

1. 电磁铁电磁铁是一种利用电流通过线圈时产生的磁场吸引铁磁物质的装置。

根据安培环路定理，可以计算电磁铁中磁场的分布情况，从而设计合适的线圈参数，使得电磁铁的吸引力能够满足实际需求。

2. 变压器变压器是一种利用电磁感应原理来改变电压的装置。

在变压器的设计和工作过程中，安培环路定理可以用来分析和计算铁芯中的磁场分布情况，从而确定绕组的布置和匝数比。

3. 电感电感是电路中常见的一种元件，它的基本单位是亨利(Henry)。

利用安培环路定理，可以计算电感器中的磁场分布情况，从而更好地理解和分析电感元件的特性。