二叉树类模板的设计与实现

二叉树的实现实验原理二叉树是一种常见的数据结构，它由节点组成，每个节点最多有两个子节点，通常称为左子节点和右子节点。

二叉树的实现原理如下：1. 节点的定义：每个节点包含一个值和两个指针，分别指向左子节点和右子节点。

节点可以使用类或结构体来表示，具体的实现方式取决于编程语言。

2. 树的定义：树由节点组成，其中一个节点被指定为根节点。

根节点没有父节点，其他节点都有且只有一个父节点。

每个节点最多有两个子节点，即左子节点和右子节点。

3. 添加节点：向二叉树中添加节点时，需要遵循以下规则：- 如果树为空，将节点作为根节点添加到树中。

- 如果节点的值小于当前节点的值，将节点添加为当前节点的左子节点。

- 如果节点的值大于等于当前节点的值，将节点添加为当前节点的右子节点。

4. 遍历树：遍历二叉树可以按照不同的顺序进行，常见的遍历方式有三种：- 前序遍历（Preorder Traversal）：先访问根节点，然后按照前序遍历方式遍历左子树，最后按照前序遍历方式遍历右子树。

- 中序遍历（Inorder Traversal）：先按照中序遍历方式遍历左子树，然后访问根节点，最后按照中序遍历方式遍历右子树。

- 后序遍历（Postorder Traversal）：先按照后序遍历方式遍历左子树，然后按照后序遍历方式遍历右子树，最后访问根节点。

遍历树的过程可以使用递归或迭代的方式来实现，具体的实现方法取决于编程语言和使用的数据结构。

5. 删除节点：删除二叉树中的节点时，需要考虑多种情况。

如果要删除的节点是叶子节点，可以直接删除它。

如果要删除的节点只有一个子节点，可以将子节点移动到要删除的节点的位置。

如果要删除的节点有两个子节点，可以选择将其中一个子节点替代要删除的节点，或者选择左子树的最大节点或右子树的最小节点替代要删除的节点。

根据上述原理，可以使用类或结构体等数据结构和递归或迭代的方式来实现二叉树。

具体的实现方法和细节可能因编程语言而异，但以上原理是通用的。

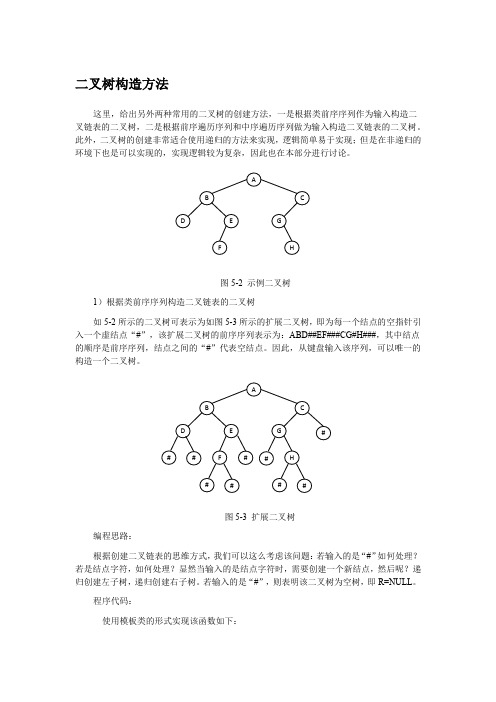
一、设计目标二叉树是形象地说既树中每个节点最多只有两个分支，它是一中重要的数据类型。

可以运用于建立家谱，公司所有的员工的职位图，以及各种事物的分类和各种机构的职位图表。

二叉树是通过建立一个链式存储结构，达到能够实现前序遍历，中序遍历，后序遍历。

以及能够从输入的数据中得知二叉树的叶子结点的个数，二叉树的深度。

在此，二叉树的每一个结点中必须包括：值域，左指针域，右指针域。

二、总体设计1．对程序中定义的核心数据结构及对其说明：typedef struct BiTNode{//创建二叉树char data;struct BiTNode *lchild,*rchild;}BiTNode,*BiTree;在开头定义了二叉树的链式存储结构，此处采用了每个结点中设置三个域，即值域，左指针域和右指针域。

2.模块的划分及其功能：本程序分为：7大模块。

二叉树的建立链式存储结构、前序遍历、求叶子结点的个数计算、中序遍历、后序遍历、深度、主函数。

1、二叉树的建立链式存储结构；首先typedef struct BiTNode：定义二叉树的链式存储结构，此处采用了每个结点中设置三个域，即值域，*lchild：左指针域和rchild：右指针域。

2、二叉树的前序遍历；利用二叉链表作为存储结构的前序遍历：先访问根结点，再依次访问左右子树。

3、二叉树的求叶子结点的个数计算；先分别求得左右子树中各叶子结点的个数，再计算出两者之和即为二叉树的叶子结点数。

4、二叉树的中序遍历；利用二叉链表作为存储结构的中序遍历：先访问左子数，再访问根结点，最后访问右子树。

5、二叉树的后序遍历；利用二叉链表作为存储结构的前序遍历：先访问左右子树，再访问根结点。

6、求二叉树的深度：首先判断二叉树是否为空，若为空则此二叉树的深度为0。

否则，就先别求出左右子树的深度并进行比较，取较大的+1就为二叉树的深度。

7、主函数。

核心算法的设计：二叉树是n个节点的有穷个集合，它或者是空集（n=0），或者同时满足以下两个条件：（1）：有且仅有一个称为根的节点；（2）：其余节点分为两个互不相交的集合T1，T2，并且T1，T2都是二叉树，分别称为根的左子树和右子树。

数学与计算机学院课程设计说明书课程名称: 数据结构与算法课程设计课程代码:题目: 线索二叉树的应用年级/专业/班: 2010级软件1班学生姓名:学号: 1127开始时间:2011 年12 月9 日完成时间:2011 年12 月23 日课程设计成绩：1指导教师签名：年月日摘要首先是对需求分析的简要阐述，说明系统要完成的任务和相应的分析，并给出测试数据。

其次是概要设计，说明所有抽象数据类型的定义、主程序的流程以及各程序模块之间的层次关系，以及ADT描述。

然后是详细设计，描述实现概要设计中定义的基本功操作和所有数据类型，以及函数的功能及代码实现。

再次是对系统的调试分析说明，以及遇到的问题和解决问题的方法。

然后是用户使用说明书的阐述，然后是测试的数据和结果的分析，最后是对本次课程设计的结论。

关键词：线索化；先序遍历；中序遍历；后续遍历线索二叉树的运用引言数据结构是计算机专业重要的专业基础课程与核心课程之一，在计算机领域应用广泛，计算机离不开数据结构。

数据结构课程设计为了能使我们掌握所学习的知识并有应用到实际的设计中的能力，对于掌握这门课程的学习方法有极大的意义。

本课程设计的题目为“线索二叉树的应用”，完成将二叉树转化成线索二叉树，采用前序、中序或后序线索二叉树的操作。

本课程设计采用的编程环境为Microsoft Visual Stdio 2008。

目录1需求分析 (3)2开发及运行平台 (4)3 概要设计 (5)4 详细设计 (7)5 调试分析 (12)6 测试结果 (13)7 结论 (18)致谢 (19)参考文献 (20)附录 (21)1、需求分析为了能更熟练精准的掌握二叉树的各种算法和操作，同时也为了开拓视野，综合运用所学的知识。

为此，需要将二叉树转化成线索二叉树，采用前序、中序或后序线索二叉树，以实现线索树建立、插入、删除、恢复线索等。

1.1任务与分析中次系统要实现对二叉树的建立，以及线索化该二叉树，同时实现对其先序、中序、后序线索话的并输出结果。

二叉树操作设计和实现实验报告一、目的：掌握二叉树的定义、性质及存储方式，各种遍历算法。

二、要求：采用二叉树链表作为存储结构，完成二叉树的建立，先序、中序和后序以及按层次遍历的操作，求所有叶子及结点总数的操作。

三、实验内容：1、分析、理解程序程序的功能是采用二叉树链表存储结构，完成二叉树的建立，先序、中序和后序以及按层次遍历的操作。

如输入二叉树ABD###CE##F##，链表示意图如下：2、添加中序和后序遍历算法//========LNR 中序遍历===============void Inorder(BinTree T){if(T){Inorder(T->lchild);printf("%c",T->data);Inorder(T->rchild);}}//==========LRN 后序遍历============void Postorder(BinTree T){if(T){Postorder(T->lchild);Postorder(T->rchild);printf("%c",T->data);}}3、调试程序，设计一棵二叉树，输入完全二叉树的先序序列，用#代表虚结点（空指针），如ABD###CE##F##，建立二叉树，求出先序、中序和后序以及按层次遍历序列，求所有叶子及结点总数。

（1）输入完全二叉树的先序序列ABD###CE##F##，程序运行结果如下：(2)先序序列:(3)中序序列:(4)后序序列:(5)所有叶子及结点总数:(6)按层次遍历序列:四、源程序代码#include"stdio.h"#include"string.h"#include"stdlib.h"#define Max 20 //结点的最大个数typedef struct node{char data;struct node *lchild,*rchild;}BinTNode; //自定义二叉树的结点类型typedef BinTNode *BinTree; //定义二叉树的指针int NodeNum,leaf; //NodeNum为结点数，leaf为叶子数//==========基于先序遍历算法创建二叉树==============//=====要求输入先序序列，其中加入虚结点"#"以示空指针的位置========== BinTree CreatBinTree(void){BinTree T;char ch;if((ch=getchar())=='#')return(NULL); //读入#，返回空指针else{T=(BinTNode *)malloc(sizeof(BinTNode)); //生成结点T->data=ch;T->lchild=CreatBinTree(); //构造左子树T->rchild=CreatBinTree(); //构造右子树return(T);}}//========NLR 先序遍历=============void Preorder(BinTree T){if(T) {printf("%c",T->data); //访问结点Preorder(T->lchild); //先序遍历左子树Preorder(T->rchild); //先序遍历右子树}}//========LNR 中序遍历===============void Inorder(BinTree T){if(T){Inorder(T->lchild);printf("%c",T->data);Inorder(T->rchild);}}//==========LRN 后序遍历============void Postorder(BinTree T){if(T){Postorder(T->lchild);Postorder(T->rchild);printf("%c",T->data);}}//=====采用后序遍历求二叉树的深度、结点数及叶子数的递归算法======== int TreeDepth(BinTree T){int hl,hr,max;if(T){hl=TreeDepth(T->lchild); //求左深度hr=TreeDepth(T->rchild); //求右深度max=hl>hr? hl:hr; //取左右深度的最大值NodeNum=NodeNum+1; //求结点数if(hl==0&&hr==0) leaf=leaf+1; //若左右深度为0，即为叶子。

二叉树的常用算法设计和实现一、引言二叉树是一种重要的数据结构，广泛应用于计算机科学中。

掌握二叉树的常用算法设计和实现对于理解和应用二叉树具有重要意义。

本文档将介绍二叉树的常用算法设计和实现，包括二叉树的遍历、查找、插入和删除等操作。

二、算法设计1. 遍历算法：二叉树的遍历是二叉树操作的核心，常用的遍历算法包括先序遍历、中序遍历和后序遍历。

每种遍历算法都有其特定的应用场景和优缺点。

2. 查找算法：在二叉树中查找特定元素是常见的操作。

常用的查找算法有二分查找和线性查找。

二分查找适用于有序的二叉树，而线性查找适用于任意顺序的二叉树。

3. 插入算法：在二叉树中插入新元素也是常见的操作。

插入操作需要考虑插入位置的选择，以保持二叉树的特性。

4. 删除算法：在二叉树中删除元素也是一个常见的操作。

删除操作需要考虑删除条件和影响，以保持二叉树的特性。

三、实现方法1. 先序遍历：使用递归实现先序遍历，可以通过访问节点、更新节点计数器和递归调用下一个节点来实现。

2. 中序遍历：使用递归实现中序遍历，可以通过访问节点、递归调用左子树和中继判断右子树是否需要访问来实现。

3. 后序遍历：使用迭代或递归实现后序遍历，可以通过访问节点、迭代处理左子树和右子树或递归调用左子树和更新节点计数器来实现。

4. 二分查找：在有序的二叉搜索树中实现二分查找，可以通过维护中间节点和边界条件来实现。

5. 线性查找：在任意顺序的二叉树中实现线性查找，可以通过顺序遍历所有节点来实现。

6. 插入和删除：针对具体应用场景和删除条件，选择适当的插入位置并维护节点的插入和删除操作。

在有序的二叉搜索树中实现插入和删除操作相对简单，而在其他类型的二叉树中则需要考虑平衡和维护二叉搜索树的特性。

四、代码示例以下是一个简单的Python代码示例，展示了如何实现一个简单的二叉搜索树以及常用的二叉树操作（包括遍历、查找、插入和删除）。

```pythonclass Node:def __init__(self, data):self.data = dataself.left = Noneself.right = Noneclass BinarySearchTree:def __init__(self):self.root = Nonedef insert(self, data):if not self.root:self.root = Node(data)else:self._insert(data, self.root)def _insert(self, data, node):if data < node.data:if node.left:self._insert(data, node.left)else:node.left = Node(data)elif data > node.data:if node.right:self._insert(data, node.right)else:node.right = Node(data)else:print("Value already in tree!") # Value already in tree!def search(self, data):return self._search(data, self.root)def _search(self, data, node):if data == node.data:return Trueelif (not node.left and data < node.data) or (notnode.right and data > node.data):return Falseelse:return self._search(data, node.left) orself._search(data, node.right)def inorder_traversal(self): # inorder traversal algorithm implementationif self.root: # If the tree is not empty, traverse it in-order.self._inorder_traversal(self.root) # Recursive function call for in-order traversal.print() # Print a new line after traversal to clear the output area for the next operation.def _inorder_traversal(self, node): # Helper function for in-order traversal algorithm implementation. Traverse the left subtreefirst and then traverse the right subtree for a given node (start with root). This method handles recursive calls for traversal operations efficiently while keeping track of nodes already visited and。

二叉树是计算机科学中常用的一种数据结构，可以用于表示各种类型的数据。

以下是一个简单的二叉树课程设计，使用C语言实现。

```c#include <stdio.h>#include <stdlib.h>// 定义二叉树节点结构体typedef struct Node {int data;struct Node *left;struct Node *right;} Node;// 创建新节点Node* createNode(int data) {Node* newNode = (Node*)malloc(sizeof(Node));if (!newNode) {printf("内存分配失败\n");return NULL;}newNode->data = data;newNode->left = NULL;newNode->right = NULL;return newNode;}// 插入节点Node* insertNode(Node* root, int data) {if (root == NULL) {return createNode(data);}if (data <= root->data) {root->left = insertNode(root->left, data); } else {root->right = insertNode(root->right, data); }return root;}// 中序遍历二叉树void inorderTraversal(Node* root) {if (root == NULL) {return;}inorderTraversal(root->left);printf("%d ", root->data);inorderTraversal(root->right);}int main() {Node* root = NULL; // 初始时，根节点为空int arr[] = {8, 3, 10, 1, 6, 14, 4, 7, 13}; // 要插入的节点数据数组int n = sizeof(arr) / sizeof(arr[0]); // 数组元素个数for (int i = 0; i < n; i++) { // 插入节点到二叉树中 root = insertNode(root, arr[i]);}printf("中序遍历二叉树的结果为："); // 中序遍历二叉树，输出结果为升序排列的节点数据数组inorderTraversal(root);printf("\n");return 0;}```。

二叉树程序设计二叉树（Binary Tree）是一种树状数据结构，其中每个节点最多有两个子节点，分别为左子节点和右子节点。

在程序设计中，涉及到二叉树的问题通常包括二叉树的构建、遍历、搜索等方面。

以下是一些常见的二叉树程序设计问题和相关的代码示例：1. 二叉树节点定义：class TreeNode:def __init__(self, value):self.value = valueself.left = Noneself.right = None2. 二叉树的构建：递归方式：def build_tree(preorder, inorder):if not preorder or not inorder:return Noneroot_value = preorder[0]root = TreeNode(root_value)root_index = inorder.index(root_value)root.left = build_tree(preorder[1:1 + root_index], inorder[:root_index])root.right = build_tree(preorder[1 + root_index:], inorder[root_index + 1:])3. 二叉树的遍历：前序遍历：def preorder_traversal(root):if root:print(root.value, end=" ") preorder_traversal(root.left) preorder_traversal(root.right)中序遍历：def inorder_traversal(root):if root:inorder_traversal(root.left)print(root.value, end=" ") inorder_traversal(root.right)后序遍历：def postorder_traversal(root):if root:postorder_traversal(root.left) postorder_traversal(root.right) print(root.value, end=" ")4. 二叉树的搜索：递归方式：def search_in_tree(root, target):return Noneif root.value == target:return rootleft_search = search_in_tree(root.left, target)right_search = search_in_tree(root.right, target)return left_search if left_search else right_search这些是一些基本的二叉树程序设计问题的示例。

二叉树问题数据结构设计摘要本文档将介绍二叉树问题的数据结构设计。

首先，我们将对二叉树的基本概念和特性进行简要说明。

然后，我们将介绍如何使用Py t ho n语言实现二叉树，并提供一些常见的二叉树问题的解决方法和相关代码示例。

1.引言二叉树是一种常用的数据结构，它由节点和连接节点的边组成，每个节点最多可以有两个子节点。

在计算机科学中，二叉树被广泛应用于搜索算法、排序算法、图像处理和网络通信等领域。

2.二叉树基本概念2.1节点二叉树中的节点是树的基本元素，它包含存储数据的值和指向其左右子节点的指针。

2.2父节点和子节点父节点是指向子节点的节点，子节点是从父节点指向的节点。

2.3根节点和叶节点根节点是树的顶部节点，它没有父节点。

叶节点是没有子节点的节点。

2.4二叉树的属性-二叉树的每个节点最多有两个子节点；-左子节点小于等于父节点，右子节点大于等于父节点；-二叉树可以为空。

3.二叉树的设计与实现在P yt ho n中，我们可以使用面向对象编程的方式来设计二叉树的数据结构，并通过一些基本操作来实现二叉树的各种功能。

以下是一个简单的二叉树类的代码示例：c l as sB in ar yT re eNod e:d e f__i ni t__(se lf,d at a):s e lf.d at a=da tas e lf.l ef t=No nes e lf.r ig ht=N on e4.常见的二叉树问题及解决方法4.1二叉树的遍历二叉树的遍历是指按照某种规定的顺序访问二叉树的所有节点。

常见的遍历方法包括先序遍历、中序遍历和后序遍历。

-先序遍历：根节点->左子树->右子树-中序遍历：左子树->根节点->右子树-后序遍历：左子树->右子树->根节点4.2二叉树的搜索二叉树的搜索是指在二叉树中查找某个特定值的节点。

常见的搜索方法包括深度优先搜索（D FS）和广度优先搜索（B FS）。

二叉树的创建与应用实例一、引言二叉树是一种非常常见的数据结构，它在很多领域都有着广泛的应用，如文件系统、计算机科学、数据挖掘等。

了解和掌握二叉树的结构和应用，对于深入理解数据结构和算法是非常有帮助的。

本篇文档将详细介绍二叉树的创建以及应用实例。

二、二叉树的基本概念二叉树是一种递归定义的数据结构，它由一个根节点和两个子节点（分别称为左子树和右子树）组成。

二叉树的每个节点最多有两个子节点，这使得二叉树具有高度优化和紧凑性的特点。

三、二叉树的创建创建二叉树通常有两种方式：手动创建和通过算法创建。

1.手动创建：手动创建二叉树需要按照二叉树的定义规则，逐个创建节点并连接它们。

这种方式的优点是直观易懂，缺点是手动创建大量的节点会比较繁琐。

2.算法创建：算法创建二叉树通常使用递归的方式，通过特定的算法步骤逐个构建节点。

这种方式可以自动化地创建大量的二叉树，而且效率较高。

四、二叉树的应用实例1.文件系统：文件系统中的目录结构可以看作是一种特殊的二叉树，其中根节点是整个文件系统的入口，左子节点表示子目录，右子节点表示文件。

通过二叉树可以方便地管理和查找文件。

2.计算机科学：在计算机科学中，二叉树常用于表示程序的执行路径，如决策树、堆栈等。

此外，二叉树也常用于数据压缩和哈希算法等。

3.数据挖掘：在数据挖掘中，二叉树常用于分类和聚类算法，如决策树、k-means等。

通过构建二叉树，可以将数据集划分为不同的类别，从而更好地理解和分析数据。

五、应用实例代码展示下面是一个简单的Python代码示例，展示了如何手动创建一个简单的二叉搜索树（BinarySearchTree,BST）：```pythonclassNode:def__init__(self,key):self.left=Noneself.right=Noneself.val=keydefinsert(root,key):ifrootisNone:returnNode(key)else:ifroot.val<key:root.right=insert(root.right,key)else:root.left=insert(root.left,key)returnrootdefinorder(root):ifroot:inorder(root.left)print(root.val),inorder(root.right)r=Node(50)r=insert(r,30)r=insert(r,20)r=insert(r,40)r=insert(r,70)r=insert(r,60)r=insert(r,80)print("Inordertraversalofthegiventree")inorder(r)#Output:20304050607080```六、总结本篇文档详细介绍了二叉树的创建以及应用实例，包括二叉树的基本概念、创建方式以及在文件系统、计算机科学、数据挖掘等领域的应用。

二叉树的建立及相关算法的实现
二叉树是一种特殊的树结构，它只允许每个节点最多有两个子树，每
个节点被称为父节点，它的子节点分别被称为左子节点和右子节点。

二叉
树的结构可以用来表示复杂的数据结构，对数据进行查询和存储，并能够
实现各种复杂的算法。

由于二叉树的结构比较简单，因此建立二叉树的技术不复杂。

通常，
我们从一个空二叉树开始，每次向树中添加一个节点，以完成树的建立。

在这里，我们主要介绍二叉树的建立，它是一种特殊的二叉树，其特点是，对于任意一个节点，它的左子树上所有节点的值均小于它的节点值，而它
的右子树上所有节点的值均大于它的节点值。

建立二叉树的一般步骤如下：
（1）构建一个空的二叉树。

（2）从根节点开始，比较插入节点和该节点的值。

（3）如果插入节点的值大于该节点的值，则插入节点放在右子树；
如果插入节点的值小于该节点的值，则插入节点放在左子树；
（4）假设一个新节点X，将要插入到该节点Y为根节点的子树中，
如果X的值大于Y的值，则将X插入到右子树上，否则将X插入到左子树上。

（5）插入过程中，继续比较X和左右子树的值。

二叉树基本操作演示程序的设计与实现2012级电器信息类X班（姓名）（学号）注意：文档以word格式提供，文件名起名规则：学号+姓名+实验报告名称一、需求分析1、创建二叉树。

按照用户需要的二叉树，构建二叉树。

2、将创建的二叉树，以树状形式输出。

3、分别以先序、中序、后序三种方式遍历访问二叉树。

4、输出二叉树的叶子结点及叶子结点的个数。

5、输出二叉树的高度。

6、将创建的二叉树，以括号形式输出。

二、概要设计为了实现以上功能，可以从三个方面着手设计。

1、主界面设计为了实现二叉树相关操作功能的管理，设计一个含有多个菜单项的主控菜单子程序以链接系统的各项子功能，方便用户使用本程序。

本系统主控菜单运行界面如图1所示。

首先请输入二叉树结点序列：请按菜单提示操作：----------------------------欢迎使用二叉树基本操作程序-------------------------------菜单选择1. 树状输出二叉树2. 先序遍历二叉树3. 中序遍历二叉树4. 后序遍历二叉树5. 输出叶子结点6. 输出叶子结点个数7. 输出二叉树的深度8. 括号形式输出二叉树9. 退出--------------------------------------------------------------------------------------------------图1 二叉树基本操作程序主菜单2、存储结构设计本程序采用二叉链式存储类型(BiTNode)存储二叉树的结点信息。

二叉树的链表中的结点至少包含3个域：数据域(data)、左孩子指针域(lchild)、右孩子指针域(rchild)。

3、系统功能设计本程序除了完成二叉树的创建功能外还设置了9个子功能菜单。

由于这9个子功能都是建立在二叉树的构造上的，所以二叉树的创建由主函数main()实现。

9个子功能的设计描述如下：⑴树状输出二叉树。

树状输出二叉树由函数TranslevelPrint()实现。

数据结构设计——⼆叉树实现⼆叉树操作设计和实现实验⽬的：掌握⼆叉树的定义、性质及存储⽅式，各种遍历算法。

实验要求：采⽤⼆叉树链表作为存储结构，完成⼆叉树的建⽴，先序、中序和后序以及按层次遍历的操作，求所有叶⼦及结点总数的操作。

1 #include <stdio.h>2 #include <stdlib.h>3 typedef char DataType;4 typedef struct node{5 DataType data;6struct node *lchild,*rchild;7 }Bnode, *BTree;8int count;9void CreateBTree(BTree *T);10void PreorderN(BTree T);11void MiddleN(BTree T);12void LatterN(BTree T);1314#define StackSize 100 /*假定预分配的栈空间最多为10*/15 typedef BTree SDataType; /*栈的元素类型设为整型*/16#define Error printf1718 typedef struct{19 SDataType data[StackSize];20int top;21 }SeqStack;2223 SeqStack * InitStack(void) /*初始栈*/24 {25 SeqStack *S = (SeqStack *)malloc(sizeof(SeqStack) * StackSize);26 S->top=-1;27 }2829int StackEmpty(SeqStack *S) /*判栈空*/30 {31return S->top==-1;32 }3334int StackFull(SeqStack *S) /*判栈满*/35 {36return S->top==StackSize-1;37 }3839void Push(SeqStack *S, SDataType x) /*进栈*/40 {41if(StackFull(S))42 Error("STACK FULL!\n"); /*上溢退出*/43else44 S->data[++S->top]=x; /*栈顶指针加1后将x进栈*/45 }4647 SDataType Pop(SeqStack *S) /*出栈*/48 {49if (StackEmpty(S))50 Error("Stack underflow"); /*下溢退出*/51else52return S->data[S->top--]; /*栈顶指针返回后将栈顶指针减1*/53 }5455 SDataType StackTop(SeqStack *S) /*取栈顶元素*/56 {57if (StackEmpty(S))58 Error("STACK EMPTY!\n");59return S->data[S->top];60 }6162 main()63 {64 BTree T;65char ch1,ch2;66 printf("\nPLEASE SELECT:\n");67 ch1='y';68while(ch1=='y' || ch1=='Y')69 {70 printf("\nA------------------------CREATE BITREE");71 printf("\nB-------------------------DLR(NO DI IGU)");72 printf("\nC----------------------Middle(NO DI IGU)");73 printf("\nD----------------------Latter(NO DI IGU)");74 printf("\nE-------------------------EXIT\n");75 scanf("\n%c",&ch2);76switch(ch2)77 {78case'A':79case'a':printf("INPUT NODE:\n");80 CreateBTree(&T);81 printf("CREATE SUCC\n");break;82case'B':83case'b':printf("BIAN LI JIE GUO\n");84 PreorderN(T);break;85case'C':86case'c':printf("Middle Bian Li Jie Guo\n");87 MiddleN(T);break;88case'D':89case'd':printf("Latter Bian Li Jie Guo\n");90 LatterN(T);break;91case'E':92case'e':ch1='n';break;93default:ch1='n';94 }95 }96 }97void CreateBTree(BTree *T)98 {99char ch;100 scanf("\n%c",&ch);101if (ch=='0')102 *T=NULL;103else104 {105 *T=(Bnode*)malloc(sizeof(Bnode));106 (*T)->data=ch;107 CreateBTree(&(*T)->lchild);108 CreateBTree(&(*T)->rchild);109 }110 }111void PreorderN(BTree T)112 {/*先序遍历⼆叉树T的⾮递归算法*/113 SeqStack *S;114 BTree p;115 p = T;116 S = InitStack();117while(!StackEmpty(S) || p != NULL)118 {119if(p)120 {121 printf("%3c",p->data); /*访问⼊栈结点的数据域*/ 122 Push(S,p); /*向左⾛到尽头*/123 p = p->lchild;124 }125else126 {127 p = Pop(S);128 p = p->rchild;129 }130 }131 }/*PreorderN */132133void MiddleN(BTree T)134 {135 SeqStack *S;136 BTree p;137 p = T;138 S = InitStack();139while(!StackEmpty(S) || p != NULL)140 {141if(p)142 {143/*向左⾛到尽头*/144 Push(S,p);145 p = p->lchild;146 }147else148 {149 p = Pop(S);150 printf("%3c",p->data);/*访问⼊栈结点的数据域*/ 151 p = p->rchild;152 }153 }154 }155156void LatterN(BTree T)157 {158 SeqStack *S1,*S2;159 BTree p;160 p = T;161 S1 = InitStack();162 S2 = InitStack();163while(!StackEmpty(S1) || p != NULL)164 {165if(p)166 {167/*向左⾛到尽头*/168 Push(S1,p);169 Push(S2,p);170 p = p->rchild;171 }172else173 {174 p = Pop(S1);175 p = p->lchild;176 }177 }178while(!StackEmpty(S2))179 {180 p = Pop(S2);181 printf("%3c",p->data);/*访问⼊栈结点的数据域*/ 182 }183 }。

精选全文完整版【数据结构】二叉树的实现//-------------------第一部分-----------------#include <stdio.h>typedef char TElemType;//建立结点typedef struct BiTree{TElemType data;struct BiTree *lchild,*rchild;}BiTree;//-------------------第二部分------------------//1、二叉树的建立：先序建立二叉树，//在创建完成二叉树之后，需要把根节点返回来，设置一个整型的临时变量//设置这个变量的目的就是为了返回根节点BiTree *CreateBiTree(BiTree *BT,int itemp){TElemType ch;BiTree *T1;//先申请一个节点T1 = (BiTree *)malloc(sizeof(BiTree));//如果失败，退出if(!T1)exit(1);//如果输入二叉树元素是“#”，说明这个元素是空的scanf("%c",&ch);if(ch !='#'){//将ch值存入新申请的节点中，新申请的节点，左右子树全为空T1->data = ch;T1->lchild = NULL;T1->rchild = NULL;//如果是根节点（只有一个），将申请的节点赋值给BTif(itemp == 0)BT = T1;//如果是左子树，将申请的节点赋值给BT的左孩子if(itemp == 1)BT->lchild = T1;//如果是右子树，将申请的节点赋值给BT的右孩子if(itemp == 2)BT->rchild = T1;//（2）创建左子树,整型变量为1，代表左子树CreateBiTree(T1,1);//（3）创建右子树,整型变量为2，代表右子树CreateBiTree(T1,2);}//返回根节点return BT;}//2、二叉树的遍历：三种方式：先序遍历、中序遍历、后序遍历//先序遍历口诀：根左右//中序遍历口诀：左根右//后续遍历口诀：左右根//（1）先序遍历二叉树void Pre_OrderTraverse(BiTree *T){//如果树存在if(T != NULL){//先输出根节点printf("%c ",T->data);//再输出左子树Pre_OrderTraverse(T->lchild);//最后输出右子树Pre_OrderTraverse(T->rchild);}}//（2）中序遍历二叉树void In_OrderTraverse(BiTree *T){//如果树存在if(T != NULL){//先遍历左子树In_OrderTraverse(T->lchild);//再输出根节点printf("%c ",T->data);//最后输出右子树In_OrderTraverse(T->rchild);}}//（3）后序遍历二叉树void Post_OrderTraverse(BiTree *T){//如果树存在if(T != NULL){//先输出左子树Post_OrderTraverse(T->lchild);//再输出右子树Post_OrderTraverse(T->rchild);//最后输出根节点printf("%c ",T->data);}}//-----------------------第三部分------------------------void main(){BiTree BT,*T;//1、以先序遍历的方式创建二叉树printf("先序建立二叉树,（每个结点为一个字符，空节点为“#”）：\n");T = CreateBiTree(&BT,0);printf("-----------------------创建树成功！-------------------------\n");printf("\n");printf("\n");printf("\n");//2、以先序遍历的方式输出二叉树printf("先序建立二叉树的结果是：\n");Pre_OrderTraverse(T);printf("\n");printf("\n");printf("\n");//3、以中序遍历的方式输出二叉树printf("中序建立二叉树的结果是：\n");In_OrderTraverse(T);printf("\n");printf("\n");printf("\n");//4、以后序遍历的方式输出二叉树printf("后序建立二叉树的结果是：\n");Post_OrderTraverse(T);printf("\n");}。

《数据结构与数据库》实验报告实验题目二叉树的基本操作及运算一、需要分析问题描述：实现二叉树（包括二叉排序树）的建立，并实现先序、中序、后序和按层次遍历，计算叶子结点数、树的深度、树的宽度，求树的非空子孙结点个数、度为2的结点数目、度为2的结点数目，以及二叉树常用运算。

问题分析：二叉树树型结构是一类重要的非线性数据结构，对它的熟练掌握是学习数据结构的基本要求。

由于二叉树的定义本身就是一种递归定义，所以二叉树的一些基本操作也可采用递归调用的方法。

处理本问题，我觉得应该：1、建立二叉树；2、通过递归方法来遍历（先序、中序和后序）二叉树；3、通过队列应用来实现对二叉树的层次遍历；4、借用递归方法对二叉树进行一些基本操作，如：求叶子数、树的深度宽度等；5、运用广义表对二叉树进行广义表形式的打印。

算法规定：输入形式：为了方便操作，规定二叉树的元素类型都为字符型，允许各种字符类型的输入，没有元素的结点以空格输入表示，并且本实验是以先序顺序输入的。

输出形式：通过先序、中序和后序遍历的方法对树的各字符型元素进行遍历打印，再以广义表形式进行打印。

对二叉树的一些运算结果以整型输出。

程序功能：实现对二叉树的先序、中序和后序遍历，层次遍历。

计算叶子结点数、树的深度、树的宽度，求树的非空子孙结点个数、度为2的结点数目、度为2的结点数目。

对二叉树的某个元素进行查找，对二叉树的某个结点进行删除。

测试数据：输入一：ABC□□DE□G□□F□□□（以□表示空格）,查找5,删除E预测结果：先序遍历ABCDEGF中序遍历CBEGDFA后序遍历CGEFDBA层次遍历ABCDEFG广义表打印A（B（C,D（E（,G）,F）））叶子数3 深度5 宽度2 非空子孙数6 度为2的数目2 度为1的数目2查找5，成功，查找的元素为E删除E后，以广义表形式打印A（B（C,D（,F）））输入二：ABD□□EH□□□CF□G□□□（以□表示空格）,查找10,删除B预测结果：先序遍历ABDEHCFG中序遍历DBHEAGFC后序遍历DHEBGFCA层次遍历ABCDEFHG广义表打印A（B(D,E(H)),C(F(,G))）叶子数3 深度4 宽度3 非空子孙数7 度为2的数目2 度为1的数目3查找10，失败。

数据结构——二叉树的实现二叉树是一种重要的数据结构，它由节点组成，每个节点最多有两个子节点：左子节点和右子节点。

二叉树的实现有多种方式，下面将介绍一种基本的实现方法。

一、二叉树节点的定义首先，我们需要定义二叉树的节点。

每个节点包含三个属性：值、左子节点和右子节点。

可以使用一个类来表示节点。

代码如下：```class BinaryTreeNode:def __init__(self, value):self.value = valueself.left = Noneself.right = None```有了节点定义以后，我们可以开始实现二叉树了。

二叉树可以由根节点表示，通过根节点可以访问整个二叉树的结构。

对于二叉树的实现，我们可以定义一个BinaryTree类。

代码如下：```class BinaryTree:def __init__(self):self.root = None```在二叉树的实现中，我们可以提供一些基本的操作，例如插入节点、删除节点、查找节点等。

下面我们来依次实现这些操作。

1.插入节点插入节点操作可以将一个新的节点插入二叉树中。

插入节点时，我们需要先找到插入位置，然后创建新的节点，将其添加到指定位置上。

代码如下：```def insert(root, value):if root is None:root = BinaryTreeNode(value)else:if value < root.value:root.left = insert(root.left, value)else:root.right = insert(root.right, value)return root```2.删除节点删除节点操作可以将一个指定的节点从二叉树中删除。

删除节点时，我们需要找到该节点，然后将其从二叉树中移除。

代码如下：```def delete(root, value):if root is None:return rootif value < root.value:root.left = delete(root.left, value)elif value > root.value:root.right = delete(root.right, value)else:if root.left is None:return root.rightelif root.right is None:return root.leftelse:temp = find_min(root.right)root.value = temp.valueroot.right = delete(root.right, temp.value)return rootdef find_min(root):while root.left is not None:root = root.leftreturn root```3.查找节点查找节点操作可以在二叉树中查找一个指定的节点。

封皮（按学校要求手工填写）成绩评定表课程设计任务书摘要树结构在客观世界中广泛存在，如族谱、各种社会组织机构等都可以用树形结构来表示；树结构在计算机中应用也很广泛，如文件夹；其中二叉树结构是比较常用的一种数据结构，简单来说每个结点最多有两个孩子。

本文采用C++语言来描述二叉树类模板的设计并实现其功能，并且采用VS2010应用程序来实现程序。

关键词：二叉树类模板；MFC目录1 需求分析 (1)2 算法基本原理 (1)3 类设计 (1)4 基于控制台的应用程序 (2)4.1类的接口设计 (2)4.2类的实现 (3)4.3主函数设计 (8)4.4基于控制台的应用程序测试 (9)5 基于MFC的应用程序 (10)5.1基于MFC的应用程序设计 (10)5.1.1 MFC程序界面设计 (11)5.1.2 MFC程序代码设计 (13)5.2基于MFC的应用程序测试 (17)结论 (20)参考文献 (21)1需求分析进行二叉树类模板的设计并实现,数据元素可以是char,int,float等多种数据类型,包括以下功能:（1）采取顺序存储结构或链式存储结构实现二叉树的存储;（2）实现二叉树的建树;（3）实现二叉树的前序、中序、后序遍历；（4）能够求解二叉树的结点总数和叶子结点总数；（5）能够求解二叉树的高度；（6）将上述功能作为类的成员函数实现，编写主函数测试上述功能。

整个二叉树类模板程序中的存储采用的是链式存储结构。

在整个二叉树类中所有数据成员和成员函数均采用公有方式，类中有一个二叉树结点的定义，有建立二叉树的成员函数，有先序、中序、后序遍历的成员函数，有求解结点数、叶子节点数、二叉树深度的成员函数，它的功能在类里定义一个调用各个成员函数的成员函数来实现对二叉树的操作，然后在主函数中通过对模板的实例化产生对象，用对象调用成员函数的方式实现预期功能。

2算法基本原理一颗二叉树有许多个结点组成，每个结点有三个区域分别存有数据和它的左右孩子指针。

实验报告(二)一、实验名称：树的操作二、实验目的：1.明确了解二叉树的链表存储结构。

2.熟练掌握二叉树的先序遍历算法。

三、实验原理：1．树型结构是一种非常重要的非线性结构。

树在客观世界是广泛存在的，在计算机领域里也得到了广泛的应用。

在编译程序里，也可用树来表示源程序的语法结构，在数据库系统中，数形结构也是信息的重要组织形式。

2．节点的有限集合（N大于等于0）。

在一棵非空数里：（1）、有且仅有一个特定的根节点；（2）、当N大于1时，其余结点可分为M（M大于0）个互不相交的子集，其中每一个集合又是一棵树，并且称为根的子树。

树的定义是以递归形式给出的。

3．二叉树是另一种树形结构。

它的特点是每个结点最多有两棵子树，并且，二叉树的子树有左右之分，其次序不能颠倒。

三、设计思路根据二叉树的结构特点采用递归的方法构造和先序遍历二叉树。

然后构造一个二叉树，先预测其输出结果再看计算机输出是否与预计符合。

四、实验内容1.二叉树实验源程序：#include <stdio.h>#include <conio.h>#include <stdlib.h>#include <malloc.h>#include <iostream># define null 0# define len sizeof(bitreptr)int f,g;typedef struct type1 /*二叉树结点类型说明*/ {char data;type1 *lchild,*rchild;}bitreptr,*bt;void preorder(bitreptr *bt) /*先序遍历二叉树*/{if(g==1) printf("先序遍历序列为：\n");g=g+1;if(bt){printf("%c",bt->data);preorder(bt->lchild);preorder(bt->rchild);}else if(g==2) printf("空树\n");}bitreptr *crt_bt() /*建立二叉树*/ {bitreptr *bt;char ch;if(f==1) printf("输入根结点，#表示结束\n");else printf("输入结点，#表示结束\n");scanf("\n%c",&ch);f=f+1;if(ch=='#') bt=null;else{bt=(bitreptr *)malloc(len);bt->data=ch;printf("%c 左孩子",bt->data);bt->lchild=crt_bt();printf("%c 右孩子",bt->data);bt->rchild=crt_bt();}return(bt);}void main(){f=1;g=1;bitreptr *newbt; newbt=crt_bt(); preorder(newbt); printf("\n");}2.程序运行结果: 构造的二叉树:先序遍历结果:五、实验总结:❶通过递归运算可以实现二叉树的先序遍历❷二叉树是按照一定的规律构造的,故其遍历也是有规律的,均可通过递归实现❸和栈一样利用二叉树的遍历可实现数值运算,如本例通过实现中序遍历可实现运算。