Matlab图形绘制技巧

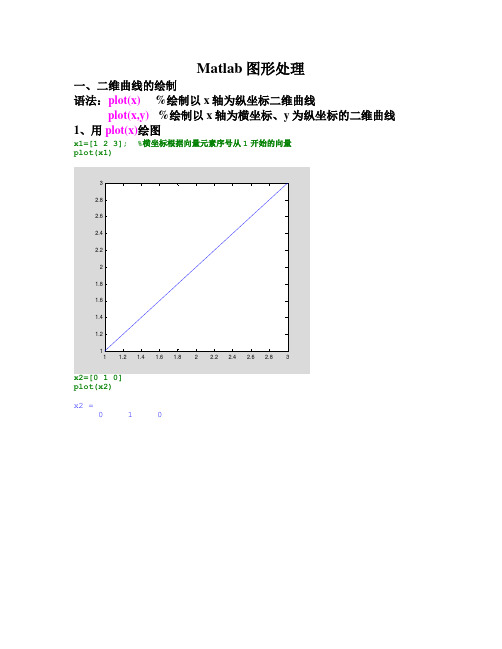
Matlab图形处理一、二维曲线的绘制语法：plot(x) %绘制以x轴为纵坐标二维曲线plot(x,y) %绘制以x轴为横坐标、y为纵坐标的二维曲线1、用plot(x)绘图x1=[1 2 3]; %横坐标根据向量元素序号从1开始的向量plot(x1)plot(x2)x2 =0 1 0x1=0:0.1:2*pi;y1=sin(x1);plot(x1,y1)y2=[1 1 0 0 1 1]; plot(x2,y2)axis([0 4 0 2])3、矩阵绘图x1=[1 2 3;4 5 6] %以矩阵的每一列作图，横坐标为向量1:2 plot(x1)x1 =1 2 3plot(x2)x2 =-1 2 04 0 -20 0 1Y=[1 2 3;4 5 6]plot(X,Y) %X是向量，其长度与Y的列数相同，X与Y的每一行绘一曲线X =-1 2 3Y =1 2 34 5 6Y1=[1 2;3 4;5 6]plot(X1,Y1) %X1的长度与Y1的行数相同，X1与Y1的每一列绘一图X1 =1 2 3Y1 =1 23 4Y2=[1 2;3 4;5 6]plot(X2,Y2) %如果X2，Y2均是矩阵，则它们的大小必须相同,矩阵X2的每一列和Y2的每一列绘一曲线X2 =1 00 -11 2Y2 =1 23 4Z2=X2+i*Y2plot(Z2) %与plot(real(Z2),imag(Z2))相同Z2 =1.0000 + 1.0000i 0 +2.0000i0 + 3.0000i -1.0000 + 4.0000i1.0000 + 5.0000i2.0000 + 6.0000ix=0:0.1:2*pi;plot(x,sin(x),x,cos(x),x,sin(2*x))6、指定图形窗口语法：figure(n) % 指定第n个窗口,窗口名为"Figure No.n",而不关闭其它窗口7、同一窗口绘制多个子图语法：subplot(m,n,k) %使m n幅子图中的第k幅成为当前图x=0:0.1:2*pi;subplot(2,2,1)plot(x,sin(x))subplot(2,2,2)plot(x,cos(x))subplot(2,2,3)plot(x,sin(2*x))subplot(2,2,4)plot(x,cos(3*x))8、曲线的线型、颜色和数据点型(见书本p140表格)语法：plot(x,y,'s') %s为类型说明的字符串参数，可以是线型，颜色和数据点型之一或三种组合.clfx=0:0.1:2*pi;plot(x,sin(x),'r-.')hold on %使当选前坐标系和图形保留plot(x,cos(x),'b:o')9、文字标注：包括图名(Title)、坐标轴(Lable)、文字注释(Text)和图例(Legend)语法：title(s) %图名xlabel(s) % x坐标名ylabel(s) % y坐标名legend(s,pos) %在指定位置建立图例legend off %擦除当前图中的图例text(xt,yt,s) %在图形的(xt,yt)处注释注：pos可取值0 (自动取最佳位置) ，1(右上角，默认位置)， 2(左上角)， 3(左下角)， 4(右下角)， -1(图右侧)，也可以直接在图中用鼠标将图例拖到满意位置.clear allclfx=0:0.1:2*pi;plot(x,sin(x))hold onplot(x,cos(x),'ro')title('y1=sin(x),y2=cos(x)')xlabel('x')legend('sin(x)','cos(x)',4) %在右下角添加图例text(pi,sin(pi),'x=\pi')10、交互式图形命令语法：[x，y]=ginput(n) %用鼠标从图形上获取n个点坐标(x,y) gtext('s') %用鼠标把字符串放置到图形上x=0:0.1:2*pi;plot(x,sin(x))[m,n]=ginput(2) %获取两点坐标gtext('2\pi') %写2pim =3.15326.1855n =-0.0029-0.00291、三维曲线：语法：plot3(x,y,z,'s') %x,y,z是同维向量时，绘制以元素为坐标的三维曲线，当x,y,z是同维的矩阵时，绘制三维曲线的条数等于矩阵的列数。

Matlab图形绘制技巧与实例展示一、介绍Matlab是一种功能强大的计算机软件，常用于科学计算和数据可视化分析。

其中，图形绘制是Matlab的一项重要功能，能够直观地展示数据和结果。

本文将探讨一些Matlab图形绘制的技巧，并通过实例展示其应用。

二、基础图形绘制Matlab提供了多种基础图形绘制函数，如plot、scatter、bar等。

这些函数可以用来绘制折线图、散点图、柱状图等常见图形。

例如我们可以使用plot函数绘制一个简单的折线图：```matlabx = 1:10;y = [1, 2, 3, 4, 5, 4, 3, 2, 1, 0];plot(x, y);```运行以上代码，就可以得到一个由点连接而成的折线图。

通过修改x和y的取值，可以得到不同形状和样式的折线图。

三、图形修饰在绘制图形时，我们通常需要添加标题、坐标轴标签、图例等进行修饰。

Matlab提供了相应的函数，如title、xlabel、ylabel、legend等。

下面是一个例子：```matlabx = 1:10;y = [1, 4, 9, 16, 25, 16, 9, 4, 1, 0];plot(x, y);title('Parabolic Curve');xlabel('X-axis');ylabel('Y-axis');legend('Curve');```执行以上代码，我们得到一个带有标题、坐标轴标签和图例的折线图。

四、子图绘制有时候，我们希望在一幅图中同时显示多个子图，以便比较它们之间的关系。

Matlab提供了subplot函数来实现这个功能。

下面是一个例子：```matlabx = 1:10;y1 = [1, 2, 3, 4, 5, 4, 3, 2, 1, 0];y2 = [0, 1, 0, 1, 0, 1, 0, 1, 0, 1];subplot(2, 1, 1);plot(x, y1);title('Subplot 1');subplot(2, 1, 2);plot(x, y2);title('Subplot 2');通过subplot函数，我们将一幅图分为两个子图，并在每个子图中绘制不同的折线图。

matlab绘图的一些技巧1.在坐标轴上任意标上感兴趣的刻度。

用XTick、YTick、ZTick。

如图1.如：x=0:0.1:10;y=x.^2;h=plot(x,y,'o',x,y);set(gca,'YTick',[0,10,25,50,80,99],'XTick',[0.5,8,10]); 用XTickLabel、YTickLabel、ZTickLabel属性把标记标签从数值改为字符串。

如图2.如将y轴上的值80用字符串代替：x=0:0.1:10;y=x.^2;h=plot(x,y,'o',x,y);set(gca,'YTickLabel','0|10|25|50|cutoff|99');图1图22.使用多个x轴和y轴XAxisLocation和YAxisLocation属性指定在图形的哪一侧放置x轴和y轴。

如图3.x1=0:0.01:10;y1=sin(x1);h1=line(x1,y1,'Color','r');ax1=gca;set(ax1,'XColor','r','YColor','r');ax2=axes('Position',get(ax1,'Position'),'XAxisLocation','top','YAxisLocation','right','Color','none',' XColor','k','YColor','k');x2=x1;y2=cos(x2);h2=line(x2,y2,'Color','k','Parent',ax2);图33.连接图形与变量（更新自变量或因变量的值）用数据源属性XDataSource、YDataSource、ZDataSource及refreshdata.可以做动画。

使用matlab绘制三维图形的方法要使用MATLAB绘制三维图形，首先需要了解MATLAB中的三维绘图函数和绘图选项。

下面将介绍一些常用的绘制三维图形的方法。

1.绘制基本的三维图形要绘制基本的三维图形，可以使用以下函数：- plot3(函数：用于在三维坐标系中绘制线条。

- scatter3(函数：用于在三维坐标系中绘制散点图。

- surf(函数：用于绘制三维曲面图。

- mesh(函数：用于绘制三维网格图。

- bar3(函数：用于绘制三维条形图。

- contour3(函数：用于绘制三维等高线图。

例如，下面的代码演示了如何使用plot3(函数绘制一个三维线条图：```x = linspace(0, 2*pi, 100);y = sin(x);z = cos(x);plot3(x, y, z, 'LineWidth', 2);xlabel('X');ylabel('Y');zlabel('Z');title('3D Line Plot');```2.添加颜色和纹理在绘制三维图形时，可以使用颜色和纹理来增加图形的信息。

MATLAB 提供了一系列函数来处理颜色和纹理，如：- colormap(函数：用于设置颜色映射。

- caxis(函数：用于设置坐标轴范围。

- shading(函数：用于设置颜色插值方法。

- texturemap(函数：用于设置纹理映射方法。

例如，下面的代码展示了如何使用纹理映射来绘制一个球体：```[X, Y, Z] = sphere(50);C = colormap('jet');surface(X, Y, Z, 'FaceColor', 'texturemap', 'CData', C);axis equal;```3.绘制多个数据集要在同一张图中绘制多个数据集，可以使用hold on和hold off命令。

一、目录1.彗星图二维彗星图三维彗星图2.帧动画3.程序动画4.色图变换5.Voronoi图和三角剖分Voronoi图三角剖分6.四面体7.彩带图彩带图三维流彩带图8.伪彩图9.切片图切片图切片轮廓线图10.轮廓图显示轮廓线显示围裙瀑布效果带光照模式的阴影图11.函数绘图轮廓线、网格图、曲面图、轮廓网格图轮廓曲面图、二维曲线、极坐标曲线图、自定义函数12.三维图形控制视点灯光效果色彩控制二、图形示例1．彗星图二维彗星图t=0:.01:2*pi;x=cos(2*t).*(cos(t).^2);y=sin(2*t).*(sin(t).^2);comet(x,y);title('二维彗星轨迹图')hold onplot(x,y)三维彗星图a=12;b=9;T0=2*pi;%T0是轨道的周期T=5*T0;dt=pi/100;t=[0:dt:T]';f=sqrt(a^2-b^2);%地球与另一焦点的距离th=12.5*pi/180;%未经轨道与x-y平面的倾角E=exp(-t/20);%轨道收缩率x=E.*(a*cos(t)-f);y=E.*(b*cos(th)*sin(t));z=E.*(b*sin(th)*sin(t));plot3(x,y,z,'g')%画全程轨线hold on,sphere(20);%画地球axis offtitle('卫星返回地球示例')x1=-18*T0;x2=6*T0;y1=-12*T0;y2=12*T0;z1=-6*T0;z2=6*T0;axis([x1 x2 y1 y2 z1 z2])% axis([-15 10 -15 10 -10 10])axis equalcomet3(x,y,z,0.02);%画运动轨线hold off2．帧动画Z=peaks;surf(Z)%绘制网格表面图axis tightset(gca,'nextplot','replacechildren');%设定axis覆盖重画模式title('帧动画播放示例')for j=1:20surf(sin(2*pi*j/20)*Z,Z)%重新绘制网格表面图，这里后面一个Z当成了颜色矩阵F(j)=getframe;%创建帧endmovie(F,20)%播放动画20次3．程序动画t=0:pi/50:10*pii=1;h=plot3(sin(t(i)),cos(t(i)),t(i),'*','erasemode','none');%设定擦除模式grid onaxis([-2 2 -2 2 -1 10*pi])title('程序动画示例')for i=2:length(t)set(h,'xdata',sin(t(i)),'ydata',cos(t(i)),'zdata',t(i));drawnowpause(0.01)end4．色图变换load spine image(X) colormap cool spinmap(10)5．Voronoi图和三角剖分Voronoi图rand('state',5)x=rand(1,10);y=rand(1,10);subplot(131)voronoi(x,y);%绘制voronoi图形axis equalaxis([-0.2 1.6 -0.5 2.5])subplot(132)[vx,vy]=voronoi(x,y);plot(x,y,'r+',vx,vy,'b-');%应用返回值绘制axis equalaxis([-0.2 1.6 -0.5 2.5])subplot(133)rand('state',5);x=rand(10,2);[v,c]=voronoin(x);%返回值v参数维voronoi顶点矩阵，返回值c参数为voronoi元胞数组for i=1:length(c)if all(c{i}~=1)patch(v(c{i},1),v(c{i},2),i);%应用色图iendendaxis equalaxis([-0.2 1.6 -0.5 2.5])box on三角剖分[x,y]=meshgrid(1:15,1:15); tri=delaunay(x,y);z=peaks(15);trimesh(tri,x,y,z)d=[-1 1];[x,y,z]=meshgrid(d,d,d);%定义一个立方体x=[x(:);0];y=[y(:);0];z=[z(:);0];%[x,y,z]分别为加上中心的立方体顶点X=[x(:) y(:) z(:)];Tes=delaunayn(X);%返回m×n的数组值tetramesh(Tes,X);%绘制四面体图camorbit(20,0);%旋转摄像目标位置7．彩带图彩带图[x,y]=meshgrid(-3:.5:3,-3:.1:3);z=peaks(x,y);三维流彩带图load wind%打开保存的数据lims=[100.64 116.67 17.25 28.75 -0.02 6.86];%定义坐标轴范围[x,y,z,u,v,w]=subvolume(x,y,z,u,v,w,lims);%lims来定义数据子集[sx sy sz]=meshgrid(110,20:5:30,1:5);%定义网格点verts=stream3(x,y,z,u,v,w,sx,sy,sz,.5);%计算彩带顶点cav=curl(x,y,z,u,v,w);%计算卷曲角速度wind_speed=sqrt(u.^2+v.^2+w.^2);%计算流速h=streamribbon(verts,x,y,z,cav,wind_speed,2);%绘制流彩带图view(3)8．伪彩图n=6%定义轮数r=(0:n)'/n;%定义轮的半径theta=pi*(-n:n)/n;%定义轮的扇区角X=r*cos(theta);Y=r*sin(theta);%定义网格顶点C=r*cos(2*theta);%定义色图pcolor(X,Y,C)%绘制伪彩图axis equal tight9．切片图切片图[x,y,z] = meshgrid(-2:.2:2,-2:.25:2,-2:.16:2); v = x.*exp(-x.^2-y.^2-z.^2);xslice = [-1.2,.8,2]; yslice = 2; zslice = [-2,0]; slice(x,y,z,v,xslice,yslice,zslice)colormap hsv切片轮廓线图[x y z v]=flow;%打开水流数据h=contourslice(x,y,z,v,[1:9],[],[0],linspace(-8,2,10));%切片轮廓线view([-12 30])10．轮廓图显示轮廓线[x,y,z]=peaks;subplot(1,2,1)meshc(x,y,z);%同时画出网格图与轮廓线title('meshc 网格图与轮廓线')axis([-inf inf -inf inf -inf inf]);subplot(1,2,2)surfc(x,y,z);%同时画出曲面图与轮廓线title('surfc 曲面图与轮廓线')axis([-inf inf -inf inf -inf inf]);显示围裙[x y z]=peaks;meshz(x,y,z);瀑布效果[X,Y,Z]=peaks(30); waterfall(X,Y,Z)带光照模式的阴影图[x,y]=meshgrid(-3:1/8:3);z=peaks(x,y);surfl(x,y,z);shading interp%着色处理colormap(gray);%灰度处理axis([-3 3 -3 3 -8 8])11．函数绘图轮廓线、网格图、曲面图、轮廓网格图%图1绘制轮廓线、网格图、曲面图、轮廓网格图subplot(221)f=['3*(1-x)^2*exp(-(x^2)-(y+1)^2)-10*(x/5-x^3-y^5)*exp(-x^2-y^2)-1/3*exp(-(x+1)^2-y^ 2)'];%定义双变量x、y的函数式ezcontour(f,[-3,3],49)%x、y为[-3 3]，网格为49×49subplot(222)ezmesh('sqrt(x^2+y^2)');subplot(223)ezsurf('real(atan(x+i*y))')%经过滤波，如果相同数据surf绘图没有滤波subplot(224)ezmeshc('y/(1+x^2+y^2)',[-5,5,-2*pi,2*pi])%x、y的数值范围分别为[-5 5]、[-2*pi 2*pi]轮廓曲面图、二维曲线、极坐标曲线图、自定义函数%图2绘制轮廓曲面图、二维曲线、极坐标曲线图、自定义函数figure(2)subplot(221)ezsurfc('sin(u)*sin(v)')subplot(222)ezplot('x^2-y^4');subplot(223)ezpolar('1+cos(t)')subplot(224)fplot('myfun',[-20 20])function Y=myfun(x)Y(:,1)=200*sin(x(:))./x(:);Y(:,2)=x(:).^2;三维曲线图%绘制三维曲线图figure(3)ezplot3('sin(t)','cos(t)','t',[0,6*pi])12．三维图形控制视点View图形旋转subplot(121)surf(peaks);title('旋转前图形'); subplot(122)h=surf(peaks); rotate(h,[1 0 1],180) title('旋转后图形');灯光效果%灯光效果(1)camlight(2)light(3)lightangle(4)lighting(5)material sphere;camlight色彩控制%色彩控制(1)缺省设置colordef、whitebg(2)色图colormap(3)浓淡处理shading load flujetimage(X)colormap(jet)subplot(131)sphere(16)axis squareshading flattitle('Flat Shading') subplot(132)sphere(16)axis squareshading facetedtitle('Faceted Shading') subplot(133)sphere(16)axis squareshading interptitle('Interpolated Shading')v。

MATLAB中的三维图形绘制与动画制作技巧引言MATLAB是一种强大的科学计算软件，广泛应用于工程、物理、数学等各个领域。

其中，三维图形绘制和动画制作是其功能的重要一部分。

本文将深入探讨MATLAB中三维图形绘制与动画制作的技巧，并给出一些实用的示例。

一、三维图形绘制1. 坐标系的设定在绘制三维图形之前，我们需要设定坐标系。

通过使用MATLAB的figure函数和axes函数，我们可以创建一个三维坐标系，并设置其属性，如坐标轴的范围、标签等。

2. 点的绘制在三维图形中，最基本的图元是点。

通过scatter3函数，我们可以绘制出一系列点的三维分布情况。

可以通过设置点的大小、颜色、透明度等属性，增加图像的美观性。

3. 曲线的绘制MATLAB提供了多种绘制曲线的函数，如plot3、line、quiver等。

通过这些函数，我们可以绘制各种样式的曲线，例如直线、曲线、矢量、流线等。

我们可以根据需要设置线条的样式、颜色、宽度等属性。

4. 曲面的绘制除了曲线，我们还可以绘制三维曲面。

通过函数mesh、surf和contour，我们可以绘制出具有平滑外形的曲面。

可以通过设置颜色映射和透明度等属性，使得曲面具有更加细腻的外观。

二、动画制作1. 创建动画对象要制作动画，我们需要先创建一个动画对象。

通过使用MATLAB的videoWriter函数，我们可以创建一个视频文件，并设置其参数，如帧率、分辨率等。

2. 绘制关键帧动画的核心是绘制一系列关键帧，并在每一帧之间进行插值。

通过在每一帧中修改图形对象的属性，我们可以实现对象的平移、旋转和缩放等变换。

通过MATLAB提供的getframe函数，我们可以将当前图像存储为一个帧对象。

3. 帧之间的插值在关键帧之间，我们需要进行插值，以平滑动画的过渡。

通过使用MATLAB 的linspace函数，我们可以生成两个关键帧之间的若干插值。

然后，我们可以在每个插值处更新图形对象的属性，从而实现动画效果。

绘制二维数据曲线图1.1 绘制单根二维曲线plot 函数的基本调用格式为：plot(x,y) 其中x和y为长度相同的向量，分别用于存储x坐标和y坐标数据。

例1-1 在0≤x≤2p区间内，绘制曲线y=2e-0.5xcos(4πx)程序如下：x=0:pi/100:2*pi;y=2*exp(-0.5*x).*cos(4*pi*x);plot(x,y)例1-2 绘制曲线。

程序如下：t=0:0.1:2*pi;x=t.*sin(3*t);y=t.*sin(t).*sin(t);plot(x,y);plot函数最简单的调用格式是只包含一个输入参数：plot(x)在这种情况下，当x是实向量时，以该向量元素的下标为横坐标，元素值为纵坐标画出一条连续曲线，这实际上是绘制折线图。

1.2 绘制多根二维曲线1．plot函数的输入参数是矩阵形式(1)当x是向量，y是有一维与x同维的矩阵时，则绘制出多根不同颜色的曲线。

曲线条数等于y矩阵的另一维数，x被作为这些曲线共同的横坐标。

(2)当x,y是同维矩阵时，则以x,y对应列元素为横、纵坐标分别绘制曲线，曲线条数等于矩阵的列数。

(3)对只包含一个输入参数的plot函数，当输入参数是实矩阵时，则按列绘制每列元素值相对其下标的曲线，曲线条数等于输入参数矩阵的列数。

当输入参数是复数矩阵时，则按列分别以元素实部和虚部为横、纵坐标绘制多条曲线。

2．含多个输入参数的plot函数调用格式为：plot(x1,y1,x2,y2,…,xn,yn)(1)当输入参数都为向量时，x1和y1，x2和y2，…，xn和yn分别组成一组向量对，每一组向量对的长度可以不同。

每一向量对可以绘制出一条曲线，这样可以在同一坐标内绘制出多条曲线。

(2) 当输入参数有矩阵形式时，配对的x,y按对应列元素为横、纵坐标分别绘制曲线，曲线条数等于矩阵的列数。

例1-3 分析下列程序绘制的曲线。

x1=linspace(0,2*pi,100);x2=linspace(0,3*pi,100);x3=linspace(0,4*pi,100);y1=sin(x1);y2=1+sin(x2);y3=2+sin(x3);x=[x1;x2;x3]';y=[y1;y2;y3]';plot(x,y,x1,y1-1)3．具有两个纵坐标标度的图形在MA TLAB中，如果需要绘制出具有不同纵坐标标度的两个图形，可以使用plotyy绘图函数。

MATLAB图形绘制技巧与实例介绍：MATLAB是一种功能强大，广泛应用于科学计算和工程领域的软件平台。

它拥有丰富的图形绘制功能，可以用于可视化数据和传达研究成果。

本文将探讨一些MATLAB图形绘制的技巧和提供一些实例，让读者了解如何高效地利用MATLAB 绘制各种类型的图形。

一、基本绘图函数MATLAB中最基本的绘图函数是plot，它可以绘制二维图形。

可以通过指定x和y向量作为输入参数，将数据点连线绘制出来。

除了plot函数，还有其他一些常用的绘图函数，如scatter用于绘制散点图，bar用于绘制条形图，hist用于绘制直方图等。

这些函数具有丰富的参数选项，可以根据需要进行调整，以得到满意的图形效果。

二、自定义图形样式在MATLAB中，可以通过一些简单的命令实现图形样式的自定义。

例如，可以通过修改线型、颜色和点标记等属性，使得图形更加美观和易读。

除了利用内置的属性选项，还可以使用一些自定义的方法，如在plot函数中添加字符串参数来自定义线型和颜色。

三、多图绘制在某些情况下，需要在一个图形窗口中展示多个图形。

MATLAB提供了subplot函数，可以将图形窗口划分为多个小的绘图区域，并在每个区域中绘制不同的图形。

这对于比较不同数据集之间的关系或展示多个实验结果非常有用。

另外，还可以使用hold on和hold off命令，以在同一个图形窗口中绘制多个图形，并在绘制后保持图形的可编辑性。

四、3D图形绘制除了二维图形，MATLAB还支持绘制三维图形。

可以使用plot3函数将数据点绘制成三维曲线或散点图。

也可以使用mesh和surf函数绘制三维表面图，这在可视化函数和曲面的形状时非常有用。

通过调整视角和添加颜色映射等设置，可以使得3D图形更加生动和具有立体感。

五、图形标注和注释为了更好地传达和解释图形的含义，MATLAB提供了一些标注和注释功能。

可以使用xlabel、ylabel和title函数添加坐标轴标签和标题。

MATLAB中的图形绘制技巧概述：MATLAB是一种用于科学计算和数据可视化的强大工具，它提供了丰富的图形绘制功能，使用户能够清晰地展示和分析数据。

本文将介绍一些MATLAB中的图形绘制技巧，帮助读者更加熟悉和灵活运用这些功能。

一、基本图形绘制1.折线图(Line Plot)：折线图是用于显示随时间、变量或其他条件变化而变化的数据的理想选择。

例如，假设我们想要展示一段时间内气温的变化趋势，可以使用MATLAB中的plot 函数来生成折线图。

通过在X轴上放置时间（日期）或变量，将温度值绘制在Y 轴上，我们可以清晰地看到气温的变化。

2.散点图(Scatter Plot)：散点图用于观察两个连续变量之间的关系。

在MATLAB中，可以使用scatter 函数生成散点图。

例如，我们可以绘制一个散点图来观察身高和体重之间的关系，每个点代表一个人，x轴表示身高，y轴表示体重。

通过观察图形，我们可以直观地看到身高和体重之间是否存在某种关联。

3.柱状图(Bar Plot)：柱状图适用于对各个组或类别之间的数值进行比较。

使用bar函数可以在MATLAB中绘制柱状图。

例如，如果我们想要比较不同地区的人口数量，可以使用柱状图将不同地区的人口数量以柱状图的形式展示出来。

不同地区的柱状图高度不同，可以直观地看到不同地区的人口数量差异。

4.饼图(Pie Chart)：饼图用于表示不同类别之间的比例关系，MATLAB中的pie函数可以用来生成饼图。

例如，我们可以使用饼图展示一份问卷调查中各个选项的比例，饼图的每个扇区表示一个选项，扇区的面积大小代表该选项占总数的比例。

通过观察饼图，我们可以更加直观地了解各个选项之间的比例关系。

二、高级图形绘制技巧1.子图(Subplot)：在MATLAB中，我们可以使用subplot函数创建一个包含多个子图的大图。

通过在subplot函数中指定行数和列数，可以将图形划分为不同的区域，并在每个区域中绘制不同的图形。