当前位置：文档之家 › 材料力学 第七章弯曲正应力(1,2)分析

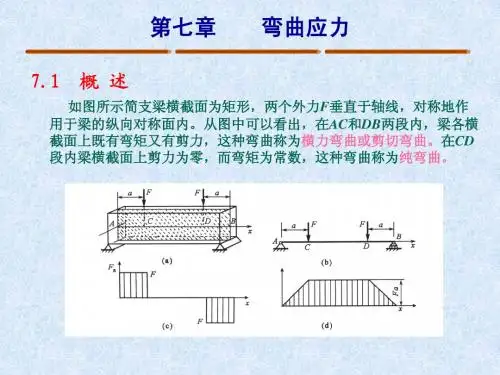
材料力学 第七章弯曲正应力(1,2)分析

  • 格式：ppt
  • 大小：1.53 MB
  • 文档页数：43

下载文档原格式

  / 43

合集下载

秦飞编著《材料力学》第7章 弯曲应力

秦飞编著《材料力学》第7章 弯曲应力
危险点发 生在什么 位置？
秦飞 编著《材料力学》 第7章 弯曲应力
14
7.1 弯曲正应力
弯曲正应力公式
各种型钢的Iz、Wz值均可以从附录的型钢规格表中查到。
常用截面：矩形截面
bh 3 Iz 12
y max
h 2
bh 2 Wz 6
h
b
对于直径为D的实心圆形截面
πD Iz 64
4
ymax
C
拉
z
M
z
C
压
拉 y y
秦飞 编著《材料力学》 第7章 弯曲应力 8
7.1 弯曲正应力
纯弯曲时梁横截面上的正应力
（2）静力平衡关系 由平面假设，横截面上只有正应力σ。纯弯曲情况下，梁横 截面上的内力只有Mz=M，轴力和 My等其他内力均为零，则
dA 0
A
中性轴
z dA 0
A
由这3个静力平衡方

y

与y成正比，沿截面高
度线性变化。
秦飞 编著《材料力学》 第7章 弯曲应力
ρ为中性层曲率半径
10
7.1 弯曲正应力
纯弯曲时梁横截面上的正应力
（4）物性关系
y 将 代入物性关系，得： y E E
可见，梁横截面上的弯曲正应力 (normal stress in bending) 与y成正比， 即 （1）沿截面高度线性分布； （2）在中性层处为零，在上、下表面 处最大。

My Iz
—弯曲正应力公式
此公式适用于所有横截面具有纵向对称轴的梁，如圆形截 面、工字形截面和T形截面。 由公式： 正比于y。 沿高度线性分布。 中性轴处=0。
秦飞 编著《材料力学》 第7章 弯曲应力 13

材料力学：第七章 弯曲变形

材料力学：第七章 弯曲变形
刚度设计依据
(1) 挠度w大小取决于M, E, I三个参数 应该取较小的M, 较大的E, I
(2) 弯矩M大小取决于载荷\约束分布及梁跨度大小
(3) 截面惯性矩I 大小和截面形状有关,
弹性模量E大小和材料有关
Iz =
y2dA,
A
当A大小一定时, y越大, I 越大
梁的合理刚度设计
选择I 较大的薄壁横截面形状
1 度静不定 选 FBy 为多余力, 去约 束, 写出位移边界条件
－变形协调条件 －物理方程
利用边界条件 解出未知力
列平衡方程,求其他约束力:
－补充方程
分析方法与步骤：
判断梁的静不定度
用多余力代替多余约
束的作用，得相当系统
相当系统
相当系统有多种选择:
计算相当系统在多余约
束处的位移，并根据变形 协调条件建立补充方程。
例题
解：
()
()
例题
例题
解：
()
()
()
例题
图示组合梁，EI=常数，求 wB 与qA
例题
解：
P378, 情况8
()
P377, 情况1,2
()
例题
图示刚架，求截面 C 的铅垂位移
例题
解：
位移w1包括AB弯曲 和AB扭转两部分
例题
矩形截面梁, 自由端承受集中载荷F作用, 该载荷与对 称轴y的夹角为θ, 用叠加法计算自由端求自由端截面形心C
的位移d
解：
例题
一般情况下
挠曲轴与外力作用面一般不重合
§6 简单静不定梁
静不定度与多余约束 简单静不定梁分析方法
静不定度与多余约束
静不定度 4-3= 1

材料力学课件第七章变曲应力(机械专业)

材料力学课件第七章变曲应力(机械专业)

A ydA M
yC ydA A ቤተ መጻሕፍቲ ባይዱ A
(c)
(a)(b)
A ydA 0
E
中性轴通过横截面形心
(a)(c)
A
y 2dA M
M EI z 1
Iz
A
y2dA－惯性矩
(d)
(d)(a)
( y )
My Iz

max
M Wz
max
Mymax Iz
静力学方面:
( y)
( y)d d y d

y
(a)
物理方面:
( y) E ( y)
dA0 (b) Fx 0, A M z 0, A ydA M (c)
第七章
弯曲应力
正应力分布
第七章
E
y
弯曲应力
(b)

(a)
dA 0 A
A
F
z
1）画弯矩图 跨中截面 C 为危险截面 危险截面上的最大弯矩
M max 1 Fl 280 kN m 4
M /kN m
C 8m
a
B
y
F
A
C
B
8m
280
x
第七章
2）计算正应力
弯曲应力
查型钢表，No. 50a 工字钢的惯性矩 Iz = 46500 cm4 ，抗弯截面 系数 Wz = 1860 cm3 危险截面 C 上的最大正应力
第七章
7.1 概 述
弯曲应力
如图所示简支梁横截面为矩形，两个外力F垂直于轴线，对称地作 用于梁的纵向对称面内。从图中可以看出，在AC和DB两段内，梁各横 截面上既有弯矩又有剪力，这种弯曲称为横力弯曲或剪切弯曲。在CD 段内梁横截面上剪力为零，而弯矩为常数，这种弯曲称为纯弯曲。

材料力学 第07章 应力状态分析与强度理论

材料力学 第07章 应力状态分析与强度理论
2
sin2a t xy cos2a
18/95
7.2 平面应力状态分析 主应力 7.2.3 主平面的方位及极值正应力 s x s y s x s y sa cos2a t xy sin2a 2 2 s x s y ds a 上式对a 求导 2 sin2a t xy cos2a da 2 s x s y 若a a0时，导数为 0 sin2a 0 t xy cos2a 0 0 2 2t xy tan2a 0 s x s y
7.2.5 应力圆
t
sx
tyx
sy
sx txy sy
D(sx,txy) 1. 确定点 D (s ,t ) x xy
O
D'(sy,tyx)
C
s
2. 确定点D' (sy,tyx) tyx= －txy 3. 连接DD'与s 轴交于点C 4. 以 C 为圆心，CD（CD'） 为半径画圆。
26/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆
sx sy sz
sxs1 100 MPas 2
0 MPas 3 120 MPa
11/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态 三个主应力中仅有一个主应力不为零 单向应力状态
s1
s1
F
A
F
12/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态
O
D'(sy,tyx)
C sx－ sx sy/2
s
27/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆 利用应力圆确定角a 斜截面上的正应力和切应力

工程力学c材料力学部分第七章 应力状态和强度理论

工程力学c材料力学部分第七章 应力状态和强度理论

无论是强度分析还是刚度分析，都需要求出应力的极值， 无论是强度分析还是刚度分析，都需要求出应力的极值，为了找 到构件内最大应力的位置和方向 需要对各点的应力情况做出分析。 最大应力的位置和方向， 到构件内最大应力的位置和方向，需要对各点的应力情况做出分析。
受力构件内一点处所有方位截面上应力的集合，称为一点的 受力构件内一点处所有方位截面上应力的集合，称为一点的 研究一点的应力状态时， 应力状态 。研究一点的应力状态时，往往围绕该点取一个无限小 的正六面体—单元体来研究。 单元体来研究 的正六面体 单元体来研究。
σ2
σ2
σ1
σ1
σ
σ
σ3
三向应力状态
双向应力状态
单向应力状态 简单应力状态
复杂应力状态 主应力符号按代数值的大小规定： 主应力符号按代数值的大小规定：
σ1 ≥ σ 2 ≥ σ 3
平面应力状态的应力分析—解析法 §7−2 平面应力状态的应力分析 解析法
图(a)所示平面应力单元体常用平面图形(b)来表示。现欲求 )所示平面应力单元体常用平面图形( )来表示。现欲求 垂直于平面xy的任意斜截面 上的应力 垂直于平面 的任意斜截面ef上的应力。 的任意斜截面 上的应力。
二、最大正应力和最大剪应力
σα =
σ x +σ y
2
+
σ x −σ y
2
cos 2α − τ x sin 2α
τα =
令
σ x −σ y
2
sin 2α + τ x cos 2α
dσ α =0 dα
σ x −σ y
2
sin 2α +τ x cos2α = 0
可见在 τ α
=0

弯曲应力(剪应力6月9日)(1)

弯曲应力(剪应力6月9日)(1)

[1 12
16
283
16
28
(14
13)2 ]

[1 12

8 103
18 10
(19
13)2 ]
26200cm4
Wz

Iz ym a x

26200 (28 13)
1748cm3
（3）正应力校核

max

M Wz
1.2 105 1748 106
1.0 1.04 1.12 1.57 2.30
（四）切应力强度条件

max

(
FQ Sz,max
I z
)max

[
]
对于等宽度截面， m ax发生在中性轴上；对于宽度变化的截面，
m ax不一定发生在中性轴上。
在进行梁的强度计算时，需注意以下问题： （1）对于细长梁的弯曲变形，正应力的强度条件是主要的，剪应
S
* z
：y以外面积对中性轴的静矩
I z ：整个截面对中性轴的惯性矩
b：y处的宽度
c
yc
y
z h
b
对于矩形：
S* z

A*

yc
b(h 2

y) [ y

h 2
2
y
]
b (h2 24

y2)
弯曲应力/弯曲时的剪应力
而
Iz

1 bh3 12


6FQ bh3
( h2 4

y2)
力的强度条件是次要的。但对于较粗短的梁，当集中力较大 时，截面上的剪力较大而弯矩较小，或是薄壁截面梁时，也 需要较核剪应力强度。

材料力学《第七章》应力状态分析

材料力学《第七章》应力状态分析

上海交通大学
受力： sadA、 tadA 受力： sxdAcosa、 txydAcosa
受力： sydAsina、 tyxdAsina
n
sx
txy
a
sa a
a
x
ta
tyx
e
切线方向上： Σ Fτ 0
σx σy σx σy σα cos2α τ xy sin2α 2 2
b
sy
τα d A ( σ x d A cos α )sin α ( τ xy d A cos α )cos α ( σ y d A sin α )cos α ( τ yx d A sin α )sin α 0
s1
一个主应力为零，其他二个主应力不为零。
3. 三向应力状态(空间应力状态)： 三个主应力均不为零。
上海交通大学
一般要找出主应力后才能确定应力状态。
四、应力状态分析步骤
s2
1. 确定构件危险截面危险点；
2. 取危险点单元体；
s3
3. 计算单元体各面应力；
4. 截面法取部分单元体； 5. 由平衡条件确定单元体斜截面上的应力。 应力状态分析方法： 解析法、图解法。
上海交通大学
三、应力状态的分类 定义：单元体 上应力为零的面称为零应力面； 单元体上只有 s 而无 t 的面称为主平面。 主平面上的正应力 s 称为主应力。
s2
s3
单元体在某一特殊方向上，三个互相垂直的截面上只有 s，而 无 t ，即为单元体的三个主平面。 用 s1 ≥ s2 ≥ s3 表示三个主应力，此单元体称为主单元体。 1. 单向应力状态： 一个主应力不为零，其他二个主应力为零。如：轴向拉伸。 2. 二向应力状态(平面应力状态)：

材料力学第07章应力状态与应变状态分析

材料力学第07章应力状态与应变状态分析

以上由单元体公式
应力圆（原变换）
下面寻求： 由应力圆
单元体公式（逆变换）
只有这样，应力圆才能与公式等价
换句话，单元体与应力圆是否有一一对应关系？
为什么说有这种对应关系？
DE R sin[180o ( 2 20 )] R sin( 2 20 )
( R cos 20 ) sin 2 ( R cos 20 )cos 2
2
cos2
xy
sin 2
同理：
x
y
2
sin 2
xy
cos2
n
Ox
图2
二、极值应力
令:d
d
0
x
y
sin202 xycos200
由此得两个驻点：
01、（
01
2
）和两个极值：
tg20
2 xy x
y
y
mm
ax in
x
y ±（x
2
y
2
）2
2 xy
0 0极值正应力就是主应力 ！
y
O
x
七、主单元体、主平面、主应力：
y
y
主单元体(Principal bidy)：
x
各侧面上剪应力均为零的单元体。
z
z
2
3
主平面(Principal Plane)：
剪应力为零的截面。 x
主应力(Principal Stress ）：
主平面上的正应力。
1
主应力排列规定：按代数值大小，
1 2 3
三向应力状态（ Three—Dimensional State of Stress）： 三个主应力都不为零的应力状态。
A

弯曲正应力强度条件

弯曲正应力强度条件

正应力强度计算（1）正应力强度条件一般情况下，梁弯曲时，各个截面上的弯矩和剪力是变化的，而且截面上的应力（包括正应力和切应力）分布是不均匀的。

对等截面梁而言，最大弯矩所在的截面称为危险截面。

危险截面上距中性轴最远的点（上下边缘处）称为危险点。

显然危险截面上危险点处的应力值即为梁内的最大正应力值，即：zz W M max max =σ 保证梁内最大正应力不超过材料的许用应力，就是梁的强度条件。

根据材料力学性能的不同，具体分以下两种情况讨论：● 塑性材料塑性材料的力学性能是许用拉应力和许用压应力相等，所以拉压许用应力不在区分，统称为许用应力，即表示为[][][]t c σσσ==。

梁横截面的形式可分为两种情况，一种是横截面关于中性轴对称，一种是横截面关于中性轴不对称。

但无论那种情况，只要使梁内绝对值最大的正应力不超过材料的许用应力值即可。

所以危险点则发生在最大弯矩作用的截面离中性轴最远的点处。

强度条件为： []z max max zM W =≤σσ 为了使横截面上最大拉压应力同时达到其许用应力，工程中通常将塑性材料梁的横截面做成关于中性轴对称的形状。

● 脆性材料脆性材料的力学性能是许用拉应力小于许用压应力，即[][]t c σσ<。

针对上述两种截面形式建立梁的弯曲正应力强度条件。

1）横截面关于中性轴对称荷载作用下在梁内产生的最大拉压应力相等，而材料的[][]t c σσ<，所以强度条件为：[]z max t max t zM W σσ≤ 2）横截面关于中性轴不对称为了充分利用材料，通常将脆性材料梁的横截面做成关于中性轴不对称的形状，且中性轴靠近受拉侧。

所以强度条件应为：[][]1122z t max t z z c max t zM y I M y I σσσσ=≤=≤ 式中：t max σ、c max σ——分别为最大拉应力和最大压应力；1z M 、2z M ——分别为产生最大拉应力和最大压应力截面上的弯矩； []t σ、[]c σ——分别为许用拉应力和许用压应力。

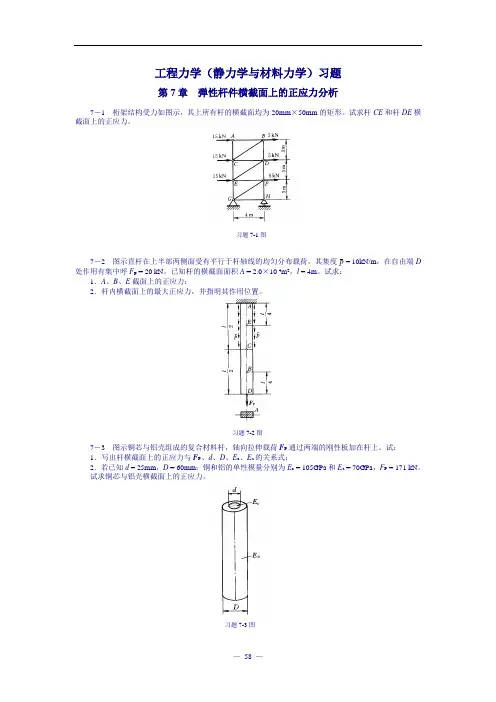
工程力学(静力学与材料力学)习题及答案 )-正应力分析

工程力学(静力学与材料力学)习题及答案 )-正应力分析

习题7-1图习题7-2图 习题7-3图工程力学（静力学与材料力学）习题第7章 弹性杆件横截面上的正应力分析7－1 桁架结构受力如图示，其上所有杆的横截面均为20mm ×50mm 的矩形。

试求杆CE 和杆DE 横截面上的正应力。

7－2 图示直杆在上半部两侧面受有平行于杆轴线的均匀分布载荷，其集度p = 10kN/m ，在自由端D 处作用有集中呼F P = 20 kN 。

已知杆的横截面面积A = 2.0×10-4m 2，l = 4m 。

试求：1．A 、B 、E 截面上的正应力；2．杆内横截面上的最大正应力，并指明其作用位置。

7－3 图示铜芯与铝壳组成的复合材料杆，轴向拉伸载荷F P 通过两端的刚性板加在杆上。

试：1．写出杆横截面上的正应力与F P 、d 、D 、E c 、E a 的关系式；2．若已知d = 25mm ，D = 60mm ；铜和铝的单性模量分别为E c = 105GPa 和E a = 70GPa ，F P = 171 kN 。

试求铜芯与铝壳横截面上的正应力。

习题7-4图 习题7-5图 习题7-6图习题7-7图 7－4 图示由铝板钢板组成的复合材料柱，纵向截荷F P 通过刚性平板沿着柱的中心线施加在其上。

试：1．导出复合材料柱横截面上正应力与F P 、b 0、b 1、h 和E a 、E s 之间的关系式；2．已知F P = 385kN ；E a = 70GPa ，E s = 200GPa ；b 0 = 30mm ，b 1 = 20mm ，h = 50mm 。

求铝板与钢板横截面上的最大正应力。

7－5 从圆木中锯成的矩形截面梁，受力及尺寸如图所示。

试求下列两种情形下h 与b 的比值：1．横截面上的最大正应力尽可能小；2．曲率半径尽可能大。

7－6 梁的截面形状为正方形去掉上、下角，如图所示。

梁在两端力偶M z 作用下发生弯曲。

设正方形截面时，梁内最大正应力为0σ；去掉上、下角后，最大正应力变为0max σσk =，试求：1．k 值与h 值之间的关系；2．max σ为尽可能小的h 值，以及这种情形下的k 值。

第七章-弯曲应力(1) (2)

第七章-弯曲应力(1) (2)
y
M
z

Q
横截面上内力 横截面上切应力

横截面上正应力
Q dA
A
M y dA
A
切应力和正应力的分布函数不知道，2个方程确定不了
切应力无穷个未知数、正应力无穷个未知数，实质是 超静定问题 解决之前，先简化受力状态 —— 理想模型方法
8
横力弯曲与纯弯曲 横力弯曲 ——
剪力Q不为零 （ Bending by transverse force ） 例如AC, DB段
E
A
(-) B
D
(+) 10kN*m
y2
C
拉应力
a
e
压应力
y1
压应力 B截面
b
d
拉应力 D截面
危险点：
a, b, d
33
（3）计算危险点应力 拉应力
a
e
压应力
校核强度
M B y2 a Iz 30 MPa （拉） M B y1 b Iz
70 MPa （压）
压应力 B截面
b
d
强度问题 弯曲问题的整个分析过程： 弯曲内力 弯曲应力 弯曲变形 刚度问题
5
本章主要内容
7.1 弯曲正应力 7.2 弯曲正应力强度条件 7.3 弯曲切应力及强度条件 7.4 弯曲中心 7.5 提高弯曲强度的一些措施
这一堂课先效仿前人，探求出来弯曲正应力
公式，然后解决弯曲正应力强度问题
6
知道公式会用，不知推导，行不行？不行。
2
解：1 画 M 图求有关弯矩
qLx qx M1 ( ) 2 2
2
2
x 1
60kNm
M max qL / 8 67.5kNm

材料力学第七章知识点总结

材料力学第七章知识点总结
研究应力状态的目的：找出一点处沿不同方向应力的变化
规律，确定出最大应力，从而全面考虑构件破坏的原因，建 立适当的强度条件。
材料力学
3、一点的应力状态的描述
研究一点的应力状态，可对一个 包围该点的微小正六面体——单 元体进行分析
在单元体各面上标上应力 各边边长 dx , dy , dz
——应力单元体
三、几个对应关系
点面对应——应力圆上某一点的坐标值对应着单元体某一截面
上的正应力和切应力；
y
σy
n
τ
H (σα ,τα )
τ yxHτ xy来自αxσx
(σy ,Dτyx)
2α A (σx ,τxy)
c
σ
σx +σ y
2
转向对应——半径旋转方向与截面法线的旋转方向一致； 二倍角对应——半径转过的角度是截面法线旋转角度的两倍。
α =α0
=
−2⎢⎡σ x
⎣
−σ y
2
sin 2α0
+τ xy
cos
2α
0
⎤ ⎥
⎦
=0
=
−2τ α 0
τα0 = 0
tg
2α 0
=
− 2τ xy σx −σ y
可以确定出两个相互垂直的平面——主平面，分别为
最大正应力和最小正应力所在平面。
主平面的方位
(α0 ; α0′ = α0 ± 900 )
主应力的大小
材料力学
四、在应力圆上标出极值应力
τ
τ max
x
R
O σ min
2α12α0A(σx ,τxy)
c
σ
σ
max
(σy ,τyx) D

材料力学-第七章应力分析

材料力学-第七章应力分析

材料⼒学-第七章应⼒分析班级学号姓名7-1 构件受⼒如图所⽰。

(1)确定危险点的位置；(2)⽤单元体表⽰危险点的应⼒状态。

7-2 已知如图所⽰的单元体中70MPa x σ=，70MPa y σ=-，70MPa xyτ=，030α=，35MPa ασ=，60.6MPa xy τ=。

试：(1)标出该单元体各⾯的应⼒⽅向；(2)画出斜截⾯并标出斜截⾯上的应⼒⽅向。

题7-1图(b) 题7-1图(a)班级学号姓名7-3 试⽤解析法求图⽰单元体斜截⾯ab 上的应⼒（图中应⼒单位为MPa ）。

(a)40(b)(c)班级学号姓名7-4 已知应⼒状态如图所⽰（图中应⼒单位为MPa ），试⽤解析法求：(1) 主应⼒的⼤⼩和主平⾯的⽅位；(2) 在单元体上绘出主平⾯的位置和主应⼒的⽅向； (3) 最⼤切应⼒。

20(a)(b)班级学号姓名7-5 已知如图所⽰应⼒状态（图中应⼒单位为MPa ），⽤⼤致⽐例画出应⼒圆。

4040 30 50 20 (a) (b) (c)班级学号姓名7-6 已知应⼒状态如图所⽰（图中应⼒单位为MPa），试⽤应⼒圆⼏何⽅法求：(1) 主应⼒的⼤⼩和主平⾯的⽅位；(2) 在单元体上绘出主平⾯的位置和主应⼒的⽅向；(3) 最⼤切应⼒。

20(a) (b)班级学号姓名7-7 图⽰锅炉的内径m 1=d ，壁厚m m 10=t ，内受蒸汽压⼒MPa 3=p 作⽤，试求： (1) 壁内的主应⼒1σ、2σ以及最⼤切应⼒max τ； (2) 斜截⾯ab 上的正应⼒与切应⼒。

7-8 平⾯应⼒状态如图所⽰（图中应⼒单位为MPa ），试求主应⼒，并画出应⼒圆。

80 80班级学号姓名7-9 试求图⽰应⼒状态的主应⼒和最⼤切应⼒（图中应⼒单位为MPa ）。

7-10 圆轴扭转-拉伸⽰意图如图所⽰。

若P =50kN ，M e =600NN·m ，且d =50mm 。

试求：（1）A 点在指定斜截⾯上的应⼒；（2）A 点主应⼒的⼤⼩及⽅向，并⽤单元体表⽰。

材料力学 第七章 应力状态与强度理论

材料力学 第七章 应力状态与强度理论

取三角形单元建立静力平衡方程
n 0
dA ( xdA cos ) sin ( xdA cos ) cos ( y dA sin ) cos ( y dA sin ) sin 0
t 0
dA ( xdA cos ) cos ( xdA cos ) sin ( y dA sin ) sin ( y dA sin ) cos 0
2 2

cos 2 x sin 2
2 x y 2 x y ( ) ( cos 2 x sin 2 )2
2
2

x y
sin 2 x cos 2
( 0) (
x y
2
2
sin 2 x cos 2 )
max x y x y 2 x 2 2 min
2
max
1 3
2
例7-2 试求例7-1中所示单元体的主应力和最大剪应力。
（1）求主应力的值
x 10MPa, y 30MPa, x 20MPa max x y x y 2 2 x min 2
复杂应力状态下（只就主应力状态说明） 有三个主应力
1 , 2 , 3
1
E
由 1引起的线段 1应变 1
由 2引起的线段 1应变 1
2
由 3引起的线段1应变 1
3
E
E
沿主应力1的方向的总应变为：
1 1 1 1
1 42.4 1 3 2 0 MPa 由 max 3 2.4 2

材料力学 第七章弯曲正应力(1,2)解析

材料力学 第七章弯曲正应力(1,2)解析

M
1.平面假设： 梁各个横截面变形后仍保持为平面，并仍垂直于变形 后的轴线，横截面绕某一轴旋转了一个角度。 2.单向受力假设： 假设各纵向纤维之间互不挤压。于是各纵向纤维均 处于单向受拉或受压的状态。
中性层 梁在弯曲变形时，凹面部分纵向纤维缩短，凸面 部分纵向纤维伸长，必有一层纵向纤维既不伸长也不 缩短,保持原来的长度，这一纵向纤维层称为中性层. 中性轴
C截面
Fb/4 拉应力 压应力 B截面
20
y 20
拉应力
压应力
可见：压应力强度条件由B截面控制，拉应力强度 条件则B、C截面都要考虑。
Fb/2
40 180
120 C 形心 86 z 134
Fb/4 考虑截面B ：
t,max
c, max
M B y1 F / 2 2 103 mm134 mm 90 MPa 4 4 Iz 5493 10 mm F 73.8 kN
c
注：强度校核（选截面、荷载） （ 1） （ 2）
[ ]t [ ]c （等截面）只须校核Mmax处
[ ]t [ ]c （等截面）
(a)对称截面情况只须校核Mmax处使
maxt [ ]t , maxc [ ]c
(b)非对称截面情况，具体分析，一般要校核 M+max与 M-max两处。
查型钢表得56b号工字钢的Wz比较接近要求值
Wz 2447cm3 2447103 mm3
此时 max
M max 153MPa Wz
误差小于5%，可用
例4-17 跨长 l= 2m 的铸铁梁受力如图，已知铸铁 的许用拉应力[ t ]=30 MPa，许用压应力[ c ] =90 MPa。试根据截面最为合理的要求，确定T字形梁 横截面的尺寸d ，并校核梁的强度 。

工程力学(材料力学部分第七章)

工程力学(材料力学部分第七章)

4 主应力及应力状态的分类
主应力和主平面
切应力全为零时的正应力称为主应力；
主应力所在的平面称为主平面；
主平面的外法线方向称为主方向。
主应力用1 , 2 , 3 表示 (1 2 3 ) 。
应力状态分类
单向应力状态
11
应力状态分类
单向应力状态 二向应力状态(平面应力状态)
三向应力状态(空间应力状态)
D点
由 y 40, yx 60
D'点
画出应力圆
52
圆心坐标
OC x y 80 (40)
2
2
20
半径
R
x
2
y
2
2 xy
80 (40) 2
(60)2
84.85 85
2
53
圆心坐标 OC 20
半径
R 85
1 OA1 OC R
E
105 MPa
3 OC R
65 MPa
D (x ,xy)
x y
2
R 1 2
x y
2
4
2 xy
38
3 应力圆上的点与单元体面上的应力的对应关系 (1) 点面对应
应力圆上某一点 的坐标值对应着 单元体某一方向面上的正应力和切应力。
39
(1) 点面对应
应力圆上某一点的坐 标 值对应着单元体某 一方向面上的正应力 和切应力。
D点对应的面与E点 对应的面的关系
主应力。
从半径CD转到CA1 的角度即为从x轴转
到主平面的角度的
两倍。
44
主应力 即为A1, B1处的正应力。
max min
x
y
2
x
2

材料力学课件第七章 应力状态分析1-2

材料力学课件第七章 应力状态分析1-2

G2 "
3.应力圆的应用
①应力圆上一点坐标代表单元体某个面上的应力；
②应力圆上半径转过2a，单元体上坐标轴转过a,且转向相同;
③圆心为平均正应力，为不变量。 ④ 半径对应极值切应力。
y yx
xy x
n
a
a x a xy
yx y
(a,a)E
B1 B O "
D' (y, yx)
G1'
D(x, xy) 2a
x
2
y
2
2 xy
②取x面，定出D( x ,xy )点；取y面，定出D'( y ,yx )点；
③连DD'交轴于C点，以C为圆心，DD1为直径作圆；
y y yx
xy x
n
a
a x x a xy
yx y
(a,a)E
B1 B O "
G1'
D(x, xy) 2a
2a0 A A1
C
'
D' (y, yx)
1. ①主平面：单元体上切应力为零的面；
②主应力：主平面上的正应力，用1、2、3 表示， 有1≥2≥3。
y
z
yx
yz
xy
zy
x x
z zx xz z
x' 1
旋转
z' 3
2 y'
2.应力状态按主应力分类：
①只有一个主应力不为零称单向应力状态；
②只有一个主应力为零称两向应力状态(平面应力状态)； ③三个主应力均不为零称三向应力状态(空间应力状态)；
③主应力大小：
max min
x
y
2
x

材料力学第七章应力应变分析

材料力学第七章应力应变分析

x
y
2
x
2
y
cos 2
xy sin 2
x
y
2
sin 2
xy cos 2
1、最大正应力的方位
令
d d
2[
x
y sin 2
2
xy cos 2 ] 0
tg 2 0
2 xy x
y
0 0
90
0 和 0+90°确定两个互相垂直的平面，一个是最大正应 力所在的平面，另一个是最小正应力所在的平面.
的方位.
m
m a
A
l
解： 把从A点处截取的单元体放大如图
x 70, y 0, xy 50
A
tan 20
2 xy x y
2 50 1.429
1
3
(70) 0
0
A
x
0
27.5 62.5
3
1
因为 x < y ，所以 0= 27.5° 与 min 对应
max min
x
2
y
(
x
2
y )2
三、应力状态的分类
1、空间应力状态
三个主应力1 、2 、3 均不等于零
2、平面应力状态
三个主应力1 、2 、3 中有两个不等于零
3、单向应力状态
三个主应力 1 、2 、3 中只有一个不等于零
2 3
2
1
1
1
1
1
3 2
2
1
例题 1 画出如图所示梁S截面的应力状态单元体.
F
5
S平面
4
3
l/2
2
l/2 1
任意一对平行平面上的应力相等

材料力学07弯曲应力ppt课件

材料力学07弯曲应力ppt课件
分离部分 ——平衡分析……
x
y 26
dA1
s
, b s
顶面有 ,存在.
两截面M 不等—— s 不等
(X 0)
左侧面
dx
N1
M
A1 sdA1 I z
A1 ydA1
右侧面
MS
z
Iz
dM
S
* z
, b( dx ) 0
Iz
FS
,
dM dx
S
z
Izb
FS
S
z
Izb
(∵切应力互等 )
2s
h
2 ( bdy )y s
bh2
M
0
4
s
4M bh2
2. 按沿梁高线性分布:
s max
M h2 Iz
s
6M bh2
s1 2 s2 3
(相差三分之一)
13
[例2]:
15KN
6KN
求B截面K点应力
B
1m
1m
解： M
3
6kNm
s
My Iz
90
K 90
60
120 ( 拉? 压应力? )
IZ
bh3 12
第七章 弯曲应力
§1 弯曲正应力 §2 正应力强度条件 §3 弯曲剪应力 §4 剪应力强度条件 梁的合理截面 §5 非对称截面梁弯曲弯曲中心 §6 考虑塑性的极限弯矩
1
概述
＋
－F
Q
Fa
－
M
CD段：只有弯矩没有剪力－ 纯弯曲
AC和BD段：既有弯矩又有剪力－ 剪切弯曲
2
剪力FS
弯矩M
切应力τ
正应力s
先分析纯弯梁横截面的正应力s ，
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
A
E
ydA 0
A
A ydA Sz 0
中性轴Z必过截面形心
横截面对Z轴的静矩
M y
A
zdA
0
A
zE
y
dA
E
A
zydA
0
zydA I yz 0 截面的惯性积（ y为对称轴）
A
M z y dA M
A
Байду номын сангаас
A
yE
y dA
M
y2dA Iz
截面对z轴的惯性矩
A
1 M
EI z
中性层的曲率公式
2）中性轴将截面分为受 拉、受压两个区域。
3）最大正应力发生在距
y
中性轴最远处。
3.简单截面的抗弯模量
dy
(1)矩形：
Wz
Iz h/2
bh3 12
2 h
y
Wz
1 6
bh2
(2)圆：
Wz
D 4
64(D / 2)
D 3
32
(3)圆环
WZ
(D4 d 4 )
64(D / 2)
D3
32
(1 4 )
式中 d
C
副梁CD:
Pa M max CD 4
M
由 (M m ax ) AB (M ) m ax CD
P (l a) P a
4
4
得 a l 2
P D
a
Pa (Mmax)CD 4
[例7-3]受均布载荷的外伸梁材料许用应力[ ] 160MPa 校核该梁的强度。
10kN / m
200
2m
4m
45 kN
1.正应力
My
IZ
2.横截面上的最大正应力
t
M y1 IZ
,
c
M y2 IZ
当中性轴是横截面的对称轴时：
若y1 y2 ymax
则 t c max
max
M ymax IZ
M
WZ
Wz
Iz y max
Wz 称为抗弯截面模量
1）沿y轴线性分布，同一 坐标y处，正应力相等。中 性轴上正应力为零。
（1） [ ]t [ ]c （等截面）只须校核Mmax处 （2） [ ]t [ ]c （等截面）
(a)对称截面情况只须校核Mmax处使
maxt [ ]t , maxc [ ]c
(b)非对称截面情况，具体分析，一般要校核 M+max与 M-max两处。
例4-14 图示简支梁由56a号工字钢制成，已知
后的轴线，横截面绕某一轴旋转了一个角度。
2.单向受力假设：
假设各纵向纤维之间互不挤压。于是各纵向纤维均 处于单向受拉或受压的状态。
中性层
梁在弯曲变形时，凹面部分纵向纤维缩短，凸面
部分纵向纤维伸长，必有一层纵向纤维既不伸长也不 缩短,保持原来的长度，这一纵向纤维层称为中性层.
中性层
中性轴
中性层与横截面的交线称为中性轴
[例7-1]：两矩形截面梁，尺寸和材料均相同， 但放置分别如图(a)、(b)。按弯曲正应力强度条 件确定两者许可载荷之比 P1／P2＝？
l
解： max1
M max1 Wz1
P1l bh2 / 6
max2
M max2 Wz2
P2l hb2 / 6
由 max 1 max 2 [ ] 得:
P1 h P2 b
M
FS
三个方面:
jastin4.swf
静力学关系 变形几何关系 物理关系
一.几何变形
M
(1)aa、bb弯成弧
线，aa缩短，bb伸 长
(2)mm、nn变形后仍
保持为直线，且仍与M
变为弧线的aa，bb正
交；
(3)部分纵向线段缩短 ，另一部分纵向线段 伸长。
mn
M
aa
bb mn
M
1.平面假设：
梁各个横截面变形后仍保持为平面，并仍垂直于变形
M xy
二.梁弯曲正应力强度I条z 件
max [ ]
max
M max WZ
[ ]
利用上式可以进行三方面的强度计算：
①已知外力、截面尺寸、许用应力，校核梁的强度；
②已知外力、截面形状、许用应力，设计截面尺寸;
Wz
M max
[ ]
③已知截面形状尺寸、许用应力，求许可载荷
[M ] Wz[ ]
三.算例
D
y
D
0
Z
y
x d D
§7-2 横力弯曲时的正应力及正应力强度条件
一.横力弯曲时的正应力
My
IZ
上式是在平面假设和单向受力假设的基础上推 导的，实验证明在纯弯曲情况下这是正确的。
对于横力弯曲，由于剪力的存在，横截面产生剪 切变形，使横截面发生翘曲，不再保持为平面。理 论证明在L/h大于5时该式的精度能满足工程要求。
梁的强度。
9 kN 4 kN
52 C
zA
C
B D
88
1m 1m 1m
C截面
2.5kN
10.5kN
4
t
2.5 88 Iz
28.8MPa
＜ t
c
2.5 52 Iz
17MPa
＜ c
M
2.5
B截面
t
4 52 Iz
27MPa ＜ t
c
4 88 Iz
46MPa ＜ c
注：强度校核（选截面、荷载）
第七章 弯曲应力
§7-1纯弯曲时梁横截面上的正应力
一. 纯弯曲： 纯弯曲：
FS = 0，M = const
F
AC
Fa
l
F
Da B
F
FS
F
横力弯曲：
F
FS ≠0，M ≠0
M
Fa
CL8TU1
CL8TU2
M
dA M
FS
dA dA
dA FS
dA
在横截面上，只有法向内力元素σdA才能合成弯 矩M，只有切向内力元素τdA才能合成剪力FS
[例7-2]主梁AB，跨度为l，采用加副梁CD的方法提高
承载能力，若主梁和副梁材料相同，截面尺寸相同，则
副梁的最佳长度a为多少？
a Pa
解：
C2
2D
A
B
l P 22
A
l 2
P2
B
主梁AB:
M max AB
P (l a) 4
(l a)/2 M
M maxAB P(l a) / 4
(l a)/2
F=150kN。试求危险截面上的最大正应力max 和同 一横截面上翼缘与腹板交界处a点处的正应力a 。
12.5
F
A
FA
5m
C
10m
B z
FB
a
166
375 kN.m 21 560
M
Fl 解：1、作弯矩图如上， M max 4 375 kN m
2、查型钢表得
一.几何方程
y
y
z d
dx
y
dx
dx
(
y)d d d
y
y
二. 物理关系
E E y
dx
dx
一点的正应力与它到中性层的距离成正比。
三.静力学方程
FN dA 0 A
M y
z dA 0
A
M z
y dA M
A
E y
设中性轴为z
M
y
z dA
FN
dA 0
A
E y dA 0
FS 25
15kN
20
15
20
M
11.25
100
解：由弯矩图可见
Mmax 20 kN m
t
M max Wz
20 103 0.1 0.22 /
6
t 30MPa< [ ]
该梁满足强度条件，安全
[例7-4]图示铸铁梁，许用拉应力[σt ]=30MPa，许
用压应力[σc ]=60MPa,Ｉz=7.63×10-6m4，试校核此