光子晶体传输矩阵教程文件

一、绪论1.1光子晶体的基本概念光子晶体是由不同介电常数的介质材料在空间呈周期排布的结构，当电磁波受到调制而形成类似于电子的能带结构，这种能带结构称为光子能带。

在合适的晶格常数和介电常数比的条件下，类似于电子能带隙，在光子晶体的光子能带间可出现使某些频率的电磁波完全不能透过的频率区域，将此频率区域称为光子带隙或光子禁带。

人们又将光子晶体称为光子带隙材料。

与一般的电子晶体类似，光子晶体也有一维、二维、三维之分。

一维光子晶体是介电常数不同的两种介质块交替堆积形成的结构。

实际上，一维光子晶体已经被广泛应用，如法布里-珀罗腔光学多层的增反/透膜等。

二维光子晶体是介电常数在二维空间呈周期性排列的结构。

光子晶体中存在光子禁带的物理机理是基于固体物理的布洛赫理论。

1.2光子带隙光子在光子晶体中的行为类似于电子在半导体晶体中的行为，通过独特的光子禁带可改变光的行为。

研究表明，光子带隙有完全光子带隙与不完全光子带隙的区分。

所谓完全光子带隙，是指在一定频率范围内，无论其偏振方向及传播方向如何，光都禁止传播，或者说光在整个空间的所有传播方向上都有能隙，且每个方向上的能隙能互相重叠。

所谓不完全光子带隙，则是相应于空间各方向上的能隙并不能完全重叠，或只在特定的方向上有能低折射率的介质在晶格中所占比率以及它们在空间的排列结构。

总的来说，折射率差别越大带隙越大，能够达到的效率也就越高。

二、光子晶体的晶体结构和能带结构特性研究2.1一维光子晶体的传输矩阵法设一维光子晶体由两种材料周期性交替排列构成，通常称一维二元光子晶体，类似固体能带理论中的Kroning-penney模型，在空气中由A、B薄层交替构成一维人工周期性结构材料，其中A材料的折射率是na，厚度为ha，B材料的折射率是nb，厚度为hb，那么周期d=a+b，A、B总层数为N。

以AB材料进行仿真计算。

仿真程序clear allna=2.35;nb=1.38;ha=63.8e-9;hb=108.7e-9;yeta1=na;yeta2=nb;yeta0=1;bo=400:1:900;derta1=(2*pi*na*ha)./(bo*1e-9);derta2=(2*pi*nb*hb)./(bo*1e-9);num=length(bo);for j=1:num;Ma=[cos(derta1(j)),-i*sin(derta1(j))./yeta1;-i*yeta1*sin(derta1(j)),cos(derta1(j))]; Mb=[cos(derta2(j)),-i*sin(derta2(j))./yeta2;-i*yeta2*sin(derta2(j)),cos(derta2(j))]; Mab=Ma*Mb;N=10;M=Mab^N;Rfan(j)=abs((M(1,1)*(yeta0)+M(1,2)*(yeta0)*(yeta0)-M(2,1)-M(2,2)*(yeta0))./(M(1, 1) *(yeta0)+M(1,2)*(yeta0)*sqrt(yeta0)+M(2,1)+M(2,2)*(yeta0)))^2;endfigure(1);plot(bo,Rfan,'k');box on;首先，我们A材料的折射率为2.35，B材料的折射率为1.38，AB材料组成的光子晶体的介质层数为10层，进行了matlab仿真，得到如下的图形然后我们更改介质层数为20层：最后我们更改介质层数为30层：对比以上三个图我们可以看出，一维二元光子晶体的投射特性与组成光子晶体的介质层数有关，介质层周期越大，越有利于形成禁带。

光子晶体一、发展背景及历史1.1 微电子的危机今天，人类进入了信息时代，电子信息产业已成为当今全球规模最大、发展最迅猛的产业，从日常生活的电视，电话等家庭用品到工作中的电子计算机，传感器以及各种电子测试设备，无处不渗透着半导体技术的影响，可以说半导体技术正日益成为我们工作和生活中不可缺少的组成部分。

微电子技术是电子信息产业的核心技术之一（另一个是软件技术），是在半导体材料上采用微米级线度加工处理的技术。

现在电子信息技术，尤其是计算机和通讯技术发展的驱动力。

来自于半导体元器件的技术突破，每一代更高性能的集成电路的问世，都会驱动各个信息技术向前跃进。

我们今天处在一个真正的技术革命时代，而微电子技术的突飞猛进是这个革命最基础的组成部分。

微电子技术所遵循的摩尔定律指出：芯片集成度每18-24个月增长一倍，价格不变。

目前主流加工技术是8英寸硅片，0.25微米线宽。

12英寸硅片0.13微米应经批量生产。

当前，半导体技术正向着高速度，高集成化方向发展。

据国际权威机构预测，到2014年，半导体芯片加工技术将达到18英寸硅片0.035微米线宽。

当集成电路线宽达到0.1微米以下时，标志着半导体制造技术及器件、工艺理论随之全面进入纳米领域。

硅基芯片的微细加工技术将可能达到极限。

届时，微电子的基础理论、材料技术和加工技术都将遇到极大的挑战：（1）首先是芯片的发热量随着工作频率的提高而迅速增加从而使芯片无法正常工作；（2）其次是现有的加工设备已经很难再继续减小芯片内部的线宽，因而通过减小线宽的方法来提高心片的工作效率和性能遇到了很大的困难；（3）最后也是最难克服的一点，随着芯片内部结构的减小，其量子效应会非常明显，电子在芯片内部的波动效应就不可以忽略，而电子的波动所造成的量子隧穿效应直接威胁着用“1”和“0”表示“开”和“关”状态的芯片最基本的结构。

导致这一结果的原因在于半导体器件的工作载体是电子，由于电子是一种费米子，具有静止质量，同时，电子之间具有库仑相互作用，当集成度很高时，产生热效应，相互干扰，这即是“电子瓶颈”效应产生的原因。

用传输矩阵法计算一维光子晶体的带隙特性研究------------------------------------------作者------------------------------------------日期一维光子晶体带隙特性研究1103011013 黄蓓粉体一班摘要：光子晶体是20世纪80年代末提出的新概念和新型人工微结构光学材料。

光子晶体以光子禁带的存在为主要特征，其典型结构为一个折射率周期变化的物体。

一维光子晶体是光子晶体最基本的构型，其折射率在一维空间方向上呈周期性分布。

一维光子晶体结构简单、易于制备，同时具备二维、三维光子晶体的性质，极有可能成为全光通信领域中的关键材料，因此具有较高的理论价值和广泛的应用前景。

关键词：光子带隙特征矩阵规律1 引言光子晶体是一种折射率周期变化的人工微结构材料 ,其典型结构为一个折射率周期变化的三维物体 ,周期为光波长量级. 光子在光子晶体中传播存在光子带隙.，频率落在光子带隙内的电磁波不能在光子晶体中传播,光子晶体的这种特性具有极大的理论价值和潜在的应用前景。

在光子晶体中掺杂后 ,会在光子能隙中引入局域模式 ,这将给激光技术和非线性光学等带来全新的应用 ,如制作零阈值激光器、光滤波器、慢光缓存器、慢光传感器等。

理论研究发现，对于含有缺陷的一维光子晶体，在光子禁带（PBG：Photonic Band Gap）的带边和缺陷模对应的频率位置，光的传输具有极低的群速度，Scalorta 等人发现在带边处，光脉冲传输速度可以降低到c/17（c 为真空中光速），大约为1.76×107m/s 。

光子晶体的理论计算已相对成熟 ,本文旨在应用现有的计算方法，建立一维光子晶体模型并讨论一维光子晶体在不同结构参数和参数下的光学传输特性。

2方法与原理2.1模型的建立一维光子晶体由两种不同相对介电常量 (εa ,εb ) 、厚度( a , b)的薄介质层交替排列构成的一维周期性结构 材料. 如图 1 所示 ,空间周期为 d = a + b ,一束频率 为 ω的光从左向右正入射到图中所示的一维周期 性结构材料中.将光波在介质层中的行 进看作是正向行进电磁波 (下行波) 和反向行进电磁 波 (上行波) 的叠加. 介质交界面处的电磁场满足边 界条件. 每一介质层与光波的相互作用可由其矩阵完全决定. 介质层两边的场矢量 E Ⅰ , H Ⅰ , E H Ⅱ的模可用特征矩阵联系起来 :E E M H H I II I II ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ 2.2数学理论推导为行进一步的计算，下面给出光子晶体的特殊矩阵表达式。

上海大学硕士学位论文图３．２一维三层介质光予晶体禁带结构幽ｓｔｍｃｔｌｌｒｅｏｆａｏｎｅ—ｄｉｍｅｎｓｉｏｎａｌｔｈｒｅｅ－ｃｏｍｐｏｎｅｎｔｐｈｏｔｏｎｉｃｃｒｙｓｔａｌＦｉｇ３２ＢａｊｌｄｇａｐⅣ＝４００，玎Ｈ＝３．２３，＂Ｍ＝２．５８，＂Ｌ＝１．３５－ｄⅣ＝ｄ吖＝ｄ＾＝１．５２ｐ卯对于由四层及更多层数介质组成基本周期的一维光子晶体结构，介质层的不同排列顺序对光子禁带则会产生影响，以一维四层介质光子晶体为例，仍然选取上述三种介质，再加上一层高折射率介质碲化铅（ｎ＝４．１）形成一维四层介质光子晶体，与上面计算相同，对于一维四层介质光子晶体（２．２２）式表示为：÷（卅ｌｌ＋聊２２）＝ｃｏｓ（２册？ｌｄｌ／丑）ｃｏｓ（２册Ｔ２ｄ２／旯）ｃｏｓ（２万Ｍ３ｄ３／丑）ｃｏｓ（２翮４ｄ４／五）Ｚ一妻（！Ｌ＋竺王）ｓｉｎ（２册１ｄＩ，＾）ｓｉｎ（２翮２ｄ２／＾）ｃｏｓ（２翮３ｄ３／丑）ｃｏｓ（２肋４ｄ４／Ａ）￡丌２一一昙（竺王＋！王）ｓｉｎ（２翮３ｄ３／＾）ｓｉｎ（２翮２ｄ２／五）ｃｏｓ（２ＭｌｄＩ／＾）ｃｏｓ（２砌４ｄ４／五）￡“２“３一妻（兰王＋！Ｌ）ｓｉｎ（２翮．“，／兄）ｓｉｎ（２册３ｄ３／五）ｃｏｓ（２翮２ｄ２／且）ｃｏｓ（２翮。

ｄ。

／五）￡门ｌｎ３一妻（兰王＋旦Ｌ）ｓｉｎ（２砌】ｄ１／五）ｓｉｎ（２删４ｄ４／五）ｃｏｓ（２刀ｗ２ｄ２／＾）ｃｏｓ（２翮３ｄ３／丑）Ｚ肛１”ｄ一妻（竺生＋竺呈）ｓｉｎ（２７聊４ｄ４／五）ｓｉｎ（２翮２ｄ２／五）ｃｏｓ（２翮３ｄ）／旯）ｃｏｓ（２翮１ｄ１／兄）Ｚ盯２“４一妻（兰王＋旦生）ｓｉｎ（２册３ｄ３／丑）ｓｉｎ（２Ｍ４ｄ４／旯）ｃｏｓ（２彻１ｄｌ／五）ｃｏｓ（２翮２ｄ２／＾）￡ｒ１４ｎ３＋妻（盟＋堕）ｓｉｎ（２删ｌｄｌ／＾）ｓｉｎ（２翮２ｄ２／五）ｓｉｎ（２翮３ｄ３／五）ｓｉｎ（２翮４ｄ４／五）２胛２聆４盯３胛１ｆ３．２、上海大学硕士学位论文幽３．３一维四层介质光子晶体禁带结构图Ｆｉｇ３．３Ｂａｎｄｇ印ｓｔｎｌｃｔｕｒｅｏｆａｏｎｅ—ｄｉｍｅｎｓｉｏｎａｌｆｏｕｒ＿ｃｏｍｐｏｎｅｎｔｐｈｏｔｏｎｉｃｃｒｙｓｔａｌ＿ｖ２１００００，ｎⅣ＝４．１，Ｈ…＝３．２３，”＂２＝２５８，Ｈ￡＝１．３５，ｄＨ＝ｄ＂Ｉ＝ｄＭ２＝ｄ￡＝１．５２脚从（３．２）式可以分析出由于各介质层的排列顺序不同，会产生三种不同的光子禁带范围，如数值模拟图３．３所示。

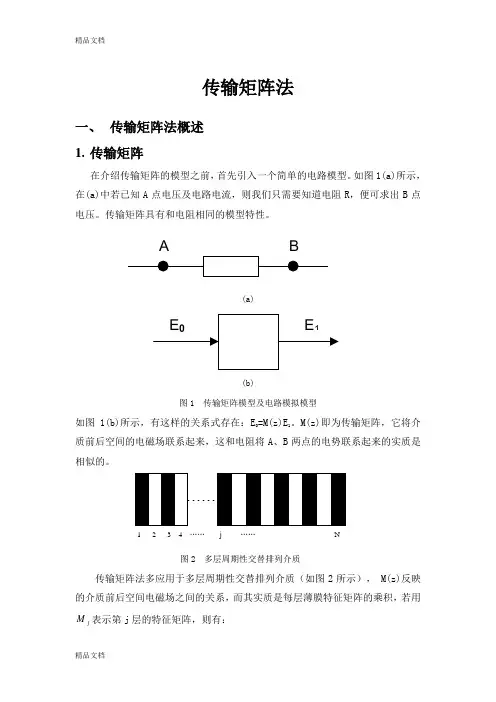
传输矩阵法一、 传输矩阵法概述 1. 传输矩阵在介绍传输矩阵的模型之前，首先引入一个简单的电路模型。

如图1(a)所示， 在(a)中若已知A 点电压及电路电流，则我们只需要知道电阻R ，便可求出B 点电压。

传输矩阵具有和电阻相同的模型特性。

(a)(b)图1 传输矩阵模型及电路模拟模型如图1(b)所示，有这样的关系式存在：E 0=M(z)E 1。

M(z)即为传输矩阵，它将介质前后空间的电磁场联系起来，这和电阻将A 、B 两点的电势联系起来的实质是相似的。

图2 多层周期性交替排列介质传输矩阵法多应用于多层周期性交替排列介质（如图2所示）， M(z)反映的介质前后空间电磁场之间的关系，而其实质是每层薄膜特征矩阵的乘积，若用j M 表示第j 层的特征矩阵，则有：1 2 3 4 …… j …… N（1）其中， （2）j δ为相位厚度，有 （3）如公式（2）所示，j M 的表示为一个2×2的矩阵形式，其中每个矩阵元都没有任何实际物理意义，它只是一个计算结果，其推导过程将在第二部分给出。

2. 传输矩阵法在了解了传输矩阵的基础上，下面将介绍传输矩阵法的定义：传输矩阵法是将磁场在实空间的格点位置展开，将麦克斯韦方程组化成传输矩阵形式，变成本征值求解问题。

从其定义可以看出，传输矩阵法的实质就是将麦克斯韦方程转化为传输矩阵，也就是传输矩阵法的建模过程，具体如下：利用麦克斯韦方程组求解两个紧邻层面上的电场和磁场，从而可以得到传输矩阵，然后将单层结论推广到整个介质空间，由此即可计算出整个多层介质的透射系数和反射系数。

传输矩阵法的特点：矩阵元少（4个），运算量小，速度快；关键：求解矩阵元；适用介质：多层周期性交替排列介质。

二、 传输矩阵的基础理论——薄膜光学理论 1.麦克斯韦方程组麦克斯韦方程组由四个场量：D 、E 、B 、H ，两个源量：J 、ρ以及反映它们之间关系的方程组成。

而且由媒质方程中的参数ε、μ、σ反映介质对电磁场的影响。

·激光物理·分析一维光子晶体的传输矩阵法与光学薄膜的菲涅耳系数矩阵法的等效性范希智，易迎彦，陈清明，刘子龙，郜洪云，祝霁洺，浦实，黎敏（武汉理工大学物理系，武汉430070）摘要：一维光子晶体与光学薄膜的结构都具有分层性，为了得它们分析方法的异同，本文比较分析了一维光子晶体能带结构的传输矩阵法与计算光学薄膜分光特性的菲涅耳系数矩阵法，结果发现两种方法在计算一维光子晶体与光学薄膜的反射率与透射率上是等效的，用菲涅耳系数矩阵法计算一维光子晶体的反射率R 与入射光波长的变化规律的实例也表明这一点，这两种方法在公式表述中的差别在于位相改变量δ的符号的正负，但不影响计算结果。

关键词：光子晶体；传输矩阵法；光学薄膜；菲涅耳系数矩阵法DOI编码：doi:10.3969/j.issn.0253-2743.2014.07.026中图分类号：O431 文献标识码：A 文章编号：0253-2743(2014)07-026-04On the Equivalence of the Transfer Matrix Method for Investigating one dimensional Photonic Crystal with the Fresnel Coefficient Matrix Method for Analyzing OpticalThin filmFAN Xi-zhi, YI Ying-yan, CHEN Qing-ming, LIU Zi-long, GAO Hong-yun, ZHU Ji-ming, PU Shi, LI Min(Department of Physics, Wuhan University of Technology, Wuhan 430070, China) Abstract: To distinguish the similarities and differences of the methods using to analyze one dimensional pho- tonic crystal(PC) and optical thin films(TF) which are provided with the similar stratified structure, the transfer ma- trix method(TMM) for analyzing the band gap of PC and the Fresnel coefficient matrix method(FCMM) for discuss- ing transmission and refection of TF were compared, and the equivalence of these two method for investigating the reflectivity and transmissivity of light of PC and TF was declared through the theory and a example of calculation of P C’s reflectance using FCMM, although existence of plus-minus of sign of variation for phase in the design formula for these two methods.Key words: Photonic Crystals; Transfer Matrix Method; Optical Thin films; Fresnel Coefficient Matrix Method光子晶体于1987年由E.Ya bolonovitc h[1]和S. John[2]分别提出。