一维光子晶体的传输矩阵编程
- 格式:ppt
- 大小:35.50 KB
- 文档页数:6

用传输矩阵法计算一维光子晶体的带隙特性研究------------------------------------------作者------------------------------------------日期一维光子晶体带隙特性研究1103011013 黄蓓粉体一班摘要:光子晶体是20世纪80年代末提出的新概念和新型人工微结构光学材料。
光子晶体以光子禁带的存在为主要特征,其典型结构为一个折射率周期变化的物体。
一维光子晶体是光子晶体最基本的构型,其折射率在一维空间方向上呈周期性分布。
一维光子晶体结构简单、易于制备,同时具备二维、三维光子晶体的性质,极有可能成为全光通信领域中的关键材料,因此具有较高的理论价值和广泛的应用前景。
关键词:光子带隙特征矩阵规律1 引言光子晶体是一种折射率周期变化的人工微结构材料 ,其典型结构为一个折射率周期变化的三维物体 ,周期为光波长量级. 光子在光子晶体中传播存在光子带隙.,频率落在光子带隙内的电磁波不能在光子晶体中传播,光子晶体的这种特性具有极大的理论价值和潜在的应用前景。
在光子晶体中掺杂后 ,会在光子能隙中引入局域模式 ,这将给激光技术和非线性光学等带来全新的应用 ,如制作零阈值激光器、光滤波器、慢光缓存器、慢光传感器等。
理论研究发现,对于含有缺陷的一维光子晶体,在光子禁带(PBG:Photonic Band Gap)的带边和缺陷模对应的频率位置,光的传输具有极低的群速度,Scalorta 等人发现在带边处,光脉冲传输速度可以降低到c/17(c 为真空中光速),大约为1.76×107m/s 。
光子晶体的理论计算已相对成熟 ,本文旨在应用现有的计算方法,建立一维光子晶体模型并讨论一维光子晶体在不同结构参数和参数下的光学传输特性。
2方法与原理2.1模型的建立一维光子晶体由两种不同相对介电常量 (εa ,εb ) 、厚度( a , b)的薄介质层交替排列构成的一维周期性结构 材料. 如图 1 所示 ,空间周期为 d = a + b ,一束频率 为 ω的光从左向右正入射到图中所示的一维周期 性结构材料中.将光波在介质层中的行 进看作是正向行进电磁波 (下行波) 和反向行进电磁 波 (上行波) 的叠加. 介质交界面处的电磁场满足边 界条件. 每一介质层与光波的相互作用可由其矩阵完全决定. 介质层两边的场矢量 E Ⅰ , H Ⅰ , E H Ⅱ的模可用特征矩阵联系起来 :E E M H H I II I II ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ 2.2数学理论推导为行进一步的计算,下面给出光子晶体的特殊矩阵表达式。

![一维三元光子晶体的传输特性研究[1]](https://uimg.taocdn.com/9456d46b01f69e314332946e.webp)
一维三元光子晶体的传输特性研究3Ξ王旭东3,刘 芳,闫珂柱(曲阜师范大学物理系,山东曲阜273165)摘要:运用光学传输矩阵理论对一维三元光子晶体传输特性进行了数值计算。
结果表明,其带隙宽度随结构参数a、b明显的改变;适当调节两个参数,得到了带隙相对宽度(Δω/ω0)为68%的带隙结构,带隙宽度几乎不随入射角的变化而改变,并且随实际操作中带来的随机误差引起的无序度的改变不明显,由此可方便地用于制作全角宽带反射镜等光学器件。
关键词:光子晶体;带隙;无序度中图分类号:O43;TN2 文献标识码:A 文章编号:100520086(2004)0120104204Studies on the Optical T ransmission Characteristics of12D Polybasic Photonic CrystalsWAN G Xu2dong3,L IU Fang,YAN Ke2zhu(Department of Physics,Qufu Normal University,Qufu273165,China)Abstract:Optical trnasmission characteristics of one dimensional polybasic photonic crystals compo sed of three kind of dielectric mediums was studied by the optical transmission matrix method.The re sults indicate the band gap change s with the variation of structure parameter a and b,a wide band gap with relative band width(Δω/ω0)of68%can be get by adjusting a and b,and its width change s lightly with the incident an2 gle,in fluence of the disorder is small com paring with binary photonic crystals.So it was sugge sted to make wide band refleceors with the photouic crystal.K ey w ords:photonic crystals;band gap;disorder1 引 言 自从1987年S.J hon[1]和E.Yblaloloath[2]提出光子晶体的概念之后,由于其广泛的应用前景和潜在的应用价值,吸引了众多科学家的兴趣。


一维ssh光子晶格能带结构matlab模拟光子晶体是一种具有周期性介质结构的材料,可以控制光的传播和调控光的性质。
其中,SSH光子晶格是一种特殊的光子晶体结构,具有非常有趣的能带结构和拓扑性质。
本文将介绍如何使用MATLAB进行一维SSH光子晶格能带结构的模拟。
首先,我们需要定义SSH光子晶格的基本参数。
一维SSH光子晶格由两种不同的介质单元组成,分别记为A和B。
我们可以定义两种介质的折射率分别为nA和nB,以及两种介质的宽度分别为dA和dB。
此外,我们还需要定义晶格的周期性,即晶格常数a。
接下来,我们可以使用MATLAB的光学工具箱中的Transfer Matrix 方法来模拟SSH光子晶格的能带结构。
Transfer Matrix方法是一种基于矩阵运算的数值计算方法,可以用来求解光在介质中的传播和反射。
首先,我们可以定义两种介质的传输矩阵。
对于介质A,其传输矩阵可以表示为:T_A = [exp(i*k*nA*dA), 0; 0, exp(-i*k*nA*dA)]其中,k是光的波矢,可以通过光的频率和折射率计算得到。
类似地,介质B的传输矩阵可以表示为:T_B = [exp(i*k*nB*dB), 0; 0, exp(-i*k*nB*dB)]然后,我们可以定义整个光子晶格的传输矩阵。
对于一个周期性为a的光子晶格,其传输矩阵可以表示为:T = T_B * T_A接下来,我们可以使用传输矩阵的特征值来计算光子晶格的能带结构。
传输矩阵的特征值可以表示光在光子晶格中的传播模式,即能带。
我们可以通过改变光的波矢k的值,来计算不同波矢下的能带结构。
最后,我们可以使用MATLAB的绘图函数来绘制一维SSH光子晶格的能带结构。
我们可以将波矢k作为横轴,能带的特征值作为纵轴,绘制出能带随波矢的变化曲线。
通过以上步骤,我们可以使用MATLAB进行一维SSH光子晶格能带结构的模拟。
这种模拟方法可以帮助我们理解SSH光子晶格的特性和性质,为光子晶体的设计和应用提供指导。



井冈山大学学报(自然科学版)26文章编号:1674-8085(2012)03-0026-05一维光子晶体全向带隙限光特性的研究*李棚1,张明存1,叶飞1,2(1.六安职业技术学院,安徽,六安237100 2.合肥工业大学,安徽,合肥230009)摘要:采用传输矩阵的计算方法研究了一维光子晶体结构对光传输特性的影响,利用MATLAB绘制不同结构参数的一维光子晶体透射率图谱。
通过绘图发现,改变一维光子晶体的结构参数,能够实现带隙宽度的最大化,同时,可以实现入射角在0到90度之间的全方向带隙限光。
选择适当的结构参数能够实现在1550nm光波附近的宽屏全向带隙限光。
关键词:光子晶体;传输矩阵法;数值分析;透射谱;带隙限光中图分类号:O436 文献标识码:A DOI:10.3969/j.issn.1674-8085.2012.03.006 RESEARCH ON THE CHARACTERISTICS OF OPTICAL TRANSMISSION WITH OMNIDIRECTIONAL BANDGAP CONTROL IN 1D PHOTONICCRYSTALLI Peng1,ZHANG Ming-cun1,YE Fei1.2( 1. Lüan V ocation Technology College, Lüan, Anhui 237100, China; 2.Hefei University of Technology, Hefei , Anhui 230009, China) Abstract: The effect of one-dimensional photonic crystal structure for optical transmission property was studied by transfer matrix computing method. MATLAB is used to draw One-dimensional photonic crystal transmittance map of different structure parameter. Through drawing, we find the larges bandgap width when the one-dimensional photonic crystal structure parameter is changed. Omni directional band gap limit of light will be implemented in angle from 0o to 90o. Broadband Omni directional bandgap limit light in a 1550nm optical wavelength near be achieved by select the appropriate structural parametersKey words: photonic crystals; transfer matrix method; numerical analysis; transmission spectrum; bandgap limit lightS. John [1]及E.Yablonovitch [2]几乎同时指出,光子系统中的光子会受到晶格周期性结构的散射,部分波段会因为干涉而形成能隙,进而在传输的光信号中出现能带。


一维光子晶体的研究方法----传输矩阵法1:绪论1.1:光子晶体研究的意义在以前对半导体材料的研究导致一场轰轰烈烈的电子工业革命,我们的科技水平有了突飞猛进的发展,并为此进入了计算机和信息为标准的信息时代。
在过去的几十年里,半导体技术正向高速,高集成化方向发展。
但这也引发了一系列的问题,比如电路中能量损失过大,导致集成体发热。
此外,由于高速处理对信号器件中的延迟提出更高的要求,半导体器件的能力已经基本达到了极限,为此科学家们把目光从电子转向广光子。
这是因为光子有着电子所不具备的优势:1.极高的信息容量和效率。
2.极快的响应速度。
3.极强的互连能力和并行能力。
4.极大地存储能力。
5.光子间的相互作用很弱,可极大地降级能力损失。
但是与集成电路相比,科学家们设想能像集成电路一样制造出集成光路,在集成光路中,光子在其中起着电子的作用,全光通过。
光子计算机将成为未来的光子产业,集成光路类似于电子产业中半导体的作用,光子产业中也存在着向集成电路的器件一样的集成光路——光子晶体,光子晶体的研究不仅仅是光通讯领域内的问题,同时也对其他相关产业将产生巨大的影响。
1.2:光子晶体的概念及应用光子晶体是八十年代未提出的新概念和新材料,迄今取得了较快的发展,光子晶体不仅具有理论价值,更具有非常广阔的应用前景,这个领域已经成为国际学术界的研究热点。
控制光子是人们长期以来的梦想,光子晶体能帮助人们实现这一梦想。
1987年Yablonol itch在讨论如何控制自发辐射和John 在讨论光子局域化时各自独立的提出了光子晶体的概念。
他们所讨论问题的共同实质是周期性电介质材料中光传播的特性,根据固体电子能带理论,晶体内部原子呈周期性排列,库仑场的叠加产生周期性势场,当电子在其中运动时受到周期性势场的布格拉散射而形成的能带结构,带与带之间有带隙,称为禁带。
能量落在禁带中的电子波不能传播。
与此相仿,当电磁波在周期性电介质结构材料中传播时由于受到调制而形成能带结构——光子能带结构,其带隙称为光带隙(PBG:photonic band gap)。
传输矩阵法研究光子晶体的反射、折射特性———以MATLAB程序实现简单介绍主要内容:1、光子晶体及计算参数简介;2、具体光子晶体模型及程序实现方法;3、其他图形的实现方法;4、图形的编辑和输出5、作业(编程练习)一、光子晶体及计算参数简介1、光子晶体一般模型光子晶体是一种折射率周期变化的人工微结构材料,其典型结构为一个折射率周期变化的三维物体,周期为光波长量级。
光子在这类材料中的行为类似于电子在凝聚态物质中的行为,可能存在着类似于半导体能带结构的禁带,称为“光子带隙”。
频率落在光子带隙内的电磁波不能在光子晶体中传播,光子晶体的这种特性具有极大的理论价值和潜在的应用前景。
一维光子晶体模型如图1:(ABABABABABABABABABABA)或(AB)5A其中a、b是两种不同介质的的厚度,εa与εb是介质的介电常数,d=a+b为光子晶体空间周期。
2、数学计算模型如图2E,H表示界Ⅰ面的an一侧的场矢量,EI,HI表示界Ⅱ面的bn一侧的场矢量,EII,HII表示界Ⅱ面的cn一侧的场矢量。
同一界面两侧,有E EI=,H HI=。
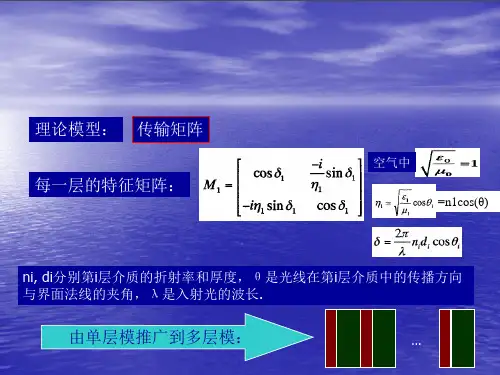
介质两层边的场矢量EI,HI,EII,HII的模可用特征矩阵联系起来:cos sinsin cosb bbb b biE E EMH H HiδδηηδδI II III II II⎡⎤-⎡⎤⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦-⎢⎥⎣⎦(1)其中cos sin sin cos jj j j j jj iM i δδηηδδ⎡⎤-⎢⎥=⎢⎥⎢⎥-⎣⎦,正入射时j j j h c ωδε=-,0j j εηεμ= (2) 即正入射时:a a a a h n a ccωωδε=-=-,b b n b cωδ=-,00a a n εημ=,0b b n εημ= 对图1所示的一维周期性结构情况有: 111211()N N N N N N E E E M M M M H H H ++I ++I ⎡⎤⎡⎤⎡⎤==⋅⋅⋅⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦111111N N Na b a b a N N N E E E A B M M M M M M H H H C D ++++++⎡⎤⎡⎤⎡⎤⎡⎤=⋅⋅⋅==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦ (3) 式中a b a b a M M M M M M =⋅⋅⋅就是一维周期性结构的特征矩阵。
一维光子晶体的各角度入射研究采用传输矩阵的方法,研究了电磁波从不同角度入射的一维光子晶体的能带结构和透射率.设电磁波从第I 层介质传到相邻第J 层介质,第I 层介质中,电场i E 为:(cos )(cos )+-i i i E = { E , E }i i i i i k z wt i k z wt e e θθ-+ 第J 层介质中,电场j E 为: (cos )(cos )+-j j j E = { E , E }j j j j i k z wt i k z wt eeθθ-+先考虑TE 波(电矢量垂直于波的传播方向),有界面处的边界条件:E 和H 都切向连续可得:+-+-i i j j E E E E +=+(1)cos cos cos cos i i i i j j j j H H H H θθθθ+-+--=-(2)H =(3)n =4)由(1)——(4)可得:++ji --i jE 11E 11cos cos cos cos E E j j j j i ii i n n n n θθθθ⎛⎫⎛⎫⎛⎫⎛⎫⎪= ⎪ ⎪⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭⎝⎭表示成电场波矢的矩阵形式:j i E E ij Q =其中ij Q 为:cos cos 11cos cos 1cos cos 211cos cos i i i i j jj j ij i i i i j j j j n n n n Q n n n n θθθθθθθθ⎛⎫+-⎪⎪=⎪-+ ⎪ ⎪⎝⎭同理,TM 波(磁矢量垂直于波的传播方向)的界面传输矩阵ij m 为:cos cos cos cos 1cos cos 2cos cos i i i i j jj j ij i ii i j j j j n n n n Q n n n n θθθθθθθθ⎛⎫+-⎪⎪= ⎪-+ ⎪ ⎪⎝⎭一段介质的位相变化矩阵:cos cos 00i ii i i i ik d i ik d e p e θθ-⎛⎫=⎪ ⎪⎝⎭ 由以上可得特征矩阵:T=ij i Q P对于两种介质A ,B (设厚度分别为A d =0.5,B d =0.5;相对介电常数分别为(1,0),(13,0),相对磁导率分别为(1,0),(1,0))组成的SL(超晶格材料是两种不同组元以几个纳米到几十个纳米的薄层交替生长并保持严格周期性的多层膜,事实上就是特定形式的层状精细复合材料)系统,其特征矩阵为:,()()BA B B A B A A T Q P d Q P d =由BLOCH 定理可得:(0,)()()()ikd T d E x w E x d w e E x w =+= 可知:[]1122c o s ()(0,)(0,)/2kd T d T d =+由此可画出能级图:图1。
·激光物理·分析一维光子晶体的传输矩阵法与光学薄膜的菲涅耳系数矩阵法的等效性范希智,易迎彦,陈清明,刘子龙,郜洪云,祝霁洺,浦实,黎敏(武汉理工大学物理系,武汉430070)摘要:一维光子晶体与光学薄膜的结构都具有分层性,为了得它们分析方法的异同,本文比较分析了一维光子晶体能带结构的传输矩阵法与计算光学薄膜分光特性的菲涅耳系数矩阵法,结果发现两种方法在计算一维光子晶体与光学薄膜的反射率与透射率上是等效的,用菲涅耳系数矩阵法计算一维光子晶体的反射率R 与入射光波长的变化规律的实例也表明这一点,这两种方法在公式表述中的差别在于位相改变量δ的符号的正负,但不影响计算结果。
关键词:光子晶体;传输矩阵法;光学薄膜;菲涅耳系数矩阵法DOI编码:doi:10.3969/j.issn.0253-2743.2014.07.026中图分类号:O431 文献标识码:A 文章编号:0253-2743(2014)07-026-04On the Equivalence of the Transfer Matrix Method for Investigating one dimensional Photonic Crystal with the Fresnel Coefficient Matrix Method for Analyzing OpticalThin filmFAN Xi-zhi, YI Ying-yan, CHEN Qing-ming, LIU Zi-long, GAO Hong-yun, ZHU Ji-ming, PU Shi, LI Min(Department of Physics, Wuhan University of Technology, Wuhan 430070, China) Abstract: To distinguish the similarities and differences of the methods using to analyze one dimensional pho- tonic crystal(PC) and optical thin films(TF) which are provided with the similar stratified structure, the transfer ma- trix method(TMM) for analyzing the band gap of PC and the Fresnel coefficient matrix method(FCMM) for discuss- ing transmission and refection of TF were compared, and the equivalence of these two method for investigating the reflectivity and transmissivity of light of PC and TF was declared through the theory and a example of calculation of P C’s reflectance using FCMM, although existence of plus-minus of sign of variation for phase in the design formula for these two methods.Key words: Photonic Crystals; Transfer Matrix Method; Optical Thin films; Fresnel Coefficient Matrix Method光子晶体于1987年由E.Ya bolonovitc h[1]和S. John[2]分别提出。