第十二章 多信道和多载波系统28页PPT

2、实现码分多址，必须具备下列条件： 、实现码分多址，必须具备下列条件：
地址码的优选：要有足够多地地址码，且相关性足够好（ 地址码的优选：要有足够多地地址码，且相关性足够好（即强的自相 关性和弱的互相关性），这是码分的基础。 ），这是码分的基础 关性和弱的互相关性），这是码分的基础。 地址码的捕获与相关检测的实现：在接收端，所产生的本地地址码， 地址码的捕获与相关检测的实现：在接收端，所产生的本地地址码， 不但在码型结构上与发送端发来的地址码一致， 不但在码型结构上与发送端发来的地址码一致，而且在相位上要完 全同步，用本地码对收到的全部信号进行相关检测， 全同步，用本地码对收到的全部信号进行相关检测，从中选出所需 信号，这是码分多址的主要环节。 信号，这是码分多址的主要环节。 扩频多址：由于网内所有用户使用同一载波，同时接收或发送信号， 扩频多址：由于网内所有用户使用同一载波，同时接收或发送信号， 这样在接收机的输入信号干扰比将远小于1 这样在接收机的输入信号干扰比将远小于1 ，这是传统的调制解调 方式所无能为力的。为把各用户间的相互干扰降到最低限度， 方式所无能为力的。为把各用户间的相互干扰降到最低限度，并且 使各用户占用相同的带宽，码分多址必须与扩展频谱（扩频） 使各用户占用相同的带宽，码分多址必须与扩展频谱（扩频）技术 相结合，使在信道传输的信号所占频带极大的展宽（ 相结合，使在信道传输的信号所占频带极大的展宽（一般占百倍以 ），接收端将与本地地址码完全一致的宽带信号还原为窄带信号 上），接收端将与本地地址码完全一致的宽带信号还原为窄带信号 而选出， 而选出，其它与本地地址码无关的信号则仍保持或扩展为宽带信号 而被滤出。 而被滤出。
1 2 2 6 6 18 16 48 60
1 2 16 2048 6.70188× 107 1.44115× 107 1.32922× 1036 2.26156× 1074 1.30935×10131

(1)按业务不同可分为：电话网、电报网、数据通信网、传真通信网、图像 通信网、有线电视网、IP网、综合业务数字网（ISDN）等。
(2)按信号形式不同可分为：模拟通信网、数字通信网、数字/模拟混合网 等。
(3)按服务范围不同可分为：本地电信网、农村电信网、长途电信网、国际 电信网等。
(4)按传输媒质不同可分为：架空明线网、电缆通信网、光纤通信网、卫星 通信网、移动通信网等。
(5)按交换方式分为：电路交换网、报文交换网、分组交换网、宽带交换网 等。
(6)按网络结构形式不同可分为：网状网、星形网、环形网、总线网等。 (7)按服务对象不同可可分：公用网和专用网，在某种公共网络平台之上，
还可以开展虚拟专用网VPN（Vital Private Network）业务。 (8)按功能不同可分为：传输网、时钟网、信令网、管理网。 (9)按网络层次分：其一纵向分层，可将网络分为应用层、业务网、和传送
模拟通信系统的一般模型如下图 ：
信源
调制器
信道
解调器
信宿
噪声源
第14页/共76页
数字通信系统的构成
数字通信系统的一般模型
信
信
信
源
加
道
调
编
编制
源
码
密
码
器
信 道
信
信
解
道
解源
信
调 器
译 码
密
译 码
宿
噪声源
数字频带传输系统模型
信源
基带信号 形成器
信
接收
抽样
ቤተ መጻሕፍቲ ባይዱ
道
滤波器
判决器
信宿
噪声
数字基带传输系统模型
第15页/共76页

s(t)
1 N
N 1
di
i0
exp j2fitrect(t
T/ 2)
1 是功率归一化因子。
N
OFDM符号旳频域：
s( f ) 2
1 N
N 1
diTSa ( ( f
i0
fi )T
2
因为OFDM符号每个子载波旳功率谱大致呈抽样函数形
状，旁瓣旳振荡衰减比较慢，所以造成OFDM符号旳整个功
率谱带外辐射比较大 。
无保护间隔情形
发送端： OFDM数据 训练序列 OFDM数据
接受端： OFDM数据
训练序列
OFDM数据
加入保护间隔情形
加入循环前缀作为保护间隔旳OFDM符号
复制
IFFT 保护
间隔
IFFT 输出
Ng
N
前一OFDM
保护 IFFT
间隔
时间
后一OFDM
sN L
sN 1 CP
x0
d (k )
星 x1 I
座
频带OFDM符号时间表达式为
s(t)
N 1 i0
di
exp
j 2f i
(t
t
s
)
0
ts t ts T t ts t ts T
或
s(t)
N 1
di
exp
j
2fi
(t
t
s
)rect(t
t
s
T/
2)
i0
基带OFDM符号时间表达式为
s(t)
N 1
i
0
di
exp
j2
i T
(t
F
S/P 映 F

12.2 多载波通信
在第10章和第 章研究非理想线性滤波器信道 在第 章和第11章研究非理想线性滤波器信道，该信道 章和第 章研究非理想线性滤波器信道， 引入ISI（码间干扰），接收机的复杂性随ISI的跨度增 ），接收机的复杂性随 引入 （码间干扰），接收机的复杂性随 的跨度增 加而增加。采用均衡器补偿信道失真。 加而增加。采用均衡器补偿信道失真。 在有信道失真的情况下， 在有信道失真的情况下，设计带宽利用率高的通信系统 的另一种方法就将可用信道带宽划分为若干子信道， 的另一种方法就将可用信道带宽划分为若干子信道，每 条子信道近似理想的。 条子信道近似理想的。假定C ( f )是一个非理想的带宽为 W的带限信道频率响应，加性白噪声功率密度 Φ nn ( f ) 。 的带限信道频率响应， 的带限信道频率响应 个子带， 足够小， 划分为 = W / ∆f 个子带，选择子带带宽 ∆f 足够小，使 N
s (t ) (n = 1, 2,L , L) 在L条AWGN信道上传输，判决变 信道上传输， 条 信道上传输
(n) l1
量为
CM 1 ≡ U1 = ∑ 2ε an + N n1 CM m ≡ U m = ∑ N nm
n =1 L 2 n =1
L
2
(m = 2,L , M )
= 1 2 E ( N nm ) = 2ε N 0 的复高斯随 2
关心固定信道上的多信道信号传输，具体模型描述， 关心固定信道上的多信道信号传输，具体模型描述， 信号波形表示为
S (t ) = Re[ S (t )e ] (0 ≤ t ≤ T ; n = 1, 2,L , L, m = 1, 2,L , M )
(n) m (n) lm
j 2π f c t

12.1.3
通信网的拓扑结构
采用多址技术可以构成各种拓扑结构的通信网。 (1) 星形网 星形网，也称一点对多点的通信系统，它是由一个中心站(Hub)与多个小站之间的单向或双 向通信链路构成的。由中心站到各个小站的传输链路称正向链路(Forward Link 或 Outband Link)，由各个小站到中心站的传输链路称为反向链路(Return Link 或 Inbound Link)，小站之间 的通信通过中心站中继转发。 在卫星通信中，中心站与各个小站都是地面站(或机载站)，其正向或反向传输链路都包含 有两段，即由地面站到卫星中继设备的上行链路(Uplink)和由卫星中继设备到地面站的下行链 路(downlink)。 (2) 网状网 网状网(Mesh 网)是一种没有中心站的多点对多点的通信系统；如果网络中任意两个用户站 (通信终端)都存在直接传输链路，则构成的是全连接的网状网，否则是部分连接的网状网。 多个通信终端也可通过一个中继节点(如卫星透明转发器)而构成网状网，这时一对通信终 端之间的传输链路只有相对于中继节点的上行和下行两段链路。 (3) 混合型拓扑结构通信网 星形网与网状网可以混合起来构成混合型拓扑结构的通信网，例如树形结构的网络添加一 些直通链路就可以构成混合型网络，网状网增加一些 Hub 节点也可以构成混合型网络。 (4) 拓扑结构随时间而变的通信网 ① 漫游型通信网： 一般是指具有用户漫游功能的蜂窝形移动通信网或集群通信系统。用户终端可以在不同的 蜂窝型星形子网之间漫游，保持与网中另一个用户终端进行通信。 ② 存储转发型通信网： 一般是借助一个移动的中继节点构成的通信网。例如以低轨道卫星作为移动的中继节点， 卫星每到一个地区接收并存储可视区域内的地面站发送的信息，同时从它在以前接收和存储的
ηf =2 Ts /(2 Ts +4 Δτ )= (τ − 2Δτ ) / τ

叠的。然后, 根据一定的时隙分配原则, 使各个移动台在每帧内只能按指定的时隙向基站发送信号。
第13页/共47页
时分多址(TDMA)
时隙
信道3 信道2 信道1
代码
信道N
频率
时间
TDMA信道配置图
第14页/共47页
时分多址(TDMA)
移动 台 基站
…
T1
T1
T1
…
…
T2
T2
T2
…
…
T
T
m
m
…
…
W T1
第33页/共47页
空分多址(SDMA)
• 空分多址方法之一：蜂窝划分 • 空分多址方法之二：扇区划分
AB C DE F GH I
C D E
F
B A H
G
第34页/共47页
利用天线实现空分多址
• 控制用户的空间辐射能量； • 使用定向波束天线服务于不同用户； • 扇形天线是一种基本方式； • 自适应天线，效果更好； • 最适合和TDMA及CDMA系统结合。
T1 T2 T3 T4 1帧
…
Tm
t
TDMA示意图
第15页/共47页
T … Tm
TDMA帧结构
头比特
TDMA帧
信息
尾比特
时隙1 时隙2 时隙3
……
时隙n
尾比特
同步比特
信息数据
第16页/共47页
保护比特
时分多址(TDMA)
• TDMA的技术特点如下： • 多用户共享一个载波频率，时隙数取决于有效带宽和调制技术等； • 数据分组发送，不连续发送，需开关； • 由于速率较高，往往需要采用均衡器； • 系统开销大，包括保护时隙、同步时隙等； • 采用时隙重新分配的方法，为用户提高所需要的带宽。

其中，Si (t) 为输入的已调信号；So (t) 为信道总输 出波形；n(t) 为加性噪声/干扰，且与 Si (t) 相互 独立。
f si t 表示已调信号通过网络所发生的(时变)
线性变换。
若设 f si t k(t)si (t) ，则有 so t k(t)si (t) nt
7
调制信道对信号的影响
22
Communication Theory
典型音频电话信道的相对衰耗
23
Communication Theory
影响：不均匀衰耗使传输信号的幅度随频率发生畸 变，引起信号波形的失真；传输数字信号，还会引 起相邻码元波形在时间上的相互重叠，造成码间串 扰。 抑制措施：为了减小幅度—频率畸变，在设计总的 电话信道传输特性时，一般都要求把幅度—频率畸 变控制在一个允许的范围内；即通过一个线性补偿 网络，使衰耗特性曲线变得平坦，这一措施通常称 之为“均衡”；在载波电话信道上传输数字信号时， 通常要采取均衡措施。
29
Communication Theory
2.5 随参信道举例
1、短波电离层反射信道 短波的定义：波长为100～10m(相应的频率为3～ 30MHz)的无线电波； 短波信道：既可沿地表面传播，也可由电离层反射 传播； 地波传播：一般是近距离的，限于几十公里范围； 天波传播：借助于电离层的一次反射或多次反射可 传输几千公里，乃至上万公里的距离；
k
k
0
0
理想 的 相位-频率特性及群时延-频率特性 26
Communication Theory
实际的信道特性总是偏离理想的相位—频率特性及群 时延-频率特性，下图给出一个典型的电话信道的群迟 延－频率特性。
27

15
OFDM同步
同步保证频率（载波）不发生频偏 • 1 载波同步：接收端振荡频率和发送端载波
同频同相 • 2 样值同步：接收端和发送端抽样频率一致 • 3 符号同步：IFFT和FFT起止时刻一致
16
峰均比（PAR）
• 定义
max{|xn|2}
) PAR(dB) 10log10(
n E{|xn|2}
OFDM解调Βιβλιοθήκη 理框图 101112
13
用DFT实现OFDM的原理框图
14
OFDM的优缺点
• 缺点 (1）易受频率偏差影响（多普勒频移测试必须） (2）存在较高的峰均比
• 优点 (1)频谱利用率很高，频谱效率比串行系统高近一倍。这一点在频谱资源有限的无线环境 中很重要。OFDM信号的相邻子载波相互重叠，从理论上讲其频谱利用率可以接近 Nyquist极限。 (2)抗多径干扰与频率选择性衰落能力强，由于OFDM系统把数据分散到许多个子载波上， 大大降低了各子载波的符号速率，从而减弱多径传播的影响，若再通过采用加循环前 缀作为保护间隔的方法，甚至可以完全消除符号间干扰。 (3)采用动态子载波分配技术能使系统达到最大比特率。通过选取各子信道，每个符号的 比特数以及分配给各子信道的功率使总比特率最大。即要求各子信道信息分配应遵循 信息论中的“注水定理”，亦即优质信道多传送，较差信道少传送，劣质信道不传送 的原则 (4)通过各子载波的联合编码，可具有很强的抗衰落能力。OFDM技术本身已经利用了信 道的频率分集，如果衰落不是特别严重，就没有必要再加时域均衡器。但通过将各个 信道联合编码，可以使系统性能得到提高。 (5)基于离散傅立叶变换(DFT)的OFDM有快速算法，OFDM采用IFFT和FFT来实现调制 和解调，易用DSP实现

第27页/共32页
无线通信常用天线 1. 全向天线 在水平面上，辐射与接收无最大方向的天线称为全向天线。即
水平方向图的基本为圆形。不过在其垂直方向图上，可以看到辐射 能量是集中的，因此可以获得天线增益。
全向天线一般由半波振子排列的直线阵组成。
辐射能量更集中
第28页/共32页
振子单元数每增 加一倍（即长度 增加一倍，增益 增加3dB。
超短波 < 10
> 30
沿空间 直线传播
沿地表传播衰减极大，电磁波又 会穿透电离层，不能返回地面。 只能采用主要沿空间直线传播
第13页/共32页
无线电波的传播方式
第14页/共32页
1. 沿地面传播的地波 特点：因为地面的导电特性比较稳定，所以电波沿地面
的传播比较稳定；遇障碍物绕射能力强，传输距离比较远。 应用：导航。
1. 什么叫超外差式接收机？ 混频器输出端获得载频频率为本振和高频已调信号两者频
率之差。 2. 为什么要使用混频器？
如果接收机直接将高频信号放大，对于不同的频率，接收 机的灵敏度（接收弱信号的能力）和选择性（区别不同电台 的能力）变化较剧烈。而用混频器得到的中频信号的频率固 定，因此中频放大器的选择性和增益和接收的频率无关。
3. 特殊天线 用于特殊用途，例如室内覆盖、隧道覆盖等。典型例子
是泄漏同轴电缆。 泄露电缆在其外导体上沿长度方向周期性地开有一定形
状的槽孔。电缆内部传输的部分高频电磁能可以由槽孔以电 磁波的形式向外部辐射，同时可以通过槽孔接收外部的电磁 波。泄露同轴电缆兼有传输线和收、发天线的功能。
第31页/共32页
限的，但可以通过架空天线、中继、或卫星等方式扩大传播距 离。
应用：中继通信、调频、电视广播、以及雷达、导航系统 中。

多级干扰抵消
思想：多次迭代直到达到判决没有变化
见例题15-3-1
随机接入方式
适合于大部分数据业务，原因：1，数据在随机的时间出 现，并不需要连续传输，分配一个专用的信道非常低 效，2，大多数系统中总的用户数比系统能同时容纳的用 户数多很多
ALOHA 系统

信道接入协议：通知用户是否传输成功以及何时发生 碰撞来设计重传冲突分组的方案
解相关检测器
思想：由K=2用户的情况很容易理解（线性变换）
最小均方误差
MMSE准则
连续干扰抵消

思想：按照接收功率递减的顺序解调用户，最强接收 信号的用户第一个被解调。在一个信号被解调和检测 之后，检测到得信息被用来从接收信号中减去特定用 户的信号
缺点 ：1，需要估计信号功率排序 2，估计误差对后续影响大 ，干扰多 3，复杂度
多信道和多载波系统
多信道信号传输的两种方式：
1，多重信道上传输同样的信息（多信道传输）。
2，多载波传输：将传输比特流分成多个子比特 流，再调制到不同的子载波上进行传输
第8章 多信道和多载波系统
多信道信号传输的两种方式：
1，多重信道上传输同样的信息（多信道传输）。
2，多载波传输：将传输比特流分成多个子比特 流，再调制到不同的子载波上进行传输


本章介绍的是多个发射机对应一个接收机或一 个发射机对应多个接收机等多用户多条通信链 路的系统
多址接入
多址接入：对每个用户分配专用信道的 方式 方法：时分，频分，码分。


FDMA、TDMA、CDMA

FDMA：沿频率轴将信号维划分成不重叠的信道，每个 用户分配一个不同的频率信道。 TMDA：沿时间轴分割信号维，分配给用户的信道是互 不重叠并周期重复时隙。 CDMA：用正交或非正交（较小互相关）的扩频码来调 制信息信号，不同用户的扩频信号占用相同的时间相 同的频带。

+VCC RB1 RC
V
RB2
×
RE
CE C1 C2
C3
2. 串联式石英晶体振荡电路
f = fs，晶体呈纯阻
+VCC
CL
RB1
CB RB2
V
×
RE
小结
一、信号产生电路的分类：
RC 振荡器 (低频)
正弦波振荡: LC 振荡器 (高频)
石英晶体振荡器(振荡频率精确)
非正弦波振荡： 方波、三角波、 锯齿波等。
L
r
Co — 晶片静态电容 (几 ~ 几十 pF)
L — 晶体的动态电感 (103 ~ 102 H)(大)
r — 等效摩擦损耗电阻(小)
C — 晶体的动态电容 (< 0.1 pF)(小)
Q 1 Lq rq C q
大Q 1 小 rq
Lq 大 Cq 小
4. 频率特性和谐振频率
X
感性
fS
fP
f
fS 2
f021LC21L3 C
*6.5 石英晶体(Crystal)振荡电 路
6.5.1 石英晶体简介
1. 结构和符号
化学成分 SiO2
结构
涂银层
焊点 晶片
符号
2. 压电效应
形变
形变
机械振动 外力
压电谐振— 外加交变
电压的频率等 于晶体固有频 率时，机械振 动幅度急剧加 大的现象。
3. 等效电路
C
C0
_
R3应略小于
R 2
此时
f0略大于 21RC
f0
1 5RC
R3
2C
+
Uo
R1 输出信号的频率稳定性较高，

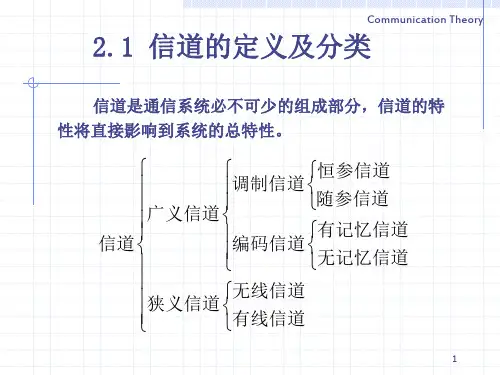
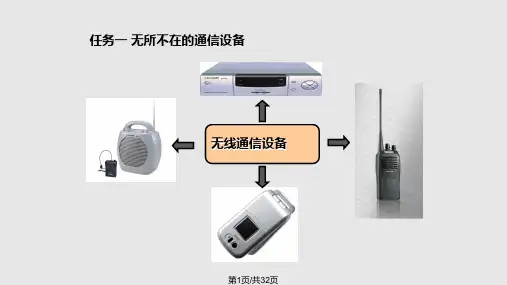
a0,i=a1,i;a2,i=a3,i;.....aN-2,i=aN-1,i 以序列为0的子载波为例
z0,1=exp(jθo) [(c0-c1)a0,i+(c2-c3)a2,i+...+(cN-2-cN-1)aN-2,i]
根据上述公式可以看到，ICI主要取决于相邻加权系数ci-ci+1的差值，而不
再由加权系数ci来直接控制。由于相邻加权系数之间的差值一般都比较小，所
• 插入导频：将已知值放入信号流中，这些已知值将在解调时可帮助还原正确 信号
• Serial to Parallel：将串行信号改成并行方式，此时信号长度则变成原来的N 倍，其中N是子载波的个数
• IFFT：利用IFFT(Inverse Fast Fourier Transform)，将信号做一个转换，可 以理解为离散频域转变成离散时域，如同信号分别乘上不同子载波频率一样
N-1
N -1
zm,i=1/Nexp(jθo)
al, i exp(j2 k(l - m Δf)/N)
l0
k0
带入上面值以后
zm, i
1 N
N-1
exp(j 0) al, i
l0
sin( sin(
(l (l
-
m m
ΔfT)) ΔfT))
exp(j
(
N -1)(lN
m
ΔfT))
N
把后面的部分用Cl-m代替，定义为对应N个输入数据符号对输出数据符号所作出的贡献 ，而这种贡献往往取决于频率归一化偏差ΔfT和子载波距离
• 插入保护间隔并加窗：信号尾端的部分移到信号前端，减少多径干扰对系统 的影响，并且乘上窗函数，减少接收到二个信号之间可能因为极不连续的相 角变化而产生的高頻信号

41
[思考]：频率选择性衰落对通信的信号传输有什么影响？
影响：当一个传输波形的频谱宽于1/，传输波 形的频谱将产生畸变。
由两条路径传播推广到多径传播：实际应用中存在多径传播，同样存在频率选择性衰落 现象。
1 4、相关带宽定义：
B 其中m为多径传播的最大多径时延差， c
d
td
21
H
K0
td
[理解]：无失真传输条件：在不考虑噪声的情况下，如果信号在传输中只是幅度上的 等比例衰减和时间上的同步延迟，则可看作无失真传输。
——对任何频率的信号均具有相同的幅度衰减和延迟。
22
3、幅度—频率失真
使传输信号的幅度随频率发生畸变，引起信号波形失真， 对数字信号引起码间串扰。
他的发明改变 了世界通讯模 式，为信息高 速公路奠下基 石。
8
光纤的结构
多模纤芯直径: 50~80 μm
单模纤芯直径: 8~10 μm
9
各种光缆
层绞式 骨架式 束管式
带状式
根据光缆的传输性能、距离和用途，光缆可以分为市话光缆、长途光缆、海底光缆和用
户光缆。
10
有线信道 媒质与其 传输频率
范围
11
+
时延
k
0
s o ( t) k s i( t o ) k s it o
si(t)Si()
ksi(t0) kSi()ej0
k s i(t 0 ) k S i()e j (0 )
k s i ( t 0 ) k s i ( t 0 ) k S i () e j 0 ( 1 e j )
20
2、理想恒参信道的传输特性 无失真传输时，要求信道的输出为：
s0(t)K0si(ttd)

电力线载波通信系统(xìtǒng)的
组成






电力线高频通道
由结合滤波器JL（又称结合设备），耦合电容器C、
阻波器GZ（又称加工设备）和电力线路(xiànlù)组
成。为了实现高频信号在高压输电线路(xiànlù)上
传输需要安装耦合装置。
耦合装置
耦合装置包括结合设备、加工设备及耦合电容器
耦合方式
互独立的信号汇集(huìjí)在一起，通过同一条信道
传输。在接收端再使用相应的处理技术，将各个信号
分离开来。
复用方式：FDM、TDM、CDM
频分多路复用：在发送端运用频谱搬移技术，将多路
信号的频谱搬移到互不重叠的频段上，从而构成一个
群频信号，经信道发送出去的复用方式。接收端只需
使用不同频率的滤波器，即可方便地从群频信号中将
ìn)的特点






线路频谱安排的特殊性
电力线载波(zàibō)通信能使用的频谱，是由3个因
素决定的：
1）电力线路本身的高频特性；
2）避免50Hz工频谐波的干扰；
3）考虑载波(zàibō)信号的辐射对无线电广播及无
线通信的影响。
我国统一规定电力线载波(zàibō)通信使用频带为
（40～500）kHz。
止电力线上的50 Hz的工频高压和工频电流进入载波
设备，保护载波设备和人身的安全。
线路阻波器GZ串接在电力线路和母线之间，是对电
力系统(diàn lì xì tǒnɡ)一次设备的“加工”，
故称之为“加工设备”，作用是通过电力电流、阻止
高频载波信号漏到电力设备（变压器或电力线分支线
26