算法合集之《母函数的性质及应用》
- 格式:pdf
- 大小:553.12 KB
- 文档页数:24

母函数(生成函数)(发生函数)(发生函数)英文:generating function我们已知道了解决组合的计数问题的几种方法,从基本的加法原理和乘法原理开始,导出了排列与组合的各种公式,证明了容斥原理,并且已用它来解决某些计数问题。
这里将论证一种方法是属于Eular 的生成函数法。
(对工程师来说,数列的母函数通称为z-变换)§1 母函数利用生成函数可以说是研究计数问题的一个最主要的一般方法:其基本思想很简单:为了获得一个数列{} 210,,0:a a a k a k=≥的知识,我们用一个母函数+++=∑=≥22100)(x a x a a xa x g kk k这里x k 是指数函数来整体地表示这个数列,称g (x )是数列{}0:kx a k 的普通母函数,这样原数列就转记为成函数。
假如能求得这个函数,则不仅原则上已确定了原数列,还可以通过对函数的运算和分析得到这个数列的许多性质。
这里如果把x k 提成)(x k μ亦称普通母函数指数函数通常选来使得没有两个不同的序列令产生同一个母函数,故序列的母函数仅只是序列的另一种表示。
如1,cos x ,cos2x ,…为指数函数,序列{}2,,1ωω的母函数为+++++=rx x x x F rcos 2cos cos1)(2ωωω另一方面,用,1,1+x ,1-x ,1+x 2,1-x 2,…,1+x r ,1-x r …作为指数函数,序列(3,2,6,0,0)的普通母函数是3+2(1+x )+6(1-x )=11-4x ,而序列(1,3,7,6,0)和(1,2,6,1,1)会产生同一母函数即,1+3(1+x )+7(1-x )=11-4x ,xx x x x 411)1()1()1(6)1(2122-=-+++-+++故函数 ,1,1,1,1,122x x x x -+-+不应做为指数函数,)(x r μ的最近常用的是r x ,以下我们仅讨论这种情况的指数函数。

母函数的概念和使用
母函数是组合数学中的一种重要工具,用于描述序列的生成函数。
它可以将序列转化为形式简单的多项式,从而方便地进行计算和推导。
形式上,对于序列$\{a_n\}$,它的母函数可以定义为:
$A(x)=\sum_{n=0}^{\infty}a_nx^n=a_0+a_1x+a_2x^2+...$
母函数$A(x)$通常被视为$x$的函数,可以进行各种计算操作,比如加法、乘法、求导等。
母函数的使用有以下几个方面:
1. 求序列的常用操作:对于给定的序列,可以通过母函数求导、乘法、加法等操作得到新的序列。
例如,序列的微分对应于母函数的求导,序列的乘法对应于母函数的乘法,序列的加法对应于母函数的加法。
2. 求序列的递推关系:通过构造序列的母函数,可以得到序列的递推关系。
递推关系描述了序列相邻项之间的关系,是解决组合计数问题的关键。
通过求解递推关系,可以得到序列的通项公式,从而得到更深入的结论。
3. 求序列的生成函数:母函数可以将序列转化为一个形式简单的多项式。
通过对母函数进行逆变换,可以得到序列的生成函数,从而用多项式的形式来表示序列。
生成函数是分析序列性
质的一种强有力的工具,可以进行各种计算和推导。
母函数在组合计数、离散数学和概率等领域中具有广泛的应用,可以解决各种组合计数问题,如排列组合、图论、走迷宫等问题。
同时,母函数也是解决一些难题的关键,在一些具有复杂递推关系的序列中起到了重要作用。

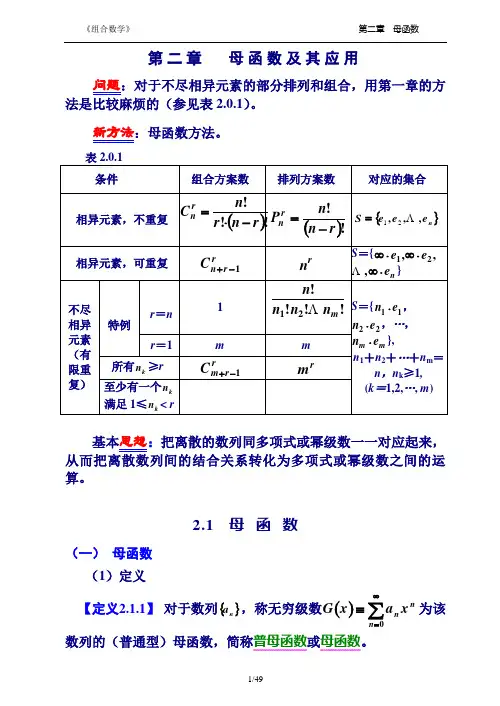
第二章 母函数及其应用问题:对于不尽相异元素的部分排列和组合,用第一章的方2.0.1)。
新方法:母函数方法。
基本思想:把离散的数列同多项式或幂级数一一对应起来,算。
2.1 母 函 数(一) 母函数 (1)定义【定义2.1.1】 对于数列{}n a ,称无穷级数()∑∞=≡0n n n x a x G 为该数列的(普通型)母函数,简称普母函数或母函数。
(2)例【例2.1.1】 有限数列rn C (r =0,1,2, …,n )的普母函数是。
()x G =nn n n n nx C x C x C C ++++ 2210=()nx +1【例2.1.2】 无限数列{1,1,…,1,…}的普母函数是()x G = +++++n x x x 21=x-11(3)说明● n a 可以为有限个或无限个;● 数列{}n a 与母函数一一对应,即给定数列便得知它的母函数;反之,求得母函数则数列也随之而定;例如,无限数列{0,1,1,…,1,…}的普母函数是+++++nx x x 20=xx-1● 这里将母函数只看作一个形式函数,目的是利用其有关运算性质完成计数问题,故不考虑“收敛问题”,而且始终认为它是可“逐项微分”和“逐项积分”的。
(4)常用母函数(二) 组合问题 (1)组合的母函数定理2.1.1 组合的母函数:设{}m m e n e n e n S ⋅⋅⋅=,,,2211 ,且n 1+n 2+…+n m =n ,则S 的r 可重组合的母函数为()x G =∏∑==⎪⎪⎭⎫ ⎝⎛mi n j j i x 10=∑=n r rr x a 0(2.1.1) 其中,r 可重组合数为rx 之系数r a ,r =0,1,2, …,n .理论依据:多项式的任何一项与组合结果一一对应(见例2.1.3)定理2.1.1的优点:● 将无重组合与重复组合统一起来处理; ● 使处理可重组合的枚举问题变得非常简单。
(2)特例推论1 {}n e e e S ,,,21 =,则r 无重组合的母函数为G (x )= (1+x )n (2.1.2)组合数为r x 之系数r n C 。






六、母函数及其应用6.1定义:称() +++++=-12321n n x a x a x a a x f 为数列{}n a 的形式幂级数,或生成函数,简称母函数。
6.2几个常用初等函数的形式幂级数展开式(1)()111<=-∑+∞=x x x n n ;(2)()()()()1!1110<-+⋅⋅-⋅=+∑+∞=x x n n x n n αααα;(3)()R x n x e n nx∈=∑+∞=0!;(4)()()()R x n x x n nn∈-=∑+∞=02!21cos ; (5)()()()R x n x x n n n∈+-=∑+∞=+012!121sin ; (6)()()()111ln 01<-=+∑+∞=-x nx x n nn ; (7)()()1121arctan 012<+-=∑+∞=+x n x x n n n。
求一个初等函数的形式幂级数的根本方法是利用泰勒展开定理,或马克劳林定理。
在定义域范围内,对上述形式幂级数再进行算术运算和解析运算,可以得到其它初等函数的形式幂级数。
我们在下文的目的,就是利用这种运算方法来求数列的通项公式。
6.3数列{}n a 及其前n 项和数列{}n S 的母函数关系定理1:记数列{}n a 的母函数为()x A ,则其n 项和数列{}n S 的母函数()()xx A x B -=1。
证明:∵ ()()∑∑∑∑+∞=-+∞=-+∞=--+∞=-++=++==21111211111n n n n n n n n n n n n n x a xS x a xa S a xSx B()()()()x A x xB a x A x xB a +=-++=11∴ ()()xx A x B -=1。
定理2:()()*121N n n n k nk ∈+=∑=。
证明:记数列{}n 的前n 项和为n S ,则数列{}n S 的母函数为()()∑∑∑∑+∞=-+∞=-+∞=--+∞=-++=++==21112111111n n n n n n n n n n n nx xS x xn S S xS x B()()()()22111111x x xB x x xB -+=--++=∴ ()()()()∑∑∞+=-∞+=--=⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-=-=22'11'2312121112111n n x n n x x n n nx x x x B ()∑+∞=-+=11121n n nx n 。
第二章 母函数及其应用问题:对于不尽相异元素的部分排列和组合,用第一章的方法是比较麻烦的(参见表2.0.1)。
新方法:母函数方法,问题将显得容易多了。
其次,在求解递推关系的解、整数分拆以及证明组合恒等式时,母函数方法是一种非常重要的手段。
表2.0.1 条件组合方案数排列方案数对应的集合相异元素,不重复()!!!r n r n C rn -⋅=()!!r n n P rn -={}n e e e S ,,, 21=相异元素,可重复rr n C 1-+rnS ={,,21e e ⋅∞⋅∞ne ⋅∞, }不尽相异元素(有限重复)特例r =n1 !!!!m n n n n 21S ={11e n ⋅,22e n ⋅,…,m m e n ⋅}, n 1+n 2+…+n m =nn k ≣1, (k =1,2,…, m )r =1mm所有n k ≣r rr m C 1-+rm至少有一个n k 满足1≢n k < r母函数方法的基本思想是把离散的数列同多项式或幂级数一一对应起来,从而把离散数列间的结合关系转化为多项式或幂级数之间的运算。
2.1 母 函 数(一)母函数(1)定义定义2.1.1 对于数列{}n a ,称无穷级数()∑∞=≡0n nnxax G 为该数列的(普通型)母函数,简称普母函数或母函数。
(2)例例2.1.1 有限数列C (n ,r ),r =0,1,2, …,n 的普母函数是()nx +1。
例2.1.2 无限数列{1,1,…,1,…}的普母函数是+++++=-nxx x x2111(3)说明● n a 可以为有限个或无限个; ● 数列{}n a 与母函数一一对应,即给定数列便得知它的母函数;反之,求得母函数则数列也随之而定;例如,无限数列{0,1,1,…,1,…}的普母函数是 +++++n x x x 20=xx-1● 这里将母函数只看作一个形式函数,目的是利用其有关运算性质完成计数问题,故不考虑“收敛问题”,而且始终认为它是可“逐项微分”和“逐项积分”的。
母函数和特征函数简介§1 母函数(生成函数)简介对于取值非负整数的随机变量,其母函数有极其良好的性质且又便于计算和分析,因此引入母函数是非常必要的。
母函数又称生成函数(Generating function)。
母函数的定义● 定义:对于数列}0,{≥n a n ,称幂级数)1(0≤∑∞=s sa n nn 为}0,{≥n a n 的母函数。
● 定义:设X 为取值于非负整数随机变量,分布率为 ,2,1,0,}{===k p x X P k k ,则称1)(?)(0≤==∑∞=s s p s E s g k kk X为随机变量X 的概率母函数,简称母函数。
一些常用分布的母函数(1)若).(~p n B X ,则n sp q s g )()(+=(2)若)(~λPo X ,则)1()(-=s e s g λ (3)若)(~p G X ,则qs pss g -=1)(母函数的基本性质(1)X 的母函数与其分布率是一一对应的,且有!)0()(k g p k k =(2)设非负整值随机变量n X X X ,,,21 相互独立,而n g g g ,,,21 分别是它们的母函数,则∑==nk kXY 1的母函数为:)()()()(21s g s g s g s g n Y =(3)设随机变量X 的母函数为)(s g ,则有:(a ))1()(g X E '=(b )2)]1([)1()1()()(g g g X Var X D '-'+''==母函数的应用(4)设n X X X ,,,21 独立同分布,且).1(~p B X i ,求∑==nk kXY 1的分布。
(5)设21,X X 独立,且2,1,).(~=i p n B X i i ,证明),(~2121p n n B X X ++。
(6)设21,X X 独立,且2,1,)(~=i Po X i i λ,证明)(~2121λλ++Po X X 。
1绪论母函数又可译为发生函数或生成函数.母函数方法是现代离散数学领域中的重要方法.它是联结离散数学与连续数学的桥梁.它是解决组合计数问题的一个重要工具之一.母函数方法是一种既简单又有用的数学方法,是一个古老方法.他源于De Moivre 在1720前后的工作,1748年欧拉在研究关于划分的问题中发展了这一方法.拉普拉期于18世纪末及19世纪初期对其进行了广泛的论述.其探究主要与概率论相关.尽管这一方法有其悠久的历史,但是正如我们将要看到的那样,这一方法有着广泛的应用.当代计算机科学家克努特(D.E.Knuth)在其名著《The art of computer programming,voll》中作了这样的论述:“…当运用母函数时,通常无需担心级数的收敛性,因为我们只是在探求得到某个问题的解的可能途径,一旦当我们用任何手段发现了解,尽管这些手段也许不严格,就有可能独立的验证这个解…例如有时很容易用数学归纳法来证明,我们甚至不必提到它是利用母函数发现的.此外,可以证明我们对母函数所做的绝大多数——如果不是所有的话——运算都能严格论证其可行而无须顾及级数的收敛性.”这段引文最后的断言是通过把母函数作为形式幂级数而得以实现的.一般情况下,母函数中的x只是一个抽象符号,并不需要对它赋予具体数值.因而不需要考虑它的收敛性.此时的变量x只是一种形式变元.对这种级数可以把它看成形式幂级数,可以按通常方式定义其加法、乘法、形式微分等运算,从而构成一个代数体系.母函数有多种类型,这里仅讨论最常见的两种:普通母函数和指数母函数.下面分别进行讨论.2母函数基本概念定义2.1. 对于数列{}0n n a ≥,称函数 120120()k k k f x a x a a x a x ≥==+++∑为数列{}0n n a ≥的普通型母函数(简称普母函数).定义2.2. 对于数列{}0n n a ≥,称函数120120()!1!2!k kk x x x f x a a a a k ≥==+++∑为数列{}0n n a ≥的指数型母函数(简称指母函数).数列与母函数可以互求.已知母函数,可求出其对应的数列;已知数列,可求出其对应的母函数.R 上的母函数的全体记为[]R x ⎡⎤⎣⎦.在集合[]R x ⎡⎤⎣⎦中适当定义加法和乘法运算,可使它成为一个整环,任何一个母函数都是这个环中的元素.定义2.3. 设0()kk k A x a x ∞==∑与0()k k k B x b x ∞==∑是R 上的两个母函数.若对任意0k ≥,有k k a b =.则称()A x 与()B x 相等.记作()()A x B x =.定义 2.4. 设α为任意实数. []0()kk k A x a x R x ∞=⎡⎤=∈⎣⎦∑,则()0()kk k A x a x αα∞==∑称作α与()A x 的数乘积.定义2.5. 设0()kk k A x a x ∞==∑与0()k k k B x b x ∞==∑是R 上的两个母函数.(1)将()A x 与()B x 相加定义为0()()()k k k k A x B x a b x ∞=+=+∑,并称()()A x B x +为()A x 与()B x 的和,把运算“+”称作加法.(2)将()A x 与()B x 相乘定义为01100()()()k k k k k A x B x a b a b a b x ∞-=⋅=+++∑,并称()()A x B x ⋅为()A x 与()B x 的积,把运算“⋅”称作乘法.3母函数的性质母函数与数列之间是一一对应的,因此,若两个母函数之间存在某种关系,那么相应的两个数列之间也必然存在一定的关系;反过来说当然也能成立.设数列{}0n n a ≥的母函数为()A x ,数列{}0n n b ≥的母函数为()B x ,我们可以得到下面的一些性质:性质3.1. 若0n n kn k b a n k-<⎧=⎨≥⎩ , 则 ()()k B x x A x =.证明: 由假设条件,有 21101211()k k k k k k B x b b x b x b x b x b x -+-+=+++++++11k k k k b x b x ++=++ 101k k a x a x +=++()01k x a a x =++()k x A x =.例3.1. 2()11!2!xx x A x e =+++= 且()B x 满足0n n kn k b a n k-<⎧=⎨≥⎩,则求()B x .解:利用性质1,()()k B x x A x =k x x e =⋅性质3.2. 若n n k b a +=,10()()k n k n n B x A x a x x -=⎡⎤=-⎢⎥⎣⎦∑.证明: 又假设条件,有2012()B x b b x b x =+++212k k k a a x a x ++=+++()12121k k k k k k k a x a x a x x ++++=+++ ()10111()k k k A x a a x a x x--=----10()k n k n n A x a x x -=⎡⎤=-⎢⎥⎣⎦∑.例3.2. 35()sin 3!5!x x A x x x ==+++,且6k k b a +=,求()B x .解: 6160()()n n n B x A x a x x -=⎡⎤=-⎢⎥⎣⎦∑356()3!5!x x A x x x ⎡⎤=---⎢⎥⎣⎦.性质3.3. 若0nn k k b a ==∑,则()()1A x B x x=-. 证明: 有假设条件,有 00b a =, 101b x a x a x =+, 22222012b x a x a x a x =++, …,012n n n n n n n b x a x a x a x a x =++++…, 把以上两边分别相加,得2222012()(1)(1)(1)B x a x x a x x x a x x x =++++++++++++22012()(1)a a x a x x x =++++++()1A x x=-. 例3.3. 21()11A x x x x =+++=- ,且0nn k k b a ==∑,则 ()2()1()11A x B x x x ==-- . 性质3.4. 若n k k nb a ∞==∑,则(1)()()1A xA x B x x -=-.这里0k n a ≥∑是收敛的.证明: 因为0k n a ≥∑是收敛的,所以n k k nb a ∞==∑是存在的.于是有0012(1)b a a a A =+++= 1120[(1)]b x a x a x A a x =++=-, 222222301[(1)]b x a x a x A a a x =++=--,…, 1011[(1)]k k k k k k k k b x a x a x A a a a x +-=++=----,….把以上各式的两边分别相加,得0()(1)[(1)]B x A A a x =+-201[(1)]A a a x +--+01[(1)]k k A a a x -+--+2(1)(1)A x x =+++20(1)a x x x -+++221(1)a x x x -+++- 21(1)k k a x x x --+++-2012[(1)()]A x a a x a x =-+++2(1)x x +++(1)()1A xA x x-=-.性质3.5. 若n n na b =, 则'()()B x xA x =.证明: 由'()A x 的定义知'11()n n n na xxA x x ∞-==∑0n n n na x ∞==∑n n n b x ∞==∑()B x =.例3.4. 已知21()11A x x x x =+++=- ,n n na b =,则()21()11x B x x x x '⎛⎫== ⎪-⎝⎭-. 性质3.6. 若1nn a b n =+, 则1()()xB x A t dt x =⎰.证明: 由假设条件,有0()xxn n n A t dt a t dt ∞==∑⎰⎰(1)xn n n b n t dt ∞==+∑⎰1n n n b x ∞+==∑=()xB x .性质3.7. 若0112200nn n n n n k n k k c a b a b a b a b a b ---==++++=∑.则2012()()()C x c c x c x A x B x =+++=证: 000c a b =()10110c x a b a b x =+ ()222021120c x a b a b a b x =++ …()()()2222001210122012()c x a b b x b x a x bb x b x a x bb x b x =++++++++++++()()22012012a a x a x bb x b x =++++++()()A x B x =.例3.5. 已知21()11n A x x x x x=+++++=- ()22()21n xB x x x nx x =++++=-()11232n n n c n +=++++=则 ()3()1xG x x =-.性质3.8. 若k k k c a b αβ=+ ,则()()()0k k k c x c x A x B x αβ∞===+∑.证明:有假设条件,有()()00kkk k k k k c x c x a b x αβ∞∞====+∑∑0kk k k k k a x b x αβ∞∞===+∑∑kk k k k k a x b x αβ∞∞===+∑∑()()A x B x αβ=+.4性质的应用利用这些性质,可以求某些数列的母函数,也可以计算数列的和.下面列出几个常见的简单数列的母函数.(1) {}111G x=- (2) {}11k G a ak=-(3) {}()21xG k x =-(4) (){}()3211xG k k x +=-(5) {}()()2311x x G k x +=-(6) ()(){}()46121xG k k k x ++=-(7) 1!x G e k ⎧⎫=⎨⎬⎩⎭(8) ()1aa G x k ⎧⎫⎛⎫=+⎨⎬ ⎪⎝⎭⎩⎭(9) ()111n n k G k x +⎧+⎫⎛⎫=⎨⎬ ⎪-⎝⎭⎩⎭ 例4.1.求序列{}5,6,7,,5,n +的母函数.解:()()25675n A x x x n x =++++++()()2235123x x x xx =+++++++(){}51G G k =+ ()()221545111x xx x x -=⋅+=---. 母函数的应用很多.求解递推关系,排列组合中,计数问题中的应用等等.利用母函数的性质,可以求某些数列的母函数,也可以计算数列的和.结束语母函数又称生成函数,是一种即简单又有用的数学方法,求解递推关系和组合计数问题中母函数是一种重要的数学方法.用母函数可以求解常系数线性齐次、非齐次递推关系、求解非线性递推关系、非常系数递推关系等等递推关系.这篇文章给出了母函数的基本知识,从最基本点开始讨论了母函数的性质.利用母函数的性质,可以求某些数列的母函数,也可以计算数列的和.参考文献【1】卢开澄,卢华明. 组合数学(第四版).北京:清华大学出版社,2006,12.【2】田秋成等编著. 组合数学. 电子工业出版社,2006,11.【3】李凡长,康宇,董海峰,段爱华编著.组合理论及其应用. 北京:清华大学出版社,2005,9.【4】冯速译. 应用组合学. 拉特格大学狄克森学院:机械工业出版社,2007,5.【5】李乔.组合学讲义(第二版).北京:高等教育出版社,2008,1.【6】孙淑玲许胤龙编著.组合数学引论.中国科学技术大学出版社,2004,1.【7】孙世新张先迪编著.组合原理及其应用.北京:国防工业出版社,2006,3.。