当前位置：文档之家 › 第2.4区间估计

第2.4区间估计

  • 格式：pdf
  • 大小：818.40 KB
  • 文档页数：56

下载文档原格式

  / 56

合集下载

第2节 区间估计

第2节 区间估计


2
~ (n 1)
2
在给定的置信度1 下,由
P{12 2 (n 1) 2 22 (n 1)} 1
得
2 的置信区间为:
2 (n 1) S 2 (n 1) S , 2 2 (n 1) 1 (n 1) 2 2
即 P X u X u 1 n 2 n 2 置信度为1 的置信区间是 ( X u , X u )
n
2
n
2
例1 包糖机某日开工包了12包糖,称得重量(单 位:克)分别为506,500,495,488,504,486,505,
2 ( n 1) S n 11 0.04 2 0.0224 2 (n 1) 19.675
故所求置信区间为: (0.0224, 0.0962)
二、两个正态总体均值差与方差比的置信区间 1、二总体均值差
1 2 的区间估计
2 X ~ N ( 1 , 12 ), Y ~ N ( 2 , 2 ) 设两总体
n2
n2
Yi 2
2
) 2 ~ 2 ( n2 )
1 故F

1
2 1 i 1 n2
(X
i
n1
i
1 )
2
2
n1 ~F (n1 , n2 ) n2
( , ) 即是 的置信度为 1 的置信区间
正态总体参数的区间估计
一、单总体均值与方差的区间估计
二、双总体均值差与方差比的区间估计
三、小结
一、单正态总体均值与方差的区间估计 1.单总体均值 的置信区间 X ~ N ( , 2 ), 2 已知时 (1)设

区间估计知识点总结

区间估计知识点总结

区间估计知识点总结区间估计的基本概念区间估计是一种用来估计参数未知真值范围的统计方法。

在假设条件下，利用样本的信息来推断总体参数，并给出一个区间，该区间包含了总体参数真值的一个估计范围。

例如，我们可以用区间估计的方法来估计总体均值、方差、比例等参数的取值范围。

区间估计的优点与点估计相比，区间估计有以下几个优点：1. 提供了参数真值的估计范围，更具有实际应用的意义。

点估计只给出了一个具体的数值，而区间估计可以反映出参数的不确定性。

2. 能够控制估计的置信水平。

在区间估计中，我们可以通过置信水平来控制估计的精度和可靠性，这使得我们可以根据需求来选择合适的置信水平。

区间估计的步骤区间估计的步骤一般包括以下几个方面：1. 确定总体分布类型。

在进行区间估计之前，我们需要对总体的分布类型进行研究，以确定区间估计的方法和技巧。

2. 挑选合适的估计方法。

不同类型的参数估计需要采用不同的估计方法，如均值的区间估计可以使用t分布、z分布或者Bootstrap方法。

因此，在进行区间估计时，需要挑选合适的估计方法。

3. 计算置信区间。

根据所选的估计方法和数据样本，我们可以计算出置信区间的上下限，从而得到参数的估计范围。

区间估计的常用方法在统计学中，常用的区间估计方法有以下几种：1. 正态分布的区间估计。

当总体服从正态分布时，我们可以使用z分布来进行参数估计。

例如，对正态总体的均值进行区间估计时，我们可以使用z分布的方法来计算置信区间。

2. t分布的区间估计。

当总体服从t分布时，我们可以使用t分布来进行参数估计。

常见的例子包括小样本的均值估计和相关系数的区间估计。

3. Bootstrap方法。

Bootstrap方法是一种非参数估计方法，它通过对原始样本进行重抽样，得到估计量的抽样分布，从而计算出参数的置信区间。

区间估计的应用区间估计作为统计推断的重要方法，在各个领域都有着广泛的应用。

在医学、社会科学、经济学和工程学等领域中，人们常常需要对总体参数进行估计，在这些领域中，区间估计可以提供参数估计的可靠性和精度，为决策提供支持。

区间估计公式正态总体二项总体与泊松总体的区间估计公式

区间估计公式正态总体二项总体与泊松总体的区间估计公式

区间估计公式正态总体二项总体与泊松总体的区间估计公式区间估计公式是统计学中常用的方法，用于估计总体参数的范围。

在正态总体、二项总体和泊松总体中，也存在相应的区间估计公式。

本文将分别介绍这三个总体的区间估计公式。

一、正态总体的区间估计公式在正态总体中，我们通常关注总体均值的估计。

假设样本容量为n，样本均值为x，总体标准差为σ。

若总体标准差已知，则总体均值的区间估计公式为：[公式1]其中zα/2是正态分布的分位数，代表了α/2的上分位数。

例如，若置信水平为95%，则α为0.05，z0.025为1.96。

若总体标准差未知，则总体均值的区间估计公式为：[公式2]其中s是样本标准差，tα/2是自由度为n-1的t分布的上分位数。

与正态分布不同，t分布考虑了样本容量的影响。

二、二项总体的区间估计公式在二项总体中，我们通常关注总体比例的估计。

假设样本容量为n，成功次数为x，总体成功率为p。

总体比例的区间估计公式为：[公式3]其中zα/2为正态分布的分位数，p为样本比例，n为样本容量。

三、泊松总体的区间估计公式在泊松总体中，我们关注总体平均到达率的估计。

假设样本容量为n，观测到的平均到达率为x。

总体平均到达率的区间估计公式为：[公式4]其中zα/2为正态分布的分位数，λ̂为样本平均到达率，n为样本容量。

以上是正态总体、二项总体和泊松总体的区间估计公式。

根据不同的总体类型和参数类型，选择合适的公式进行区间估计。

这些公式可以帮助我们对总体参数进行估计，并提供了对估计结果的置信区间，从而更好地理解总体特征。

在实际应用中，我们可以根据采样数据和问题背景选择适合的区间估计方法，得出有意义的结论。

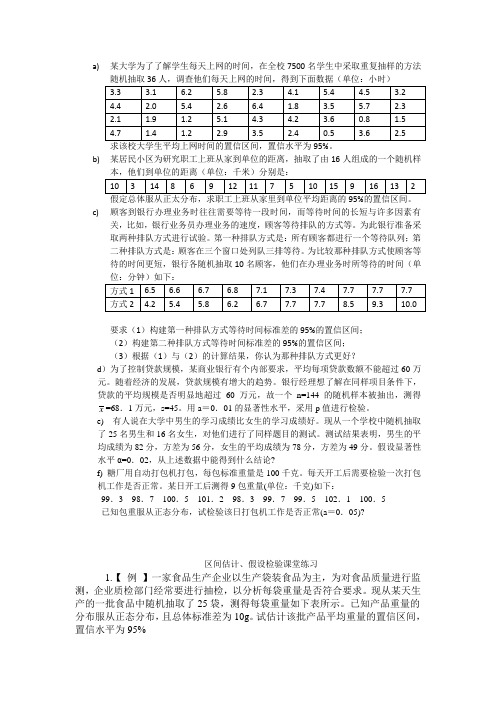
区间估计、假设检验练习题

区间估计、假设检验练习题

a)某大学为了了解学生每天上网的时间，在全校7500名学生中采取重复抽样的方法求该校大学生平均上网时间的置信区间，置信水平为95%。

b)某居民小区为研究职工上班从家到单位的距离，抽取了由16人组成的一个随机样本，他们到单位的距离（单位：千米）分别是：假定总体服从正太分布，求职工上班从家里到单位平均距离的95%的置信区间。

c)顾客到银行办理业务时往往需要等待一段时间，而等待时间的长短与许多因素有关，比如，银行业务员办理业务的速度，顾客等待排队的方式等。

为此银行准备采取两种排队方式进行试验。

第一种排队方式是：所有顾客都进行一个等待队列；第二种排队方式是：顾客在三个窗口处列队三排等待。

为比较那种排队方式使顾客等待的时间更短，银行各随机抽取10名顾客，他们在办理业务时所等待的时间（单要求（1）构建第一种排队方式等待时间标准差的95%的置信区间；（2）构建第二种排队方式等待时间标准差的95%的置信区间；（3）根据（1）与（2）的计算结果，你认为那种排队方式更好？d）为了控制贷款规模，某商业银行有个内部要求，平均每项贷款数额不能超过60万元。

随着经济的发展，贷款规模有增大的趋势。

银行经理想了解在同样项目条件下，贷款的平均规模是否明显地超过60万元，故一个n=144的随机样本被抽出，测得x=68．1万元，s=45。

用a＝0．01的显著性水平，采用p值进行检验。

e) 有人说在大学中男生的学习成绩比女生的学习成绩好。

现从一个学校中随机抽取了25名男生和16名女生，对他们进行了同样题目的测试。

测试结果表明，男生的平均成绩为82分，方差为56分，女生的平均成绩为78分，方差为49分。

假设显著性水平α=0．02，从上述数据中能得到什么结论?f) 糖厂用自动打包机打包，每包标准重量是100千克。

每天开工后需要检验一次打包机工作是否正常。

某日开工后测得9包重量(单位：千克)如下：99．3 98．7 100．5 101．2 98．3 99．7 99．5 102．1 100．5已知包重服从正态分布，试检验该日打包机工作是否正常(a＝0．05)?区间估计、假设检验课堂练习1.【例】一家食品生产企业以生产袋装食品为主，为对食品质量进行监测，企业质检部门经常要进行抽检，以分析每袋重量是否符合要求。

第2章-总体特征数的点估计与区间估计

第2章-总体特征数的点估计与区间估计

( x − y ) − ( µ1 − µ 2 ) ( n1 − 1) s1 + (n 2 − 1) s 2 n1 + n 2 − 2
2 2
∼ t(n1+ n2 –2)
（2-11） ）
1 1 + n1 n 2
服从 n1+ n2–2 个自由度的 t 分布。 分布。 其中 s12， 22 分别是这两个样本{x1, x2, …, xn} s 分别是这两个样本 的样本方差。 的样本容量。 和 {y1, y2, …, yn}的样本方差。n1、n2 分别表示总体 xi 和 yi 的样本容量。 的样本方差
2.2 几种统计量的抽样分布 统计量： 称作统计量。 统计量：样本 {x1 ，x2，…, x n} 的函数 f (x1, x2, …, xn) 称作统计量。 2.2.1 样本平均数 x 的抽样分布
1 若样本用{x 表示， 计算公式是 若样本用 1 ，x2，…, x n}表示，已知样本平均数 x 的计算公式是 x = 表示 n
x−µ
σ2
n
) 。把 x 标准化为 Z， 标准化为 ，
σ/ n
分布。 ∼ N(0, 1) , Z 渐近服从 N(0, 1)分布。 分布
2.4 2.0 1.6 1.2 T=200
总体中抽样， 从χ2(3)总体中抽样，随着样本容量加大， 0.8 总体中抽样 随着样本容量加大， T=4, 15, 200，样本平均数的分布越来 ， 越近似正态分布。 越近似正态分布。 File：central-limit-1 ： File： 5 central1 。 ：
2.2.4 统计量 F 的抽样分布 相互独立， 定理 3：若 xi ∼ χ2(n1)，yi ∼ χ2(n2), 且 xi 与 yi 相互独立，则统计量 ： ， F=

应用数理统计_3版(孙荣恒编著)PPT模板

应用数理统计_3版(孙荣恒编著)PPT模板

4.3.1正交表
3
4.3.2正交表的分析
2
§4.2*双因素方差分析
4.2.1数学模型 4.2.2方差分析
4
习题四
第五章线性回归模型
第五章线性回归模 型
§5.1线性模型 §5.2最小二乘法估计 §5.3检验、预测与控制 §5.4带有线性约束的线性回归模型 习题五
第五章线性回归模型
§5.2最小二乘法估计
5.2.1β的最小二乘 法估计
5.2.2最小二乘法估 计量的性质
5.2.3例子
第五章线性回归模型
§5.3检验、预测与控制
5.3.1线性 模型与回归 系数的检验
5.3.2预测 与控制
第五章线性回 归模型
§5.4带有线性约束的线性回归模 型
5.4.2βH的 性质
5.4.1拉格 朗日乘子法
5.4.3对假设 H0:Hβ=d的 检验
计
0 5
2.5.5先验分布
的选取
0 6
2.5.6最大后验
估计
第二章参数估计
§2.5贝叶斯(Bayes)估计
02
2.5.8离散型分布 中参数的贝叶斯估
计与极大似然估计
01
2.5.7贝叶斯区间
估计
第二章参数估计
§2.6截尾寿命试验中指数分布和几何分布的参数估计
A
2.6.1指数 分布中参 数的点估
计
B
§1.2多元 正态分布 与正态二
次型
§1.3抽 样分布
定理
§1.4分 位数
习题一
第二章参数估计
第二章参 数估计
0 1
§2.1点估计常用 方法
0 2
§2.2评价估计量 好坏的标准

区间估计思想

区间估计的思想1.用样本的估计量的某个取值直接作为总体参数的估计值例如：用样本均值直接作为总体均值的估计；用两个样本均值之差直接作为总体均值之差的估计2.无法给出估计值接近总体参数程度的信息–由于样本是随机的，抽出一个具体的样本得到的估计值很可能不同于总体真值–一个点估计量的可靠性是由它的抽样标准误差来衡量的，这表明一个具体的点估计值无法给出估计的可靠性的度量区间估计(interval estimate)1.在点估计的基础上，给出总体参数估计的一个区间范围，该区间由样本统计量加减估计误差而得到2.根据样本统计量的抽样分布能够对样本统计量与总体参数的接近程度给出一个概率度量比如，某班级平均分数在75～85之间，置信水平是95%样本统计量(点估计)置信区间置信下限置信上限x95%-1.96x+1.96x-2.58x+2.58x90%的样本-1.65x+1.65xxσxzxσμα2±=已知总体服从正态分布ሻX~N(μ,σ2，若从总体中抽取一个容量为n 的样本，则样本均值x 的抽样分布为ቁx~N(μ,σ2n，对其进行标准化，得到：~(0,1)x Z N μ-=则在1-α的置信度下，上式可写成：即在1-α的置信度下的置信区间为2()1x P Z αμα-≤=-22()1P x Z x Z αασσμα-≤≤+=-22(,x Z x Z αασσ-+例：一家食品生产企业以生产袋装食品为主，为对食品质量进行监测，企业质检部门经常要进行抽检，以分析每袋重量是否符合要求。

现从某天生产的一批食品中随机抽取了25袋，测得每袋重量如下表所示。

已知产品重量的分布服从正态分布，且总体标准差为10g。

试估计该批产品平均重量的置信区间，置信水平为95%。

解：已知Ｘ~N (μ，102)，n =25,1-α=95%，z α/2=1.96根据样本数据计算得:ഥx=105.36由于原总体是正态总体，且方差已知，故总体均值μ在1-α置信水平下的置信区间为2x z nασ±10105.36 1.96105.36 3.9225=±⨯=±()101.44,109.28=谢谢观看。

数理统计课件 2.4.1--2.4.3区间估计

12.4 区间估计一、 区间估计的概念参数的点估计是用θ的一个估计值),,(ˆ1n x x θ估计未知参数θ.优点： 简便、直观缺点：没有反映估计的精确度，也未给出估计值的偏差范围。

为了弥补点估计的不足，可采用另一种估计方式—－区间估计。

定义2.11. 设总体X 的分布函数为θθ),,(x F 为未知参数，),,,(21n X X X 是来自总体X 的样本。

如果存在两个统计量),,,(ˆˆ2111n X X X θθ=,),,,(ˆˆ2122n X X X θθ=，对于给定的(01)αα<<，使得αθθθ−=<<1}ˆˆ{21P (2.33) 则称区间(1ˆθ,2ˆθ)为参数θ的置信度为α−1的置信区间，1ˆθ称为置信下限，2ˆθ称为置信上限。

所谓θ的区间估计，就是要在给定α值的前提下，去寻找两个统计量1ˆθ和2ˆθ，使其满足式(2.33)。

如何寻找θ的置信区间？2下面给出寻求未知参数θ的置信区间的一般步骤： 寻求未知参数θ的置信区间的一般步骤：(1). 设法找到一个包含样本1(,,)n X X …和待估参数θ的函数12(,,,;)n U U X X X θ= ，除θ外U 不含其他未知参数，U 的分布可求出且与θ无关； (2). 对于给定的置信度α−1,由等式{}1P c U d α<<=−适当地确定两个常数c, d ；(3). 求解不等式 12(,,,;)n c U d θ<ΧΧΧ<得 1ˆθ12212ˆ(,,,)(,,,)n n θθΧΧΧ<<ΧΧΧ 从而有1ˆ{P θ12212ˆ(,,,)(,,,)}1n nθθαΧΧΧ<<ΧΧΧ=− 故（1ˆθ,2ˆθ）就是所求的置信区间。

二、数学期望的置信区间1、已知DX ，求EX 的置信区间设总体X 服从正态分布N(µ,2σ)，其中2σ已知。

现求总体均值µ的置信区间.设12,,,n ΧΧΧ 是来自总体X 的样本，自然用X 对µ作为点估计，因为，2(,)nN σµΧ∼故3X U =由正态分布表（附表1）可知，对于给定的α，存在一个值2u α，使得 2{||}1P U u αα<=−这里2u α是标准正态分布的α/2上侧分位数。

西安交大西工大 考研备考期末复习概率论与数理统计 区间估计

且标准差为 10, 试求糖包的平均重量 的1 置信区间(分别取 0.10 和 0.05).
解 10, n 12,
计算得 x 502.92,
(1) 当 0.10时, 1 0.95,
2 查表得 u / 2 u0.05 1.645,
x
n u / 2
502.92
10 1.645 498.17, 12
E(ˆ ) 为估计量 ˆ 的偏差。
例1 设总体 X 的k 阶矩k E( X k ) (k 1)存在,
又设 X1, X2 ,, Xn 是 X 的一个样本，试证明不论
总体服从什么分布, k 阶样本矩
Ak
1 n
n i 1
X
k i
是
k 阶总体矩k的无偏估计.
证 因为 X1, X2 ,, Xn 与 X 同分布，
则 称 随 机 区 间[ˆ1,ˆ2 ]是 的 置 信 度 为1 的 置 信 区 间,ˆ1和ˆ2分 别 称 为 置 信 度 为1 的 双 侧 置 信 区 间 的置 信下 限和 置信 上限, 1 为置 信度.
关于定义的说明
被估计的参数虽然未知, 但它是一个常数, 没有随机性, 而区间[ˆ1,ˆ2 ]是随机的.
例5 若总体 X 的 E( X ) 和D( X ) 存在,则样
本均值 X 是总体均值的相合估计.
解：E( X ) E( X )
D( X )
lim D( X ) lim
0
n
n n
一般地,样本的 k 阶原点矩
Ak
1 n
n
X
k i
i 1
是总体 X
的 k 阶原点矩 E(X k ) 的相合估计.由此可见,矩
由 P(-1.75≤U≤2.33)=0.95

2.4 正态总体参数的区间估计


解： 这是两个正态总体参数比较问题，从 两方面比较：均值差异、方差差异，但均 值差异比较必须知道方差有无差异，因此 在两总体方差未知的情况下，先看方差有 无差异，无差异后进行均值差异估计。
2 2 设 X A ~ N ( µ A ,σ A ), X B ~ N ( µ B ,σ B ) ，
2 2 x A = 120, S A = 445.82, x B = 101, S B = 425.33
2 SA = 1.048, F0.05 (11,6) = 5.37, F 0.05 (11,6) = 0.258 2 1− SB 2 2
2 σA = 2 σ B 的 95%置信区间是[0.195,4.07]，
其中包含有“1” ，可以认为 σ = σ
2 A
2 B
1 1 + ) n1 n2
代入
2 (n1 − 1) S12 + (n2 − 1) S 2 ( X 1 − X 2 ± t α (n1 + n2 − 2) n1 + n2 − 2 2
≤ µ1 − µ2 ≤ X1 − X 2 + zα
2
2 σ12 σ 2
n1
+
n2
} = 1− α
( X 1 − X 2 ± zα
2
σ 12
n1
+
2 σ2
n2
)
2 σ 12 = σ 2 = σ 2 未知时 2）当
X 1 − X 2 − ( µ1 − µ 2 ) ( n1 − 1) S + ( n2 − 1) S n1 + n2 − 2
2.4.2 两个正态总体方差比的区间估计
由于 于是对于给定 α
P{F
1−
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
ˆ , ˆ 那么 [ 1 2 ] 就是 的一个置信度为1 的置信区间.
二、正态总体数学期望的置信区间
设给定置信度为 1 , 并设 (X 1 , X 2 , 和修正样本方差.
(1) 2为已知, 求 的置信区间
选取X 作为的估计，又因为 X N (,
, X n )T
*2 为总体 N ( , 2 )的样本, X , S n 分别是样本均值
2
3 查表可确定 t ( n 1).
2
t (n 1)
2
t (n 1)
2
4° 作等价变形
T t ( n 1)
2
X t ( n 1) 2 Sn / n


X t ( n 1) 2 Sn / n
Sn Sn X t ( n 1) X t ( n 1) n 2 n 2
查 t ( n 1) 分布表可知 : t0.025 (11) 2.201,
* sn 12.35 于是 t / 2 ( n 1) 2.201 7.85, n 12
得的置信度为95%的置信区间 [495.07, 510.77].
三、正态总体方差的区间估计
根据实际需要, 只介绍 未知的情况.
n
注 置信区间不唯一，但上述结论区间长度最小
例1 包糖机某日开工包了12 包糖,称得重量(单位: 克)分别为506, 500, 495, 488, 504, 486, 505,
513, 521, 520, 512, 485. 假设重量服从正态分布, 且标准差为 10, 试求糖包的平均重量 的 1
2 n 1 1 1 2 n
ˆ ˆ (X , X , 2 2 1 2
, X n ) 满足 ˆ ˆ } 1 , P{ 1 2
ˆ, ˆ ]是 的置信度为1 的置信区 则称随机区间[ 1 2 ˆ和 ˆ 分别称为置信度为1 的双侧置信区间 间,
1 2
x

n
u / 2
10 502.92 1.645 507.67, 12
即 的置信度为90% 的置信区间为
[498.17, 507.67].
( 2) 当 0.05 时, 1

2
0.975,
查表得
u / 2 u0.025 1.96,
同理可得的置信度为95%的置信区间为
2
n
),
1 取

X U ~ N (0,1), / n
2 给定，要求：
P U u / 2
2 2
1,

2
( u ) ( u ) 1 , 2( u ) 1 1 , ( u ) 1
2
,
2
3 查表可确定 u .
的置信度为1 的置信区间 Sn Sn [X t ( n 1)，X t ( n 1)]， n 2 n 2
* 简写成 X S n t ( n 1) . /2 n
例2 有一大批糖果,现从中随机地取16袋, 称得重 量(克)如下: 506 508 499 503 504 510 497 512
区间估计解决了上述问题，从而克服了点估 计的不足之处.
2. 置信区间与置信度
定义2.11 设总体 X 的分布函数 F ( x; ) 含有一个 未知参数 , 对于给定值 (0 1), 若由样本X 1 , ˆ ˆ (X , X , , X )和 X , , X 确定的两个统计量
. 2 1 / 2 ( n 1)
* n 1S n
注 此置信区间长度并非最短 注意: 在密度函数不对称时,
如 2 分布和 F分布, 习惯上仍取对称的分位点
来确定置信区间(如图).
例4 (续例2) 求例2中总体标准差的置信度为0.95 的置信区间. 解

2
0.025,
[497.26, 508.58].
从此例可以看出 , 当置信度1 较大时, 置信区间也较大 ; 当置信度1 较小时, 置信区间也较小.
( 2) 为未知, 求 的置信区间
2
1 取

X T ~ t ( n 1), Sn / n
2 给定，要求：
P T t ( n 1) 1 ,
6.2022 其误差不大于 2 .1315 .1315 2 6,.61 (克). t (15) t0.025 (15 )2 16 2 这个误差的可信度为 95%. x 503.75 , sn 6.2022,
例3 (续例1)如果只假设糖包的重量服从正态分布
N ( , 2 ), 试求糖包重量 的 95% 的置信区间. * S n 此时 未知 , n 12 , 解 X t ( n 1 ) . / 2 n * 0.05, x 502.92, sn 12.35,
置信区间 (分别取 0.10 和 0.05).
解
10, n 12,

0.95,
计算得 x 502.92,
2 查表得 u / 2 u0.05 1.645,
(1) 当 0.10时, 1
x

u / 2 502.92 10 1.645 498.17, n 12
ˆ 与参数真值 不足之处：未给出估计值量 0 的误差及估计的可靠程度.
例如
E ( X ) ，
ˆ x — 样本均值的观察值
问： 误差 x 多大？
用 X 估计 的可靠程度如何？
即 给定： 0 1
使 P{ X } 1
很小 较大
中的 ？
方差 2的置信度为 1 的置信区间
*2 ( n 1) S * 2 ( n 1) S n n , 2 . 2 / 2 ( n 1) 1 / 2 ( n 1)
推导过程如下:
因为 S 是 2 的无偏估计,
根据第1章第三节定理1.12可知
于是得方差 的置信度为1 的置信区间
2
*2 ( n 1) S * 2 ( n 1) S n n , 2 . 2 / 2 ( n 1) 1 / 2 ( n 1)
进一步可得: 标准差 的一个置信度为1 的置信区间
* n 1 S n , 2 ( n 1) /2
sn
6.2022,
得 的置信度为95% 的置信区间
6.2022 503 . 75 2 . 1315 即 [500.4, 507.1]. 16
就是说估计袋装糖果重量的均值在500.4克与
507.1克之间, 这个估计的可信程度为95%.
* S n X t ( n 1 ) ，n 16 , 若依此区间内任一值作 为 的近似值 / 2 n
第2.4节
区间估计
一、区间估计的概念
二、正态总体数学期望的置信区间
三、正态总体方差的区间估计
四、两个正态总体均值差的区间估计
五、两个正态总体方差比的区间估计 六、单侧置信区间 七、非正态总体参数的区间估计
一、区间估计基本概念
1. 问题的提出
ˆ 来估计参数， 点估计法： 找一个统计量
ˆ ( ˆ 的观察值) 0
其中仅包含待估参数 , 并且u的分布已知 且不依赖于任何未知参数(包括 ).
2 对于给定的置信度1 , 定出两个常数 c, d , 使 P{c u( X 1 , X 2 , , X n ; ) d } 1 .
3° 求解不等式
ˆ ˆ, a u( X 1 , X 2 , , X n ; ) b 1 2 ˆ ˆ ( X , X , , X ), ˆ ˆ (X , X , , X ) 其中 1 1 1 2 n 2 2 1 2 n
ˆ , ˆ ]. 而不能说参数以 1 的概率落入随机区间[ 1 2
另外定义中的表达式 ˆ ˆ } 1 P{ 1 2 还可以描述为:
若反复抽样多次(各次得到的样本容量相等,都是n) ˆ , ˆ ], 每个样本值确定一个区 间 [
1 2
每个这样的区间或包含 的真值或不包含 的真值,
514 505 493 496 506 502 509 496
设袋装糖果的重量服从正态分布, 试求总体均值
的置信度为0.95 的置信区间.
解
0.05, n 1 15,
2
查 t ( n 1) 分布表可知 : t (15) t0.025 (15) 2.1315,
计算得 x 503.75,
只依赖于样本的界限(构造统计量)
ˆ1 ˆ1 (X1,…Xn) ˆ2 ˆ2 (X1,…Xn)
内. 这里有两个要求:
(ˆ1 ˆ2 )
ˆ ,ˆ ] 一旦有了样本，就把 估计在区间 [ 1 2
ˆ ,ˆ ] 1. 要求 以很大的可能被包含在区间 [ 1 2 ˆ ˆ } 要尽可能大. 内，就是说，概率P{ 1 2 即要求估计尽量可靠.
* n 1 S n , 2 ( n 1) /2
2. 估计的精度要尽可能的高. 如要求区间 长度 ˆ2 ˆ1 尽可能短，或能体现该要求的其 它准则. 可靠度与精度是一对矛盾，一般是在
保证可靠度的条件下尽可能提高精度.
3. 求置信区间的一般步骤(共3步)
1 寻求一个样本 X 1 , X 2 , u u( X 1 , X 2 , , X ) S
2
*2 n
~ 2 ( n 1),
*2 ( n 1) S n 2 2 则 P 1 / 2 ( n 1) / 2 ( n 1) 1 , 2 *2 *2 ( n 1) S n ( n 1) S n 2 即 P 2 2 1 , 1 / 2 ( n 1) / 2 ( n 1)