电子科技大学DSP课件
- 格式:ppt
- 大小:609.00 KB
- 文档页数:35

第 1章DSP 概念绪论结构 特点DSP原理 理及应用I电子信 信息工程TI的 DSP设计 流程CCS 软件1第 1章DSP 概念绪论正在学习:DSP概念¾DSP概念:① Digital Signal Processin ng 数字信号处理(理论 论和方法) ② Digital Signal Processor 数字信号处理器(实现数字信号处理的微处理器 实 )结构 特点TI的 DSPx’(t) x (t) 放大器x(t)抗混叠 滤波器 输入通道ADCx(n)其它数字系统设计 流程DSP硬件 输出通道CCS 软件放大器 重建 y(t) 滤波器 y’(t y (t) DAC y(n) 其它数字系统 2第 1章DSP 概念绪论正在学习:DSP概念结构 特点¾微处理器发展的几个 个方向: ① 通用CPU ② 微控制器MCU/AR RM ③ DSP处理器 ④ FPGATI的 DSP设计 流程CCS 软件3第 1章DSP 概念绪论正在学习:DSP结构¾ DSP处理器结构特点 ①采用哈佛结构 ②采用多总线结构 ②采用多 线结构 ③采用硬件乘累加(MAC)单元 单 ④采用流水线技术 ⑤采用特殊的程序控制方式 式(如零开销循环) ⑥采用特殊的寻址方式(如 如循环寻址、位倒序寻址)和高效的特 殊指令 ⑦采用丰富的片内外设结构 特点TI的 DSP设计 流程CCS 软件4第 1章DSP 概念绪论正在学习:DSP结构①采用哈佛结构地 地址总线结构 特点冯诺依曼结构存储器: 数据和指令CPU数据 据总线TI的 DSP哈佛结构程序存储器: 仅存放指令地 地址总线地址总线CPU程序 序总线 数据总线数据存储器: 仅存放数据设计 流程改进的哈佛结构CCS 软件地 程序存储器: 地址总线 存放指令和 数据 程序 序总线地址总线CPU缓存 数据总线数据存储器: 仅存放数据5第 1章DSP 概念 取指 结构 特点绪论正在学习:DSP结构②采用流水技术译码 取指 寻址 译码 取指 取数 寻址 译码 取指 第五级流水 运算 算 取数 数 寻址 址 译码 码 取指 指 存储 运算 取数 寻址 译码 取指 第一级流水 存储 运算 取数 寻址 译码 第二级流水 存储 运算 取数 寻址 第三级流水 存储 运算 取数 第四级流水 存储 运算 存储TI的 DSP设计 流程第六级流水 水综合来看 每条指令都是在 综合来看,每条指令都是在 在 个指令周期内执行的。

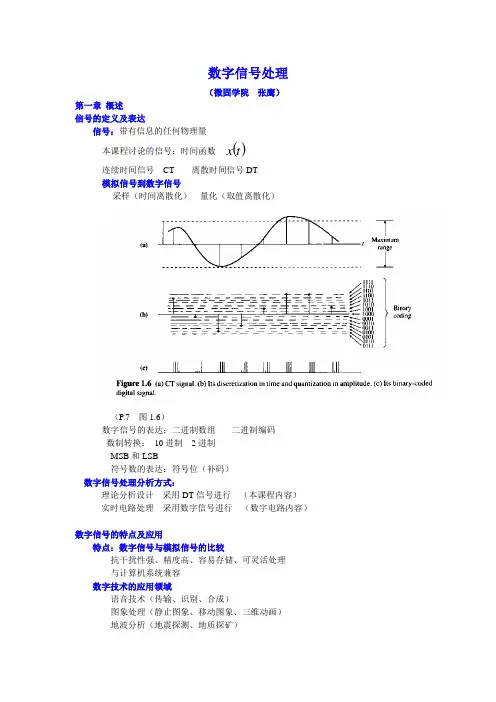
数字信号处理(微固学院张鹰)第一章概述信号的定义及表达信号:带有信息的任何物理量本课程讨论的信号:时间函数()t x连续时间信号CT 离散时间信号DT模拟信号到数字信号采样(时间离散化)量化(取值离散化)(P.7 图1.6)数字信号的表达:二进制数组----二进制编码数制转换:10进制---2进制MSB和LSB符号数的表达:符号位(补码)数字信号处理分析方式:理论分析设计采用DT信号进行(本课程内容)实时电路处理采用数字信号进行(数字电路内容)数字信号的特点及应用特点:数字信号与模拟信号的比较抗干扰性强、精度高、容易存储、可灵活处理与计算机系统兼容数字技术的应用领域语音技术(传输、识别、合成)图象处理(静止图象、移动图象、三维动画)地波分析(地震探测、地质探矿)谐振分析(高层建筑、桥梁、机翼等)自动控制实时检测本课程的主要教学安排:主要内容:(50学时)数字信号的频率分析:定义、变换与计算(22学时)频率定义、CTFS与DTFS、CTFT与DTFT、DFT与FFT数字信号的频率处理:滤波器设计(26学时)LTI系统分析理想滤波器与低阶数字滤波;FIR滤波器设计、IIR滤波器设计数字滤波器结构与误差分析教材与参考书:教材:《Digital Signal Processing –spectral computation and filterdesign 》(Third edition)(美) Chi-Tsong Chen电子工业出版社2002版《数字信号处理基础》(加)Joyce Van de Vegte 著侯正信王国安等译电子工业出版社2003版《信号与系统计算机练习—利用MA TLAB》John R.Buck刘树棠译西安交通大学出版社2000版主要工具:MATLAB :信号波形图、频谱计算与分析滤波器设计及系统频率特性分析考核方式:平时作业30%考试(笔试、开卷)70%MATLAB的基本应用方法命令窗口(Command window)的使用:输入各类变量或函数名称,按回车即得到当前变量或函数值;输入各类命令,按回车即得到该命令执行结果;若需要输入多行命令或程序,各行间用“;”间隔;M文件的编制与调试执行打开空白文件或已经有的文件,进行程序文件的输入编辑;各行间用“;”间隔;一行中“%”以后内容为注释部分,不影响程序执行;程序编制完毕后,可以按“F5”键保存执行,注意根据屏幕提示建立文件名称;如果出现错误,可在命令窗口看到错误类型及位置,根据错误检测信息对程序进行调试;MATLAB命令及函数信号的表达方式及作图在MA TLAB中,任何变量或函数均表现为向量,任何向量的元素编号均从1开始;序列(向量)表达方式设定坐标向量n和信号向量x;x和n为长度相同的向量,向量的编号从1开始;n=[-2 :0.1:2]坐标向量可以直接逐点写出:n=[2 3 4 5 6 7];也可以采用起点,终点和步长的形式写出:n=[-2 :0.1:2] ;信号向量可以直接逐点写出:x=[1 2 3 4 3 2];也可以采用与n 有关的函数运算形式写出:例如: x=3*n x=exp(j*(pi/8)*n)作图: 采用stem (n ,x ) 作出离散图形 DT 信号采用plot (n ,x ) 作出连续图形(折线连接) CT 信号作图时主要通过合理设置n 的范围及步长来保证变量坐标的正确性;可以利用title ,axis等函数为图形设置说明和坐标范围;特别注意:作图时必须保证坐标向量与信号向量长度完全一致;0101:离散序列的作图直接表现离散序列n=[2 3 4 5 6 7];x=[1 2 3 4 3 2];stem(n,x);0102:将图形表现为连续曲线n=[2 3 4 5 6 7];x=[1 2 3 4 3 2];plot(n,x);0203:信号表现为坐标向量的函数n=[2 3 4 5 6 7];x=exp(j*(pi/8)*n);plot(n,x);0204:图形说明和坐标范围的设置n=[-20:0.5:20];x=exp(j*(pi/8)*n);plot(n,x),title('n=[-20:0.5:20];x=exp(j*(pi/8)*n);plot(n,x)');axis([-20,20,-2,2]);第二章 DTFS 和CTFS---周期信号的频率分量信号的时域表达形式:连续时间信号CT 离散时间信号DTDT 信号由CT 信号采样得出CT 信号()t x 采样信号()nT x DT 信号 []n x周期信号:每隔一段时间重复的信号 ()(),...2,1±±=+=k kT t x t x 信号变化快慢的描述:周期T :信号重复的时间间隔频率0ω:单位时间内信号重复的次数频域表达形式人类接受的自然信号主要以频率形式表达:声音 色彩信号分析的重要任务:从时域信号得出频域信号频率的定义----单频率时间信号CT 信号的频率与周期性密切相关标准信号 ()t t x 01s in ω= ()t t x 02c o s ω=()t j t e t x t j 003sin cos 0ωωω+==上述信号均为周期信号,周期为T ;频率均为 0ω;周期与频率的关系 02ωπ=T 0ω 取值范围 ()∞∞-,DT 信号的频率 (仿照CT 信号定义)DT 信号由CT 信号采样得到;周期信号的采样不一定为周期信号;对于DT 信号,频率与周期没有直接对应关系;仿照CT 信号定义基本信号()Tn nT x 01sin ω= ()Tn nT x 02cos ω=()Tn j Tn e nT x Tn j 003sin cos 0ωωω+==上述信号频率均为 )在主值区域内的对应值T d 0(ωω=要点:信号nT j e 0ω的时域性质:非周期性频率性质:多重性频率范围 d ω 取值范围 ]/,/(T T ππ-Nyquist frequency ranged ω与采样频率有关CT 与DT 信号频率之间的关系:P. 29f d 与采样频率有关,位于]5.0,5.0(s s f f -范围内;将高频按周期折合到低频(主值区);例 p.27 2.1 2.2付氏级数及频率分量一般周期时间信号的频率:采用单频率信号表达CTFS (连续时间付氏级数)定义式 (周期信号:周期为P )()∑∞-∞==m t jm m e c t x 0ω P /20πω=()⎰-=Pt jm m dt e t x P c 01ω 存在条件:()t x 绝对可积,而且在一个周期内间断点和极值点有限;频率分量:CTFS coefficient / frequency component 通常为复数: Magnitude phase phase 的范围],(ππ- 共轭对称性:奇偶性()k FS a t x -**−→←()t x k areal {}k k a a Re :even{}k k a a ∠Im : oddreal and even real and evenreal and odd imaginary and odd周期信号频率分量的计算 (例 P.38)要点:P /20πω=2.4 利用简单分解求m c⎩⎨⎧≠==−→←000(m m A c A m FS常数) ⎩⎨⎧≠==−→←nm n m B c Be m FS t jn 00ω 2.5 利用公式求矩形脉冲的m c ()P m a m c ta t t x m FS 00sin 201ωω=−→←⎩⎨⎧≤=其余 2.6 利用公式求冲激串(sampling function )的m c()()Tc kT t t r m FS k 1=−→←-=∑∞-∞=δ 周期信号的时间范围:),(∞-∞ 双边信号一般周期信号的频率范围:),(∞-∞若对于所有的0,=>m c M m ,则称为带限信号;频率分量的意义:平均功率: 只与magnitude 有关phase 的影响:对信号波形的影响对视频有影响,对音频没有影响DTFS (离散时间付氏级数)定义式[]∑==N m nT jm md e c n x 0ω []∑=-=Nn nT jm md e n x N c 01ω 频率分量讨论:md c 的周期性 只有N 个独立系数共轭对称性:奇偶性m 的取值范围:应使 NT m m /20πω=的范围为]/,/(T T ππ-时移的影响: 线性相位变化例 p.48—542.8 利用公式直接计算系数 N=32.9 利用公式直接计算系数 N=42.10 时移的作用时移不影响DTFS 系数的幅度,只在系数中加入线性相位;利用MATLAB 计算频率分量DTFS 系数的FFT 计算重要函数 c=(1/N)*fft(x) x=N*ifft(c)应用要点:x和c的序列都为N个元素,下标排列都为[ 1 …..N],分别对应于离散时间n [0….N-1]和离散频率m [0….N-1];DTFS可以利用任何一个周期进行计算;在采用FFT的时候,输入数据必须从n=0到N-1;利用shift()函数(P.56)可以使频率向量排布在对称区间内:N为odd时,下标0在正中,N为even时,下标0偏左;利用m=ceil(-(N-1)/2):ceil((N-1/2)可以得到对应的横坐标;注意:c为周期序列,周期为N;例:2.8 2.9 程序P2.2 (P.57 )例2.8题的求解N=3;T=0.5; x=[-2 1 –0.6];例2.9题的求解N=4;T=1; x=[ 2.5 -0.4 1 -2];%program 2.2N=3;T=0.5; x=[-2 1 –0.6];D=2*pi/(N*T);X=fft(x/N);m=ceil(-(N-1)/2):ceil((N-1)/2);w=m*D;subplot(2,1,1),stem(w,abs(shift(X))),title('(a)');subplot(2,1,2),stem(w,angle(shift(X))*180/pi),title('(b)');CTFS系数的FFT计算问题:x为连续信号;m取值范围为无限大区间;方案:在一个周期内取N点对x进行采样(离散化);求出DTFS系数---周期序列;取主值范围内的序列即为对应CTFS系数;当x为带限信号时,在满足采样定理条件下可以得出准确的CTFS系数;例2.4题的求解 2.12%program 2.2P=2*pi/0.3;N=11;T=P/N;D=2*pi/P;n=0:N-1;x=-1.2+0.8*sin(0.6*n*T)-1.6*cos(1.5*n*T);X=fft(x/N);m=ceil(-(N-1)/2):ceil((N-1)/2);w=m*D;subplot(2,1,1),stem(w,abs(shift(X))),title('(a)');subplot(2,1,2),stem(w,angle(shift(X))*180/pi),title('(b)');对于带限信号,在满足采样定理的条件下,不同大小的N值(采样数量)得到的幅频分量相同;若采样周期不够小,则将产生频率混叠失真;例2.3 频率混叠的影响例2.5题的求解通过改变采样点数量N,可以比较混叠的影响大小%program 2.4hold on;N=42;P=4;T=P/N;D=2*pi/P;x=[ones(1,q+1) zeros(1,N-2*q-1) ones(1,q)];X=fft(x/N);m=ceil(-(N-1)/2):ceil((N-1)/2);stem(m*D,shift(X),'b','fill');对于在足够逼近条件下,magnetude 可以得到足够良好近似值;(能量逼近);但计算出的phase 不会得出良好近似值(通常不采用);关键:N 的选取(足够大以获得良好近似,足够小以减少运算量)根据设定的精确度,求出最小的N :令N=2n ,选定n 的特定值,再逐1增加;重复计算在Nyquist 范围内的系数差,直到系数差小于设定值为止;例2.6 根据设定最大误差,自动选取最小采样点数量,并求出满足要求的频谱例2.5题的求解% program 2.6a=1;b=100;P=4;D=2*pi/P;beta=1;while b>betaN1=2^a;T1=P/N1;q1=floor(1/T1);x1=[ones(1,q1+1) zeros(1,N1-2*q1-1) ones(1,q1)];X1=fft(x1/N1);N2=2*N1;T2=P/N2;q2=floor(1/T2);x2=[ones(1,q2+1) zeros(1,N2-2*q2-1) ones(1,q2)];X2=fft(x2/N2);m1p=0:N1/2;d=max(abs(abs(X1(m1p+1))-abs(X2(m1p+1))));mm=max(abs(X1(m1p+1)));b=d/mm*100;a=a+1;endN2,bm=-N2/2+1:N2/2;stem(m*D,abs(shift(X2)));对此程序作少数改动可以得到对其他信号的计算:P.73 例2.14平均功率计算CT 信号 ∑∞-∞==m m av c P 2 DT 信号 ∑-==102N m md av c P例2.15分别采用时域序列和频谱序列求信号平均功率例2.4题的信号功率P=2*pi/0.3;N=11;T=P/N;n=0:N-1;x=-1.2+0.8*sin(0.6*n*T)-1.6*cos(1.5*n*T);P1=sum(x.^2)*T/PX=fft(x/N);P2=sum(abs(X).^2)例2.16采用频谱序列求信号平均功率例2.5题的信号功率%program 2.9N=1024;D=2*pi/4;x=[ones(1,257) zeros(1,511) ones(1,256)];X=fft(x/N);mu=floor(5/D);m=2:mu+1;p=abs(X(1))^2+2*sum(abs(X(m)).^2)第三章 CTFT 和DTFT---一般信号的频谱实际信号都是非周期信号(非双边信号)周期信号对应于离散频率分量(离散频谱)非周期信号对应于连续频谱CTFT 连续时间信号的付氏变换 定义式()()⎰∞∞-=ωωπωd e X t x t j 21 ()()⎰∞∞--=dt e t x X t j ωω 频谱存在条件:()t x 绝对可积,而且在一个周期内间断点和极值点有限;例 3.1 e at u(t) 的频谱()()01<-−→←=a a j t u e t x FT at ωP.85 图3.1例3.2 w a (t )的频谱:时域窗口函数()()ωωa at a t t w t x FTa sin 201−→←⎩⎨⎧>≤==P.87 图3.2主瓣:高2a ,宽2π/a旁瓣:宽π/a 零点:n π/a窗口宽度与主瓣/旁瓣宽度成反比;窗口的时移不改变幅频特性,只引入线性相位; 例3.3 模拟理想低通滤波器 :频域窗口函数()()⎩⎨⎧≤=−→←==ωωωωωπωπω其余01sin sin cFTc c c H t c t t t xP.89 图3.3CT 周期信号的频谱()020ωωπδω-−−→←FTt j e步骤:将CT 周期信号先展开为CTFS ,再进行逐项变换; 若干常用信号的频谱(P.91 图3.4)()ωπδ21−→←FT()()000s in ωωπδωωπδω++--−→←j j t FT()()000c o s ωωπδωωπδω++-−→←FT t()()ωωπδj t u FT1+−→←例 3.4 冲激串的CTFT()()∑∑∞-∞=∞-∞=-−→←=m FTk tjm m Tet r 020ωωδπω频谱的性质()()ωj X t x F−→←连续有界:若()t x 绝对可积,则()ωX 有界并连续;奇偶性:()()ωj X t xF -−→←**P.94 表3.1时间实函数----幅频偶、相频奇 时间实偶----频谱实偶 时间实奇----频谱虚奇 时移与频移:()()ωωj X e t t x t j F00-−→←-()()()00ωωω-−→←j X t x e Ft j时移引入线性相位,频移对应复指数调制 时间尺度变换:()⎪⎭⎫⎝⎛−→←a j X a at x Fω1()()ωj X t x F-−→←-时间压缩对应频谱扩展Parseval’s relation 能量的频率分布()()ωωπd j X dt t x E 2221⎰⎰∞+∞-∞+∞-==能量只与幅频特性有关,时移不影响信号能量分布周期信号与非周期信号的能量对比 周期信号能量为无限大,平均功率为∑∞-∞==m mavc P 2,非零功率只存在于离散频率点;绝对可积的非周期信号能量为()()ωωπd j X dt t x E2221⎰⎰∞+∞-∞+∞-==,在任何特定频率点能量为零,能量分布于频率区间上;连续时间信号截断对于频谱的影响只有极少数信号可以求出频谱的解析表达式; 绝大多数实际信号只能采用数值方式求解频谱;对无限长时间连续信号,在实际计算时必须考虑截断并离散化;时域截断模型:以窗口函数乘以时间函数 ()()t w t x a ⋅时域乘积对应于频域卷积:()()()()⎰∞∞--=*ϖϖωϖπωωd X W W X a a 21其中 ()ωωωa W asin 2=单频率信号的截断效果 (P.104 图3.8)使单频率展宽,出现主瓣(高L=2a 、宽4π/L )和旁瓣(高<0.2L 、宽2π/L ); 对于有限带宽信号,截断导致带外泄露(能量)和纹波现象; L 越小,上述效应越显著;对于连续信号,增大L 可以将上述效应削弱到可以忽略的程度; 例3.5()()t u e t x t 1.0-=的频谱:采用不同宽度的窗口截断;(P.104 图3.8)Gibbs 现象用付氏变换表达时间函数时,当频谱信号含有不连续点时,频谱的纹波将会变窄并靠近该点,但纹波不会随L 的无限增大而消失,而是趋于一个常量(宽度无限小,高度约为不连续变化量的9%);(P.105 图3.9)将频谱变换为时间函数时存在相同的现象; 采用矩形窗口截断信号必然出现Gibbs 现象。







