电力变压器铁芯柱截面的优化设计
- 格式:doc
- 大小:400.36 KB
- 文档页数:14



电力变压器铁心柱截面的优化设计之程序实现(MATLAB)附录7.1 附录 1funf='f=-1*(x(1)*sqrt(325^2-x(1)^2)+x(2)*(sqrt(325^2-x(2)^2)-sqrt(325 ^2-x(1)^2))+x(3)*(sqrt(325^2-x(3)^2)-sqrt(325^2-x(2)^2))+x(4)*(sqrt(3 25^2-x(4)^2)-sqrt(325^2-x(3)^2))+x(5)*(sqrt(325^2-x(5)^2)-sqrt(325^2-x(4)^2))+x(6)*(sqrt(325^2-x(6)^2)-sqrt(325^2-x(5)^2))+x(7)*(sqrt(325^ 2-x(7)^2)-sqrt(325^2-x(6)^2))+x(8)*(sqrt(325^2-x(8)^2)-sqrt(325^2-x(7 )^2))+x(9)*(sqrt(325^2-x(9)^2)-sqrt(325^2-x(8)^2))+x(10)*(sqrt(325^2-x(10)^2)-sqrt(325^2-x(9)^2))+x(11)*(sqrt(325^2-x(11)^2)-sqrt(325^2-x( 10)^2))+x(12)*(sqrt(325^2-x(12)^2)-sqrt(325^2-x(11)^2))+x(13)*(sqrt(3 25^2-x(13)^2)-sqrt(325^2-x(12)^2))+x(14)*(sqrt(325^2-x(14)^2)-sqrt(32 5^2-x(13)^2)));' ; %最大面积的目标函数fung='g=[x(2)-x(1)+5;x(3)-x(2)+5;x(4)-x(3)+5;x(5)-x(4)+5;x(6)-x(5)+5; x(7)-x(6)+5;x(8)-x(7)+5;x(9)-x(8)+5;x(10)-x(9)+5;x(11)-x(10)+5;x(12)-x(11)+5;x(13)-x(12)+5;x(14)-x(13)+5];'; %宽度逐级递减的约束条件fun=[funf fung];x0=[180 185 190 195 200 205 210 215 225 225 230 235 240 245]; %初始值options=[];vlb=[85 80 75 70 65 60 55 50 45 40 35 30 25 20]; %下界vub=[395 390 385 380 375 370 365 360 355 350 345 340 335 330]; %上界[x,options]=constr(fun,x0,options,vlb,vub);y=zeros(1,14);x=x.*2;x=(round(x./10)).*10; %以10 为倍数的宽度for i=1:14yy=sum(y',1);y(i)=sqrt(325^2-x(i)^2)-yy;endy=round(y);xys=x.*y;sum(s',1)(ans)/((325^2)*pi)7.2 附录 2max=0;hh1=395;yy1=(325^2-hh1^2)^(1/2);ss1=hh1*yy1;for b=1:6hh2=385+(b-3)*5;yy2=(325^2-(hh2)^2)^(1/2)-yy1;ss2=hh2*yy2;for c=1:6hh3=375+(c-3)*5;yy3=(325^2-(hh3)^2)^(1/2)-yy1-yy2;ss3=hh3*yy3;for d=1:6hh4=365+(d-3)*5;yy4=(325^2-(hh4)^2)^(1/2)-yy1-yy2-yy3;ss4=hh4*yy4;for e=1:6hh5=355+(e-3)*5;yy5=(325^2-(hh5)^2)^(1/2)-yy1-yy2-yy3-yy4;ss5=hh5*yy5;for f=1:6hh6=345+(f-3)*5;yy6=(325^2-(hh6)^2)^(1/2)-yy1-yy2-yy3-yy4-yy5;ss6=hh6*yy6;for g=1:6hh7=335+(g-3)*5;yy7=(325^2-(hh7)^2)^(1/2)-yy1-yy2-yy3-yy4-yy5-yy6;ss7=hh7*yy7;for h=1:6hh8=325+(h-3)*5;yy8=(325^2-(hh8)^2)^(1/2)-yy1-yy2-yy3-yy4-yy5-yy6-yy7;ss8=hh8*yy8;for i=1:6hh9=315+(i-3)*5;yy9=(325^2-(hh9)^2)^(1/2)-yy1-yy2-yy3-yy4-yy5-yy6-yy7-yy8;ss9=hh9*yy9;for j=1:6hh10=305+(j-3)*5;yy10=(325^2-(hh10)^2)^(1/2)-yy1-yy2-yy3-yy4-yy5-yy6-yy7-yy8-yy9;ss10=hh10*yy10;for k=1:6hh11=285+(k-3)*5;yy11=(325^2-(hh11)^2)^(1/2)-yy1-yy2-yy3-yy4-yy5-yy6-yy7-yy8-yy9-yy10; ss11=hh11*yy11;for l=1:6hh12=265+(l-3)*5;yy12=(325^2-(hh12)^2)^(1/2)-yy1-yy2-yy3-yy4-yy5-yy6-yy7-yy8-yy9-yy10-yy11;ss12=hh12*yy12;for m=1:6hh13=245+(m-3)*5;yy13=(325^2-(hh13)^2)^(1/2)-yy1-yy2-yy3-yy4-yy5-yy6-yy7-yy8-yy9-yy10-yy11-yy12;ss13=hh13*yy13;for n=1:6hh14=225+(n-3)*5;yy14=(325^2-(hh14)^2)^(1/2)-yy1-yy2-yy3-yy4-yy5-yy6-yy7-yy8-yy9-yy10-yy11-yy12-yy13;ss14=hh14*yy14;ss=ss1+ss2+ss3+ss4+ss5+ss6+ss7+ss8+ss9+ss10+ss11+ss12+ss13+ss14;if max<ssmax=ss;hh=[hh1,hh2,hh3,hh4,hh5,hh6,hh7,hh8,hh9,hh10,hh11,hh12,hh13,hh14]; yy=[yy1,yy2,yy3,yy4,yy5,yy6,yy7,yy8,yy9,yy10,yy11,yy12,yy13,yy14]; sss=[ss1,ss2,ss3,ss4,ss5,ss6,ss7,ss8,ss9,ss10,ss11,ss12,ss13,ss14]; endend,end,end,end,end,end,end,end,end,end,endendend7.3 附录 3t=s;for i=length(s)-1:-1:1t=[t s(i)]; %将23 级面积全部合并为一数组endnn=squre/7; %平均分割时的面积ss=0;w=30000; %误差设置的初始值sss=[];while length(sss)~=7w=w-1000;for i=1:23ss=ss+t(i);if nn-w<=ss<=nn+wsss=union(sss,ss);ss=0;endendendsss %油道分割的各级面积。



电力变压器铁芯柱截面的优化设计电力变压器铁芯柱截面的优化设计是指通过调整变压器铁芯柱的截面形状和尺寸,以提高变压器的效率和功率因素,减少能量损耗和材料成本,并满足电力系统对变压器的性能要求。
下面将从设计原理、优化方法和实例应用三个方面进行阐述。
设计原理:电力变压器的铁芯柱由硅钢片叠压而成,用于传导磁场并提供磁耦合效果。
铁芯柱的优化设计是在保持磁路特性不变的前提下,寻找最佳的截面形状和尺寸,以提高变压器的性能。
常用的设计原理包括:最小损耗设计原理、最小材料成本设计原理、最佳功率因素设计原理等。
优化方法:1.目标函数选择:优化设计的第一步是选择适当的目标函数,如变压器的效率、功率因素、磁损耗、铁芯材料成本等。
2.参数选择:确定需要优化的设计参数,如铁芯柱的截面形状和尺寸、硅钢片的厚度等。
3.优化算法选择:根据设计要求和目标函数选择合适的优化算法,如遗传算法、粒子群算法、模拟退火算法等。
4.建立数学模型:根据电磁学原理和变压器的特性建立数学模型,包括磁场方程、电流方程、能量损耗方程等。
5.参数求解:利用所选的优化算法对数学模型进行求解,得到最优的设计参数。
6.优化结果分析:对优化结果进行分析,包括目标函数值、设计参数值的变化情况等。
实例应用:以提高变压器效率为目标,假设需要优化的设计参数为铁芯柱的截面形状和尺寸。
首先,在建立数学模型时考虑铁芯柱的几何形状和磁导率等因素,并确定合适的目标函数,如功率因素。
然后,选择适当的优化算法对数学模型进行求解,得到最优的设计参数。
最后,将优化结果与初始设计进行对比,分析优化效果。
总结:电力变压器铁芯柱截面的优化设计是一项复杂的任务,需要综合考虑磁路特性、电力系统要求和经济性等因素。
通过选择合适的目标函数和优化算法,建立数学模型并进行参数求解,可以得到最优的设计参数,提高变压器的性能和经济效益。
在实际应用中,还需考虑制造工艺、材料特性和现实情况等因素,以实现优化设计的有效落地。

变压器铁心截面优化设计是电力系统中重要的工程技术问题,优化设计可提高变压器的效率和性能,降低能耗和成本。
基于matlab的变压器铁心截面优化设计可以通过模拟和分析来实现,本文将介绍基于matlab的变压器铁心截面优化设计的理论和方法,并结合实例进行详细说明。
一、变压器铁心截面优化设计理论1.1 变压器铁心的作用和优化设计目标变压器铁心是变压器的核心部件,其主要作用是传导磁场和减少磁通的漏磁损耗。
优化设计的目标是在满足磁通密度和损耗限制的情况下,尽量减小铁心的截面积,以降低铁心材料的使用成本,并提高变压器的效率。
1.2 变压器铁心截面优化设计的数学模型变压器铁心的优化设计可以通过数学建模和优化算法来实现。
常见的数学模型包括磁场分布模型和损耗模型,优化目标包括最小截面积和最小损耗。
基于matlab的优化工具箱可以方便地实现这些数学模型和优化算法。
二、基于matlab的变压器铁心截面优化设计方法2.1 建立变压器铁心的磁场分布模型通过有限元分析方法,可以建立变压器铁心的磁场分布模型。
利用matlab中的pde工具箱可以方便地进行有限元分析,得到铁心的磁场分布和磁通密度分布。
在优化设计中,需要根据工作条件和限制条件进行合理的磁场分布设置。
2.2 建立变压器铁心的损耗模型变压器铁心的损耗包括铁损和铜损。
铁损是由于铁心磁化和磁滞引起的损耗,铜损是由于铜导体电阻引起的损耗。
利用matlab中的矢量分析工具箱,可以方便地建立变压器铁心的损耗模型,并进行损耗的计算和分析。
2.3 基于matlab的优化算法在建立了变压器铁心的磁场分布模型和损耗模型之后,可以利用matlab中的优化工具箱进行优化设计。
常用的优化算法包括遗传算法、粒子裙算法、模拟退火算法等,这些算法可以用于求解磁场分布和损耗的最优设计方案,并得到最小截面积和最小损耗的优化结果。
三、案例分析以某一具体变压器为例,假设其工作条件和限制条件已知,利用基于matlab的变压器铁心截面优化设计方法,可以得到最优的铁心截面积和损耗分布。

电力变压器铁心柱截面的优化设计(一)(2)电力变压器铁心柱截面的优化设计(一)1.整个铁心柱的硅钢片出了长度,其它如厚度,表面绝缘漆膜厚度,平整度都相同;2.硅钢片之间是没有形变的压紧;3.叠片系数是确定的已知数;4.油道对称分布;5.不考虑工艺过程的影响。
3 符号说明第i级叠片的的厚度;第i级叠片的宽度;叠片系数;铁心柱理论外接圆的直径,也等于理论线圈内筒直径;第i根油道与直径之间的;油道分割出来的分块 ___;多级阶梯形前i级厚度之和;线圈内筒的公差值;4 问题分析 4. 问题背景变压器是一种应用电磁感应原理把电能从一个电路传到另一个电路的电磁装置。
它在电路中起变压,变流,变电阻的作用。
它由三部分组成:铁心,起导磁,助磁作用;而是初级线圈,接电源,起激磁作用;三是次级线圈接负载,利用不同次初级线圈匝数比,实现变压,变流,变电阻的作用。
在变压器的构成里,铁心柱是很一个十分重要的组成部件。
因为铁心柱的形状,截 ___,叠片的选择,叠片的相关工艺过程都会影响将来变压器的使用效果和寿命,以及使用成本。
我国变压器制造业通常采用全国统一的标准铁心设计图纸,根据多年的生产经验,在 ___的生产研究过程中,各生产厂产生了对已有设计方案的疑问:能否改进及如何改进这些设计,才能在提高使用效益的同时降低变压器成本。
4.1. 铁心柱是 ___在线圈筒里面的,理论上,在线圈的直径确定了的情况下,铁心柱的有效 ___越大,铁心的电阻越大,使铁心的铁损最小,因而可以减少能量损耗,变压器的使用性能会越好,使用寿命较长。
为了充分利用空间和便于生产,铁心柱截面长采用多级阶梯形结构,用不同长度的硅钢片,堆叠成不同厚度的级,并且选择合适的级数去逼近与之配合的铁心线圈圆,期望得到的有效 ___最大,获得更大的电阻。
截面优化设计是以保证到达设计标准为前提,尽可能改善和提高产品的使用效果,使产品竞争力提升。
4.2 公差是生产中允许工件尺寸和几何形状变动的范围,用来限制误差。

变压器铁心截面的优化设计
巫付专;刘建风;等
【期刊名称】《郑州纺织工学院学报》
【年(卷),期】2000(011)004
【摘要】介绍了解析法、动态规划法和实际处理分三步进行优化设计,使变压器铁心有效面积达到最大的方法,提供了四组备选数据,认为使铁心有效截面积在直径不变的情况下达到最大,其实际意义非常显著。
【总页数】3页(P70-72)
【作者】巫付专;刘建风;等
【作者单位】中原工学院电气系,河南郑州450007;郑州电气装备总厂,河南壮族450006
【正文语种】中文
【中图分类】TM402
【相关文献】
1.电力变压器铁心柱截面的优化设计 [J], 潘淑平;王晓玲;张秀兰
2.电力变压器铁心柱截面优化设计 [J], 夏立伟;汪旭旭;辛巍;范杨
3.立体卷铁心变压器铁心柱截面的优化设计 [J], 许凯旋
4.电力变压器铁心柱截面的优化设计 [J], 周文洲;覃金南
5.电力变压器铁心柱截面优化设计 [J], 陈仲;
因版权原因,仅展示原文概要,查看原文内容请购买。

电力变压器铁心柱截面的优化设计发表时间:2019-05-28T11:04:39.507Z 来源:《电力设备》2018年第35期作者:郭旭[导读] 摘要:电力变压器在电力系统运行的过程中起着非常大的作用,电力变压器可以对电压进行调节和控制,从而保证整个电力系统运行的稳定性和安全性。
(国网内蒙古东部电力有限公司通辽供电公司内蒙古通辽 028000)摘要:电力变压器在电力系统运行的过程中起着非常大的作用,电力变压器可以对电压进行调节和控制,从而保证整个电力系统运行的稳定性和安全性。
振动既是变压器故障的致因之一,又是识别变压器绕组变形故障的重要表征。
本文从振动的角度出发,结合电力变压器绕组变形故障的实际,对基于振动的电力变压器绕组变形故障诊断方法进行简要的分析。
关键词:振动;电力变压器绕组变形;故障诊断方法一、变压器振动信号分析在运行过程中变压器之所以会产生振动,是因为变压器内部铁芯和绕组的震动,电力变压器在稳定运行时,硅钢片的磁致伸缩会导致变压器内部的铁芯震动,同时由于有电流经过绕组,在绕组、线饼、线匝之间产生的点动力会引起绕组的震动,这种震动与变压器内部的电动力有直接的关系,所以在震动在外在表现形式上的震动频率与变压器自身的负载电流基数有直接的数据关系,在理想状态下变压器的振动信号的基频是负载电流基频的两倍,即100Hz。
因为变压器内部振动信号与其内部电力运行的相关性,所以在电力变压器运行过程中其振动信号基本上能够反应出其内部的故障信息,但是电力变压器故障检测活动中这种相关性表现的并不直接,在变压器运行过程中即使没有故障也其振动信息也会随着变压器内部负载的变化而变化,也就说变压器振动信号的变化只是其绕组变形故障的必要条件,要对变压器绕组故障进行诊断还需要有其他信息的支持,需要有其他诊断手段的帮助。
二、一般振动诊断方法对于如何初步确定故障位置,理论界和一线管理人员都有一些方法,如通过延时效应定位、通过相位差定位等。
0背景在变压器的产品设计中,铁心截面设计非常关键,为了达到节材降耗的目的,应对铁心直径更细分档,并使某一直径的铁心截面最大化,这对于规模较大的中小型变压器厂尤为重要。
本文将对改进及如何改进铁心截面设计,提高使用效果的同时减低变压器的成本做重点论述。
1约束条件变压器的心柱截面一般采用多级圆形截面,为了提高心柱截面的利用率,必须增大心柱的几何截面与外接圆截面的比例。
为达到此目的,有两条途径,其一是提高叠压系数,其二是在给定直径D 时,增加多级圆形截面的几何面积。
提高叠压系数,受到工厂剪切、叠压等工艺条件限制,在一定工艺水平下,它是一个常数。
然而在给定直径下,增大铁心几何截面积确实一个较为有效的办法。
采用优化设计得方法,在给定直径时,铁心的多级圆形截面的几何面积达到最大。
如果通过优化,能使给定直径的圆形几何截面积增大1%,其意义也是很大的。
假设原铁心中磁密1.74T,比较饱和,而优化后,截面增大1%,则磁通密度可下降至1.72T,饱和情况会得到较大的缓解。
铁心截面优化有以下三方面内容:1)对应于某铁心直径的级数不变时,在该直径下多级圆形截面的几何面积达到最大。
2)级数增加一级,若给定直径的最大几何面积较原级数对应的几何面积有较大增加,可以考虑增加一级。
3)级数减少一级,若给定直径的最大几何面积较原级数对应的几何面积无明显减少,可考虑减少一级。
当然,对于标准化的铁心截面系列,其级数要符合递变规律。
2模型由于制造工艺的要求,硅钢片的宽度一般取为5或10的倍数(单位:毫米)。
因为在多级阶梯形和线圈之间需要加入一定的撑条来起到固定的作用,所以一般要求第一级的厚度最小为26毫米,硅钢片的宽度最小为20毫米。
令S πr2为铁心利用率。
对直径d,以(x 1,x 2,…,x n )为其各级的宽度,(y 1,y 2,…,y n )为相应的厚度。
面积函数为S i =2x i y i ,x 与y 的关系为y i =(r 2-x 2)12-i -1t =1∑y ti=1,2,…,n ,可得以下模型:max S i =2x i y i x iω[]=x iω各级宽度必须为ω的倍数y i ≧26第一级厚度必须大于26mm x n ≧20第n 级宽度大于20mm x 1≧x 2≧…≧x n 各级宽度逐级递增此模型为非线性整数规划。
学科代码:080618学号:0914********贵州师范大学(本科)毕业论文题目:变压器心式铁心优化设计学院:机械与电气工程学院专业:电气信息工程年级:2009级姓名:樊伟指导教师:霍慧芝(副教授)完成时间:2013年5月5日目录摘要............................................................................................................................... Abstract ......................................................................................................................... 引言............................................................................................................................... 第一章概述.................................................................................................................1.1 电力变压器性能参数的确定................................................................................1.2 电力变压器电磁计算的一般步骤........................................................................1.2.1 电力变压器设计计算应注意的问题...............................................................1.2.2 电力变压器设计步骤.......................................................................................1.2.3 电力变压器电磁计算的一般步骤................................................................... 第二章电力变压器铁芯直径计算方法的优化设计.................................................2.1 影响铁芯直径选择的主要因素............................................................................2.2 电力变压器铁芯直径设计一般方法....................................................................2.2.1 常用基本公式...................................................................................................2.2.2 半经验公式的推导...........................................................................................2.2.3 相关参数的计算...............................................................................................2.2.3.1 铁芯直径经验系数K D.................................................................................2.2.3.2 每柱容量S Z..................................................................................................2.3 电力变压器铁芯直径计算方法的优化设计........................................................2.3.1 铁芯直径计算方法比较...................................................................................2.3.2 铁芯直径计算方法优化设计........................................................................... 第三章电力变压器铁芯截面的优化设计.................................................................3.1 铁芯截面选取的一般方法....................................................................................3.2 铁芯截面积的优化设计........................................................................................3.2.1 铁芯截面优化设计问题分析...........................................................................3.2.2 数学模型假设...................................................................................................3.2.3 数学模型的建立...............................................................................................3.2.3.1 符号说明......................................................................................................3.2.3.2 数学模型的建立..........................................................................................3.2.4 数学模型的求解...............................................................................................3.3 考虑油道的铁芯截面优化设计............................................................................3.3.1 截面优化设计问题分析...................................................................................3.3.2 数学模型假设...................................................................................................3.3.3 数学模型的建立...............................................................................................3.3.3.1 符号说明......................................................................................................3.3.3.2 数学模型假设..............................................................................................3.3.4 数学模型的求解............................................................................................... 第四章电力变压器铁芯公差带的优化设计.............................................................4.1 电力变压器公差带简介........................................................................................4.2 电力变压器公差带的优化设计............................................................................4.2.1 公差带优化设计的问题分析...........................................................................4.2.2 数学模型的假设...............................................................................................4.2.3 数学模型的建立...............................................................................................4.3 数学模型的求解.................................................................................................... 第五章结论及展望.....................................................................................................5.1 对铁芯直径的简便设计........................................................................................5.2 填充系数的提高....................................................................................................5.3 公差带的设计........................................................................................................ 参考文献....................................................................................................................... 致谢...............................................................................................................................摘要铁芯是变压器计算中很重要的部分,铁芯相关参数计算的合理与否,直接影响到了变压器的技术经济指标。
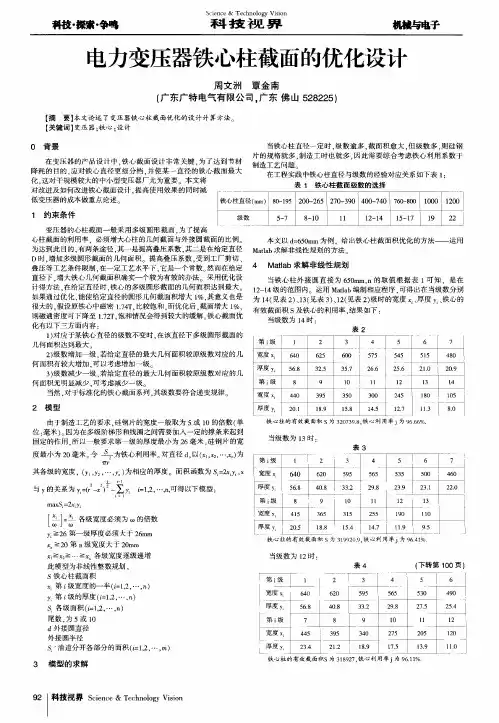
电力变压器铁心柱截面的优化设计[摘要]:针对变压器铁心柱截面优化设计,建立数学模型并用 matlab 函数 constr 编程与搜索法求解,有计算速度快,稳定性好等特点,铁心利用率比较原设计图纸算法可提高3.8%左右,具有一定的实用价值。
对于直径为 800mm 的铁心柱,原设计级数为 17 级,通过对模型求解,发现级数为 12 级时,仍能达到 96% 的铁心截面积利用率,则可减少10级叠片的叠压,因此可在生产设计时考虑采用12级的叠片设计方案。
关键词:铁心利用率;非线整数性规划;搜索领域;尾数调整1 问题的提出电力变压器设计中一个很重要的环节就是铁心柱的截面如何设计。
变压器铁心截面在圆 形的线圈里。
为充分利用线圈内空间,心式铁心柱截面常采用多级阶梯型结构,如图 1:各 小阶梯(又称为“级” )均为矩形。
截面在圆内是上下轴对称的,阶梯的每级都是由许多种 宽度的硅钢片迭起来的,如何构造各个小矩形,使几何截面积最大?这就是电力变压器铁心 柱截面积的优化问题。
为了改善铁心柱内部的散热,在某些相邻阶梯形之间留下一些水平空隙,放入冷却油。
油道的位置应使其分割的各部分铁心柱截面积近似相等。
因此在确定各级的设计后,还要考 虑油道的设计。
2 符号约定S 铁心柱截面积i x 第i 级宽度的一半 ( ) n i ,..., 2 , 1 = i y 第i 级的厚度( ) n i ,..., 2 , 1 = iS 各级面积( ) n i ,..., 2 , 1 = w尾数,为5 或 10d外接圆直径 r外接圆半径¢ iS 油道分开各部分的面积( )m i ,..., 2 , 1 = 3 问题的分析与模型的建立我国变压器制造业通常采用全国统一的标准铁心设计图纸,根据多年的生产经验,各生 产厂存在着对已有设计方案的疑问:能否改进及如何改进这些设计,才能在提高使用效益的 同时降低变压器成本。
所以以往在设计大直径多级铁心柱时,工厂一般采用作图法,即在图 纸上经过反复核算,画出较好的铁心截面积设计方案,实际上与最优解的偏差较大;近年来 由于计算机的应用及数学软件的发展, 产生了建立数学模型并利用计算机使用多种方法求解 的思想。
电力变压器铁心柱截面的优化设计(一)(3)电力变压器铁心柱截面的优化设计(一)5.3.1 因为我们采用的方法是:先根据油道分割出来的各小块的___基本相等,确定出油道的具 ___置,然后在满足第一小问中关于制造工艺的约束的情况下,用硅钢片填充各个分区块,使各个区块的铁心 ___最大,即以各个区块铁心柱 ___最大为目标,然后 ___之和最大为目标函数,求最优方案。
Setp.1 确定油道的位置和宽度,根据几何关系可得如 ___程组:方程组联立求解求得油道的位置:求得的第一根油道的尺寸为:,求得的第二根油道的尺寸为:,,在获得有油道的精确位置之后,然后用硅钢片去填充每一个由油道分割出来的小区块,并且让填充的 ___最大:第一个区块的填充 ___为: ,并让第二个区块的填充 ___为:, 并让第三个区块的填充 ___为:,并让总的填充 ___,即为铁心柱几何截___的二分之一目标函数: Setp.2 第一根油道与水平的那根直径之间的填充最优方案:求解上述模型就可得到第一分块的多级阶梯截 ___最大的最优方案。
Setp.3 求第一根油道和第二根油道之间,最优填充方案:求解上述模型可以得到第一根油道和第二根油道之间区块最佳填充方案。
Setp.4 求解第二根油道和圆顶部之间区块的最优填充方案:求解上述模型可求得第二根油道和圆顶之间的最优填充方案。
5.3.2 模型求解利用MATLAB进行优化计算得到如下最优设计方案1级 2级 3级 4级 5级 6级 7级 8级 9级 10级第一分块 645 40 第二分块 620 600 570 82 55 62 第三分块 635 630 625 615 610 600 595 585 580 570 25 21 19 32 14 26 12 22 10 19 第一模块 ___ 51600 第二模块 ___ mj=59590 第三模块 ___ mj =60720 总 ___(不包括油道) 292220 ___占用比 88.1%7 模型评价与扩展本文建立的模型属于含多个整数变量的非线性整数规划模型。
电力变压器铁芯柱截面的优化设计摘要针对变压器铁心柱截面优化设计,建立数学模型,利用动态规划法计算变压器铁心柱截面最优解,通过matlab程序实现。
当直径为650毫米,叠片系数为0.98的时候,计算出级数为14级的时候有效面积最大,铁心柱截面的最大有效面积为314163.5平方毫米,面积利用率为94.72%。
运用动态规划方法计算任何铁心直径截面的最优解,既准确又快捷。
利用vb进行编程,导出可执行软件。
只要输入铁心柱的直径,级数,最小片宽还有叠片系数就能很快的算出铁心几何面积和有效截面积,以及各级的宽度和厚度。
而对于线圈的内筒直径和铁心柱的外接圆的公差带的设计,结合前一题的铁心柱截面的设计,对铁心柱直径的基本尺寸至500mm的,我们根据二者的最优配合,得出其上下偏差和公差,继而得到它们的公差带。
对于基本尺寸500mm至3150mm的没有推荐的最优配合,综合考虑各因素的影响,可采用其常用配合,得出他们的公差带。
同样利用vb进行编程,导出可执行软件,只用输入基本尺寸,然后选择公差代号和过程等级,就可上下偏差和公差。
根据铁心柱直径确定要增加的油道数,根据油道使分割相邻两边的面积近似相等,算出各个被分割的面积的大小,确定油道的位置。
关键词:动态规划最优解公差带基本尺寸有效面积一问题的重述电力变压器的设计中很重要的一个环节就是铁心柱的截面如何设计为了充分利用线圈内空间又便于生产管理,心式铁心柱截面常采用多级阶梯形结构,截面在圆内上下轴对称,左右也轴对称。
阶梯形的每级都是由许多同种宽度的硅钢片迭起来的。
如何构造各个小矩形,使几何截面积最大?这就是电力变压器铁心柱截面积的优化问题。
为了改善铁心柱内部的散热,在某些相邻阶梯形之间留下一些水平空隙,放入冷却油。
油道的位置应使其分割的各部分铁心柱截面积近似相等。
因此在确定各级的设计后,还要考虑油道的设计。
问题一:当铁心柱外接圆直径为650毫米时,如何确定铁心柱截面的级数、各级宽度和厚度,才能使铁心柱的有效截面积最大。
问题二:实际生产中线圈的内筒直径和铁心柱的外接圆直径不是精确地相等,而留有一定的间隙以便于安装和维修,设计的两个直径的取值范围称为各自的公差带。
因此可以在设计铁心截面时稍微增加铁心柱的外接圆的直径以使得铁心柱有更好的截面形状。
请结合铁心柱截面的设计而设计出二者的公差带。
问题三:铜导线在电流流过时发热造成的功率损耗简称为铜损;铁心在磁力线通过时发热造成的功率损耗简称为铁损。
为了改善铁心内部的散热,铁心柱直径为380毫米以上时须设置冷却油道。
简单地说,就是在某些相邻阶梯形之间留下6毫米厚的水平空隙,空隙里充满油,变压器工作时油上下循环带走铁心里的热量。
具体油道数可按表2选取。
油道的位置应使其分割的相邻两部分铁心柱截面积近似相等。
分别针对问题一和问题二的情况,增加油道要求再给出设计,并指出油道的位置。
二 模型的假设1 叠片之间的空隙不会对叠积片截面积有影响2 加入油道后对铁心的形状不产生影响。
3 不考虑日光辐射对变压器升温的影响。
4 厂家能生产任何尺寸大小的所需叠片。
三 符号说明n 铁心柱级数i a 第i 级的厚度 (i=1,2…..n ) i A 第1级厚度的一半到第i 级厚度之和i b 第i 级的宽度 (i=1,2…..n )i s 第i 级的面积 (i=1,2…..n )S 铁心柱截面几何面积S 有效 铁心柱截面有效面积R 外接圆直径r 外接圆半径K 叠片系数'i S 油道分开各部分的面积()m i ,...,2,1=四 模型的分析与建立我国变压器制造业通常采用全国统一的标准铁心设计图纸,根据多年的生产经验,各生产厂存在着对已有设计方案的疑问:能否改进及如何改进这些设计,才能在提高使用效益的同时降低变压器成本。
所以以往在设计大直径多级铁心柱时,工厂一般采用作图法,即在图纸上经过反复核算,画出较好的铁心截面积设计方案,实际上与最优解的偏差较大;近年来由于计算机的应用及数学软件的发展,产生了建立数学模型并利用计算机使用多种方法求解的思想。
本文的重点主要在计算机求解与数据分析。
铁心截面的优化设计问题是一个多变量、多极值的非线性问题。
问题一:变压器铁心截面最优设计是指在铁心的约束条件下的最大截面。
穷举法是常用的方法之一,即将各种可能的叠积尺寸均试算一遍,从中选取一组使截面为最大时的叠积尺寸。
但当铁心直径较大,级数较多时,不适合用穷举法,而适合用动态规划方法。
用该方法计算任何铁心直径截面的最优解,既准确又快捷,结果令人满意。
对于变压器铁心柱的级宽,都可以通过已知的直径算出相应的厚度,因此可以转化为以各级的宽度为变量的数学模型。
铁心柱有效截面的面积,等于多级铁心柱的几何截面积(不包括油道)乘以叠片系数。
当叠片系数一定的时候,几何面积越大,有效面积也越大。
以第一级面积的一半加上从第二级到第n 级矩形的几何面积作为目标函数,其值越大越减少能量损耗[1]。
1122n i i S a b a b =+∑约束条件:由勾股定理可知,第i 级矩形的宽度的一半的平方,与第一级厚度的一半到第i 厚度之和平方之和,小于等于圆柱形半径的平方。
222()2i i b A r +≤第i 级的宽度一定是5的倍数第i 级的宽度一定大于第i+1级的宽度1i i b b +>第1级的宽度不小于26毫米 最后一级的宽度最小为20毫米126a ≥ 20n b ≥;因为20n b ≥,片宽尾数是5或0,那么片宽的可行值为205b k =+,k=1,2,3…..m; 式中()/5n m R b =-; 对应的叠积厚为22(/2)i i A r b =-;在片宽可行值结合中任意选取n 个片宽子集,就是一个可行的叠积方案。
对任意一级片宽最多有m-n+1个元素可供选择。
例如,对于铁心直径为650,级数为14,最小片宽为20,这时m=126,即片宽b 可行值集合有126个元素,依次为{645,640,635···25,20},相应的叠积厚A 可行集合{56.78,69.42,80.00···324.76,324.85}.将叠积厚和片宽(,)i i b A 视为一点的坐标,所以对于每一级来说均有113(=126-14+1)个点可以选择,对于第一级有(645,56.78),(640,69.42)······113个可以选择,依次类推[2][3]。
根据铁心截面优化设计的分析,目标函数为112m ax(2)ni i S a b a b =+∑。
*S K S=有效。
问题二:首先对于铁心柱直径的选取,虽然铁心柱的直径越大其截面积越大,同时铁心的利用率也会增大,但是随着电力变压器的工作,变压器铁心的温度将要升高,而其通常要求温升不超过80K ,由于变压器油的允许温升限值为55K ,所以铁心对油的温升为25K 。
小型变压器的铁心,因为铁心直径小,单位高度铁心柱体积产生的热量为20p g πr ,式中0p 是单位重量耗损W/kg ,g 是单位体积重量kg/3m 。
单位高度传热面是2πr ,由此可得单位热负荷是20p g πr /2πr=r 0p g/2。
对小容量变压器,通过单位高度铁心柱表面传热的温升不会有问题;但大型变压器的铁心直径很大,单位面积热负荷大,且热传导路径很长。
在铁心内部传导出所产生的耗损,可能会发生铁心的过热,导致与其相邻的部件受到热损坏或者使油过度老化。
通过计算对比,对于此题,铁心柱的直径上限我们取为3150mm 。
要设计出最优化的公差带,最要考虑公差等级的选择,基准制和其配合。
确定公差等级应综合考虑各种因素,如果选择公差等级过高,当然可以满足使用要求,但加工难度大,成本高。
选择公差等级过低,加工容易,成本低,未必能保证使用要求。
所以,公差等级的选择应在满足使用要求的前提下,尽量选用较低的公差等级。
保证产品质量,满足使用要求是选择时应首先考虑的因素,然后考虑如何能更加经济,选择比较合适的、尽量低的公差等级,我们在此采用类比法选择公差等级。
通常,高于5级的等级用于量规或者精密零件上,5~12级用于配合尺寸,13~18级用于非配合尺寸。
基准制的选择与使用要求无关,不管选择基孔制还是基轴制,都可以达到预期的目的,实现配合性质。
但从工艺的经济性和结构的合理性考虑问题,对于中小尺寸优先选用基孔制。
因为基准孔的极限偏差是一定的,加工简易,比较经济。
若使用基轴制,就要配备许多的设配,所以选用基孔制可以取得明显的经济效果。
配合种类的选择,实质上是确定线圈的内筒和铁心柱的外接圆配合应具有一定的间隙或者过盈,满足使用要求,保证机器正常工作。
当基准制、公差等级确定后,基准孔或者基准轴的公差带就确定了,关键就是选择配合公差带的位置。
而对于选择配合件,我们同样采用类比法,根据使用要求,工作条件确定配合类别。
而对于本题的变压器这类要求装拆方便的,应该选用间隙配合。
本题,我们对基本尺寸至500mm 规定的配合最优选择中(见附录三表7),线圈的内筒和铁心柱的外接圆公差的等级关系以IT8为界。
IT8的线圈的内筒可与同级的或高一级的铁心柱的外接圆配合(例如H8/f8,H8/f7);高于IT8的线圈内筒均采用与高一级的铁心柱的外接圆配合(例如H7/f6);低于IT8的线圈内筒、铁心柱均采用同级配合(例如H10/d10),这是因为在常用尺寸段中,轴较孔的加工容易控制。
而对于基本尺寸在500mm 至3150mm 配合的选择,由于500mm 至3150mm 段零件通常是单件小批量生产,往往采用配作或修配的制造方式,不一定要求达到互换性;在实际使用中,对大尺寸零件的结合往往只要求保证配合的特性,而不强求保持严格的基本尺寸;大尺寸线圈的内径达到的测量精度一般比铁心柱的外接圆更高一些等特点,因此,我们采用基孔制同级线圈内径、铁心柱的外接圆配合,无需算出其最优的配合。
而计算所需要的标准公差数值参照附录二的表6。
问题三:对小容量变压器,通过单位高度铁心柱表面传热的温升不会有问题;但大型变压器的铁心直径很大,单位面积热负荷大,且热传导路径很长,在铁心内部传导出所产生的损耗,可能会发生铁心的过热。
油道的位置应使其分割的相邻两部分铁心柱截面积近似相等。
油道处于相邻两级间,i S '取油道间的面积。
1n 211.....S S S S +++='21112n2.....n n S S S S ++'=+++······112...m mm n n n S S S S +++'=+++; 油道为m 时,将铁心柱截面分为m+1部分,即1S ',2S ',···mS ',1+'m S ,要求各部分面积必须近似相等,则各级面积应与1+m S 近似相等, 即 1+≈'m S S i 1,...,2,1+=m i 。