金属及各类晶体配位数计算图总结共140页文档

既有共价键又有金属键和范 1、在晶体学中配位数与晶胞类型有关；
2、离子晶体中指一个离子周围最近的异电性离子的数目；
德华力，属于混合型晶体 它可以描述晶体中粒子排列的紧密程度，粒子排列越紧密，配位数越大，结合能越低，晶体结构越稳定。 C的杂化方式：SP 2
谢谢！
谢谢观看
铜型
采用这种堆 积的典型代
表
空间利用率
配位数
Po
52℅
6
Na K Fe
68℅
8
Mg Zn Ti
74℅
12
Cu Ag Au
74℅
12
混合型晶体
1、在晶体学中配位数与晶胞类型有关； 非密置层堆积——简单立方堆积 配位数：在晶体中与离子（或原子）直接相连的离子（或原子）数。 半径越小，金属键越强 如碱金属 3、配位化学中，化合物中性原子周围的配位原子的数目。 概念：一个粒子周围最近邻的粒子数称为配位数。 半径越小，金属键越强 如碱金属 金属晶体的原子堆积模型 金属晶体的原子堆积模型
在提到配位数时应当分析其所处环境。
• 1、在晶体学中配位数与晶胞类型有关； • 2、离子晶体中指一个离子周围最近的异电性离子的数目； • 3、配位化学中，化合物中性原子周围的配位原子的数目。
配位数：在晶体中与离子（或原子）直接相连的离 子（或原子）数。
金属晶体的原子堆积模型
非密置层，配位 数是4
金属晶体配位数计算
影响金属键强弱的因素
金属阳离子的半径
半径越小，金属键越强
如碱金属
金属阳离子的电荷数 电荷越多，金属键越强；如
Al>Mg>Na 金属阳离子的堆积方式
配位数
概念：一个粒子周围最近邻的粒子数称为配位数。

解析：
① Ni原子的配位数为: Ni原子的数目为: 8×1/8 + 6×1/2 =4 ②晶体的密度为: m= 4M/NA ; V= a3 ,a2+a2+a2 = (4r)2 3a2=16r2→a=4d/3 p=m/v=4M/NA/4d/3= 3M/dNA
探究3：已知铜晶胞是面心立方晶胞，该晶胞的 边长为3.6210-10m ，每一个铜原子的质量为 1.05510-25kg ，试回答下列问题： （1）一个晶胞中“实际”拥有的铜原子数是多 少？ （2）该晶胞的体积是多大？ （3）利用以上结果计算金属铜的密度。 （4）计算空间利用率。
探究1：单质晶体中原子的堆积方式
如下图所示，其晶胞特征如下图乙所示，原子之间 相互位置关系的平面图如下图丙所示。
甲
乙
丙
若已知Ni的原子半径为d，NA代表阿伏加德罗常数，Ni的 相对原子质量为M，请回答： ①晶胞中Ni原子的配位数为___ ___ _ ，一个晶胞中Ni 原子的数目为_ _； ②该晶体的密度为______ _ （用字母表示）。
a
3
100 %
晶胞的有关计算


1） 利用晶胞参数可计算晶胞体积(V)，根据相对分子 质量(M)、晶胞中粒子数(Z)和阿伏伽德罗NA，可计算 晶体的密度 ：M·Z/NA·V 2）已知棱长，求某线段。晶胞中各线段间的关系如下：



3 ）空间利用率：指构成晶体的微粒在整个晶体空间中 所占有的体积百分比。 球体积 空间利用率 = ———— 100% 晶胞体积
配位数：在晶体中与离子直接相连的 离子数。
1、简单立方堆积
-配位数：6
6 1 4 3 2 1 4 3 5 2
2、钾型（体心立方堆积）

笨，没有学问无颜见爹娘 ……” • “太阳当空照，花儿对我笑，小鸟说早早早……”
配位数
概念：一个粒子周围最近邻的粒子数称为配位数。
它可以描述晶体中粒子排列的紧密程度，粒 子排列越紧密，配位数越大，结合能越低， 晶体结构越稳定。
在提到配位数时应当分析其所处环境。
• 1、在晶体学中配位数与晶胞类型有关； • 2、离子晶体中指一个离子周围最近的异电性离子的数目； • 3、配位化学中，化合物中性原子周围的配位原子的数目。
配位数：在晶体中与离子（或原子）直接相连的离 子（或原子）数。
金属晶体的原子堆积模型
非密置层，配位 数是4
密置层，配位数 是6
非密置层堆积——简单立方堆积
1、简单立方堆积
-配位数：6
1
4
2
3
6146源自2352.体心立方堆积——钾型
2.体心立方堆积——钾型
5
6
8
7
1
2
4
3
-配位数：8
二.密置层堆积
金属晶体的空间结构
影响金属键强弱的因素
金属阳离子的半径
半径越小，金属键越强
如碱金属
金属阳离子的电荷数 电荷越多，金属键越强；如
Al>Mg>Na 金属阳离子的堆积方式
• 你怎么称呼老师？ • 如果老师最后没有总结一节课的重点的难点，你
是否会认为老师的教学方法需要改进？ • 你所经历的课堂，是讲座式还是讨论式？ • 教师的教鞭 • “不怕太阳晒，也不怕那风雨狂，只怕先生骂我
3. 六方最密堆积——镁型
配位数：12
7 19
8 2
6
3
5
4
10
11
12
4.面心立方最密堆积——铜型

8
Mg Zn Ti
74℅
12
Cu Ag Au
74℅
12
混合型晶体
在提到配位数时应当分析其所处环境。
2、离子晶体中指一个离子周围最近的异电性离子的数目；
半径越小，金属键越强 如碱金属
六方最密堆积——镁型
六方最密堆积——镁型
配位数：在晶体中与离子（或原子）直接相连的离子（或原子）数。
电荷越多，金属键越强；
金属晶体配位数计算
影响金属键强弱的因素
金属阳离子的半径
半径越小，金属键越强
如碱金属
金属阳离子的电荷数 电荷越多，金属键越强；如
Al>Mg>Na 金属阳离子的堆积方式
配位数
概念：一个粒子周围最近邻的粒子数称为配位数。 2、离子晶体中指一个离子周围最近的异电性离子的数目；
非密置层堆积——简单立方堆积 概念：一个粒子周围最近邻的粒子数称为配位数。 它可以描述晶体中粒子排列的紧密程度，粒子排列越紧密，配位数越大，结合能越低，晶体结构越稳定。 它可以描述晶体中粒子排列的紧密程度，粒子排列越紧密，配位数越大，结合能越低，晶体结构越稳定。 概念：一个粒子周围最近邻的粒子数称为配位数。 半径越小，金属键越强 如碱金属
2.体心立方堆积——钾型
5
6
8
7
1
2
4
3
-配位数：8
3. 六方最密堆积——镁型
配位数：12
7 19
8 2
6
3
5
4
10
11
12
4.面心立方最密堆积——铜型
堆积模型
简单立方 体心立方 钾型 立方最密 镁型 面心立方最密
铜型
采用这种堆 积的典型代

(4)能否 把“NaCl”称为分子式？
练习
－的距离为 a cm，该晶体密度为
（1）设NaCl晶胞的边长为acm，则
示晶为胞中Na+和Cl-的最近距离（( 即小)立
方体的边长）为 a/2 cm，则晶胞中 同种离子的最近距离为 a/2 cm。
(2)晶胞的边长为acm，求NaCl晶 体的密度。
ρ=
M / NA×晶胞所含粒子数 晶胞的体积
镁型[六方密堆积] （Be Mg ⅢB ⅣB ⅦB ）
12
6
3
54
12
6
3
54
12
6
3
54
A B A B A
找镁型的晶胞
1200
每个晶胞含原子数： 2 配位数： 12
空间占有率：
六方密堆积（镁型）的空间利用率计算：
四点间的夹角均为60°
先求S
在镁型堆积中取出六方晶胞，平行六面体的底是
平行四边形，各边长a=2r，则平行四边形的面积：
找铜型的晶胞
面心立方最密堆积的空间占有率 =74%
金属晶体的四种堆积模型对比
堆积模型
采纳这种堆积 的典型代表
空间利用率
配位数
简单立方
Po（钋）
52%
6
体心立方 （钾型）
K、Na、Fe
68%
8
六方最密 （镁型）
Mg、Zn、Ti
74%
12
面心立方最密 （铜型）
Cu, Ag, Au
74%
12
晶胞
原子晶体
金刚石
该晶胞实际分摊到的碳原子数为 (4 + 6 ×1/2 + 8 ×1/8) = 8个。
小结：高考常见题型 （一） 晶胞中微粒个数的计算， 求化学式

非密置层，配位数 是4
密置层，配位数是 6
第5页，本讲稿共15页
非密置层堆积——简单立方堆积
第6页，本讲稿共15页
1、简单立方堆积
-配位数：6
1
4
2
3
6
1
4
6
2
3
5
第7页，本讲稿共15页
2.体心立方堆积——钾型
第8页，本讲稿共15页
2.体心立方堆积——钾型
5
6
8
7
1
2
4
3
-配位数：8
第9页，本讲稿共15页
二.密置层堆积
第10页，本讲稿共15页
3. 六方最密堆积——镁型
配位数：12
7
1
9
6 5
8
2 3
4
10
11
12
第12页，本讲稿共15页
堆积模型
简单立方 体心立方 钾型 立方最密 镁型 面心立方最密
铜型
采用这种堆 积的典型代
表
空间利用率
配位数
第3页，本讲稿共15页
在提到配位数时应当分析其所处环境。
• 1、在晶体学中配位数与晶胞类型有关； • 2、离子晶体中指一个离子周围最近的异电性离子的数目； • 3、配位化学中，化合物中性原子周围的配位原子的数目。
配位数：在晶体中与离子（或原子）直接相连的离子（或 原子）数。
第4页，本讲稿共15页
金属晶体的原子堆积模型
金属晶体配位数计算
第1页，本讲稿共15页
影响金属键强弱的因素
金属阳离子的半径
金属阳离子的电荷数 金属阳离子的堆积方式
半径越小，金属键越强 如碱金属
电荷越多，金属键越强；如 Al>Mg>Na

02
越紧密，配位数越大，结合能越低，晶体结构越稳
定。
在提到配位数时应当分析其所处环 境。
配位数：在晶体中与离子（或原子） 直接相连的离子（或原子）数。
1. 在晶体学中配位数与晶胞类 型有关；
2. 离子晶体中指一个离子周围 最近的异电性离子的数目；
3. 配位化学中，化合物中性原 子周围的配位原子的数目。
采用这种堆积的 典型代表
空间利用 率
配位数
简单立方
Po
52℅
6
体心立方 钾型
Na K Fe
68℅
8Байду номын сангаас
立方最密 镁型
Mg Zn Ti
74℅
12
面心立方最密 铜型
Cu Ag Au
74℅
12
混合型晶体
C的杂化方式： SP2
既有共价键又有金属键和范德华力，属于混合型晶体
谢谢！
汇报人姓名
汇报日期
金属晶体的原 子堆积模型
非密置层，配 位数是4
密置层，配位 数是6
非密置层堆积——简单立方堆积
-配位数：6
1、简单立方堆积
1
4
2
3
6
1
4
6
2
3
5
2.体心立方堆积——钾型
2.体心立方堆积——钾型
-配位数：8
二.密置层堆积
3. 六方最密堆积——镁型
配位数：12
面心立方最密 堆积——铜型
堆积模型
金属晶体的空间结 构
金属晶体
单击此处添加正文具体内容
影响金属键强弱的因 素
金属阳离子的堆积方 式
半径越小，金属键越 强 如碱金属
金属阳离子的电荷数

金属晶体
金属晶体的空间结构
精选课件
1
影响金属键强弱的因素
金属阳离子的半径
半径越小，金属键越强
如碱金属
金属阳离子的电荷数 电荷越多，金属键越强；如
Al>Mg>Na 金属阳离子的堆积方式
精选课件
2
配位数
概念：一个粒子周围最近邻的粒子数称为配位数。
它可以描述晶体中粒子排列的紧密程度，粒 子排列越紧密，配位数越大，结合能越低， 晶体结构越稳定。
精选课件
3
在提到配位数时应当分析其所处环境。
• 1、在晶体学中配位数与晶胞类型有关； • 2、离子晶体中指一个离子周围最近的异电性离子的数目； • 3、配位化学中，化合物中性原子周围的配位原子的数目。
配位数：在晶体中与离子（或原子）直接相连的离 子（或原子）数。
精选课件
4
金属晶体的原子堆积模型
非密置层，配位 数是4
8 2
6
3
5
4
Hale Waihona Puke 101112
精选课件
11
4.面心立方最密堆积——铜型
精选课件
12
Po
52℅
6
Na K Fe
68℅
8
Mg Zn Ti
74℅
12
Cu Ag Au
74℅
12
精选课件
13
混合型晶体
既有共价键又有金属键和范 德华力，属于混合型晶体 C的杂化方式：SP 2
精选课件
14
谢谢！
精选课件
15
感谢亲观看此幻灯片，此课件部分内容来源于网络， 如有侵权请及时联系我们删除，谢谢配合！
精选课件
密置层，配位数

立方ZnS型离子晶体:
所属晶系: 立方; 点阵: 立方F; 结构基元及每个晶胞中结构基元的数目: ZnS, 4个; Zn和S离子的配位数都是4；
CaF2型离子晶体:
所属晶系: 立方; 点阵: 立方F; 结构基元及每个晶胞中结构基元的数目: CaF2, 4个; Ca和F离子的配位数分别是8和4；
三、在配位化合物(简称配合物) 中

配位场理论认为中心原子的内层轨道受 周围配体的影响，也即关系到配位数。 例如，Ni2+离子与H2O和NH3等具有小的相 互排斥力的弱场配体，生成配位数为 6 的【Ni(H2O)6】2+和【Ni(NH3)6】2+等八面 体配离子;与Br-和I-等具有大的相互排斥 力的弱场配体则趋向于生成配位数为4的 【NiBr4】2-和【NiI4】2-等正四面体配离 子；与CN-等强场配体则生成配位数为4
3.典型结构的配位数 (1)六角密积和立方密积的配位数都是十二。即晶体中最
大配位数为十二。
(2)当晶体不是由全同的粒子组成时，相应的配位数要发
生变化—减小。由于晶体的对称性和周期性的特点，以
及粒子在结合成晶体时，是朝着结合能最小、最稳固的
方向发展。因此，相应的配位数只能取:
8(CsCl型结构)、6(NaCl型结构)、4(金刚石型结构)、
3(层状结构)、2(链状结构)。
4.氯化铯型结构的配位数
如图所示，大球(半径为R)中心为立方体顶角，小 球(半径为r)位于立方体的中心。 如果大球相切，则
立方体的边长为：
空间对角线的长度为： ak
a 2R
Cs

3a 2 3 R
RCl - 1.81 A rC s 1.69 A
o o

4 3 4 3 3 2 r 2 ( a) 3 3 4 100% 68% 3 3 a a
空间利用率计算
例2：求面心立方晶胞的空间利用率.
解：晶胞边长为a，原子半径为r. 由勾股定理： a 2 + a 2 = (4r)2 a = 2.83 r 每个面心立方晶胞含原子数目： 8 1/8 + 6 ½ = 4 = (4 4/3 r 3) / a 3 = (4 4/3 r 3) / (2.83 r ) 3 100 % = 74 %
解：体心立方晶胞：中心有1个原子， 8个顶点各1个原子，每个 原子被8个 晶胞共享。每个晶胞含有几个原子:1 &半径为r 、晶胞边长为a ，根据勾股定理， 得：2a 2 + a 2 = (4r) 2 2 2 3a 16r
3 r a 4
空间利用率 = 晶胞含有原子的体积 / 晶胞体积 100% =
配位数：在晶体中与离子直接相连的离子数。
1、简单立方堆积 -配位数：6
6 1 4 3 2 1 4 3 5 2
2、钾型（体心立方堆积） -配位数：8
5 8 1 4 3
6
7 2
3. 镁型（立方紧密堆积）
配位数：12
6
5 10 7
1
8
9
2
3
4
11
12
空间利用率计算
例1：计算体心立方晶胞中金属原子的空间利用率。

配位数
概念：一个粒子周围最近邻的粒子数称为配位数。
它可以描述晶体中粒子排列的紧密程度，粒子排 列越紧密，配位数越大，结合能越低，晶体结构 越稳定。
第二页，共14页。
在提到配位数时应当分析其所处环境。
• 1、在晶体学中配位数与晶胞类型有关； • 2、离子晶体中指一个离子周围最近的异电性离子的数目； • 3、配位化学中，化合物中性原子周围的配位原子的数目。
配位数：在晶体中与离子（或原子）直接相连的离 子（或原子）数。
第三页，共14页。
金属晶体的原子堆积模型
非密置层，配位数 是4
第四页，共14页。
密置层，配位数是 6
非密置层堆积——简单立方堆积
第五页，共14页。
1、简单立方堆积
1 4
3
-配位数：6
6
1
2
4
6
2
3
5
第六页，共14页。
2.体心立方堆积——钾型
第七页，共14页。
2.体心立方堆积——钾型
5
6
8
7
1
2
4
3
第八页，共14页。
-配位数：8
二.密置层堆积
第九页，共14页。
3. 六方最密堆积——镁型
配位数：12
7
1
9
6
5
8
2
3 4
10
11
12
第十页，共14页。
4.面心立方最密堆积——铜型
第十一页，共14页。
堆积模型
简单立方 体心立方 钾型 立方最密 镁型 面心立方最密 铜
金属晶体金属晶体的空间结构影响金属键强弱的因素金属阳离子的电荷数金属阳离子的堆积方式金属阳离子的半径半径越小金属键越强如碱金属电荷越多金属键越强

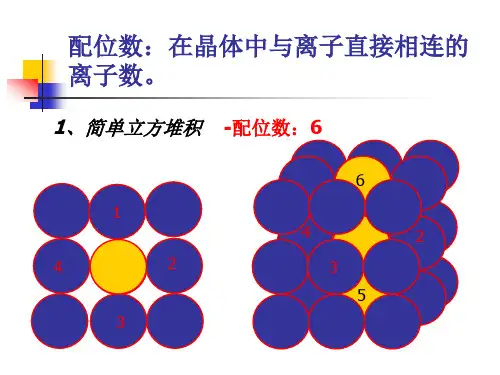
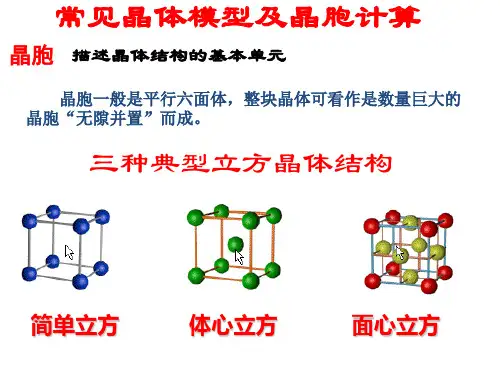
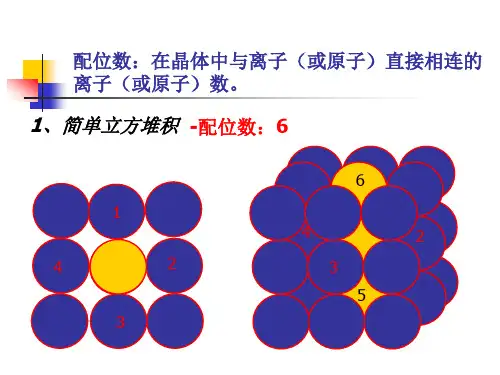
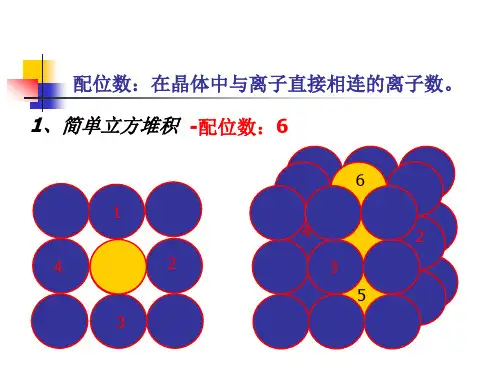
二.晶体的配位数，密度，距离，空间利用率计算1.课本模型图一个CO2分子周围阳离子的配位数是阳离子的配位数是有个分子紧邻阴离子的配位数是阴离子的配位数是阳离子周围的阳离子阳离子周围最近的阳离子数阴离子周围的阴离子阴离子周围最近的阴离子数CaF2CaF2F-的配位数是简单立方堆积体心立方堆积Ca2+的配位数是配位数是配位数是Ca2+周围的最近Ca2+数是F- 周围最近的F-数是面心立方最密堆积六方最密堆积金刚石配位数是配位数是配位数是标出A,B,C各层的原子2、在自然界中TiO2有金红石、板钛矿、锐钛矿三种晶型，其中金红石的晶胞如右图所示，则其中Ti4+的配位数为化学式为3.晶体中距每个X原子周围距离最近的Q原子有个．每个Q原子周围距离最近的X原子有个,Z原子周围距离最近的X有个,每个X原子周围距离最近的Z原子有个,每个Z原子周围距离最近的Q原子有个4.若en代表乙二胺（）则配合物[Pt(en)2]Cl4中心离子的配位数为。

σ链数目为。

配离子[PtEn）2]4+的配位数为，该配离子含有的微粒间的作用力类型有5.立方氮化硼，其结构和硬度都与金刚石相似。

（1）晶胞边长为361.5pm，立方氮化硼的密度是g/cm3．（只要求列算式）．（2）如图是立方氮化硼晶胞沿z轴的投影图，请在图中圆球上涂“●”和画“×”分别标明B与N的相对位置．6.列式表示(NA表示阿伏伽德罗常数的值)（1）钋原子半径为r pm，相对原子质量为M,晶体钋的密度空间利用率（2）钠原子半径为a pm,晶体钠的密度空间利用率（3）银原子半径为d cm，银晶体的密度空间利用率（4）锌原子半径为b nm 锌晶体的密度空间利用率7.列式并计算（1）铁原子半径为r pm铁晶体有2种分别是钾型铜型，铁晶体的钾型铜型密度之比为（2）金刚石原子半径为r pm列式并计算表示空间利用率8.（1）已知CaF2晶体密度为dg/cm3则F﹣与F﹣的最短距离为nm,F﹣与Ca2+最短距离为pm. （2）CaF2的Ca2+,F-半径分别为r1,r2 pm，把晶胞看成阳离子刚性球堆积，阴离子填充其中列式表示CaF2晶胞空间利用率Ca2+间最近距离，F-间最近距离9.已知氧化镍的密度为ρg/cm3；其纳米粒子的直径为Dnm，列式表示其比表面积m2/g。

晶体结构总结一、离子晶体晶体结构离子晶体的结构类型的制约因素主要是离子的电荷比（决定数量比）和半径大小比（决定配位数），离子的电子组态在一定程度上也会影响它的晶体结构，这三个性质综合起来还会决定离子键的共价性成分，后者过分强烈时，将使离子晶体转变为原子晶体，其间存在离子晶体到原子晶体的过渡型。

离子半径比r+－与配位数和晶体构型的关系堆积方式体心立方堆积面心立方最密堆积六方最密堆积三、原子晶体1.金刚石、晶体硅的结构：金刚石的晶体结构如下图所示，每个碳原子以sp3杂化与相邻的4个碳原子形成4个共价键，把晶体内所有的C原子连结成一个整体，形成空间网状结构，这种结构使金刚石具有很大的硬度和熔沸点。

由金刚石晶胞得，在一个金刚石晶胞中，含有8个C原子。

晶体硅具有金刚石型的结构。

只需将金刚石中的C原子换成Si原子，即得到硅的结构。

2.SiO2的结构:在每个Si—Si键中插入1个O原子，即得到SiO2的晶体结构，如下图所示，每个Si原子与4个氧原子形成1个Si—O四面体，Si原子配位数为4，O原子配位数为2.四、分子晶体水凝结变成冰，冰晶体中，H2O分子之间存在范德华力和氢键，其晶体结构如下图所示：CO2晶体俗称干冰，CO2分子之间通过范德华力结合，其晶胞如下图所示：注意：在干冰晶体结构中，每个CO2分子周围与之最近且等距离CO2分子的个数有12个。

五、混合型晶体混合型晶体又称过渡型晶体，石墨是典型的混合型晶体。

晶体的微粒之间存在两种或两种以上的作用力，这样的晶体就是混合型晶体。

石墨是层状结构，C原子采用sp2杂化轨道，与相邻的三个C原子以σ键相连结。

每个C原子周围形成三个σ键，键角120°。

每个C原子还有一个2p轨道，其中有一个2p电子。

这些2p 轨道都垂直于sp2杂化轨道的平面，因此互相平行，形成了大π键。

大π键中的电子沿层面方向的活动能力很强，与金属中的自由电子具有相似之处，所以石墨具有金属光泽，并具有良好的导电和导热性。