河南豫东八校必修一模块训练

豫东名校2022--2023学年高一年上期第一次联合调研考试物理试卷(考试时间:75分钟试卷满分:100分)注意事项:1.答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后,将本试卷和答题卡一并交回。

一、单项选择题:本题共7小题，每小题4分，共28分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 下面各图的文字叙述正确的是( )A.图1中，19.19 s表示时刻B.图2中，跳水运动员在裁判眼里可以看作质点C.图3中，高铁车厢里显示的速度为瞬时速度D.图4中，两人对跳伞员的描述不同是因为参考系不同2. 一个质点做方向不变的直线运动，加速度的方向始终与速度方向相同，但加速度大小逐渐减小直至为零。

在此过程中( )A.速度逐渐减小，位移逐渐增大，当加速度减小到零时，速度达到最小值B.速度逐渐增大，位移逐渐增大，当加速度减小到零时，速度达到最大值C.速度逐渐减小，位移逐渐增大，当加速度减小到零时，位移将不再增大D.速度逐渐增大，位移逐渐减小，当加速度减小到零时，位移达到最小值3. 关于质点在某段时间内的位移和路程，下列说法正确的是( )A.位移为零，该质点一定是静止的B.路程为零，该质点一定是静止的C.沿直线运动的质点，位移大小一定等于其路程D.沿曲线运动的质点，位移大小可能大于其路程4. 如图所示，气垫导轨上滑块经过光电门时，遮光条将光遮住，电子计时器可自动记录遮光时间Δt ，测得遮光条的宽度为Δx ，用ΔΔx t 近似代表滑块通过光电门时的瞬时速度，为使ΔΔx t更接近瞬时速度，正确的措施是( )A.换用宽度更窄的遮光条B.提高测量遮光条宽度的精确度C.使滑块的释放点更靠近光电门D.增大气垫导轨与水平面的夹角5. 2020年7月，在青岛附近海域国产大型水陆两栖飞机“鲲龙”AG600成功实现海上首飞。

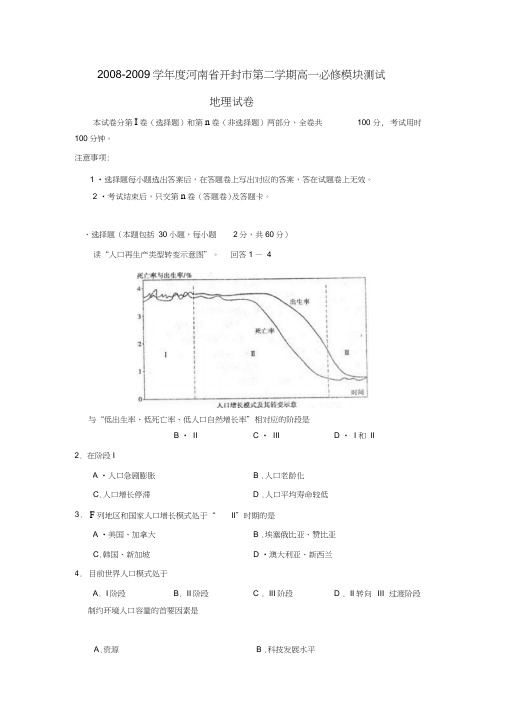
2008-2009学年度河南省开封市第二学期高一必修模块测试地理试卷100分钟。

注意事项:1 •选择题每小题选出答案后，在答题卷上写出对应的答案，答在试题卷上无效。

与“低出生率、低死亡率、低人口自然增长率”相对应的阶段是制约环境人口容量的首要因素是本试卷分第I 卷（选择题）和第n 卷（非选择题）两部分，全卷共100 分, 考试用时2 •考试结束后，只交第n 卷（答题卷）及答题卡。

、选择题（本题包括 30小题，每小题 2分，共60分）读“人口再生产类型转变示意图”。

2. 在阶段IB • IIC • IIID • I 和 IIA •人口急剧膨胀B .人口老龄化C .人口增长停滞D .人口平均寿命较低 3.F 列地区和国家人口增长模式处于“II ”时期的是A •美国、加拿大B .埃塞俄比亚、赞比亚C .韩国、新加坡D •澳大利亚、新西兰4. 目前世界人口模式处于A . I 阶段B . II 阶段C . III 阶段D . II 转向 III 过渡阶段回答1 — 4题。

C .人口的文化水平D •人口的生活消费水平6.关于全球环境人口容量的叙述，乐观者认为A •现今世界人口已超过了全球的环境人口容量B .未来世界人口不会达到全球环境人口容量的极限值C .未来全球的环境人口容量可稳定在110亿或略多一些D •由于环境污染和生态退化等问题，全球人口不能再增长了 读“伦敦的城市规则和布局示意”图回答7〜8题。

9.下列叙述正确的是7•伦敦的城市地域结构模式属于A .同心圆模式B .扇形模式C .多核心模式D &为改善城市环境，伦敦采取的主要措施是A .分散和减少大城市职能 B. 在城市周围建设新城和卫星城( ).块状模式( )C. 把以政治职能为主的首都和城市的经济职能完全分离D. 选择新址，建新首都读“荷兰圩田居民点设置规划”图，回答 9〜11题。

住宅区•扩建裔城 •…大伦敦界 ——内轮牧界A. 该区居民点分为A、B、C三级B. 数目最多的是A级居民点C. B级居民点服务于圩田上的所有居民D. C级居民点设施最完善10•各级居民点的服务范围在空间上的关系是（）A .重叠交错，层层嵌套B .界线分明，彼此相离C.界线分明，偶有交错 D .同级嵌套，偶有交错11•不同等级的城市服务范围的理论主要用来指导（）A .城市工业生产和产品的类型B .郊区农业生产和作物种类的配置C. 区域规划、城市建设和商业网点的布局D. 交通运输和道路的建读“城市化水平随时间变化”图，回答12〜13题城沟人口比W鳴100；------------------------2012.发达国家城市化进程大部分处于( )A. a阶段B. b阶段C. c阶段 D . a阶段和b阶段13.在b阶段中( )A .人口向郊区大量聚集B. 市区出现交通拥挤、住房紧张、环境恶化等问题C. 城市化发展较慢D. 出现逆城市化现象14.新疆吐哈盆地的瓜果农业区位选择的主导因素是内可以通过的最大车流量。

河南省八校2021高三〔上〕第一次联考数学试卷〔文科〕一、选择题：本大题共12小题，每题5分，共60分，在每题给出的四个选项中，只有一项为哪一项符合题目要求的．1．设集合A={x|x2﹣5x+6=0}，B={x|y=log2〔2﹣x〕}，那么A∩〔∁R B〕=〔〕A．{2，3} B．{﹣1，6} C．{3} D．{6}2．设复数z1，z2在复平面内的对应点关于虚轴对称，z1=2+i，那么z1z2=〔〕A．﹣5 B．5C．﹣4+i D．﹣4﹣i3．设a，b为实数，那么“a＞b＞0是＜〞的〔〕A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分又不必要条件4．一个几何体的三视图是一个正方形，一个矩形，一个半圈，尺寸大小如下图，那么该几何体的外表积是〔〕A．πB．3π+4 C．π+4 D．2π+45．向量=〔sin〔α+〕，1〕，=〔4，4cosα﹣〕，假设⊥，那么sin〔α+〕等于〔〕A．﹣B．﹣C．D．6．等差数列{a n}中，S n是前n项和，S1=﹣6，S5﹣S2=6，那么|a1|+|a2|+|a3|+|a4|+|a5|﹣=〔〕A．0 B．6C．12 D．187．某程序框图如图，当输入x=3时，那么输出的y=〔〕A．1 B．2C．4D．88．函数f〔x〕是R上的可导函数，f〔x〕的导数f′〔x〕的图象如图，那么以下结论正确的选项是〔〕A．a，c分别是极大值点和极小值点B．b，c分别是极大值点和极小值点C．f〔x〕在区间〔a，c〕上是增函数D．f〔x〕在区间〔b，c〕上是减函数9．设a=2﹣0.5，b=log3π，c=log42，那么〔〕A．b＞a＞c B．b＞c＞a C．a＞b＞c D．a＞c＞b10．中心在原点，焦点在x轴上的双曲线，一条渐近线方程是y=x，那么双曲线的离心率是〔〕A．B．C．D．211．函数f〔x〕=+ax2+2bx+c的两个极值分别为f〔x1〕和f〔x2〕，假设x1和x2分别在区间〔﹣2，0〕与〔0，2〕内，那么的取值范围为〔〕A．〔﹣2，〕B．[﹣2，]C．〔﹣∞，﹣2〕∪〔，+∞〕D．〔﹣∞，﹣2]∪[，+∞〕12．函数f〔x〕=lnx+x﹣，那么函数的零点所在的区间是〔〕A．〔，〕B．〔，〕C．〔，1〕D．〔1，2〕二、填空题：〔本大题共4小题，每题5分，共20分〕13．假设函数y=f〔x〕的值域是[1，3]，那么函数F〔x〕=1﹣2f〔x+3〕的值域是_________．14．数列{a n}中，S n是前n项和，且S n=2a n+1，那么数列的通项a n=_________．15．假设函数f〔x〕=x3+a|x﹣1|在[0，+∞〕上单调递增，那么实数a的取值范围是_________．16．以下5个命题，其中正确的选项是命题_________〔写出所有正确的命题代号〕①函数y=x+，x∈[1，4]的最大值是4；②底面直径和高都是2的圆柱侧面积，等于内切球的外表积；③在抽样过程中，三种抽样方法抽取样本时，每个个体被抽取的可能性不相等；④F1，F2是椭圆+=1〔a＞0〕的两个焦点，过F1点的弦AB，△ABF2的周长是4a；⑤“∀x∈R，|x|＞x〞的否认，“∃x∈R，|x|≤x〞．三、解答题：解容许写出必要的文字说明、证明过程或演算步骤．〔共70分〕17．〔12分〕设△ABC的内角A，B，C的对边分别为a，b，c，且b=3，c=2，S△ABC=．〔Ⅰ〕求角A的值；〔Ⅱ〕当角A钝角时，求BC边上的高．18．〔12分〕抛掷一枚质地不均匀的骰子，出现向上点数为1，2，3，4，5，6的概率依次记为p1，p2，p3，p4，p5，p6，经统计发现，数列{p n}恰好构成等差数列，且p4是p1的3倍．〔Ⅰ〕求数列{p n}的通项公式．〔Ⅱ〕甲、乙两人用这枚骰子玩游戏，并规定：掷一次骰子后，假设向上点数为奇数，那么甲获胜，否那么已获胜，请问这样的规那么对甲、乙二人是否公平？请说明理由；〔Ⅲ〕甲、乙、丙三人用这枚骰子玩游戏，根据掷一次后向上的点数决定胜出者，并制定了公平的游戏方案，试在下面的表格中列举出两种可能的方案〔不必证明〕．方案序号甲胜出对应点数乙胜出对应点数丙胜出对应点数①②19．〔12分〕矩形ABCD，ED⊥平面ABCD，EF∥DC，EF=DE=AD=AB=2，O为BD中点．〔Ⅰ〕求证：EO∥平面BCF；〔Ⅱ〕求几何体ABCDEF的体积．20．〔12分〕抛物线y=x2，过点P〔0，2〕作直功l，交抛物线于A、B两点，O为坐标原点．〔Ⅰ〕求证：•为定值；〔Ⅱ〕求三角形AOB面积的最小值．21．〔12分〕函数f〔x〕=，其中a∈R〔Ⅰ〕假设a=0，求函数f〔x〕的定义域和极值；〔Ⅱ〕当a=1时，试确定函数g〔x〕=f〔x〕﹣1的零点个数，并证明．四、选考题〔请考生在第22、23、24题中任选一题作答，如果多做，那么按所做第一题记分．〕选修4-1：几何证明选讲22．〔10分〕如图，D，E分别为△ABC的边AB，AC上的点，且不与△ABC的顶点重合，AE的长为m，AC的长为n，AD，AB的长是关于x的方程x2﹣14x﹣mn=0的两个根．〔Ⅰ〕证明：C，B，D，E四点共圆；〔Ⅱ〕假设∠A=90°，且m=4，n=6，求C，B，D，E所在圆的半径．五、选考题〔请考生在第22、23、24题中任选一题作答，如果多做，那么按所做第一题记分．〕选修4-4：坐标素与参数方程23．圆C的极坐标方程为ρ=2cosθ，直线l的参数方程为〔t为参数，t∈R〕．〔Ⅰ〕求直线l的普通方程和圆C的直角坐标方程；〔Ⅱ〕求直线l与圆C相交的弦长．六、选考题〔请考生在第22、23、24题中任选一题作答，如果多做，那么按所做第一题记分．〕选修4-5：不等式选讲24．设函数f〔x〕=|2x+1|﹣|x﹣3|〔1〕求函数y=f〔x〕的最小值；〔2〕假设f〔x〕≥ax+恒成立，求实数a的取值范围．高三数学〔文〕试题参考答案一选择题：13.[5,1]--二填空题： 14. 12n n a -=- 15. [3,0]- 16. ②⑤ 三解答题：17. 〔本小题总分值12分〕解：〔Ⅰ〕由题设3,2,ABC b c S ∆===和1sin 2ABC S bc A ∆=得，132sin 2A ⨯⨯=，∴sin A =…………………………4分 ∴60A =或120A =………………….………………6分 〔Ⅱ〕由120A =…………………………………………7分由余弦定理得，29412cos12019a =+-=，∴a =………10分 设BC 边上的高为h ，由三角形面积相等得，h =⇒=12分题号1 2 3 4 5 6 7 8 910 11 12 答案 A B A B B C A C A DCC19. 〔本小题总分值12分〕证明：〔Ⅰ〕在矩形ABCD 中，取BC 的中点G ，连接FG ，OG 由O 为BD 中点知，OG ∥DC ，OG =12DC ，又EF ∥DC ，EF = 12AB= 12DC ∴OG ∥EF 且OG=EF ，∴OGFE 是平行四边形，……………4分∴EO ∥FG ，又FG ⊂平面BCF ，∴EO ∥平面BC F ……………………6分解：〔Ⅱ〕连接AC ，AF ，那么几何体ABCDEF 的 体积为A EDCF F ABC V V V --=+………………………7分 由ED ⊥平面ABCD ，ABCD 为矩形得，AD ⊥平面EDCF ， ∴AD 是四棱锥A EDCF -的高，又EF ∥DC ，∴EDCF 是直角梯形，又EF=DE=AD=12AB=2， ∴1162433A EDCF EDCF V S AD -=⨯⨯=⨯⨯=………………………9分在三棱锥F ABC -中，高ED=2，∴11842333F ABC ABC V S ED -∆=⨯⨯=⨯⨯=…………………………11分∴几何体ABCDEF 的体积为820433V =+=…………………………12分20. 〔本小题总分值12分〕证明：〔Ⅰ〕设过点(0,2)P 的直线l ：2y kx =+，由2214y kx y x =+⎧⎪⎨=⎪⎩得，2480x kx --=令1122(,),(,)A x y B x y ，∴12124,8x x kx x +==-………………4分 ∴2212121212116OA OB x x y y x x x x ⋅=+=+844=-+=-为定值……6分 解：〔Ⅱ〕由〔Ⅰ〕知，12||||AB x x =-==，原点到直线l 的距离d =……………10分∴1||2AOB S AB d ∆=⨯⨯=≥ 当0k =时，三角形AOB 面的最小，最小值是………………12分A B CDO EFG21．〔本小题总分值12分〕解：〔Ⅰ〕函数()1xe f x x =+的定义域为{|,x x ∈R 且1}x ≠-，………………2分2()(1)xxe f x x '=+．令()0f x '=，得0x =．当x 变化时，()f x 和()f x '的变化情况如下： x (,1)-∞- (1,0)- 0(0,)+∞ ()f x ' － － 0 ＋ ()f x↘ ↘ 极小 ↗ 所以()f x 的单调减区间为(,1)-∞-，(1,0)-；单调增区间(0,)+∞．故当0x =时，函数()f x 有极小值(0)1f =. ……………… 5分〔Ⅱ〕结论：函数()g x 存在两个零点．证明过程如下：由题意，函数2()11xe g x x x =-++．因为22131()024x x x ++=++>．所以函数()g x 的定义域为R ．求导，得22222e (1)e (21)e (1)()(1)(1)x x x x x x x x g x x x x x ++-+-'==++++，…………………… 7分令()0g x '=，得10x =，21x =，当x 变化时，()g x 和()g x '的变化情况如下： x (,0)-∞ 0(0,1) 1 (1,)+∞ ()g x ' + 0 — 0+ ()g x↗极大 ↘ 极小 ↗故函数()g x 的单调减区间为(0,1)；单调增区间为(,0)-∞，(1,)+∞． 当0x =时，函数()g x 有极大值(0)0g =； 当1x =时，函数()g x 有极小值e(1)13g =-. ………………………… 10分 因为函数()g x 在(,0)-∞单调递增，且(0)0g =，所以对于任意(,0)x ∈-∞，()0g x ≠. 因为函数()g x 在(0,1)单调递减，且(0)0g =，所以对于任意(0,1)x ∈，()0g x ≠.因为函数()g x 在(1,)+∞单调递增，且e(1)103g =-<，2e (2)107g =->， 所以函数()g x 在(1,)+∞上存在唯一0x ，使得0()0g x =，故函数()g x 存在两个零点〔即0和0x 〕． ……………… 12分请考生在第22、23、24三题中任选一题做答，如果多做，那么按所做的第一题记分。

河南省豫东八校必修一模块训练（二）一、选择题（本大题共12小题，每小题5分，共60分）1.集合{2|90}x x -=的所有元素之和为 （ ）A.3B.-3C.0D.9 2.( ) A.（0,2）B.[0,2]C.[0,2)D.(0,2] 3．函数()f x0 ）A ．是奇函数但不是偶函数B ．是偶函数但不是奇函数C ．既是奇函数又是偶函数D ．既不是奇函数又不是偶函数 4.若偶函数)(x f 在),0(+∞上是减函数，则下列关系式中成立的是（ ）ABC D 5. 若方程xx )1ln(=+的根在区间))(1,(Z kk k ∈+上，则k的值为（ ）A ．1-B ．1C ．1-或2D ． 1-或16.已知[0,1]x ∈，则函数y 的值域是（ ）A ．]13,12[--B ．]3,1[C ．]3,12[-D ．]12,0[-7．设f(x)=⎪⎩⎪⎨⎧>+≤--1||,111||,2|1|2x x x x ，则1(())2f f 等于（ ）A ．21B ．134C ．59- D ． 4125 8．三个数26.0=a ，6.0log 2=b ，6.02=c 之间的大小关系是( )A ．b <a <cB ．a <c <bC ．a <b <cD ．b <c <a9．函数|1|ln )(-=x x f 的图象大致是( )10．设()f x 是偶函数，且在(0,)+∞内是减函数，又(3)0f -=，则0)(>x xf 的解集是( )A ．{}|303x x x -<<>或 B. {}|33x x x <->或 C. {}|3003x x x -<<<<或 D. {}|303x x x <-<<或11．定义在R 上的函数()x f 满足()()x f x f -=+1，当[]1,0∈x 时()2121+--=x x f ， 则=⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛29925f fA ． 21-B ．0C ．21D ． 112．在x y 2=、x y 2log =、2x y =这三个函数中，当1201x x <<<时，使()()222121x f x f x x f +>⎪⎭⎫ ⎝⎛+恒成立的函数个数是：A ．0B ．1C ． 2D ． 3二、填空题（本大题共4小题，每小题5分，共20分）13. 已知2=(3--1)m y m m x 是幂函数，则m =__________14.函数212log (23)y x x =--的单调递增区间是_____________..15.已知,2)1(x x x f +=+则函数)(x f 的解析式为______.16.设函数22460()6log (1)0x x x f x x x ⎧-+≥=⎨--<⎩，，，若互不相同的三个实数123x x x ，，满足123()()()f x f x f x ==，则123x x x ++的取值范围是 .三、解答题：（本大题共6小题，第17题10分，其余每小题12分，共70分）.17．已知集合{}52|≤≤-=x x A ，集合{}121-≤≤+=p x p x B ，若B B A = ,求实数p 的取值范围。

豫东名校2022--2023学年高一年上期第一次联合调研考试英语试卷考生注意:1.本试赛分选择题和非选择题两部分。

满分150 分，考试时间120分钟。

2.答题前，考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚。

3.考生作答时，请将签蜜答在答题卡上。

选择题每小题选出答量后，用2B铅笔把答题卡上对应题目的签案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，超出答题区域书写的答案无效，在试题卷、草稿纸上作答无效。

4.本卷命题范围:必修一，一、二单元。

第一部分听力(共两节，满分30分)第一节(共5小题;每小题15分，满分7.5分)听下面5段对话，选出最佳选项。

1. What does the woman invite the man to do?A. Go bike riding.B.Meet a friend.C. Do some writing.2. What are the speakers talking about?A.Their friends.B. Their favorite food.C. Their hobbies.3. What color hair does the speakers English teacher have?A. Brown.B. Black.C. Grey.4. What will the woman probably study next year?A.History.B. Chemistry.C. Math.5. Why does the woman talk to the man?A.To thank him.B. To congratulate him.C.To ask for advice.第二节(共15小题;每小题15分,满分22.5分)听下面5段对话或独白，选出最佳选项。

听第6段材料，回答第6、7题。

河南省豫东名校2022-2023学年高三上学期摸底联考语文试题一、论述类文本阅读阅读下面的文字，完成下列小题。

哲学社会科学在认识世界、启迪思想、传承文明、创新理论、文化交流等方面发挥着至关重要的作用，能够在多重文化意义之下重叠的生活世界里架起不同解释之间共同认识的桥梁。

发挥哲学社会科学在融通中外文化交流中的价值融通作用。

中国特色社会主义对世界文明的一大贡献是创造了中国式现代化道路和人类文明新形态。

中国特色哲学社会科学揭示了人类文明新形态关于文化与民族、国家、世界关系的真理性原则：携手构建人类命运共同体，这是打造人类和平发展的“共同屋顶”，提出“和平、发展、公平、正义、民主、自由”的全人类共同价值；提出相互尊重、公平正义、合作共赢，建设更具包容性、普惠性的国际秩序；提出共商、共建、共享，建设更加公正合理的全球治理体系；提出不对抗、不冲突，相互尊重，合作共赢建设新型大国关系；倡议并推动“一带一路”建设，建设具有天下意义的共同发展平台。

中国智慧、中国方案、中国力量对跨文化交流的世界哲学的贡献是以文明对话论突破和超越文明等级论。

发挥哲学社会科学在融通中外文化交流中的方法论互学作用。

只有当哲学社会科学拥有有效接受对象、其价值得以传递时，才意味着中外文化交流的实现。

文化交流的方法论需要把“什么是”和“怎么样”结合起来，构建真理与价值相统一的哲学社会科学方法论体系。

在“时间同质化、空间一体化”的互联网时代，中国社会哲学工作者一方面要在文化各个层面展现出中华民族所特有的生存智慧、精神特质、文化血脉；另一方面要融入并丰富世界价值共识，及时地告诉世界一个真实的中国、立体的中国、全面的中国、负责任的社会主义大国，从而有利于推动营造中国当前发展的良好外部环境。

关于文明本质，中国哲学社会科学提出“多彩、平等、包容”的中国思维，为跨文化交流提供了一种新的概念范畴；关于文明关系，中国哲学社会科学提出了“交流、互鉴、共存”的中国主张，为跨文化交流丰富了内容范畴；关于文明发展，中国哲学社会科学提出建构“共商、共建、共享”的中国方案，为跨文化交流指明了方向性目标。

2022-2023学年河南省豫东名校上册高一上册12月质量检测数学模拟试题第I 卷一、选择题:本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

公众号高中试卷资料下载1.已知2:0p x x -<，那么命题p 的一个必要不充分条件是()A.01x << B.11x -<< C.1223x << D.122x <<2.命题“x ∀∈R ，25110x x -+≤”的否定是()A.x ∀∈R ，25110x x -+> B.x ∃∉R ，25110x x -+>C.x ∃∈R ，25110x x -+≤ D.x ∃∈R ，25110x x -+>3.已知0a >，0b >且11149a b +=，则当a b +取到最小值时，a b =()A.49B.94C.23D.324.已知关于x 的不等式210ax bx -+>的解集为()2,,m m ⎛⎫-∞+∞ ⎪⎝⎭，其中0m >，则1b m+的最小值为().A.4B. C.2D.15.设函数()y f x =的定义域为R ；对于任一给定的正数p ，定义函数(),(),(),(),p f x f x p f x p f x p ≤⎧=⎨>⎩则称()p f x 为()f x 的“p 界函数”.若函数2()21f x x x =--，则下列结论：①2(2)2f =；②2()f x 的值域为[2,2]-，③()2f x 在[1,1]-上单调递减；④函数2(1)y f x =+为偶函数.其中正确的结论共有()A.4个B.3个C.2个D.1个6.在同一坐标系内，函数(0)ay x a =≠和1y ax a=-的图象可能为()A. B.C. D.7.已知2log 3a =，0.42b -=， 2.10.5c =，则它们的大小关系是()A.c b a <<B.a c b<< C.a b c << D.b c a<<8.函数20225log (1)3y x x =+--的定义域为()A.(,3)(3,)-∞+∞ B.(1,3)(3,)+∞ C.()1,+∞ D.(3,)+∞二、选择题:本题共4小题，每小题5分，共20分。

政治必修一第二、三单元训练题[2014·豫北豫东十校联考]针对我国当前存在的“天价工资”“灰色收入”“隐性收入”“同工不同酬”“多劳不多得”等不合理的分配现象，党和国家十分关注和重视分配制度改革。

回答1～2题。

1．党和国家之所以十分关注和重视分配制度改革，是因为①收入分配差距是分配不公的重要体现②分配制度改革事关人民福祉和经济发展③收入分配公平是社会公平的基本内容④合理的收入分配制度是社会发展的前提A．①②B．①④C．②③ D．③④2. 面对我国当前收入分配不公的现实，可采取以下措施()①提高居民收入在国民收入分配中的比重②实现劳动报酬增长和劳动生产率提高同步③通过立法限制过高收入，取缔非法收入④初次分配中注重效率，再分配中注重公平A．①②B．①③C．②④D．③④3．从2014年1月1日起，重庆最低工资标准提高至一档1250元/月，二档1150元/月，非全日制职工最低小时工资标准也有提高。

对上调最低工资标准可能带来的影响，在下列选项中错误的是()A．有利于发挥政府在再分配中重要作用B．有利于缩小收入差距，提高居民消费水平C．有利于推动企业技术创新，提高效益D．有利于保护劳动者权益，实现社会公平4.[2013·皖南八校联考]1914年1月，福特公司将技术工人的日工资从80美分提高到5美元。

福特这么做是因为其员工离职率之高超出正常水平，公司每年需雇佣6万人才能保证1万人的用工需求。

尽管加薪后人工成本大幅提升，但在第一年，福特公司的利润几乎翻了一番，希望进入福特公司的工人成群结对地涌来。

这一案例表明()①再分配应更加注重社会公平②公平的实现有助于效率的提高③企业应自觉维护劳动者权益④分配政策对企业经济效益具有决定性影响A．①③B．②③C．②④D．①④5．在美国等经济发达国家，从事慈善事业已经成为富裕阶层的一种普遍追求，像比尔·盖茨这样成功的企业家也是全球最为著名的慈善家。