当前位置：文档之家 › 东北大学材料成型力学讲义

东北大学材料成型力学讲义

  • 格式：ppt
  • 大小：2.69 MB
  • 文档页数：40

下载文档原格式

  / 40

合集下载

东北大学材料成型力学ppt课件

东北大学材料成型力学ppt课件


a
f
在边界点，r = R 时，σr=0, rz 0 ; 由剪应力互
等 zr 0 则边界处满足塑性条件
h
zr r o
r
za ra
2
3
2 zra
s2
R
za s
z
s
2 s
3h
(R r)
7
(3) 接触表面分区情况
由
r rb f zb k
则
zb
s
3f
f k
f f z
rb
（1） f < 0.58，d/h >2[η(f )+1] 三区共存
（2） f < 0.58, 2[η(f)+1]≥d/h≥2 两区共存，常摩擦应力区消失
（3） 当d/h≤2， f为任何值，接触表面只有摩擦应力递减区
（4） f ≥0.58 两区共存,常摩擦系数区消失
9
4） 摩擦应力递减区接触表面压应力分布曲线方程
m 称为摩擦因子，取值0-1
5
（5）其他假设
3.2 圆柱体镦粗
3.2.1 接触表面压应力分布曲线方程
（1） 常摩擦系数区接触表面压应力分布曲线方程
{ f f z
d r 2 f z 0
dr
h
d r d z 0
z
z
a
f
zr r
ho
r
d z 2 f z 0
dr
h
在边界点，r=R时，σr=0,
2f
zb s e h (Rrb ) rb d ( f )
h 2h
常 常摩
摩 摩擦
擦 系 数 区
擦 应 力 区
应 力 递 减 区
8
( f ) 1 ln f 3
【材料课件】材料成型工程学第二讲[1]

【材料课件】材料成型工程学第二讲[1]

【材料课件】材料成型工程学第二讲 [1]
2) 咬入条件的确定(分析金属刚被咬入时的受力)
【材料课件】材料成型工程学第二讲 [1]
受力分析
【材料课件】材料成型工程学第二讲 [1]
结论
【材料课件】材料成型工程学第二讲 [1]
物理概念
• 根据物理概念: • 摩擦系数可用摩擦角表示.即摩擦角的正
切就是摩擦系数f. • tgβ=f • 则 tgβ≥tgα • β≥α • 轧制过程中的咬入条件为摩擦角大于咬
– 由咬入条件 α≤β可知: • 凡是使α降低及β增加的因素,均有利于咬入 • (1) 降低α
•实际生产中以带有楔形端咬入后利用稳定轧制阶段剩余摩擦力,实现咬入. •利用外推力将轧件强制推入轧辊中,外力作用使轧件前端被压扁,相当于楔形外 端降低压下量,有利于咬入.
【材料课件】材料成型工程学第二讲 [1]
• Δh＝H－h • ΔL＝Lh －LH • ΔB＝Bh －BH • 式中 h ，H —— 轧件轧后、轧前高度； • Lh，LH—— 轧件轧后、轧前长度； • Bh，BH—— 轧件轧后、轧前宽度；
【材料课件】材料成型工程学第二讲 [1]
轧制时表示各向变形系数的关 系式
【材料课件】材料成型工程学第二讲 [1]
计算举例
• 已知 D=850 钢锭尺寸 550*550/480*480/1200 • 采用热轧 试问? • 1)当咬入角为30°,采用小头进钢轧制,能否实
现轧制过程. • 2)当压下量为120时,能否实现自然咬入(假定咬
入条件于前面一致) • 3) 求压下量为50时的α及L.
【材料课件】材料成型工程学第二讲 [1]
• 1)从理论讲,改钢锭如何轧制可使轧件轧 一道次厚度最小,轧后厚度为多大.
材料成型力学第一章

材料成型力学第一章


m1 m2 m3
n1 x n2 xy n3 xz
yx zx l1 l 2 y zy m1 m2 yz z n1 n2
T
l3 m3 n3

存在不变量 有主状态
2 2 2 I 3 x y z 2 xy yz zx x yz y zx z xy
三个实根。即所求主应力。
按代数值大小排列
σ1 2 3
主状态下过一点任意一个微分面上的合应力？法向正应力？切向剪应力？
2 2 2 2 S 2 S x S y S z2 12 l 2 2 m 2 3 n 2
x yx zx xy y zy 0 xz yz z
I 1 I 2 I 3 0
3 2
特征方程
I1 x y z
其中
2 2 2 I 2 x y y z z x xy yz zx
x l1l3 y m1 m3 z n1n3 xy (l3 m1 l1m3 ) yz (m1 n3 m3 n1 ) zx (l1n3 l3 n1 )
x y yz zy yz zy xz zx
2 n
l m 1 3 l 2 3
2 3 2 2 2 2 3 2 2 3 2

2 2 1

2 2
2

2 3
2
2
2
2


m
2 2 2 3
2 2
二元函数求极值
2 ( 2
《材料成型原理》教学大纲(金属凝固原理及塑性成形原理部分,基础知识点概括,考研必备)

《材料成型原理》教学大纲(金属凝固原理及塑性成形原理部分,基础知识点概括,考研必备)


§ 9–1 液态金属的脱氧 先期脱氧（焊接） 、预脱氧（熔炼） 、沉淀脱氧、扩散脱氧、真空脱氧；各种脱氧原理 的概念及优、缺点；锰、硅沉淀的脱氧的比较，温度、熔渣的性质对其脱氧效果的影响； § 9–2 液态金属的脱碳反应 液态金属的脱碳精炼反应原理、目的及工艺原则； § 9–3 液态金属的脱硫 液态金属的脱硫原理及脱硫效果的影响因素、目的及工艺原则； § 9–4 液态金属的脱磷 液态金属的脱磷原理及脱磷效果的影响因素、目的及工艺原则；
小于 180o，所以，非均质形核功Δ G he 远小于均质形核功Δ G ho ， 越小，Δ G he 小，夹杂界面
的非均质形核能力越强，形核过冷度越小； §3-4 晶体长大 液-固界面自由能及界面结构类型、本质及其判据；晶体长大方式
第四章 单相及多相合金的结晶
本章从凝固过程溶质再分配的规律谈起，着重讨论所涉及到的“成分过冷”条件及其对 合金凝固组织的影响规律、 单相固溶体合金及多相合金的凝固。 并为后续章节的内容的讨论 奠定基础。 §4-1 凝固过程中溶质再分配
《材料成型原理》教学大纲
总学时： 96→ 总学分： 6 一、 课程的目的和任务 《材料成型原理》 是材料成形及控制专业主要的院定必修课之一。 本课程的任务是对材 料的凝固成形、塑性成形、焊接成形等近代材料成形技术中共同的物理现象、基本规律及各 成形技术的基本原理、理论基础、分析问题的方法加以阐述，使学生对材料成形过程及原理 有深入广泛的实质性理解，为后续的成形技术具体工艺方法、设备控制等课程的学习，为开 发新材料及其成形技术、分析和解决成形过程中的质量缺陷问题奠定理论基础。 二、 本课程的基本要求 1. 了解液态金属和合金的结构、性质，掌握液态金属与合金凝固结晶的基本规律及结 晶过程中的伴随现象，了解冶金处理对凝固组织与材料性能的影响。 2. 掌握材料成形过程中的物理、化学冶金现象及内部规律 。 3. 掌握塑性成形力学基础理论、塑性成形过程中的分析方法与原理。 三、 与其它课程的联系与分工 本课程的理论基础是数学、物理、物理化学、冶金传输原理、工程力学、金属学与热处 理。本课程重点在于阐述成形技术的理论基础、基本原理、分析问题的方法，而不涉及具体 成形工艺方法及参数。 各种具体的成形工艺方法、 原理过程及控制等将在后续专业课程中学 习。 四、 课程内容与学时分配 章次 一 二 三 四 五 六 七 八 九 十 十一 十二 十三 十四 十五 十六 十七 十八 十九 内容 绪论 液态金属的结构和性质 凝固温度场 金属凝固热力学与动力学 单相及多相合金的结晶 铸件宏观组织及其控制 特殊条件下的凝固与成形 液态金属与气相的相互作用 液态金属与渣相的相互作用 液态金属的净化与精炼 焊接热影响区的组织与性能 凝固缺陷及控制 粉末冶金原理 金属塑性成形的物理基础 应力分析 应变分析 屈服准则 材料本构关系 金属塑性变形与流动问题 塑性成形力学的工程应用 总学时数 2 4 6 4 4 2 4 4 4 4 4 12 4 4 6 4 3 8 4 9 课堂讲授学时数 2 4 4 4 4 2 4 4 4 4 4 8 4 4 6 4 3 6 2 9 2 2 4 2 实验时数
第5章 凝固-材料科学基础东北大学

第5章 凝固-材料科学基础东北大学

●
凝固后
液相浓度随凝固距离的变化规律
x k0 1 C L ( x) C0 (1 ) L
平衡凝固
●
固体中溶质的分布曲线为：
x k0 1 C s ( x) k 0C0 (1 ) L
液相完全混合
（2）夜相不完全混合 液体中在液固接触面有层流边界层， 存在溶质的聚集边界层以外对流混合均匀
●
2 由：dΔG/dr = 0，得晶核的临界半径： Gv 2Tm3 3 16 16 临界形核功： GK 3(Gv ) 2 3( Lm T ) 2 rk
过冷度ΔT越大，临界晶核的尺寸越小， 临界形核功减少， 形核的几率增大。 ● 过冷度ΔT为0时，临界形核功和临界晶核的尺寸为∞， 形核不可能发生。 2 16 2 临界晶核的表面积： AK 4 (rk ) 2 G v 1 所以： G K AK
●
ΔG =ΔGv•4/3•πr3 + σ•4πr2
3
● 临界晶核形成时自由能是升高的，液固两相体积自由能的差只能补偿
形成临界晶核表面所需能量的2/3，另外的1/3需要靠液相中的 能量起伏来补充。
● 形核的条件：结构起伏和能量起伏达到一定临界值
原子扩散几率因子
2 形核率(nucleation ratio) 控制形核率的主要因素： 1) 形核功因子： exp（―ΔGk/（RT））， 体系中出现高于能量ΔGk所出现的几率 2) 原子扩散几率因子： exp（―ΔGA/（RT））， ΔGA为原子越过液固相的激活能. 形核率
' k
2 L / S Gv
2 3 cos cos 3 G Gk ( ) 4
● 非均匀形核与均匀形核具有相同的临界半径；
随着过冷度增加，临界半径和临界形核功下降， 有利形核；
材料成形力学课程教学大纲

材料成形力学课程教学大纲

材料成形力学课程教学大纲课程名称：材料成形力学英文名称：Mechanics for Mater i a I s Process i ng课程编号：x2010491学时数：40其中实验（实训）学时数：4课外学时数:学分数：2.5适用专业：材料成型及控制工程一、课程的性质和任务本课程是材料成型及控制工程专业本科学生的专业基础理论课，目的在于使本学科本科生了解材料加工必要的力学知识，为以金属材料为主的塑性加工成形过程的力能计算和变形计算打下必要的专业理论基础。

本课程的主要内容为材料的塑性加工力学，首先从应力和应变分析入手，建立求解塑性加工成形问题的基本方程，进而结合塑性加工实际讲解了主要解析方法：工程法、滑移线法和上界法，并给出了许多实例。

二、课程教学内容的基本要求、重点和难点（1）绪论（2学时）从金属塑性加工过程的概念出发，了解工件的两种不同成形方式。

基本成形方式包括锻造、轧制、挤压、拉拔、冲压、拉伸成形、弯曲和剪切等；组合成形方式包括锻造■轧制、轧制-挤压、拉拔-轧制、轧制-弯曲、轧制-剪切等。

按变形时的温度特征分为热变形、冷变形和温变形。

（2）应力与应变（10学时）掌握应力、点应力状态、主应力、应力张量不变量、偏差应力分量和球应力分量的概念以及主应力图; 掌握应变、主应变、应变张力不变量、应变张量分解、•点附近的应变分析和主应变图，掌握变形与位移方程关系方程的数学表达和相互间的关联。

了解应力坐标变换、应力椭球面、应变速率概念，了解变形表示法、应力应变曲线和变形体模型。

重点：本章节为本课程的基础内容，必须深入理解和全面掌握；其中一点应力状态的数学表达式、特征方程、应力张量不变量、主剪应力、偏差应力分量等需重点掌握；应变的矢量和张量特性，也需掌握。

难点：对应力坐标变换、应力张量、偏差应力、变形与位移关系方程的数学表达理解。

（3）变形力学方程（8学时）深入理解变形力学体系的数学描述方法，掌握直角坐标系的力学平衡微分方程。

材料成形原理-第一章(1)液态金属的结构和性质 PPT课件

材料成形原理-第一章(1)液态金属的结构和性质 PPT课件


1.1固态金属的加热、膨胀及熔化
1.1.2 金属的加热膨胀
当温度升高时，原子振动能量
图1-2 加热时原子间距和 原子势垒的变化
增加，振动频率和振幅增大。以双
原子模型为例，假设左边的原子被
固定不动而右边的原子是自由的。
则随着温度的升高，原子间距将由 R0→R1→R2→R3→R4；原子的能 量也不断升高，由 W0→W1→W2→W3→W4。原子间 距随温度升高而增加，即产生膨胀， 如图1-2所示。膨胀只改变原子的
5、缺点 （1 ）铸件尺寸均一性差； （2） 与压力加工和粉末冶金相比金属的利用率低； （3 ）内在质量比锻件差； （4 ）工作环境粉尘多、温度高、劳动强度大、生产效率低等
2、我国铸造技术的发展
我国铸造技术已有5000年的悠久历史 铸造技术的成就推动了农业、兵器制造、 天文、医药、音乐、艺术等方面的进步
1.2 液态金属的结构
液态金属的结构分析(表观特征)
㊣ 具有流动性 （液体最显著的性质）；
㊣ 可完全占据容器的空间并取得容器内腔的形
表
状 （类似于气体，不同于固体）；
观 ㊣ 不能够象固体那样承受剪切应力，表明液体
特
的原子或分子之间的结合力没有固体中强
征
（类似于气体，不同于固体）；
㊣ 具有自由表面 （类似于固体，不同于气
沧州铁狮的历史照片
湖北当阳铁塔，铸造 于北宋嘉佑六年（公 元1061年），八面十 三层 ，高16.945米, 据铭文记载的铁塔重 七万六千六百斤,当时 是就地设炉分层铸造, 采用堆土法而建起来, 各层之间重叠摆放,没 有焊接 ,整个塔身玲 珑隽秀,从上到下,自 里而外全生铁浇铸,仅 塔刹在 清代以青铜重 铸.
中国和美国1996～2001年铸件产量（万吨）
材料成型原理备课笔记.

材料成型原理备课笔记.

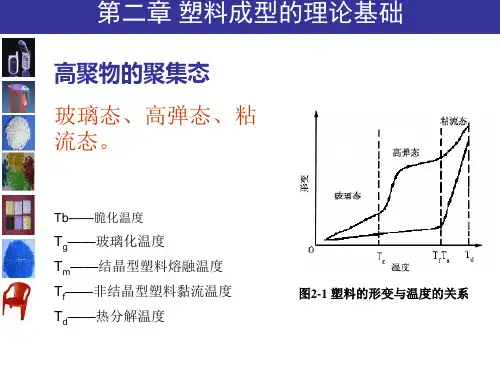
第二篇材料成形力学原理第十三章金属塑性成形的物理基础基本要求：1．掌握金属塑性、抗力及其影响因素；2．了解金属变形机理和变形特征。

第一节 概述一、金属塑性成形的特点定义——塑性是指金属材料在外力作用下发生变形而不破坏其完整性的能力。

人们利用金属的这种特性，使其在外力作用下改变形状，并获得一定力学性能。

这种加工方法，称为金属塑性加工或塑性成形。

用途——金属塑性加工在汽车、拖拉机、船舶、兵器、航空和家用电器等行业都有广泛的应用。

如汽车的大梁和覆盖件是冲压出来的，曲轴、连杆和齿轮的毛坯是锻造出来的。

优点：１．生产效率高，适用于大批量生产２．改善了金属的组织和结构３．材料利用率高４．尺寸精度高二、塑性成形工艺的分类（一）体积成形体积成形是在塑性成形过程中靠体积的转移和重新分配来实现的。

1．锻造 锻造可分为自由锻和模锻。

自由锻是在空气锤或水压机上将毛坯锻成一定的形状和尺寸。

自由锻不使用专用的模具，它的形状和尺寸主要靠工人的熟练技巧来保证。

锻件的尺寸精度较低，生产效率不高，主要适用于单件、小批量生产，以及大型锻件的生产。

模锻是在锻压机器的压力作用下，使金属在模具的孔型中产生塑性变形，获得与模腔形状、尺寸相同的零件，保证相当高的尺寸精度，且生产效率高，适合于大批量生产。

模锻可分开式模锻和闭式模锻。

2．轧制 轧制是将金属坯料通过两个旋转轧辊间的特定孔型，使其形成一定截面形状的成形方法。

利用轧制方法可获得型材、板材和管材。

轧制可分为纵轧、横轧和斜轧。

3．拉拔 拉拔是将金属坯料的前端施以一定的拉力，使它通过锥型的凹模型腔、改变其截面的形状和尺寸的一种加工方法。

拉拔是生产棒材、线材和管材的主要方法，它的生产效率很高。

4．挤压 挤压是使大截面的毛坯在凸模的强大压力作用下产生塑性流动，迫使金属从模具型腔中挤出，从而获得一定形状和较小截面尺寸的工件。

由于金属在挤压模具中受三向压应力作用，挤压成形零件的力学性能极佳。

这种加工方式也特别适用于塑性较差的材料成形。

材料科学基础(东北大学)第六章

材料科学基础(东北大学)第六章


Al2O3 A
LiTaO3
0.2m
LiTaO3颗粒内裂纹发生大角度偏转的TEM照片
Domain Crack
LiTaO3 Particle
如：铁电/压电性畴转变增韧机制，在压电陶瓷材料中，利用使产生裂纹
的外应力转变为电能，从而达到增韧的目的。
ZrO2 颗粒弥散在其他陶瓷 ( 包括 ZrO2 本身 ) 基体中，由于两者具有不同
的热膨胀系数，烧结完成后，在冷却过程中，ZrO2颗粒周围则有不同的
受力情况，当它受到压抑，四方相ZrO2（t-ZrO2）的相变也将受到压抑。 使得瓷体中部分t- ZrO2 在烧成冷却过程中以亚稳态保存下来。 在室温时, ZrO2 颗粒仍以四方相存在, 它有一种力图膨胀而变成单斜相 的自发倾向； 当外力作用时, 陶瓷的内应力可使四方相的ZrO2粒子解除约束,发生四方 相ZrO2( t- ZrO2) 转变成单斜相( m- ZrO2) 的马氏体相变, 引起体积膨胀。
1/ 2
式中E1为主裂纹尖端含有微裂纹材料的弹性模量，fs为显微裂纹密 度，W为过程区宽度的一半，为显微裂纹引起的膨胀应变。
微裂纹增韧同样对温度和粒子尺寸很敏感，合适的颗粒尺寸是大于应力诱 发相变的临界尺寸而小于自发产生危险裂纹的临界尺寸，并且应减小 基质与粒子间的热失配，使其产生最大的相变张应力。 微裂纹的密度大到一定程度后，就会使裂纹相互连接，形成大裂纹，反而 使韧性下降。
替代式溶质原子在基体晶格中造成的畸变大都是球 面对称的，因而强化效果要比填隙式原子小
6.1.2 形变强化（加工硬化）
定义 强化机理
金属在塑性变形过程中位错密度不断增加，使弹性应 力场不断增大，位错间的交互作用不断增强，因而位
错的运动越来越困难—位错强化
材料成型力学第二章

材料成型力学第二章

27变形抗力模型271变形抗力的概念271变形抗力的影响因素1变形温度变形程度40055085090028平面变形和轴对称问题的变形力学方程281平面变形问题xzyzxzyzxyxy几何方程本构方程xyxy力平衡微分方程密赛斯屈服准则静定问题282轴对称变形问题几何方程应力特点zrzrzrzr假设非静定问题一矩形件在刚性槽内压缩如图所示如果忽略锤头槽底侧壁与工件的摩擦试求工件尺寸为hbl垂直纸面方向为l时的锤头压力p和侧壁压力n已知应力状态如图所示试写出力平衡微分方程mises屈服准则tresca屈服准则
可以表示成如下的简化形式
∂ σ ij ∂x j
= 0
∑M
x
=0
∂τ zy ∂τ yz dy dz dz dy τ zy + − τ yz dxdz =0 dz dxdy + τ zy dxdy − τ yz + dy dxdz 2 ∂z ∂y 2 2 2
y
dz
τ yx +
τ yx
y
dy
dy
σx τ yx
dx
τ zx
σx +
σx
x
dx
∂τ zx τ = τ zx + dz ∂z
1 zx
z
τ zx +
τ zx
z x
dz
o
∑X =0
∂τ yx ∂σ x dx dydz − σ x dydz + τ yx + dy dxdz − τ yx dxdz σ x + ∂x ∂y
x z
x+dx z+dz
x
0
z
2.1 力平衡微分方程
材料成型PPT课件

材料成型PPT课件

很显然与交联度有对应关系，但是不相等，因为交联 度不可能达到百分之百。
22.3.2聚聚合合物物在的模流内变的行流为动
入口效应、离模膨胀
Unstable flow
挤出胀大现象
B
A
C
胀大比 die
B D max D0
在工程实践中考虑入口效应的目的有两个：
➢1 保证制品的成型质量，在必要时避免或减 小入口效应。
➢2 在确定注射压力时，在考虑所有流道（包 括浇口）总长引起的压力损耗的同时，还要 考虑入口效应引起的压力损失
•鲨鱼皮形 •波浪形 •竹节形 •螺旋形 •不规则破裂
2.3 聚合物的加热与冷却
• 热源：
– 外热：电阻丝（经济、简单、方便、温度波动 较大）；微波（适合较厚发泡成型）；红外线；
热油（温度控制精确，设备复杂，成本高）； 热水、蒸气。
– 内热：摩擦热
Q
1 J
a
2
• 冷却：水（注射模、挤出定型模、中空模
低分子多为此类
宾汉 流体
假塑 性流 体
膨胀
(τy 和η为常数)
n<1
凝胶糊、良溶 在剪切力增大到一 剂的浓溶液 定值后才能流动。
大多数聚合物 剪切增加，粘度下
熔体、溶液、 降。原因为分子
糊
“解缠”
2.2 聚合物的流变行为
拉伸粘度
如果引起聚合物熔体的流动不是剪切应力
而是拉伸应力时，仿照式（2—2）即有拉
聚合物的结晶
有结晶倾向
两类聚合物
无结晶倾向
结晶过程是聚合物由非晶态转变为晶态的过程，发生 在Tg和Tm温度之间。
结晶度：聚合物是不可能完全结晶的，仅有 有限的结晶度，而且结晶度依聚合物结晶的历史 不同而不同。

材料成型概论第二章材料成型的基础1


3.晶粒出现方向性；
4.除晶粒内部变形外，在晶界上 也发生变形。
31
加工过程中的硬化
加工硬化
多晶体塑性变形将导致金属的力学、物理和化学
性能的改变。随着变形程度↑，则有： １.变形抗力（σS σb 硬度）↑ ２.塑性（伸长率 压缩率 ）↓ ３.同时使电阻升高、抗腐蚀性和导热性↓
32
加工过程中的软化
2.Mises屈服条件: 形变能定值理论。
当变形金属内的变形剪切能达到一个临界值时，
金属就由弹性变形进入塑性变形。
（1 2 )2 ( 2 3 )2 （1 3 )2 2 s2
又称精确塑性条件。 对于板带轧制，简化为：σ1－σ3 = 1.15σS＝K K：平面变形抗力。
35
金属的冷变形和热变形
（0.25～0.3）TM ℃
只有加工硬化作用而无回复与再结晶现象的变形
过程叫冷变形。加工温度低于材料的再结晶回复
温度的塑性加工方法。 冷变形特点如下： 冷变形后的产品尺寸精度高，表面光洁，可以生 产极细的丝、极薄的箔和细薄的管； 材料经冷变形变形后呈现加工硬化，变形抗力增
高，塑性下降，加工过程中需退火，增加能耗；
性能都近于冷加工的优良产品。
38
2.1.2.2 金属的塑性

塑性变形 ：
形状和尺寸的不可逆变化是通过原子的定向位移实 现的．
多晶体塑性变形的主要机制:位错的运动 金属和合金的塑性取决于： 一是：自然属性
应力超过弹性极限，材料发生的不可逆的永久变形。
二是：塑性加工过程外界条件
变化
39
塑性变形的不均匀性原因与后果

内力产生的原因:
1）平衡外力；
2）由于工件的整体性，各部分的不均匀变形、不 均匀加热和冷却、不均匀相变等必将互相限制， 因此物体内部出现了自相平衡的内力。 • 如加热不均;

东北大学考研金属塑性成型力学课后问题详解

1-6 已知物体内某点的应力分量为xσ=yσ=20MPa，xyτ=10MPa，其余应力分量为零，试求主应力大小和方向。

解：zyxIσσσ++=1=40MPa2222)(zxyzxyxzzyyxIτττσσσσσσ+++++-==-300 MPa22232xyzzxyyzxzxyzxyzyxIτστστστττσσσ---+==03004023=+-σσσ1σ=30MPa2σ=10 MPa3σ=01-7已知变形时一点应力状态如图1-34所示，单位为MPa，是回答下列问题？（1）注明主应力；（2）分解该张量；（3）给出主变形图；（4）求出最大剪应力，给出其作用面。

解：（1）注明主应力如下图所示：（2）分解该张量；⎪⎪⎪⎭⎫⎝⎛-⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎪⎭⎫⎝⎛---11666765＋＝（3）给出主变形图（4）最大剪应力127523113±=+-±=-±=σστ MPa 其作用面为1-8已知物体内两点的应力张量为a 点1σ=40 MPa ，2σ=20 MPa ，3σ=0；b 点：y x σσ==30 MPa ，xy τ=10 MPa ，其余为零，试判断它们的应力状态是否相同。

解：a 点MPa I 603211=++=σσσ)(1332212σσσσσσ++-=I =-800 MPa 3213σσσ=I =0z y x I σσσ++=1=60 MPa2222)(zx yz xy x z z y y x I τττσσσσσσ+++++-==-800 MPa 22232xyz zx y yz x zx yz xy z y x I τστστστττσσσ---+==0 其特征方程一样，则它们的应力状态相同。

1-10 某材料进行单向拉伸试验，当进入塑性状态时的断面积F=100mm 2，载荷为P=6000N ； （1）求此瞬间的应力分量、偏差应力分量与球分量； （2）画出应力状态分解图，写出应力张量； （3）画出变形状态图。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

z x y 2
平面变形时
1 1 1 2 2 y x y xy 3 2 x 4
max
1 1 2 2 1 3 x y xy 2 4 1 p k 2 p 3 p k
1 2
屈服时
4.1.2 基本假设
假设变形材料为各向同性的刚－塑性材料
即 假设塑性区各点的变形抗力是常数
4.1.3 基本概念
(1) 滑移线、滑移线网和滑移线场
max
1 2 2 x y xy k 4
规 定
1) 使体素顺时针转的切应 力方向为 线方向；反 之为 线方向。 2） 线各点的切线与所取 的x 轴的正向夹角为 ， 逆时针转为正，顺时针 转为负 。
沿 线
4.3 滑移线场的几何性质 性质1 在同一条滑移线上，由点a 到点b，静水压力的变化
与滑移线的切线的转角成正比.
pa 2ka pb 2kb
pa pb 2k a b
y b
a o
滑移线
p 2k
b
a
x
性质2 在已知的滑移线场内，只要知道一点的静水压力， 即可求出场内任意一点的静水压力，从而可以计算出各点的 应力分量.
cos2 sin 2 ctg 1 sin 2 cos2 ctg ctg
dp 2k dx 2k dx ctg 0 x y
沿 线
p 2k c2
pa 2ka pb 2kb pa 2ka pb 2kb
多媒体课件
材料成形力学
主 讲
东北大学
王平
材料与冶金学院
第4章 滑移线场理论及其应用
概述
1、滑移线场的绘制
2、应力状态的求解
y
o
x
4.1 滑移线场的基本概念
4.1.1 平面塑性变形的基本方程式
1 1 m x y z x y 8 z 2 p 3 2 P；定义为静水压力
cos2 sin 2 tan 1
sin 2 cos2 tan tan
dp 2k dx 2k dx tan 0 x y
p 2k c1
沿 线
dp 2k dxcos2 sin 2 ctg 2k dxsin 2 cos2 ctg 0 x y
dy tan dx
dy tan 90 0 cot dx


y

P y dx o

dy
滑移线微分方程
p p dp dx dy x y
d dx dy x y
x
x
沿 线
dp 2k dxcos2 sin 2 tan 2k dxsin 2 cos2 tan 0 x y
x yx 0 x y
xy x y y 0
p 2k cos 2 2k sin 2 0 x x y
（1） （2）
p 2k sin 2 2k cos 2 0 y x y
方程（1）乘 dx + 方程（2）乘dy
2
b
2
1
1
d
pb pa 2k a b
a c
性质3 直线滑移线上各点的静水压力相等。因直线滑 移线上各点的夹角相等.
p 0
性质4 汉基(Hencky)第一定理:同族的两条滑移线与另族滑 移线相交，其相交处两切线间的夹角是常数. A B B（沿a 线） p A 2k A pB 2k B C（沿b 线）
p k k p
yx
3
状态图
xy
x
1
k y , yx 莫尔圆
3
2

o

1
x , xy -k
3
p +k
I
+ max = k
B 2
p/4
P

p/4
-k p
y
y
+ yx P
+ yx
-
+ yx
1 y
xy
- xy
2 A II
C
1பைடு நூலகம்
x
xy
构成右手坐标系， 3），
1 在一、三象限。
o
y

k P
k

x

（2） 平面变形时的基本方程 张量
1 x yx 0 T xy y 0 0 0 0 z 0
y
0 1 3 2 0
0 0 3
y

B C
C
pB 2k B pC 2kC
pC p A 2k A C 2 B
A D（沿b 线）
B
A D
D
p A 2k A pD 2kD
D C （沿a 线） pD 2kD pC 2kC
p p dy dx dy 2 k dx cos 2 sin 2 x y dx x dy 2k dx sin 2 cos 2 0 dx y
x
- max = k 2 = ( x+ y)/ 2 =- p
x 3
y p k sin 2 p k sin 2
x p k sin 2 p k sin 2
基本应力方程
xy k cos2
4.2 汉基应力方程