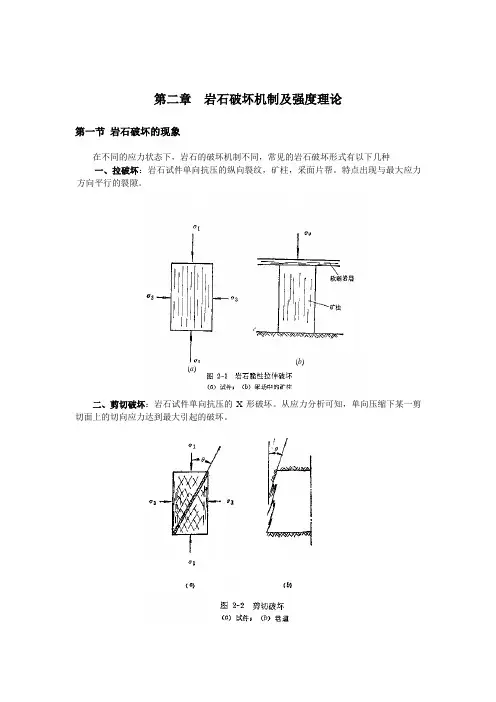
第二章 岩石破坏机制及强度理论
第一节 岩石破坏的现象
在不同的应力状态下，岩石的破坏机制不同，常见的岩石破坏形式有以下几种
一、拉破坏：岩石试件单向抗压的纵向裂纹，矿柱，采面片帮。特点出现与最大应力方向平行的裂隙。
二、剪切破坏：岩石试件单向抗压的X 形破坏。从应力分析可知，单向压缩下某一剪切面上的切向应力达到最大引起的破坏。
(a ) (b )
三、重剪破坏：即沿原有的结构面的滑动、重剪破坏
主要的机制：岩体受剪切作用或者受拉应力的作用、三向受压情况下多数为剪切应力的作用，侧向压力较小时可能是拉神破坏，实际工程中可能是不同机制的组合，但侧向应力较大时，可以认为剪切应力是岩石重剪破坏的主要破坏机制。
从岩石破坏的现象看，从小到几厘米的岩块到大的工程岩体，破坏形式雷同，并可归纳为两种，拉断与剪坏，因此有一定的规律可寻。
对岩石破坏的研究：
在单向条件下可以从实验得到破坏的经验关系。但是三向受力条件下，不同应力的组合有无穷多种，因此无法仅仅依靠实验得到破坏的经验关系，因此在一般应力状态，对岩石破坏的研究需要结合理论分析和试验研究两个方面。现代关于岩石破坏的理论分析一般归结为、寻求破坏时的主应力之间的关系
123(,)f σσσ=
研究的方法有：理论分析；2、试验研究；3、理论研究结合试验研究。
第二节 岩石拉伸破坏的强度条件
一、最大线应变理论
该理论的主要观点是，岩石中某个面上的拉应变达到临界值时破坏，而与所处的应力状态无关。强度条件为
c εε≤ (2-1)
c ε—拉应变的极限值，ε—拉应变。
若岩石在破坏之前可看作是弹性体，在受压条件下σ1>σ2>σ3下， 3ε是最小主应力。按弹性力学有3
3E E
σμ
εσσ=
-12（+），即33E εσμσσ=-12（+）。若3ε<0则产生拉应变。由于E >0，因此产生拉应变的条件是
3σμσσ-12（+）<0，3μσσσ12（+）>
若3ε=0ε<0则产生拉破坏，此时抗拉强度为0t E
σε＝?0t E σε＝。
按最大线应变理论30εε≥破坏，即
312()t σμσσσ-+≥ (2-2)
式中0ε是允许的拉应变。
二、格里菲斯理论
格里菲斯理论的主要观点是：材料内微小裂隙失稳扩展导致材料的宏观破坏。 格里菲斯理论的主要依据是：1）、任何材料中总有各种微小微纹；2）、裂纹尖端的有严重的应力集中，即应力最大，并且有拉应力集中的现象；3）、当这种拉应力集中达到拉伸强度时微裂纹失稳扩展，导致材料的破坏。
格里菲斯理论的来源：由玻璃破坏得到的启示。 格里菲斯理论的基本假设为：
1、岩石的裂隙可视为极扁的扁椭圆裂隙；
2、裂隙失稳扩展可按平面应力问题处理；
3、裂隙之间互不影响。
按格里菲斯理论，裂纹失稳扩展条件为 1）、当1330σσ+>时，满足
21313()8()0t σσσσσ-++= (2-2)
时发生破坏。
2)、当1330σσ+<时，满足
8c t σσ=- (2-3)
时发生破坏。式中。σ c —单向抗压强度，σ t —单向抗拉强度。
按格氏理论，岩石的拉压强度是抗拉强度的8倍。
按照格里菲斯理论，岩石破坏的微观机制是微裂隙的受拉破坏，宏观机制是微裂隙的失稳扩展并汇合成宏观裂隙。
三、修正的格里菲斯理论
格里菲斯理论没有考虑裂隙受压和裂隙面摩擦的情况，只能用于裂隙严格受拉的情况，因此Maclintock 和Walsh 考虑到裂隙在压应力作用下的混发生闭合的情况，对格里菲斯理论进行了修正，得到了修正的格里菲斯准则
123311
(1)(1)(1)
t
f f σσσσσσ=
-+-+ (2-4)
式中t σ—岩石的抗拉强度。由于抗拉强度测量比较困难。因此用抗压强度代替抗拉强度。
当310,c σσσ==时从上式可求出
c σ= (2-5)
将(2-5) 式代入(2-4)式可得到以抗压强度表示的修正的格里菲斯准则。
3
11c c σσσσ= (2-6)
式中f 是裂隙面的摩擦系数。
研究裂纹的两种方法：1、椭圆坐标；2、数学裂纹。 以上是二维理论，其进一步的假设为：
1、岩体内遍布微裂隙，且裂隙可理想化为格里菲斯裂纹；
2、岩体内裂纹均匀分布，但裂纹之间没有相互作用。
第三节、岩石剪切破坏的强度条件
一、莫尔强度理论
莫尔强度理论的基本观点：莫尔强度理论认为，材料在压应力作用下的屈服和破坏，主要是在材料内部某一截面上的剪应力到达一定限度，但也和作用于该截面上的正应力有关。
莫尔强度理论的来源：最早起源于对金属摩擦的研究。对岩石力学而言，主要来源于土力学。
根据对摩擦的研究，滑动面上的剪切位移既与剪应力有关，又与正应力有关，剪切破坏的一般示意图如下。
因此，强度准则的一般形式为
()f τσ= (2-6) 上式一般是非线性关系，因此在τ－σ图上一般是曲线，直线是其特例，也是最简单的情况。
下图是几种典型的剪切破坏()f τσ=曲线
二、绘制()f τσ=的方法：
按照莫尔理论测定岩石的强度，有以下几种方法：
1、由三轴压缩实验测定破坏时的σ1和σ3，由此绘制一系列极限应力图，这些圆的包络即是强度曲线()f τσ=。
2、由剪切试验(斜剪或直剪)，得到破坏时的一系列τa
和σa (方法见前一条)，由此拟合
曲线。
3、按单向抗拉强度和单向抗压试验求强度曲线。
)c t
c t
σστσσσ-=
+
(2－7) 7
6
以下讨论式(2－6)的导出过程。按图2-8，从抗压和抗拉两个实验绘制莫尔圆，可确定如下曲线
c tg τσφ=+
设摩擦角为φ，则单向受压时的剪应力和正应力为
cos 2
c
στφ=
，sin 2
2
c
c
σσσφ=
-
单向受拉时的剪应力和正应力为
cos 2
t
t στφ=
，sin 2
2
t
t
t σσσφ=
+
直线斜率为
t t tg ττφσσ-=+?()cos ()()sin t t t tg σσφ
φσσσσφ
-=+-- ? 22()cos ()sin ()sin t t t σσφσσφσσφ-=+-+ ? ()sin t t σσσσφ-=+
8 2-8
? sin t
t
σσφσσ-=
+ 纵坐标上的点C 确定的方法
0cos 2t C σφτ=+,0t
tg τ
φσ=
? 0t tg τσφ=?
? 0(s i n )2
2
t
t
tg σστφφ=+
?
(s i n c o s )
2
t
C t g t g σφφφφ=
++ 由辅助三角形
tg φ=
，cos c t φ=；sin c t
c t σσφσσ-=+
代入上式得到
?
2t c t C σ=
?
22C =
= ?
C =
=
因此
)c t c t
σστσ
σσσ-=
=+
然后根据图2－9可以得到各个量的几何关系，得出(2－7)式。
2-9 t
σσ+t
σσ-φ
三、库仑—莫尔理论
按莫尔强度理论得到的岩石强度曲线一般是曲线，直线是其特例。在莫尔理论的基础上，库仑假设岩石的剪切强度曲线是直线，称为库仑—莫尔理论。按照库仑—莫尔理论，对于图2—7所示的岩石的直剪情况下的破坏，剪切强度τ可按下式确定
C tg τσφ=+ (2-8)
或者
C f τσ=+? (2-8a)
上式中的绝对值表示剪切破坏与滑移方向无关。式中，σ—作用在剪切面上的正应力，φ—岩石的内摩擦角，f —岩石的内摩擦系数，C —岩石的纯剪切强度(即剪切滑移面上的正应力
0σ=时的剪切强度)，也称内聚力，粘结力。
但工程岩体的应力状态比图(2-7)所示的更复杂，为了便于将莫尔—库仑理论推广到一般的应力状态，需要有比式(2-8)更方便的公式，为此首先介绍应力莫尔圆。 应力莫尔圆简介
考虑两种平面直角坐标Oxy Ox y ''和中应力分量的变换
如果坐标系Oxy 中的应力分量,,x y xy σστ已知，则对于图2-10的情况容易导出
''''11()()cos 2sin 222
11()()cos 2sin 2221()sin 2cos 22x x
y x y xy y x y x y xy x y y x xy σσσσσατασσσσσατατσσατα?=++-+??
?
=+--+??
?
=--??
''',y x x τσ是坐标系''oy x 坐标中应力分量。若在主应力空间，则0=xy τ，1σσ=x ，2σσ=y ，
因此
y y
图 2-10
???
???
?-=-++=ασστασσσσσ2sin )(212cos )(2
1)(2131''3131'y x x (a )
x x y στ'''和也可看作是与1σ成α角的平面上的法向应力和剪应力，即可写为
???
???
?-=-++=ασστασσσσσαα2sin )(212cos )(2
1)(21313131 (2-9) 下面讨论αατσ,的几何表示。将(2-9)式改写为
???????=-+-=-αατ
ασσσσσασσ2sin )(2
1)(212cos )(21313131 (2-10)
从(2-10)式可以求出，
222121311[()]()24
αασσστσσ-++=-
在ααστ,平面上，上式表示一个圆，圆心在σ轴上]0),(21[31σσ+，半径为)(2
131σσ-，被称为莫尔应力圆，在不引起误解的情况下，用στ,表示与1σ成α角的平面上的正应力和
剪应力αατσ,。
图2-12的应力莫尔圆，是公式(2-10)的几何表示。
考虑下面的试验。试件受1σ和3σ的作用，31σσ>。试件中的某个面与1σ的夹角为α，则在31,σσ作用下，该斜面上的法向应力ασ，和剪应力ατ就是应力莫尔圆上的P 点的横坐标和纵坐标。对比图2-10和2-11试件内与1σ成α角的面，就是莫尔应力圆上与σ成α2角的点。因此从圆心]0),(2
1
[31σσ+起做与σ轴为α2角的射线，它与射线与σ轴夹角为α2，
1
,σx y 3
图 2-11
应力莫尔圆的交点为P 。从图2-11可以看出，P 点的横坐标ασ和纵坐标ατ分别为
ασσσσσα2cos )(21)(213131-++=
； ασστα2sin )(2
1
31-= (2-11a ，b )
如果将(2-11)式中的στ,理解为图2-13所示的α面上的剪应力和正应力，则(2-11)式可以推广到受压岩石的剪切破坏。 将(2-11)代入(2-8)，得出
131313111
()sin 2[()()cos 2]222
C f σσασσσσα-=+++-? 整理上式可得
131311
()(sin 2cos 2)()22
f f C σσαασσ--?-?+= (2-12) 式(2-12)中，13,σσ是作用在岩石上的载荷，其大小是已知的，而受压岩石的剪切破坏面无法事先知道，即剪切破断角α是未知的。因此无法使用(2-8)式判断岩体的剪切破坏。
显然破
图 2-13
图2-12
坏在C 取最大值的面上发生。由于(2-12)式仅仅与角度α有关。这意味着只有当0d C
da
=，即(2-12)式取极值时才可能发生，将(2-12)式对剪切破断角α导，得到
13130()cos2()sin 2f σσασσφ=-+-
? cos2sin 2a f a -= ?12tg a f
=-
注意到f tg φ=，则
11
2tg a tg f
φ=-
= (2-13) 从上式可以求出 sin cos 2cos sin 2φα
φα
=-
? sin sin 2cos2cos 0φααφ+=
或者
cos(2)0αφ-=
要是上式满足，必然有
22
π
φα-=
或者
42
π
φ
α=
+
(2-14)
式中α是破断角，即与最小主应力的夹角，φ是摩擦角。
库仑—莫尔准则(2-13)式是τσ-平面上的直线，应力莫尔圆是τσ-图上的一个圆，应力莫尔圆上点的纵坐标横坐标分别表示和岩样内某一截面上的剪应力和法向应力。因此τσ-面内强度曲线和应力莫尔图的交点是受压岩样剪切破坏时的剪应力和法向应力，α是破断角。用(2-12)式判断岩体的破坏也不是十分方便。
在岩石的三轴抗压压缩实验中1σ和3σ是已知的，因此下面讨论用1σ和3σ表示的库仑—摩尔准则。
从下图可以看出：
α
σ
图2-14
1
σ
13
sin ,2
R AB AB AO OB σσφ-=
==+ (a )
而
13
,2
AO C ctg OB σσφ+=?=
(b )
因此
13
2
AB C ctg σσφ+=?+
(c )
将(b )、(c )代入(a )，得到
13
13
()sin 2
2
C ctg σσσσφφ-+=?+
或者
1313()sin 2cos C σσσσφφ-=++
整理上式，并令1sin 2cos ,1sin 1sin c C N φφ
σφφ
+=
=
--，可以得到 13c N σσσ=+ (2-15)
式中c σ－单向抗压强度。(2-15)式是库仑—莫尔准则一种常用的形式，在粘聚力c 和内摩擦角已知的情况下使用。
213tan c σσασ=+ (2-16)
(2-16)式是库仑－莫尔准则的另一种形式。其导出过程如下：
22
π
φα-=
[(2-14)式]，因此
21sin 1sin(2)1cos 22sin 2π
φααα+=+-=-=
21sin 1sin(2)1cos 22cos 2
π
φααα-=--=+=
这样N = 222
1sin 2sin tan 1sin 2cos φα
αφα
+==-，将它代入(2-15)式，得到(2-16)式。 库仑－莫尔准则与单轴抗压强度和单轴抗拉强度的关系
令(2-15)式中的侧向应力3σ=0，得到单向抗压强度
2cos 1sin c C φ
σφ
=
-
但是，另一方面，(2-15)式中的纵向应力3σ=0，得到的 3c
t N
σσσ=-
≠ 不是压应力作用下岩石的抗拉强度t σ。分析如下：
由于岩石的摩擦系数大于零，即0f <<∞，则(2-13)式表明2tg a 位于第二象限，因此
22
π
απ<<，4
2
π
π
απ<<
做辅助三角型
f
-
1
借助于辅助三角型，可以得到
sin 2a =
，cos 2a =
将sin 2a ，cos2a 和tg f φ=代入(2-15)式，得到
122
13132()(1)()C f f σσσσ=-+-+
122
1313()(1)
()2f f C σσσσ-+-+<
时不破坏
122
1313()(1)
()2f f C σσσσ-+-+>
时不破坏
1313(()2f C σσσσ-+=
C f f f f 2)1()1(2321=++--+σσ (2-17)
处于极限状态。显然
13
13
13
sin 2(
cos 2)2
2
2
a a tg C σσσσσσφ-+--+
<
另一方面，从库仑准则的适用条件0>ασ，并利用应力的坐标变换公式(2-11a ，b )，得到
0)2cos 1()2cos 1(2cos )()(2313131>-++=-++=ασασασσσσσα
改写上式得到
0)11()11(2
32
1>++
++-
f
f f
f σσ
或者
0)]1()1([1123212
>+++-++f f f f f σσ (2-18a )
由于012>+f ，因此0>ασ要求
13))0f f σσ+> (2-18b )
联立(2-18)式和(2-18)式，得出
C f f 2)1(221>-+σ 或者 C f f >-+)1(21σ (2-19)
注意到
?
??222
2
cos sin tan =
=f ，????2222
2cos sin cos tan 11+=+=+f 因此
?
?
?cos sin cos 112-
=
-+f f 这样从(2-19)式得到
2
sin 1cos cos sin cos 11c
C C σ???
?
?σ=-=
-
>
(2-20)
上式表明，按照库仑—莫尔准则，即1σ的最小值为
2
c
σ>0。因此只有21c σσ>时，(2-15)式
c N σσσ+=31才成立。这样证明了不能令(2-15)式中的纵向应力1σ=0，因此
3c
t N
σσσ=-
≠
不是岩样的拉应力。不等式2
1c
σσ>
也给出了库仑—莫尔准则的适用范围。
???
???
?
≤-=>
=++--+)2()
2
(2)1()1(1312321c t c
C f f f f σσσσσσσσ
将(2-15)式改写为
N
N c
σσσ-
=
1
3 (2-21)
在31~σσ图上，(2-21)式是一条直线，斜率t
c σσβ2
/arctan
=。当03=σ时，c σσ=1；当03=σ时，N
c
23σσ-=。上图表明库仑—莫尔准则的有效范围为线段AP 。
库仑—莫尔准则不仅适合与土，还适合于完整岩石，它合理地给出了剪切破坏所需要的应力和剪切破坏方向。为了能得出发生剪切破坏时应力的大小，利用(2-18b )式给出发生时的
图2-15
应力状态1σ，3σ与岩石的抗拉、抗压强度的关系。从(2-18b )式
122
1313()(1)
()2f f C σσσσ-+-+≥ (2-22)
单向压缩时30σ=， 1c σσ=，则(2-22)式变为
122
2(1)
c C f f
σ=
+- (2-22)
单向拉伸时10σ=， 3t σσ=-。从(2-22)式得出
122
2(1)
t C S f f
=
++ (2-23)
1
22122(1)(1)c t f f
f f
σσ++=
+- (2-24) 在上述两种情况下，有1c σσ=，
1
1c σσ=；和3t σσ=-，31t
σσ=-。合并两式得到 3
11c t
σσσσ-= (2-25a ) 和
132c
c t
σσσσσ=+
(2-25b ) 这些关系已在实践中得到证实。
库仑—莫尔准则小结
1、库仑—莫尔准则中包含的物理量、意义及相互关系 粘结力C （也被称为内聚力或固有剪切强度）；摩擦角系数f （f = tan φ）；摩擦角φ；破断角α；单轴抗压强度C σ;系数N 。
破断角与摩擦角之间的关系
2
4?
π
α+
=
粘结力、摩擦角和单轴抗压强度之间的关系
2cos 1sin C C φ
σφ=
- 系数N 与摩擦角之间的关系
1sin 1sin N φ
φ
+=
-
2、库仑—莫尔准则的几种形式
(1)、C f =-στ，(原理形式，在剪切面已知条件下才适用，实际使用不方便)； (2)、2
,2
,cos sin 3
13
1σσσσστ??στ+=
-=
+=m m m m C ，(方便使用，但不常使用)；
(3)、c σασσ+=231tan (以破断角α和单轴抗压强度C σ表示的准则，有时使用)； (4)、13c N σσσ=+ (以1σ，3σ和C σ表示的准则，最方便使用)
第四节、对强度理论的评价
目前使用的有关岩石的各种强度理论和强度准则都有一定的局限性，因而有一定的使用范围
1、莫尔理论
较适合于松散材料，也适合于完整岩石，裂隙岩体的强度和破裂面的方向与该理论预计的有较大差别；不能充分解释拉伸破坏；将剪断和滑移两个相继的过程结作为一个过程处理。
对库仑—莫尔准则理论的评价：
1、可以解释岩石在三向等压时不破坏的现象（在右半区敞开）；
2、可以解释岩石在三向受拉可以破坏的现象（在左半区封闭）；
3、可以解释岩石抗拉强度小于抗压强度的现象；
4、不能充分解释拉伸破坏。
库仑—莫尔准则较全面地反映了岩石的强度特点，不仅适用于塑性材料，也适用于脆性材料的剪切破坏；由于岩石大多是剪切破坏，故适用性较广、简单实用。库仑—莫尔准则不能说明强度的非线性变化，因此比较较粗糙；
2、最大线应变理论
最大线应变理论与破坏的物理过程想抵触，因为张破裂势必涉及到局部拉应力集中，并不一定在最小主应力方向上发生。
3、格里菲斯理论
可以说明裂隙开始时的情况。但对岩石这样的非均匀材料，裂隙开始时的应力要低于破坏时的应力，而且两者之间的关系复杂，因此还不能用来说明岩石的拉伸破坏。
表明实践岩石的破坏渐进破坏。由于岩石的非均匀性，岩体内一点的受力达到强度时发生破坏，将应力转移到周围岩体，导致周围岩体应力增大，于是破坏依次发展，直至形成宏观破裂面。非均匀的岩体。
岩石岩体区别:岩石可以瞧作就是一种材料,岩体就是岩石与各种不连续面的组合体;岩石可以瞧作就是均质的,岩体就是非均质的(在一定的工程范围内);岩石具有弹、塑、粘弹性,岩体受结构面控制,性质更复杂,强度更低;岩体通常就是指一定工程范围内的地质体,岩石则无此概念。 岩石力学就是一门研究岩石在外界因素(如荷载、水流、温度变化等)作用下的应力、应变、破坏、稳定性及加固的 学科。又称岩体力学,就是力学的一个分支。研究目的在于解决水利、土木工程等建设中的岩石工程问题。它就是 一门新兴的,与有关学科相互交叉的工程学科,需要应用数学、固体力学、流体力学、地质学、土力学、土木工程学 等知识,并与这些学科相互渗透。 研究对象:对象:岩石—对象—岩石材料—地壳中坚硬的部分; 复杂性:地质力学环境的复杂性(地应力、地下水、物理、化学作用等) 研究的基本内容: 基本理论岩体地应力 材料实验——三大部分→岩体的强度 工程应用岩体的变形
裂隙水力学 研究方法: 物理模拟→岩石物理力学性质常规实验,地质力学模型试验; 数学模型→如有限元等数值模拟; 理论分析→用新的力学分支,理论研究岩石力学问题; 由于岩石中存在各种规模的结构面(断裂带、断层、节理、裂隙)→致使岩石的物理力学性质→不连续、不均匀、各 向异性→因此,有必要引入刻划不均一程度的参数。 各向异性:指岩石的强度、变形指标(力学性质)随空间方位不同而异的特性。 岩石的基本物理力学性质 岩石力学问题的研究首先应从岩石的基本物理力学性质研究入手, 1.岩石的容重:指单位体积岩石的重量。2、比重(Gs)指岩石干重量除以岩石的实体积(不含孔隙体积)的干容重与4?c 水的容重的比值。3、孔隙率(n%)指岩石内孔隙体积与总体积之比。4、天然含水量:指天然状态下,岩石的含水量与岩石干重比值的百分比。5、吸水率:指岩石在常温条件下浸水48小时后,岩石内的含水量与岩石干容重的比值。6、饱与含水率:指岩样在强制状态(真空、煮沸或高压)下,岩样最大吸水量与岩石干重量比值。7、饱水分数:指岩石吸水
东 北 大 学 继 续 教 育 学 院 工程力学（一）X 试 卷（作业考核 线上2） A 卷（共 3 页） 总分 题号 一 二 三 四 五 六 七 八 九 十 得分 一、选择题（15分） 1．已知1F ，2F ，3F ，4F 为作用于刚体上的平面力系，其力矢关系如图所示为平行四边形。由此可知（ D ）。 A. 力系可合成为一个力偶； B. 力系可合成为一个力； C. 力系简化为一个力和一个力偶； D. 力系的合力为零，力系平衡 2．内力和应力的关系（ D ） A. 内力小与应力 B. 内力等于应力的代数和 C. 内力为矢量，应力为标量 D. 应力是分布内力的集度 3．梁发生平面弯曲时，其横截面绕（ B ）旋转。 A.梁的轴线； B.中性轴； C.截面的对称轴； D.截面的上（或下）边缘。 二、通过分析计算选出正确答案，（15分） 图示结构由梁DC 、CEA 两构件铰接而成，尺寸和载荷如图。已知：2qa M ，qa P 2 。如求A 、 B 处约束反力： 1. 简便的解题步骤为（ D ）； 1 F 3 F 2 F 4 F
A ．先整体分析，再分析 CAE 构件； B ．先分析DBC 构件，再整体分析； C ．先分析CAE 构件，再分析DBC 构件； D ．先分析DBC 构件，再分析CEA 构件。 2. 由DBC 构件分析，可以求得（ C ）； A ．F By B ．F Cy 、F Ay C ．F By 、F Cy D ．F Ay 3. F By 、F Ay 、M A 分别等于（ A ）。 A ． qa 29， qa 23， 225qa B ． qa 25， qa 29， 223 qa C ． qa 23， qa 29， qa 25 D ． qa 29， qa 25， qa 2 3 三、已知变截面钢轴上的外力偶矩1800b m N m ，1200c m N m ，剪切弹性模量 98010Pa G ，轴的尺寸见图，试求最大切应力max 和最大相对扭转角AC 。（15分） 解：1）画扭矩图 最大扭矩值3kNm 2）最大切应力 AB 段：36max max 333 1616310Nm 36.210Pa =36.2MPa 0.075m AB AB P T T W d BC 段：36max max 333 1616 1.210Nm 48.810Pa =48.8MPa 0.05m BC BC P T T W d T 3kNm 1.2kNm
《岩石力学》期末试卷及答案 姓名 学号 成绩 一、 选择题(每题1分，共20分) 1. 已知岩样的容重为γ，天然含水量为0w ，比重为s G ，40C 时水的容重为w γ，则该岩样的饱和容重m γ为（ A ） A. ()()w s s G w G γγ++-011 B. ()()w s s G w G γγ+++011 C. ()()γγ++-s s w G w G 011 D. ()()w s s G w G γγ+--011 2. 岩石中细微裂隙的发生和发展结果引起岩石的（ A ） A ．脆性破坏 B. 塑性破坏 C. 弱面剪切破坏 D. 拉伸破坏 3. 同一种岩石其单轴抗压强度为c R ，单轴抗拉强度t R ，抗剪强度f τ之间一般关系为（ C ） A.f c t R R τ<< B. f t c R R τ<< C. c f t R R <<τ D. t f c R R <<τ 4. 岩石的蠕变是指（ D ） A. 应力不变时，应变也不变； B. 应力变化时，应变不变化； C. 应力变化时，应变呈线性随之变化； D. 应力不变时应变随时间而增长 5. 模量比是指（A ） A ．岩石的单轴抗压强度和它的弹性模量之比 B. 岩石的 弹性模量和它的单轴抗压强度之比 C ．岩体的 单轴抗压强度和它的弹性模量之比 D ．岩体的 弹性模量和它的单轴抗压强度之比 6. 对于均质岩体而言，下面岩体的那种应力状态是稳定状态（ A ） A.??σσσσsin 23131<++-cctg B.?? σσσσsin 23131>++-cctg C. ??σσσσsin 23131=++-cctg D.??σσσσsin 23131≤++-cctg 7. 用RMR 法对岩体进行分类时，需要首先确定RMR 的初始值，依据是（ D ） A ．完整岩石的声波速度、RQD 值、节理间距、节理状态与地下水状况 B. 完整岩石的强度、RQD 值、节理间距、节理状态与不支护自稳时间 C. 完整岩石的弹性模量、RQD 值、节理间距、节理状态与地下水状况 D. 完整岩石的强度、RQD 值、节理间距、节理状态与地下水状况 8. 下面关于岩石变形特性描述正确的是（ B ） A. 弹性就是加载与卸载曲线完全重合，且近似为直线 B. 在单轴实验中表现为脆性的岩石试样在三轴实验中塑性增强 C. 加载速率对应力－应变曲线没有影响 D. 岩基的不均匀沉降是由于组成岩基的不同岩石材料含水量不同导致的 9. 下面关于岩石水理性质描述正确的是（ B ）
一、单选题： 1. (满分:5) A. B. C. D. 2. (满分:5) A. A B. B C. C D. D 3.关于材料的力学一般性能，有如下结论，试判断哪一个是正确的： (满分:5) A. 脆性材料的抗拉能力低于其抗压能力； B. 脆性材料的抗拉能力高于其抗压能力； C. 韧性材料的抗拉能力高于其抗压能力； D. 脆性材料的抗拉能力等于其抗压能力。 4.平面汇交力系的合成结果是( )。 (满分:5) A. 一扭矩 B. 一弯矩 C. 一合力 D. 不能确定
5.将构件的许用挤压应力和许用压应力的大小进行对比，可知( )，因为挤压变形发生在局部范围，而压缩变形发生在整个构件上。 (满分:5) A. 前者要小些 B. 前者要大些 C. 二者大小相等 D. 二者可大可小 6. (满分:5) A. A B. B C. C D. D 7. (满分:5) A. A B. B C. C D. D 8.直径为d、长度为l、材料不同的两根轴，在扭矩相同的情况下，最大切应力，最大相对扭转角。 (满分:5) A. 相同、相同 B. 不同、相同 C. 相同、不同
D. 不同、不同 9. (满分:5) A. A B. B C. C D. D 10. (满分:5) A. 减小轴的长度 B. 改用高强度结构钢 C. 提高轴表面的粗糙度 D. 增加轴的直径 11. (满分:5) A. 前者不变，后者改变 B. 两者都变 C. 前者改变，后者不变 D. 两者都不变 12. (满分:5) A. A B. B C. C D. D 13.作用与反作用定律适用于下列哪种情况( )。 (满分:5)
第六章地下工程灾害预报与防治 第四节、岩爆发生的现象、机理与防治 一、岩爆发生的现象 岩爆是矿井进入深部开采以后更容易遇到的严重的灾害之一。 有记录的岩爆发生的历史 我国岩爆发生的基本情况 岩爆是岩石动力破坏的一种特殊形式 采矿引起岩石破坏的主要形式 1、岩块的冒落或坍落 原因：采矿导致节理岩体的松动。危害：砸伤作业人员、损坏支护。 2、松散岩层变形 原因：在强大地应力作用下，松软岩体的明显变形。危害：损坏支护，改变巷道断面和形状。 3、凿岩爆破等动载荷下的破坏； 4、岩爆、煤与瓦斯突出等动力现象 岩爆发生的一些实例 岩爆的危害：造成人员设备的巨大损失并引起作业人员的恐慌。 岩爆与通常的岩体破坏现象的区别 通常的岩体石破坏发生时的主要现象：1、通常的岩石破坏不会有猛烈的声响和(大量)能量的瞬间释放；2、破坏过程缓慢；3、要进一步施加外载或做功才能发生破坏；4、比较容易预报。 岩爆发生的现象和特点：1、破坏范围大、能量大；2、无明显前兆的情况下，自行发生破坏，难以预报；3、破坏时可以有巨大声响，破坏及其迅速；4、小扰动下会引发岩爆；5、岩爆有滞后发生的现象；6、岩爆引起的岩体突然破坏不需要外界向系统进一步输入能量，因此与爆破载荷引起的岩体动力破坏有实质区别。 岩爆发生的初步的定义(从现象上)： 岩爆是岩石（体）猛烈破坏并释放大量能量的现象。 岩爆是岩石（体）的一种特殊的破坏形式，并可以得出如下结论： 1、岩爆不能简单地等同与岩石的破坏； 2、岩爆所表现出的岩石破坏的动力性，不同于爆破引起的岩石动力破坏。 问题与思考：岩爆与普通岩石破坏的根本区别是什么？ “科学研究的区分，就是根据科学对象所具有的特殊的矛盾性。因此，对某一现象所特有的某种矛盾的研究，就构成某一门学科的对象。”（毛泽东《矛盾论》） 库克认为：“岩体发生破坏，引起矿体—围岩力学系统平衡状态破坏时，若其释放的能量大于消耗的能量，将产生岩爆。” 岩爆与通常岩石破坏的本质区别在于：1、破坏的突然性；2、破坏过程中有多余的(有时是大量的)能量释放。 二、经典力学关于非稳定平衡和突然破坏的研究 1、压杆失稳
2020年硕士研究生统一入学考试 矿山岩体力学 第一部分考试说明 一、考试性质 矿山岩体力学学是东北大学资源与土木工程学院采矿工程专业、矿业工程专业硕士生（采矿方向）入学考试的专业基础考试科目，考试对象为参加东北大学资源与土木工程学院采矿工程专业、矿业工程专业（采矿方向）2020年全国硕士研究生入学考试的准考考生。 二、考试形式与试卷结构 1. 答卷方式：闭卷，笔试 2. 答题时间：180分钟 3. 考试题型及比例(均为约占) 术语解释15% 简答题15% 计算题20% 分析、论述题30% 应用题20% 4. 参考书目 赵文. 《岩石力学》，中南大学出版社，2010 蔡美峰. 《岩石力学与工程》，科学出版社，2002 郑永学. 《矿山岩体力学》，冶金工业出版社，1988 Brady B.H.G., Brown E.T./佘诗刚、朱万成、赵文等译. 《地下采矿 岩石力学/Rock Mechanics for Underground Mining》，科学出版社， 2010
第二部分考查要点 一、基础知识 1．完整岩石的物理性质、力学性质、影响因素等； 2．岩体结构及岩体力学性质，结构面的力学性质、岩体质量评价；3．地应力及其测量方法； 4．岩石支护与加固 5．相似材料模型 6．岩石力学数值分析方法分类及其适用条件 二、露天矿边坡 1．露天边坡稳定性的影响因素、破坏形式； 2．稳定性分析和计算； 3．露天矿边坡的治理。 三、金属矿床地下开采 1.与地压有关的概念，围岩与支架力学模型； 2.巷道地压、竖井地压、采场地压、地压控制方法； 3.采空区处理、井巷维护原则与支护
东北大学继续教育学院 岩石力学试卷（作业考核线上2） B 卷（共 6 页） 一、 1、岩石与岩体的关系是（ B ）。 （A）岩石就是岩体（B）岩体是由岩石和结构面组成的 （C）岩石是岩体的主要组成部分 2、流变性质指材料的应力应变关系与（ B ）因素有关系的性质。 （A）强度（B）时间（C）载荷大小（D）材料属性 3、比较岩石抗压强度、抗剪强度和抗拉强度的大小为（ C ）。 （A）抗压强度<抗剪强度<抗拉强度（B）抗压强度>抗拉强度>抗剪强度 （C）抗压强度>抗剪强度>抗拉强度 4、影响岩体力学性质各向异性的主要因素为（ B ）。 （A）地下水（B）结构面（C）构造应力场 5、巴西试验是一种间接测定岩石（ B ）强度的试验方法。 （A）抗压（B）抗拉（C）抗剪 6、蠕变是指介质在大小和方向均不改变的外力作用下，介质的（B ）随时间的变化而 增大的现象。 （A）应力（B）应变（C）粘性 7、下列参数不是岩石强度指标的为（ A ）。 （A）弹性模量（B）内聚力（C）摩擦角 8、在地应力测量中以下那种方法不属于直接测量法（D ） （A）扁千斤顶法（B）声发射法（C）水力劈裂法（D）全应力解除法 9、按照库仑—莫尔强度理论，若岩石强度曲线是一条直线，则岩石破坏时破裂面与最大 主应力作用方向的夹角为（ C ）。 （A）45°（B）（C）（D）60° 10、岩石质量指标RQD是（A）以上岩芯累计长度和钻孔长度的百分比。 （A）10cm（B）20cm（C）30cm 11、下列关于岩石长期强度S∞和瞬间强度S0的关系正确的是（D）。 （A）S∞＞S0 （B）S∞≤S0 （C）S∞≥S0 （D）S∞＜S0 12、下列关于库伦强度理论论述不正确的是（B） (A) 库伦准则是摩尔强度理论的一个特例(B)适用于受拉破坏 (C) 适用于岩石压剪破坏(D)适用于结构面压剪破坏 13、关于格里菲斯强度理论论述不正确的是（C） (A)岩石抗压强度为抗拉强度的8倍
第一部分 填空题 1、岩石力学定义 ①岩石力学是研究岩石的力学性态的理论和应用的科学，是探讨岩石对其周围物理环境中力场的反应的科学。识记（1分/空） ②岩石力学是研究岩石在荷载作用下的应力、变形、破坏规律以及工程稳定性等问题。识记（1分/空） 2、岩石力学研究容 ①岩石力学研究的主要领域可概括为基本原理、实验室和现场试验、实际应用。识记（1分/空） 3、岩石力学研究方法 ①岩石力学研究方法主要有工程地质研究法、试验法、数学力学、分析法、综合分析法。理解（1分/空） 4、岩石的常用物理指标 ①在工程上常用到的物理指标有：容量、比重、孔隙率、吸水率、膨胀性、崩解性等。识记（1分/空） ②岩石的容量γ是指岩石的单位体积（包括岩石孔隙体积）的重力，单位是3/m KN 与岩石密度ρ的关系为：8.9?=ργ。 识记（1分/空） ③岩石的密度ρ是指岩石的单位体积的质量（包括孔隙体积）单位是3/m kg 与岩石容重γ的关系为：8.9?=ργ。识记（1分/空） ④岩石的比重就是岩石的干的重力除以岩石的实际体积，再与4。C 时水的容重相比。计算公式是：s w s s W G νγ= 。识记（1分/
空） ⑤孔隙率是指岩石试样中孔隙体积与岩石试样总体积的百分比，工程设计上所用的孔隙率常是利用w s d r G γη- =1计算出来。识 记（1分/空） ⑥孔隙率是反映岩石的密度和岩石质量的重要参数。孔隙率愈大表示岩石中的空隙和细微裂隙愈多，岩石的抗压强度随之是降低。理解（1分/空） ⑦表示岩石吸水能力的物理指标有吸水率和饱和吸水率，两者的比值被称为饱水系数，它对于判别岩石的抗冻性具有重要意义。理解应用（1分/空） ⑧岩石的吸水能力大小，一般取决于岩石所含孔隙的多少以及孔隙和细裂隙的连通情况。岩石中包含的孔隙和细微裂隙愈多，连通情况愈好，则岩石吸入的水量就愈多。理解（1分/空） ⑨岩石的抗冻性就是岩石抵抗冻融破坏的性能，一般用抗冻系数和重力损失率两个物理指标来表示。识记（3分/空） 5、岩石的渗透性及水对岩石的性状影响 ①岩石的渗透性是指在水压力的作用下，岩石的孔隙和裂隙透过水的能力。表示岩石渗透能力的物理指标是渗透系数k 。识记（1分/空） ②渗透系数的物理意义是介质对某种特定流体的渗透能力，它的大小取决于岩石的物理特性和结构特征。理解（1分/空） ③水对岩石性状的影响主要表现在岩石的抗冻性、膨胀性、崩解性、软化性。 ④岩石的软化是指岩石与水相互作用时降低强度的性质，常用的物理指标为软化系数，即饱和抗压强度与抗压强度的比值。识记（1分/空） ⑤岩石的膨胀性是指岩石浸水后体积增大的性质。这种现象的发生必备条件是岩石中含有粘土矿物。表示岩石的膨胀性能的
工程力学材料力学 （北京科技大学与东北大学） 第一章 轴向拉伸和压缩 1-1：用截面法求下列各杆指定截面的内力 解： (a):N 1=0,N 2=N 3=P (b):N 1=N 2=2kN (c):N 1=P,N 2=2P,N 3= -P (d):N 1=-2P,N 2=P (e):N 1= -50N,N 2= -90N (f):N 1=0.896P,N 2=-0.732P 注（轴向拉伸为正，压缩为负） 1-2：高炉装料器中的大钟拉杆如图a 所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b 所示；拉杆上端螺纹的内 径d=175mm 。以知作用于拉杆上的静拉力P=850kN ，试计算大钟拉杆的最大静应力。 解： σ1= 2118504P kN S d π= =35.3Mpa σ2=2228504P kN S d π= =30.4MPa ∴σmax =35.3Mpa 1-3：试计算图a 所示钢水包吊杆的最大应力。以知钢水包及其所盛钢水共重90kN ，吊杆的尺寸如图b 所示。 解： 下端螺孔截面：σ1=1 90 20.065*0.045P S = =15.4Mpa 上端单螺孔截面：σ2=2P S =8.72MPa 上端双螺孔截面：σ3= 3P S =9.15Mpa ∴σmax =15.4Mpa 1-4：一桅杆起重机如图所示，起重杆AB 为一钢管，其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm 2。已知起重量
P=2000N ， 试计算起重机杆和钢丝绳的应力。 解： 受力分析得： F 1*sin15=F 2*sin45 F 1*cos15=P+F 2*sin45 ∴σAB = 1 1F S =-47.7MPa σBC =2 2F S =103.5 MPa 1-5：图a 所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又 两层钢板构成,如c 所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力. 解: F=6P S 1=h*t=40*4.5=180mm 2 S2=(H-d)*t=(65-30)*4.5=157.5mm 2 ∴σmax=2F S =38.1MPa 1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求; (1) AC. CD DB 各段的应力和变形. (2) AB 杆的总变形. 解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa; △ l AC =NL EA =AC L EA σ=-0.01mm △ l CD =CD L EA σ=0 △ L DB =DB L EA σ=-0.01mm (2) ∴AB l ?=-0.02mm 1-7:一圆截面阶梯杆受力如图所示,已知 材料的弹性模量E=200Gpa,试求各段的应力和应变. 解: AC AC AC L NL EA EA σε===1.59*104 ,
岩石力学复习题B 一、选择题 1、岩石与岩体的关系是（ B ）。 （A）岩石就是岩体（B）岩体是由岩石和结构面组成的 （C）岩石是岩体的主要组成部分 2、大部分岩体属于（ C ）。 （A）均质连续材料（B）非均质材料 （C）非均质、非连接、各向异性材料 3、比较岩石抗压强度、抗剪强度和抗拉强度的大小为（ C ）。 （A）抗压强度<抗剪强度<抗拉强度（B）抗压强度>抗拉强度>抗剪强度（C）抗压强度>抗剪强度>抗拉强度 4、影响岩体力学性质各向异性的主要因素为（ B ）。 （A）地下水（B）结构面（C）构造应力场 5、巴西试验是一种间接测定岩石（ B ）强度的试验方法。 （A）抗压（B）抗拉（C）抗剪 6、蠕变是指介质在大小和方向均不改变的外力作用下，介质的（ B ）随时 间的变化而增大的现象。 （A）应力（B）应变（C）粘性 7、下列参数不是岩石强度指标的为（ A ）。 （A）弹性模量（B）内聚力（C）摩擦角 8、格里菲斯准则认为岩石的破坏是由于（ A ）。 （A）拉应力引起的拉裂破坏（B）压应力引起的剪切破坏 （C）压应力引起的拉裂破坏 9、按照库仑—莫尔强度理论，若岩石强度曲线是一条直线，则岩石破坏时破裂面与最大主应力作用方向的夹角为（ C ）。 （A）45°（B）45 2 ? ?+ （C） 45 2 ? ?- （D）60° 10、岩石质量指标RQD是（A ）以上岩芯累计长度和钻孔长度的百分比。A
（A ）10cm （B ）20cm （C ）30cm 11、下列关于岩石长期强度S ∞和瞬间强度S 0的关系正确的是（D ）。 （A ）S ∞＞S 0 （B ）S ∞≤S 0 （C ）S ∞≥S 0 （D ）S ∞＜S 0 12 A 13 C 二、 填空题 １． 就破坏机理而言，岩石材料破坏的主要形式有（ 断裂破坏 ）和 （ 流变破坏 ）两种。 ２． 岩石的弹性变形特性常用（ 弹性模量 ）和（ 泊松比 ）两 个常数来表示。 ３． 岩石变形性质按卸载后变形是否可以恢复可分为（ 弹性变形 ）和 （ 塑性变形 ）两类。 ４． 岩石的剪切模量G 可用岩石的弹性模量E 和泊松比μ计算，其计算公式为 （ 2(1)E μ+ ）；同样岩石的拉梅常数λ也可以用岩石的弹性模量 E 和泊松比μ计算，其公式为（ (1)(12)E μ μμ+- ）。 ５． 岩体基本质量应由受（ 岩石坚硬程度 ）和 （ 岩体完整程度 ）。 ６． 巴西劈裂试验中，P 为劈裂破坏时最大压力，D 为岩石圆盘的直径，T 为岩 石圆盘厚度，则岩石抗拉强度的公式为（ 2t P DT σπ= ）。 7本构关系，强度准则 8 松动和蠕动
工程力学基础复习题B 一、 空心圆轴外力偶矩如图示，已知材料[]100MPa τ=，9 8010 Pa G =?，[]3θ= ， 60mm D =，50mm d =，试校核此轴的强度和刚度。 解：1）画扭矩图 最大扭矩值2kNm 2）最大切应力 ()()3max max 34343 1616210Nm 93.6MPa 10.0510.6m AB P T T W d τπαπ??====-?- 3）最大单位长度扭转角 ()() 3m a x 449244 32180180 32210180 2.68m 180100.0510.6AB AB P T T GI G D θπππαπ???=? =?==-???- []max =93.6MPa <100MPa ττ=，[]max 2.68m 3θθ=<= ， 安全。 二、 梁受力如图示，求约束反力并画出剪力图和弯矩图。 解：1）约束反力 0,200N 0y By F F =-=∑ ； ()200N By F =↑ 0,200N 4m 150Nm 0B M =?+=∑；()950Nm B M =顺时针 2）画剪力图和弯矩图 2kNm m =3－ S F 200N M 400Nm － 550Nm 950Nm
三、 已知矩形截面梁，高度80m m h =，宽度60m m b =，1m a =，分布载荷 6k N m q =,[]170MPa σ=，试校核梁的强度。 解：1）约束反力 0B M =∑ ； 220A aF aq a Fa -?+=；1 2A F qa = ； 0A M =∑ ； 2230B aF aq a aF -?-=； 5 2 B F qa =; 2）画剪力图和弯矩图 3）危险截面在B 处，23261016kN m B M qa ==??=? 236max 22266661093.810Pa =93.8MPa 0.060.08 z M M qa W bh bh σ???=====?? []m a x 93.8M P a <100M P a σσ== 安全。 四、 直角折杆AD 放置水平面内，A 端固定，D 端自由。已知折杆直径0.1m d =受力如图， 15kN F =、210kN F =、3kN P =，[]120MPa σ=，试用第三强度理论校核此杆 的强度。 10kN z =+ － 12 qa 32 qa qa 218 qa 2 qa ＋ －
一章： 1.叙述岩体力学的定义.：岩体力学主要是研究岩石和岩体力学性能的一门学科，是探讨岩石和岩体在其周围物理环境（力场、温度场、地下水等）发生变化后，做出响应的一门力学分支。 2.何谓岩石？何谓岩体？岩石与岩体有何不同之处？（1）岩石：由矿物或岩屑在地质作用下按一定规律聚集而形成的自然物体。（2）岩体：一定工程范围内的自然地质体。（3）不同之处：岩体是由岩石块和各种各样的结构面的综合体。 3.何谓岩体结构？岩体结构的两大要素是什么？ （1）岩体结构是指结构面的发育程度及其组合关系；或者是指结构体的规模、形态及其排列形式所表现的空间形态。（2）结构体和结构面。 4. 岩体结构的六大类型？ 块状、镶嵌、层状、碎裂、层状碎裂、松散结构。 5.岩体有哪些特征？（1）不连续；受结构面控制，岩块可看作连续。（2）各向异性；结构面有一定的排列趋势，不同方向力学性质不同。（3）不均匀性；岩体中的结构面方向、分布、密度及被结构面切割成的岩块的大小、形状和镶嵌情况等在各部位不同，各部位的力学性质不同。（4）赋存地质因子特性（水、气、热、初应力）都会对岩体有一定作用。 二章：岩石物理力学性质有哪些？ 岩石的质量指标，水理性质指标，描述岩石风化能力指标，完整岩石的单轴抗压强度，抗拉强度，剪切强度，三向压缩强度和各种受力状态相对应的变形特性。影响岩石强度特性的主要因素有哪些？对单轴抗压强度的影响因素有承压板、岩石试件尺寸及形状（形状、尺寸、高径比），加载速率、环境（含水率、温度）。对三相压缩强度的影响因素：侧向压力、试件尺寸与加载速率、加载路径、空隙压力。 什么是岩石的应力应变全过程曲线？所谓应力应变全过程曲线是指在刚性实验机上进行实验所获得的包括岩石达到峰值应力之后的应力应变曲线。 2.4简述岩石刚性实验机的工作原理？：压力机加压（贮存弹性应能）岩石试件达峰点强度（释放应变能）导致试件崩溃。AA′O2O1面积—峰点后，岩块产生微小位移所需的能。ACO2O1面积——峰点后，刚体机释放的能量（贮存的能量）。ABO2O1——峰点后，普通机释放的能量(贮存的能量)。当实验机的刚度大于岩石的刚度，才有可能记录下岩石峰值应力后的应力应变曲线。 莫尔强度理论，格尔菲斯强度理论和E.hoek和E.T.brown提出的经验理论的优缺点？：莫尔强度理论优点是使用方便，物理意义明确；缺点是1不能从岩石破坏机理上解释其破坏特征2忽略了中间主应力对岩石强度的影响；格尔菲斯强度理论优点是明确阐明了脆性材料破裂的原因、破裂所需能量及破裂扩展方向；缺点是仅考虑岩石开裂并非宏观上破坏的缘故。E.hoek和E.T.brown提出的经验理论与莫尔强度理论很相似其优点是能够用曲线来表示岩石的强度，但是缺点是表达式稍显复杂。 典型的岩石蠕变曲线有哪些特征？典型的岩石蠕变曲线分三个阶段第Ⅰ阶段：称为初始蠕变段或者叫瞬态蠕变阶段。在此阶段的应变一时间曲线向下弯曲；应变与时间大致呈对数关系，即ε∝㏒t。第Ⅱ阶段：称为等速蠕变段或稳定蠕变段。在此阶段内变形缓慢，应变与时间近于线性关系。第Ⅲ阶段：称为加速蠕变段非
17秋东北大学东大17春学期《岩石力学》在线作业3 一、单选题（共15 道试题，共75 分。） 1. 下列属于表面力的有（） A. 重力 B. 流体压力 C. 剪应力 D. 拉力 正确答案： 2. 下列不是结构面的力学性质主要因素（）。 A. 法向变形 B. 抗压强度 C. 切向变形 D. 抗剪强度 正确答案： 3. 平面滑动时滑动面的倾角与滑动面的摩擦角的关系为（）。 A. β>φ B. β<φ C. β≥φ D. β=φ 正确答案： 4. 构造应力的作用方向为（）。 A. 铅垂方向 B. 近水平方向 C. 断层的走向方向 D. 倾斜方向 正确答案： 5. 下列不是喷出岩常见的岩石的是（） A. 玄武岩 B. 安山岩 C. 流纹岩 D. 花岗岩 正确答案： 6. 已知某岩石饱水状态与干燥状态的抗压强度之比为0.72，则该岩石（）。 A. 软化性强，工程地质性质不良 B. 软化性强，工程地质性质较好 C. 软化性弱，工程地质性质较好 D. 软化性弱，工程地质性质不良
正确答案： 7. 流变性质指材料的应力应变关系与（）因素有关系的性质。 A. 强度 B. 时间 C. 载荷大小 D. 材料属性 正确答案： 8. 在胶结物看，下列哪种胶结强度最低（） A. 硅质 B. 钙质 C. 铁质 D. 泥质 正确答案： 9. 剪胀（或扩容）发生的原因是由于（） A. 岩石内部裂隙闭合引起的 B. 压应力过大引起的 C. 岩石的强度大小引起的 D. 岩石内部裂隙逐渐张开的贯通引起的 正确答案： 10. 岩质边坡发生曲折破坏时，一般是在下列哪种情况下？（） A. 岩层倾角大于坡面倾角 B. 岩层倾角小于坡面倾角 C. 岩层倾角与坡面倾角相同 D. 岩层是直立岩层 正确答案： 11. 不同形式的结构体对岩体稳定性的影响程度由大到小的排列次序为（） A. 聚合型结构体>方形结构体>菱形结构体>锥形结构体 B. 锥形结构体>菱形结构体>方形结构体>聚合型结构体 C. 聚合型结构体>菱形结构体>文形结构体>锥形结构体 D. 聚合型结构体>方形结构体>锥形结构体>菱形结构体 正确答案： 12. 岩石破坏类型由剪应力引起的是（） A. 劈裂 B. 剪断 C. 单轴拉断 D. 崩落 正确答案： 13. 岩质边坡发生岩块翻转破坏的最主要的影响因素是（）。 A. 裂隙水压力 B. 边坡坡度 C. 岩体性质 D. 节理间距比 正确答案： 14. 关于格里菲斯强度理论论述不正确的是（）
教学大纲 第一章概论 §1.1岩石力学的基本概念——什么是岩石力学？ 传统的概念和理论 美国科学院岩石力学委员会定义 岩石力学固体力学和其他力学学科的本质区别 岩石力学的重新定义 §1.2岩石力学的应用——岩石力学服务于哪些工程领域采矿工程 水利水电工程 隧道和公路建设工程 土木建筑工程 石油工程 海洋勘探与开发工程 核电站建设与核废料处理工程 地热开发工程 地震监测与预报工程 §1.3岩石力学与工程研究的特点 力学荷载条件的特殊性和多因素性 研究对象的复杂性和不确定性 研究内容的广泛性和工程实用性
研究方法的多样性、系统性和综合性第二章岩石的物理力学性质 §2.1岩石的物理性质 孔隙度 密度，容重 渗透性 声波速度（在岩石中的传播速度）§2.2岩石力学性质的试验和研究非限制性压缩强度试验 点荷载强度试验 三轴压缩强度试验 拉伸强度试验 剪切强度试验 全应力—应变曲线及破坏后强度试验第三章岩石与岩体分类 §3.1按地质组成分类 具有结晶组织的岩石 具有碎屑组织的岩石 非常细颗粒的岩石 有机岩石 §3.2按力学效应分类 均质连续体 弱面体
散体 §3.3按岩体结构分类 完整块状结构 层状结构 碎裂结构 散体结构 §3.4 CSIR岩体质量分级 CSIR岩体质量分级指标体系 RMR岩体质量评分标准 §3.5 NG1隧道岩体质量分级 NG1岩体质量分级指标体系 Q岩体质量评分标准 第四章岩石强度理论（破坏准则）§4.1莫尔—库仑破坏准则 §4.2经验破坏准则 §4.3格里菲斯破坏准则 §4.4各向异性岩体的破坏 第五章岩石流变理论 §5.1岩石流变的基本概念 §5.2 流变模型 三个流变元件模型 圣维南(St. Venant)体 马克斯威尔Maxwell体
第二章岩石破坏机制及强度理论 第一节岩石破坏的现象 在不同的应力状态下，岩石的破坏机制不同，常见的岩石破坏形式有以下几种 一、拉破坏：岩石试件单向抗压的纵向裂纹，矿柱，采而片帮。特点出现与最大应力 方向平行的裂隙。 " (b) (
3)试件)戏道
三.重剪破坏：即沿原有的结构而的滑动、重剪破坏 主要的机制：岩体受剪切作用或者受拉应力的作用、三向受压情况下多数为剪切应力的作用，侧向压力较小时可能是拉神破坏，实际工程中可能是不同机制的组合，但侧向应力较大时，可以认为剪切应力是岩石重剪破坏的主要破坏机制。 从岩右?破坏的现彖看，从小到几厘米的岩块到大的工程岩体，破坏形式雷同，并可归纳 为两种，拉断与剪坏，因此有一定的规律可寻。 对岩石破坏的研究： 在单向条件下可以从实验得到破坏的经验关系。但是三向受力条件下，不同应力的组合有无穷多种，因此无法仅仅依靠实验得到破坏的经验关系，因此在一般应力状态，对岩石破坏的研究需要结合理论分析和试验研究两个方而。现代关于岩石破坏的理论分析一般归结为、寻求破坏时的主应力之间的关系 b] =/(bg) 研究的方法有：理论分析：2、试验研究；3、理论研究结合试验研究。 第二节岩石拉伸破坏的强度条件 一、最大线应变理论 该理论的主要观点是，岩石中某个面上的拉应变达到临界值时破坏，而与所处的应力状态无关。强度条件为 叫(2-1) < 一拉应变的极限值，￡ —拉应变。门 囹2-4住仲敲坏
……………………………………密…………封……………线………………………………… 1、岩石力学的定义（5分） 2、何为岩石的强度？表示岩石强度的指标有哪些？（5分） 3、试述学过的岩石破坏准则(要求列举4个)列出相应的表达式且说明各自的适用情况。（7分） 第1页共6 页
……………………………………密…………封……………线………………………………… 4、什么是岩体初始应力？试简要说明研究岩体原始应力的工程意义？（5分） 5、详细介绍压力拱理论？（8分） 6、什么叫滑坡？滑坡动面的形式有几种？（5分） 7、什么叫岩基极限承载力？计算时应考虑哪能些条件？（5分） 第2页共6 页
……………………………………密…………封……………线………………………………… 二、作图题：（5分） 直剪破坏试验全过程曲线可分几段？各区段的特点是什么？ 三、选择题：（2/题）（共10分） 1、模量比是指： a. 岩石的 单轴抗压强度和它的弹性模量之比。（ ） b. 岩石的 弹性模量和它的单轴抗压强度之比。（ ） c. 岩体的 单轴抗压强度和它的弹性模量之比。（ ） d.岩体的 弹性模量和它的单轴抗压强度之比。（ ） 2、室内静荷载单轴抗压强度试验要求加荷速度： a.0.5_0.8MPa/s （ ） b. 0.5_1.0MPa/s （ ） c. 0.3_0.5MPa/s （ ） d. 0.3_0.8MPa/s （ ） 3、 a. γ μ)1(+= E k （ ） b. γμ)1(-=E k （ ） c. γμγE k = （ ） d. μ γ+=1E k （ ） 4、下列研究岩石弹性、塑性和粘性等力学性制裁的理想力学模型中，哪一种被称为凯尔文模型？（ ） （A ）弹簧模型 （ ） （B ）缓冲模型 （ ） （C ）弹簧与缓冲器并联 （ ）（D ）弹簧与缓冲器串联 （ ） 5、岩坡发生在岩石崩塌破坏的坡度，一般认为是（ ）。 （a ）>45°时 （b ）>60°时 （c ）>75°时 （d ）90°时 第 3页 共 6 页 \
工程力学（一）复习题A 一．已知变截面钢轴上外力偶矩1800b m N m =?，1200c m N m =?，剪切弹性模量98010Pa G =?，轴的尺寸见图，试求最大切应力max τ和最大相对扭转角 AC ?。 解：1）画扭矩图 最大扭矩值 2）最大切应力 AB 段：36max max 333 1616310Nm 36.210Pa =36.2MPa 0.075m AB AB P T T W d τππ??====?? BC 段：36max max 333 1616 1.210Nm 48.810Pa =48.8MPa 0.05m BC BC P T T W d τππ??====?? 3）最大相对扭转角 AB 段：32 494 32323100.750.6810rad 80100.075AB AB AB AB AB AB T l T l GI G d ?ππ-???====???? BC 段：32494 3232 1.2100.50.61110rad 80100.05 BC BC BC BC BC BC T l T l GI G d ?ππ-???====???? ()220.6110.6810 1.2910rad AC AB BC ???--=+=+?=? 最大切应力为max =48.8MPa BC τ，最大相对扭转角2max 1.2910rad ?-=?
二．梁受力如图示，求约束反力并画出剪力图和弯矩图。 解：1）约束反力 25 5(),()2 Ay A F qa M qa =↑=逆时针 ； 2）画剪力图和弯矩图 三．T 形截面悬臂梁，材料的许用拉应力[]40MPa t σ=，许用压应力 []160MPa c σ=，截面对形心轴z 的惯性矩64101.810cm z I -=?，19.64cm y =，试 计算梁的许可载荷F 。 + 5qa 4qa 252 qa 2 2qa ＋ C 2 2qa
岩石岩体区别：岩石可以看作是一种材料，岩体是岩石与各种不连续面的组合体；岩石可以看作是均质的，岩体是非均质的（在一定的工程范围内）；岩石具有弹、塑、粘弹性，岩体受结构面控制，性质更复杂，强度更低；岩体通常是指一定工程范围内的地质体，岩石则无此概念。 岩石力学是一门研究岩石在外界因素（如荷载、水流、温度变化等）作用下的应力、应变、破坏、稳定性及加固的学科。又称岩体力学，是力学的一个分支。研究目的在于解决水利、土木工程等建设中的岩石工程问题。它是一门新兴的，与有关学科相互交叉的工程学科，需要应用数学、固体力学、流体力学、地质学、土力学、土木工程学等知识，并与这些学科相互渗透。 研究对象：对象：岩石—对象—岩石材料—地壳中坚硬的部分； 复杂性：地质力学环境的复杂性（地应力、地下水、物理、化学作用等） 研究的基本内容： 基本理论岩体地应力 材料实验——三大部分→岩体的强度 工程应用岩体的变形 仅供学习与参考
裂隙水力学 研究方法：物理模拟→岩石物理力学性质常规实验，地质力学模型试验； 数学模型→如有限元等数值模拟； 理论分析→用新的力学分支，理论研究岩石力学问题； 由于岩石中存在各种规模的结构面（断裂带、断层、节理、裂隙）→致使岩石的物理力学性质→不连续、不均匀、各向异性→因此，有必要引入刻划不均一程度的参数。 各向异性：指岩石的强度、变形指标（力学性质）随空间方位不同而异的特性。 岩石的基本物理力学性质 岩石力学问题的研究首先应从岩石的基本物理力学性质研究入手， 1.岩石的容重：指单位体积岩石的重量。 2.比重（Gs）指岩石干重量除以岩石的实体积（不含孔隙体积）的干容重与4?c水的容重的比值。 3.孔隙率（n%）指岩石内孔隙体积与总体积之比。 4.天然含水量：指天然状态下，岩石的含水量与岩石干重比值的百分比。 5.吸水率：指岩石在常温条件下浸水48小时后，岩石内的含水量与岩石干容重的比值。 6.饱和含水率：指岩样在强制状态（真空、煮沸或高压）下，岩样最大吸水量与岩石干重量比值。 7.饱水 仅供学习与参考
第二章 岩石破坏机制及强度理论 第一节 岩石破坏的现象 在不同的应力状态下，岩石的破坏机制不同，常见的岩石破坏形式有以下几种 一、拉破坏：岩石试件单向抗压的纵向裂纹，矿柱，采面片帮。特点出现与最大应力方向平行的裂隙。 二、剪切破坏：岩石试件单向抗压的X 形破坏。从应力分析可知，单向压缩下某一剪切面上的切向应力达到最大引起的破坏。 (a ) (b )
三、重剪破坏：即沿原有的结构面的滑动、重剪破坏 主要的机制：岩体受剪切作用或者受拉应力的作用、三向受压情况下多数为剪切应力的作用，侧向压力较小时可能是拉神破坏，实际工程中可能是不同机制的组合，但侧向应力较大时，可以认为剪切应力是岩石重剪破坏的主要破坏机制。 从岩石破坏的现象看，从小到几厘米的岩块到大的工程岩体，破坏形式雷同，并可归纳为两种，拉断与剪坏，因此有一定的规律可寻。 对岩石破坏的研究： 在单向条件下可以从实验得到破坏的经验关系。但是三向受力条件下，不同应力的组合有无穷多种，因此无法仅仅依靠实验得到破坏的经验关系，因此在一般应力状态，对岩石破坏的研究需要结合理论分析和试验研究两个方面。现代关于岩石破坏的理论分析一般归结为、寻求破坏时的主应力之间的关系 123(,)f σσσ= 研究的方法有：理论分析；2、试验研究；3、理论研究结合试验研究。 第二节 岩石拉伸破坏的强度条件 一、最大线应变理论 该理论的主要观点是，岩石中某个面上的拉应变达到临界值时破坏，而与所处的应力状态无关。强度条件为 c εε≤ (2-1) c ε—拉应变的极限值，ε—拉应变。
若岩石在破坏之前可看作是弹性体，在受压条件下σ1>σ2>σ3下， 3ε是最小主应力。按弹性力学有3 3E E σμ εσσ= -12（+），即33E εσμσσ=-12（+）。若3ε<0则产生拉应变。由于E >0，因此产生拉应变的条件是 3σμσσ-12（+）<0，3μσσσ12（+）> 若3ε=0ε<0则产生拉破坏，此时抗拉强度为0t E σε＝?0t E σε＝。 按最大线应变理论30εε≥破坏，即 312()t σμσσσ-+≥ (2-2) 式中0ε是允许的拉应变。 二、格里菲斯理论 格里菲斯理论的主要观点是：材料内微小裂隙失稳扩展导致材料的宏观破坏。 格里菲斯理论的主要依据是：1）、任何材料中总有各种微小微纹；2）、裂纹尖端的有严重的应力集中，即应力最大，并且有拉应力集中的现象；3）、当这种拉应力集中达到拉伸强度时微裂纹失稳扩展，导致材料的破坏。 格里菲斯理论的来源：由玻璃破坏得到的启示。 格里菲斯理论的基本假设为： 1、岩石的裂隙可视为极扁的扁椭圆裂隙； 2、裂隙失稳扩展可按平面应力问题处理； 3、裂隙之间互不影响。 按格里菲斯理论，裂纹失稳扩展条件为 1）、当1330σσ+>时，满足 21313()8()0t σσσσσ-++= (2-2)