东北大学岩石力学讲义岩石破坏机制及强度理论
- 格式:docx
- 大小:257.66 KB
- 文档页数:17

第六章地下工程灾害预报与防治第四节、岩爆发生的现象、机理与防治一、岩爆发生的现象岩爆是矿井进入深部开采以后更容易遇到的严重的灾害之一。
有记录的岩爆发生的历史我国岩爆发生的基本情况岩爆是岩石动力破坏的一种特殊形式采矿引起岩石破坏的主要形式1、岩块的冒落或坍落原因:采矿导致节理岩体的松动。
危害:砸伤作业人员、损坏支护。
2、松散岩层变形原因:在强大地应力作用下,松软岩体的明显变形。
危害:损坏支护,改变巷道断面和形状。
3、凿岩爆破等动载荷下的破坏;4、岩爆、煤与瓦斯突出等动力现象岩爆发生的一些实例岩爆的危害:造成人员设备的巨大损失并引起作业人员的恐慌。
岩爆与通常的岩体破坏现象的区别通常的岩体石破坏发生时的主要现象:1、通常的岩石破坏不会有猛烈的声响和(大量)能量的瞬间释放;2、破坏过程缓慢;3、要进一步施加外载或做功才能发生破坏;4、比较容易预报。
岩爆发生的现象和特点:1、破坏范围大、能量大;2、无明显前兆的情况下,自行发生破坏,难以预报;3、破坏时可以有巨大声响,破坏及其迅速;4、小扰动下会引发岩爆;5、岩爆有滞后发生的现象;6、岩爆引起的岩体突然破坏不需要外界向系统进一步输入能量,因此与爆破载荷引起的岩体动力破坏有实质区别。
岩爆发生的初步的定义(从现象上):岩爆是岩石(体)猛烈破坏并释放大量能量的现象。
岩爆是岩石(体)的一种特殊的破坏形式,并可以得出如下结论:1、岩爆不能简单地等同与岩石的破坏;2、岩爆所表现出的岩石破坏的动力性,不同于爆破引起的岩石动力破坏。
问题与思考:岩爆与普通岩石破坏的根本区别是什么?“科学研究的区分,就是根据科学对象所具有的特殊的矛盾性。
因此,对某一现象所特有的某种矛盾的研究,就构成某一门学科的对象。
”(毛泽东《矛盾论》)库克认为:“岩体发生破坏,引起矿体—围岩力学系统平衡状态破坏时,若其释放的能量大于消耗的能量,将产生岩爆。
”岩爆与通常岩石破坏的本质区别在于:1、破坏的突然性;2、破坏过程中有多余的(有时是大量的)能量释放。





![岩石的强度理论及破坏判据[详细]](https://uimg.taocdn.com/b87c145d5ef7ba0d4b733ba7.webp)


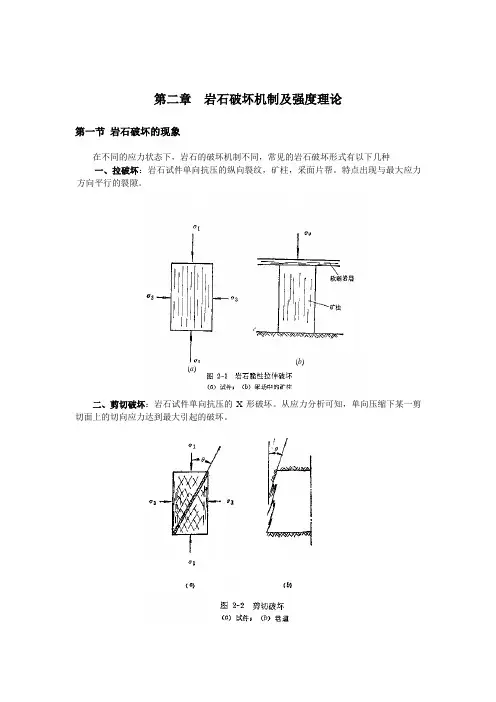
第二章 岩石破坏机制及强度理论第一节 岩石破坏的现象在不同的应力状态下,岩石的破坏机制不同,常见的岩石破坏形式有以下几种一、拉破坏:岩石试件单向抗压的纵向裂纹,矿柱,采面片帮。
特点出现与最大应力方向平行的裂隙。
二、剪切破坏:岩石试件单向抗压的X 形破坏。
从应力分析可知,单向压缩下某一剪切面上的切向应力达到最大引起的破坏。
(a ) (b )三、重剪破坏:即沿原有的结构面的滑动、重剪破坏主要的机制:岩体受剪切作用或者受拉应力的作用、三向受压情况下多数为剪切应力的作用,侧向压力较小时可能是拉神破坏,实际工程中可能是不同机制的组合,但侧向应力较大时,可以认为剪切应力是岩石重剪破坏的主要破坏机制。
从岩石破坏的现象看,从小到几厘米的岩块到大的工程岩体,破坏形式雷同,并可归纳为两种,拉断与剪坏,因此有一定的规律可寻。
对岩石破坏的研究:在单向条件下可以从实验得到破坏的经验关系。
但是三向受力条件下,不同应力的组合有无穷多种,因此无法仅仅依靠实验得到破坏的经验关系,因此在一般应力状态,对岩石破坏的研究需要结合理论分析和试验研究两个方面。
现代关于岩石破坏的理论分析一般归结为、寻求破坏时的主应力之间的关系123(,)f σσσ=研究的方法有:理论分析;2、试验研究;3、理论研究结合试验研究。
第二节 岩石拉伸破坏的强度条件一、最大线应变理论该理论的主要观点是,岩石中某个面上的拉应变达到临界值时破坏,而与所处的应力状态无关。
强度条件为c εε≤ (2-1) c ε—拉应变的极限值,ε—拉应变。
若岩石在破坏之前可看作是弹性体,在受压条件下σ1>σ2>σ3下, 3ε是最小主应力。
按弹性力学有33E Eσμεσσ=-12(+),即33E εσμσσ=-12(+)。
若3ε<0则产生拉应变。
由于E >0,因此产生拉应变的条件是3σμσσ-12(+)<0,3μσσσ12(+)>若3ε=0ε<0则产生拉破坏,此时抗拉强度为0tEσε=⇒0t E σε=。

第五章岩石的爆破破碎机理本章重点:1、爆破破坏的几种假说;2、单个药包作用下的破坏特征3、霍布金逊效应;4、爆破漏斗;5、装药量计算;难点:1、应力波在岩体中传播引起的应力状态;2、能量利用对岩石破坏影响。
前面学习了爆破器材和爆破方法,那么炸药包是如何把炸药能量传递给岩石的呢?由于爆炸的特殊性,尚不能彻底解决。
5.1 岩石爆破破坏原因的基本理论三大类情况一、爆炸气体产物膨胀压力破坏理论爆炸产生高压气体作用于孔眼壁岩层,产生应力场,引起应变,产生径向位移,产生径向压应力,径向压力衍生切向拉应力,当切向应力大于岩石的抗拉强度时,则产生径向裂隙。
气体膨胀的结果①产生径向压应力,径向位移;②衍生切向拉应力;③不同质点位移产生剪应力;④径向抛掷。
二、冲击波引起应力波反射破坏理论炸药爆炸产生的爆轰波传播到孔壁的结果①产生压力波;②在自由面反射成拉应力波;③拉伸破坏这种理论依据是破碎是从自由面处开始的。
三、膨胀气体与冲击波所引起的应力波共同作用理论上面的两种作用分处于不同的阶段,炸药爆炸产生的应力波,使①在近区形成压碎;②在压碎区之外造成径向裂隙;③气体的气楔作用使裂隙进一步扩张,直到停止。
根据这一原理,可以针对不能特性的岩石和破碎要求,选用不同特性的炸药,使炸药的能量利用率最高,而破碎效果最好。
岩石的波阻抗值较高时,要求有较高的应力波波峰值。
波阻抗=c ⨯ρ5.2单个药包爆破作用分析一、内部作用:单药包埋置很深时,或采用有机玻璃模拟爆破时可以观察到爆破破坏的内部作用。
岩石分为三个破坏区:①压缩区(粉碎区)5000-10000MPa的超高压远大于最坚韧岩石的动抗压强度,形成粉碎区,不大于药室半径的2倍。
②破坏区能量在粉碎区消耗后,冲击波衰减为应力波,引起质点径向位移,从而产生环向拉应变,并引发径向裂隙。
由压应力而产生的弹性变形能会引起岩石质点的向心运动而产生径向拉伸应力,从而形成环向裂隙。
高压气体对裂隙扩展的作用(应力集中区,格里非斯理论)③震动区不能引起岩石破坏的能量导致弹性震动,范围较大。
精品文档第二章岩石破坏机制及强度理论岩石破坏的现象第一节在不同的应力状态下,岩石的破坏机制不同,常见的岩石破坏形式有以下几种:岩石试件单向抗压的纵向裂纹,矿柱,采面片帮。
特点出现与最大应力一、拉破坏方向平行的裂隙。
)(b) (a形破坏。
从应力分析可知,单向压缩下某一剪二、剪切破坏:岩石试件单向抗压的X 切面上的切向应力达到最大引起的破坏。
精品文档.精品文档三、重剪破坏:即沿原有的结构面的滑动、重剪破坏主要的机制:岩体受剪切作用或者受拉应力的作用、三向受压情况下多数为剪切应力的作用,侧向压力较小时可能是拉神破坏,实际工程中可能是不同机制的组合,但侧向应力较大时,可以认为剪切应力是岩石重剪破坏的主要破坏机制。
并可归纳从小到几厘米的岩块到大的工程岩体,破坏形式雷同,从岩石破坏的现象看,为两种,拉断与剪坏,因此有一定的规律可寻。
对岩石破坏的研究:不同应力的组合在单向条件下可以从实验得到破坏的经验关系。
但是三向受力条件下,对岩石破因此在一般应力状态,有无穷多种,因此无法仅仅依靠实验得到破坏的经验关系,坏的研究需要结合理论分析和试验研究两个方面。
现代关于岩石破坏的理论分析一般归结为、寻求破坏时的主应力之间的关系???)(,?f321、理论研究结合试验研究。
、试验研究;3研究的方法有:理论分析;2岩石拉伸破坏的强度条件第二节一、最大线应变理论岩石中某个面上的拉应变达到临界值时破坏,而与所处的应力该理论的主要观点是,状态无关。
强度条件为(2-1)???c—拉应变的极限值,—拉应变。
??c精品文档.精品文档?是最小主应力。
σ下,σ>σ>若岩石在破坏之前可看作是弹性体,在受压条件下3123??????3,E>0<0则产生拉应变。
由于,即。
若按弹性力学有?????)?(?+)E?(?+32312133EE因此产生拉应变的条件是????????)>((?++)<0,312132??????t?E==。
第二章岩石破坏机制及强度理论第一节岩石破坏的现象在不同的应力状态下,岩石的破坏机制不同,常见的岩石破坏形式有以下几种一、拉破坏:岩石试件单向抗压的纵向裂纹,矿柱,采而片帮。
特点出现与最大应力 方向平行的裂隙。
"(b)(</,图27岩石脳性拉伸破以 ©)试件■ <W 采场中的犷住二、剪切破坏:岩石试件单向抗压的X 形破坏。
从应力分析可知,单向压缩下某一剪 切面上的切向应力达到最大引起的破坏。
((&) 图2“2菊切破坏53)试件)戏道三.重剪破坏:即沿原有的结构而的滑动、重剪破坏主要的机制:岩体受剪切作用或者受拉应力的作用、三向受压情况下多数为剪切应力的作用,侧向压力较小时可能是拉神破坏,实际工程中可能是不同机制的组合,但侧向应力较大时,可以认为剪切应力是岩石重剪破坏的主要破坏机制。
从岩右•破坏的现彖看,从小到几厘米的岩块到大的工程岩体,破坏形式雷同,并可归纳为两种,拉断与剪坏,因此有一定的规律可寻。
对岩石破坏的研究:在单向条件下可以从实验得到破坏的经验关系。
但是三向受力条件下,不同应力的组合有无穷多种,因此无法仅仅依靠实验得到破坏的经验关系,因此在一般应力状态,对岩石破坏的研究需要结合理论分析和试验研究两个方而。
现代关于岩石破坏的理论分析一般归结为、寻求破坏时的主应力之间的关系b] =/(bg)研究的方法有:理论分析:2、试验研究;3、理论研究结合试验研究。
第二节岩石拉伸破坏的强度条件一、最大线应变理论该理论的主要观点是,岩石中某个面上的拉应变达到临界值时破坏,而与所处的应力状态无关。
强度条件为叫(2-1) < 一拉应变的极限值,£ —拉应变。
门囹2-4住仲敲坏若岩石在破坏之前可看作是弹性体,在受压条件下0,>02>«3下,§是最小主应力。
按弹性力学有6 =¥-牛9+6),即凸=巧-/g+还)。
若5<0则产生拉应变。
由于E>0, 因此产生拉应变的条件是6-“((7^(7? <0 • ”(b] + 6)>O\若®二£。
<0则产生拉破坏,此时抗拉强度为%=冬=> 6=E“ oE按最大线应变理论s>勺破坏,即6 —“(b|+b2)nq (2-2)式中是允许的拉应变。
» 2-1几种岩石的拉忡应««««(mm)试比hfd e(石KSA41t石英MB412OJOO】仞启英逍c282O.OOOC81石艾岩Q 41t O.OQOL30不英岩E412O.OOH132席君A412oeooix熔計B4120 •泗33玄近占B4130.000175苏找若S4Z.50/00173孫若A410•切冈必砾岩E<J20.^00073砾冷c4】20.000083砂君4120.000090戻甘A门20.0002IfiPI S B412 C.OOOIJOnt sc282 C.OOOU95二.格里菲斯理论格里菲斯理论的主要观点是:材料内微小裂隙失稳扩展导致材料的宏观破坏。
格里菲斯理论的主要依据是:I)、任何材料中总有各种微小微纹:2)、裂纹尖端的有严重的应力集中,即应力最大,并且有拉应力集中的现象:3)、当这种拉应力集中达到拉伸强度时微裂纹失稳扩展,导致材料的破坏。
格里菲斯理论的来源:由玻璃破坏得到的启示。
格里菲斯理论的基本假设为:1、岩石的裂隙可视为极扁的扁椭圆裂隙:2、裂隙失稳扩展可按平而应力问题处理:3、裂隙之间互不影响。
按格里菲斯理论,裂纹失稳扩展条件为1)、当0+3巧>0时,满足时发生破坏。
2).当°+36<0时,满足6 = -8(7, (2-3) 时发生破坏。
式中。
C—单向抗压强度,I—单向抗拉强度。
按格氏理论,岩右•的拉压强度是抗拉强度的8倍•按照格里菲斯理论,岩仃破坏的微观机制是微裂隙的受拉破坏,Z;•观机制是微裂隙的失稳扩展并汇合成宏观裂隙。
三.修正的格里菲斯理论格里菲斯理论没有考虑裂隙受压和裂隙而摩擦的情况,只能用于裂隙严格受拉的情况,因此Maclintock和Walsh考虑到裂隙在压应力作用下的混发生闭合的情况,对格里菲斯理论进行了修正,得到了修正的格里菲斯准则q=一舌——------------- —(2-4)(1 一二)(1 + /2) — /(1 + 丄)厲©式中4—岩石的抗拉强度。
由于抗拉强度测量比较困难。
因此用抗压强度代替抗拉强度。
当6 =0, q =4时从上式可求出(2-5)将(2・5)式代入(24)式可得到以抗压强度表示的修(2-6)正的格里菲斯准则。
式中/是裂隙而的摩擦系数。
研究裂纹的两种方法:1、椭圆坐标:2、数学裂纹。
以上是二维理论,其进一步的假设为:1、岩体内遍布微裂隙,且裂隙可理想化为格里菲斯裂纹:2、岩体内裂纹均匀分布,但裂纹之间没有相互作用。
第三节.岩石剪切破坏的强度条件一、莫尔强度理论莫尔强度理论的基本观点:莫尔强度理论认为,材料在压应力作用下的屈服和破坏,主要是在材料内部某一截面上的剪应力到达一上限度,但也和作用于该截而上的正应力有关。
莫尔强度理论的来源:最早起源于对金属摩擦的研究。
对岩石力学而言,主要来源于上力学。
根据对摩擦的研究,滑动面上的剪切位移既与剪应力有关,又与正应力有关,剪切破坏的一般示意图如下。
T———A熨2-6推劝柑块的推力丁与P关系因此,强度准则的一般形式为r = f(a)(2-6) 上式一般是非线性关系,因此在T 一。
图上一般是曲线,直线是其特例,也是最简单的情况。
下图是几种典型的剪切破坏r = /(a)曲线图2-7几种岩石强度曲线花卤自砂岩](o山岩$ (d)土二、绘制r = f(a)的方法:按照莫尔理论测定岩石的强度,有以下几种方法:1、由三轴压缩实验测上破坏时的。
丨和。
3,由此绘制一系列极限应力图,这些圆的包络即是强度曲线r = f(a) o2、由剪切试验(斜剪或直剪),得到破坏时的一系列♦和。
a(方法见前一条),由此拟合曲线。
3、按单向抗拉强度和单向抗压试验求强度曲线。
r =返叵+ (2-7)2 a a,因2-8英尔包络级閔以下讨论式(2-6)的导出过程。
按图2-8,从抗压和抗拉两个实验绘制莫尔圆,可确泄 如下曲线T = C + 6g©设摩擦角为0,则单向受压时的剪应力和正应力为单向受拉时的剪应力和正应力为(J o a t = —+ —sind f2 2直线斜率为dig嘶cr + q(cr + q)-(cr-q)sin0(<j 一q)cos‘ 0 = (£F + q)sin0-(cT + a;)sin' ©O C~2-企sina=—cos^ , 2=>国2-8按抗拉“抗压碩度求强度曲线O圈2-9 岩石在a 作用下能否破坏判断=>▲ O_6 sm0 =(7 + 0纵坐标上的点C 确定的方法C = ¥cos0+q 丄=30 2 6 => G=Qx 曲=> a a T — ( f 4- 1ain /AVp/A 4a \ 2亠山艸〃&労 =>aC = T-(Jg0 + t0sin0 + cos0)由辅助三角形ige=代入上式得到=>6 (q -q)(q+0) + C -0)'+4吓 q 2q'+20q 2j4qq(°.+0)2 2jqQg+q)=>因此「_6 6 _V^TJ — - -- ~ ----- --------2 J°Q , 2一屋*异斗屋仆+ = 622^^2吓然后根据图2-9可以得到乞个量的几何关系.得岀(2 — 7)式。
7 一 oCT-CT,(W )0 -q) | Jgg )J4qq q.+q q+q三. 库仑一莫尔理论按莫尔强度理论得到的岩石强度曲线一般是曲线,直线是其特例。
在莫尔理论的基础上, 库仑假设岩石的剪切强度曲线是直线,称为库仑一莫尔理论。
按照库仑一莫尔理论,对于图 2-7所示的岩石的直剪情况下的破坏,剪切强度r 可按下式确左(2-8)(2-8a)上式中的绝对值表示剪切破坏与滑移方向无关。
式中,b —作用在剪切而上的正应力,0- 岩石的内摩擦角,/ —岩石的内摩擦系数,C —岩石的纯剪切强度(即剪切滑移而上的正应力 <7 = 0时的剪切强度),也称内聚力,粘结力。
但工程岩体的应力状态比图(2-7)所示的更复杂,为了便于将莫尔一库仑理论推广到一 般的应力状态,需要有比式(2-8)更方便的公式,为此首先介绍应力莫尔圆。
应力莫尔圆简介考虑两种平而直角坐标O 小和Oxy 中应力分量的变换图 2-10如果坐标系O 小中的应力分量已知,则对于图2-10的情况容易导出6 = 70 + a )+ 范 -6)cos 2a + r… sin2a S = +(6 + U )- + © - S )cos 2ct + q sin 2a 匚 y =扣,- 6)血 2a - g cos 2a“y 是坐标系"op 坐标中应力分虽:。
若在主应力空间,则r tv = 0 , 因此或者p| = C + 6g0= -(CFj +<73)+ 了(巧-cr 3)cos 2aGy =[(S —6)sin 2a图 2-11q ,和也可看作是与6成a 角的平面上的法向应力和剪应力,即可写为o a =丄(6 +6)+丄(巧 一6)cos2a <T a = —(a, -crjsin 2a下而讨论cr 。
,讣的几何表示。
将(2-9)式改写为:(巧 一6) cos2° =乙一卜巧 + 6) -(a, 一crjsin 2a = T a从(2-10)式可以求岀,[乙一*(0+6)尸 + 疋=土(0-6)‘在J' °a 平而上,上式表示一个圆,圆心在b 轴上(CT ] +6),0】,半径为- 6), 被称为莫尔应力圆,在不引起误解的情况下,用厂,o ■表示与5成。
角的平面上的正应力和 剪应力乙,T a .图2-12的应力莫尔圆,是公式(2-10)的几何表示。
考虑下面的试验。
试件受6和6的作用,6 >6。
试件中的某个而与巧的夹角为a, 则在6,6作用下,该斜而上的法向应力//和剪应力G 就是应力莫尔圆上的P 点的横 坐标和纵坐标。
对比图2-10和2-11试件内与6成&角的而,就是莫尔应力圆上与成加角 的点。
因此从圆心[y (CT| +CFj ), 0]起做与(J 轴为加角的射线,它与射线与<7轴夹角为加,(2-9)(2-10)6应力莫尔圆的交点为几 从图2」1可以看出,P 点的横坐标无和纵坐标-分别为乙=丄(6+6)+丄(6 — 6)cos2a ;r a = -(a { -cr jsin 2a(2-1 la, b)图2・13如果将(2-11)式中的人理解为图2・13所示的a 面上的剪应力和正应力,则(2J1)式可 以推广到受压岩石的剪切破坏。