二叉搜索树(BinarySearchTree).

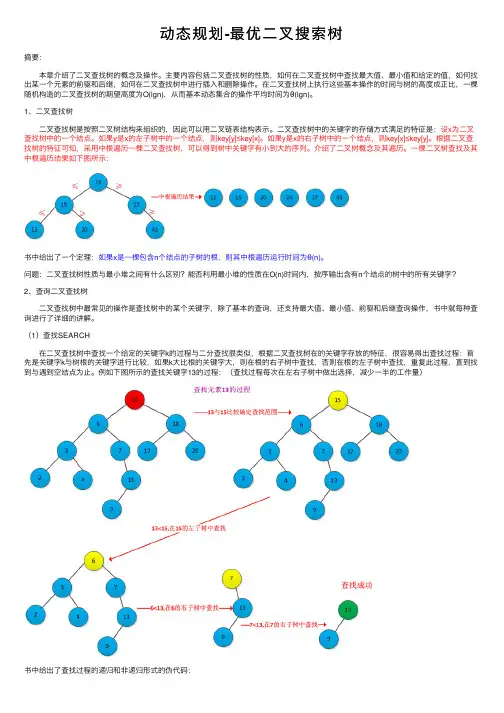
动态规划-最优⼆叉搜索树摘要： 本章介绍了⼆叉查找树的概念及操作。

主要内容包括⼆叉查找树的性质，如何在⼆叉查找树中查找最⼤值、最⼩值和给定的值，如何找出某⼀个元素的前驱和后继，如何在⼆叉查找树中进⾏插⼊和删除操作。

在⼆叉查找树上执⾏这些基本操作的时间与树的⾼度成正⽐，⼀棵随机构造的⼆叉查找树的期望⾼度为O(lgn)，从⽽基本动态集合的操作平均时间为θ(lgn)。

1、⼆叉查找树 ⼆叉查找树是按照⼆叉树结构来组织的，因此可以⽤⼆叉链表结构表⽰。

⼆叉查找树中的关键字的存储⽅式满⾜的特征是：设x为⼆叉查找树中的⼀个结点。

如果y是x的左⼦树中的⼀个结点，则key[y]≤key[x]。

如果y是x的右⼦树中的⼀个结点，则key[x]≤key[y]。

根据⼆叉查找树的特征可知，采⽤中根遍历⼀棵⼆叉查找树，可以得到树中关键字有⼩到⼤的序列。

介绍了⼆叉树概念及其遍历。

⼀棵⼆叉树查找及其中根遍历结果如下图所⽰：书中给出了⼀个定理：如果x是⼀棵包含n个结点的⼦树的根，则其中根遍历运⾏时间为θ(n)。

问题：⼆叉查找树性质与最⼩堆之间有什么区别？能否利⽤最⼩堆的性质在O(n)时间内，按序输出含有n个结点的树中的所有关键字？2、查询⼆叉查找树 ⼆叉查找树中最常见的操作是查找树中的某个关键字，除了基本的查询，还⽀持最⼤值、最⼩值、前驱和后继查询操作，书中就每种查询进⾏了详细的讲解。

（1）查找SEARCH 在⼆叉查找树中查找⼀个给定的关键字k的过程与⼆分查找很类似，根据⼆叉查找树在的关键字存放的特征，很容易得出查找过程：⾸先是关键字k与树根的关键字进⾏⽐较，如果k⼤⽐根的关键字⼤，则在根的右⼦树中查找，否则在根的左⼦树中查找，重复此过程，直到找到与遇到空结点为⽌。

例如下图所⽰的查找关键字13的过程：（查找过程每次在左右⼦树中做出选择，减少⼀半的⼯作量）书中给出了查找过程的递归和⾮递归形式的伪代码：1 TREE_SEARCH(x,k)2 if x=NULL or k=key[x]3 then return x4 if(k<key[x])5 then return TREE_SEARCH(left[x],k)6 else7 then return TREE_SEARCH(right[x],k)1 ITERATIVE_TREE_SEARCH(x,k)2 while x!=NULL and k!=key[x]3 do if k<key[x]4 then x=left[x]5 else6 then x=right[x]7 return x（2）查找最⼤关键字和最⼩关键字 根据⼆叉查找树的特征，很容易查找出最⼤和最⼩关键字。

二叉排序树1．二叉排序树定义二叉排序树（Binary Sort Tree）或者是一棵空树；或者是具有下列性质的二叉树：（1）若左子树不空，则左子树上所有结点的值均小于根结点的值；若右子树不空，则右子树上所有结点的值均大于根结点的值。

（2）左右子树也都是二叉排序树，如图6-2所示。

2．二叉排序树的查找过程由其定义可见，二叉排序树的查找过程为：（1）若查找树为空，查找失败。

（2）查找树非空，将给定值key与查找树的根结点关键码比较。

（3）若相等，查找成功，结束查找过程，否则：①当给值key小于根结点关键码，查找将在以左孩子为根的子树上继续进行，转（1）。

②当给值key大于根结点关键码，查找将在以右孩子为根的子树上继续进行，转（1）。

3．二叉排序树插入操作和构造一棵二叉排序树向二叉排序树中插入一个结点的过程：设待插入结点的关键码为key，为将其插入，先要在二叉排序树中进行查找，若查找成功，按二叉排序树定义，该插入结点已存在，不用插入；查找不成功时，则插入之。

因此，新插入结点一定是作为叶子结点添加上去的。

构造一棵二叉排序树则是逐个插入结点的过程。

对于关键码序列为：｛63，90，70，55，67，42，98，83，10，45，58｝，则构造一棵二叉排序树的过程如图6-3所示。

4．二叉排序树删除操作从二叉排序树中删除一个结点之后，要求其仍能保持二叉排序树的特性。

设待删结点为*p（p为指向待删结点的指针），其双亲结点为*f，删除可以分三种情况，如图6-4所示。

（1）*p结点为叶结点，由于删去叶结点后不影响整棵树的特性，所以，只需将被删结点的双亲结点相应指针域改为空指针，如图6-4（a）所示。

（2）*p结点只有右子树或只有左子树，此时，只需将或替换*f结点的*p子树即可，如图6-4（b）、（c）所示。

（3）*p结点既有左子树又有右子树，可按中序遍历保持有序地进行调整，如图6-4（d）、（e）所示。

设删除*p结点前，中序遍历序列为：① P为F的左子女时有：…，Pi子树，P，Pj，S子树，Pk，Sk子树，…，P2，S2子树，P1，S1子树，F，…。

2024年研究生考试考研计算机学科专业基础(408)自测试卷(答案在后面)一、单项选择题（本大题有40小题，每小题2分，共80分）1、在计算机网络中，TCP协议工作在哪一层？A. 物理层B. 数据链路层C. 网络层D. 传输层2、假设有一个采用补码表示的8位寄存器，如果该寄存器的内容是10000000，则其对应的十进制数值是多少？A. -127B. -128C. 0D. 1283、以下哪项不是数据库事务应满足的ACID特性之一？A. 原子性B. 一致性C. 隔离性D. 持久性E. 可用性4、在计算机系统中，以下哪种存储器属于随机存取存储器（RAM）？A、只读存储器（ROM）B、光盘存储器C、硬盘存储器D、动态随机存取存储器（DRAM）5、下列哪个选项描述了编译器的功能？A、将汇编语言翻译成机器语言B、将高级语言翻译成机器语言C、将机器语言翻译成高级语言D、将二进制代码转换成源代码6、在数据结构中，以下哪种数据结构可以实现高效的查找操作？A、链表B、数组C、栈D、哈希表7、在下列寻址方式中，哪种寻址方式需要两次访问内存？A. 直接寻址B. 立即数寻址C. 寄存器间接寻址D. 基址变址寻址8、设有3个作业J1、J2、J3，它们的到达时间和运行时间如下表所示。

若采用短作业优先(SJF)调度算法，则这3个作业的平均等待时间是多少？作业到达时间运行时间J106J224J342A. 6B. 8C. 10D. 129、下面关于虚拟存储器的说法，哪个是正确的？A. 虚拟存储器允许程序访问比主存更大的地址空间。

B. 虚拟存储器可以完全避免碎片问题。

C. 虚拟存储器的实现不需要硬件支持。

D. 虚拟存储器中所有页面都在内存中。

10、计算机网络的OSI七层模型中，负责处理数据传输的层次是：A. 应用层B. 表示层C. 会话层D. 传输层13、在某计算机系统中，若一个文件的物理结构采用链接结构存储，则下列说法正确的是：A. 适合于随机存取B. 存储空间利用率高，但不支持随机访问C. 不利于文件长度动态增长D. 文件的逻辑记录不必连续存放16、在计算机科学中，下列哪个术语描述了一个由有限个状态组成的模型，用于描述有限个输入的序列，并产生输出？A. 有限自动机B. 状态机C. 数据结构D. 程序19、关于操作系统中的进程状态转换，以下哪个选项是正确的？A. 进程从就绪状态直接转换为阻塞状态B. 进程从运行状态直接转换为就绪状态C. 进程从阻塞状态直接转换为运行状态D. 进程从创建状态直接转换为运行状态22、在计算机科学中，以下哪种排序算法的平均时间复杂度是O(nlogn)？A. 冒泡排序B. 快速排序C. 插入排序D. 选择排序25、在计算机系统中，以下哪个设备通常用于存储大量数据？A. 硬盘驱动器（HDD）B. 光驱C. 显卡D. CPU28、以下关于C++中虚函数和纯虚函数的说法，正确的是（）A. 虚函数一定有函数体，纯虚函数必须有函数体B. 纯虚函数可以出现在类中，但不能被实例化C. 虚函数只能在派生类中重写，纯虚函数只能在基类中重写D. 虚函数和纯虚函数都是成员函数，都可以在类定义中给出函数体31、在计算机网络中，以下哪个协议是用于传输电子邮件的？A. HTTPB. FTPC. SMTPD. TCP34、以下关于数据结构中二叉搜索树的描述，错误的是：A. 二叉搜索树是一种特殊的二叉树，其中每个节点都有一个关键字。

分治法1、二分搜索算法是利用（分治策略）实现的算法。

9. 实现循环赛日程表利用的算法是（分治策略）27、Strassen矩阵乘法是利用（分治策略）实现的算法。

34．实现合并排序利用的算法是（分治策略）。

实现大整数的乘法是利用的算法（分治策略）。

17．实现棋盘覆盖算法利用的算法是（分治法）。

29、使用分治法求解不需要满足的条件是（子问题必须是一样的）。

不可以使用分治法求解的是（0/1背包问题）。

动态规划下列不是动态规划算法基本步骤的是（构造最优解）下列是动态规划算法基本要素的是（子问题重叠性质）。

下列算法中通常以自底向上的方式求解最优解的是（动态规划法）备忘录方法是那种算法的变形。

（动态规划法）最长公共子序列算法利用的算法是（动态规划法）。

矩阵连乘问题的算法可由（动态规划算法B）设计实现。

实现最大子段和利用的算法是（动态规划法）。

贪心算法能解决的问题：单源最短路径问题，最小花费生成树问题，背包问题，活动安排问题，不能解决的问题：N皇后问题，0/1背包问题是贪心算法的基本要素的是（贪心选择性质和最优子结构性质）。

回溯法回溯法解旅行售货员问题时的解空间树是（排列树）。

剪枝函数是回溯法中为避免无效搜索采取的策略回溯法的效率不依赖于下列哪些因素（确定解空间的时间）分支限界法最大效益优先是（分支界限法）的一搜索方式。

分支限界法解最大团问题时，活结点表的组织形式是（最大堆）。

分支限界法解旅行售货员问题时，活结点表的组织形式是（最小堆）优先队列式分支限界法选取扩展结点的原则是（结点的优先级）在对问题的解空间树进行搜索的方法中,一个活结点最多有一次机会成为活结点的是( 分支限界法).从活结点表中选择下一个扩展结点的不同方式将导致不同的分支限界法,以下除( 栈式分支限界法)之外都是最常见的方式.（1）队列式(FIFO)分支限界法：按照队列先进先出（FIFO）原则选取下一个节点为扩展节点。

（2）优先队列式分支限界法：按照优先队列中规定的优先级选取优先级最高的节点成为当前扩展节点。

数据结构之⼆叉树（BinaryTree）⽬录导读 ⼆叉树是⼀种很常见的数据结构，但要注意的是，⼆叉树并不是树的特殊情况，⼆叉树与树是两种不⼀样的数据结构。

⽬录 ⼀、⼆叉树的定义 ⼆、⼆叉树为何不是特殊的树 三、⼆叉树的五种基本形态 四、⼆叉树相关术语 五、⼆叉树的主要性质（6个） 六、⼆叉树的存储结构（2种） 七、⼆叉树的遍历算法（4种） ⼋、⼆叉树的基本应⽤：⼆叉排序树、平衡⼆叉树、赫夫曼树及赫夫曼编码⼀、⼆叉树的定义 如果你知道树的定义（有限个结点组成的具有层次关系的集合），那么就很好理解⼆叉树了。

定义：⼆叉树是n(n≥0)个结点的有限集，⼆叉树是每个结点最多有两个⼦树的树结构，它由⼀个根结点及左⼦树和右⼦树组成。

（这⾥的左⼦树和右⼦树也是⼆叉树）。

值得注意的是，⼆叉树和“度⾄多为2的有序树”⼏乎⼀样，但，⼆叉树不是树的特殊情形。

具体分析如下⼆、⼆叉树为何不是特殊的树 1、⼆叉树与⽆序树不同 ⼆叉树的⼦树有左右之分，不能颠倒。

⽆序树的⼦树⽆左右之分。

2、⼆叉树与有序树也不同（关键） 当有序树有两个⼦树时，确实可以看做⼀颗⼆叉树，但当只有⼀个⼦树时，就没有了左右之分，如图所⽰：三、⼆叉树的五种基本状态四、⼆叉树相关术语是满⼆叉树；⽽国际定义为，不存在度为1的结点，即结点的度要么为2要么为0，这样的⼆叉树就称为满⼆叉树。

这两种概念完全不同，既然在国内，我们就默认第⼀种定义就好）。

完全⼆叉树：如果将⼀颗深度为K的⼆叉树按从上到下、从左到右的顺序进⾏编号，如果各结点的编号与深度为K的满⼆叉树相同位置的编号完全对应，那么这就是⼀颗完全⼆叉树。

如图所⽰：五、⼆叉树的主要性质 ⼆叉树的性质是基于它的结构⽽得来的，这些性质不必死记，使⽤到再查询或者⾃⼰根据⼆叉树结构进⾏推理即可。

性质1：⾮空⼆叉树的叶⼦结点数等于双分⽀结点数加1。

证明：设⼆叉树的叶⼦结点数为X，单分⽀结点数为Y，双分⽀结点数为Z。

Java常见的七种查找算法1. 基本查找也叫做顺序查找，说明：顺序查找适合于存储结构为数组或者链表。

基本思想：顺序查找也称为线形查找，属于无序查找算法。

从数据结构线的一端开始，顺序扫描，依次将遍历到的结点与要查找的值相比较，若相等则表示查找成功；若遍历结束仍没有找到相同的，表示查找失败。

示例代码：public class A01_BasicSearchDemo1 {public static void main(String[] args){//基本查找/顺序查找//核心：//从0索引开始挨个往后查找//需求：定义一个方法利用基本查找，查询某个元素是否存在//数据如下：{131, 127, 147, 81, 103, 23, 7, 79}int[] arr ={131,127,147,81,103,23,7,79};int number =82;System.out.println(basicSearch(arr, number));}//参数：//一：数组//二：要查找的元素//返回值：//元素是否存在public static boolean basicSearch(int[] arr,int number){//利用基本查找来查找number在数组中是否存在for(int i =0; i < arr.length; i++){if(arr[i]== number){return true;}}return false;}}2. 二分查找也叫做折半查找，说明：元素必须是有序的，从小到大，或者从大到小都是可以的。

如果是无序的，也可以先进行排序。

但是排序之后，会改变原有数据的顺序，查找出来元素位置跟原来的元素可能是不一样的，所以排序之后再查找只能判断当前数据是否在容器当中，返回的索引无实际的意义。

基本思想：也称为是折半查找，属于有序查找算法。

用给定值先与中间结点比较。

比较完之后有三种情况：•相等说明找到了•要查找的数据比中间节点小说明要查找的数字在中间节点左边•要查找的数据比中间节点大说明要查找的数字在中间节点右边代码示例：package com.itheima.search;public class A02_BinarySearchDemo1 {public static void main(String[] args){//二分查找/折半查找//核心：//每次排除一半的查找范围//需求：定义一个方法利用二分查找，查询某个元素在数组中的索引//数据如下：{7, 23, 79, 81, 103, 127, 131, 147}int[] arr ={7,23,79,81,103,127,131,147};System.out.println(binarySearch(arr,150));}public static int binarySearch(int[] arr,int number){//1.定义两个变量记录要查找的范围int min =0;int max = arr.length-1;//2.利用循环不断的去找要查找的数据while(true){if(min > max){return-1;}//3.找到min和max的中间位置int mid =(min + max)/2;//4.拿着mid指向的元素跟要查找的元素进行比较if(arr[mid]> number){//4.1 number在mid的左边//min不变，max = mid - 1；max = mid -1;}else if(arr[mid]< number){//4.2 number在mid的右边//max不变，min = mid + 1;min = mid +1;}else{//4.3 number跟mid指向的元素一样//找到了return mid;}}}}3. 插值查找在介绍插值查找之前，先考虑一个问题：为什么二分查找算法一定要是折半，而不是折四分之一或者折更多呢？其实就是因为方便，简单，但是如果我能在二分查找的基础上，让中间的mid点，尽可能靠近想要查找的元素，那不就能提高查找的效率了吗？二分查找中查找点计算如下：mid=(low+high)/2, 即mid=low+1/2*(high-low);我们可以将查找的点改进为如下：mid=low+(key-a[low])/(a[high]-a[low])*(high-low)，这样，让mid值的变化更靠近关键字key，这样也就间接地减少了比较次数。

18个查找函数查找函数是计算机编程中常用的工具之一，用于在给定数据集中快速找到目标元素。

这些函数广泛应用于各种编程语言和领域，包括数据处理、数据库查询、图形算法等。

本文将介绍18个常见的查找函数，并逐步回答与之相关的问题。

1. 线性查找（Linear Search）线性查找是最简单的一种查找方法，它逐个地比较目标元素与数据集中的每个元素，直到找到目标或遍历完整个数据集。

但是，线性查找的时间复杂度较高，适用于小规模数据集或未排序的数据。

问题1：线性查找的时间复杂度是多少？答：线性查找的时间复杂度为O(n)，其中n是数据集的大小。

2. 二分查找（Binary Search）二分查找是一种高效的查找算法，要求数据集必须是有序的。

它通过将数据集分成两半，并与目标元素进行比较，从而逐步缩小查找范围。

每次比较都可以将查找范围缩小一半，因此该算法的时间复杂度较低。

问题2：二分查找要求数据集必须是有序的吗？答：是的，二分查找要求数据集必须是有序的，这是保证算法正确性的前提。

3. 插值查找（Interpolation Search）插值查找是对二分查找的改进，它根据目标元素与数据集中最大和最小元素的关系，估算目标所在位置，并逐步逼近目标。

这种方法在被查找的数据集分布较为均匀时能够显著提高查找效率。

问题3：何时应该使用插值查找而不是二分查找？答：当被查找的数据集分布较为均匀时，插值查找能够提供更好的性能。

而对于分布不均匀的数据集，二分查找可能更适用。

4. 斐波那契查找（Fibonacci Search）斐波那契查找是一种利用斐波那契数列的性质进行查找的算法。

它类似于二分查找，但将查找范围按照斐波那契数列进行划分。

这种方法在数据集较大时能够降低比较次数，提高查找效率。

问题4：为什么使用斐波那契数列进行划分？答：斐波那契数列具有递增的性质，能够将查找范围按照黄金分割比例进行划分，使得划分后的两部分大小接近，提高了查找的效率。

二叉树算法的应用领域
二叉树算法在计算机科学和相关领域中有广泛的应用。

以下是一些常见的应用领域：
1. 数据库系统：二叉树被广泛用于数据库系统中的索引结构，如二叉搜索树（Binary Search Tree，BST）和平衡二叉树（如AVL树、红黑树）等，以提高数据的检索效率。

2. 文件系统：用于文件系统的目录结构，如B树和B+树，能够高效地组织和管理文件系统中的数据。

3. 编译器：语法分析阶段使用语法树（也是一种树结构）来表示源代码的语法结构，其中二叉树是语法树的一种常见形式。

4. 网络路由：路由表中的路由信息通常使用树状结构，如二叉树，以便高效地搜索和决定数据包的路由。

5. 图形学：在计算机图形学中，二叉树可以用于场景图（Scene Graph）的表示，用于管理和渲染三维场景中的对象。

6. 人工智能：决策树是一种特殊的二叉树，广泛应用于机器学习和数据挖掘中的分类和决策问题。

7. 操作系统：进程调度和资源管理中可能使用树结构来组织和管理进程。

8. 游戏开发：在游戏中，空间分区树（如四叉树和八叉树）常用于加速空间查询和碰撞检测。

9. 密码学：Merkle树是一种二叉树结构，被广泛用于区块链中的交易验证和Merkle证明。

10. 网络和通信：Huffman编码树用于数据压缩，而霍夫曼解码树用于解压缩。

这只是二叉树算法应用的一小部分。

它们在计算机科学的各个领域中都发挥着关键的作用，提高了数据结构和算法的效率和性能。

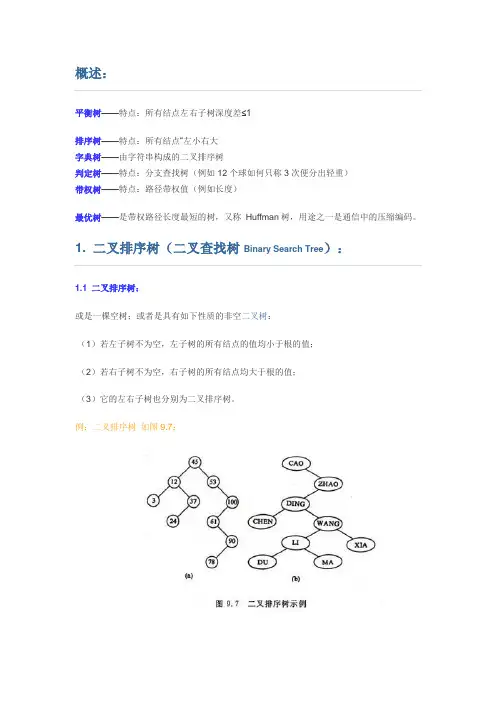
平衡树——特点：所有结点左右子树深度差≤1排序树——特点：所有结点―左小右大字典树——由字符串构成的二叉排序树判定树——特点：分支查找树（例如12个球如何只称3次便分出轻重）带权树——特点：路径带权值（例如长度）最优树——是带权路径长度最短的树，又称Huffman树，用途之一是通信中的压缩编码。

1.1 二叉排序树：或是一棵空树；或者是具有如下性质的非空二叉树：（1）若左子树不为空，左子树的所有结点的值均小于根的值；（2）若右子树不为空，右子树的所有结点均大于根的值；（3）它的左右子树也分别为二叉排序树。

例：二叉排序树如图9.7：二叉排序树的查找过程和次优二叉树类似，通常采取二叉链表作为二叉排序树的存储结构。

中序遍历二叉排序树可得到一个关键字的有序序列，一个无序序列可以通过构造一棵二叉排序树变成一个有序序列，构造树的过程即为对无序序列进行排序的过程。

每次插入的新的结点都是二叉排序树上新的叶子结点，在进行插入操作时，不必移动其它结点，只需改动某个结点的指针，由空变为非空即可。

搜索,插入,删除的复杂度等于树高，期望O(logn),最坏O(n)(数列有序,树退化成线性表).虽然二叉排序树的最坏效率是O(n),但它支持动态查询,且有很多改进版的二叉排序树可以使树高为O(logn),如SBT,AVL,红黑树等.故不失为一种好的动态排序方法.2.2 二叉排序树b中查找在二叉排序树b中查找x的过程为：1. 若b是空树，则搜索失败，否则：2. 若x等于b的根节点的数据域之值，则查找成功；否则：3. 若x小于b的根节点的数据域之值，则搜索左子树；否则：4. 查找右子树。

[cpp]view plaincopyprint?1.Status SearchBST(BiTree T, KeyType key, BiTree f, BiTree &p){2. //在根指针T所指二叉排序樹中递归地查找其关键字等于key的数据元素，若查找成功，3. //则指针p指向该数据元素节点，并返回TRUE，否则指针P指向查找路径上访问的4. //最好一个节点并返回FALSE，指针f指向T的双亲，其初始调用值为NULL5. if(!T){ p=f; return FALSE;} //查找不成功6. else if EQ(key, T->data.key) {P=T; return TRUE;} //查找成功7. else if LT(key,T->data.key)8. return SearchBST(T->lchild, key, T, p); //在左子树继续查找9. else return SearchBST(T->rchild, key, T, p); //在右子树继续查找10.}2.3 在二叉排序树插入结点的算法向一个二叉排序树b中插入一个结点s的算法，过程为：1. 若b是空树，则将s所指结点作为根结点插入，否则：2. 若s->data等于b的根结点的数据域之值，则返回，否则：3. 若s->data小于b的根结点的数据域之值，则把s所指结点插入到左子树中，否则：4. 把s所指结点插入到右子树中。

二叉查找树例题
二叉查找树（Binary Search Tree）是一种特殊的二叉树，每个节点的键值都大于左子树任意节点的键值，小于右子树任意节点的键值。

这种结构使得在二叉查找树中查找、插入和删除元素的操作都变得相对简单。

以下是一个简单的二叉查找树的例题：
题目：给定一个未排序的整数数组，检查是否存在重复元素。

解题思路：
这道题可以使用二叉查找树解决。

我们可以遍历数组中的每个元素，并将它们插入到二叉查找树中。

如果存在重复元素，则插入操作会失败，我们就可以提前返回结果。

如果不存在重复元素，则插入所有元素后，我们遍历二叉查找树即可验证结果。

具体实现如下：
1. 定义一个二叉查找树节点类，包含键值和左右子节点。

2. 定义一个二叉查找树类，包含根节点和插入、查找、遍历等方法。

3. 遍历给定的未排序整数数组，将每个元素插入到二叉查找树中。

如果插入失败（即该元素已存在于二叉查找树中），则说明存在重复元素，返回true。

4. 如果插入所有元素后都没有返回true，则遍历二叉查找树中的所有节点，检查它们的键值是否在给定的未排序整数数组中出现过。

如果出现过，则说明存在重复元素，返回true；否则返回false。

时间复杂度：O(nlogn)，其中n 是给定数组的长度。

空间复杂度：O(n)，其中n 是给定数组的长度。

二叉排序树的概念
二叉排序树，也称为二叉搜索树（Binary Search Tree，BST），是一种常用的数据结构，它具有以下特点：
1、结构特点：二叉排序树是一种二叉树，其中每个节点最多有两个子节点（左子节点和右子节点），且满足以下性质：
（1）左子树上的所有节点的值都小于根节点的值；
（2）右子树上的所有节点的值都大于根节点的值；
（3）左右子树都是二叉排序树。

2、排序特性：由于满足上述性质，二叉排序树的中序遍历结果是一个有序序列。

即，对二叉排序树进行中序遍历，可以得到一个递增（或递减）的有序序列。

3、查找操作：由于二叉排序树的排序特性，查找某个特定值的节点非常高效。

从根节点开始，比较目标值与当前节点的值的大小关系，根据大小关系选择左子树或右子树进行进一步的查找，直到找到目标值或者遍历到叶子节点为止。

4、插入和删除操作：插入操作将新节点按照排序规则插入到合适的位置，保持二叉排序树的特性；删除操作涉及节点的重新连接和调整，保持二叉排序树的特性。

二叉排序树的优点在于它提供了高效的查找操作，时间复杂度为O(log n)，其中n为二叉排序树中节点的个数。

它也可以支持其他常见的操作，如最小值和最大值查找、范围查找等。

然而，二叉排序树的性能受到数据的分布情况的影响。

当数据分
布不均匀时，树的高度可能会增加，导致查找操作的效率下降。

为了解决这个问题，可以采用平衡二叉树的变种，如红黑树、AVL 树等，以保持树的平衡性和性能。

算法设计与分析考试题目及答案Revised at 16:25 am on June 10, 2021I hope tomorrow will definitely be better算法分析与设计期末复习题一、 选择题1.应用Johnson 法则的流水作业调度采用的算法是DA. 贪心算法B. 分支限界法C.分治法D. 动态规划算法塔问题如下图所示;现要求将塔座A 上的的所有圆盘移到塔座B 上,并仍按同样顺序叠置;移动圆盘时遵守Hanoi 塔问题的移动规则;由此设计出解Hanoi 塔问题的递归算法正确的为：B3. 动态规划算法的基本要素为C A. 最优子结构性质与贪心选择性质 B ．重叠子问题性质与贪心选择性质 C ．最优子结构性质与重叠子问题性质 D. 预排序与递归调用4. 算法分析中,记号O 表示B , 记号Ω表示A , 记号Θ表示D ; A.渐进下界 B.渐进上界 C.非紧上界 D.紧渐进界 E.非紧下界5. 以下关于渐进记号的性质是正确的有：A A.f (n)(g(n)),g(n)(h(n))f (n)(h(n))=Θ=Θ⇒=Θ B. f (n)O(g(n)),g(n)O(h(n))h(n)O(f (n))==⇒= C. Ofn+Ogn = Omin{fn,gn} D. f (n)O(g(n))g(n)O(f (n))=⇔=Hanoi 塔A. void hanoiint n, int A, int C, int B { if n > 0 {hanoin-1,A,C, B; moven,a,b;hanoin-1, C, B, A; } B. void hanoiint n, int A, int B, int C { if n > 0 {hanoin-1, A, C, B; moven,a,b; hanoin-1, C, B, A; }C. void hanoiint n, int C, int B, int A { if n > 0 { hanoin-1, A, C, B; moven,a,b; hanoin-1, C, B, A; }D. void hanoiint n, int C, int A, int B { if n > 0 {hanoin-1, A, C, B; moven,a,b;hanoin-1, C, B, A; }6.能采用贪心算法求最优解的问题,一般具有的重要性质为：AA. 最优子结构性质与贪心选择性质B．重叠子问题性质与贪心选择性质C．最优子结构性质与重叠子问题性质D. 预排序与递归调用7. 回溯法在问题的解空间树中,按D策略,从根结点出发搜索解空间树;广度优先 B. 活结点优先 C.扩展结点优先 D. 深度优先8. 分支限界法在问题的解空间树中,按A策略,从根结点出发搜索解空间树;A．广度优先 B. 活结点优先 C.扩展结点优先 D. 深度优先9. 程序块A是回溯法中遍历排列树的算法框架程序;A.B.C.D.10.xk的个数;11. 常见的两种分支限界法为DA. 广度优先分支限界法与深度优先分支限界法；B. 队列式FIFO分支限界法与堆栈式分支限界法；C. 排列树法与子集树法；D. 队列式FIFO分支限界法与优先队列式分支限界法；12. k带图灵机的空间复杂性Sn是指BA.k带图灵机处理所有长度为n的输入时,在某条带上所使用过的最大方格数;B.k带图灵机处理所有长度为n的输入时,在k条带上所使用过的方格数的总和;C.k带图灵机处理所有长度为n的输入时,在k条带上所使用过的平均方格数;D.k带图灵机处理所有长度为n的输入时,在某条带上所使用过的最小方格数;13. N P类语言在图灵机下的定义为DA.NP={L|L是一个能在非多项式时间内被一台NDTM所接受的语言}；B.NP={L|L是一个能在多项式时间内被一台NDTM所接受的语言}；C.NP={L|L是一个能在多项式时间内被一台DTM所接受的语言}；D.NP={L|L是一个能在多项式时间内被一台NDTM所接受的语言}；14. 记号O的定义正确的是A;A.Ogn = { fn | 存在正常数c和n0使得对所有n≥n0有：0≤ fn ≤cgn }；B.Ogn = { fn | 存在正常数c和n0使得对所有n≥n0有：0≤ cgn ≤fn }；>0使得对所有n≥n0C.Ogn = { fn | 对于任何正常数c>0,存在正数和n有：0 ≤fn<cgn }；>0使得对所有n≥n0D.Ogn = { fn | 对于任何正常数c>0,存在正数和n有：0 ≤cgn < fn }；15. 记号Ω的定义正确的是B;A.Ogn = { fn | 存在正常数c和n0使得对所有n≥n0有：0≤ fn ≤cgn }；B.Ogn = { fn | 存在正常数c和n0使得对所有n≥n0有：0≤ cgn ≤fn }；>0使得对所有n≥n0有：C.gn = { fn | 对于任何正常数c>0,存在正数和n0 ≤fn<cgn }；D.gn = { fn | 对于任何正常数c>0,存在正数和n0 >0使得对所有n≥n0有：0 ≤cgn < fn }；二、 填空题1. 下面程序段的所需要的计算时间为 2O(n ) ;2.3.4. 5.6. 用回溯法解题的一个显着特征是在搜索过程中动态产生问题的解空间;在任何时刻,算法只保存从根结点到当前扩展结点的路径;如果解空间树 中从根结点到叶结点的最长路径的长度为hn,则回溯法所需的计算空间通常为Ohn ;7. 回溯法的算法框架按照问题的解空间一般分为子集树算法框架与排列树算法框架;8. 用回溯法解0/1背包问题时,该问题的解空间结构为子集树结构; 9.用回溯法解批处理作业调度问题时,该问题的解空间结构为排列树结构; 10.用回溯法解0/1背包问题时,计算结点的上界的函数如下所示,请在空格中填入合适的内容：11. n m12. 用回溯法解图的m着色问题时,使用下面的函数OK检查当前扩展结点的每一个儿子所相应的颜色的可用性,则需耗时渐进时间上限Omn;13.;设分分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用fn个单位时间;用Tn表示该分治法解规模为|P|=n的问题所需的计算时间,则有：(1)1 ()(/)()1O nT nkT n m f n n=⎧=⎨+>⎩通过迭代法求得Tn的显式表达式为：log1log()(/)nmk j jmjT n n k f n m-==+∑试证明Tn的显式表达式的正确性;2. 举反例证明0/1背包问题若使用的算法是按照p i/w i的非递减次序考虑选择的物品,即只要正在被考虑的物品装得进就装入背包,则此方法不一定能得到最优解此题说明0/1背包问题与背包问题的不同;证明：举例如：p={7,4,4},w={3,2,2},c=4时,由于7/3最大,若按题目要求的方法,只能取第一个,收益是7;而此实例的最大的收益应该是8,取第2,3 个;3. 求证：Ofn+Ogn = Omax{fn,gn} ;证明：对于任意f1n∈ Ofn ,存在正常数c1和自然数n1,使得对所有n≥n1,有f1n≤ c1fn ;类似地,对于任意g1n ∈ Ogn ,存在正常数c2和自然数n2,使得对所有n≥n2,有g1n ≤c2gn ;令c3=max{c1, c2}, n3 =max{n1, n2},hn= max{fn,gn} ;则对所有的 n ≥ n3,有f1n +g1n ≤ c1fn + c2gn≤c3fn + c3gn= c3fn + gn≤ c32 max{fn,gn} = 2c3hn = Omax{fn,gn} .4. 求证最优装载问题具有贪心选择性质;最优装载问题：有一批集装箱要装上一艘载重量为c 的轮船;其中集装箱i 的重量为Wi;最优装载问题要求确定在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船; 设集装箱已依其重量从小到大排序,x 1,x 2,…,x n 是最优装载问题的一个最优解;又设1min{|1}i i nk i x ≤≤== ;如果给定的最优装载问题有解,则有1k n ≤≤;证明： 四、 解答题1. 机器调度问题;问题描述：现在有n 件任务和无限多台的机器,任务可以在机器上得到处理;每件任务的开始时间为s i ,完成时间为f i ,s i <f i ;s i ,f i 为处理任务i 的时间范围;两个任务i,j 重叠指两个任务的时间范围区间有重叠,而并非指i,j 的起点或终点重合;例如：区间1,4与区间2,4重叠,而与4,7不重叠;一个可行的任务分配是指在分配中没有两件重叠的任务分配给同一台机器;因此,在可行的分配中每台机器在任何时刻最多只处理一个任务;最优分配是指使用的机器最少的可行分配方案;问题实例：若任务占用的时间范围是{1,4,2,5,4,5,2,6,4,7},则按时完成所有任务最少需要几台机器提示：使用贪心算法画出工作在对应的机器上的分配情况;2. 已知非齐次递归方程：f (n)bf (n 1)g(n)f (0)c =-+⎧⎨=⎩ ,其中,b 、c 是常数,gn 是n 的某一个函数;则fn 的非递归表达式为：nnn i i 1f (n)cb b g(i)-==+∑;现有Hanoi 塔问题的递归方程为：h(n)2h(n 1)1h(1)1=-+⎧⎨=⎩ ,求hn 的非递归表达式;解：利用给出的关系式,此时有：b=2, c=1, gn=1, 从n 递推到1,有： 3. 单源最短路径的求解;问题的描述：给定带权有向图如下图所示G =V,E,其中每条边的权是非负实数;另外,还给定V 中的一个顶点,称为源;现在要计算从源到所有其它各顶点的最短路长度;这里路的长度是指路上各边权之和;这个问题通常称为单源最短路径问题;解法：现采用Dijkstra 算法计算从源顶点1到其它顶点间最短路径;请将此过程填入下表中;4. 请写出用回溯法解装载问题的函数; 装载问题：有一批共n 个集装箱要装上2艘载重量分别为c1和c2的轮船,其中集装箱i 的重量为wi,且121ni i w c c =≤+∑;装载问题要求确定是否有一个合理的装载方案可将这n 个集装箱装上这2艘轮船;如果有,找出一种装载方案;解：void backtrack int i{用分支限界法解装载问题时,对算法进行了一些改进,下面的程序段给出了改进部分；试说明斜线部分完成什么功能,以及这样做的原因,即采用这样的方式,算法在执行上有什么不同;初始时将;也就是说,重量仅在搜索进入左子树是增加,因此,可以在算法每一次进入左子树时更新bestw 的值;43 2 110030maxint10 - {1} 初始 dist5 dist4 dist3 dist2 u S 迭代7. 最长公共子序列问题：给定2个序列X={x 1,x2,…,xm }和Y={y 1,y2,…,yn },找出X 和Y 的最长公共子序列;由最长公共子序列问题的最优子结构性质建立子问题最优值的递归关系;用cij 记录序列Xi 和Yj 的最长公共子序列的长度;其中, Xi={x1,x2,…,xi}；Y j={y1,y2,…,yj};当i=0或j=0时,空序列是Xi 和Yj 的最长公共子序列;故此时Cij=0;其它情况下,由最优子结构性质可建立递归关系如下：00,0[][][1][1]1,0;max{[][1],[1][]},0;i j i ji j c i j c i j i j x y c i j c i j i j x y ⎧==⎪=--+>=⎨⎪-->≠⎩在程序中,bij 记录Cij 的值是由哪一个子问题的解得到的;8.1.2.3.4.5.用回溯法解问题时,应明确定义问题的解空间,问题的解空间至少应包含___________;6.动态规划算法的基本思想是将待求解问题分解成若干____________,先求解___________,然后从这些____________的解得到原问题的解;7.以深度优先方式系统搜索问题解的算法称为_____________;背包问题的回溯算法所需的计算时间为_____________,用动态规划算法所需的计算时间为____________;9.动态规划算法的两个基本要素是___________和___________;10.二分搜索算法是利用_______________实现的算法;二、综合题50分1.写出设计动态规划算法的主要步骤;2.流水作业调度问题的johnson算法的思想;3.若n=4,在机器M1和M2上加工作业i所需的时间分别为ai 和bi,且a 1,a2,a3,a4=4,5,12,10,b1,b2,b3,b4=8,2,15,9求4个作业的最优调度方案,并计算最优值;4.使用回溯法解0/1背包问题：n=3,C=9,V={6,10,3},W={3,4,4},其解空间有长度为3的0-1向量组成,要求用一棵完全二叉树表示其解空间从根出发,左1右0,并画出其解空间树,计算其最优值及最优解;5.设S=｛X1,X2,···,Xn｝是严格递增的有序集,利用二叉树的结点来存储S中的元素,在表示S的二叉搜索树中搜索一个元素X,返回的结果有两种情形,1在二叉搜索树的内结点中找到X=Xi ,其概率为bi;2在二叉搜索树的叶结点中确定X∈Xi ,Xi+1,其概率为ai;在表示S的二叉搜索树T中,设存储元素Xi的结点深度为C i ；叶结点Xi,Xi+1的结点深度为di,则二叉搜索树T的平均路长p为多少假设二叉搜索树Tij=｛Xi ,Xi+1,···,Xj｝最优值为mij,Wij= ai-1+bi+···+bj+aj,则mij1<=i<=j<=n递归关系表达式为什么6.描述0-1背包问题;三、简答题30分1.流水作业调度中,已知有n个作业,机器M1和M2上加工作业i所需的时间分别为ai 和bi,请写出流水作业调度问题的johnson法则中对ai和bi的排序算法;函数名可写为sorts,n2.最优二叉搜索树问题的动态规划算法设函数名binarysearchtree答案：一、填空1．确定性有穷性可行性 0个或多个输入一个或多个输出2.时间复杂性空间复杂性时间复杂度高低3. 该问题具有最优子结构性质4.{BABCD}或{CABCD}或{CADCD｝5.一个最优解6.子问题子问题子问题7.回溯法8. on2n omin{nc,2n}9.最优子结构重叠子问题10.动态规划法二、综合题1.①问题具有最优子结构性质；②构造最优值的递归关系表达式；③最优值的算法描述；④构造最优解；2. ①令N1={i|ai<bi},N2={i|ai>=bi}；②将N1中作业按ai的非减序排序得到N1’,将N2中作业按bi的非增序排序得到N2’；③N1’中作业接N2’中作业就构成了满足Johnson法则的最优调度;3.步骤为：N1={1,3},N2={2,4}；N 1’={1,3}, N2’={4,2}；最优值为：384.解空间为{0,0,0,0,1,0,0,0,1,1,0,0,0,1,1,1,0,1, 1,1,0,1,1,1}; 解空间树为：该问题的最优值为：16 最优解为：1,1,0 5.二叉树T 的平均路长P=∑=+ni 1Ci)(1*bi +∑=nj 0dj *aj{mij=0 i>j6.已知一个背包的容量为C,有n 件物品,物品i 的重量为W i ,价值为V i ,求应如何选择装入背包中的物品,使得装入背包中物品的总价值最大; 三、简答题 1.void sortflowjope s,int n {int i,k,j,l;fori=1;i<=n-1;i++ag=0 k++; ifk>n break;ag==0ifsk.a>sj.a k=j; swapsi.index,sk.index; swapsi.tag,sk.tag;} }l=i;<sj.b k=j;swapsi.index,sk.index; ag,sk.tag; }mij=Wij+min{mik+mk+1j} 1<=i<=j<=n,mii-1=0}2.void binarysearchtreeint a,int b,int n,int m,int s,int w{int i,j,k,t,l;fori=1;i<=n+1;i++{wii-1=ai-1;mii-1=0;}forl=0;l<=n-1;l++Init-single-sourceG,s2. S=Φ3. Q=VGQ<> Φdo u=minQS=S∪{u}for each vertex 3do 4四、算法理解题本题10分根据优先队列式分支限界法,求下图中从v1点到v9点的单源最短路径,请画出求得最优解的解空间树;要求中间被舍弃的结点用×标记,获得中间解的结点用单圆圈○框起,最优解用双圆圈◎框起;五、算法理解题本题5分设有n=2k个运动员要进行循环赛,现设计一个满足以下要求的比赛日程表：①每个选手必须与其他n-1名选手比赛各一次；②每个选手一天至多只能赛一次；③循环赛要在最短时间内完成;1如果n=2k,循环赛最少需要进行几天；2当n=23=8时,请画出循环赛日程表;六、算法设计题本题15分分别用贪心算法、动态规划法、回溯法设计0-1背包问题;要求：说明所使用的算法策略；写出算法实现的主要步骤；分析算法的时间;七、算法设计题本题10分通过键盘输入一个高精度的正整数nn的有效位数≤240,去掉其中任意s个数字后,剩下的数字按原左右次序将组成一个新的正整数;编程对给定的n 和s,寻找一种方案,使得剩下的数字组成的新数最小;样例输入178543S=4样例输出13一、填空题本题15分,每小题1分1．规则一系列运算2. 随机存取机RAMRandom Access Machine；随机存取存储程序机RASPRandom Access Stored Program Machine；图灵机Turing Machine3. 算法效率4. 时间、空间、时间复杂度、空间复杂度5．2n6．最好局部最优选择7. 贪心选择最优子结构二、简答题本题25分,每小题5分1、分治法的基本思想是将一个规模为n的问题分解为k个规模较小的子问题,这些子问题互相独立且与原问题相同；对这k个子问题分别求解;如果子问题的规模仍然不够小,则再划分为k个子问题,如此递归的进行下去,直到问题规模足够小,很容易求出其解为止；将求出的小规模的问题的解合并为一个更大规模的问题的解,自底向上逐步求出原来问题的解;2、“最优化原理”用数学化的语言来描述：假设为了解决某一优化问题,需要依次作出n个决策D1,D2,…,Dn,如若这个决策序列是最优的,对于任何一个整数k,1 < k < n,不论前面k个决策是怎样的,以后的最优决策只取决于由前面决策所确定的当前状态,即以后的决策Dk+1,Dk+2,…,Dn也是最优的;3、某个问题的最优解包含着其子问题的最优解;这种性质称为最优子结构性质;4、回溯法的基本思想是在一棵含有问题全部可能解的状态空间树上进行深度优先搜索,解为叶子结点;搜索过程中,每到达一个结点时,则判断该结点为根的子树是否含有问题的解,如果可以确定该子树中不含有问题的解,则放弃对该子树的搜索,退回到上层父结点,继续下一步深度优先搜索过程;在回溯法中,并不是先构造出整棵状态空间树,再进行搜索,而是在搜索过程,逐步构造出状态空间树,即边搜索,边构造;5、PPolynomial问题：也即是多项式复杂程度的问题;NP就是Non-deterministicPolynomial的问题,也即是多项式复杂程度的非确定性问题;NPCNP Complete问题,这种问题只有把解域里面的所有可能都穷举了之后才能得出答案,这样的问题是NP里面最难的问题,这种问题就是NPC问题;三、算法填空本题20分,每小题5分1、n后问题回溯算法1 Mj&&Li+j&&Ri-j+N2 Mj=Li+j=Ri-j+N=1;3 tryi+1,M,L,R,A4 Aij=05 Mj=Li+j=Ri-j+N=0 2、数塔问题; 1c<=r2trc+=tr+1c 3trc+=tr+1c+1 3、Hanoi 算法 1movea,c2Hanoin-1, a, c , b 3Movea,c 4、1pv=NIL 2pv=u3 v ∈adju 4Relaxu,v,w四、算法理解题本题10分五、18天2分；2当n=23=8时,循环赛日程表3分;六、算法设计题本题15分 1贪心算法 Onlogn ➢ 首先计算每种物品单位重量的价值Vi/Wi,然后,依贪心选择策略,将尽可能多的单位重量价值最高的物品装入背包;若将这种物品全部装入背包后,背包内的物品总重量未超过C,则选择单位重量价值次高的物品并尽可能多地装入背包;依此策略一直地进行下去,直到背包装满为止; ➢ 具体算法可描述如下：void Knapsackint n,float M,float v,float w,float x {Sortn,v,w; int i;for i=1;i<=n;i++ xi=0; float c=M;for i=1;i<=n;i++ {if wi>c break; xi=1; c-=wi; }if i<=n xi=c/wi; }2动态规划法 Oncmi,j 是背包容量为j,可选择物品为i,i+1,…,n 时0-1背包问题的最优值;由0-1背包问题的最优子结构性质,可以建立计算mi,j 的递归式如下;void KnapSackint v,int w,int c,int n,int m11 {int jMax=minwn-1,c;for j=0;j<=jMax;j++ /mn,j=0 0=<j<wn/ mnj=0;1 2 3 4 5 6 7 82 1 43 6 5 8 73 4 1 2 7 8 5 64 3 2 1 8 7 6 55 6 7 8 1 2 3 4 6 5 8 7 2 1 4 37 8 5 6 3 4 1 28 7 6 5 4 3 2 1for j=wn;j<=c;j++ /mn,j=vn j>=wn/mnj=vn;for i=n-1;i>1;i--{ int jMax=minwi-1,c;for j=0;j<=jMax;j++ /mi,j=mi+1,j 0=<j<wi/mij=mi+1j;for j=wi;j<=c;j++/mn,j=vn j>=wn/mij=maxmi+1j,mi+1j-wi+vi;}m1c=m2c;ifc>=w1m1c=maxm1c,m2c-w1+v1;}3回溯法 O2ncw:当前重量 cp:当前价值 bestp：当前最优值voidbacktrack int i//回溯法 i初值1{ifi>n //到达叶结点{ bestp=cp; return; }ifcw+wi<=c //搜索左子树{cw+=wi;cp+=pi;backtracki+1;cw-=wi;cp-=pi;}ifBoundi+1>bestp//搜索右子树backtracki+1;}七、算法设计题本题10分为了尽可能地逼近目标,我们选取的贪心策略为：每一步总是选择一个使剩下的数最小的数字删去,即按高位到低位的顺序搜索,若各位数字递增,则删除最后一个数字,否则删除第一个递减区间的首字符;然后回到串首,按上述规则再删除下一个数字;重复以上过程s次,剩下的数字串便是问题的解了;具体算法如下：输入s, n;while s > 0{ i=1; //从串首开始找while i < lengthn && ni<ni+1{i++;}deleten,i,1; //删除字符串n的第i个字符s--;}while lengthn>1&& n1=‘0’deleten,1,1; //删去串首可能产生的无用零输出n;。

二叉树是一种常见的数据结构，用于存储和组织数据。

以下是二叉树存取数据的一些基本原则：
1. 二叉搜索树原则（Binary Search Tree, BST）：如果你使用的是二叉搜索树，那么它满足以下条件：
-左子树上的节点的值都小于当前节点的值。

-右子树上的节点的值都大于当前节点的值。

这个特性使得在二叉搜索树中进行数据的存取操作更高效，因为你可以根据节点的值与目标值的比较结果来决定向左子树还是右子树搜索。

2. 存取操作的时间复杂度：对于一颗具有n个节点的二叉树，存取操作的平均时间复杂度为O(log n)。

这是因为在一个平衡的二叉树中，每次存取操作可以将搜索空间缩小一半。

3. 递归遍历：常用的二叉树遍历方法包括前序遍历、中序遍历和后序遍历。

这些遍历方法可以帮助你按照特定顺序获取二叉树中的所有数据。

递归是实现这些遍历方法的一种常见方式。

-前序遍历：根节点-> 左子树-> 右子树
-中序遍历：左子树-> 根节点-> 右子树
-后序遍历：左子树-> 右子树-> 根节点
4. 层序遍历：层序遍历是一种广度优先的遍历方法，它按照树的层级顺序逐层遍历二叉树节点。

这种遍历方法可以帮助你按照层级顺序获取二叉树中的所有数据。

以上是二叉树存取数据的一些基本原则。

根据你的具体需求和使用场景，可能会有其他特定的存取规则和操作方式。

数据结构基本英语词汇I like ITPUB!数据结构基本英语词汇数据抽象 data abstraction数据元素 data element数据对象 data object数据项 data item数据类型 data type抽象数据类型 abstract data type逻辑结构 logical structure物理结构 phyical structure线性结构 linear structure非线性结构 nonlinear structure基本数据类型 atomic data type固定聚合数据类型 fixed-aggregate data type可变聚合数据类型 variable-aggregate data type 线性表 linear list栈 stack队列 queue串 string数组 array树 tree图 grabh查找，线索 searching更新 updating排序(分类) sorting插入 insertion删除 deletion前趋 predecessor后继 successor直接前趋直接后继双端列表循环队列immediate predecessor immediate successor deque(double-ended queue) cirular queue指针 pointer先进先出表(队列) first-in first-out list 后进先出表(队列) last-in first-out list 栈底 bottom栈定 top弹出 pop队头 front队尾 rear上溢 overflow下溢 underflow数组 array矩阵 matrix多维数组 multi-dimentional array以行为主的顺序分配 row major order以列为主的顺序分配 column major order三角矩阵对称矩阵稀疏矩阵转置矩阵truangular matrix symmetric matrix sparse matrix transposed matrix链表 linked list线性链表 linear linked list 单链表 single linked list多重链表 multilinked list循环链表 circular linked list 双向链表 doubly linked list 十字链表 orthogonal list广义表 generalized list链 link指针域 pointer field链域 link field头结点 head 头指针 head 尾指针 tail 串 string node pointer pointer空白(空格)串 blank string 空串(零串) null string子串 substring树 tree子树 subtree森林 forest根 root叶子 leaf结点 node深度 depth双亲 parents孩子 children兄弟 brother祖先 ancestor子孙 descentdant二叉树 binary tree平衡二叉树 banlanced binary tree 满二叉树 full binary tree彻底二叉树 complete binary tree 遍历二叉树 traversing binary tree 二叉排序树 binary sort tree二叉查找树 binary search tree线索二叉树 threaded binary tree 哈夫曼树 Huffman tree有序数 ordered tree无序数 unordered tree判定树 decision tree双链树 doubly linked tree数字查找树 digital search tree树的遍历 traversal of tree先序遍历 preorder traversal中序遍历 inorder traversal后序遍历 postorder traversal图 graph子图 subgraph有向图无向图彻底图连通图digraph(directed graph) undigraph(undirected graph) complete graph connected graph非连通图 unconnected graph强连通图 strongly connected graph 弱连通图 weakly connected graph 加权图 weighted graph有向无环图 directed acyclic graph 稀疏图 spares graph稠密图 dense graph重连通图 biconnected graph二部图 bipartite graph边 edge弧 arc路径 path回路(环) cycle弧头弧尾源点终点汇点headtail source destination sink权 weight连接点 articulation point 初始结点 initial node终端结点 terminal node 相邻边 adjacent edge相邻顶点 adjacent vertex 关联边 incident edge入度 indegree出度 outdegree最短路径 shortest path 有序对 ordered pair无序对 unordered pair简单路径简单回路连通分量邻接矩阵simple pathsimple cycle connected component adjacency matrix邻接表 adjacency list邻接多重表 adjacency multilist遍历图 traversing graph生成树 spanning tree最小(代价)生成树 minimum(cost)spanning tree 生成森林 spanning forest拓扑排序 topological sort偏序 partical order拓扑有序 topological orderAOV 网 activity on vertex networkAOE 网 activity on edge network关键路径 critical path匹配 matching最大匹配 maximum matching增广路径 augmenting path增广路径图 augmenting path graph查找 searching线性查找(顺序查找) linear search (sequential search) 二分查找 binary search分块查找 block search散列查找 hash search平均查找长度 average search length电脑专业术语散列表 hash table散列函数 hash funticion直接定址法 immediately allocating method数字分析法 digital analysis method平方取中法 mid-square method折叠法 folding method除法 division method随机数法 random number method排序 sort内部排序 internal sort外部排序 external sort插入排序 insertion sort随小增量排序 diminishing increment sort选择排序 selection sort堆排序 heap sort快速排序归并排序基数排序外部排序quick sort merge sort radix sort external sort平衡归并排序 balance merging sort二路平衡归并排序 balance two-way merging sort 多步归并排序 ployphase merging sort置换选择排序 replacement selection sort文件 file主文件 master file顺叙文件 sequential file索引文件 indexed file索引顺叙文件 indexed sequential file索引非顺叙文件 indexed non-sequential file直接存取文件 direct access file多重链表文件 multilist file倒排文件 inverted file目录结构 directory structure树型索引 tree index数据结构基本英语词汇数据抽象 data abstraction数据元素 data element数据对象 data object免费考研网 freekaoyan数据项 data item数据类型 data type抽象数据类型 abstract data type逻辑结构 logical structure物理结构 phyical structure线性结构 linear structure非线性结构 nonlinear structure基本数据类型 atomic data type固定聚合数据类型 fixed-aggregate data type可变聚合数据类型 variable-aggregate data type 线性表 linear list栈 stack队列 queue串 string数组 array树 tree图 grabh查找，线索 searching更新 updating排序(分类) sorting插入 insertion删除 deletion前趋 predecessor后继 successor直接前趋直接后继双端列表循环队列immediate predecessor immediate successor deque(double-ended queue) cirular queue指针 pointer先进先出表(队列) first-in first-out list 后进先出表(队列) last-in first-out list栈底栈定压入弹出队头队尾上溢下溢bottom toppushpopfront rear overflow underflow数组 array矩阵 matrix多维数组 multi-dimentional array以行为主的顺序分配 row major order以列为主的顺序分配 column major order三角矩阵对称矩阵稀疏矩阵转置矩阵truangular matrix symmetric matrix sparse matrix transposed matrix链表 linked list线性链表 linear linked list 单链表 single linked list多重链表 multilinked list 循环链表 circular linked list 双向链表 doubly linked list 十字链表 orthogonal list广义表 generalized list链 link指针域 pointer field链域 link field头结点 head 头指针 head 尾指针 tail 串 string node pointer pointer空白(空格)串blank string 空串(零串) null string子串 substring树 tree子树 subtree森林 forest根 root叶子结点深度层次双亲leaf node depth level parents孩子 children兄弟 brother祖先 ancestor子孙 descentdant二叉树 binary tree平衡二叉树 banlanced binary tree 满二叉树 full binary tree彻底二叉树 complete binary tree遍历二叉树 traversing binary tree 二叉排序树 binary sort tree二叉查找树 binary search tree线索二叉树 threaded binary tree 哈夫曼树 Huffman tree有序数 ordered tree无序数 unordered tree判定树 decision tree双链树 doubly linked tree数字查找树 digital search tree树的遍历 traversal of tree先序遍历 preorder traversal中序遍历 inorder traversal后序遍历 postorder traversal图 graph子图 subgraph有向图无向图彻底图连通图digraph(directed graph) undigraph(undirected graph) complete graph connected graph非连通图 unconnected graph强连通图 strongly connected graph 弱连通图 weakly connected graph 加权图 weighted graph有向无环图 directed acyclic graph 稀疏图 spares graph稠密图 dense graph重连通图 biconnected graph二部图 bipartite graph边 edge顶点 vertex弧 arc路径 path回路(环) cycle弧头 head弧尾 tail源点 source终点 destination汇点 sink权 weight连接点 articulation point初始结点 initial node终端结点 terminal node相邻边 adjacent edge相邻顶点 adjacent vertex 关联边 incident edge入度 indegree出度 outdegree最短路径 shortest path 有序对 ordered pair无序对 unordered pair简单路径简单回路连通分量邻接矩阵simple pathsimple cycle connected component adjacency matrix邻接表 adjacency list邻接多重表 adjacency multilist遍历图 traversing graph生成树 spanning tree最小(代价)生成树 minimum(cost)spanning tree生成森林 spanning forest拓扑排序 topological sort偏序 partical order拓扑有序 topological orderAOV 网 activity on vertex networkAOE 网 activity on edge network关键路径 critical path匹配 matching最大匹配 maximum matching增广路径 augmenting path增广路径图 augmenting path graph查找 searching线性查找(顺序查找) linear search (sequential search) 二分查找 binary search分块查找 block search散列查找 hash search平均查找长度 average search length散列表 hash table散列函数 hash funticion直接定址法 immediately allocating method数字分析法 digital analysis method平方取中法 mid-square method折叠法 folding method除法 division method随机数法 random number method排序 sort内部排序 internal sort外部排序 external sort插入排序 insertion sort随小增量排序 diminishing increment sort 选择排序 selection sort堆排序 heap sort快速排序归并排序基数排序外部排序quick sort merge sort radix sort external sort平衡归并排序 balance merging sort二路平衡归并排序 balance two-way merging sort多步归并排序 ployphase merging sort置换选择排序 replacement selection sort文件 file主文件 master file顺叙文件 sequential file索引文件 indexed file索引顺叙文件 indexed sequential file索引非顺叙文件 indexed non-sequential file直接存取文件 direct access file多重链表文件 multilist file倒排文件 inverted file目录结构 directory structure树型索引 tree indexfreekaoyanfreekaoyan免费考研网 freekaoyan数据抽象 data abstraction | wo:Eb yM数据元素 data element 9U k %F[5W数据对象 data object r6t^ }数据项 data item ct jP(数据类型 data type eC+ >}5cn抽象数据类型e* o4t 7J逻辑结构 logical structure E 0&g o5物理结构线性结构 linear structure E(+ m3EBh非线性结构 nonlinear structure #s C |0+gcEa2z, )基本数据类型 atomic data type E : 9 / U固定聚合数据类型 fixed-aggregate data type zH{S ?J<^可变聚合数据类型 variable-aggregate data type pJ~=E<n 1%线性表 linear list bLh..- $栈 stack -c y8t$T队列 queue s+O a :! c串 string K~o7T| i数组 array $ t Tu I树 tree kEnx @9+DL图(`6< kg5O查找，线索 searching K -m p5V更新 updating @ Zf,f5oTk排序(分类) sorting > - A *zGv插入 insertion TH p la@/'删除 deletion -E}G1e 1:_P &~Lh S前趋 predecessor V H0u d后继 successor y ~CT= )直接前趋 immediate predecessor CMEeBk3E5直接后继 immediate successor ()VV #<v2双端列表 deque(double-ended queue) /I7y wG P 循环队列 cirular queue sTd W [T指针 pointer { U?Enew先进先出表(队列) first-in first-out list .lfE` LX K 后进先出表 ( 队列)栈底 bottom vXi z4hi0/栈定 top N- J f.. m压入 push 720<rD tR}弹出 pop Zu:V@JUN f队头 front }&v~-2 iJ队尾上溢 overflow 2 kcs6 e 7下溢 underflow P;krZ <kQen * wFE数组 array JA1A`y.aC矩阵 matrix ^qn 2b=多维数组以行为主的顺序分配以列为主的顺序分配三角矩阵 truangular matrix m:1 . ];kg对称矩阵 symmetric matrix 2G 3_L*r稀疏矩阵 sparse matrix U s;6YV_ 1转置矩阵 transposed matrix a W(2.Y4tZXS- &,链表 linked list `5A:=/ p线性链表 linear linked list M,d {= R8单链表 single linked list ,Y^ 9F0Mpm 多重链表 multilinked list ZE d _+a%循环链表 circular linked list Q 2M8{sf X 双向链表十字链表 orthogonal list OX`;wn)} C 广义表g Cn u;y链 link L;TR}'Xz指针域 pointer field ;K SXw1h链域 link field J > n !f_头结点 head node = WW. 9/ 2头指针尾指针 tail pointer nX /K 1Hd串 string t R[ BqDJQ空白(空格)串空串 ( 零串 )子串 substring 0L=V^0Ob3F|& Qs.2d K树 tree ->U+Cg= Di子树 subtree f;P CD* o<森林 forest D}6AB>Enq根 root x(c aOt叶子leaf F d 6x'%,g结点node K Vd]Y1p7深度depth i(W%Sj(<wJ层次level ,U:Feb3*zH双亲parents G/O9! L4}孩子 children ^)fLN!SxQw兄弟 brother %W (XP祖先 ancestor UO [m/3Fs子孙 descentdant .*#g/fgl1<vKlF%% t二叉树 binary tree qWMMr !:'4平衡二叉树满二叉树 full binary tree K. V彻底二叉树 complete binary tree ISb} A^{$ 遍历二叉树 traversing binary tree fVu&M& 5p 二叉排序树 binary sort tree gbQVK kM,H二叉查找树 binary search tree >c>* .qdp 线索二叉树 threaded binary tree < K Lq r+哈夫曼树 Huffman tree Q )y <[ C有序数 ordered tree g 7H &v'M无序数 unordered tree W c$8 =b 7判定树 decision tree Ee h@!双链树 doubly linked tree q! 0xnb数字查找树 digital search tree ~LjI * <pG HuvjCYr树的遍历 traversal of tree zO0 ZkDu&先序遍历 preorder traversal Xh( _ SkS3中序遍历 inorder traversal j^3&e B0后序遍历 postorder traversal H E*' Eo # Lx#Gj图 graph !b{gVE -*:子图有向图 digraph(directed graph) 1 J] xhv无向图 undigraph(undirected graph) & htNnse 彻(底图 complete graph S7 ehg连通图 connected graph H1 -~1PW`非连通图 unconnected graph S $f 1LoC强连通图 strongly connected graph `AfU9A42d 弱连通图 weakly connected graph b_M&oB y = 加权图 weighted graph Z*;Vx/ 5l有向无环图 directed acyclic graph 'TKf K ^J& 稀疏图 spares graph Zm{BW @>)B稠密图 dense graph p < j {重连通图二部图 bipartite graph h jE8$=tXU 9h{ ~mv边 edge | p I顶点弧 arc gG5 f{_ n路径 path u ; ?'ZA回路(环) cycle {S9<Qu21'-弧头 head 2 9 v3 )弧尾 tail )Z x$5 zXr源点 source ,A|p 2; (3终点 destination Mx, uX 6汇点 sink DS GcE>权 weight {Vk:H$W{ J连接点 articulation point SKO t/W{<初始结点 initial node `Ll/ lCG终端结点 terminal node G W[Ii { d相邻边 adjacent edge jq, /$9相邻顶点 adjacent vertex b[BYj U.sc关联边 incident edge yb|,1/vB|入度 indegree Pw SM6/t/K出度 outdegree I[ !~nP:最短路径 shortest path ` zwp;q i4有序对 ordered pair Xp Q}}HC]无序对 unordered pair $ sx& E2!]简单路径 simple path +<R* V#FSu简单回路 simple cycle D f}& hJ连通分量 connected component sY ttQ e邻接矩阵 adjacency matrix #OD) ;1邻接表 adjacency list A%W <JyW}邻接多重表 adjacency multilist zDw s E c遍历图 traversing graph QiK Q r生成树最小(代价)生成树 minimum(cost)spanning tree j? C i -g;生成森林 spanning forest - ;t5h(ip[6>zyBE0拓扑排序 topological sort x/{ {A%N偏序 partical order `' % WX> `拓扑有序 topological order #`! K SRPAOV 网 activity on vertex network I 1aM5AOE 网关键路径M (%,A`APA匹配 matching ,3ST . m4&最大匹配增广路径 augmenting path AU6e p7增广路径图 augmenting path graph _>Z <1 Ko[IFVt6 M'查找 searching ;kmv<GvT:'线性查找(顺序查找) linear search (sequential search) l &G Q 二分查找 binary search 8t8 .v;gq分块查找 block search t ; , ?散列查找平均查找长度 average search length [b'UP y&^*=i /^ l /c散列表 hash table ~v 5 W+| {散列函数 hash funticion J], t4}kO直接定址法 immediately allocating method HV9~ ZyZ0数字分析法平方取中法 mid-square method ?@&va ]折叠法 folding method Ra @l_eT7i除法 division method # -!jIO8随机数法 random number method w <i1#;P7.} |? t nwf排序 sort U`Zi6 iA内部排序 internal sort jh~k =czN外部排序插入排序 insertion sort 7m 'k /j0随小增量排序 diminishing increment sort Q182 >选择排序 selection sort b 34& $g堆排序 heap sort F]bg# LL l快速排序 quick sort &zM$ 4$H归并排序 merge sort jqB{l~E 1基数排序 radix sort twiI { Rk=外部排序 external sort }`( { m)平衡归并排序 balance merging sort #W6 -lP 0二路平衡归并排序 balance two-way merging sort y m # 4 多步归并排序 ployphase merging sort }e0 z>1 n置换选择排序 replacement selection sort u^ B) %! |^ A E2e }3n_文件 file `0xoS54Vh主文件 master file u<Ej .w;B顺叙文件 sequential file kRq (%d4索引文件 indexed file {|<hM i Xa索引顺叙文件 indexed sequential file -,7h%RR}BW索引非顺叙文件 indexed non-sequential file c H ' 0 直接存取文件多重链表文件 multilist file 'S|xat8NjL倒排文件 inverted file K [P v _目录结构 directory structure bQy A#M:uX树型索引 tree index。