小白专场:是否同一棵二叉搜索树(1)
- 格式:pdf
- 大小:267.42 KB
- 文档页数:14


AVL树自平衡的二叉搜索树AVL树是一种自平衡的二叉搜索树,它是根据其发明者 G.M. Adelson-Velsky 和 Evgenii Landis 的姓氏首字母而得名。
AVL树解决了传统二叉搜索树由于插入或删除操作导致树结构不平衡而引发的性能问题。
1. 什么是二叉搜索树?二叉搜索树,又称二叉排序树或二叉查找树,是一种特殊的二叉树结构。
在二叉搜索树中,每个节点都包含一个键值,并且节点的左子树中的键值小于节点的键值,右子树中的键值大于节点的键值。
2. 为什么需要自平衡?传统的二叉搜索树在执行插入或删除操作时,可能会导致树结构不平衡,使得树的高度远大于理想情况下的最小高度。
当树的高度增加后,查找、插入、删除等操作的时间复杂度也会增加,进而影响整体性能。
3. AVL树的自平衡特性AVL树通过保持树的平衡性来提高性能。
对于每一个节点,AVL 树通过计算其左右子树的高度差(平衡因子)来判断是否需要进行旋转操作来保持树的平衡。
当平衡因子超过一定阈值时,进行相应的旋转操作来维持平衡。
4. AVL树的旋转操作AVL树的旋转操作包括左旋和右旋。
左旋操作将当前节点的右子树变为新的根节点,而右旋操作则恰恰相反。
通过旋转操作,AVL树可以在保持二叉搜索树性质的同时,实现树的自平衡。
5. AVL树的插入操作在进行插入操作时,AVL树首先按照二叉搜索树的规则找到插入位置,并插入新的节点。
然后,从插入节点开始沿着路径向上逐层检查平衡因子,若遇到不平衡的节点,执行相应的旋转操作来恢复树的平衡。
6. AVL树的删除操作在进行删除操作时,AVL树首先按照二叉搜索树的规则找到待删除的节点,并执行删除操作。
然后,从删除节点的父节点开始沿着路径向上逐层检查平衡因子,若遇到不平衡的节点,执行相应的旋转操作来恢复树的平衡。
7. AVL树的平衡性保证AVL树的自平衡操作保证了树的高度始终保持在理想情况下的最小高度的常数倍。
通过对平衡因子的检查并执行旋转操作,AVL树能够有效地保持树的平衡性,使得查找、插入、删除等操作能够在较快的时间内完成。

二叉搜索树的详解所谓二叉搜索树,就是指对包括树本身的任何一棵子树,左子树的值要小于根节点,右子树的值要大于根节点。
以便在搜索的时候能够从根节点开始一直往下检索。
在搜索树构造合理的情况下复杂度是。
这里主要介绍二叉搜索树的创建和查询以及增加节点和删除节点。
先定义节点的结构体:为了索引更加方便,定义了父节点。
二叉搜索树的创建二叉搜索树的显示二叉搜索树的插入二叉搜索树的删除完整代码:链接:密码:二叉搜索树的创建二叉搜索树的创建分为直接创建和随机创建。
所谓直接创建,就是拿到一系列树以后,根据原有数据的顺序依次以增加节点的方式扩展原二叉搜索树。
而随机创建就是指创建二叉树的过程随机的从给定树种随机选取一个点加入二叉搜索树。
先来介绍直接创建的办法:先创建根节点判空寻找下一个节点插入的位置这里有两点要注意的:是用来表示往下后的父节点。
新节点要插入的位置的父节点,它一定不会是有两个孩子的节点。
如果比插入点的值要大,则父节点一定没有左孩子;如果比插入点的值要小,则没有右孩子。
插入节点直接创建的整个函数为:二叉树的查找这里要注意的是,我们认为在二叉查找数中的关键字是没有重复,如果有重复的只会查找到其中一个,而无法保证返回所有的值。
用递归的方法是最简单的方法:如果为空,或者找到关键词搜索左子树搜索右子树二叉树的显示(层次遍历)二叉树的层次遍历现在主要事采用队列的方法来处理:队列的原理性的内容随便百度都有,这里直接上源码值得注意的是,虽然我们定义的节点是带有父节点的内容,但是实际上我们的遍历算法并没有用到父节点,具有一般适应性。
记录层数初始化遍历过程判断是否还有节点判断和上一个节点是不是同一层,如果不是则分行将节点加入暂存数组并记录层数在这里,效果如下所示642578二叉树的插入二叉树的删除只有右子树只有左子树寻找代替节点的节点,右子树的最小节点即可代替如果即将代替的节点,如果恰好不是的子节点处理节点挪走后的续接问题,值得注意的是由于节点是右子树的最小节点,所以节点不会有左子树。


⼆叉树常见⾯试题(进阶)⼀、常见题型1. 求两个节点的最近公共祖先;2. 求⼆叉树中最远的两个节点的距离;3. 由前序遍历和中序遍历重建⼆叉树(如:前序序列:1 2 3 4 5 6 - 中序序列:3 2 4 1 6 5);4. 判断⼀棵树是否是完全⼆叉树;5. 将⼆叉搜索树转换成⼀个排序的双向链表。
要求不能创建任何新的结点,只能调整树中结点指针的指向;6.求⼆叉树的宽度;7. 判断⼀棵⼆叉树是否是平衡⼆叉树;8.判断⼀颗⼆叉树是否是另⼀颗树的⼦树。
⼆、解题思路分析1.两个节点的最近公共祖先求两个节点的最近公共祖先可分为三种情况,分别为:(1)求搜索⼆叉树的最近公共祖先。
根据搜索⼆叉树的性质,左⼦树的所有节点⽐根节点⼩,右⼦树的所有节点⽐跟节点⼤。
如果两个节点都⽐根节点⼩,则递归左⼦树;如果两个节点都⽐跟节点⼤,则递归右⼦树;否则,两个节点⼀个在左⼦树,⼀个在右⼦树,则当前节点就是最近公共祖先节点。
1 Node* GetAncestor(Node* root, Node* x1, Node* x2)//1.该⼆叉树为搜索⼆叉树2 {3 assert(x1 && x2);4if (x1->_data <= root->_data && x2->_data <= root->_data)5 {6return GetAncestor(root->_left, x1, x2);//两个节都⼩于根节点,最近公共祖先在左⼦树中7 }8else if (x1->_data > root->_data && x2->_data > root->_data)9 {10return GetAncestor(root->_right, x1, x2);//两个节都⼤于根节点,最近公共祖先在左⼦树中11 }12else13return root; //⼀个在左⼦树,⼀个在右⼦树,找到公共祖先1415 }(2)三叉链,带⽗节点时求最近公共祖先,⼆叉树节点有指向⽗节点的指针。

⼀、⼆叉搜索树(BSTree)的概念参考⽹址:⼆叉搜索树⼜被称为⼆叉排序树,那么它本⾝也是⼀棵⼆叉树,那么满⾜以下性质的⼆叉树就是⼆叉搜索树:1、若左⼦树不为空,则左⼦树上左右节点的值都⼩于根节点的值2、若它的右⼦树不为空,则它的右⼦树上所有的节点的值都⼤于根节点的值3、它的左右⼦树也要分别是⼆叉搜索树===================================================================⼆、⼆叉搜索树的插⼊1、搜索插⼊之前我们先来说说它的搜索,像上图这样的⼀棵⼆叉搜索树,我们要查找某⼀个元素是很简单的。
因为它的节点分布是有规律的,所以查找⼀棵元素只需要如下的步骤就可以了:2、插⼊由于⼆叉搜索树的特殊性质确定了⼆叉搜索树中每个元素只可能出现⼀次,所以在插⼊的过程中如果发现这个元素已经存在于⼆叉搜索树中,就不进⾏插⼊。
否则就查找合适的位置进⾏插⼊。
第⼀种情况:_root为空直接插⼊,return true;第⼆种情况:要插⼊的元素已经存在如上⾯所说,如果在⼆叉搜索树中已经存在该元素,则不再进⾏插⼊,直接return false;第三种情况:能够找到合适位置===================================================================三、⼆叉搜索树的删除对于⼆叉搜索树的删除操作,主要是要理解其中的⼏种情况,写起来还是⽐较简单的。
当然⼀开始还是需要判断要删除的节点是否存在于我们的树中,如果要删除的元素都不在树中,就直接返回false;否则,再分为以下四种情况来进⾏分析:》要删除的节点⽆左右孩⼦》要删除的节点只有左孩⼦》要删除的节点只有右孩⼦》要删除的节点有左、右孩⼦删除⽅法解释:对于第⼀种情况,我们完全可以把它归为第⼆或者第三种情况,就不⽤再单独写⼀部分代码进⾏处理;》如果要删除的节点只有左孩⼦,那么就让该节点的⽗亲结点指向该节点的左孩⼦,然后删除该节点,返回true;》如果要删除的节点只有右孩⼦,那么就让该节点的⽗亲结点指向该节点的右孩⼦,然后删除该节点,返回true;对于上⾯这两种情况我们还应该在之前进⾏⼀个判断,就是判断这个节点是否是根节点,如果是根节点的话,就直接让根节点指向这个节点的左孩⼦或右孩⼦,然后删除这个节点。

阿里巴巴客服面试题及答案面试要通过层层考验,刷题肯定是必不可少的。
这一次面试题,不仅是知识的收获,还将间接地与技术大牛们做了直观的沟通,了解他们的出题思路与考察要点,并加以消化吸收。
这对自己技术能力本身就是一种极大的提升。
走上编程之路,不断丰富自己方能与世接轨,努力做最优秀的自己。
面试题001:如何实现一个高效的单向链表逆序输出?参考答案下面是其中一种写法,也可以有不同的写法,比如递归等。
面试题002:已知sqrt (2)约等于1.414,要求不用数学库,求sqrt (2)精确到小数点后10位。
考察点1.基础算法的灵活应用能力(二分法学过数据结构的同学都知道,但不一定往这个方向考虑;如果学过数值计算的同学,应该还要能想到牛顿迭代法并解释清楚)。
2.退出条件设计。
参考答案1. 已知sqrt(2)约等于1.414,那么就可以在(1.4, 1.5)区间做二分查找,如:a.high=>1.5b.low=>1.4c.mid => (high+low)/2=1.45d. 1.45*1.45>2 ? high=>1.45 : low => 1.45e.循环到c2. 退出条件前后两次的差值的绝对值<=0.0000000001, 则可退出。
代码示例:面试题003:给定一个二叉搜索树(BST),找到树中第K小的节点。
考察点1. 基础数据结构的理解和编码能力2. 递归使用示例如下图,输入K=3,输出节点值3说明:保证输入的K满足1<=K<=(节点数目)参考答案树相关的题目,第一眼就想到递归求解,左右子树分别遍历。
联想到二叉搜索树的性质,root大于左子树,小于右子树,如果左子树的节点数目等于K-1,那么root就是结果,否则如果左子树节点数目小于K-1,那么结果必然在右子树,否则就在左子树。
因此在搜索的时候同时返回节点数目,跟K做对比,就能得出结果了。
复杂度分析:时间复杂度: O(N),节点最多遍历一遍空间复杂度:O(1),(如果算上递归深度可以当做O(logN))面试题004:LRU缓存机制。


Search trees:实例--二叉搜索树什么是二叉搜索树二叉搜索树(Binary Search Tree)是一棵有序的二叉树,所以我们也可以称它为二叉排序树(不知道二叉树的童鞋,先看看二叉树:传送门)。
具有以下性质的二叉树我们称之为二叉搜索树:若它的左子树不为空,那么左子树上的所有值均小于它的根节点;若它的右子树不为空,那么右子树上所有值均大于它的根节点。
它的左子树和右子树分别也为二叉搜索树。
2、二叉搜索树的结构二叉搜索树能够高效的进行一下操作:①插入一个数值②查询是否包含某个数值③删除某个数值根据实现的不同,还可以实现其他各种操作,这是一种使用性很高的数据结构。
我们来看一个例子:这就是二叉搜索树的存储结构,所有的节点,都满足左子树上的比自己小,而右子树上的所有节点比自己大。
二叉搜索树因为其有序性,所以它能够高效的管理数的集合(1)查询我们查找是否存在17:<1>根节点是7,因为小于17,所以去右子树查找<2>走到节点12,还是小于17,所以继续往右子树找<3>走到节点17,此时找到17。
(2)插入我们使用查找的方式进行插入,以数字6为例,如图所示:(3)删除删除操作相对之前的其他两种操作,就略显复杂一些。
一般来说我们可以分为三种情况:<1>需要删除的节点没有左儿子,那么就把右儿子提上去<2>需要删除的节点的左儿子没有右儿子,那么就把左儿子提上去<3>不满足上述的两种情况的话,就把左子树中最大的节点放到要删除的节点上。
3、二叉搜索树的复杂度无论我们执行哪一个操作,其所花的时间都和树的高度成正比。
我们不难得知,二叉搜索树的平均复杂度为O(log n)。
4、二叉搜索树的实现通过上述的了解,我们大致已经知道二叉搜索树的工作原理。
所以现在我们就来简单的实现二叉搜索树基本的增删查的功能,代码如下:[cpp]view plain copy1.//表示节点的结构体2.struct node{3.int val;4.node*lch,*rch;5.};6.//插入整数x7.node*insert(node*p,int x){8.if(p==NULL){9.node*newNode=new node;10.newNode->val=x;11.newNode->lch=newNode->rch=NULL;12.p=newNode;13.}else{14.if(x<p->val)p->lch=insert(p->lch,x);15.else p->rch=insert(p->rch,x);16.}17.return p;18.}19.//查找整数x20.bool find(node*p,int x){21.if(p==NULL)return false;22.else if(p->val==x)return true;23.else if(p->val>x)return find(p->lch,x);24.else return find(p->rch,x);25.}26.//删除整数x27.node*remove(node*p,int x){28.if(p==NULL)return NULL;29.else if(x<p->val)p->lch=remove(p->lch,x);30.else if(x>p->val)p->rch=remove(p->rch,x);31.//情况<1>32.else if(p->lch==NULL){33.node*q=p->rch;34.delete p;35.return q;36.}37.//情况<2>38.else if(p->lch->rch==NULL){39.node*q=p->lch;40.q->rch=p->rch;41.delete p;42.return q;43.}44.//情况<3>45.else{46.node*q;47.for(q=p->lch;q->rch->rch!=NULL;q=q->rch);48.node*r=q->rch;49.q->rch=r->lch;50.r->lch=p->lch;51.r->rch=p->rch;52.delete p;53.return r;54.}55.return p;56.}Heaps;实例--斐波那契堆斐波纳契堆(Fibonacci Heap)于1984年由Michael L.Fredman与Robert E.Tarjan 提出,1987年公开发表,名字来源于运行时分析所使用的斐波那契数。

二叉树笔试题
以下是10道常见的二叉树笔试题:
1. 二叉树前序遍历的非递归实现方法是什么?
2. 如何求一棵二叉树的深度?
3. 如何判断一个二叉树是平衡二叉树?
4. 给定一棵二叉树和一个节点,如何找到该节点在中序遍历中的下一个节点?
5. 如何实现用两个栈来实现二叉树的后序遍历?
6. 如何通过中序遍历和后序遍历构建一棵二叉树?
7. 如何判断两棵二叉树是否相同?
8. 如何找到一棵二叉树中的最大路径和?
9. 如何将一棵二叉搜索树转换成一个有序的双向链表?
10. 如何判断一个二叉树是否是完全二叉树?
以上是常见的二叉树笔试题目,希望对您有所帮助。
同时,也希望您在掌握相关知识的基础上,能够熟练解答这些问题。
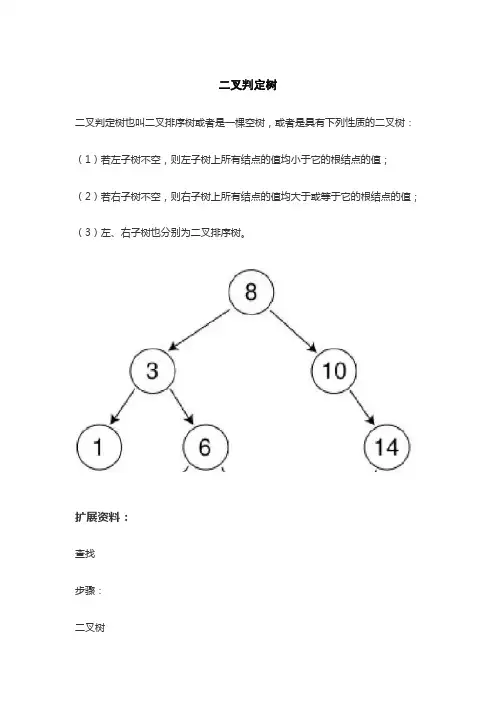
二叉判定树
二叉判定树也叫二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:(1)若左子树不空,则左子树上所有结点的值均小于它的根结点的值;(2)若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;(3)左、右子树也分别为二叉排序树。
扩展资料:
查找
步骤:
二叉树
若根结点的关键字值等于查找的关键字,成功。
否则,若小于根结点的关键字值,递归查左子树。
若大于根结点的关键字值,递归查右子树。
若子树为空,查找不成功。
平均情况分析(在成功查找两种的情况下):
在一般情况下,设P(n,i)为它的左子树的结点个数为i 时的平均查找长度。
如图的结点个数为n = 6 且i = 3; 则P(n,i)= P(6, 3)= [ 1+ ( P(3) + 1) * 3 + ( P(2) + 1) * 2 ] / 6= [ 1+ ( 5/3 + 1) * 3 + ( 3/2 + 1) * 2 ] / 6
注意:这里P(3)、P(2) 是具有3 个结点、2 个结点的二叉分类树的平均查找长度。
在一般情况,P(i)为具有i 个结点二叉分类树的平均查找长度。
平均查找长度= 每个结点的深度的总和/ 总结点数。
二叉排序树的概念
二叉排序树,也称为二叉搜索树(Binary Search Tree,BST),是一种常用的数据结构,它具有以下特点:
1、结构特点:二叉排序树是一种二叉树,其中每个节点最多有两个子节点(左子节点和右子节点),且满足以下性质:
(1)左子树上的所有节点的值都小于根节点的值;
(2)右子树上的所有节点的值都大于根节点的值;
(3)左右子树都是二叉排序树。
2、排序特性:由于满足上述性质,二叉排序树的中序遍历结果是一个有序序列。
即,对二叉排序树进行中序遍历,可以得到一个递增(或递减)的有序序列。
3、查找操作:由于二叉排序树的排序特性,查找某个特定值的节点非常高效。
从根节点开始,比较目标值与当前节点的值的大小关系,根据大小关系选择左子树或右子树进行进一步的查找,直到找到目标值或者遍历到叶子节点为止。
4、插入和删除操作:插入操作将新节点按照排序规则插入到合适的位置,保持二叉排序树的特性;删除操作涉及节点的重新连接和调整,保持二叉排序树的特性。
二叉排序树的优点在于它提供了高效的查找操作,时间复杂度为O(log n),其中n为二叉排序树中节点的个数。
它也可以支持其他常见的操作,如最小值和最大值查找、范围查找等。
然而,二叉排序树的性能受到数据的分布情况的影响。
当数据分
布不均匀时,树的高度可能会增加,导致查找操作的效率下降。
为了解决这个问题,可以采用平衡二叉树的变种,如红黑树、AVL 树等,以保持树的平衡性和性能。
阿里篇1.1.1 如何实现一个高效的单向链表逆序输出?1.1.2 已知sqrt(2)约等于1.414,要求不用数学库,求sqrt(2)精确到小数点后10位1.1.3 给定一个二叉搜索树(BST),找到树中第K 小的节点1.1.4 LRU缓存机制1.1.5 关于epoll和select的区别,以下哪些说法是正确的1.1.6 从innodb的索引结构分析,为什么索引的key 长度不能太长1.1.7 MySQL的数据如何恢复到任意时间点?1.1.8 NFS 和SMB 是最常见的两种NAS(Network Attached Storage)协议,当把一个文件系统同时通过NFS 和SMB 协议共享给多个主机访问时,以下哪些说法是错误的1.1.9 输入ping IP 后敲回车,发包前会发生什么?1.2.0 请解释下为什么鹿晗发布恋情的时候,微博系统会崩溃,如何解决?1.2.1 现有一批邮件需要发送给订阅顾客,且有一个集群(集群的节点数不定,会动态扩容缩容)来负责具体的邮件发送任务,如何让系统尽快地完成发送?1.2.2 有一批气象观测站,现需要获取这些站点的观测数据,并存储到Hive 中。
但是气象局只提供了api 查询,每次只能查询单个观测点。
那么如果能够方便快速地获取到所有的观测点的数据?1.2.3 如何实现两金额数据相加(最多小数点两位)1.2.4 关于并行计算的一些基础开放问题1.2.5 请计算XILINX公司VU9P芯片的算力相当于多少TOPS,给出计算过程与公式1.2.6 一颗现代处理器,每秒大概可以执行多少条简单的MOV指令,有哪些主要的影响因素1.2.7 请分析MaxCompute 产品与分布式技术的关系、当前大数据计算平台类产品的市场现状和发展趋势1.2.8 对大数据平台中的元数据管理是怎么理解的,元数据收集管理体系是怎么样的,会对大数据应用有什么样的影响1.2.9 你理解常见如阿里,和友商大数据平台的技术体系差异以及发展趋势和技术瓶颈,在存储和计算两个方面进行概述1.3.0 在云计算大数据处理场景中,每天运行着成千上万的任务,每个任务都要进行IO 读写。
二叉检索树
二叉排序树(Binary Sort Tree),又称二叉查找树(Binary Search Tree),亦称二叉搜索树。
是数据结构中的一类。
在一般情况下,查询效率比链表结构要高。
一棵空树,或者是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(2)若右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(3)左、右子树也分别为二叉排序树;
【注】:以上的三种定义在不同的数据结构教材中均有不同的定义方式但是都是正确的在开发时需要根据不同的需求进行选择
【注2】:没有键值相等的结点。
⼆叉树查找 对于符号表,要⽀持⾼效的插⼊操作,就需要⼀种链式结构。
但单链表⽆法使⽤⼆分查找,因为⼆分查找的⾼效来⾃于能够快速通过索引取得任何⼦数组的中间元素,链表只能遍历(详细描述)。
为了将⼆分查找的效率和链表的灵活性结合,需要更复杂的数据结构:⼆叉查找树。
具体来说,就是使⽤每个结点含有两个链接的⼆叉查找树来⾼效地实现符号表。
⼀棵⼆叉查找树(BST)是⼀棵⼆叉树,其中每个结点都含有⼀个 IComparable 类型的键以及相关联的值,且每个结点的键都⼤于其左⼦树的任意结点的键⽽⼩于右⼦树的任意结点的键。
1.实现API 1.数据结构public class BinarySearchTreesST<Key, Value> : BaseSymbolTables<Key, Value>where Key : IComparable{private Node root;//⼆叉树根节点///<summary>///嵌套定义⼀个私有类表⽰⼆叉查找树上的⼀个结点。
///每个结点都含有⼀个键,⼀个值,⼀条左连接,⼀条右连接和⼀个结点计数器。
///变量 N 给出了以该结点为根的⼦树的结点总数。
/// x.N = Size(x.left) + Size(x.right) + 1;///</summary>private class Node{public Key key;public Value value;public Node left, right;public int N;public Node(Key key,Value value,int N){this.key = key;this.value = value;this.N = N;}}public override int Size(){return Size(root);}private int Size(Node x){if (x == null)return0;elsereturn x.N;}} ⼀棵⼆叉查找树代表了⼀组键(及其相应的值)的集合,⽽⼀个可以⽤多棵不同的⼆叉查找树表(起始根结点不同,树就不同),下⾯是⼀种情况。
⼆叉排序树1 定义 ⼆叉排序树,⼜称为⼆叉查找树。
它或者是⼀颗空树,或者是具有下列性质的⼆叉树。
(1)若它的左⼦树不为空,则左⼦树上所有结点的值都⼩于它的根结点的值; (2)若它的右⼦树不为空,则右⼦树上所有结点的值都⼤于它的根结点的值; (3)它的左、右⼦树也分别为⼆叉排序树。
2 ⼆叉排序树查找操作//⼆叉树的⼆叉链表结点结构定义typedef struct BiTNode {int data;struct BiTNode *lchild;struct BiTNode *rchild;}BiTNode;typedef struct BiTNode *BiTree;//递归查找⼆叉树中是否存在key//指针f指向key的双亲,初始值为NULL//若查找成功,则指针p指向该数据元素结点,并返回true//若查找失败,则指针p指向查找路径上指向的最后⼀个结点,并返回falseStatus SearchBST(BiTree T, int key, BiTree f, BiTree *p) {if (!T) { //查找不成功*p = f;return false;} else if (key == T->data) { //查找成功*p = f;return true;} else if (key < T->data) {SearchBST(T->lchild, key, f, p); //在左⼦树继续查找} else {SearchBST(T->rchild, key, f, p); //在右⼦树继续查找}}。
二叉排序树的判定代码1.引言概述部分的内容可以介绍二叉排序树及其重要性。
可以参考以下示范:1.1 概述二叉排序树(Binary Search Tree,BST)是一种重要的数据结构,在计算机科学领域具有广泛的应用。
它是一种基于二叉树的数据结构,其中每个节点都包含一个键及其对应的值。
通过比较节点的键,可以将整个树组织为一个有序的结构。
二叉排序树具有以下特性:- 左子树中的所有节点的键值小于根节点的键值。
- 右子树中的所有节点的键值大于根节点的键值。
- 左、右子树也都是二叉排序树。
二叉排序树的重要性主要体现在以下几个方面:首先,二叉排序树可以高效地支持搜索和插入操作。
由于二叉排序树的有序性质,我们可以使用二叉树的搜索算法快速地找到特定键对应的值。
而插入操作也是非常高效的,只需要根据节点的键值逐层比较并插入到合适的位置即可。
其次,二叉排序树可以支持有序遍历操作。
有序遍历是指按照节点的键值升序或降序的方式遍历整棵树。
这种遍历方式对于需要按照一定顺序处理数据的场景非常有用,比如对于某种排序算法的输入数据进行预处理。
此外,二叉排序树还可以支持高效的删除操作。
删除一个节点时,我们可以根据节点的键值快速找到该节点,并根据不同情况进行删除操作。
相比其他数据结构,二叉排序树的删除操作更加简洁高效。
综上所述,二叉排序树是一种重要的数据结构,具有高效的搜索、插入、遍历和删除等操作,对于解决许多实际问题具有重要作用。
本文将介绍二叉排序树的定义以及判定二叉排序树的算法,希望能对读者深入理解和应用二叉排序树提供帮助。
1.2 文章结构文章结构部分的内容可以包括以下内容:文章结构部分旨在介绍本文的整体结构,并简要描述各个部分的内容安排。
本文将按照以下结构进行叙述:1. 引言:本部分旨在引入文章的主题和背景,并对问题进行概述。
首先介绍二叉排序树及其重要性,然后简要介绍本文的目的和组织结构。
2. 正文:本部分是文章的核心,详细介绍了二叉排序树的定义和判定算法。