重庆市铜梁中学校高三数学下学期模拟测试(一)试题 理

2021-2021学年重庆市铜梁中学高三〔下〕3月月考数学试卷〔理科〕参考答案与试题解析一、选择题：本大题10小题，每题5分，共50分.在每题给出的四个备选项中，只有一项为哪一项符合题目要求的.1．〔5分〕设全集U=R，集合M={y∈R|y=2x，x＞0}，N={x∈R|2x﹣x2＞0}，那么M∩N为〔〕A．〔1，2〕 B．〔1，+∞〕 C．[2，+∞〕 D．〔﹣∞，0]∪〔1，+∞〕考点：交集及其运算．分析：求函数y=2x的值域y的范围即可求出集合M，解不等式2x﹣x2＞0即能求出集合N，而后求M∩N．解答：解：∵函数y=2x，〔x＞0〕的值域为y＞1，∴集合M={y∈R|y=2x，x＞0}={y|y＞1}，即：所有大于1的实数构成集合M，也可写成M={x|x＞1}，又∵N={x∈R|2x﹣x2＞0}={x∈R|x〔x﹣2〕＜0}={x|0＜x＜2}，∴M∩N={x|1＜x＜2}，用区间表示为〔1，2〕．应选A．点评：解决此题的关键在于要明确集合中元素指的是谁，明确了这一点，此题变得就简单了．2．〔5分〕在各项都为正数的等比数列{a n}中，首项为3，前3项和为21，那么a3+a4+a5=〔〕A．189 B．84 C．72 D．33考点：等比数列的前n项和；等比数列的性质．专题：计算题．分析：首先设出等比数列{a n}的公比为q，根据前3项的和为21，得到3+3q+3q2=21，解之得q=2或﹣3．再结合等比数列{a n}中，各项都为正数，得到公比也是正数，所以取q=2〔﹣3舍去〕，最后利用前3项的和为21以及公比为2，可以求出a3+a4+a5的值．解答：解：设等比数列{a n}的公比为q，那么∵首项为3，前3项和为21，∴3+3q+3q2=21，解之得q=2或﹣3∵在等比数列{a n}中，各项都为正数∴公比q为正数，q=2〔﹣3舍去〕∴a3+a4+a5=q2〔a1+a2+a3〕=4×21=84应选B点评：此题以一个特殊的等比数列为载体，通过求连续3项和的问题，着重考查了等比数列的通项、等比数列的性质和前n项和等知识点，属于根底题．3．〔5分〕以下说法正确的有〔〕个①“〞是“θ=30°〞的充分不必要条件②假设命题p：∃x∈R，x2﹣x+1=0，那么¬p：∀x∈R，x2﹣x+1≠0③命题“假设a=0，那么ab=0”的否命题是：“假设a≠0，那么ab≠0”④a，b∈R+，假设log3a＞log3b，那么．A．0B．1C．2D．3考点：命题的真假判断与应用．专题：阅读型．分析：对于①，由，不一定有θ=30°．由θ=30°，一定有，然后由充分条件与必要条件的定义判断；对于②，命题p是特称命题，其否认是全程命题，注意格式的书写；对于③，把原命题的条件和结论分别取否认即可得到其否命题，由此可判断给出的否命题是否正确；对于④，由对数函数的性质得到a与b的大小，进一步由指数函数的性质得到．由以上分析可得答案．解答：解：由，得：θ=30°+k360°或θ=150°+k360°〔k∈Z〕，反之，由θ=30°，一定有，∴“〞是“θ=30°〞的必要不充分条件，命题①错误；命题p：∃x∈R，x2﹣x+1=0的否认为¬p：∀x∈R，x2﹣x+1≠0，∴命题②正确；命题“假设a=0，那么ab=0”的否命题是：“假设a≠0，那么ab≠0”，∴命题③正确；a，b∈R+，假设log3a＞log3b，那么a＞b，∴，∴命题④正确．所以正确的命题是②③④．应选D．点评：此题考查了命题的真假判断与应用，考查了充分条件与必要条件的判断方法，考查了命题的否命题与命题的否认，特别是全程命题和特称命题的否认一定要注意格式的书写，全程命题p：∀x∈M，p〔x〕，它的否认￢p：∃x∈M，￢p〔x〕．特称命题p：∃x∈M，p〔x〕，它的否认￢p：∀x∈M，￢p〔x〕．此题是根底题．4．〔5分〕某空间几何体的三视图如以下列图，该空间几何体的体积是〔〕A．B．10 C．D．考点：由三视图求面积、体积．专题：空间位置关系与距离．分析：通过三视图判断几何体的形状，通过三视图的数据，求出几何体的体积即可．解答：解：由三视图可知，几何体是底面为直角三角形，高为4的三棱锥，其放在棱长分别为4，4，5的长方体中的图形如以下列图．底面直角三角形的直角边长分别为：4，5，棱锥的高为：4；所以棱锥的体积为：××4×5×4=．应选C．点评：此题考查直观图与三视图的关系，三视图判断几何体的形状的解题的关键，考查计算能力．5．〔5分〕锐角α满足，那么sin2α等于〔〕A．B．C．D．考点：三角函数的恒等变换及化简求值．专题：计算题．分析：先根据二倍角公式以及和差角公式对条件两边整理得cosα﹣sinα=，再两边平方即可得到结论．解答：解：∵cos2α=cos2α﹣sin2α=〔cosα﹣sinα〕〔cosα+sinα〕；①cos〔﹣α〕=〔cosα+sinα〕；②∵锐角α满足，③∴由①②③得，cosα﹣sinα=，两边平方整理得：1﹣sin2α=⇒sin2α=．应选：A．点评：此题主要考查三角函数的恒等变换及化简求值．解决这类题目的关键在于对公式的熟练掌握及其应用．6．〔5分〕按以下程序框图来计算：如果输入的x=5，应该运算〔〕次才停止．A．2B．3C．4D．5考点：程序框图．专题：计算题；概率与统计．分析：根据题意，该框图的含义是计算3x﹣2的值，在所得3x﹣2的值不大于200时用此值代替x并进入下一步循环，直到所得结果大于200时输出结果并终止程序，由此即可得到此题答案．解答：解：由题意，该程序按如下步骤运行经过第一次循环得到x=3×5﹣2=13，不满足x＞200，进入下一步循环；经过第二次循环得到x=3×13﹣2=37，不满足x＞200，进入下一步循环；经过第三次循环得到x=3×37﹣2=109，不满足x＞200，进入下一步循环；经过第四次循环得到x=3×109﹣2=325，因为325＞200，结束循环并输出x的值因此，运算进行了四次后，输出x值而程序停止应选：C点评：此题给出程序框图，求循环体执行的次数，属于根底题．解题的关键是先根据题中的数学模逐步进行运算，直到满足终止循环的条件而输出x的值，使问题得以解决．7．〔5分〕〔2021•桂林模拟〕从9名学生中选出4人参加辨论比赛，其中甲、乙、丙三人至少有两人入选的不同选法的种数为〔〕A．36 B．96 C．63 D．51考点：计数原理的应用．专题：计算题；分类讨论．分析：此问题可以分为两类计数，三人中有两人参加与三人都参加，计数时分两步解决，先取甲、乙、丙三人至少有两人，第二步再相应从其余六人中取人凑够四人解答：解：由题意9名学生中选出4人参加辨论比赛，其中甲、乙、丙三人至少有两人入选的不同选法有两类，一类是三人中有两人参加，入选种数为C32×C62=45一类是三人都参加，入选种数为C33×C61=6所以总的入选种数有45+6=51应选D点评：此题考查计数原理的应用，解题的关键是根据题设中的问题对问题正确分类，再利用计数原理求得选法种数8．〔5分〕设实数x，y满足条件假设目标函数z=ax+by〔a＞0，b＞0〕的最大值为12，那么的最小值为〔〕A．B．C．D．4考点：根本不等式；简单线性规划的应用．专题：计算题．分析：由可得2a+3b=6，那么=〔2a+3b〕〔〕×，然后利用根本不等式可求最小值解答：解：不等式表示的平面区域如以下列图阴影局部，当直线ax+by=z〔a＞0，b＞0〕过直线4x﹣y﹣10=0与直线x﹣2y+8=0的交点〔4，6〕时，目标函数z=ax+by〔a＞0，b＞0〕取得最大12∴4a+6b=12即2a+3b=6那么=〔2a+3b〕〔〕×==当且仅当即a=b=时取等号应选A点评：此题综合地考查了线性规划问题和由根本不等式求函数的最值问题．要求能准确地画出不等式表示的平面区域，并且能够求得目标函数的最值．9．〔5分〕〔2021•南开区二模〕假设函数y=f〔x〕〔x∈R〕满足f〔x+2〕=f〔x〕且x∈[﹣1，1]时，f〔x〕=1﹣x2，函数g〔x〕=，那么函数h〔x〕=f〔x〕﹣g〔x〕在区间[﹣5，5]内的与x轴交点的个数为〔〕A．5B．7C．8D．10考点：函数的零点与方程根的关系．专题：压轴题；数形结合．分析：由f〔x+2〕=f〔x〕，知函数y=f〔x〕〔x∈R〕是周期为2的函数，进而根据f〔x〕=1﹣x2与函数g〔x〕=的图象得到交点为8个．解答：解：因为f〔x+2〕=f〔x〕，所以函数y=f〔x〕〔x∈R〕是周期为2函数，因为x∈[﹣1，1]时，f〔x〕=1﹣x2，所以作出它的图象，那么y=f〔x〕的图象如以下列图：〔注意拓展它的区间〕再作出函数g〔x〕=的图象，容易得出到交点为8个．应选C．点评：注意周期函数的一些常见结论：假设f〔x+a〕=f〔x〕，那么周期为a；假设f〔x+a〕=﹣f〔x〕，那么周期为2a；假设f〔x+a〕=，那么周期为2a；另外要注意作图要细致．10．〔5分〕〔2021•甘肃三模〕过双曲线的左焦点F〔﹣c，0〕，〔c＞0〕，作圆：x2+y2=的切线，切点为E，延长FE交双曲线右支于点P，假设=〔+〕，那么双曲线的离心率为〔〕A．B．C．D．考点：圆与圆锥曲线的综合．专题：综合题；压轴题．分析：由题设知|EF|=，|PF|=2，|PF′|=a，再由|PF|﹣|PF′|=2a，知2﹣a=2a，由此能求出双曲线的离心率．解答：解：∵|OF|=c，|OE|=，∴|EF|=，∵，∴|PF|=2，|PF'|=a，∵|PF|﹣|PF′|=2a，∴2﹣a=2a，∴，应选C．点评：此题考查双曲线的性质和应用，解题时要认真审题，仔细解答二、填空题：本大题共6小题，考生作答5小题，每题5分，共25分.11．〔5分〕复数，是z的共轭复数，那么等于 1 ．考点：复数代数形式的乘除运算；复数求模．专题：计算题．分析：利用复数的运算法那么和共轭复数的定义及其复数的模的计算公式即可得出．解答：解：∵=﹣i，∴，∴．故答案为1．点评：熟练掌握复数的运算法那么和共轭复数的定义及其复数的模的计算公式是解题的关键．12．〔5分〕〔2021•房山区二模〕一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图〔如图〕．为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10000人中再用分层抽样方法抽出100人作进一步调查，那么在[2500，3000〕〔元〕月收入段应抽出25 人．考点：分层抽样方法．专题：压轴题．分析：直方图中小矩形的面积表示频率，先计算出[2500，3000〕内的频率，再计算所需抽取人数即可．解答：解：由直方图可得[2500，3000〕〔元〕月收入段共有10000×0.0005×500=2500人按分层抽样应抽出人故答案为：25点评：此题主要考查直方图和分层抽样，难度不大．13．在△ABC中，角A，B，C所对边长分别为a，b，c，假设a2，c2，b2成等差数列，那么角C的最大值为60°．考点：余弦定理；等差数列的通项公式．专题：解三角形．分析：由a2，c2，b2成等差数列，理由等差数列的性质列出关系式，再利用余弦定理表示出cosC，将得出的关系式代入并利用根本不等式变形求出cosC的最大值，根据C为三角形的内角，利用余弦定理即可求出C的最大值．解答：解：∵a2，c2，b2成等差数列，∴2c2=a2+b2，∴cosC=≥==，当且仅当a=b时取等号，∵C为三角形的内角，∴0＜C≤60°，那么C的最大值为60°．故答案为：60°点评：此题考查了余弦定理，根本不等式的运用，以及等差数列的性质，熟练掌握余弦定理是解此题的关键．14．〔5分〕在实数范围内，不等式|2x﹣1|+|2x+1|≤6的解集为[﹣，] ．考点：绝对值不等式的解法．专题：不等式的解法及应用．分析：由的不等式可得可得①，或②，或③．分别求得①②③的解集，再取并集，即得所求．解答：解：由不等式|2x﹣1|+|2x+1|≤6，可得①，或②，或③．解①得﹣≤x＜﹣，解②得﹣≤x＜，解③得≤x≤．把①②③的解集取并集可得不等式的解集为[﹣，]．故答案为[﹣，]点评：此题主要考查分式不等式的解法，表达了等价转化和分类讨论的数学思想，属于中档题．15．〔5分〕圆的参数方程为为参数〕，直线l的极坐标方程为3ρcosθ+4ρsinθ+m=0，假设圆与直线相切，那么实数m= 2或﹣8 ．考点：参数方程化成普通方程；直线与圆的位置关系；点的极坐标和直角坐标的互化．专题：直线与圆．分析：把圆的参数方程化为直角坐标方程，把直线l的极坐标方程化为直角坐标方程，利用圆心到直线的距离等于半径求出m 的值．解答：解：圆的参数方程为为参数〕，化为普通方程，即〔x﹣1〕2+y2=1．直线3ρcosθ+4ρsinθ+m=0 即 3x+4y+m=0．圆与直线相切，∴圆心〔1，0〕到直线的距离等于半径．∴=1，解得m=2或m=﹣8，故答案为：2或﹣8．点评：此题考查把参数方程化为普通方程，把极坐标方程化为直角坐标方程的方法，直线和圆相切的性质，把参数方程化为普通方程，把极坐标方程化为直角坐标方程是解题的突破口．16．〔5分〕〔2021•广东〕如图，AB，CD是半径为a的圆O的两条弦，他们相交于AB的中点P，，∠OAP=30°，那么CP= ．考点：与圆有关的比例线段．专题：计算题；压轴题．分析：先由垂径定理可得直角三角形PAO，从而用a表示BP，再利用圆中线段相交弦关系得关于CP的等式，即可求得CP．解答：解：因为点P是AB的中点，由垂径定理知，OP⊥AB．在Rt△OPA中，．由相交弦定理知，BP•AP=CP•DP，即，所以．故填：．点评：此题考查的是直角三角形的性质、勾股定理及垂径定理的综合应用，此题还考查与圆有关的比例线段、圆中的切割线定理，属于根底题．三、解答题：本大题共6小题，共75分.解容许写出文字说明、证明过程或演算步骤. 17．〔13分〕向量，设函数〔I〕求f〔x〕的解析式，并求最小正周期；〔II〕假设函数g〔x〕的图象是由函数f〔x〕的图象向右平移个单位得到的，求g〔x〕的最大值及使g〔x〕取得最大值时x的值．考点：平面向量数量积的运算；两角和与差的正弦函数；三角函数的周期性及其求法；函数y=Asin〔ωx+φ〕的图象变换．专题：计算题；三角函数的图像与性质；平面向量及应用．分析：〔I〕根据向量数量积的坐标运算公式，结合三角恒等变换公式化简，得数f〔x〕=sin〔2x+〕+，再由三角函数的周期公式即可算出求最小正周期T；〔II〕根据函数图象平移的公式，可得g〔x〕=f〔x﹣〕=sin2x+，结合正弦函数的图象与性质，可得当x=+kπ〔k∈Z〕，g〔x〕=sin2x+取得最大值+，得到此题的答案．解答：解：〔I〕∵向量，∴函数=cos2x+sinxcosx=〔1+cos2x〕+sin2x=sin〔2x+〕+即f〔x〕的解析式为y=sin〔2x+〕+，最小正周期为T==π；〔II〕将f〔x〕的图象向右平移个单位，得到y=f〔x﹣〕=sin[2〔x﹣〕+]+，即y=sin2x+的图象，因此g〔x〕=sin2x+令2x=+2kπ〔k∈Z〕，得x=+kπ〔k∈Z〕∴当x=+kπ〔k∈Z〕，g〔x〕=sin2x+取得最大值+即[g〔x〕]max=+，相应的x=+kπ〔k∈Z〕点评：此题以向量的数量积运算为载体，求函数y=Asin〔ωx+φ〕+k的图象与性质．着重考查了平面向量数量积的坐标公式和三角函数的图象与性质等知识，属于根底题．18．〔13分〕〔2021•陕西〕某项选拔共有三轮考核，每轮设有一个问题，能正确答复以下问题者进入下一轮考核，否那么即被淘汰，某选手能正确答复第一、二、三轮的问题的概率分别为、、，且各轮问题能否正确答复互不影响．〔Ⅰ〕求该选手被淘汰的概率；〔Ⅱ〕该选手在选拔中答复以下问题的个数记为ξ，求随机变量ξ的分布列与数学期望．考点：离散型随机变量及其分布列；离散型随机变量的期望与方差．专题：计算题．分析：〔Ⅰ〕求该选手被淘汰的概率可先求其对立事件该选手不被淘汰，即三轮都答对的概率；〔Ⅱ〕ξ的可能值为1，2，3，ξ=i表示前i﹣1轮均答对问题，而第i次答错，利用独立事件求概率即可．解答：解：〔Ⅰ〕记“该选手能正确答复第i轮的问题〞的事件为A i〔i=1，2，3〕，那么，，．∴该选手被淘汰的概率===．〔Ⅱ〕ξ的可能值为1，2，3.，=，P〔ξ=3〕=P〔A1A2〕=P〔A1〕P〔A2〕=．∴ξ的分布列为∴=．点评：此题考查互斥、对立、独立事件的概率，离散型随机变量的分布列和期望等知识，同时考查利用概率知识分析问题、解决问题的能力．19．〔13分〕〔2021•烟台一模〕定义在R上的函数f〔x〕=ax3+bx2+cx+3同时满足以下条件：①f〔x〕在〔0，1〕上是减函数，在〔1，+∞〕上是增函数；②f′〔x〕是偶函数；③f 〔x〕在x=0处的切线与直线y=x+2垂直．〔Ⅰ〕求函数y=f〔x〕的解析式；〔Ⅱ〕设g〔x〕=4lnx﹣m，假设存在x∈[1，e]，使g〔x〕＜f′〔x〕，求实数m的取值范围．考点：利用导数研究函数的单调性；函数恒成立问题；利用导数研究曲线上某点切线方程．专题：综合题．分析：〔Ⅰ〕求出f′〔x〕=3ax2+2bx+c，由f〔x〕在〔0，1〕上是减函数，在〔1，+∞〕上是增函数，得到f′〔1〕=3a+2b+c=0，再由函数的奇偶性和切线方程能够求出函数y=f〔x〕的解析式．〔Ⅱ〕假设存在x∈[1，e]，使4lnx﹣m＜x2﹣1，即存在x∈[1，e]，使m＞4lnx﹣x2+1，由此入手，结合题设条件，能够求出实数m的取值范围．解答：解：〔Ⅰ〕f′〔x〕=3ax2+2bx+c∵f〔x〕在〔0，1〕上是减函数，在〔1，+∞〕上是增函数，∴f′〔1〕=3a+2b+c=0…①…〔1分〕由f′〔x〕是偶函数得：b=0②…〔2分〕又f〔x〕在x=0处的切线与直线y=x+2垂直，f′〔0〕=c=﹣1③…〔3分〕由①②③得：，即…〔4分〕〔Ⅱ〕由得：假设存在x∈[1，e]，使4lnx﹣m＜x2﹣1，即存在x∈[1，e]，使m＞4lnx﹣x2+1 设h〔x〕=4lnx﹣x2+1m＞h min，对h〔x〕求导，导数在〔0，〕大于零，〔，e〕小于零，即h〔x〕先递增再递减，当x=．m取最大值+∞，x=e 时，m取最小值5﹣e2．∴实数m的取值范围是〔5﹣e2，+∞〕．点评：此题考查函数解析式的求法和求实数的取值范围，考查化归与转化、分类与整合的数学思想，培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识．20．〔12分〕如图，四棱锥A﹣BCDE中，△ABC是正三角形，四边形BCDE是矩形，且平面ABC⊥平面BCDE，AB=2，AD=4．〔Ⅰ〕假设点G是AE的中点，求证：AC∥平面BDG；〔II〕假设点F为线段AB的中点，求二面角B﹣CE﹣F的正切值．考点：二面角的平面角及求法；直线与平面平行的判定．专题：空间位置关系与距离；空间角．分析：〔Ⅰ〕利用三角形的中位线定理和线面平行的判定定理即可证明；〔2〕利用线面垂直的判定和性质定理、面面垂直的性质定理、二面角的定义即可得出．解答：〔Ⅰ〕证明：连接CE、BD，设CE∩BD=O，连接OG，由三角形的中位线定理可得：OG∥AC，∵AC⊄平面BDG，OG⊂平面BDG，∴AC∥平面BDG．〔Ⅱ〕∵平面ABC⊥平面BCDE，DC⊥BC，∴DC⊥平面ABC，∴DC⊥AC，在Rt△ACD中，CD==．取BC的中点M，连接AM，那么AM⊥平面BCDE．取BM 的中点N，连接FN，那么FN∥AM，∴FN⊥平面BCDE．过点N作NP⊥CE，垂足为P，连接FP，由三垂线定理可得FP⊥CE．∴∠FPN为二面角B﹣CE﹣F的平面角．在Rt△CNP 中，NP=CNsin∠NCP==．在Rt△FNP 中，==．点评：熟练掌握三角形的中位线定理、线面平行的判定定理、线面及面面垂直的判定和性质定理、二面角的定义是解题的关键．21．〔12分〕〔2021•甘肃一模〕设椭圆的右焦点为F1，直线与x轴交于点A ，假设〔其中O为坐标原点〕．〔1〕求椭圆M的方程；〔2〕设P是椭圆M上的任意一点，EF为圆N：x2+〔y﹣2〕2=1的任意一条直径〔E、F为直径的两个端点〕，求的最大值．考点：圆与圆锥曲线的综合；平面向量数量积的运算；椭圆的标准方程．专题：综合题．分析：〔1〕先求出点A，F1的坐标，利用，即可求得椭圆的方程；〔2〕方法1：设圆N：x2+〔y﹣2〕2=1的圆心为N，那么==，从而求的最大值转化为求的最大值；方法2：设点E〔x1，y1〕，F〔x2，y2〕，P〔x0，y0〕，根据E，F的中点坐标为〔0，2〕，可得所以=．根据点E在圆N上，点P在椭圆M上，可得==，利用，可求的最大值；方法3：①假设直线EF的斜率存在，设EF的方程为y=kx+2，由，解得，再分别求得、，利用，可求的最大值；②假设直线EF的斜率不存在，此时EF的方程为x=0，同理可求的最大值．解解：〔1〕由题设知，，，…〔1分〕答：由，得．…〔3分〕解得a2=6．所以椭圆M的方程为．…〔4分〕〔2〕方法1：设圆N：x2+〔y﹣2〕2=1的圆心为N，那么…〔6分〕=…〔7分〕=．…〔8分〕从而求的最大值转化为求的最大值．…〔9分〕因为P是椭圆M上的任意一点，设P〔x0，y0〕，…〔10分〕所以，即．…〔11分〕因为点N〔0，2〕，所以．…〔12分〕因为，所以当y0=﹣1时，取得最大值12，…〔13分〕所以的最大值为11，…〔14分〕方法2：设点E〔x1，y1〕，F〔x2，y2〕，P〔x0，y0〕，因为E，F的中点坐标为〔0，2〕，所以…〔6分〕所以…〔7分〕=〔x1﹣x0〕〔﹣x1﹣x0〕+〔y1﹣y0〕〔4﹣y1﹣y0〕==．…〔9分〕因为点E在圆N上，所以，即．…〔10分〕因为点P在椭圆M上，所以，即．…〔11分〕所以==．…〔12分〕因为，所以当y0=﹣1时，．…〔14分〕方法3：①假设直线EF的斜率存在，设EF的方程为y=kx+2，…〔6分〕由，解得．…〔7分〕因为P是椭圆M上的任一点，设点P〔x0，y0〕，所以，即．…〔8分〕所以，…〔9分〕所以．…〔10分〕因为，所以当y0=﹣1时，取得最大值11，…〔11分〕②假设直线EF的斜率不存在，此时EF的方程为x=0，由，解得y=1或y=3．不妨设，E〔0，3〕，F〔0，1〕．…〔12分〕因为P是椭圆M上的任一点，设点P〔x0，y0〕，所以，即．所以，．所以．因为，所以当y0=﹣1时，取得最大值11，…〔13分〕综上可知，的最大值为11，…〔14分〕点评：此题以向量为载体，考查椭圆的标准方程，考查向量的数量积，考查配方法求函数的最值，综合性强，属于中档题．22．〔12分〕设数列{b n}满足b1=1，b n+1=2b n+1，假设数列{a n}满足：a1=1，且当n≥2，n∈N*时，〔I〕求b2，b3，b4及b n；〔II 〕证明：，〔注：〕．考点：数列递推式；等比数列的通项公式；数列的求和．专题：综合题；压轴题；等差数列与等比数列．分〔I〕由b1=1，b n+1=2b n+1，分别令n=1和n=2，先求出b2和b3，再由b n+1=2b n+1，利用析：构造法求出{b n}的通项公式．〔II〕先证明=〔n≥2，n∈N*〕，由该结论得〕=2〔++…++〕，再由++…++=1++…+，利用放缩法即可证明结论；解答：〔Ⅰ〕解：∵b1=1，b n+1=2b n+1，∴b2=2×1+1=3，b3=2×3+1=7，b4=2×7+1=15，∵b n+1=2b n+1，∴b n+1+1=2〔b n+1〕，所以{b n+1}为公比为2的等比数列，首项为2，∴b n+1=〔b1+1〕•2n﹣1=2•2n﹣1=2n，∴b n=2n﹣1．〔II〕证明：a1=1，a n=b n〔〕〔n≥2且n∈N*〕，∴=++…+，=++…++，∴﹣=，∴=，∴=〔n≥2且n∈N*〕．所以〕=×…×=×…×=×ׅוa n+1=וa n+1=2•=2〔++…++〕，而++…++=1++…+，当k≥2时，=＜=2〔〕，∴1++…+=1+2[〔﹣〕+〔﹣〕+…+〔﹣〕=1+2〔﹣〕＜＜．点评：此题考查数列的通项公式的求法，考查不等式的证明，考查数列、不等式知识，考查化归与转化、分类与整合的数学思想，培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识．。

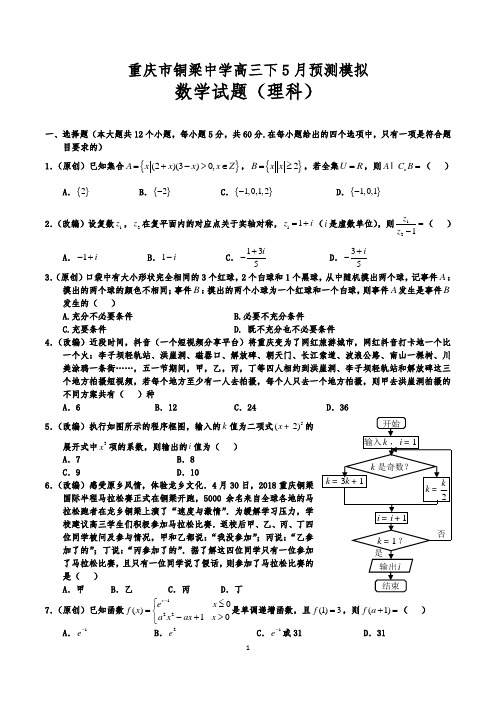
重庆市铜梁中学高三下5月预测模拟数学试题（理科）一、选择题（本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的） 1．（原创）已知集合{}(2)(3)0,A x x x x Z =+->∈，{}2B x x =≥，若全集U R =，则u A C B =（ ）A ．{}2B ．{}2-C ．{}1,0,1,2-D ．{}1,0,1- 2．（改编）设复数1z ，2z 在复平面内的对应点关于实轴对称，11z i =+（i 是虚数单位），则121z z =-（ ） A ．1i -+ B ．1i - C ．135i +-D ．35i+- 3．（原创）口袋中有大小形状完全相同的3个红球，2个白球和1个黑球，从中随机摸出两个球，记事件A ：摸出的两个球的颜色不相同；事件B ：摸出的两个小球为一个红球和一个白球，则事件A 发生是事件B 发生的（ ）A.充分不必要条件B.必要不充分条件C.充要条件D. 既不充分也不必要条件 4．（改编）近段时间，抖音（一个短视频分享平台）将重庆变为了网红旅游城市，网红抖音打卡地一个比一个火：李子坝轻轨站、洪崖洞、磁器口、解放碑、朝天门、长江索道、波浪公路、南山一棵树、川美涂鸦一条街……，五一节期间，甲，乙，丙，丁等四人相约到洪崖洞、李子坝轻轨站和解放碑这三个地方拍摄短视频，若每个地方至少有一人去拍摄，每个人只去一个地方拍摄，则甲去洪崖洞拍摄的不同方案共有（ ）种A ．6B ．12C ．24D ．36 5．（改编）执行如图所示的程序框图，输入的k 值为二项式5(2)x +的展开式中3x 项的系数，则输出的i 值为（ ）A ．7B ．8C ．9D ．10 6．（改编）感受原乡风情，体验龙乡文化．4月30日，2018重庆铜梁国际半程马拉松赛正式在铜梁开跑，5000余名来自全球各地的马拉松跑者在龙乡铜梁上演了“速度与激情”．为缓解学习压力，学校建议高三学生们积极参加马拉松比赛．返校后甲、乙、丙、丁四位同学被问及参与情况，甲和乙都说：“我没参加”；丙说：“乙参加了的”；丁说：“丙参加了的”．据了解这四位同学只有一位参加了马拉松比赛，且只有一位同学说了假话，则参加了马拉松比赛的是（ ）A ．甲B ．乙C ．丙D ．丁7．（原创）已知函数1220()10x e x f x a x ax x -⎧≤=⎨-+>⎩是单调递增函数，且(1)3f =，则(1)f a +=（ ）A ．1e -B ．2eC ．1e -或31D ．318．（原创）已知不等式组0160x y x kx y -≤⎧⎪≥⎨⎪-+≤⎩表示的平面区域是面积为4的等腰直角三角形，点(,)P x y 是该区域内一点，则2z x y =-的最大值为（ ）A.3-B.1C.3D.6 9．（原创）已知函数()sin 2cos2f x a x x =+的图像关于直线6x π=对称，将函数()f x 的图像向右平移6π个单位得到函数()g x 的图像，若α为锐角，则()g α的取值范围是（ ）A ．(1,2]-B ．(0,2] C．( D ．[2,2]- 10．（原创）某三棱锥的三视图如图所示，其三个视图都是直角三角形，该三棱锥的外接球表面积为1S ，正视图中的三角形是一个圆锥的轴截面，且该圆锥的侧面积为2S ，则1S :2S =（ ） A.9:8 B.27:4C.18:D.9:11．（改编）点1F ，2F 是双曲线C ：22221(0,0)x y a b a b-=>>的左右焦点，点P 在双曲线C 上，且1PF ⊥12F F ，1PF 与x 轴交于点Q ，O 为坐标原点，若四边形1OF PQ 有内切圆，则双曲线C 的离心率为（ ）A ．2 D ．312．（原创）已知直线l ：20kx y k --+=与函数3233()y x x x a a R =-++∈的图像有三个不同交点()11,A x y ，()22,B x y ，()33,C x y ， 123x x x <<，对任意的实数k ，都有AB BC =，则1232132()()y y y x a x x ++=++（ ）A ．1B ．2C ．3D ．4二、填空题（本大题共4小题，每小题5分，共20分） 13．（改编）《九章算术》是中国古代第一部数学专著，是《算经十书》中最重要的一种，该书中有这样一个问题：“某贾人擅营，月入益功疾（注：从第2月开始，每月比前一月多入相同数量的铜钱），3月入25贯，全年（按12个月计）共入510贯”，则该贾人上半年共入 贯．14．（原创）圆C ：22450x y x +--=截直线l ：2y kx =+所得的弦长为2，则直线l 的倾斜角为 ． 15．（原创）已知(sin ,2cos )αα=a ，(1,1)=-b ，且⊥a b ，则2()=+a b ．16．（原创）已知ABC ∆的三个内角A 、B 、C 所对的边分别为a 、b 、c ，若2c =，a b =，sin 3sin()A B C =-，则ABC ∆的面积为 ．俯视图侧视图三、解答题（共70分．解答应写出文字说明、证明过程或演算步骤．第17——21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答）（一）必考题：共60分17.（改编）（本小题满分12分）已知数列{}n a 的前n 项和为n S ，且344n n S a =-．（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设2log n n b a =，求数列2221(1)n n b n ⎧⎫+⎨⎬+⎩⎭的前n 项和n T ．18．（原创）（本小题满分12分）调研考试后，某校对甲、乙两个班的数学考试成绩进行分析，统计成绩后，（Ⅰ）规定：大于或等于100分为优秀，100分以下为非优秀．完成列联表，并判断能否在犯错误的概率不超过90%的前提下认为“成绩与班级有关系”？ （Ⅱ）将甲乙两班各分数段的频率视为概率，现在从该校所有的学生中用随机抽样的方法每次抽取1人，共抽取3次，记被抽取的3人中成绩在[)100,120的人数为X ，若每次抽取的结果是相互独立的，求X 的分布列、数学期望()E X 和方差()D X ． ，其中n a b c d =+++.19．（改编）（本小题满分12分）如图，在四棱锥P ABCD -中，PA PB PD ==，BA AD =，BA ⊥AD ，O 为BD 的中点，22OA OC ==，3OP =． （Ⅰ）求证：AC ⊥PD ；（Ⅱ）线段PD 上是否存在点E ，使得二面角E AC P --？若存在，确定E 点的位置；若不存在，请说明理由．20．（原创）（本小题满分12分）已知椭圆C ：22221(0)x y a b a b +=>>过点，直线l 与椭圆C 交于不重合的两点P ，Q ，点M 是PQ 的中点，点O 为坐标原点，且当直线OM 和直线l 的斜率都存在时，它们的斜率之积为定值14-． （Ⅰ）求椭圆C 的标准方程；（Ⅱ）若0OP OQ =，试判断点O 到直线l 的距离是否为定值？若是定值，求出该值；若不是，请说明理由．21．（本小题满分12分）已知函数ln 1()x f x a x+=-. （Ⅰ）若函数()f x 有两个零点，求实数a 的取值范围； （Ⅱ）若函数21()ln 22ag x x x ax =-+有两个极值点，试判断函数()g x 的零点个数.（二）选考题：共10分．请考生在第22、23两题中任选一题作答．如果多做，则按所做的第一题计分．在答题卡上一定要把自己所选做的题号对应的方框涂黑． 22．（改编）（本小题满分10分）选修4——4：坐标系与参数方程在直角坐标系xOy 中，曲线1C 的参数方程为22cos 2sin x y θθ=+⎧⎨=⎩（θ为参数），以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线2C 的极坐标方程为sin()4πρθ+=.（Ⅰ）求曲线1C 的极坐标方程和2C 的直角坐标方程；（Ⅱ）若射线l ：θα=（0ρ>）分别交1C ，2C 于,A B 两点，求||||OA OB 的最大值. 23．（改编）（本小题满分10分）选修4——5：不等式选讲已知函数()2121f x x x =++-，不等式()4f x ≤的解集为M ． （Ⅰ）求M ；（Ⅱ）证明：当,a b M ∈时，2a b a b ++-≤．数学试题（理科）参考答案一、选择题1——5 DABBC ； 6——10 CDCAD ； 11——12 CB. 二、填空题（本大题共4小题，每小题5分，共20分．）13.165； 14．4p； 15.185；三、解答题17.解:（Ⅰ）当1n =时，11344a a =-，得14a =，…………………………………………1分当2n ≥时，11344n n S a --=-，∴1344n n n a a a -=-，即14n n a a -= …………………4分 故{}n a 是以4为首项，4为公比的等比数列，∴4nn a =；…………………………………6分（Ⅱ）2log 2n n b a n ==，2222222121111(1)4(1)4(1)n n n b n n n n n ⎛⎫++==- ⎪+++⎝⎭，...............9分 2221111(14223n T =-+-+ (22222)11112)1(1)4(1)4(1)n nn n n n ⎛⎫++-=-= ⎪+++⎝⎭.…………12分 18．（本小题满分12分）解：（Ⅰ）列联表如图所示，……………………………2分22120(18382242)0.6 2.70660604080K ⨯⨯-⨯==<⨯⨯⨯，所以不能在犯错误的概率不超过90%的前提下认为“成绩与班级有关系”；…………………………………………………………6分 （Ⅱ）由题意可得成绩在[)100,120的概率45P =, X 的取值依次为0,1,2,3,且23,5XB ⎛⎫ ⎪⎝⎭，所以()3032270C 15125P X ⎛⎫==-= ⎪⎝⎭， ()121322541C 155125P X ⎛⎫⎛⎫==-= ⎪⎪⎝⎭⎝⎭，()22322362C 155125P X ⎛⎫⎛⎫==-= ⎪ ⎪⎝⎭⎝⎭，()333283C 5125P X ⎛⎫=== ⎪⎝⎭，…10分 所以X 的分布列为26()355E X =⨯=，2318()35525D X =⨯⨯=．……………………………………………12分 19．（本小题满分12分）解：（Ⅰ）∵PB PD =，O 是BD 的中点，∴PO ⊥BD ，………………………………1分∵BA AD =，BA ⊥AD ，∴OA OB OD ==，AO BD ⊥，………………………………2分 ∵PA PD =，PO PO =，∴PAO PDO ∆≅∆，∴90POA POD ∠=∠=，即PO AC ⊥，……………………………………………………4分 又AC BD ⊥，PO BD O =，∴AC ⊥面PBD ，∴AC ⊥BD ；………………………6分（Ⅱ）由（Ⅰ）知，PO ⊥BD ，PO ⊥OA ，∴PO ⊥平面ABCD ，以O 为坐标原点，OB 、OC 、OP 分别为x ，y ，z 轴建立如图所示的空间直角坐标系，…………………………7分则0,0,3P （），02,0A -（，），0,10C （,），2,0,0D -（），设(01)PE tPD t uur uu u r=<<，则030AC =(,,)，(2,0,33)AE AP PE t t u u u r u u u r u u r=+=--，设平面EAC的法向量(,,)x y z m =，则302(33)0y tx t z ì=ïïíï-+-=ïî，取33x t =-，则2z t =， ∴(33,0,2)t t =-m ，取平面PAC 的一个法向量1,(0)0,=n ，………………10分∴cos ,m n <>==，解得13t =， ∴存在点E ，使得二面角E AC P --，E 为靠近P 的三等分点.……12分20．（本小题满分12分）解：（Ⅰ）设11(,)P x y ，22(,)Q x y ，00(,)M x y ，则2211221x y a b +=，2222221x y a b+=，………………1分两式相减得222212122211()()0x x y y a b -+-=，即1212222212121110l OM k ky y y y a b x x x x a b-++创=+=-+， 即2214l OM b k k a =-=-，∴224a b =；…………………………………………………………3分又221314a b+=，解得24a =，21b =，∴椭圆C 的方程为2214x y +=；………………4分 （Ⅱ）当直线l 的斜率不存在时，设l 的方程为x t =，则12x x t ==，21214t y y =-， ∵OP OQ ⊥，∴12120x x y y +=，∴22104t t +-=，解得t =?，此时点O 到直线l的距离d =；…………………………………………………………6分当直线l 的斜率存在时，设l ：y kx m =+，代入椭圆方程得222(14)8440k x kmx m +++-=，∵0∆>，∴22410k m -+>，且122814kmx x k +=-+，21224414m x x k -=+，22221212121224()()()14m k y y kx m kx m k x x km x x m k -=++=+++=+. ∵OP OQ ⊥，∴12120x x y y +=，即2222244401414m m k k k --+=++，∴22514m k +=， 由225114m k +=≥和22410k m -+>，得245m >即可， ∴点O 到直线l的距离d = 综上所述，点O 到直线l的距离是定值，且d =……………………………………12分 21．（本小题满分12分）解：（Ⅰ）令ln 1()x x xφ+=，由题意知()y x φ=的图像与y a =的图像有两个交点， 2ln '()x x xφ-=，当01x <<时，'()0x φ>，∴()x φ在(0,1)上单调递增； 当1x >时，'()0x φ<，∴()x φ在(1,)+∞上单调递减；∴max ()(1)1x φφ==，又∵0x →时，()x φ→-∞，∴(0,1)x ∈时，()(,1)x φ∈-∞，又∵1x >时，()(0,1)x φ∈，综上可知，当且仅当(0,1)a ∈时，y a =与()y x φ=的图像有两个交点，即函数()f x 有两个零点；……………………………………………………………………………………………6分 （Ⅱ）因为函数()g x 有两个极值点，由'()ln 10g x x ax =+-=，得ln 10x a x +-=有两个不同的根1x ，2x （设12x x <）， 由（Ⅰ）知，1201x x <<<，01a <<，且ln 1(1,2)i ix a i x +==， 且函数()g x 在1(0,)x ，2(,)x +∞上单调递减，在12(,)x x 上单调递增， 则21()ln 22i i i i a g x x x ax =-+ln 111ln (1,2)222i i i i ix x x x i x +=-+=， 令11ln 1()ln 222t h t t t t t +=-+，则2ln 11ln '()222t t h t t +-=-+22(1)ln 02t t t-=≥， 所以函数()h t 在(0,)+∞上单调递增，故()()110g x g <=，()()210g x g >=，又0x →，()02a g x →>；x →+∞，()g x →-∞， 所以函数()g x 恰有三个零点. ………………………………………………………………12分22.解：（Ⅰ）曲线1C 的普通方程为()2224x y -+=，所以极坐标方程为4cos ρθ=，……3分 2C 的直角坐标方程为2x y +=；……………………………………………………………5分 （Ⅱ）设A 、B 两点的极坐标分别为()()12,,,A B ραρα，则14cos ρα=，22cos sin ραα=+，…………………………………………………………7分故12||2cos (cos sin ))1||4OA OB ρπααααρ==+=++， 当8πα=时，||||OA OB1.……………………………………………………10分 23．（本小题满分10分）解：（Ⅰ）11112222442444x x x x x ⎧⎧⎧≥-<<≤-⎪⎪⎪⎨⎨⎨⎪⎪⎪≤≤-≤⎩⎩⎩或或，解得11x -≤≤，即[]1,1M =-；……………5分（Ⅱ）当,a b M ∈时，即11,11a b -≤≤-≤≤，得1,1a b ≤≤，当()()0a b a b +-≥时，22a b a b a ++-=≤，………………………………………7分 当()()0a b a b +-<时，22a b a b b ++-=≤，………………………………………9分 所以2a b a b ++-≤；………………………………………………………………………10分 另解：当,a b M ∈时，即11,11a b -≤≤-≤≤，得1,1a b ≤≤()()222222222224,224,a a b a b a b a b a b b a b ⎧≥++-=++-=⎨<⎩……………………………………7分 由于221,1,a b ≤≤则2244,44a b ≤≤，故()24a b a b ++-≤，……………………………9分 所以2a b a b ++-≤．………………………………………………………………………10分。

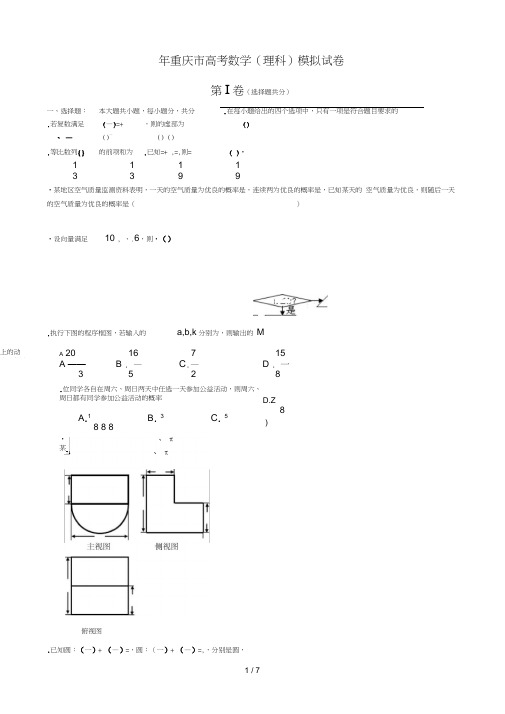
年重庆市高考数学（理科）模拟试卷第I 卷（选择题共分）一、选择题： 本大题共小题，每小题分，共分 .在每小题给出的四个选项中，只有一项是符合题目要求的.若复数满足 (—)=+ ，则的虚部为()、 — ()—() ().等比数列{}的前项和为.已知=+ ,=,则=( )•1 1 1 1 3 3 9 9•某地区空气质量监测资料表明，一天的空气质量为优良的概率是，连续两为优良的概率是，已知某天的 空气质量为优良，则随后一天的空气质量为优良的概率是（）•设向量满足10 , 、.6，则•（）.执行下图的程序框图，若输入的a,b,k 分别为，则输出的 MA 2016 7 15 A ——B . —C .—D . 一 3528.位同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日都有同学参加公益活动的概率 A .1B . 3C . 58 8 8•某D.Z8 ).已知圆：（一）+ （—）=，圆：（一）+ （—）=,，分别是圆，上的动点，为轴71俯视图几何函数的三视图如图所示，则该几何的体积为、n已知点（—），（），（），直线=+ （ ＞）将△分割为面积相等的两部分，则的取值范围是 （）.AB 1 丄 A B2, OB ； = O B2= , AP = AB ； +A B 2.若 OP v 1 ,则 OA 的取值范围是(2第口卷（非选择题 共分）、填空题 本大题共小题，考生作答小题，每小题分，共分，把答案填在答题卡相应位置上（x-y ）（x ，y ）8的展开式中x 2y 2的系数为•（用数字填写答案）函数f x =sin x 2：「：;-2sin cos x 亠门］的最大值为若函数（）（—）（++ ）的图像关于直线—对称，则 （）的最大值是考生注意：、、三题为选做题，请从中任选两题作答，若三题全做，则按前两题给分 .如图，在△中，/ = °,/ = °,=，过作△的外接圆的切线，丄，与外接圆交于点,x = 2 +t一.已知直线I 的参数方程为丿（t 为参数），以坐标原点为极点， x 正半轴为y =3+t极轴线l 与曲线C 的公共点的极经 r 二..若关于实数的不等式- + + ＜无解，则实数的取值范围是.三、解答题：本大题共小题，共分 .解答应写出文字说明，证明过程或演算过程 （本小题满分分）已知函数f （x ）=』3si ＞0,—》＜工i 的图像关于直线x＜ 2 2丿两个最高点的距离为 -：.（）求•，和::的值；5^2-4417 -1 6-2^2 41•（） 在平面上,_323对称，且图像上相邻()若f.（本小题满分分）某商场举行的“三色球”购物摸奖活动规定：在一次摸奖中，摸奖者先从装有个红球与个白球的袋中任意<a摸出个球，再从装有个蓝球与个白球的袋中任意摸出个球. 三等奖如下：其余情况无奖且每次摸奖最多只能获得一个奖级.（）求一次摸奖恰好摸到个红球的概率；（）求摸奖者在一次摸奖中获奖金额的分布列与期望根据摸出个球中红球与蓝球的个数，设一、.（本小题满分分）如图，三棱柱中，，，/（I ）证明丄；（n ）若平面丄平面，，求直线 与平面所成角的正弦值。

重庆市铜梁中学2025届高考数学全真模拟密押卷考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。

选择题必须用2B 铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．函数()()sin f x A x ωϕ=+（0A >，0>ω， 2πϕ<）的部分图象如图所示，则,ωϕ的值分别为（ ）A ．2，0B ．2，4π C ．2， 3π-D ．2，6π 2．已知函数()f x 的定义域为[]0,2，则函数()()282x g x f x =+-的定义域为（ ） A ．0,1 B ．[]0,2 C ．[]1,2D ．[]1,33．已知a R ∈若（1-ai ）( 3+2i )为纯虚数，则a 的值为 （ ） A ．32-B ．32C ．23-D ．234．《九章算术》“少广”算法中有这样一个数的序列：列出“全步”（整数部分）及诸分子分母，以最下面的分母遍乘各分子和“全步”，各自以分母去约其分子，将所得能通分之分数进行通分约简，又用最下面的分母去遍乘诸（未通者）分子和以通之数，逐个照此同样方法，直至全部为整数，例如：2n =及3n =时，如图：记n S 为每个序列中最后一列数之和，则6S 为（ ） A ．147B ．294C ．882D ．17645．已知当m ，[1n ∈-，1)时，33sin sin22mnn m ππ-<-，则以下判断正确的是( )A ．m n >B ．||||m n <C ．m n <D ．m 与n 的大小关系不确定6．()f x 是定义在()0,∞+上的增函数，且满足：()f x 的导函数存在，且()()f x x f x '<，则下列不等式成立的是（ ） A ．()()221f f < B ．()()3344ff <C ．()()2334f f <D ．()()3223f f <7．执行如图所示的程序框图，输出的结果为（ ）A ．193B ．4C ．254D ．1328．已知抛物线C ：214y x =的焦点为F ，准线为l ，P 是l 上一点，直线PF 与抛物线交于A ，B 两点，若2PA AF =，则AB 为( )A ．409B ．40C ．16D ．1639． “2b =”是“函数()()2231f x b b x α=--（α为常数）为幂函数”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件10．波罗尼斯（古希腊数学家，的公元前262-190年）的著作《圆锥曲线论》是古代世界光辉的科学成果，它将圆锥曲线的性质网罗殆尽，几乎使后人没有插足的余地．他证明过这样一个命题：平面内与两定点距离的比为常数k （k ＞0，且k≠1）的点的轨迹是圆，后人将这个圆称为阿波罗尼斯圆．现有椭圆2222x y a b+=1（a ＞b ＞0），A ，B 为椭圆的长轴端点，C ，D 为椭圆的短轴端点，动点M 满足MA MB=2，△MAB 面积的最大值为8，△MCD 面积的最小值为1，则椭圆的离心率为（ ）A ．3B ．3C ．2D ．211．设1F ，2F 是双曲线()2222:10,0x yC a b a b-=>>的左，右焦点，O 是坐标原点，过点2F 作C 的一条渐近线的垂线，垂足为P ．若1PF =，则C 的离心率为（ ）AB C ．2D ．312．二项式22)nx+的展开式中只有第六项的二项式系数最大，则展开式中的常数项是( ) A ．180B ．90C ．45D ．360二、填空题：本题共4小题，每小题5分，共20分。

重庆市铜梁一中等三校2024届高三10月联考数学试卷学校：___________姓名：___________班级：___________考号：___________一、选择题1．设集合,,则( )A. B. C.或 D.R2．已知命题,,那么是( )A., B.,C., D.,3．为了得到函数的图象,只要把函数图象上所有的点( )4．( )5．已知为了破解某密码,在最坏的情况下,需要进行2512次运算．现在有一台计算机,每秒能进行2.5×1014次运算,那么在最坏的情况下,这台计算机破译该密码所需的时间大约A.秒 B.秒 C.秒 D.秒6．在中,,则角B 的最大值为( )7．对于函数,有下列结论：①最小正周期为;②最大值为2;③减区间为;④对称中心为．则上述结论正确的个数是( )A.1B.2C.3D.4{}1A x x =>{}2B x x =≤A B = ∅{}12x x <≤{1x x ≤}2x >1:p x ∃>210x ->p ⌝1x ∀>210x ->1x ∀>210x -≤1x ∃>210x -≤1x ∃≤210x -≤2sin 3y x =π2sin 35y x ⎛⎫=+ ⎪⎝⎭22π5πsin sin 1212-=1393.1610⨯1391.5810⨯1401.5810⨯1403.1610⨯ABC △AC =4=2()(sin cos )2f x x x x =++π7π,ππ()1212πk k k ⎡⎤++∈⎢⎥⎣⎦Z ππ,0()6k k ⎛⎫-+∈ ⎪⎝⎭Z8．已知函数的解集为( )A. B. C. D.二、多项选择题9．已知，，且，则下列结论中正确的是( )A.有最小值3有最大值410．已知正八边形ABCDEFGH ,其中,则( )B.11．已知定义在R上偶函数,满足,则下列结论正确的是( )A.的图象关于对称B.C.若函数在区间上单调递增,则在区间上单调递增D.若函数在区间上解析式为,则在区间上的解析式为12．已知函数及其导函数满足,且,则( )A.在上单调递增B.在上有极小值三、填空题的的()f x =()e x f x >()0,11,1e ⎛⎫ ⎪⎝⎭()1,e ()1,+∞0x >0y >3x y +=ln ln x y +2y +22OA =0OE OG ++= OA OD -⋅= EH += 4GH +=+ ()f x ()()22f x f x +-=()f x 1x =()()4f x f x +=()f x []0,1()f x []2021,2022()f x ()0,1()ln 1f x x =+()f x ()2,3()()ln 11f x x =-+()f x ()f x '()()()2ln 1xf x f x x x '-=+()10f =()f x ()1,+∞()f x 1,12⎛⎫ ⎪⎝⎭()f x13．设,则“”是“”成立的___________条件．（填“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”）14．在边长为4的等边中,已知,点P 在线段上,且___________.15．函数点处切线方程为___________.16．已知函数,则不等式的解集是____________.四、解答题17．已知函数的图像上相邻两条对称轴的距的最大值与最小值之差为1,且的图像的一个对称中心是．（1）求函数的解析式;（2）若方程在区间上有解,求实数m 的取值范围．18．已知函数的图象关于原点对称．（1）求a 的值;（2）当时,恒成立,求实数k的取值范围．19．如图,在四边形中,,（1）求角A 的值;（2）若,,,求四边形的面积20．已知函数.（1）求的单调区间;的x ∈R cos 0x =sin 1x =ABC △23AD AB = CD 12AP mAC AB =+ 1()e ln(1)x f x x +=-(0,(0))f ()11x x f x e e x --=-+()()2432f x f x -+-≤()()πsin ,0,0,2f x A x A ωφωφ⎛⎫=+>>< ⎪⎝⎭()f x ()f x 3π,016⎛⎫ ⎪⎝⎭()f x ()f x m =π0,4⎡⎤⎢⎥⎣⎦(2))(2lna a x f x x -=∈-R [3,5]x ∈()ln()f x x k <+ABCD BD AD <sin cos 36ππA A ⎛⎫⎛⎫-+= ⎪ ⎪⎝⎭⎝⎭AB =3AD =1CD =2C CBD ∠=∠ABCD ()2ln 3f x x x =+()f x（2）求过点的切线方程.21．在中，角A ，B ，C 所对的边分别为a ，b ，c ，（1）求角C 的大小；（2）若22．已知函数,.（1）讨论的单调性并求极值.（2）设函数（为的导函数）,若函数在内有两个不同的零点,求实数a 的取值范围.()f x 1(,0)2-ABC △tan C =ABC △()21f x ax a =--()e e x g x x =-()g x ()()()h x g x f x '=-()g x '()g x ()h x ()0,1参考答案1．答案：D 解析：因为,,所以.故选：D.2．答案：B 解析：已知命题,,则为：,.故选：B.3．答案：D 解析：因为,所以把函数图象上的所的图象.故选:D.4．答案：D解析：由题意知,所以故选：D.5．答案：B解析：设在最坏的情况下,这台计算机破译该密码所需的时间为x 秒,则所以,,所以．故选：B.6．答案：A{}1A x x =>{}2B x x =≤A B =R 1:p x ∃>210x ->p ⌝1x ∀>210x -≤ππ2sin 32sin 3155y x x ⎡⎤⎛⎫==-+ ⎪⎢⎥⎝⎭⎣⎦π2sin 35y x ⎛⎫=+ ⎪⎝⎭2sin 3y x =5ππ5πsin cos()12212=-=2222π5ππππsin sin sin cos cos 121212126-=-=-=x =51251214142lg lg lg 2lg(2.510)512lg 2(lg 2513)2.510x ==-⨯=-+⨯512lg 2(2lg 513)512lg 2(22lg 2)13514lg 215139.2=-+=---=-≈139.21390.2139101010 1.5810x ≈=⨯≈⨯解析：设,则,由余弦定理可得当且仅当,则.故选：A.7．答案：B解析：.,①正确;,时,②错误;,,,因此减区间为,③正确;令,,解得,此时,故对称中心为,故④错误.所以,上述结论正确的个数是2个.故选：B.8．答案：B解析：函数因,则不等式成立必有,即令时,,当时,,因此,函数在上单调递减,在上单调递增,又,AB x =0x >222281cos 288AB BC AC x x B AB BC x x +-+===+≥=⋅x =πB <<π04B <≤()()222sin cos 2sin cos 2sin cos 2f x x x x x x x x x=+=+++1sin 2212sin 2π3x x x ⎛⎫=+=++ ⎪⎝⎭2ππ2T ==23ππ2πx k +=+k ∈Z ()max 3f x =π3π2π22π32k x k +≤+≤+k ∈Z 7πππ12k x k +≤≤+k ∈Z ()π7ππ,π1212k k k ⎡⎤++∈⎢⎥⎣⎦Z π2π3x k +=k ∈Z π6x =-+∈Z ()1f x =ππ,162k ⎛⎫-+ ⎪⎝⎭k ∈Z ()f x =21ln e e ()e e 1ln 1ln x x x x f x x x +>⇔>⇔>++0x >()e x f x >1ln 0x +>x >()g x =x >()x '=1x <<()0g x '<1x >()0g x '>()g x 1(,1)e(1,)+∞()e (1ln )()x f x g x g x >⇔+>当时,,于是得,即,令,当时,,函数在上单调递减,,,因此,无解,时,,于是得,即,此时,函数在上单调递增,,,不等式解集为,所以不等式的解集为.故选：B.9．答案：BD解析：对于A 选项，因为，，且，所以由当且仅当，当且仅当时等号成立，故B 正确；对于C 选项，因为，时等号成立，故C 错误对于D 选项，因为，，令，解得或（舍），令，解得，令，解得，故，此时，，故D 正确故选：BD10．答案：ABC解析：分别以,所在的直线为x 轴和y 轴,建立如图所示的平面直角坐标系,1x >ln 11x +>1ln x x +>1ln 0x x +->()1ln h x x x =+-1x >1()10h x x'=-<()h x (1,)+∞1x ∀>()(1)0h x h <=1ln x x +>1x <<0ln 11x <+<1ln x x +<1ln 0x x +-<1()10h x x'=->()h x 1(,1)e 1(,1)e x ∀∈()(1)0h x h <=1ln x x +<1(,1)e()e x f x >1(,1)e0x >0y >3x y +=3x y +=≥xy ≤x y ==ln ln ln x y xy +=≤2222233(3)69(2)33222x y x x x x +=+-=-+=-+≥2,1x y ==41()41453333333x y y x x y x y ⎛⎫++=+++≥+= ⎪⎝⎭1y ≥=2x =1y =2232()(3)3f y xy y y y y ==-=-+(03)y <<2()360f y y y '=-+=2y =0y =2()360f y y y '=-+>02y <<2()360f y y y '=-+<23y <<32max ()(2)2324f y f ==-+⨯=1x =2y =HD BF易知作,垂足为M ,则．因为,所以,同理可得其余各点坐标,,,,,,故A 正确;,,,所以,故C 正确;,,,故选：ABC.11．答案：BC解析：对于A 选项,因为,则函数的图象关于点对称,A 错;对于B 选项,因为且函数为偶函数,所以,可得,所以,,所以,对任意的,,B 对;对于C 选项,因为,若函数在区间上单调递增,则在区间上单调递增,C 对;对于D 选项,当时,,,所以,,D 错.360458AOH HOG AOB EOF FOG DOE COB COD ︒∠=∠=∠=∠=∠=∠=∠=∠==︒AM HD ⊥OM AM =2OA =OM AM ==(A (0,2)B -E (G (2,0)D (2,0)H -(0,(0OE OG =-++=++ 2(0·OA OD =+⨯=- (2AH =- (2EH =- (4,0)AH EH +=- 4AH EH +== (2AH =- (2GH =-+ (4AH GH +=-+ 4AH GH =+=- ()()22f x f x +-=()f x ()1,1()()22f x f x +-=()f x ()()22f x f x +-=()()22f x f x ++=()()22f x f x +=-x ∈R ()()4f x f x +=()()4f x f x +=()f x []0,1()f x []2021,2022()2,3x ∈()21,0x -∈-()20,1x -∈()()()()()22222ln 211ln 2f x f x f x x x =--=--=--+=--⎡⎤⎣⎦故选：BC.12．答案：ABD解析：设,所以（C 为常数）,所以,又,所以,所以,,当时,,单调递减,当,单调递增,所以在因为,所以在上有极小值可知A,B 都正确．,,当,单调递减,当,单调递增,所以的极小值即最小值为,当时,,,所以,当时,,,所以,()g x =()()()2ln 1xf x f x g x x x'-'==+()ln g x x x C =+()()2ln f x xg x x x Cx ==+()10f =0C =()2ln f x x x =()()2ln 1f x x x '=+0x <<()0f x '<()f x x >()0f x '>()f x ()f x x =1<<1<<()f x 1,12⎛⎫ ⎪⎝⎭()ln g x x x =()ln 1g x x '=+0x <<()0x '<()g x x >()0x '>()g x ()g x 1e g ⎛⎫= ⎪⎝⎭()()()1ln f x f x x x x x-=-01x <<10x -<ln 0x <()()0f x f x x ->1x >10x ->ln 0x >()()0f x f x x->而当时,,所以故D 正确．故选：ABD.13．答案：必要不充分解析：当时,,显然不一定成立;反之,,则必然成立．故答案为：必要不充分.解析：因为,所以,又,即,因为点P 在线段上,所以P ,C ,D 三点共线,由平面向量三点共线定理得,,即所以,又是边长为4的等边三角形,.15．答案：解析：,所以切点为,,,所以切线的斜率为.故该切线方程为,即.故答案为：.16．答案：解析：构造函数,那么是单调递增函数,1x =()()1101f f -=()f x -cos 0x =sin 1x =±sin 1x =sin 1x =cos 0x =23AD AB = 32AB AD = 12AP mAC AB =+ 1324AP mAC AB mAC AD =+=+ CD 314m +=m =1142AP AC AB =+ ABC △22211111cos 60421644AC AB AC AC AB AB ⎛⎫+=++ ⎪⎝⎭ 1111164416716424=⨯+⨯⨯⨯+⨯=e 0x y +=(0)0f =(0,0)111()e ln(1)e 1x x f x x x ++'=-+⋅- (0)e f '∴=-e -e y x =-e 0x y +=e 0x y +=[1,)+∞111()()1(1)x x g x f x e x e --=-=-+-()g x且向左移动一个单位得到,的定义域为R ,且,所以为奇函数,图象关于原点对称,所以图象关于对称．不等式等价于,等价于,结合单调递增可知,,所以不等式的解集是．故答案为：．17．答案：（1）（2）解析：（1）因为函数.又.因为的最大值与最小值之差为1,故,又由的图像的一个对称中心是,故,则故当时,,故.（2）,,,,若方程在区间上有解,则,1()(1)x x h x g x e x e=+=-+()h x 1()()xx hx e x h x e-=--=-()h x ()g x (1,0)()()2432f x f x-+-≤(2)1(43)10f x f x --+--…()()2430g x g x -+-≤()()()224332g x g x g x ∴-≤--=-⎡⎤⎣⎦()g x 232x x -≤-1x ∴≥()()2432f x f x -+-≤[1,)+∞[1,)+∞()1πsin 424f x x ⎛⎫=+ ⎪⎝⎭12⎡⎤⎢⎥⎣⎦(f x π4=0ω>=4=()f x 21A =A =()f x 3π,016⎛⎫⎪⎝⎭()3π4πZ 16k k φ⨯+=∈(3ππ,Z 4k k φ=-∈1k =π4φ=()1πsin 424f x x ⎛⎫=+ ⎪⎝⎭π0,4x ⎡⎤∈⎢⎥⎣⎦ ππ5π4,444x ⎡⎤∴+∈⎢⎥⎣⎦πsin 44x ⎡⎤⎛⎫∴+∈⎢⎥ ⎪⎝⎭⎣⎦()12f x ⎡⎤∴∈⎢⎥⎣⎦()f x m =π0,4⎡⎤⎢⎥⎣⎦12m ⎡⎤∈⎢⎥⎣⎦故实数m 的取值范围是18．答案：（1）-1（2）解析：（1）因为函数的图象关于原点对称,所以函数,所以,则,解得,当时,当时,,且,满足题意,综上,可得a 的值为-1;（2）由,得恒成立,即当,恒成立,令显然在恒成立,所以在上单调递减,则的最大值为,所以,即实数k 的取值范围为．解析：（1）12⎡⎤⎢⎥⎣⎦(2,)+∞()f x ()f x =()()f x f x -=-22ln ln 22ax ax x x +-=----22ln 022ax ax x x +-⎛⎫⋅= ⎪---⎝⎭1=1a =±1a =()lnf x =1a =-()lnf x =,2)(2,)-∞-+∞ 22()lnln ()22x x f x f x x x ---===---+()ln()f x x k <+2ln ln()2xx k x +<+-[3,5]x ∈22xk x x +>--2()2x g x x x +=-=-22(2)4()(2)x g x x ---'=-()0g x '<[3,5]x ∈()g x [3,5]x ∈()g x (3)2g =2k >(2,)+∞πππππ2sin cos cos cos 3636A A A A ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-+=--+ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦因为解得,得（2）在中,,在,,,,的面积为20．答案：（1）的单调递增区间是：,单调递减区间是：（2）解析：(1)的定义域为,,所以的单调递增区间是：,单调递减区间是：.（2）由题意可得点不在曲线上,设切点为,因为,2cos 21cos cos ππ1π324326A A A ⎛⎫++ ⎪⎛⎫⎛⎫⎝⎭=++== ⎪ ⎪⎝⎭⎝⎭=⇒0πA <<π23A <+<π32A ∴+=2A +=A =A =AD <A <π6A ∴=ABD △BD ==△sin C CBD =⇒∠=∠2sin cos in 2CBD CBD CB C D C BD ∠=∠⇒∠∠=∠ π03CBD <∠< cos CBD ∴∠=π6CBD =C ∴∠=CDB =ABCD 1π13sin 1262ABD BCD S S S =+=⨯+=V V ()f x 1(,)e +∞1(0,e12212y x x ⎛⎫=+=+ ⎪⎝⎭()f x (0,)+∞()2ln 2f x x '=+()0f x x '>⇒>()00f x x '<⇒<<()f x 1(,)e +∞1(0,e 1(,0)2-()f x 00(,)x y ()2ln 2f x x '=+所以所求切线的斜率所以.因为点是切点,所以,所以,即.设,明显在上单调递增,且,所以有唯一解,则所求切线的斜率,故所求切线方程为.21．答案：（1）（2）解析：（1）因为.即，得.所以或(不成立，舍去)，从而，又，所以（2）由（1）知是锐角三角形，则因为所以设，因为，02ln 2k x =+=000002ln 2ln 1y x x x x =+++00(,)x y 0002ln 3y x x =+0000002ln 2ln 12ln 3x x x x x x =++++002ln 20x x -=+()2ln 2f x x x +-=()f x (0,)+∞()10f ＝002ln 20x x -=+01x =2k =12212y x x ⎛⎫=+=+ ⎪⎝⎭π3C =tan C ==sin cos sin cos cos sin cos sin C A C B C A C B +=+sin cos cos sin cos sin sin cos C A C A C B C B -=-sin()sin()C A B C -=-C A B C -=-π()C A B C -=--2C A B =+πA B C ++=C =A B +=ABC π0,22ππ0,32A A ⎧<<⎪⎪⎨⎪<-<⎪⎩A <<21sin sin sin sin 22sin ABC c AB S abC A B C ==⋅==△2c =sin sin y A B =2π3B A =-所以，，从而，即，所以边c 的取值范围是.22．答案：（1）见解析（2）解析：（1）因为在R 上单调递增,所以当时,当时,所以在上单调递减,在上单调递增,所以的极小值为,无极大值.（2）因为,所以,当时,,所以当或时,在上单调,至多只有一个零点,不满足题意,当时,由可得,当时,,单调递减,当时,,单调递增,所以要使函数在内有两个不同的零点,则有,由可得,下面证明当时,令,则,2π1111π1sin sin sin sin 2cos 2sin 23244264y A A A A A A A A ⎫⎛⎫⎛⎫=-=+=+-=-+⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎭A <<π26A <-<13,24y ⎛⎫∈ ⎪⎝⎭2[4,6)c =c ∈()e 2,1-()e e x g x '=-1x <()0g x '<1x >()0g x '>()g x (),1-∞()1,+∞()g x ()10g =()()()()e e 21e 2e 1x x h x g xf x ax a ax a '=-=----=--++()e 2x h x a '=-()0,1x ∈()e 1,e x ∈21a ≤2e a ≥()h x ()0,112e a <<e 20x a -=()ln 2x a =()()0,ln 2x a ∈()0h x '<()h x ()()ln 2,1x a ∈()0h x '>()h x ()h x ()0,1()()()()00ln 2010h h a h ⎧>⎪<⎨⎪>⎩()()0010h h >⎧⎪⎨>⎪⎩e 21a -<<e 21a -<<()()ln 20h a <()()()()ln 232ln 2e+1m a h a a a a ==--()()12ln 2m a a '=-所以当时,,单调递增,当时,,单调递减,所以,所以当时,综上：实数a 的取值范围为.e a ⎛∈- ⎝()0m a '>()ma a ⎫∈⎪⎪⎭()0m a '<()m a ()maxe 10m a m ==+<e 21a -<<()()ln 20h a <()e 2,1-。

2015届重庆市铜梁中学校高三下学期模拟测试（一）数学（理）试题一、选择题：本大题共10小题，每小题5分，共50分。

1．已知集合2{1},{M x y x N y y ==+==，则M N = （ ）A ．{(0,1)}B ．{1}x x ≥-C ．{0}x x ≥D ．{1}x x ≥2．设复数z 满足()(1)1,(z i i i i ++=-是虚数单位），则z =（ ）A ．1B ．2C ．3D ．43．命题“若1,x >则22x >”的否定是（ ）A ．21,2x x ∀>≤B ．21,2x x ∃>>C ．21,2x x ∃>≤D ．21,2x x ∃≤>4．若22nx ⎫⎪⎭展开式中只有第六项的二项式系数最大，则展开式中的常数项是（ ）A ．180B ．120C ．90D ．455．一个圆锥被过其顶点的一个平面截去了较少的一部分几何体，余下的几何体的三视图如下图，则余下部分的几何体的体积为( )A ．169πB ． 169π+C ．89π+D ．163π+6．若抛物线()2:20C y px p =>上一点到焦点和x 轴的距离分别为5和3，则此抛物线的方程为（ ）A ．22y x = B ．)24y x =-C ．22y x =或218y x =D ．23y x =或)24y x =-7．如图所示的算法中，令tan a θ=，sin b θ=，cos c θ=，,,a b c 若在集合π3π,44θθθ⎧-<<≠⎨⎩ππ0,,42⎫⎬⎭中，给θ取一个值，,,a b c 输出的结果是sin θ，则θ的值所在范围是（ ）A ． π,04⎛⎫- ⎪⎝⎭B ．π0,4⎛⎫ ⎪⎝⎭C ．ππ,42⎛⎫⎪⎝⎭D ．π3π,24⎛⎫ ⎪⎝⎭8．已知菱形ABCD 的边长4，150ABC ∠= ，若在菱形内任取一点，则该点到菱形的四个顶点的距离均大于1的概率为（ ） A ．4πB ．14π-C ．8πD ．18π-9．已知ABC ∆的三个内角,,A B C 所对的边分别为,,a b c ，若1b a c b -=-=且2C A =，则cos C =（ ） A ．12B ．14C ．16D ．1810．已知函数221(1)()(2)1(1)x x f x x x ⎧-⎪=⎨--+⎪⎩＜≥，则关于x 的方程1(1)f x a x +-=的实根个数最多为（ ）A ．5个B ．6个C ．7个D ．8个第Ⅱ卷（非选择题，共100分）二、填空题：本大题共6小题，考生作答5小题，每小题5分，共25分。

年重庆市高考数学（理科）模拟试卷第Ⅰ卷（选择题 共分）一、选择题：本大题共小题，每小题分，共分.在每小题给出的四个选项中，只有一项是符合题目要求的. . 若复数满足 (－)＝＋ ，则的虚部为 ( )、－ （）－ （） （）. 等比数列{}的前项和为.已知＝＋，＝，则＝( )． ．13 ．13- ．19 ．19-．某地区空气质量监测资料表明，一天的空气质量为优良的概率是，连续两为优良的概率是，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是（ ）. . . . ．设向量满足10，6，则⋅ ( )． ． ． ．. 执行下图的程序框图，若输入的,,a b k 分别为，则输出的MA .203B .165C .72D .158. 位同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日都有同学参加公益活动的概率A .18B .38C .58D .78 ．某几何函数的三视图如图所示，则该几何的体积为( )、π 、π、π 、π. 已知圆：(－)＋(－)＝，圆：(－)＋(－)＝，，分别是圆，上的动点，为轴上的动点，则＋的最小值为( )．侧视图俯视图．41-．6-. 已知点(－)，()，()，直线＝＋(＞)将△分割为面积相等的两部分，则的取值范围是( )．．()．1122⎛⎫- ⎪ ⎪⎝⎭．1123⎛⎤- ⎥ ⎝⎦ ．11,32⎡⎫⎪⎢⎣⎭ . 在平面上，1AB ⊥2AB ，1OB ＝2OB ＝，AP ＝1AB ＋2AB .若OP ＜12，则OA 的取值范围是( )．．0,2⎛ ⎝⎦．22⎛ ⎝⎦．2⎛ ⎝．2⎛ ⎝ 第Ⅱ卷（非选择题 共分）二、填空题 本大题共小题，考生作答小题，每小题分，共分，把答案填在答题卡相应位置上.. 8()()x y x y -+的展开式中22x y 的系数为 .(用数字填写答案) . 函数()()()sin 22sin cos f x x x ϕϕϕ=+-+的最大值为.. 若函数()(－)(＋＋)的图像关于直线－对称，则()的最大值是.考生注意：、、三题为选做题，请从中任选两题作答，若三题全做，则按前两题给分.．如图，在△中，∠＝°，∠＝°，＝，过作△的外接圆的切线，⊥，与外接圆交于点，则的长为．.已知直线l 的参数方程为⎩⎨⎧+=+=t y t x 32（t 为参数），以坐标原点为极点，x 正半轴为极轴线l 与曲线C 的公共点的极经=ρ..若关于实数的不等式－＋＋＜无解，则实数的取值范围是．三、解答题：本大题共小题，共分.解答应写出文字说明，证明过程或演算过程..（本小题满分分）已知函数()()⎪⎭⎫ ⎝⎛<≤->+=220sin 3πϕπωϕω，x x f 的图像关于直线3π=x 对称，且图像上相邻两个最高点的距离为π.（）求ω和ϕ的值； （）若⎪⎭⎫ ⎝⎛<<=⎪⎭⎫ ⎝⎛326432παπαf ，求⎪⎭⎫ ⎝⎛+23cos πα的值. .（本小题满分分）某商场举行的“三色球”购物摸奖活动规定：在一次摸奖中，摸奖者先从装有个红球与个白球的袋中任意摸出个球，再从装有个蓝球与个白球的袋中任意摸出个球．根据摸出个球中红球与蓝球的个数，设一、二、三等奖如下：其余情况无奖且每次摸奖最多只能获得一个奖级． ()求一次摸奖恰好摸到个红球的概率； ()求摸奖者在一次摸奖中获奖金额的分布列与期望()．.(本小题满分分)如图，三棱柱中，， ，∠°.（Ⅰ）证明⊥;（Ⅱ）若平面⊥平面，，求直线 与平面所成角的正弦值。

2022年重庆铜梁中学高三数学理模拟试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 复数等于A．1+2i B．1—2i C．2+i D．2一i参考答案：D【知识点】复数的基本概念与运算L4=2-i【思路点拨】两个复数相除，分子和分母同时乘以分母的共轭复数，再利用虚数单位i的幂运算性质进行准确化简运算．2. 若x∈（，1），a＝lnx，b＝，c＝，则a，b，c的大小关系是A．c＞b＞a B．b＞c＞a C．a＞b＞c D．b＞a＞c参考答案：B略3. 下列命题中真命题的个数是（1）“”的否定是“?x∈R，x2﹣2sinx＜5”；（2）“∠AOB为钝角”的充要条件是“”；（3）函数的图象的对称中心是．（）A．0 B．1 C．2 D．3参考答案：B【考点】命题的真假判断与应用．【分析】（1）根据含有量词命题的否定定义判定；（2）根据向量的夹角与数量积的关系判定；（3）由y=tanx的对称中心为（，0），k∈Z判定【解答】解：对于（1），“”的否定是“?x∈R，x2﹣2sinx＜5”，正确；对于（2），“∠AOB为钝角”的充要条件是“”且不共线，故错；对于（3），∵y=tanx的对称中心为（，0），k∈Z，∴由2x+=，k∈Z，得x=﹣，故错故选：B4. 已知R，R，则A．4 B．3 C．2 D．1参考答案：A5. 已知复数是正实数，则实数a的值为( )A. 0B. 1C. －1D. ±1参考答案：C【分析】将复数化成标准形式，由题意可得实部大于零，虚部等于零，即可得到答案.【详解】因为为正实数，所以且，解得.故选：C【点睛】本题考查复数的基本定义，属基础题.6. 不等式成立的一个充分不必要条件是（）A．或B．或C． D．参考答案：D7. 已知函数，则方程（为正实数）的实数根最多有 K]A．6个 B．4个 C．7个 D．8个参考答案：B8.直线xsinβ＋ycosθ＝2＋sinθ与圆(x－1)2＋y2＝4的位置关系是( )A．相离 B．相切 C．相交 D．以上都有可能参考答案：答案:B9. 平面向量，共线的充要条件是（）A. ，方向相同B. 存在不全为零的实数，，C. ，D.，两向量中至少有一个为零向量参考答案：B略10. 将4名实习教师分配到高一年级三个班实习，每班至少安排一名教师，则不同的分配方案有（）种A．12 B． 36 C．72 D．108参考答案：B 略二、填空题:本大题共7小题,每小题4分,共28分11. 在平面直角坐标系xOy中，角与角均以Ox为始边，它们的终边关于y轴对称.若sin=，则sin=_________．参考答案：1/312. 若某几何体的三视图 (单位：cm) 如图所示，则此几何体的表面积是 cm．参考答案：命题意图：考查学生的空间想象能力及面积公式的运用。

2 1133正视图 侧视图俯视图 21 重庆市铜梁中学2013届高三下学期二轮复习定时练习（一）数学（理）试题一、选择题（本大题10个小题，每小题5分，满分50分，每小题给出的四个选项中，只有一项符合题目要求） 1．已知集合(){}{}222=log ++2,,=1,A x y x x x R B x y x x R =-∈=-∈，则A B ⋂=（ ）A.()1,2-B.[]1,2-C.()1,1-D.(]11-，2. 条件甲：⎩⎨⎧<<<+<3042xy y x ；条件乙：⎩⎨⎧<<<<3210y x ，则甲是乙的( )A. 充要条件B. 充分而不必要条件C. 必要而不充分条件D. 既不充分也不必要条件3．已知等比数列{}n a 的公比为正数，且2395=2a a a g ，2=1a ，则1=a （ ）A.12B.22C.2D.2 4.已知2,(2)()2a b a b a b ==+-=-r r r r r r ,则a r 与b r的夹角为( )A.3πB.23π C.6πD.56π 5. 右图给出的是计算1111++++24620L 的值的一个 程序框图，其中判断框内应填入的条件是( )A .>10iB <10i . C.>20i D.<20i 6. 已知某几何体的三视图如图所示，则该几何体的体积为（ ）A.32B.52C.43D. 537. 某班班会准备从甲、乙等7名学生中选派4名学生发言，要求甲、乙两人至少有一人参加。

当甲、乙同时参加时，他们两人的发言不能相邻，那么不同的发言顺序的种数为（ ）A. 360B.520C.600D. 7208. 一直线与圆222()()(0)x a y b r r -+-=>相交于A B 、两点，且A B 、两点关于直线22x y += 对称，则过点(2,2)(,4)a b P b Q a --、两点的直线的斜率的最小值为（ ） A. 2 B. 1 C. 2 D. 22 9. 将函数()=2sin 2+4f x x π⎛⎫⎪⎝⎭的图像向右平移()>0ϕϕ个单位，再将图像上每一点横坐标缩短到原来的12倍，所得图像关于直线=4x π对称，则ϕ的最小正值为( )A.8π B.38π C.34π D.2π10．点P 的底边长为23，高为2的正三棱柱表面上的动点，MN 是该棱柱内切球的一条直径，则PM PN ⋅u u u u r u u u r取值范围是( )A ．[0，2]B ．[0，3]C ．[0，4]D ．[—2，2]二、填空题（本大题共6小题，每小题5分，其中11--13为必做题，14--16为选做题只需选做2个小题，共25分） 11. 设复数13=+22i ω-，则化简复数21ω的结果是 。

命题人： 李超一、选择题1．已知全集U ＝R ，A ＝{x |x ≤0}，B ＝{x |x ≥1}，则集合∁U (A ∪B )＝( )A ．{x |x ≥0}B ．{x |x ≤1}C ．{x |0≤x ≤1}D ．{x |0＜x ＜1}2．设函数f (x )＝log 2x ，则“a ＞b ”是“f (a )＞f (b )”的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件3．等于（）A ．B ．C ．D ．4．下列函数中，定义域是R 且为增函数的是( )A ．y ＝e －xB ．y ＝x 3C ．y ＝ln xD ．y ＝|x |5. 函数f (x )＝log2x －11的定义域为( )A ．(0，2)B ．(0，2]C ．(2，＋∞)D ．[2，＋∞)6．已知，则f(3)为（ ）A ．2B ．3C ．4D ．5 7．若，则的取值范围是（ ）A ．B ．C ．D ．8．设的值为（ ）A ．B ．C ．－1D ．19．奇函数f (x )的定义域为R .若f (x ＋2)为偶函数，且f (1)＝1，则f (8)＋f (9)＝( )A ．－2B ．－1C ．0D ．110．是定义在非零实数集上的函数，为其导函数，且时，，记，则（ ）A ．B ．C ．D ． 二、填空题11．已知，则的值为_________12．把函数y = sin(2x+)的图象向右平移个单位, 再将横坐标缩小为原来的, 则其解析式为 .13．在平面直角坐标系xOy 中，若曲线y ＝ax 2＋x b (a ，b 为常数)过点P (2，－5)，且该曲线在点P 处的切线与直线7x ＋2y ＋3＝0平行，则a ＋b 的值是________．14．若函数f (x )(x ∈R )是周期为4的奇函数，且在[0，2]上的解析式为f (x )＝sin πx ，1<x≤2，x （1－x ），0≤x≤1，则f 429＋f 641＝______．15．已知f (x )是定义在R 上且周期为3的函数，当x ∈[0，3)时，f (x )＝21.若函数y ＝f (x )－a 在区间[－3，4]上有10个零点(互不相同)，则实数a 的取值范围是________．三、解答题16．已知函数（8分）（1）求f(x)的定义域；（2）判断f(x)的奇偶性并证明；17．已知函数（1）求曲线在点处的切线方程；（2）求函数的极值；18．已知函数，，（Ⅰ）若曲线在点处的切线方程为，求实数的值；（Ⅱ）若，求函数的最大值．19．已知函数f (x )＝A sin 3π，x ∈R ，且f 125π＝22.（1）求A 的值；(2)若f (θ)－f (－θ)＝，θ∈2π，求f －θπ20．已知函数f (x )＝2cos x (sin x ＋cos x )．（1）求f 45π的值；(2)求函数f (x )的最小正周期及单调递增区间．21．定义在非零实数集上的函数满足且是区间上的增函数（1）求的值；（2）求证：；（3）解不等式.。