2019-2020年初中数学竞赛专题培训第十三讲梯形.docx

与平行四边形同样，梯形也是一种特别的四边形，此中等腰梯形与直角梯形据有重要地位，本讲就来研究它们的相关性质的应用．例 1 如图 2-43 所示．在直角三角形 ABC中， E 是斜边 AB上的中点， D 是 AC的中点，DF∥ EC交 BC延伸线于 F．求证：四边形 EBFD是等腰梯形．剖析因为E，D是三角形ABC边 AB，AC的中点，所以 ED∥ BF．别的，还要证明 (1)EB=DF；(2)EB 不平行于DF．证因为 E， D 是△ ABC的边 AB， AC的中点，所以2019-2020 年初中数学比赛专题培训第十三讲梯形又已知 DF∥ EC，所以 ECFD是平行四边形，所以EC=DF．①又 E 是 Rt △ ABC斜边 AB上的中点，所以EC=EB．②由①，②EB=DF．下边证明 EB 与 DF 不平行．若 EB∥ DF，因为 EC∥ DF，所以有 EC∥ EB，这与依据定义， EBFD是等腰梯形．例 2 如图 2-44 所示． ABCD是梯形， AD∥ BC，BD交于 O.求∠ BCD的度数．EC与 EB交于 E 矛盾，所以EB DF．AD＜ BC，AB=AC且 AB⊥ AC，BD=BC，AC，剖析因为△ BCD是等腰三角形，若能确立极点∠CBD的度数，则底角∠BCD可求．由等腰 Rt △ ABC可求知斜边 BC(即 BD)的长．又梯形的高，即 Rt△ ABC斜边上的中线也可求出．通过添协助线可结构直角三角形，求出∠BCD的度数．解过 D作 DE⊥ EC于 E，则 DE的长度即为等腰 Rt △ ABC斜边上的高 AF．设 AB=a，因为△ABF也是等腰直角三角形，由勾股定理知AF2+BF2=AB2，即又22222BC=AB+AC=2AB=2a ，因为 BC=DB，所以，在Rt△ BED中，从而∠ EBD=30°( 直角三角形中30°角的对边等于斜边一半定理的逆定理) ．在△ CBD 中，例 3 如图 2-45 所示．直角梯形 ABCD中， AD∥ BC，∠ A=90°，∠ ADC=135°， CD的垂直均分线交 BC于 N，交 AB 延伸线于 F，垂足为 M．求证： AD=BF．剖析 MF 是 DC的垂直均分线，所以ND=NC．由 AD∥ BC及∠ ADC=135°知，∠ C=45°，从而∠ NDC=45°，∠ DNC=90°，所以ABND是矩形，从而推知△BFN是等腰直角三角形，从而AD=BN=BF．证连结 DN．因为 N 是线段 DC的垂直均分线MF上的一点，所以ND=NC．由已知， AD∥BC及∠ ADC=135°知∠C=45°，从而∠NDC=45°．在△ NDC中，∠DNC=90° (= ∠ DNB)，所以 ABND是矩形，所以AF∥ ND，∠ F=∠ DNM=45°．△ BNF是一个含有锐角45°的直角三角形，所以BN=BF．又AD=BN，所以 AD=BF．例 4 如图 2-46 所示．直角梯形 ABCD中，∠ C=90°， AD∥ BC， AD+BC=AB， E 是 CD的中点．若 AD=2， BC=8，求△ ABE的面积．剖析因为 AB=AD+BC，即一腰 AB的长等于两底长之和，它启迪我们利用梯形的中位线性质 ( 这个性质在教材中是梯形的重要性质，我们将在下一讲中深入研究它，这里只引用它的结论 ) ．取腰 AB 的中点 F，( 或 BC)．过A 引 AG⊥ BC于 G，交 EF 于 H，则 AH， GH分别是△ AEF与△ BEF的高，所以2222-(8-2)2，AG=AB-BG =(8+2)=100-36=64所以 AG=8．这样 S△ABE(=S △AEF+S△BEF) 可求．解取 AB中点 F，连结 EF．由梯形中位线性质知EF∥ AD(或 BC)，过 A 作 AG⊥ BC于 G，交 EF于 H．由平行线均分线段定理知，AH=GH且 AH，GH均垂直于EF．在 Rt△ ABG中，由勾股定理知222AG=AB-BG=(AD+BC)2-(BC-AD) 2=102-6 2=82，所以 AG=8，从而 AH=GH=4，所以S△ABE=S△AEF+S△BEF例 5 如图 2-47 所示．四边形 ABCF中， AB∥ DF，∠ 1=∠2， AC=DF， FC＜ AD．(1)求证： ADCF是等腰梯形；(2) 若△ ADC的周长为16 厘米 (cm) ， AF=3 厘米， AC-FC=3厘米，求四边形ADCF的周长．剖析欲证ADCF是等腰梯形．归纳为证明AD∥ CF， AF=DC，不要忘了还需证明AF不平行于 DC．利用已知相等的因素，应从全等三角形下手．计算等腰梯形的周长，明显要注意利用 AC-FC=3厘米的条件，才能将△ ADC的周长过渡到梯形的周长．解 (1) 因为 AB∥ DF，所以∠ 1=∠ 3．联合已知∠ 1=∠ 2，所以∠ 2=∠ 3，所以EA=ED．又 AC=DF，所以 EC=EF．所以△ EAD及△ ECF均是等腰三角形，且顶角为对顶角，由三角形内角和定理知∠3=∠ 4，从而 AD∥ CF．不难证明△ACD≌△ DFA(SAS)，所以 AF=DC．若 AF∥ DC，则 ADCF是平行四边形，则 AD=CF与 FC＜ AD矛盾，所以 AF 不平行于 DC．综上所述， ADCF是等腰梯形．(2)四边形 ADCF的周长=AD+DC+CF+AF．①因为△ADC的周长 =AD+DC+AC=16(厘米 ) ，②AF=3(厘米 ) ，③FC=AC-3，④将②，③，④代入①四边形 ADCF的周长 =AD+DC+(AC-3)+AF=(AD+DC+AC)-3+3=16( 厘米 ) ．例 6 如图 2-48 所示．等腰梯形 ABCD中，AB∥ CD，对角线 AC，BD所成的角∠ AOB=60°，P， Q， R 分别是 OA，BC， OD的中点．求证：△PQR是等边三角形．剖析第一从P，R分别是OA，OD中点知，欲证等边三角形PQR的边长应等于等腰梯形腰长之半，为此，只要证明QR，QP等于腰长之半即可．注意到△OAB与△ OCD均是等边三角形， P， R 分别是它们边上的中点，所以，BP⊥ OA，CR⊥ OD．在 Rt △ BPC与 Rt △ CRB中， PQ，RQ分别是它们斜边BC(即等腰梯形的腰) 的中线，所以，PQ=RQ=腰 BC之半．问题获解．证因为四边形 ABCD是等腰梯形，由等腰梯形的性质知，它的同一底上的两个角及对角线均相等．从而推知，∠ OAB=∠ OBA及∠ OCD=∠ODC．又已知， AC与 BD成 60°角，所以，△ODC与△ OAB均为正三角形．连结 BP， CR，则 BP⊥ OA，CR⊥ OD．在 Rt △ BPC与 Rt△CRB 中， PQ， RQ分别是它们的斜边 BC上的中线，所以又 RP是△ OAD的中位线，所以因为 AD=BC，③由①，②，③得PQ=QR=RP，即△ PQR是正三角形．说明此题证明惹人注视之处有二：(1) 充足利用特别图形中特别点所带来的性质，如正三角形OAB边 OA上的中点P，可带来 BP⊥ OA的性质，从而又引出直角三角形斜边中线PQ等于斜边 BC之半的性质．(2)等腰梯形的“等腰”就如一座桥梁“接通”了“两岸”的髀使△ PQR的三边相等．。

精锐教育学科教师辅导讲义
）作双高转化为一个矩形两个直角三角形；
）延长两腰构成一个三角形；
）作一腰平行线构成一个平行四边形和一个三角形；
（涉及对角线的题目）
构成一个△ABF，统一两底到BF．
，AB=_____，S梯形ABCD
，AB≠AD，对角线AC，BD相交于点
DOC；④△AOD∽△BOC．请把其中正确结论的序号填在横线上：
的面积为_______.
互余，AD=5，BC=13，∠C=60
2cm和7cm，一腰长为3cm，则另一腰
中，AD∥BC，AD=3，BC=7，E
°，则较短的腰长为
．如图，已知等腰梯形ABCD
19 B．20 C
，则图中面积相等的三角形的对数有（
以D为中心逆时针旋转
ABCD，使点B落在
①△AOB∽△COD; ②△
BM⊥CM．
中，AD∥BC，AB=DC，∠
；（2）△DEC是等边三角形．
BAD=90°，E是DC•的中点
精锐教育网站：电话：400—010—0868 11。

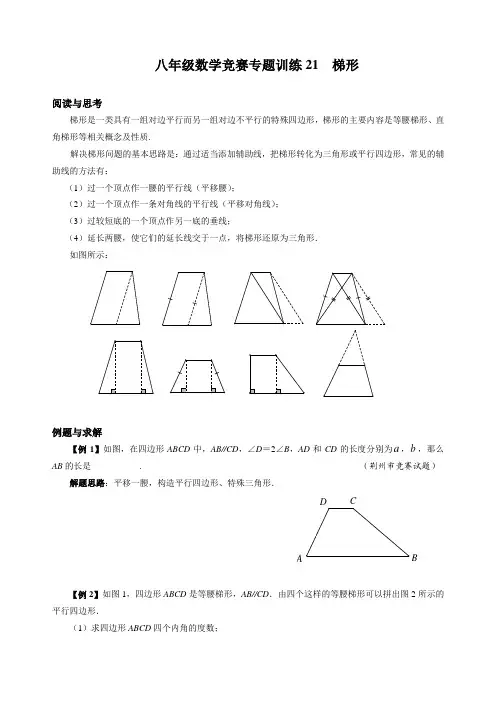
八年级数学竞赛专题训练21 梯形阅读与思考梯形是一类具有一组对边平行而另一组对边不平行的特殊四边形，梯形的主要内容是等腰梯形、直角梯形等相关概念及性质.解决梯形问题的基本思路是：通过适当添加辅助线，把梯形转化为三角形或平行四边形，常见的辅助线的方法有：（1）过一个顶点作一腰的平行线（平移腰）；（2）过一个顶点作一条对角线的平行线（平移对角线）；（3）过较短底的一个顶点作另一底的垂线；（4）延长两腰，使它们的延长线交于一点，将梯形还原为三角形．如图所示：例题与求解【例1】如图，在四边形ABCD中，AB//CD，∠D＝2∠B，AD和CD的长度分别为a，b，那么AB的长是___________. （荆州市竞赛试题）解题思路：平移一腰，构造平行四边形、特殊三角形．AB【例2】如图1，四边形ABCD是等腰梯形，AB//CD．由四个这样的等腰梯形可以拼出图2所示的平行四边形．（1）求四边形ABCD四个内角的度数；（2）试探究四边形ABCD 四条边之间存在的等量关系，并说明理由；（3）现有图1中的等腰梯形若干个，利用它们你能拼出一个菱形吗？若能，请你画出大致的示意图． （山东省中考试题） 解题思路：对于（1）、（2），在观察的基础上易得出结论，探寻上、下底和腰及上、下底之间的关系，从作出梯形的常见辅助线入手；对于（3），在（2）的基础上，展开想象的翅膀，就可设计出若干种图形．图2图1A【例3】如图，在等腰梯形ABCD 中，AD//BC ，AB ＝DC ，且AC ⊥BD ，AF 是梯形的高，梯形的面积是49cm 2，求梯形的高.（内蒙古自治区东四盟中考试题） 解题思路：由于题目条件中涉及对角线位置关系，不妨从平移对角线入手．B【例4】 如图，在等腰梯形ABCD 中，AB//DC ，AB ＝998，DC ＝1001，AD ＝1999，点P 在线段AD 上，问：满足条件∠BPC ＝900的点P 有多少个？（全国初中数学联赛试题） 解题思路：根据AB ＋DC ＝AD 这一关系，可以在AD 上取点构造等腰三角形．D【例5】如图，在等腰梯形ABCD中，CD//AB，对角线AC，BD相交于O，∠ACD＝600，点S，P，Q分别为OD，OA，BC的中点．（1）求证：△PQS是等边三角形；（2）若AB＝5，CD＝3，求△PQS的面积；（3）若△PQS的面积与△AOD的面积的比是7：8，求梯形上、下两底的比CD：AB．（“希望杯”邀请赛试题）解题思路：多个中点给人以广泛的联想：等腰三角形性质、直角三角形斜边中线、三角形中位线等.A【例6】如图，分别以△ABC的边AC和BC为一边，在△ABC外作正方形ACDE和CBFG，点P是EF的中点，求证：点P到边AB的距离是AB的一半．（山东省竞赛试题）解题思路：本题考查了梯形中位线定理、全等三角形的判定与性质．关键是要构造能运用条件EP＝PF的图形．EF能力训练A级1. 等腰梯形中，上底：腰：下底＝1：2：3，则下底角的度数是__________.（天津市中考试题）2. 如图，直角梯形ABCD中，AB⊥BC，AD＝3，BC＝5，将腰DC绕点D逆时针方向旋转900至DE，连接AE，则△ADE的面积为______________. （宁波市中考试题）3．如图，在等腰梯形ABCD 中，AB//CD ，∠A ＝060，∠1＝∠2，且梯形的周长为30cm ，则这个等腰梯形的腰长为______________.第3题图第4题图第2题图ABAB4.如图，梯形ABCD 中，AD//BC ，EF 是中位线，G 是BC 边上任一点，如果222cm S GEF =∆，那么梯形ABCD 的面积为__________. （成都市中考试题）5.等腰梯形的两条对角线互相垂直，则梯形的高h 和中位线的长m 之间的关系是 ( )A ．m ＞hB ．m ＝hC ．m ＜hD ．无法确定6. 梯形ABCD 中，AB//DC ，AB ＝5，BC ＝23，∠BCD ＝045，∠CDA ＝060，则DC 的长度是( )A .3327+B ．8 C.219 D.38+ E. 338+（美国高中考试题）7．如图，在等腰梯形ABCD 中，AC ＝BC ＋AD ，则∠DBC 的度数是 ( )A.300B.450C.600D.900（陕西省中考试第7题图第8题图BBAC第9题图B8．如图，在直角梯形ABCD 中，AD//BC ，AB ⊥BC ，AD ＝2，BC ＝DC ＝5，点P 在BC 上移动，则当P A ＋PD 取最小值时，△APD 中边AP 上的高为( )A ．17172 B ．17174 C ．17178 D ．3 （鄂州市中考试题）9．如图，在等腰梯形ABCD 中，AD //BC ，AB ＝CD ，点P 为BC 边上一点，PE ⊥AB ，PF ⊥CD ，BG ⊥CD ，垂足分别为E ，F ，G ．求证 ：PE ＋PF ＝BG ．（哈尔滨市中考试题）10. 如图，在梯形ABCD 中，AD//BC ，E ，F 分别为AB ，AC 中点，BD 与EF 相交于G ．求证：)(21AD BC GF -=．BC11.如图，等腰三角形ABC 中，AB ＝AC ，点E 、F 分别是AB 、AC 的中点，CE ⊥BF 于点O ． 求证：（1）四边形EBCF 是等腰梯形；（2）2222BE BC EF =+． （深圳市中考试题）B12.如图1，在等腰梯形ABCD 中，AD//BC ，E 是AB 的中点，过点E 作EF//BC 交CD 于点F ，AB ＝4，BC ＝6，∠B ＝060．（1）求点E 到BC 的距离；（2）点P 为线段EF 上的一个动点，过P 作PM ⊥EF 交BC 于点M ，过M 作MN//AB 交折线ADC 于点N ，连接PN ，设EP ＝x ．①当点N 在线段AD 上时（如图2），△PMN 的形状是否发生改变？若不变，求出△PMN 的周长；若改变，请说明理由．②当点N 在线段DC 上时（如图3），是否存在点P ，使△PMN 为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由． （江西省中考试题)图5(备用图)图4(备用图)图2图1图3B B BC B BB 级1. 如图，在梯形ABCD 中，AB//DC ，AD ＝BC ，AB ＝10，CD ＝4，延长BD 到E ，使DE ＝DB ，作 EF ⊥AB 交BA 的延长线于点F ，则AF ＝__________.（山东省竞赛试题）第2题图第1题图EBF2.如图，在梯形ABCD 中，AD//BC ，AB ＝DC ＝10cm ，AC 与BD 相交于G ，且∠AGD ＝060，设E 为CG 中点，F 是AB 中点，则EF 长为_________.（“希望杯”邀请赛试题）3.用四条线段：7,9,13,14====d c b a 作为四条边，构成一个梯形，则在所构成的梯形中，中位线的长的最大值为_________. （湖北赛区选拔赛试题）4.如图，梯形ABCD 的两条对角线AC ，BD 相交于O 点，且AO ：CO ＝3：2，则两条对角线将梯形分成的四个小三角形面积之比为=∆∆∆∆AOB COB DOC AOD S S S S :::_________. （安徽省中考试题）MABBC第4题图 第5题图 第6题图5.如图，在四边形ABCD 中，AD//BC ，E 是AB 的中点，若△DEC 的面积为S ，则四边形ABCD 的面积为 ( )A ．S 25 B ．2S C ．S 47 D ．S 49（重庆市竞赛试题）6.如图，在梯形ABCD 中，AD//BC ，∠B ＝020，∠C ＝070，E ，M ，F ，N 分别为AB ，BC ，CD ， DA 的中点，已知BC ＝7，MN ＝3，则EF 的值为 ( )A ．4B ．214C ．5D ．6 （全国初中数学联赛试题）7.如图，梯形ABCD 中，AB//DC ，E 是AD 的中点，有以下四个命题：①若AB ＋DC ＝BC ，则∠BEC ＝090；②若∠BEC ＝090，则AB ＋DC ＝BC ；③若BE 是∠ABC 的平分线，则∠BEC ＝090； ④若AB ＋DC ＝BC ，则CE 是∠DCB 的平分线.其中真命题的个数是 ( )A ．1个B ．2个C ．3个D ．4个（重庆市竞赛试题）第8题图第7题图NDAC B8.如图，四边形ABCD 是一梯形，AB//CD ，∠ABC ＝090，AB ＝9cm ，BC ＝8cm ，CD ＝7cm ，M 是AD 的中点，从M 作AD 的垂线交BC 于N ，则BN 的长等于 ( )A ．1cmB ．1.5cmC ．2cmD ．2.5cm（“希望杯”邀请赛试题）9.如图，在梯形ABCD 中，AB//DC ，M 是腰BC 的中点，MN ⊥AD .求证：AD MN S ABCD ⋅=四边形（山东省竞赛试题）AB10.如图，在梯形ABCD 中，AD//BC ，分别以两腰AB ，CD 为边向两边作正方形ABGE 和正方形DCHF ，设线段AD 的垂直平分线l 交线段EF 于点M.求证：点M 为EF 的中点.（全国初中数学联赛试题）GH11.已知一个直角梯形的上底是3，下底是7，且两条对角线的长都是整数，求此直角梯形的面积.（“东方航空杯”上海市竞赛试题）12.如图1，平面直角坐标系中，反比例函数)0,0(>>=x k xky 的图象经过矩形OABD 的边BD 的三等分点（BD DF 31=）交AB 于E ，AB ＝12，四边形OEBF 的面积为16. （1）求k 值.（2）已知)0,13(C ，点P 从A 出发以0.5cm/s 速度沿AB 、BD 向D 运动，点Q 从C 同时出发，以1.5cm/s 的速度沿CO ，OA ，AB 向B 运动，其中一个动点到达端点时，另一个动点也随之停止运动.从运动开始，经过多少时间，四边形PQCB 为等腰梯形（如图2）.（3）在（2）条件下，在梯形PQCB 内是否有一点M ，使过M 且与PB ，CQ 分别交于S ，T 的直线把PQCB 的面积分成相等的两部分，若存在，请写出点M 的坐标及CM 的长度；若不存在，请说明理由.图2图1专题21梯形例1 a ＋b例2⑴上底角为120°，下底角为60°；⑵梯形的上底等于下底的一半，且等于腰长； ⑶能拼出菱形，以下图形供参考：例3 7cm 提示：过A 作AE ∥BD 交CB 延长线于E ，则S △AEC ＝S 梯形ABCD . 例4(1）如图a ，若E 为AD 中点，则∠BEC ＝90°且CE,BE 分别平分∠BCD ，∠ABC ； ⑵如图b ，在BC 上取一点M ，使AB ＝MB ，连结AM,DM ，则∠AMD ＝90°； ⑶如图c ，将a ，b 组合，则四边形GEHM 为矩形.图a 图b 图c ∴当P 为AD 中点时，可以证明∠BPC ＝90°；在AD 上截取AP ＝AB ，可以证明∠BPC ＝90°，故满足条件∠BPC ＝90°的点P 有2个.例5⑴连结SC,PB .∴△OCD,△OAB 均为等边三角形，S ，P ，Q 分别为OD,OA,BC 中点， ∴SQ ＝12BC ＝12AD ＝SP ＝PQ .故△SPQ 为等边三角形.⑵∵SB ＝12DO ＋OB ＝132,CS ＝323,BC ＝7.∴△SPQ 的边长SQ ＝12BC ＝72.∴S △SPQ ＝34×(72)2＝49316.(3）设CD ＝a ，AB ＝b (a <b ),BC 2＝SC 2＋BS 2＝(32a )2＋(b ＋a2)2＝a 2＋b 2＋ab . ∴S △SPQ ＝316(a 2＋ab ＋b 2).又S △AOD S △COD ＝b a ，则S △AOD ＝34ab . 又S △AOD S △COD ＝b a ,则S △AOD ＝34ab .∵S △PQS S △AOD ＝78,∴8×316 (a 2＋ab ＋b 2)＝7×34ab . 即2a 2－5ab ＋2b 2＝0，化简得a b ＝12. 故CD ：AB ＝1:2.例6如图，分别过E,F ,C,P 作AB 的垂线，垂足依次为R ，S ，T ，Q ，则PQ 就是点P 到AB 的距离，且有ER ∥PQ ∥CT ∥FS ，故四边形ERSF 为直角梯形，PQ ＝12(ER ＋FS ).易证Rt △AER ≌Rt △CAT ，Rt △BFS ≌Rt △CBT ，∴ER ＝AT ，FS ＝BT ，又AT ＋BT ＝AB ＝ER ＋FS ， 故PQ ＝12AB .A 级1.60°2.33.6cm4.82cm 25.B6.D7.C8.C 提示:如图，作点D 关于直线BC 的对称点D '，连结DD '交BC 于E ，连结AD '交BC 于P ，过D 作DF ⊥AP 于F ,故P A ＋PD 此时最小.由BE ＝AD ＝2，EC ＝3，则可得：DE ＝4，∴DD '＝8,则AD '＝217. 又∵AD '·DF ＝AD ·DD ',则DF ＝81717.9.提示：过P 点作PQ ⊥BG 于Q ，证明PE ＝BQ .10.提示：连结DF 并延长交于BC 于H ，则GF ＝12BH ，AD ＝CH . 11.略12.⑴ 3⑵①当点N 在线段AD 上运动时，△PMN 形状不发生改变，其周长为3＋7＋4.②当点在线段DC 上运动时，△PMN 的形状发生改变，但MNC 恒为等边三角形，过E 作EG BC 于G 。

梯形（第1课时）教学任务分析教学目标知识技能探索并掌握梯形的有关概念和基本性质，探索、了解并掌握等腰梯形的性质．数学思考能够运用梯形的有关概念和性质进行有关问题的论证和计算，进一步培养学生的分析问题能力和计算能力．解决问题通过添加辅助线，把梯形的问题转化成平行四边形或三角形问题，使学生体会图形变换的方法和转化的思想．情感态度在应用等腰梯形的性质的过程养成独立思考的习惯，在数学学习活动中获得成功的体验．重点等腰梯形的性质及其应用．难点解决梯形问题的基本方法（将梯形转化为平行四边形和三角形及正确运用辅助线），及梯形有关知识的应用．教学流程安排活动流程图活动的内容和目的活动1 看一看活动2 说一说活动3 画一画活动4 猜一猜验一验活动5 试一试活动6 练一练活动7 理一理观察梯形图片，引入本节课的学习内容．通过回忆小学学过的梯形知识了解梯形定义、各部分名称及分类．通过画图了解梯形和三角形的转化关系及等腰三角形和等腰梯形的联系。

探究得到等腰梯形的性质．用学过的知识验证猜想的结论通过解决具体问题，寻找解决梯形问题的方法．通过练习，提高运用知识的能力，寻找解决问题的方法通过整理回顾，巩固知识、提高能力、渗透思想．教学过程设计问题与情景师生行为设计意图[活动1] 看一看观察图片，有你熟悉的图形吗？（生活中只要注意观察就会发现很多我们熟悉的图形，数学就在我们身边）引入课题。

观察手中的各种图形，对它们进行分类，你是依据什么进行分类的？两组对边分别平行的是平行四边形只有一组对边平行的是梯形演示图片，学生欣赏．引出课题根据学生的回答引出梯形的概念，强调梯形和平行四边形的区别。

梯形：一组对边平行而另一组对边不平行．由现实中实际问题入手，设置问题情境，引出本课主题．通过学生观察图片和归纳图形的特点，培养学生的观察、概括能力．[活动2] 说一说回忆小学的梯形知识说一说梯形的一些基本概念：（1）（如图）：底、腰、高．（2）等腰梯形：两腰相等的梯形叫做等腰梯形．（3）直角梯形：有一个角是直角的梯形叫做直角梯形．学生在小学已经对梯形有一定的感性认识，因此教师让学生自己介绍1）中的基本概念，在聆听学生发言后，教师可以强调：①梯形与四边形的关系；②上、下底的概念是由底的长短来定义的，而并不是指位置来说的．熟悉图形，明确概念，为探究图形性质做准备．[活动3] 画一画在下列所给图中的每个三角形中画一条线段，（1）怎样画才能得到一个梯形？（2）在哪些三角形中，能够得到一个等腰梯形？在学生独立探究的基础上，学生分组交流．教师参与小组活动，指导、倾听学生交流．针对不同认识水平的学生，引导其正确作图．本次活动教师应重点关注：（1）学生在活动过程中能否发现梯形与三角形之间的联系，他们之间的转化方法．（2）学生能否将等腰三角形转化为等腰梯形．（3）学生能否主动参与探究活动，在讨论中发表自己的见解，倾听他人的意见，对不同的观点进行质疑，从中获益．等腰梯形的性质与等腰三角形相仿，因此在活动3中设计了第（2）题，在推导等腰梯形性质或需要添加辅助线时，可以借助等腰三角形来研究．尤其是根据等腰三角形是轴对称图形，可得到等腰梯形是轴对称图形这条性质，为活动4种开展探究奠定了基础．问题与情景师生行为设计意图[活动4]做—做探索等腰梯形的性质（引入用轴对称解决问题的思想）．在一张方格纸上作一个等腰梯形，连接两条对角线．（1）这个图形是轴对称图形吗？对称轴在哪里？你能发现哪些相等的线段和相等的角？学生画图并通过观察猜想；（2）这个等腰梯形的两条对角线的长度有什么关系？学生按照实验步骤，独立完成画图过程，观察图形，思考教师提出的问题，猜想、验证、归纳结论．针对不同认识水平的学生，教师指导学生活动．师生共同归纳：①等腰梯形是轴对称图形，上下底的中点连线是对称轴．②等腰梯形两腰相等．③等腰梯形同一底上的两个角相等．④等腰梯形的两条对角线相等．教学中要注意引导学生证明等腰梯形的性质，尤其在证明“等腰梯形同一底上的两个角相等”这条性质时，“平移腰”和“作高”这两种常见的辅助线，在教学中头一次出现，可以借此机会，给学生介绍这两种辅助线的添加方法．[活动5] 试一试例1 （教材P118的例1）略．例 2 如图，梯形ABCD中，AD∥BC，∠B=70°，∠C=40°，AD=6cm，BC=15cm．求CD的长．师生共同分析，寻找解决问题的方法和策略．例1是等腰梯形性质的直接运用，请学生分析、解答，教师聆听，同时注意指导学生，在证明△EAD是等腰三角形时，要用到梯形的定义“上下底互相平行（AD∥BC）”这一点．分析：设法把已知所给的条件都移到一个三角形中，便可以解决问题．其方法是：平移一腰，过点A作AE∥DC交BC于E，因此四边形AECD是平行四边形，由已知又可以得到△ABE是等腰三角形（EA=EB），因此CD=EA=EB=BC—EC=BC—AD=9cm．解：（略）通过题目的练习与讲解应让学生知道：解决梯形问题的基本思想和方法就是通过添加适当的辅助线，把梯形问题转化为已经熟悉的平行四边形和三角形问题来解决．在教学时应让学生注意它们的作用，掌握这些辅助线的使用对于学好梯形内容很有帮助．活动6 练一练：小试牛刀1、判断题：（1）一组对边平行的四边形是梯形（2）一组对边平行且不相等的四边形是梯形（3）等腰梯形的两个底角相等. （4）等腰梯形的对角线相等.2、填空题:(1)已知等腰梯形的一个锐角等于75°,则其它三个角分别等于___________________.(2)梯形ABCD中,AD∥BC,AB ⊥BC,且∠C=45°,AB=3,AD=2,则BC=_____. 练习1是让学生了解有关梯形的容易理解错的地方。

初中数学梯形知识点总结与回顾梯形是初中数学中一个非常重要的几何形体。

学习完梯形的相关知识点不仅有助于学生更好地掌握初中数学，还能够为他们今后的数学学习打下坚实的基础。

本文将对初中数学梯形的相关知识点进行总结与回顾。

一、梯形的定义及特点梯形是指在同一平面内的两条平行线段中，其中一条长于另一条的四边形，它的两条并不相邻的边(非平行边)叫做斜边，另外两条平行的边称作底边。

要点总结如下：1、两直线平行。

2、相邻两边互不垂直。

3、斜边的两端在底边的两侧。

二、梯形的性质1、对角线定理梯形的两条对角线的交点称为交点，连接交点和两个对角线中的底边中点，得到的线段叫做中线。

中线的长度等于梯形的两底的长度之和的一半。

2、高度定理梯形的两个非平行边的中点连线是梯形的高，高的长度是梯形两个平行边的长度之差的一半。

3、面积公式梯形的面积等于上下底之和乘以高的一半。

S=(a1+a2)×h/24、判断是否为梯形一个四边形是梯形的条件是其中两条边平行，而剩下的两条边不平行。

三、梯形的分类1、等腰梯形梯形两个非平行边相等，两个非平行边上角度相等。

2、普通梯形梯形没有相等的两个非平行边。

3、直角梯形一条底边上有一个直角的梯形，斜边长的边就是斜边，其余同普通梯形。

四、梯形的求解1、求解梯形的面积根据面积公式，得到梯形面积的公式为S=(a1+a2)×h/2。

就是上底加下底的和乘以高再除以2。

2、求解梯形的高度根据高度定理，对于一个梯形，它的高等于两个底之差的一半。

H=(a1-a2)/2.3、求解梯形的周长梯形周长的计算方法非常简单。

周长等于上底、下底和两条斜边之和。

五、梯形的应用梯形是学习初中的数学中一个非常重要的几何形体。

学生们在学习完梯形的相关知识点后，可以运用这些知识点来解决一些实际问题。

例如，当学生在测量一个不规则长方形的面积时，可以通过画出一个梯形来求解。

此外，在建造房屋时，建筑师们也需要应用梯形的相关知识点来计算出房屋的面积和高度。

梯 形【知识提要】1．一组对边平行而另一组对边不平行的四边形叫做梯形，一腰垂直于底的梯形叫做直角梯形；两腰相等的梯形叫做等腰梯形。

2．等腰梯形的性质：等腰梯形在同一底上的两个内角相等；两条对角线相等。

3．等腰梯形的判定定理：在同一底上的两个内角相等的梯形是等腰梯形。

4．梯形中位线定理：梯形的中位线平行于两底，并且等于两底和的一半。

例1 如图1，梯形ABCD 中，AD ∥BC ，E ，F 分别是AD ，BC 的中点，若∠B ＋∠C=90°AD=7，BC=15，则EF 的长是 。

例2 如图2，梯形ABCD 中，AD ∥BC ，E 是AB 的中点，CE 恰好平分∠BCD ，若AD=3，BC=4，则CD 的长是（ ）。

（A ）5 （B ）6 （C ）7 （D ）8第11届（2000年）初二培训例3 用四条线段：a=14，b=13，c=9，d=7作为四条边构成一个梯形，则在所构成的梯形中，中位线的长的最大值是（ ）。

（A ）13.5 （B ）11.5 （C ）11 （D ）10.5第11届（2000年）初二第1试例4 如图3，已知四边形ABCD 中，AD ∥BC ，若∠DAB 的角平分线AE 交CD 于E ，连结BE ，且BE 恰好平分∠ABC ，则AB 的长与AD ＋BC 的长的大小关系是（ ）。

（A ）AB>AD ＋BC （B ）AB=AD ＋BC （C ）AB<AB ＋BC （D ）无法确定第8届（1997年）初二第2试AB CDEF 图1A BCDE图2AＣＥＤ图3例5 在凸四边形ABCD 中，AB ∥CD ，且AB ＋BC=CD ＋DA ，则（ ）。

（A ）AD>BC （B ）AD<BC（C ）AD=BC （D ）AD 与BC 的大小关系不能确定第13届（2002年）初二第1试例6 如图4，四边形ABCD 为等腰梯形，AD ∥BC ，AD<BC,点O 平分BC 且OA=OB ，若CD=54，BD=58，那么BC= 。

中考数学 梯形专题【基础知识概述】一、梯形：1．梯形的定义：一组对边平行而另一组对边不平行的四边形叫做梯形． 2．特殊梯形: (1)等腰梯形：两腰相等的梯形． (2)直角梯形：一腰垂直于底的梯形． 3．等腰梯形的性质(1) 等腰梯形的两腰相等．(2) 等腰梯形在同一底上的两个角相等． (3) 等腰梯形的对角线相等． 3．等腰梯形的判定(1)定义：两腰相等的梯形是等腰梯形．(2)在同一底上的两个角相等的梯形是等腰梯形． (3)对角线相等的梯形是等腰梯形．二、梯形中常用的辅助线的添法：三、多边形：1．多边形的定义：在平面内，由一些不在同一条直线上的线段首尾顺次相接组成的封闭图形叫多边形．2．多边形内角和定理：n 边形的内角和等于(n-2)·180°． 3．多边形外角和定理：多边形的外角和等于360°． 4．多边形的对角线(1)从n 边形的一个顶点，可以引(n-3)条对角线，将多边形分成(n-2)个三角形． (2)n 边形共有2)3( n n 条对角线.四、中心对称图形：把一个图形绕某一点旋转180°，如果旋转后的图形能够和原来的图形互相重合．那么这个图形叫作中心对称图形，这个点就是它的对称中心．中心对称图形上的每一对对应点所连成的线段都被对称中心平分。

例1．（1）某多边形的内角和与外角和共1080°，则多边形的边数是___________.（2）________边形的内角和是外角和的2倍； _______边形的内角和与外角和相等． （3）n 边形的每一个内角都相等，它的一个外角与一个内角的比是1∶3，n 边形的对角线有_____条．（1）作两高 （2）平移腰 （3）平移对角线 （4）延长两腰 中点 （6）构造全等三角中点 中点 （5）作中位线ABCD等腰梯形的常见辅助线的作法【法一：平移对角线，然后两条对角线和底构成一个等腰三角形】例2：已知等腰梯形ABCD 中，AD ∥BC ，AC ⊥BD ，AD=3㎝，BC=7㎝，求BD 的长.和梯形的面积变式：如图,等腰梯形中, ,,且 ,是高,是中位线,求证：．【法二：平移梯形一腰或两腰,把梯形的腰、两底角等转移到一个三角形中,同时还得到平行四边形】例3：如图,在梯形ABCD 中,.求证：.变式：如图，四边形ABCD 中，AB ‖CD ，B D ∠=∠2,若AD=a,AB=b,则CD 的长是 .A D BCBCD A【法三：遇到梯形一腰中点的问题可以作出梯形的中位线,中位线与上、下底都平行,且三线段有数量关系. 或利用“等积变形”,连结梯形上底一端点和另一腰中点,并延长与下底延长线交于一点,构造全等三角形解决问题】例4：如图，E 是梯形ABCD 的腰AD 的中点，且AB+CD=BC ，试说明 1. BE 平分∠ABC. CE 平分∠BCD 2. CE ⊥BE 3. ABCD BCE S S 21变式：1.已知：如图,在梯形 中,是 的中点,且 .求证：.2.如图，在梯形ABCD 中，AD ∥BC ，E 是CD 的中点，若△AEB 的面积为S ，则梯形ABCD 的面积为（ ） A.S 25B.2SC.S 47D.S 49【法四：从梯形上底的两端向下底引垂线作高,可以得到一个矩形和两个直角三角形．然后利用构造的直角三角形和矩形解决问题】例5：如图，ABCD 是梯形，AB ∥DC,AB=5，BC=23，∠BCD=45°，∠CDA=60°，DC 的长度AD BC EA BCD1S 2SS 3BCDA 【法五：即延长两腰相交于一点，可使梯形转化为三角形】例6 如图，在梯形ABCD 中，AD//BC ，∠B=50°，∠C=80°，AD=2，BC=5，求CD 的长。