第七章光的量子性普朗克公式能量子

格式：ppt
大小：826.00 KB
文档页数：16

下载文档原格式

第七章光的量子性

Vg应与光强有关，实际却与光的频率有关。 Vg应与光强有关，实际却与光的频率有关。矛盾应与光强有关
3.照射时间长，积累能量多，只要照射足够长时间，总会有照射时间长，积累能量多，只要照射足够长时间，
电子逸出，有电流。实际却是若入射光频率ν 电子逸出，有电流。实际却是若入射光频率ν <ν0 ，无论照入射光频率射多长时间，无光电流产生。射多长时间，无光电流产生。矛盾光很弱，必须要照射长时间才能积累足够的能量，长时间，积累足够的能量 4.光很弱，必须要照射长时间，才能积累足够的能量，使电子从金属表面逸出。但实际却只要不管I 多弱，子从金属表面逸出。但实际却只要 ν >ν0，不管I0多弱，一照上去，就有光电流产生。矛盾照上去，就有光电流产生。
普适常数就是黑体的单色幅出度。普适常数就是黑体的单色幅出度。
∴基尔霍夫定律
M(ν ,T ) = Mb (ν ,T ) A(ν ,T )
T=5000k T=3000k
讨论:
1.同样温度下，黑体的辐射最大。 1.同样温度下，黑体的辐射最大。同样温度下 2.绝对黑体不存在，黑体模型。 2.绝对黑体不存在，黑体模型。绝对黑体不存在 3.黑体是否一定是黑的？黑色物体是否就是黑体？ 3.黑体是否一定是黑的？黑色物体是否就是黑体？黑体是否一定是黑的
一、黑体
黑体—在任何温度状态下全部吸收任何波长的电磁波. 黑体在任何温度状态下全部吸收任何波长的电磁波. 在任何温度状态下全部吸收任何波长的电磁波由
∴
Mb (ν ,T ) = f (ν ,T ) Ab (ν ,T )
黑体
Ab (ν , T ) = 1
Mb (ν ,T )
可见光 T=6000k

第七章光的量子性光电效应爱因斯坦的量子解释

因此，光电倍增管的灵敏度比普通光电管高几百万倍，微弱的光照就可产生很大的电流。
11
五. 光子的质量和动量
光子不仅具有能量，也具有动量和质量。但光子又是以光速运动，牛顿力学便不适用。按照狭义相对论的观点，质量和能量具有如下关系： 2
E mc
因此，光子的质量为：Fra bibliotekE h m 2 2 c c
有时光电效应直接产生的电流很小，需要将其放大，光电倍增管由此而诞生。
光电倍增管由光窗、光电阴极、电子光学系统、电子倍增系统和阳极五个主要部分组成。如图
Hamamatsu R3896光电倍增管
10
在光电阴极脱出的电子在加速电场的作用下，以提高的能量打在第一阴极上，一个电子可以打出几个电子，称为次发射，然后再打在第二阴极上，可打出更多电子，如此下去，一级级放大，可放大105～106倍。
4
2. 由爱因斯坦方程
1 2 h m m A0 2
可以看出，对于给定的金属，逸出功A0一定，则最大初动能1/2mv2m与频率成线性关系。 3. 红限存在的解释。如果入射光的频率过低，以致 h<A0，则电子就不能克服金属的束缚而脱出金属表面。即使入射光很强，也就是这种光子的数目很多，但仍不会产生光电效应。只有>0=A0/h时,才会有光电效应产生。 4. 当一个光子与一个电子发生碰撞时，电子立即得到光子的全部能量，无需能量的积累时间，故光电效应的驰豫时间很短。
5
爱因斯坦的光子假设和方程对光电效应的成功解释，说明了它的正确性。但当初人们受经典电磁理论的束缚较重，实验上又未能获得全面的验证，所以爱因斯坦的假设并没有立即得到人们的承认。
爱因斯坦曾经说过：“倘若光电方程正确无误，取直角坐标系将遏止电压表征为入射光频率的函数，则遏止电压必定是一条直线，他的斜率与金属材料性质无关。”

光的量子性

12
O
P
Q
S
例. 用频率为 1 的单色光照射某种金属时，测的光电子的最大动能为 Ek1；用频率为 2 的单色光照射另一种金属时，测的光电子的最大动能为 Ek2，若 Ek1> Ek2 则：（A） 1 一定大于 2 ；（B） 1 一定小于 2 ；（C） 1 一定等于 2 ；（D） 1 可能大于也可能小于 2 .
11
4
2010-6-18
例 .某金属的光电效应中，所发射的光电
子的初动能 Ek 随入射光频率的变化关
系如图所示，由图可知逸出功 W 和普朗 1 克常数 h 为： m v2 2 (A)A=OQ；h=OR; (B)A=OR; h=PQ; (C)A=OP; h=OP/OQ ; (D)A=QS; h=QS/OS .
2010-6-18
0
§1 黑体辐射和普朗克的能量子假说
一. 基本概念 1. 热辐射分子的热运动使物体辐射电磁波
头部热辐射像
1
2. 单色辐出度 3. 总辐出度
M (T ) dM d
M (T ) M (T )d
0
W m 3
4. 吸收比，反射比
( , T ) ( , T ) 1
二.爱因斯坦的光量子论 1.普朗克假定是不协调的只涉及发射或吸收,未涉及辐射在空间的传播。 2.爱因斯坦认为: • 光在发射或吸收时,具有粒子性;光在空间传播时,也具有粒子性 • 电磁辐射由以光速c运动的局限于空间某一小范围的光量子（光子）组成， = h • 光量子具有“整体性”
9
3. 对光电效应的解释
13
例. 用波长 =410 nm 的单色光照射某金属表面，若产生的光电子的最大动能 Ek=1.00eV，试求能使该金属发生光电效应的入射光的最大波长是多少？

能量子假说光量子论

zxc
三
用爱因斯坦量子理论解释康普顿散射
光子与电子弹性碰撞
E h h 光子动量 p c c
能量守恒： h 0 m0 c 2 h mc2 (2-1)
h 0 h 动量守恒： n0 n mv c c
zxc
(2-2)
能量守恒：h 0 m0 c 2 h mc2
zxc
h 2 mVm W
2
mVm h h 0
5、光电效应应用
1）光电管：
光电信号转换
2）光电二极管：固态光电探测器
3）光电倍增管：由10-15个倍增阴极组成，增大光电流104--105
倍，探测弱光。
4）光电成像器件：（光电导摄象管）将辐射图象转换成为可观测、记录、传输、存储和进行处理的图象，广泛应用于天文学、空间科学、X射线放射学、高速摄影等。 5）光敏电阻：
M (T ) T 4
斯特藩常数
5.67051108W / m2 K 4
2）维恩位移定律（1893）黑体辐射出的光谱中辐射最强的波长 m 与黑体温度 T 之间满足关系维恩常数
mT b
（1911年诺贝尔物理奖）
b 2.897756 103 mK
黑体在不同温度下，其单色辐出度M（，T）的峰值所对
h 2 1 cos 2c sin 0 m0 c 2m 2 c 2 m 2 v 2 m 2 c 2 0 m0 2 2 2 2 2 2 1 v 2 c v2 ( E 2 p 2c 2 E0 ) zxc c

4
玻尔兹曼常数 k =1.38065810-23J/K
但实际并非如此----紫外灾难。

普朗克公式光子能量的公式

普朗克公式光子能量的公式普朗克公式是描述物体辐射能量的量子化现象的公式，由德国物理学家马克斯·普朗克于1900年提出。

此公式被用来解释黑体辐射的谱线分布，成为量子力学的起点之一，为后来的量子理论打下了基础。

下面将详细介绍普朗克公式以及光子能量的计算公式。

首先，我们来看一下普朗克公式的表达形式。

普朗克公式可以表示为：E=h*ν其中，E表示光子能量，h是普朗克常数，ν表示光子的频率。

普朗克常数h的数值为6.63×10^(-34)J·s。

该常数是量子力学中的基本物理常数之一，与光子的能量密切相关。

光子的频率ν表示的是光的震动次数，是指单位时间内振动的次数。

频率与光子能量之间的关系由普朗克公式给出，可以看出光子的能量与频率成正比。

我们知道，光的波动性与粒子性都是存在的，光的能量可以用光子能量来表示。

光子是光的量子，具有能量、动量等粒子的特性。

光子能量与光子的频率呈正比，频率越高，光子能量越大。

根据普朗克公式，我们可以计算光子的能量。

以可见光为例，可见光的频率范围为4×10^14Hz到8×10^14Hz。

假设光的频率为7×10^14Hz，则根据普朗克公式，计算得到光子的能量为：E=6.63×10^(-34)J·s*7×10^14Hz=4.641×10^(-19)J这就是光子的能量。

这个能量非常微小，对比于常见的物质的能量，可以说是非常微弱的。

根据普朗克公式，我们可以进一步了解光的量子化现象。

根据公式，我们可以看到光子能量和频率之间的关系是线性的，而不是连续的。

这就意味着，光的能量不是连续变化的，而是量子化的。

这一发现对量子力学的发展起到了重要的推动作用。

普朗克公式揭示了能量的离散性，为后来的量子理论奠定了基础。

它也是量子力学中能量量子化的重要证据之一总结起来，普朗克公式是描述物体辐射能量的量子化现象的公式，根据该公式，光子的能量与光子的频率成正比。

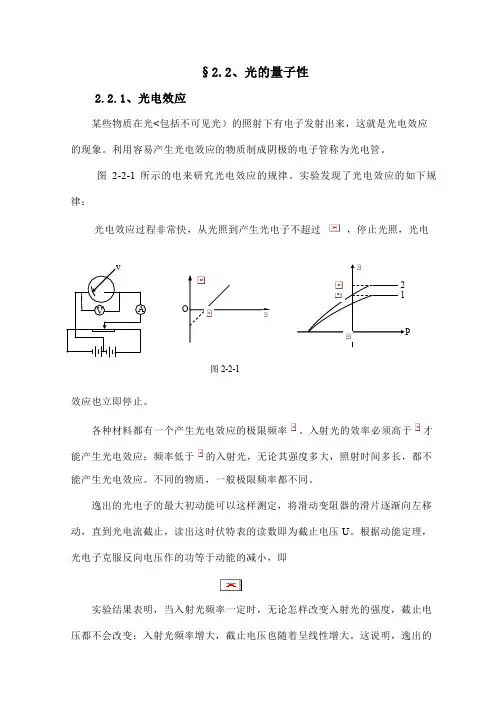
2. 2. 光的量子性

§2.2、光的量子性2.2.1、光电效应某些物质在光<包括不可见光）的照射下有电子发射出来，这就是光电效应的现象。

利用容易产生光电效应的物质制成阴极的电子管称为光电管。

图2-2-1所示的电来研究光电效应的规律。

实验发现了光电效应的如下规律：光电效应过程非常快，从光照到产生光电子不超过，停止光照，光电效应也立即停止。

各种材料都有一个产生光电效应的极限频率。

入射光的效率必须高于才能产生光电效应；频率低于的入射光，无论其强度多大，照射时间多长，都不能产生光电效应。

不同的物质，一般极限频率都不同。

逸出的光电子的最大初动能可以这样测定，将滑动变阻器的滑片逐渐向左移动，直到光电流截止，读出这时伏特表的读数即为截止电压U 。

根据动能定理，光电子克服反向电压作的功等于动能的减小，即实验结果表明，当入射光频率一定时，无论怎样改变入射光的强度，截止电压都不会改变；入射光频率增大，截止电压也随着呈线性增大。

这说明，逸出的图2-2-1光电子的最大初动能只能随入射光频率增大而增大，与入射光强度无关。

最大初动能与入射光频率的关系如图2-2-1所示。

在入射光频率一定条件下，向右移动变阻器的滑动片，光电流的强度随着逐渐增大，但当正向电压增大到某一值后继续再增大时，光电流维持一个固定图2-3值不变，此时光电流达到饱和。

增大入射光的强度P，饱和光电流也随着成正比地增大。

如图2-2-1所示。

2.2.2、光子说光电效应的四个特点中，只有第四个特点够用电磁来解释，其他特点都与电磁场理论推出的结果相矛盾。

爱因斯坦于1905年提出的光子说，完美地解释了这一现象。

光子说指出：空间传播的光<以及其他电磁波）都是不连续的，是一份一份的，每一份叫做一个光子。

光子的能量跟它的频率成正比即E=hv式中h为普朗克恒量。

光子也是物质，它具有质量，其质量等于光子也具有动量，其动量等于根据能量守恒定律得出：上式称为爱因斯坦光电效应方程。

式中W称为材料的逸出功，表示电子从物而中逸出所需要的最小能量。

光的量子性

( 0)
M b ( , T )
经典理论在这种短波的失败称为发散困难或“紫外灾难”。
7.3 普朗克辐射公式一、普朗克假设
能量子
器壁振子的能量不能连续变化，而只能够处于某些特殊状态，这些状态的能量分立值为 0, 0 , 2 0 ,n 0
其中n是整数， 0 称为能量子，简称量子：
hv kT
1
讨论
⒈ 短波近似：
h kT , e
h kT
1, 有 e
h kT
1
h kT
e 1

h kT
,
M b , T c 3 f T
2h 3 M b , T e c2
普朗克公式
维恩位移定律
⒉ 长波近似：
h kT , 有e
7.7 德布罗意波
一.光的波粒两象性
E mc2 h
p E h c c
二.实物粒子的波粒二象性 1. 物质波 1924年德布罗意假设：实物粒子和光一样，也具有波粒二象性，满足 h h p mv （它既不是机械波，也不是电磁波。） 2. 实验验证： 1927年戴维孙-革末的电子衍射实验证实了德布罗意的假设
二、热辐射基尔霍夫定律
⒈热辐射
热辐射的光谱是连续光谱，并且辐射谱的性质与温度有关。热辐射不一定需要高温，任何温度的物体都发出一定的热辐射。在室温下（不可见的红外光）→500℃（暗红色的可见光）→1500℃（明亮的白炽光、） ⒉单色辐出度M(,T)
从物体表面单位面积发出的、频率在附近的单位频率间隔内的辐射功率（W/(m2 . Hz) ）。即：
dW M , T d
⒊辐出度M0 (T)

7.3普朗克辐射公式和能量子假说

可以算出,腔内在-+d频率范围内,本征模数为
8 2 d ,
c3
瑞利根据热力学中能量均分定理, 认为每一本征振动的动能和势能各占KT/2.因此在-+d频率范围内的能量为
( ,T )d
8 2
c3
kTd ,
式中为黑体腔内的能量密度，K 为玻耳兹曼常数．可以证明
(
,T
)
4 c
r0
(
,T
).
证明
因此有
0,0,2的0,振3动0 几率有如下
0
2 0
30
1: e kT : e kT : e kT
所以,平均能量为
m 0
m0e kT
m0
m 0
0
0
h
h
.
e kT
e kT 1 e kT 1
m0
壁上振子分布应与驻波分布相同, 因此单位体积内频率范围
在 ~ d 内的能量密度为
( )d
8h 3
m1
2L1 cos ,
m2
2L2 cos ,
m3
2L3 cos
.
m1 , m2 , m3 0, 1, 2,
波矢又可以表示为:
kx m1 L1 ,
k y m2 L2 ,
kz m3 L3 .
k 2 2 2 , c / c
k2
2
(
m1 L1
)2
( m2 L2
)2
( m3 L3
k2
( 2 )2
c
k
2 x
k
2 y
k
2 z
可知振动波矢数,即是半径为 2/c的球体内体元数.
因m1、m2、m3为正整数，故对应1/8球体内的体元数：

光学教程(姚启钧) 第7章光的量子性

第7章
光的量子性
Quantum Properties of Light
光的电磁理论揭示了光的电磁波本质，成功地解释了光的干涉、衍射和偏振等光学现象。但是19世纪末以来，许多重要实验的结果与经典电磁波理论相违背，用波动理论解释这些实验中光的行为时遇到了不可克服的困难。这迫使人们对光的本性作进一步的探索，从而导致了光的量子性概念的建立。光的量子性概念的确立及随后量子理论的发展，使人们对微观世界的认识产生了深刻的变化。本章将通过黑体辐射、光电效应和康普顿效应等在科学史上具有重大意义的实验结果及基本规律来阐明光的量子特性。
3
或
M B ( , T )

5
1
——称为普朗克黑体辐射公式普朗克公式与黑体辐射的实验曲线符合的很好。
光学教程
26
普朗克的假设和公式，不仅从理论上解决了黑体辐射问题，而且他的能量量子化的新思想对近代物理学的发展具有深远的影响。从此开创了一个物理学新领域－量子理论。
本节结束
光学教程
19
第7章
光的量子性
Quantum Property of Light
§7.2 普朗克公式能量子
Planck Blackbody Formula and Energy Quantum
斯忒藩－玻尔兹曼定律只给出黑体辐射所发射的包括一切波长（或频率）在内的辐射总能量，而没有涉及到单色辐出度MB(,T)的函数形式。为了从理论上导出与实验结果相符的MB(,T)的解析表达式，19世纪末的许多科学家作出了巨大的努力。
当0时，由瑞利－金斯公式 kT 可得： WB (T ) M B ( , T )d 2c 4 d 0 0 这显然是错误的。经典理论与实验结果在短波部分的严重偏离，在物理学史上，被称为“紫外灾难”。

第七章光的量子性第二节普朗克辐射公式

第七章光的量子性第二节普朗克辐射公式普朗克辐射公式是描述黑体辐射的经典物理学理论，由德国物理学家马克斯·普朗克在1900年提出。

该公式对于理解光的量子性起到了重要的先导作用，为量子力学的发展提供了关键线索。

本节将从普朗克辐射公式的推导、具体表达形式以及其在物理学中的应用等几个方面进行介绍。

首先，我们来看一下普朗克辐射公式的推导过程。

马克斯·普朗克通过对黑体辐射的研究，提出了一个假设，即黑体辐射的能量不是连续的，而是以一种离散的形式存在，这就是所谓的能量量子化的假设。

根据这个假设，普朗克得出了一个公式，即普朗克辐射公式。

在推导普朗克辐射公式时，普朗克引入了一个新的常数，即普朗克常数h，表示能量的量子。

普朗克辐射公式的具体形式为：E = hv接下来，我们来看一下普朗克辐射公式在物理学中的应用。

首先，普朗克辐射公式为热力学的发展提供了重要的依据。

黑体辐射的研究促进了热力学第二定律的建立，同时也揭示了能量的离散性质。

其次，普朗克辐射公式对量子力学的诞生起到了关键作用。

在推导过程中，普朗克通过引入能量量子化的假设，奠定了光的量子性的基础。

这一假设启发了爱因斯坦等物理学家，从而推动了量子力学的发展。

此外，普朗克辐射公式还在其他领域中得到了广泛的应用，如原子物理学、光学等。

最后，我们来总结一下。

普朗克辐射公式是描述黑体辐射的一个经典物理学理论，通过引入能量量子化的假设，奠定了光的量子性的基础。

普朗克辐射公式的推导过程中，普朗克引入了一个常数h，即普朗克常数，表示能量的量子。

该公式在物理学中得到了广泛的应用，不仅对热力学的发展有重要影响，还对量子力学的建立起到了关键作用。

普朗克光量子假说的基本内容

量子假说普朗克最大贡献是在1900年提出了能量量子化，其主要内容是：黑体是由以不同频率作简谐振动的振子组成的，其中电磁波的吸收和发射不是连续的，而是以一种最小的能量单位ε=hν，为最基本单位而变化着的，理论计算结果才能跟实验事实相符，这样的一份能量ε，叫作能量子。

其中v是辐射电磁波的频率，h=6.62559*10^-34Js，即普朗克常数。

也就是说，振子的每一个可能的状态以及各个可能状态之间的能量差必定是hv的整数倍。

受他的启发，爱因斯坦于1905年提出，在空间传播的光也不是连续的，而是一份一份的，每一份叫一个光量子，简称光子，光子的能量E跟光的频率v成正比，即E=hv。

这个学说以后就叫光量子假说。

光子说还认为每一个光子的能量只决定于光子的频率，例如蓝光的频率比红光高，所以蓝光的光子的能量比红光子的能量大，同样颜色的光，强弱的不同则反映了单位时间内射到单位面积的光子数的多少。

普朗克黑体辐射定律：大约是在1894年，普朗克开始把心力全部放在研究黑体辐射的问题上，他曾经委托过电力公司制造能消耗最少能量，但能产生最多光能的灯泡，这一问题也曾在1859年被基尔霍夫所提出：黑体在热力学平衡下的电磁辐射功率与辐射频率和黑体温度的关系。

帝国物理技术学院（Physikalisch-Technischer Reichsanstalt）对这个问题进行了实验研究，但是经典物理学的瑞利-金斯公式无法解释高频率下的测量结果，但这定律却也创造了日后的紫外灾难，威廉·维恩给出了维恩位移定律，可以正确反映高频率下的结果，但却又无法符合低频率下的结果。

这些定律之所以能发起有一小部分是普朗克的贡献，但大多数的教科书却都没有提到他。

普朗克在1899年就率先提出解决此问题的方法，叫做“基础无序原理”（principle of elementary disorder），并把瑞利-金斯定律和维恩位移定律这两条定律使用一种熵列式进行内插，由此发现了普朗克辐射定律，可以很好地描述测量结果，不久后，人们发现他的这项新理论是没有实验证据的，这也让普朗克他在当时感到稍稍的无奈。

能量量子化光的波粒二象性物质波

能量量子化光的波粒二象性物质波●考纲预览●1 普朗克能量子假说黑体和黑体辐射 Ⅰ 德布罗意关系式的定量计算不作要求2 光电效应Ⅰ 3光的波粒二象性物质波Ⅰ■预习内容■：教科版选修3—5 P 19-P 34 创新设计P-P◇知识整理◇：一、普朗克能量子假说黑体和黑体辐射1．普朗克认为，振动着的带电微粒的能量只能是某一最小能量值ε的，这个不可再分的最小能量值ε叫做，能量子公式为ε= 。

当带电微粒辐射或吸收能量时，也是以这个最小能量为单位辐射或吸收的。

2．黑体辐射电磁波的强度按波长的分布只与有关，如图所示。

二、光电效应1．在光(包括不可见光)的照射下从物体发射出的现象叫光电效应。

发射出来的电子叫。

这一现象是由首先发现的。

2．规律（1）存在电流。

（2）存在和。

212e c c m v eU = （3）光电子的最大初动能与入射光的有关，而与入射光的强弱。

（4）效应具有。

光电效应的发生几乎是的，一般不超过 s ； 3．方程：4．E k -ν曲线(如图所示)，由E k -ν曲线可以得到的物理量：（1）：图线与ν轴交点的横坐标。

（2）：图线与E k 轴交点的纵坐标的绝对值。

（3）：图线的斜率。

三、光子说1．内容课前准备区1500K 1300K 1700K 1100K辐射强度波长 O 2μm 4μm 图1 黑体辐射实验规律辐射本领波长O 图2 辐射强度与波长关系瑞利公式实验曲线维恩公式光是地不连续传播的，每一份叫做一个，光子的能量跟它的成正比，即E= (h叫普朗克恒量，h=6.63×10-34J·s)。

2．意义（1）解释了现象；（2）说明了光具有性。

四、光的波粒二象性1．干涉、衍射和偏振表明具有性，光电效应和康普顿效应表明光具有_____ 性，因此现代物理学认为：光具有性。

2．产生的效果往往显示出波动性，产生的效果往往显示出粒子性。

3．的光，其波动性越显著，的光，其粒子性越显著。

《光学》光的量子性71√

光学课件目录
30
1 2 mv eU a 2 U a U 0
(1)
(2)
1 2 mv e eU 0 2
结论：光电子初动能和入射光频率成正比，与入射光光强无关。 3、存在截止频率（红限）对于给定的金属, 当照射光频率 0 小于某一数值 (称为红限)时, 无论照射光多强都不会产生光电效应。
2019/3/10
济南大学物理学院
光学课件目录
15
§7.1.3 黑体辐射的实验规律一、绝对黑体如果一个物体能全部吸收投射在它上面的辐射而无反射，这种物体称为绝对黑体，简称黑体。
a0 ( , t ) 1.
基尔霍夫定律中的普适函数就是黑体的光谱辐出度
e( , t ) r0 ( , t ).
2019/3/10
济南大学物理学院
光学课件目录
31
因为初动能大于零，因而产生光电效应的条件是：
U0 0 . k
0 红限频率（截止频率）
U 0 / k。
4 . 光电效应瞬时响应性质
实验发现，无论光强如何微弱，从光照射到光电
子出现只需要 109 s 的时间。
结论：光电效应的产生几乎无需时间的累积。
（n为正整数）
2019/3/10
济南大学物理学院
光学课件目录
Hale Waihona Puke 23对于频率为的谐振子最小能量为
h
h ——称为普朗克常数。
h 6.63 1034 J s
振子在辐射或吸收能量时，从一个状态跃迁到另一个状态。在能量子假说基础上，普朗克给出了黑体辐射公式。二、普朗克公式
r0 ( , T ) 2hc
e0 ( , T )

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

15
4. 在光电效应驰豫时间问题上，用波动论解释也陷入困境。按照波动论，光波能量是连续传递的，金属中的电子从入射光中获得足够的能量总需要一定的时间，并且光越弱，需要积累的时间越长。
可见，光的波动理论不能解释光电效应的实验规律，说明光的波动论在光电效应问题上又陷入了困境，需要理论创新。
16
J. Jeans 1877－1946
上式称为瑞利－金斯公式，c为光速，k为波耳兹曼常数，k＝1.38×10－23J/K.
3
理论曲线和实验曲线的比较：
由图可以看出，维恩公式在波长较短时与实验结果符合的较好，在长波段与实验结果产生了明显的偏离。而瑞利－金斯公式在波长很长时与实验结果符合较好，在短波部分与实验结果完全不符。
3
或
M B ( , T )
2hc2
1 e
hc kT

5
1
——称为普朗克黑体辐射公式普朗克公式与黑体辐射的实验曲线符合的很好。
7
普朗克的假设和公式，不仅从理论上解决了黑体辐射问题，而且他的能量量子化的新思想对近代物理学的发展具有深远的影响。从此开创了一个物理学新领域－量子理论。
可以证明，维恩公式和瑞利－金斯公式分别是普朗克公式在短波和长波段的极限情况，也可由它导出斯特藩－玻耳兹曼定律和维恩位移定律。可见普朗克的能量子假设说在黑体辐射中取得了巨大的成功。因而获得了1918年诺贝尔物理学奖。
当0时，由瑞利－金斯公式可得： kT WB (T ) M B ( , T )d 2c 4 d 0 0 这显然是错误的。经典理论与实验结果在短波部分的严重偏离，在物理学史上，被称为“紫外灾难”。
4
二. 普朗克公式能量子
普朗克既注意到维恩公式在长波(即低频）方面的不足，又注意到了瑞利－金斯在短波（即高频）方面的不足，为了找到一个符合黑体辐射的表达式， 1900年，他大胆提出了与经典理论相矛盾的，能量量子化假设。他假设： 1. 黑体由许多带电的线性振子组成，振子振动时向外辐射电磁波，各振子的频率不同，每一振子发出一种单色辐射，而整个黑体则发出连续辐射。
13
二. 光电效应与光的波动理论的矛盾
金属内部的电子受原子的束缚不能脱出金属表面，如果电子获得足够的能量，可以摆脱束缚而脱出金属表面。 1. 从光是电磁波的观点来看，光电子的脱出是由于照射到金属表面的光波使金属内的电子作受迫振动，使光波的能量转化为电子的能量。
按照光的波动论，入射光强越大，光波的振幅越大，光波供给电子的能量也越大，电子飞出金属表面后的初动能也应越大，可见光电子的最大初动能应该随入射光强的增加而增加。但实验事实是最大初动能与光强无关。
当两极间加正向电压时，光电流随电压的增加而增加，并在电压足够大时趋向于饱和。
im
i
I2
V g
o
V
这说明入射光强一定时，单位时间从阴极脱出的光电子数n是一定的，当电压大到足以把所有产生的光电子全部拉向阳极时，光电流就达到饱和值Im，再增加电压时电流不会继续增加，则饱和电流为：
I 0 ne
§7.3 普朗克公式能量子
Planck Blackbody Formula and Energy Quantum
斯忒藩－玻尔兹曼定律只给出黑体辐射所发射的包括一切波长（或频率）在内的辐射总能量，而没有涉及到单色辐出度MB(,T)的函数形式。
为了从理论上导出与实验结果相符的MB(,T)的解析表达式，19世纪末的许多科学家作出了巨大的努力。
1
由于他们的理论没有超出经典物理学的传统概念。所以没有取得完全成功。最具代表性的是维恩公式和瑞利－金斯公式。
一. 维恩公式和瑞利－金斯公式
1896年，维恩根据热力学原理，并假设辐射按波长的分布类似于与麦克斯韦速度分布律，导出下列公式：
M B ( , T )
C1

5
e
2 T
C
C1和C2为常数，上式称为维恩公式。
14
2. 光的波动理论也不能解释光电子的最大初动能与入射光频率的线性关系。
因为按照光的波动论，当入射光频率与金属中电子固有频率一致时，产生共振，此时光波传给电子的能量最大，电子脱出后的初动能最大，当入射光为其它频率时，电子受迫振动的振幅较小，从入射光中得到的能量较小，光电子的初动能也较小。即光电子的最大初动能与入射光的频率不会是线性关系。 3. 光的波动论也不能解释红限的存在。按照光的波动论，光的能流密度正比于振幅的平方，不论入射光频率如何，只要足够强，都能提供给电子脱出金属表面所需的能量，即不存在频率红限问题。
普朗克
5
2. 与经典物理中能量变化是连续的概念不同，谐振子的能量只能取某些分立值，这些分立值是某一最小能量单元的整数倍，即，2，3等。这些允许的能量值称为谐振子的能级。称为能量子。所以振子的能量是不连续的。
振子从一个能级跃迁到一个能级而辐射或吸收电磁波时，能量变化也是不连续的，能量的不连续变化称为能量量子化。
1. 饱和电流I0与入射光强成正比，而遏止电压Vg与光强无关。即光电子的最大初动能与入射光强无关。
Hale Waihona Puke 2. 遏止电压Vg与入射光频率成线性关系，即有
Vg k ( 0 )
实验发现，斜率k与阴极材料无关。 3. 光电效应存在截止频率。对每一种材料都存在一个入射光频率0，当入射光的频率小于0时，无论光强多大，照射时间多长，都无光电子发射。频率0称为光电效应的截止频率或频率红限。不同的材料具有不同的红限频率。 4. 光电效应的驰豫时间非常短。光照与光电子发射几乎是同时的。
8
§7.3 光电效应
Photoelectric Effect
金属及其化合物在光波的照射下发射电子的现象称为光电效应，所发射的电子称为光电子。
一. 光电效应的实验规律
当光照射阴极K时，便有光电子脱出，脱出的光电子受电场加速飞向阳极A，而形成电流，这种电流称为光电流。
A
K
9
实验发现，当以一定强度的单色光照射阴极时，改变加在两极上电压V，测得电压V与电流I的关系曲线如图。
10
由曲线可知，电压为零时，光电流并不为零，这说明光电子从阴极脱出时具有初速度，因而具有初动能。
虽无外加电场，但部分电子依靠初动能，仍能到达阳极而形成光电流。
im
i
I2
V g
o
V
当加反向电场时，电场对光电子有阻止作用，只有少量初动能较大的光电子可克服电场到达阳极而形成光电流。随着反向电压的增加，到达阳极A的光电子数减少，光电流也减小。当反向电压到达某一值－Vg时，光电流为零，即最大初动能的光电子也不能到达阳极。Vg称为遏止电压。
2
随后，1900年英国物理学家瑞利（L. Rayleigh, 1842 -1919）和金斯（ J. Jeans1877－1946 ）把分子运动论中的能量按自由度均分原理应用于电磁辐射，导出：
M B ( , T ) 2c
kT
4
Rayleigh,1904年获诺贝尔物理学奖(由于氩原子的发现）
3. 能量子与谐振子的频率成正比:
h
h＝6.626×10－34J/s，称为普朗克常数。
6
4.普朗克根据上述假设，由玻耳兹曼分布，得出谐振子的平均能量为： 0 (k , T ) h e kT 1
得出黑体辐射的单色辐出度的表达式为：
2h 1 M B ( , T ) h c 2 e kT 1
11
遏止电压与最大初动能之间的关系为：
I
Io3 Io2 Io1
1 2 eV g mV m 2
当以同频率，但光强不同的光照射阴极时，有不同的饱和电流。但遏止电压不变。如图
|Vg|
Vg O
光电伏安特性曲线
V
若改变入射光的频率，可得遏止电压与入射光的频率成线性关系。如图
O ν0 ν
分析光电效应的实验结果，可得出下述规律：

第七章光的量子性普朗克公式能量子

合集下载