学科竞赛-NOIP2014提高组复赛试题_2

NOIP2014普及组复赛试题解答3. 螺旋矩阵【问题描述】一个n 行n列的螺旋矩阵可由如下方法生成：从矩阵的左上角（第1行第1列）出发，初始时向右移动：如果前方是未曾经过的格子，则继续前进，否则右转；重复上述操作直至经过矩阵中所有格子。

根据经过顺序，在格子中依次填入1，2，3，…，n2，便构成了一个螺旋矩阵。

现给出矩阵大小n以及i和j,请你求出该矩阵中第i行第j列的数是多少。

【分析】这是个蛇形填数问题。

如果采用先枚举二维数组再找对应的元素方法，由于1 ≤n ≤30,000，需要建立一个 30,000× 30,000的二维数组，结果会发生数据溢出且超出运行内存上限（128M)。

我们可以采用类似贪吃蛇的方法，让它在N×N个方格内自外向内逐格移动，控制其向右转的方向，并计算其长度。

解法一#include<cstdio>using namespace std;bool pd(int,int) ;int i,j;bool p;int main(){int n,x,y,u,d,l,r,tot=0; // U为上边界，D为下边界，L为左边界，R为右边界；freopen("matrix.in","r",stdin);freopen("matrix.out","w",stdout);scanf("%d%d%d",&n,&i,&j);d=n;r=n;u=1;l=1; //各边界赋初值；x=1;y=0;p=true;while((tot<n*n)&&p){while((y<r)&&p){++y;++tot;pd(x,y);}--r;//在上侧边界上向右移动，当上侧一行的结束时，控制其右边界向左缩一列；while((x<d)&&p){++x;++tot;pd(x,y);}--d;//在右侧边界上向下移动，当右侧一列的结束时，控制其下边界向上缩一行；while((y>l)&&p){--y;++tot;pd(x,y);}++l;//在下侧边界上向左移动，当下侧一行的结束时，控制其左边界向右缩一列；while((x>u+1)&&p){--x;++tot;pd(x,y);}++u;//在左侧边界上向上移动，当左侧一列的结束时，控制其上边界向下缩一行；}printf("%d\n",tot);fclose(stdin);fclose(stdout);return 0;}bool pd(int x,int y) //判断是否到达目的地，如果到达则停止枚举；{if((x==i)&&(y==j))p=false;return P;}解法二：在上一个解法中，如果遇到极端情况时，可能需要枚举达900000000次，这显然太慢了些，我们可以根据贪吃移动的特点对程序进行优化。

1.珠心算测验注意看清题意：其中有多少个数，恰好等于集合中另外两个(不同的)数之和。

这样的题意加上100的规模，建议暴力3个for:#include<cstdio>#include<cstring>#include<algorithm>#include<iostream>using namespace std;int n;int a[105];int main(){freopen("count.in","r",stdin);freopen("count.out","w",stdout);scanf("%d",&n);for(int i=1; i<=n; i++){scanf("%d",&a[i]);}sort(a+1,a+n+1);int res=0;for(int i=1; i<=n; i++){int ok=0;for(int j=1; j<=n && !ok; j++) if(j!=i){for(int k=1; k<=n && !ok; k++) if(a[k]!=a[j]){if(a[j]+a[k]==a[i]) ok=1;}}res+=ok;}printf("%d\n",res);return 0;}2.比例简化L很小，还是枚举，然后比较的话建议用乘法比较，避免精度问题：#include<cstdio>#include<cstring>#include<iostream>using namespace std;int A,B,L;int gcd(int a,int b){if(b==0) return a;return gcd(b,a%b);}int main(){freopen("ratio.in","r",stdin);freopen("ratio.out","w",stdout);scanf("%d%d%d",&A,&B,&L);int ba=1000000,bb=1;for(int i=1; i<=L; i++){for(int j=1; j<=L; j++){if(gcd(i,j)==1 && i*B>=j*A){if(ba*j>=bb*i){ba=i, bb=j;}}}}printf("%d %d\n",ba,bb);return 0;}3.螺旋矩阵没一圈的数量有规律的，最外面一圈(n-1)*4，然后每往里n-2，直到后要么只有一个点，要么4个点。

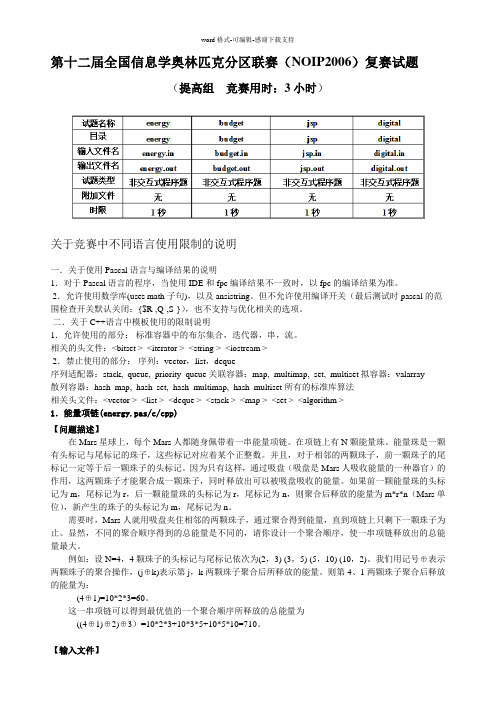
第十二届全国信息学奥林匹克分区联赛（NOIP2006）复赛试题（提高组竞赛用时：3小时）关于竞赛中不同语言使用限制的说明一．关于使用Pascal语言与编译结果的说明1．对于Pascal语言的程序，当使用IDE和fpc编译结果不一致时，以fpc的编译结果为准。

2．允许使用数学库(uses math子句)，以及ansistring。

但不允许使用编译开关（最后测试时pascal的范围检查开关默认关闭：{$R-,Q-,S-}），也不支持与优化相关的选项。

二．关于C++语言中模板使用的限制说明1．允许使用的部分：标准容器中的布尔集合，迭代器，串，流。

相关的头文件：<bitset > <iterator > <string > <iostream >2．禁止使用的部分：序列：vector，list，deque序列适配器：stack, queue, priority_queue 关联容器：map, multimap, set, multiset 拟容器：valarray 散列容器：hash_map, hash_set, hash_multimap, hash_multiset 所有的标准库算法相关头文件：<vector > <list > <deque > <stack > <map > <set > <algorithm >1．能量项链(energy.pas/c/cpp)【问题描述】在Mars星球上，每个Mars人都随身佩带着一串能量项链。

在项链上有N颗能量珠。

能量珠是一颗有头标记与尾标记的珠子，这些标记对应着某个正整数。

并且，对于相邻的两颗珠子，前一颗珠子的尾标记一定等于后一颗珠子的头标记。

因为只有这样，通过吸盘（吸盘是Mars人吸收能量的一种器官）的作用，这两颗珠子才能聚合成一颗珠子，同时释放出可以被吸盘吸收的能量。

第十届全国信息学奥林匹克分区联赛（NOIP2004）复赛试题（提高组竞赛用时：3小时）1、津津的储蓄计划(Save.pas／dpr／c／cpp)【问题描述】津津的零花钱一直都是自己管理。

每个月的月初妈妈给津津300元钱，津津会预算这个月的花销，并且总能做到实际花销和预算的相同。

为了让津津学习如何储蓄，妈妈提出，津津可以随时把整百的钱存在她那里，到了年末她会加上20％还给津津。

因此津津制定了一个储蓄计划：每个月的月初，在得到妈妈给的零花钱后，如果她预计到这个月的月末手中还会有多于100元或恰好100元，她就会把整百的钱存在妈妈那里，剩余的钱留在自己手中。

例如11月初津津手中还有83元，妈妈给了津津300元。

津津预计11月的花销是180元，那么她就会在妈妈那里存200元，自己留下183元。

到了11月月末，津津手中会剩下3元钱。

津津发现这个储蓄计划的主要风险是，存在妈妈那里的钱在年末之前不能取出。

有可能在某个月的月初，津津手中的钱加上这个月妈妈给的钱，不够这个月的原定预算。

如果出现这种情况，津津将不得不在这个月省吃俭用，压缩预算。

现在请你根据2004年1月到12月每个月津津的预算，判断会不会出现这种情况。

如果不会，计算到2004年年末，妈妈将津津平常存的钱加上20％还给津津之后，津津手中会有多少钱。

【输入文件】输入文件save.in包括12行数据，每行包含一个小于350的非负整数，分别表示1月到12月津津的预算。

【输出文件】输出文件save.out包括一行，这一行只包含一个整数。

如果储蓄计划实施过程中出现某个月钱不够用的情况，输出-X，X表示出现这种情况的第一个月；否则输出到2004年年末津津手中会有多少钱。

【样例输入1】29023028020030017034050908020060【样例输出1】-7【样例输入2】29023028020030017033050908020060【样例输出2】1580【问题描述】在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。

Day1铺地毯【问题描述】为了准备一个独特的颁奖典礼，组织者在会场的一片矩形区域（可看做是平面直角坐标系的第一象限）铺上一些矩形地毯。

一共有n 张地毯，编号从1 到n。

现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设，后铺的地毯覆盖在前面已经铺好的地毯之上。

地毯铺设完成后，组织者想知道覆盖地面某个点的最上面的那张地毯的编号。

注意：在矩形地毯边界和四个顶点上的点也算被地毯覆盖。

【输入】输入文件名为 carpet.in。

输入共 n+2 行。

第一行，一个整数 n，表示总共有n 张地毯。

接下来的 n 行中，第i+1 行表示编号i 的地毯的信息，包含四个正整数a，b，g，k，每两个整数之间用一个空格隔开，分别表示铺设地毯的左下角的坐标（a，b）以及地毯在x轴和y 轴方向的长度。

第 n+2 行包含两个正整数x 和y，表示所求的地面的点的坐标（x，y）。

【输出】输出文件名为 carpet.out。

输出共 1 行，一个整数，表示所求的地毯的编号；若此处没有被地毯覆盖则输出-1。

【输入输出样例 1】【输入输出样例说明】如下图，1 号地毯用实线表示，2 号地毯用虚线表示，3 号用双实线表示，覆盖点（2，2）的最上面一张地毯是3 号地毯。

【输入输出样例 2】【输入输出样例说明】如上图，1 号地毯用实线表示，2 号地毯用虚线表示，3 号用双实线表示，点（4，5）没有被地毯覆盖，所以输出-1。

【数据范围】对于 30%的数据，有n≤2；对于 50%的数据，0≤a, b, g, k≤100；对于 100%的数据，有0≤n≤10,000，0≤a, b, g, k≤100,000。

【一句话题意】给定n个按顺序覆盖的矩形，求某个点最上方的矩形编号。

【考察知识点】枚举【思路】好吧我承认看到图片的一瞬间想到过二维树状数组和二维线段树。

置答案ans=-1，按顺序枚举所有矩形，如果点在矩形内则更新ans。

注意题中给出的不是对角坐标，实际上是(a,b)与(a+g,b+k)。

1．某监狱里有个很长的走廊，走廊中一个接一个地有N个房间。

每个房间中锁着一个犯人。

一天夜里，狱警决定玩一个无聊游戏。

第1轮中，他喝了一口威士忌，然后打开每个房间。

第2轮，他喝了一口威士忌，然后按2的倍数遍历每个房间。

第3轮，他又喝了一口威士忌，然后遍历所有3的倍数的房间。

依次类推。

在遍历中，如果房间是锁着的，则打开；否则锁上。

他这样重复N轮，最终醉酒。

这时有些囚犯看到自己房间的锁被打开了，他们立即逃跑。

对于有N个房间的走廊，最终会有多少囚犯逃脱？输入：输入数据的第一行中有一个整数，表示有多少组测试数据。

接下来的若干行每行包含一个值为5-100的整数，这是房间的数目。

输出：对应输入数据输出多行，每行一个整数，表示逃脱的囚犯数量。

样例输入：25100样例输出：210var n,num,s,m,i,k,j:integer;a:array[0..200]of boolean;begin readln(num);for i:=1 to num dobegin readln(n);fillchar(a,sizeof(a),true);for j:=1 to n dofor k:=1 to n doif k mod j=0 then a[k]:=not a[k];s:=0;for j:=1 to n doif a[j]=false then inc(s);writeln(s);end;end. 输入3 10 35 50输出3 5 7输入3 22 68 99 输出 4 8 9输入5 10 30 60 85 100 输出 3 5 7 9 10一个自然数，若它的素因数至少是两重的（相同的素因数至少个数为二个，如：24=2*2*2*3，则称该数为“漂亮数”。

若相邻的两个自然数都是“漂亮数”，就称它们为“孪生漂亮数”，例如8和9就是一对“孪生漂亮数”。

输入X,Y,编程找出[X,Y]之间的所有“孪生漂亮数”。

如输入2 25,则输出8 924 25var i,n,a,t,x,y,s:longint; f :boolean;begin readln(x,y);a:=x;repeata:=a+1;n:=a;f:=false; i:= 2 ;while n >= i do begint:=0;while n mod i = 0 do begint:=t+1;n := n div i;end;if t>=2 then f:=true;i := i+1;end;if f then beginn:=a+1;f:=false; i:= 2 ;while n >= i do begint:=0;while n mod i = 0 do begint:=t+1;n := n div i;end;if t>=2 then f:=true;i := i+1;end; end;if f then begin s:=s+1; writeln(a,’‘,a+1);end;until a=y;readln;end.输入50 120输出63 64 75 76 80 81 98 99 99 100 116 117 120 121 输入354 480 输出360 361 363 364 368 369 。

1. 珠心算测验【问题描述】 珠心算是一种通过在脑中模拟算盘变化来完成快速运算的一种计算技术。

珠心算训练，既能够开发智力，又能够为日常生活带来很多便利，因而在很多学校得到普及。

某学校的珠心算老师采用一种快速考察珠心算加法能力的测验方法。

他随机生成一个正整数集合，集合中的数各不相同，然后要求学生回答：其中有多少个数，恰好等于集合中另外两个（不同的）数之和？ 最近老师出了一些测验题，请你帮忙求出答案。

【输入】输入文件名为count.in 。

输入共两行，第一行包含一个整数n ，表示测试题中给出的正整数个数。

第二行有n 个正整数，每两个正整数之间用一个空格隔开，表示测试题中给出的正整数。

【输出】输出文件名为count.out 。

输出共一行，包含一个整数，表示测验题答案。

【输入输出样例】 count.in count.out 4 1 2 3 42【样例说明】由1+2=3，1+3=4，故满足测试要求的答案为2。

注意，加数和被加数必须是集合中的两个不同的数。

【数据说明】对于100%的数据，3 ≤ n ≤ 100，测验题给出的正整数大小不超过10,000。

2.比例简化【问题描述】在社交媒体上，经常会看到针对某一个观点同意与否的民意调查以及结果。

例如，对某一观点表示支持的有1498人，反对的有902人，那么赞同与反对的比例可以简单的记为1498:902。

不过，如果把调查结果就以这种方式呈现出来，大多数人肯定不会满意。

因为这个比例的数值太大，难以一眼看出它们的关系。

对于上面这个例子，如果把比例记为5:3，虽然与真实结果有一定的误差，但依然能够较为准确地反映调查结果，同时也显得比较直观。

现给出支持人数A，反对人数B，以及一个上限L，请你将A比B化简为A’比B’，要求在A’和B’均不大于L且A’和B’互质（两个整数的最大公约数是1）的前提下，A’/B’≥A/B 且A’/B’ - A/B的值尽可能小。

【输入】输入文件名为ratio.in。

老师给笑笑布置了一份作业，笑笑不知如何解决。

老师给了一串很长的数列，要求从中找出连续的一段来使的总和最大。

【输入文件】：第一行包含一个整数n，表示数列的长度。

(n<=100000)第二行包含n个整数来描述这个数列，每个整数的的绝对值不超过1000。

【文件输出】：文件中只有一个整数，为最大的连续段总和。

【输入样例】:51 -23 1 -4【输出样例】4vars:array[1..10000] of longint;n,ii,t,ans:longint;beginreadln(n);for i:=1 to n doread(s[i]);t:=s[1];ans:=s[1];for i:=2 to n dobeginif t<0 then t:=s[i] else t:=t+s[i];if t>ans then ans:=t;end;writeln(ans);end.输入61 5 4 -2 63 输出17输入1024 -12 9 11 7 20 -8 15 3 18 输出87输入710 8 9 -5 12 6 11 输出51输入205 12 19 20 -7 -6 18 22 19 8 11 33 15 32 17 -30 4 14 24 -13输出230【问题描述】鲁宾逊先生有一只宠物猴，名叫多多。

这天，他们两个正沿着乡间小路散步，突然发现路边的告示牌上贴着一张小小的纸条：“欢迎免费品尝我种的花生！——熊字”。

鲁宾逊先生和多多都很开心，因为花生正是他们的最爱。

在告示牌背后，路边真的有一块花生田，花生植株整齐地排列成矩形网格（如图1）。

有经验的多多一眼就能看出，每棵花生植株下的花生有多少。

为了训练多多的算术，鲁宾逊先生说：“你先找出花生最多的植株，去采摘它的花生；然后再找出剩下的植株里花生最多的，去采摘它的花生；依此类推，不过你一定要在我限定的时间内回到路边。

”我们假定多多在每个单位时间内，可以做下列四件事情中的一件：1)从路边跳到最靠近路边（即第一行）的某棵花生植株；2)从一棵植株跳到前后左右与之相邻的另一棵植株；3)采摘一棵植株下的花生；4)从最靠近路边（即第一行）的某棵花生植株跳回路边。

NOIP2013一、单项选择题（共15 题，每题1.5 分，共计22.5 分；每题有且仅有一个正确选项）1.一个32 位整型变量占用（）个字节。

A. 4B. 8C. 32D. 1282.二进制数11.01 在十进制下是（）。

A. 3.25B. 4.125C. 6.25D. 11.1253.下面的故事与（）算法有着异曲同工之妙。

从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事：‚从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事：‘从前有座山，山里有座庙，庙里有个老和尚给小和尚讲故事....’‛A. 枚举B. 递归C. 贪心D. 分治4.1948 年，（）将热力学中的熵引入信息通信领域，标志着信息论研究的开端。

A. 冯·诺伊曼（John von Neumann）B. 图灵（Alan Turing）C. 欧拉（Leonhard Euler）D. 克劳德·香农（ClaudeShannon）5.已知一棵二叉树有2013 个节点，则其中至多有（）个节点有2 个子节点。

A. 1006B. 1007C. 1023D. 10246.在一个无向图中，如果任意两点之间都存在路径相连，则称其为连通图。

右图是一个有5 个顶点、8 条边的连通图。

若要使它不再是连通图，至少要删去其中的（）条边。

A. 2B. 3C. 4D. 57.斐波那契数列的定义如下：F1 = 1, F2 = 1, Fn = Fn –1 + Fn –2 (n ≥3)。

如果用下面的函数计算斐波那契数列的第n 项，则其时间复杂度为（）。

int F(int n){if (n <= 2)return 1;elsereturn F(n - 1) + F(n - 2);}A. O(1)B. O(n)C. O(n2)D. O(Fn)8.二叉查找树具有如下性质：每个节点的值都大于其左子树上所有节点的值、小于其右子树上所有节点的值。

那么，二叉查找树的（）是一个有序序列。