山东省潍坊市2013届高三第二次模拟文科数学_Word版

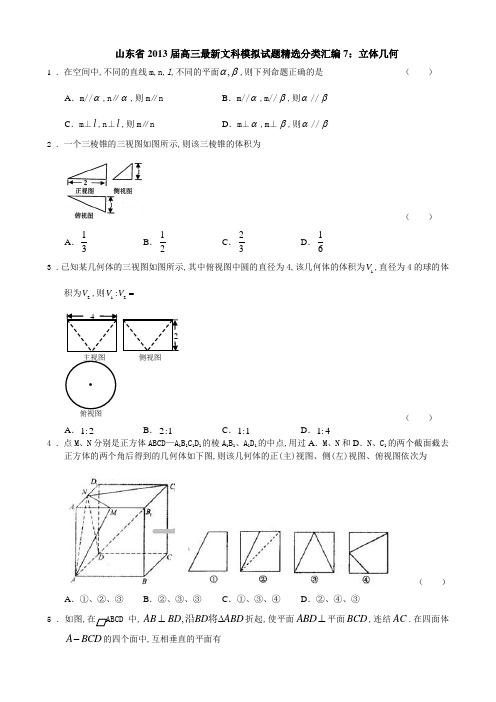
山东省2013届高三最新文科模拟试题精选分类汇编7：立体几何1 ．在空间中,不同的直线m,n,l ,不同的平面,αβ,则下列命题正确的是（ ）A ．m//α,n∥α,则m∥nB ．m//α,m//β,则α//βC ．m⊥l ,n⊥l ,则m∥nD ．m⊥α,m⊥β,则α//β2 ．一个三棱锥的三视图如图所示,则该三棱锥的体积为（ ）A ．13B ．12C ．23D ．163 ．已知某几何体的三视图如图所示,其中俯视图中圆的直径为4,该几何体的体积为1V ,直径为4的球的体积为2V ,则12:V V =（ ）A ．1:2B ．2:1C ．1:1D ．1:44 ．点M 、N 分别是正方体ABCD —A 1B 1C 1D 1的棱A 1B 1、A 1D 1的中点,用过A ．M 、N 和D ．N 、C 1的两个截面截去正方体的两个角后得到的几何体如下图,则该几何体的正(主)视图、侧(左)视图、俯视图依次为（ ）A ．①、②、③B ．②、③、③C ．①、③、④D ．②、④、③5 ．如图,中,,AB BD BD ABD ⊥∆沿将折起,使平面ABD ⊥平面BCD ,连结AC .在四面体A BCD -的四个面中,互相垂直的平面有侧视图（ ）A ．1对B ．2对C ．3对D ．4对6 ．如右图,一个由两个圆锥组合而成的空间几何体的正视图和侧视图都是边长为1、一个内角为60°的菱形,俯视图是圆及其圆心,那么这个几何体的体积为（ ）A．12B ．6ππC ．12π D．67 ．已知m,n 是两条不同直线,,αβ是两个不同平面,给出四个命题:①若,,m n n m αβα=⊂⊥ ,则αβ⊥ ②若,m m αβ⊥⊥,则//αβ ③若,,m n m n αβ⊥⊥⊥,则αβ⊥ ④若//,////m n m n αβ,则//αβ 其中正确的命题是 （ ）A ．①②B ．②③C ．①④D ．②④8 ．某几何体的三视图如右图所示,则该几何体的表面积为A ．π)55(+B ．π)5220(+俯视图左视图主视图C ．π)1010(+D ．π)525(+9 ．一个几何体的三视图如右图所示,则它的体积为（ ）A ．203 B．403C ．20D ．4010．一个几何体的三视图如图所示,其中俯视图与左视图均为半径是2的圆,则这个几何体的体积是（ ）A ．323πB ．8πC ．163πD ．32π11．有一平行六面体的三视图如图所示,其中俯视图和左视图均为矩形,则这个平行六面体的表面积为（ ）A．B．6+C．30+D ．4212．已知四面体S ABC -的所有棱长都相等,它的俯视图如下图所示,的正方形;则四面体S ABC -外接球的表面积为正视图 俯视图左视图第11题图（ ）A ． 6πB ．4πC ．8πD ．3π13．已知直线l ⊥平面α,直线m ⊂平面β,下列命题正确的是①l m a ⊥⇒∥β；②l ∥m αβ⇒⊥③l αβ⊥⇒∥m ④α∥l m β⇒⊥（ ） A ．①② B ．③④C ．②④D ．①③14．已知m ,n 为两条不同的直线,α、β为两个不同的平面,则下列命题中正确的是（ ）A ．若l m ⊥,l n ⊥,且,m n α⊂,则l α⊥B ．若平面α内有不共线的三点到平面β的距离相等,则βα//C ．若n m m ⊥⊥,α,则α//nD ．若α⊥n n m ,//,则α⊥m15．具有如图所示的正视图和俯视图的几何体中,体积最大的几何体的表面积为（ ）A ．3B ．C ．72π (D)1416．一个几何体的三视图如图所示,则该几何体的体积为（ ）A．1B．13C．12D．3217．如图,,且一个内角为60°的菱形,俯视图为正方形,那么这个几何体的表面积为（）A．B．C．4 D．818．右图是一个几何体的正(主)视图和侧(左)视图,其俯视图是面积为.则该几何体的表面积是（）A．8 B．20+C．16 D．24+19．一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为（）A．9B．10C．11D．22320．一空间几何体的三视图如图所示,则此几何体的直观图为21．一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是（ ）A ．1B ．2C ．3D ．422．一个几何体的三视图如图所示,其中的长度单位为cm,则该几何体的体积为( )cm 3.（ ）A ．18B ．48C ．45D ．54 23．一个底面是正三角形的三棱柱的侧视图如图所示,则该几何体的侧面积．．．等于（ ）A B ．6C ．第5题图24．如图,已知球O 的面上有四点,,,A B C D ,DA ⊥平面ABC ,AB BC ⊥,2DA AB BC ===,则球O的体积与表面积的比为__________25．一空间几何体的三视图如图所示,该几何体的体积为163π+,则图中x 的值为_______________.26．已知矩形ABCD 的顶点都在半径为5的球O 的球面上,且8,AB BC ==则棱锥O —ABCD 的体积为______.27．已知一圆柱内接于球O,且圆柱的底面直径与母线长均为2,则球为O 的表面积为_____. 28．某几何体的三视图如图所示,则它的表面积是________29．某几何体的三视图如右图所示,则该几何体的表面积等于_______30．31．已知在如图的多面体中,AE ⊥底面BEFC ,//AD //EF BC ,12BE AD EF BC ===,G 是BC 的中点.(1)求证://AB 平面DEG ;(2)求证:EG ⊥平面BDF .32．如图,在多面体ABCDEFG 中,平面ABC ∥平面DEFG ,AD ⊥平面DEFG ,BA AC ⊥,DG ED ⊥,EF ∥DG .且1,2AC AB ED EF ==== , 4AD DG ==.(Ⅰ)求证:BE ⊥平面DEFG ; (Ⅱ)求证:BF ∥平面ACGD ; (Ⅲ)求三棱锥A FBC -的体积.ADFEBGC第20题图33．如图,斜三棱柱111A B C ABC -中,侧面11AAC C⊥底面ABC ,底面ABC 是边长为2的等边三角形,侧面11AAC C 是菱形,160A AC ∠=,E 、F 分别是11AC 、AB 的中点.求证:(1)EC ABC ⊥平面;(2)求三棱锥1A EFC -的体积.34．如图所示,PA⊥平面ABCD,四边形ABCD 为正方形,且2PA=AD=2,E 、F 、G 分别是线段PA 、PD 、CD 的中点.(Ⅰ)求异面直线EF 与AG 所成角的余弦值; (Ⅱ)求证:BC∥面EFG;(Ⅲ)求三棱锥E-AFG 的体积.35．如图,在四棱锥S-ABC 中,底面ABCD 是矩形,SA ⊥底面ABCD,SA=AD,点M 是SD 的中点,AN ⊥SC,且交SC于点N.(I)求证:SB∥平面ACM;ADE FP G1ABCD E G F(II)求证:平面SAC⊥平面AMN.ADNM平面ABCD,P为36．在如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面⊥DN的中点.BD⊥;(Ⅰ)求证:MC(Ⅱ)在线段AB是是否存在点E,使得AP//平面NEC,若存在,说明其位置,并加以证明;若不存在,请说明理由.37．已知某几何体的直观图和三视图如下图所示,其主(正)视图为矩形,左(侧)视图为等腰直角三角形,俯视图为直角梯形.(I)求证:BC∥平面C1B1N;(Ⅱ)求证:BN⊥平面C1B1 N;(Ⅲ)求此几何体的体积.38．如图,已知平面ABEF ⊥平面A B C D,四边形ABEF 为矩形,四边形ABCD 为直角梯形,90,DAB AB CD ∠=︒ ,4,28AD AF AB CD ====.(Ⅰ)求证:AF 平面BCE ; (Ⅱ)求证:AC ⊥平面BCE ; (Ⅲ)求四棱锥C ABEF -的体积.39．如图(1),在等腰梯形CDEF 中,CB 、DA 是梯形的高,2AE BF ==,AB =现将梯形沿CB 、DA 折起,使EF//AB 且2EF AB =,得一简单组合体ABCDEF 如图(2)示,已知,,M N P 分别为,,AF BD EF 的中点.(1)求证://MN 平面BCF ;(2)求证:AP ⊥平面DAE ;(3)若2AD =,求四棱锥F-ABCD 的体积.D C B AE FM NP FE A BCD 40．如图,已知三棱柱ABC 一A 1B 1C 1中,AA 1⊥底面ABC,AC=BC,M,N 分别是棱CC 1,AB 的中点.(1)求证:CN⊥平面ABB 1A 1; (2)求证:CN//平面AMB 1.41．在如图所示的几何体中,ABC ∆是边长为2的正三角形,1,AE AE =⊥平面ABC,平面BCD ⊥平面ABC,BD=CD,且.BD CD ⊥(I)AE//平面BCD;(II)平面BDE ⊥平面CDE.42．如图,已知AB ⊥平面ACD,DE//AB,△ACD 是正三角形,2,AD DE AB ==且F 是CD 的中点.(I)求证:AF//平面BCE;(II)求证:平面BCE ⊥.43．已知正三棱柱111ABC A B C -中,AB =2,1AA =,点D 为AC 的中点,点E 在线段1AA 上(I)当1:1:2AE EA =时,求证1DE BC ⊥;(Ⅱ)是否存在点E,使三棱锥1C BDE -的体积恰为三棱柱111ABC A B C -体积的13,若存在,求AE 的长,若不存在,请说明理由.44．如图,PA 垂直于矩形ABCD 所在的平面,2,AD PA CD ===E 、F 分别是AB 、PD 的中点.(I)求证:AF//平面PCE; (II)求证:平面PCE ⊥平面PCD;(III)求四面体PEFC 的体积.第19题图45．如图,五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面ABF是等边三角形,棱EF//BC,且EF=12 BC.(I)证明:EO//面ABF;(Ⅱ)若EF=EO,证明:平面EFO⊥平面ABE.46．在如图所示的几何体中,四边形ABCD为矩形,EA⊥平面ABCD,EF// AB,AB=4,AE=EF =2.(1)若G为BC的中点,求证:FG∥平面BDE;(2)求证:AF⊥平面FBC.47．如图,四边形ABCD中,AB AD⊥,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD⊥平面EFDC,设AD中点为P.( I )当E为BC中点时,求证:CP//平面ABEF(Ⅱ)设BE=x,问当x为何值时,三棱锥A-CDF的体积有最大值?并求出这个最大值.48．如图所示,ABCD 是边长为a 的正方形,△PBA 是以角B 为直角的等腰三角形,H 为BD 上一点,且 AH⊥平面PDB.(1)求证:平面ABCD⊥平面APB;(2)点G 为AP 的中点,求证:AH=BG.49．如图,四棱锥P A B C D-中,底面A B C D 是平行四边形,90ACB ∠= ,平面PAD ⊥平面ABCD,1PA BC ==,PD AB ==、F 分别为线段PD 和BC 的中点 (I)求证://CE 平面PAF; (Ⅱ)求三棱锥P AEF -的体积.50．如图,在四棱锥P —ABCD 中,平面PAB ⊥平面ABCD,AB=AD,60BAD ∠=,E,F 分别是AP,AB 的中点. 求证:(I)直线EF//平面PBC;(II)平面DEF ⊥平面PAB.51．如图,几何体111ABCD B C D -中,四边形ABCD 为菱形,60BAD ∠=,AB a =,面111B C D ∥面ABCD ,1BB 、1CC 、1DD 都垂直于面ABCD ,且1BB =,E 为1CC 的中点. (Ⅰ)求证:1DB E ∆为等腰直角三角形;(Ⅱ)求证:AC ∥面1DB E .52．已知四棱锥P-ABCD 中,底面ABCD 是菱形,PA=PD,∠BAD=60°,E 是AD 的中点,点Q 在侧棱PC 上.(1)求证:AD⊥平面PBE; (2)若Q 是PC 的中点,求证PA∥平面BDQ;(3)若3P BCDE Q ABCD V V --=,试求CP CQ的值.53．如图所示,PA ^平面ABC ,点C 在以AB 为直径的⊙O 上,30CBA ? ,2PA AB ==,点E 为线段PB 的中点,点M 在弧AB 上,且OM ∥AC .(1)求证:平面MOE ∥平面PAC ;(2)求证:平面PAC ^平面PCB ;(3)求三棱锥O PBC -的体积.M EB OCAP54．如图,已知在直四棱柱ABCD -A 1B 1C 1D 1中,DC AD ⊥,AB //DC ,DC =DD 1=2AD =2AB =2.(Ⅰ)求证:⊥DB 平面B 1BCC 1;(Ⅱ)设E 是DC 上一点,试确定E 的位置,使得D 1E //平面A 1BD ,并说明理由.1第20题图。

山东省潍坊市2013年高考模拟考试数 学（文史类） 2013 4本试卷共4页，分第1卷（选择题）和第Ⅱ卷（非选择题）两部分共150分考试时间120分钟．第Ⅰ卷（选择题共60分）注意事项：1．答第1卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上2．每题选出答案后，用2B 铅笔把答题卡对应题目的答案标号涂黑如需改动，用橡皮擦干净后， 再改涂其它答案标号一、 选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中只有一项是符合题目要求的1．复数31i z i=+复平面内对应的点位于 A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限【答案】C 3(1)111=11(1)(1)222i i i i i z i i i i i -----====--+++-，对应点的坐标为11(,)22--，为第三象限，选C.2．在△ABC 中，“30A ∠= ”是“1sin 2A =”的 A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件【答案】A 由1sin 2A =得30360A k =+⋅ 或150360A k =+⋅ ，所以“30A ∠= ”是“1sin 2A =”的充分不必要条件，选A.3．集合{}{}2|60,|,04A x x x B y y x x =+-≤==≤≤．则()R A B = ð A ．[]3,2- B ． [)(]2,00,3- C ． []3,0- D ．[)3,0-【答案】D 由{}2|60{32}A x x x x x =+-≤=-≤≤，{}|,04{02}B y y x x y y ==≤≤=≤≤，所以{20}R B x x x =><或ð，所以(){30}R A B x x =-≤< ð，所以选D.4．已知双曲线22221x y a b-=的实轴长为2，焦距为4，则该双曲线的渐近线方程是 A ．3y x =± B ．33y x =± C ．3y x =± D ．2y x =± 【答案】C 由题意知22,24a c ==，所以1,2a c ==，所以223b c a =-=。

各地解析分类汇编:函数（2）1 【山东省兖州市2013届高三9月入学诊断检测 文】下列函数中，既是偶函数，又在区间（1,2）内是增函数的为( )A y=cos2x ，x ∈R B. y=log 2|x|，x ∈R 且x ≠0C. y=2xxe e --，x ∈R D.31y x =+，x ∈R【答案】B【解析】A,B 为偶函数，C 为奇函数，D 为非奇非偶函数，排除C,D.当0x >时，22log log y x x ==单调递增，选B.2 【山东省兖州市2013届高三9月入学诊断检测 文】函数ln xy x=的图像大致是( )A ．B ．C ．D ．【答案】A【解析】函数的定义域为(0,)+∞，当01x <<时，0y <，当1x =时，0y =，当1x >时，0y >，综上可知选A.3 【山东省烟台市莱州一中20l3届高三第二次质量检测 （文）】函数()()l g 21x f x =+-的定义域为 A.(),1-∞B.(]0,1C.()0,1D.()0,+∞【答案】C【解析】要使函数有意义，则有21010x x ⎧->⎨->⎩，即01x x >⎧⎨<⎩，所以01x <<，即函数定义域为()0,1，选C.4 【山东省烟台市莱州一中20l3届高三第二次质量检测 （文）】三个数60.7，0.76，log 0.76的大小顺序是 A.0.76＜log 0.76＜60.7B.0.76＜60.7＜log 0.76C.log 0.76＜60.7＜0.76D. 60.70.7log 60.76<<【答案】D【解析】0.761>,600.71<<,0.7log 60<，所以60.70.7log 60.76<<，选D. 5 【山东省烟台市莱州一中20l3届高三第二次质量检测 （文）】定义运算ab c dad bc =-，函数()123x xx f x --+=图象的顶点坐标是(),m n ，且k 、m 、n 、r 成等差数列，则k+r 的值为 A.-5B.14C.-9D.-14【答案】C【解析】由定义可得22()(1)(3)2()43(2)7f x x x x x x x =-+--=+-=+-，函数图象的定点坐标为(2,7)--，即2,7m n =-=-。

山东省2014届高三文科数学一轮复习之2013届名校解析试题精选分类汇编5：数列一、选择题1 ．（【解析】山东省青岛一中2013届高三1月调研考试文科数学）已知数列{n a }满足*331log 1log ()n n a a n ++=∈N ,且2469a a a ++=,则15793log ()a a a ++的值是 （ ）A ．15-B ．5-C ．5D ．15【答案】B 【解析】由*331log 1log ()n n a a n ++=∈N ,得313log log 1n n a a +-=,即13log 1n na a +=,解得13n n a a +=,所以数列{}n a 是公比为3的等比数列.因为3579246()a a a a a a q ++=++,所以35579933a a a ++=⨯=.所以5515791333log ()log 3log 35a a a ++==-=-,选 B ．2 ．（【解析】山东省德州市2013届高三3月模拟检测文科数学）若正项数列{}n a 满足1111n n ga ga +=+,且a 2001+a 2002+a 2003+a 2010=2013,则a 2011+a 2012+a 2013+a 2020的值为（ ）A ．2013·1010B ．2013·1011C ．2014·1010D ．2014·1011【答案】A 由条件知1111lg1n n n n a ga ga a ++-==,即110n naa +=为公比是10的等比数列.因为102001201020112020()a a q a a ++=++ ,所以1020112020201310a a ++=⋅ ,选A ．3 ．（【解析】山东省实验中学2013届高三第一次诊断性测试数学（文）试题）在各项均为正数的等比数列{}n a 中,31,1,s a a ==则2326372a a a a a ++=（ ）A ．4B ．6C ．8D．8-【答案】C 【解析】在等比数列中,23752635,a a a a a a a ==,所以22232637335522a a a a a a a a a ++=++22235()11)8a a =+=+==,选C ．4 ．（【解析】山东省济宁市2013届高三1月份期末测试（数学文）解析）已知函数()()2cos f n n n π=,且()()1,n a f n f n =++则123100a a a a +++⋅⋅⋅+=（ ）A ．100-B ．0C ．100D ．10200【答案】A 解:若n 为偶数,则()()221=(1)(21)na f n f n n n n =++-+=-+,为首项为25a =-,公差为4-的等差数列;若n 为奇数,则()()221=(1)21n a f n f n n n n =++-++=+,为首项为13a =,公差为4的等差数列.所以123100139924100()()a a a a a a a a a a +++⋅⋅⋅+=+++++++ 50495049503450(5)410022⨯⨯=⨯+⨯+⨯--⨯=-,选A ． 5 ．（【解析】山东省济南市2013届高三3月高考模拟文科数学）等差数列}{n a 中,482=+a a ,则它的前9项和=9S （ ）A ．9B ．18C ．36D ．72【答案】B 在等差数列中,28194a a a a +=+=,所以1999()941822a a S +⨯===,选 B ．6 ．（【解析】山东省实验中学2013届高三第三次诊断性测试文科数学）已知各项为正的等比数列{}n a 中,4a 与14a 的等比数列中项为22,则1172a a +的最小值 （ ）A ．16B ．8C ．22D ．4【答案】B 【解析】由题意知224149a a a ==,即9a =.所以设公比为(0)q q >,所以22971192228a a a a q q +=+=+≥=,2=,即42q =,所以q =,所以最小值为8,选B ．7 ．（【解析】山东省德州市2013届高三上学期期末校际联考数学（文））在各项均为正数的数列{a n }中,对任意m 、*n N Î都有m n m a a +=·n a 若636,a =则9a 等于 （ ）A ．216B ．510C ．512D ．l024【答案】A 解:由题意可知26336a a ==,所以36a =,所以93636636216a a a a +===⨯= ,选A ．8 ．（【解析】山东省潍坊市2013届高三上学期期末考试数学文（a ））如果等差数列{}n a 中,15765=++a a a ,那么943...a a a +++等于 （ ）A ．21B ．30C ．35D ．40【答案】C 【解析】在等差数列中,由15765=++a a a 得663155a a ==，.所以3496...=77535a a a a +++=⨯=,选C ．9 ．（山东省淄博市2013届高三复习阶段性检测（二模）数学（文）试题）已知等差数列{}n a 的前n 项和为n S ,满足1313113a S a ===，则 （ ）A ．14-B ．13-C ．12-D ．11-【答案】D 在等差数列中,1131313()132a a S +==,所以1132a a +=,即113221311a a =-=-=-,选 D ．10．（【解析】山东省枣庄市2013届高三3月模拟考试 数学（文）试题）两旅客坐火车外出旅游,希望座位连在一起,且仅有一个靠窗,已知火车上的座位的排法如表格所示,则下列座位号码符合要求的是（ ）A ．48,49B ．62,63C ．84,85D ．75,76【答案】C 根据座位排法可知,做在右窗口的座位号码应为5的倍数,所以C 符合要求.选 C ．11．（山东省威海市2013届高三上学期期末考试文科数学）{}n a 为等差数列,n S 为其前n 项和,已知77521a S ==，，则10S =（ ）A ．40B ．35C ．30D ．28【答案】【答案】A 设公差为d ,则由77521a S ==，得1777()2a a S +=,即17(5)212a +=,解得11a =,所以716a a d =+,所以23d =.所以1011091092101040223S a d ⨯⨯=+=+⨯=,选 （ ）A ．12．（【解析】山东省济宁市2013届高三1月份期末测试（数学文）解析）已知在等比数列{}n a 中,1346510,4a a a a +=+=,则该等比数列的公比为 （ ）A ．14B ．12C ．2D ．8【答案】B 解:因为31346()a a q a a +=+,所以34613514108a a q a a +===+,即12q =,选B ．13．（【解析】山东省实验中学2013届高三第三次诊断性测试文科数学）已知等差数列{}n a 的公差为d 不为0,等比数列{}n b 的公比q 是小于1的正有理数,若211,d b d a ==,且321232221b b b a a a ++++是正整数,则q 的值可以是 （ ）A ．71 B ．-71 C ．21 D ．21-【答案】C 【解析】由题意知21312,23a a d d a a d d =+==+=,22222131,b b q d q b b q d q ====,所以2222221232222212349141a a a d d d b b b d d q d q q q ++++==++++++,因为321232221b b b a a a ++++是正整数,所以令2141t q q=++,t 为正整数.所以2114t q q ++=,即21014t q q ++-=,解得q ===,因为t 为正整数,所以当8t =时,12122q -+===.符合题意,选C ．14．（【解析】山东省滨州市2013届高三第一次（3月）模拟考试数学（文）试题）已知数列{}n a 为等差数例,其前n 项的和为n S ,若336,12a S ==,则公差d = （ ）A ．1B ．2C ．3D ．53【答案】B 在等差数列中,13133()3(6)1222a a a S ++===,解得12a =所以解得2d =,选 B ． 15．（【解析】山东省济南市2013届高三上学期期末考试文科数学）已知数列{}n a 的前n 项和为n S ,且122-=n S n , 则=3a（ ）A ．-10B ．6C ．10D ．14【答案】C 解:22332231(221)10a S S =-=⨯--⨯-=,选 C ．16．（【解析】山东省临沂市2013届高三3月教学质量检测考试（一模）数学（文）试题）已知等差数列{n a }中,74a π=,则tan(678a a a ++)等于（ ）A ．B ．C ．-1D ．1【答案】C 在等差数列中6787334a a a a π++==,所以6784tan()tan14a a a π++==-,选 C ． 17．（【解析】山东省烟台市2013届高三5月适应性练习（一）文科数学）已知等比数列{a n }的公比q=2,前n硕和为S n .若S 3=72,则S 6等于 （ ）A ．312B ．632C ．63D ．1272【答案】B 【解析】3131(12)77122a S a -===-,所以112a =.所以6161(12)6363122a S a -===-,选 B ．二、填空题18．（【解析】山东省青岛市2013届高三第一次模拟考试文科数学）设n S 是等差数列{}n a 的前n 项和,1532,3a a a ==,则9S =_____________ ;【答案】54- 由1532,3a a a ==得1143(2)a d a d +=+,即12d a =-=-,所以919899298542S a d ⨯=+=⨯-⨯=-. 19．（山东省青岛即墨市2013届高三上学期期末考试 数学（文）试题）等比数列}{n a ,2=q ,前n 项和为=24a S S n ，则____________. 【答案】215解:在等比数列中,4141(12)1512a S a -==-,所以4121151522S a a a ==.20．（【解析】山东省实验中学2013届高三第一次诊断性测试数学（文）试题）数列{}n a 满足113,1,n n n n a a a a A +=-=表示{}n a 前n 项之积,则2013A =_____________.【答案】1-【解析】由113,1,n n n a a a a +=-=得11n n na a a +-=,所以231233a -==,312a =-,43a =,所以{}n a 是以3为周期的周期数列,且1231a a a =-,又20133671=⨯,所以6712013(1)1A =-=-.21．（山东省淄博市2013届高三复习阶段性检测（二模）数学（文）试题）在如图所示的数阵中,第9行的第2个数为___________.【答案】66 每行的第二个数构成一个数列{}n a ,由题意知23453,6,11,18a a a a ====,所以3243543,5,7,a a a a a a -=-=-=12(1)123n n a a n n --=--=-,等式两边同时相加得22[233](2)22n n n a a n n -+⨯--==-,所以()222223,2n a n n a n n n =-+=-+≥,所以29929366a =-⨯+=.22．（【解析】山东省泰安市2013届高三第一轮复习质量检测数学（文）试题）正项数列{}n a 满足:()222*121171,2,2,2,n n n a a a a a n N n a +-===+∈≥=则______.【答案】因为()222*112,2n n n a a a n N n +-=+∈≥,所以数列2{}n a 是以211a =为首项,以2221413d a a =-=-=为公差的等差数列,所以213(1)32n a n n =+-=-,所以1n a n =≥,所以7a ==23．（【解析】山东省潍坊市2013届高三第一次模拟考试文科数学）现有一根n 节的竹竿,自上而下每节的长度依次构成等差数列,最上面一节长为10cm,最下面的三节长度之和为114cm,第6节的长度是首节与末节长度的等比中项,则n=_____.【答案】16 设对应的数列为{}n a ,公差为,(0)d d >.由题意知110a =,12114n n n a a a --++=,261n a a a =.由12114n n n a a a --++=得13114n a -=,解得138n a -=,即2111(5)()n a d a a d -+=+,即2(105)10(38)d d +=+,解得2d =,所以11(2)38n a a n d -=+-=,即102(2)38n +-=,解得16n =.24．（【解析】山东省济宁市2013届高三第一次模拟考试文科数学 ）已知等差数列{n a }中,35a a +=32,73a a -=8,则此数列的前10项和10S =____.【答案】190【解析】由7348a a d -==,解得2d =,由3532a a +=,解得110a =.所以101109101902S a d ⨯=+=. 25．（【解析】山东省潍坊市2013届高三第二次模拟考试文科数学）已知等差数列{}n a 的前n 项和为n S ,若2,4,3a 成等比数列,则5S =_________.【答案】40因为2,4,3a 成等比数列,所以232416a ==,所以38a =.又153535()525584022a a a S a +⨯====⨯=. 26．（【解析】山东省烟台市2013届高三上学期期末考试数学（文）试题）已知等比数列{a n }中,6710111,16a a a a ==g g ,则89a a g 等于_______【答案】4【解析】在等比数列中2676()10a a a q ==>g ,所以0q >,所以289670a a a a q =>g .所以67101116a a a a =,即289()16a a =g ,所以894a a =g .27．（【解析】山东省泰安市2013届高三上学期期末考试数学文）下面图形由小正方形组成,请观察图1至图4的规律,并依此规律,写出第n 个图形中小正方形的个数是___________.【答案】(1)2n n +【解析】12341,3,6,10a a a a ====,所以2132432,3,4a a a a a a -=-=-=, 1n n a a n --=,等式两边同时累加得123n a a n -=+++ ,即(1)122n n n a n +=+++=,所以第n 个图形中小正方形的个数是(1)2n n + 三、解答题28．（【解析】山东省烟台市2013届高三上学期期末考试数学（文）试题）已知数列{a n }的前n 项和为S n ,且22n n S a =-.(1)求数列{a n }的通项公式;(2)记1213(21)n n S a a n a =+++-g g L g ,求S n【答案】29．（【解析】山东省潍坊市2013届高三上学期期末考试数学文（a ））设数列{}n a 为等差数列,且9,553==a a ;数列{}n b 的前n 项和为n S ,且2=+n n b S . (I)求数列{}n a ,{}n b 的通项公式; (II)若()+∈=N n b a c nnn ,n T 为数列{}n c 的前n 项和,求n T . 【答案】30．（【解析】山东省滨州市2013届高三第一次（3月）模拟考试数学（文）试题）已知数列{}n a 的前n 项和是n S ,且11()2n n S a n *+=∈N (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设113log (1)()n n b S n *+=-∈N ,令122311n T b b b b =++11n n b b ++,求n T . 【答案】31．（【解析】山东省临沂市2013届高三5月高考模拟文科数学）已知点(1,2)是函数()(01)x f x a a a =≠＞且的图象上一点,数列{}n a 的前n 项和()1n S f n =-. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)将数列{}n a 前2013项中的第3项,第6项,,第3k 项删去,求数列{}n a 前2013项中剩余项的和.【答案】解:(Ⅰ)把点(1,2)代入函数()x f x a =,得2a =.()121,n n S f n ∴=-=-当1n =时,111211;a S ==-= 当2n ≥时,1n n n a S S -=-1(21)(21)n n -=---12n -=经验证可知1n =时,也适合上式,12n n a -∴=.(Ⅱ)由(Ⅰ)知数列{}n a 为等比数列,公比为2,故其第3项,第6项,,第2013项也为等比数列,首项31324,a -==公比32012201328,2a ==为其第671项∴此数列的和为67120134(18)4(21)187--=- 又数列{}n a 的前2013项和为2013201320131(12)21,12S ⨯-==--∴所求剩余项的和为2013201320134(21)3(21)(21)77----=32．（【解析】山东省实验中学2013届高三第三次诊断性测试文科数学）已知数列}{n a 的前n 项和为n S ,且)(14*∈+=N n a S n n . (Ⅰ)求21,a a ;(Ⅱ)设||log 3n n a b =,求数列{}n b 的通项公式.【答案】解:(1)由已知1411+=a S ,即31,14111=∴+=a a a ,又1422+=a S ,即91,1)42221-=∴+=+a a a a （;(2)当1>n 时,)1(41)1(4111+-+=-=--n n n n n a a S S a ,即13--=n n a a ,易知数列各项不为零(注:可不证不说),311-=∴-n n a a 对2≥n 恒成立, {}n a ∴是首项为31,公比为-31的等比数列,n n n n a ----=-=∴3)1()31(3111,n a n n -==∴-3log ||log 33,即n b n -=33．（【解析】山东省泰安市2013届高三上学期期末考试数学文）在等差数列{}n a 中,13a =,其前n 项和为n S ,等比数列{}n b 的各项均为正数,11b =,公比为q ,且222212,,n n S b S q a b b +==求与; 【答案】34．（【解析】山东省济宁市2013届高三1月份期末测试（数学文）解析）设数列{}n a 的前n 项和为n S ,若对于任意的正整数n 都有23n n S a n =-.(I)设3n n b a =+,求证:数列{}n b 是等比数列,并求出{}n a 的通项公式; (II)求数列{}n nb 的前n 项和T n .【答案】35．（【解析】山东省德州市2013届高三3月模拟检测文科数学）数列{}n a 是公差不小0的等差数列a 1、a 3,是函数2()1(66)f x n x x =-+的零点,数列{}n b 的前n 项和为n T ,且*12()n n T b n N =-∈ (1)求数列{}n a ,{}n b 的通项公式;(2)记n n n c a b =,求数列{}n c 的前n 项和S n .【答案】36．（【解析】山东省德州市2013届高三上学期期末校际联考数学（文））已知数列{a n }的公差为2的等差数列,它的前n 项和为n S ,且1321,1,1a a a +++成等比数列. (I)求{a n }的通项公式; (2)13{},.4n n n n T T S <记数列的前项求证: 【答案】37．（【解析】山东省济南市2013届高三上学期期末考试文科数学）已知等差数列{}n a 的前n 项和为n S ,且满足24a =,3417a a +=. (1)求{}n a 的通项公式; (2)设22n a n b +=,证明数列{}n b 是等比数列并求其前n 项和n T .【答案】解:(1)设等差数列{}n a 的公差为d .由题意知3411212317,4,a a a d a d a a d +=+++=⎧⎨=+=⎩解得,11a =,3d =, ∴32n a n =-(n N *∈) (2)由题意知, 2322n a n n b +==(n N *∈),3(1)33122n n n b ---==(,2n N n *∈≥)∴333312282n n n n b b --===(,2n N n *∈≥),又18b = ∴{}n b 是以18b =,公比为8的等比数列()()818881187n nn T -==-- 38．（山东省烟台市2013届高三3月诊断性测试数学文）设{a n }是正数组成的数列,a 1=3.若点()2*11,2()n n n a aa n N ++-∈在函数321()23f x x x =+-的导函数()y f x '=图像上. (1)求数列{a n }的通项公式; (2)设12n n nb a a +=⋅,是否存在最小的正数M,使得对任意n *N ∈都有b 1+b 2++b n <M 成立?请说明理由.【答案】39．（【解析】山东省济宁市2013届高三第一次模拟考试文科数学 ）(本小题满分l2分)设数列{n a }满足:a 1=5,a n+1+4a n =5,(n ∈N*)(I)是否存在实数t ,使{a n +t }是等比数列?(Ⅱ)设数列b n =|a n |,求{b n }的前2013项和S 2013.【答案】解:(I)由+1+4=5n n a a 得+1=4+5n n a a -令()+1+=4+n n a t a t -,得+1=45n n a a t -- 则5=5t -,=1t - 从而()+11=41n n a a --- .又11=4a -, {}1n a ∴-是首项为4,公比为4-的等比数列,∴存在这样的实数=1t -,使{}+n a t 是等比数列(II)由(I)得()11=44n n a --⋅- ()=14nn a ∴--{1+4, 41==n n n n n n b a -∴为奇数，为偶数()()()()()123420132013122013=++=1+4+41+1+4+41++1+4S b b b ∴--1232013=4+4+4++4+1 201420144441=+1=143--- 40．（【解析】山东省枣庄市2013届高三3月模拟考试 数学（文）试题）已知等比数列13212{}1,6,,8n a q a a a a a >=-的公比且成等差数列.(1)求数列{a n }的通项公式;(2)设(1),: 1.n n nn n b b a +=≤求证 【答案】41．（【解析】山东省青岛市2013届高三第一次模拟考试文科数学）已知N n *∈,数列{}n d 满足2)1(3nn d -+=,数列{}n a 满足1232n n a d d d d =+++⋅⋅⋅+;数列{}n b 为公比大于1的等比数列,且42,b b 为方程064202=+-x x 的两个不相等的实根.(Ⅰ)求数列{}n a 和数列{}n b 的通项公式;(Ⅱ)将数列{}n b 中的第．1a 项,第．2a 项,第．3a 项,,第．n a 项,删去后剩余的项按从小到大的顺序排成新数列{}n c ,求数列{}n c 的前2013项和.【答案】解:(Ⅰ)2)1(3n n d -+= ,∴1232n n a d d d d =+++⋅⋅⋅+3232nn ⨯== 因为42,b b 为方程064202=+-x x 的两个不相等的实数根. 所以2042=+b b ,6442=⋅b b 解得:42=b ,164=b ,所以:n n b 2=(Ⅱ)由题知将数列{}n b 中的第3项、第6项、第9项删去后构成的新数列{}n c 中的奇数列与偶数列仍成等比数列,首项分别是12b =,24b =公比均是,8201313520132462012()()T c c c c c c c c =+++⋅⋅⋅+++++⋅⋅⋅+ 1007100610062(18)4(18)208618187⨯-⨯-⨯-=+=-- 42．（【解析】山东省潍坊市2013届高三第一次模拟考试文科数学）已知数列{}n a 的各项排成如图所示的三角形数阵,数阵中每一行的第一个数1247,,,,a a a a ⋅⋅⋅构成等差数列{}n b ,n S 是{}n b 的前n 项和,且1151,15b a S ===( I )若数阵中从第三行开始每行中的数按从左到右的顺序均构成公比为正数的等比数列,且公比相等,已知916a =,求50a 的值; (Ⅱ)设122111n n n nT S S S ++=++⋅⋅⋅+,求n T.【答案】解:(Ⅰ){}n b 为等差数列,设公差为155,1,15,51015,1d b S S d d ==∴=+== 1(1)1.n b n n ∴=+-⨯=设从第3行起,每行的公比都是q ,且0q >,2294,416,2,a b q q q === 1．+2+3++9=45,故50a 是数阵中第10行第5个数, 而445010102160.a b q ==⨯= (Ⅱ)12n S =++ (1),2n n n ++=1211n n n T S S ++∴=++21nS +22(1)(2)(2)(3)n n n n =++++++22(21)n n ++11112(1223n n n n =-+-+++++11)221n n +-+ 1122().121(1)(21)n n n n n =-=++++43．（山东省青岛即墨市2013届高三上学期期末考试 数学（文）试题）等差数列}{n a 中,9,155432==++a a a a . (Ⅰ)求数列}{n a 的通项公式;(Ⅱ)设213+=n a n b ,求数列},21{n n b a +的前n 项和n S 【答案】解:(Ⅰ)设数列{}由题意得首项的公差为,1a d a n且⎩⎨⎧=+=+⎩⎨⎧==++941563915115432d a d a a a a a 即 解得⎩⎨⎧==211d a所以数列{}12-=n a a n n 的通项公式为 (Ⅱ)由(Ⅰ)可得n n n a b 3231==+ 所以n n n n b a 3..21=+ 所以+++=323.33.23.11n S 13.+n n两式相减得++++-=433333(22n S 13.)3+++n n n 10 分43).12(323..1233.31313111+++-+=-+=+---=n n n n n n S n n n 即）（）（44．（【解析】山东省潍坊市2013届高三第二次模拟考试文科数学）某工厂为扩大生产规模,今年年初新购置了一条高性能的生产线,该生产线在使用过程中的维护费用会逐年增加,第一年的维护费用是4万元,从第二年到第七年,每年的维护费用均比上年增加2万元,从第八年开始,每年的维护费用比上年增加25%(I)设第n 年该生产线的维护费用为n a ,求n a 的表达式; (Ⅱ)设该生产线前n 年维护费为n S ,求n S .【答案】45．（山东省威海市2013届高三上学期期末考试文科数学）已知数列{}n a ,15a =-,22a =-,记()A n =12n a a a +++ ,23()B n a a =+1n a +++ ,()C n =342+n a a a +++ (*N n ∈),若对于任意*N n ∈,()A n ,()B n ,()C n 成等差数列.(Ⅰ)求数列{}n a 的通项公式; (Ⅱ) 求数列{}||n a 的前n 项和.【答案】解:(Ⅰ)根据题意()A n ,()B n ,()C n 成等差数列∴()+()2()A n C n B n =整理得2121253n n a a a a ++-=-=-+= ∴数列{}n a 是首项为5-,公差为3的等差数列 ∴53(1)38n a n n =-+-=- (Ⅱ)38,2||38,3n n n a n n -+≤⎧=⎨-≥⎩记数列{}||n a 的前n 项和为n S .当2n ≤时,2(583)313222n n n n S n +-==-+ 当3n ≥时,2(2)(138)313714222n n n n S n -+-=+=-+综上,2231322231314322n n n n S n n n ⎧-+≤⎪⎪=⎨⎪-+≥⎪⎩ 46．（【解析】山东省实验中学2013届高三第一次诊断性测试数学（文）试题）已知{}n a 是公比大于1的等经数列,13,a a 是函数9()10f x x x=+-的两个零点(1)求数列{}n a 的通项公式;(2)若数列{}n a 满足312312,80n n b og n b b b b =+++++≥ 且,求n 的最小值.【答案】47．（【解析】山东省济南市2013届高三3月高考模拟文科数学）正项等比数列}{n a 的前n 项和为n S ,164=a ,且32,a a 的等差中项为2S . (1)求数列}{n a 的通项公式; (2)设12-=n n a n b ,求数列}{n b 的前n 项和n T .【答案】解:(1)设等比数列}{n a 的公比为)0(>q q ,由题意,得⎪⎩⎪⎨⎧+=+=)(2161121131q a a q a q a q a ,解得⎩⎨⎧==221q a所以n n a 2= (2)因为12122--==n n n n a n b ,所以12753224232221-+++++=n n nT , 121275322123222141+-+-++++=n n n nn T , 所以12127532212121212143+--+++++=n n n n T122411)411(21+---=n n n 12233432+⋅+-=n n故2181612992n n nT ++=-⋅ 48．（山东省淄博市2013届高三复习阶段性检测（二模）数学（文）试题）等比数列．．．．{}n c 满足(){}1*1104,n n n n c c n N a -++=⋅∈数列的前n 项和为n S ,且2log .n n a c =(I)求,n n a S ;(II)数列{}{}1,41n n n n n b b T b S =-满足为数列的前n 项和,是否存在正整数m,()1m >,使得16,,m m T T T 成等比数列?若存在,求出所有m 的值;若不存在,请说明理由.【答案】解: (Ⅰ)40,103221=+=+c c c c ,所以公比4=q10411=+c c 得21=c121242--=⋅=n n n c所以212log 221n n a n -==-21()[1(21)]22n n n a a n n S n ++-=== (Ⅱ)由(Ⅰ)知211114122121n b n n n ⎛⎫==- ⎪--+⎝⎭于是11111112335212121n n T n n n ⎡⎤⎛⎫⎛⎫⎛⎫=-+-++-= ⎪ ⎪ ⎪⎢⎥-++⎝⎭⎝⎭⎝⎭⎣⎦假设存在正整数()1m m >,使得16,,m m T T T 成等比数列,则216213121m m m m ⎛⎫=⨯ ⎪++⎝⎭, 整理得24720m m --=, 解得14m =-或 2m = 由,1m N m *∈>,得2m =, 因此,存在正整数2m =,使得16,,m m T T T 成等比数列49．（【解析】山东省临沂市2013届高三3月教学质量检测考试（一模）数学（文）试题）已知等比数列{n a }的首项为l,公比q≠1,n S 为其前n 项和,a l ,a 2,a 3分别为某等差数列的第一、第二、第四项.(I)求n a 和n S ;(Ⅱ)设21n n b log a +=,数列{21n n b b +}的前n 项和为T n ,求证:34n T <.【答案】50．（【解析】山东省烟台市2013届高三5月适应性练习（一）文科数学）在等差数列{}n a 中,a 1 =3,其前n项和为S n ,等比数列{b n }的各项均为正数,b 1 =1,公比为q,且b 2 +S 2 =12, q=22S b . (1)求a n 与b n ; (2)设数列{C n }满足c n =1nS ,求{n c }的前n 项和T n . 【答案】51．（【解析】山东省青岛一中2013届高三1月调研考试文科数学）已知等差数列{}n a 的首项1a =1,公差d>0,且第2项、第5项、第14项分别为等比数列{}n b 的第2项、第3项、第4项. (1)求数列{}n a 与{}n b 的通项公式; (2)设数列{n c }对n ∈N +均有11c b +22c b ++nnc b =1n a +成立,求1c +2c 3c ++2012c . 【答案】.解答:(1)由已知得2a =1+d, 5a =1+4d, 14a =1+13d,∴2(14)d +=(1+d)(1+13d), ∴d=2, n a =2n-1又2b =2a =3,3b = 5a =9 ∴数列{n b }的公比为3,n b =3⋅23n -=13n -(2)由11c b +22c b ++nnc b =1n a + (1) 当n=1时,11c b =2a =3, ∴1c =3当n>1时,11c b +22c b ++11n n c b --= n a (2) (1)-(2)得nnc b =1n a +-n a =2 ∴n c =2n b =2⋅13n - 对1c 不适用∴n c =131232n n n -=⎧⎨∙≥⎩∴123c c c +++2012c =3+2⋅3+2⋅23++2⋅20113=1+2⋅1+2⋅3+2⋅23++2⋅20113=1+2⋅20121313--=2012352．（【解析】山东省泰安市2013届高三第一轮复习质量检测数学（文）试题）设等比数列{}n a 的前n 项和为,415349,,,n S a a a a a =-成等差数列.(I)求数列{}n a 的通项公式;(II)证明:对任意21,,,k k k R N S S S +++∈成等差数列.【答案】。

KS5U2013山东省高考压轴卷文科数学考试时间：120分钟 满分：150分本试卷分第I 卷和第Ⅱ卷两部分，共4页．满分150分．考试时间120分钟．考试结束后，将本试卷和答题卡一并交回． 注意事项：1．答题前，考生务必用0．5毫米黑色签字笔将姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上．2．第I 卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号．3．第II 卷必须用0．5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带．不按以上要求作答的答案无效。

4．填空题请直接填写答案，解答题应写出文字说明、证明过程或演算步骤。

第Ⅰ卷(共60分)一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有 一项是符合题目要求的.1．复数2()1i i-（其中i 为虚数单位）的虚部等于（ ） A ．i - B ． 1- C ． 1 D ．02．已知集合2{|03},{|540}M x x N x x x =<<=-+≥，则M N = （ ）A ．{|01}x x <≤B ．{|13}x x ≤<C ．{|04}x x <≤D ．{|0x x <或4}x ≥3．如果等差数列{}n a 中，34512a a a ++=，那么127a a a +++= ( )A ．14B ．21C ．28D ．354．函数121xf (x )lnx x =+-的定义域为( ) A . (0，+∞) B . (1，+∞) C . (0，1) D . (0，1) (1，+∞) 5．若实数x ，y 满足不等式组：⎩⎪⎨⎪⎧x －y ≥－1，x ＋y ≥1，3x －y ≤3，则该约束条件所围成的平面区域的面积是( ) A ．3 B.52C ．2D ．2 2 6．设sin （4πθ+）=13，sin2θ=（ ） A ．79- B ．19- D ．19 D ．797. 若直线10x y -+=与圆22()2x a y -+=有公共点，则实数a 取值范围是（ ） A ．[－3，－1] B ．[－1，3] C ．[－3,l ] D ．（－∞，－3] ⋃ [1．+∞） 8.（2013青岛市一模）已知m 、n 、l 是三条不同的直线，α、β、γ是三个不同的平面，给出以下命题：①若,//m n αα⊂，则//m n ； ②若l m l n m ⊥=⋂⊥⊂⊂,,,,βαβαβα，则n m ⊥；③若//n m ，m α⊂，则//n α；④若//αγ，//βγ，则//αβ．其中正确命题的序号是（ ） A. ②④ B. ②③ C. ③④ D. ①③ 9．（2013日照市一模）右图是一个几何体的正（主）视图和侧（左）视图，其俯视图是面积为.则该几何体的表面积是（ ）A.20+B.24+C.8D.1610. 已知函数()f x 是R 上的奇函数，若对于0x ≥，都有()2()f x f x +=，[)()()20,2,log 1x f x x∈=+当时时，()()20132012f f -+的值为（ ）A.2-B.1-C.1D.211．函数y ＝e sin x (－π≤x ≤π)的大致图象为 ( )．12．定义平面向量之间的一种运算“⊙”如下：对任意的a=（m ，n ），b=（p ，q ），令a ⊙b= mq －np ，下面说法错误的是（ ）A ．若a 与b 共线，则a ⊙b =0B ．a ⊙b =b ⊙aC ．对任意的λ∈R ，有（λa ）⊙b =λ（a ⊙b ）D ．（a ⊙b ）2+（a·b ）2= |a|2|b|2第Ⅱ卷(非选择题，共90分)二、填空题：本大题共4小题．每小题4分．共16分． 13．执行如右图的程序框图，那么输出S 的值是． 14.（2013滨州一模）已知抛物线28y x =-的准线过双曲线2213x y m -=的右焦点，则双曲线的离心率为 . 15．某校对高三年级的学生进行体检，现将高三男生的体重(单位：kg)数据进行整理后分成六组，并绘制频率分布直方图(如图)．已知图中从左到右第一、第六小组的频率分别为0.16,0.07，第一、第二、第三小组的频率成等比数列，第三、第四、第五、第六小组的频率成等差数列，且第三小组的频数为100，则该校高三年级的男生总数为16．观察下列等式：231111222⨯=-⨯，2231411112223232⨯+⨯=-⨯⨯⨯，2333141511112223234242⨯+⨯+⨯=-⨯⨯⨯⨯，……，由以上等式推测到一个一般的结论：对于n ∈*N ，2314121122232(1)2n n n n +⨯+⨯++⨯=⨯⨯+ ； 三、解答题:本大题共6小题，共74分. 17. (本小题满分12分)（2013济南市一模）在ABC ∆中，边a 、b 、c 分别是角A 、B 、C 的对边，且满足cos (3)cos b C a c B =-. （Ⅰ）求B cos ；（Ⅱ）若4BC BA ⋅=，b =a ，c 的值.18．（本小题满分12分）在如图所示的几何体中，AB ⊥平面ACD ，DE ⊥平面ACD ，△ACD 为等边三角形，AD ＝DE ＝2AB ，F 为CD 的中点．（Ⅰ）求证：AF ∥平面BCE ；（Ⅱ）求证：平面BCE ⊥平面CDE .19.（本小题满分12分）某市芙蓉社区为了解家庭月均用水量（单位：吨），从社区中随机抽查100户，获得每户2013年3月的用水量，并制作了频率分布表和频率分布直方图（如图）.(Ⅰ)分别求出频率分布表中a 、b 的值，并估计社区内家庭月用水量不超过3吨的频率； (Ⅱ）设321、A 、A A 是月用水量为[0，2)的家庭代表.21、B B 是月用水量为[2，4]的家庭代表.若从这五位代表中任选两人参加水价听证会，请列举出所有不同的选法，并求家庭代表21、B B 至少有一人被选中的概率.20. (本小题满分12分）已知等比数列{}n a 的所有项均为正数，首项1a ＝1，且435,3,a a a 成等差数列.（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）数列{1n n a a λ+-}的前n 项和为n S ，若n S ＝21(*)nn N -∈，求实数λ的值. 21．（本小题满分13分）已知椭圆的中心在原点，焦点在x 轴上，一个顶点为(0,1)B -，且其右焦点到直线0x y -+=的距离为3.（Ⅰ）求椭圆方程；（Ⅱ）设直线过定点3(0,)2Q ，与椭圆交于两个不同的点M N 、，且满足BM BN =．求直线的方程.22．（本小题满分13分）已知函数()2ln ()af x ax x a x=--∈R ． （Ⅰ）若3a =，求曲线()y f x =在点(1,(1))f 处的切线方程；（Ⅱ）求函数()f x 的单调区间；（Ⅲ）设函数()ag x x=-．若至少存在一个0[1,]x e ∈，使得00()()f x g x >成立，求实数a 的取值范围．参考答案1．B【解析】2222222(1)i i i i i ===---,所以虚部为1-，故应选B . 2．A【解析】2{|540}{| 1 4}{|01}N x x x x x or x M N x x =-+≥=≤≥⇒=<≤3．C【解析】因为34512a a a ++=，所以44a =，所以1274728a a a a +++== .4.B【解析】要使函数有意义，则有001x x x ≥⎧⎪⎨>⎪-⎩，即0(1)0x xx ≥⎧⎨->⎩，所以解得1x >，即定义域为(1，+∞)，故应选B .5．C【解析】可行域为直角三角形，其面积为S ＝12×22×2＝2.6．A【解析】因为sin （4πθ+）=13，即12,sin cos =2233θθθθ+=+所以，两边平方，得：2+sin cos=9θθ12，所以7sin 2=-9θ2。

山东省2013届高三最新文科模拟试题精选分类汇编10：概率1 ．在区间]5,1[和]6,2[内分别取一个数,记为a 和b ,则方程)(12222b a by a x <=-表示离心率小于5的双曲线的概率为 （ ）A ．21B ．3215 C ．3217 D ．3231 2 ． ABC ∆中,8,6,10AB AC BC ===,顶点A B C 、、处分别有一枚半径为1的硬币(顶点A B C、、分别与硬币的中心重合).向ABC ∆内部投一点,那么该点落在阴影部分的概率为（ ）A ．124π-B ．148π-C ．24πD ．48π3 ．设[]0,5p 在上随机地取值,则关于x 的方程210x px ++=有实数根的概率为（ ）A ．15B ．25C ．35D ．454 ．从{}1,2,3,4,5中随机选取一个数为a 从{}2,3,4中随机选取一个数b,则b a >的概率是 （ ）A ．45B ．35C ．25D ．155 ．沙糖桔是柑桔类的名优品种,因其味甜如砂糖故名.某果农选取一片山地种植沙糖桔,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(4045,,⎤⎦(((455050555560,,,,,⎤⎤⎤⎦⎦⎦进行分组,得到频率分布直方图如图 3.已知样本中产量在区间(4550,⎤⎦上的果树株数是产量在区间(5060,⎤⎦上的果树株数的43倍. (1)求a ,b 的值;(2)从样本中产量在区间(5060,⎤⎦上的果树随机抽取两株,求产量在区间(5560,⎤⎦上的果树至少有一株被抽中的概率.图3a6 ．已知向量a=(1,-2),b=(x ,y ),若x ,y ∈[1,4],则满足0a b ⋅>的概率为_____.7 ．在区间[]0,4内随机取两个数a 、b, 则使得函数22()f x x ax b =++有零点的概率为___________.8 ．海曲市教育系统为了贯彻党的教育方针,促进学生全面发展,积极组织开展了丰富多样的社团活动,根据调查,某中学在传统民族文化的继承方面开设了“泥塑”、“剪纸”、“曲艺”三个社团,三个社团参加的人数如表所示:为调查社团开展情况,学校社团管理部采用分层抽样的方法从中抽取一个容量为n 的样本,已知从“剪纸”社团抽取的同学比从“泥塑”社团抽取的同学少2人. (I)求三个社团分别抽取了多少同学;(II)若从“剪纸”社团抽取的同学中选出2人担任该社团活动监督的职务,已知“剪纸”社团被抽取的同学中有2名女生,求至少有1名女同学被选为监督职务的概率.9．为了解社会对学校办学质量的满意程度,某学校决定用分层抽样的方法从高中三个年级的家长委员会中共抽取6人进行问卷调查,已知高一、高二、高三的家长委员会分别有54人、1 8人、36人. (I)求从三个年级的家长委员会中分别应抽的家长人数;(Ⅱ)若从抽得的6人中随机抽取2人进行训查结果的对比,求这2人中至少有一人是高三学生家长的概率.10．有编号为A 1,A 2,A 3,,A 6的6位同学,进行100米赛跑,得到下面的成绩:其中成绩在13秒内的同学记为优秀.(l)从上述6名同学中,随机抽取一名,求这名同学成绩优秀的概率;(2)从成绩优秀的同学中,随机抽取2名,用同学的编号列出所有可能的抽取结果,并求这2名同学的成绩都在12.3秒内的概率. 11．一个均匀的正四面体上分别有1,2,3,4四个数字,现随机投掷两次,正四面体面朝下的数字分别为b ,c .(1)记z =(b -3)2+(c -3)2,求z =4的概率;(2)若方程x 2-bx -c =0至少有一根x ∈{1,2,3,4},就称该方程为“漂亮方程”,求方程为“漂亮方程”的概率.12．学校游园活动有一个游戏项目:箱子里装有3个红球,2个白球,这些球除颜色外完全相同.每次游戏从箱子里摸出3个球,若摸出的是3个红球为优秀;若摸出的2个红球1个白球为良好;否则为合格.(I)求在1次游戏中获得优秀的概率;(II)求在1次游戏中获得良好及以上的概率13．甲、乙两名考生在填报志愿时都选中了A 、B 、C 、D 四所需要面试的院校,这四所院校的面试安排在同一时间.因此甲、乙都只能在这四所院校中选择一所做志愿,假设每位 同学选择各个院校是等可能的,试求:(Ⅰ)甲、乙选择同一所院校的概率;(Ⅱ)院校A 、B 至少有一所被选择的概率.14．某种零件按质量标准分为1,2,3,4,5五个等级,现从一批该零件中随机抽取20个,对其等级进行统计分析,得到频率分布表如下:(I)在抽取的20个零件中,等级为5的恰有2个,求m,n;(Ⅱ)在(I)的条件下,从等级为3和5的所有零件中,任意抽取2个,求抽取的2个零件等级恰好相同的概率.15．以下茎叶图记录了甲组3名同学寒假假期中去图书馆A 学习的次数和乙组4名同学寒假假期中去图书馆B 学习的次数. 乙组记录中有一个数据模糊,无法确认,在图中以x 表示.(1)如果x =7,求乙组同学去图书馆学习次数的平均数和方差; (2)如果x =9,从学习次数大于8的学生中选两名同学,求选出的两名同学恰好分别在两个图书馆学习且学习的次数和大于20的概率.x 8 29 乙组 第18题图16．高三某班有两个数学课外兴趣小组,第一组有2名男生,2名女生,第二组有3名男生,2名女生.现在班主任老师要从第一组选出2人,从第二组选出1人,请他们在班会上和全班同学分享学习心得. (Ⅰ)求选出的3人均是男生的概率;(Ⅱ)求选出的3人中有男生也有女生的概率.17．中国共产党第十八次全国代表大会期间,某报刊媒体要选择两名记者去进行专题采访,现有记者编号分别为1,2,3,4,5的五个男记者和编号分别为6,7,8,9的四个女记者.要从这九名记者中一次随机选出取两名,每名记者被选到的概率是相等的,用符号(,)x y 表示事件“抽到的两名记者的编号分别为x 、y ,且x y <”.(1)共有多少个基本事件?并列举出来;(2)求所抽取的两记者的编号之和小于17但不小于11或都是男记者的概率.18．一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.(I)从袋中随机抽取一个球,将其编号记为a ,然后从袋中余下的三个球中再随机抽取一个球,将其编号记为b .求关于x 的一元二次方程2220x ax b ++=有实根的概率;(II)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n.若以(,)m n 作为点P 的坐标,求点P 落在区域⎩⎨⎧<-+≥-050y x y x 内的概率.19．为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30 .第6小组的频数是7.(Ⅰ)求这次铅球测试成绩合格的人数;(Ⅱ)若由直方图来估计这组数据的中位数,指出它在第几组内,并说明理由;(Ⅲ)若参加此次测试的学生中,有9人的成绩为优秀,现在要从成绩优秀的学生中,随机选出2人参加“毕业运动会”,已知a 、b 的成绩均为优秀,求两人至少有1人入选的概率.。

临沂一中2013届高三第二次阶段测试 文科数学试题 2012.12.20一.选择题.(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1.设集合{}{}22|log (2),|540==-=-+<A x y x B x x x ，则A B = ( ).A ∅B ()2,4C ()2,1-D ()4,+∞2.“a=1”是“直线x+y =0和直线x-ay =0互相垂直”的A 充分不必要条件B 必要不充分条件C 充要条件D 既不充分也不必要条件3.若()1,a b a a b ==⊥- 且，则向量,a b的夹角为A.45°B.60°C.120°D.135°4.已知圆的方程为08622=--+y x y x ，过点)5,3(A 的直线被圆所截，则截得的最短弦的长度为 ( ).....A B C D5.方程033=--m x x 在[0，1]上有实数根，则m 的最大值是（ ） A.0 B.-2 C. 811-D. 16.在A B C ∆中，a b c ，，分别为角A B C ，，所对边，若2cos a b C =，则此三角形一定是( ). A ．等腰直角三角形 B ．直角三角形 C ．等腰三角形 D ．等腰或直角三角形7.已知)1()(),1()(>=>=b b x g a a x f xx,当2)()(21==x g x f 时，有21x x >,则b a ,的大小关系是（ ）A ．b a >B ．b a ≥C ．b a <D ．b a ≤ 8.如图是一个几何体的三视图．若它的表面积为7π，则正（主）视图中a = （ ）. A ．1 BCD ．29.等比数列}{n a 的前n 项和为321,2,4,a a a S n 且成等差数列， 若11=a ，则4S 等于（ ）A ．7B ．8C ．15D ．1610.已知,m n 是两条直线，,αβ是两个平面，给出下列命题：①若,n n αβ⊥⊥，则 //αβ；第7题②若平面α上有不共线的三点到平面β的距离相等，则//αβ；③若,n m 为异面直线,//,,//n n m m αββα⊂⊂，则//αβ．其中正确命题的个数是()．A ．3个B ．2个C ．1个D ．0个11.已知函数)(x f 是定义在(,)-∞+∞上的奇函数，若对于任意的实数0≥x ，都有)()2(x f x f =+，且当[)2,0∈x 时，)1(l o g )(2+=x x f ，则)2012()2011(f f +-的值为（ ）A. -1B. -2C. 2D. 112.如图，1F 、2F 分别是双曲线)0,0(12222>>=-b a bya x 的两个焦点，以坐标原点O 为圆心，1F O 为半径的圆与该双曲线左 支交于A 、B 两点，若△AB F 2是等边三角形，则双曲线的离心率为 （ ）.A．2 C1 D．1+二.填空题(本大题共4小题，每小题4分，共16分) 13.已知抛物线2y ax=的准线方程为2y =-，则实数a 的值为14．已知2tan()5αβ+=,1tan()44πβ-=,那么tan()4πα+= ______________.15．如图是某学校一名篮球运动员在五场比赛中所得分数的茎叶图，则该运动员在这五场比赛中得分的方差为_________.89103516．若实数x ，y 满足121y y x x y m ≥⎧⎪≤-⎨⎪+≤⎩，如果目标函数z x y =-的最小值为2-，则实数m=_________.三.解答题.(共74分)17.(本题满分12分) 已知向量m ＝(sin ωx ＋cos ωx ，3cos ωx )，n ＝(cos ωx －sin ωx,2sin ωx )，其中ω>0，函数f (x )＝m ·n ，若f (x )相邻两对称轴间的距离为π2.(1)求ω的值，并求f (x )的最大值及相应x 的集合；(2)在△ABC 中，a 、b 、c 分别是A 、B 、C 所对的边，△ABC 的面积S ＝53，b ＝4，f (A )＝1，求边a 的长．18. (本题满分12分)某高级中学共有学生2000名，各年级男、女生人数如下表：已知在全校学生中随机抽取1名，抽到高二年级女生的概率是0.19. (1)求x 的值；(2)现用分层抽样的方法在全校抽取48名学生，问应在高三年级抽取多少名？ (3)已知y ≥245, z ≥245,求高三年级中女生比男生多的概率.19.(本题满分12分)如图，四棱锥P —ABCD 中，PD ⊥平面ABCD ，底面ABCD 为矩形，PD=DC=4，AD=2，E 为PC 的中点. （1）求证：AD ⊥PC ； （2）求三棱锥P-ADE 的体积；（3）在线段AC 上是否存在一点M ，使得PA//平面EDM ，若存在，求出AM 的长；若不存在，请说明理由.20.(本题满分12分)已知点(1，31)是函数,0()(>=a a x f x 且1≠a )的图象上一点，等比数列}{n a 的前n 项和为c n f -)(,数列}{n b )0(>n b 的首项为c ，且前n 项和n S 满足1n n S S --=（2n ≥).(1) 求数列}{n a 和}{n b 的通项公式；(2) 若数列{}11+n n b b 前n 项和为n T ，问10002012n T >的最小正整数n 是多少? .21．(本题满分13分)已知函数21()ln ()2f x x a x a R =-∈.（1）若)(x f 在2=x 时取得极值，求a 的值； （2）求)(x f 的单调区间；（3）求证：当1>x 时，3232ln 21x x x <+22.(本题满分13分)已知椭圆C 的中心在坐标原点,焦点在x 轴上,离心率2e =.直线l :220x y -+=与椭圆C 相交于E F 、两点, 且EF =(1)求椭圆C 的方程；(2)点(2,0)P -， A 、B 为椭圆C 上的动点,当P A P B ⊥时,求证:直线A B 恒过一个定点.并求出该定点的坐标.临沂一中2013届高三第二次阶段考试(文数)参考答案 2012.201-5 B C A C A 6-10 D C D C B 11-12 A D13. 18 14.32215. 6.8 16. 817. (1) f (x )＝cos 2ωx －sin 2ωx ＋23sin ωx cos ωx ＝cos2ωx ＋3sin2ωx ＝2sin ⎝⎛⎭⎫2ωx ＋π6....................2分由题意可得T ＝π，∴ω＝1.................................3分 ∴f (x )＝2sin ⎝⎛⎭⎫2x ＋π6..............................................4分 当sin ⎝⎛⎭⎫2x ＋π6＝1时，f (x )有最大值2，∴2x ＋π62k π＋π2，∴x ＝k π＋π6(k ∈Z )..................5分∴x 的集合为{x |x ＝π6＋k π，k ∈Z }................................6分(2)f (A )＝2sin ⎝⎛⎭⎫2A ＋π6＝1∴sin ⎝⎛⎭⎫2A ＋π6＝12 0<A <π，∴2A ＋π6＝5π6......................8分 ∴A ＝π3，S ＝12bc sin π3＝53，∴c ＝5..........................10分由余弦定理得：a 2＝16＋25－2×4×5cos π321，∴a ＝21.........................12分18. 解：（1）∵0.192000x = ∴ 380x =..........2分（2）初三年级人数为y ＋z ＝2000－373－377－380－370）＝500..............4分 现用分层抽样的方法在全校抽取48名学生，应在初三年级抽取的人数为：48500122000⨯=名.............................................................6分 （3）设初三年级女生比男生多的事件为A ，初三年级女生男生数记为（y ，z ）；由（2）知 500y z += ，且 ,y z N ∈,基本事件空间包含的基本事件有：（245，255）、（246，254）、（247，253）、……（255，245）共11个.............................8分事件A 包含的基本事件有：（251，249）、（252，248）、（253，247）、(254,246)、(255,245) 共5个 ............................................10分 ∴5()11P A =.......................................12分19（1）证明：因为PD ⊥平面ABCD.所以PD ⊥AD.又因为ABCD 是矩形，所以AD ⊥CD.……………………………………2分 因为,D CD PD =⋂ 所以AD ⊥平面PCD.又因为⊂PC 平面PCD ，所以AD ⊥PC.………………………………4分（2）解：因为AD ⊥平面PCD ， V P-ADE =V A-PDE ，…………………………………6分 所以AD 是三棱锥A —PDE 的高.因为E 为PC 的中点，且PD=DC=4，所以.444212121=⎪⎭⎫⎝⎛⨯⨯⨯==∆A PDC PDE S S 又AD=2， 所以.38423131=⨯⨯=⋅=∆-PDE PDE A S AD V ………………………………8分（3）取AC 中点M ，连结EM 、DM ，因为E 为PC 的中点，M 是AC 的中点，所以EM//PA ，又因为EM ⊂平面EDM ，PA ⊄平面EDM ，所以PA//平面EDM.…………………………………………………………10分 所以.521==AC AM即在AC 边上存在一点M ，使得PA//平面EDM ，AM 的长为5.………12分20.(1)()113f a ==Q ,()13xf x ⎛⎫∴= ⎪⎝⎭................1分()1113a f c c =-=- ,()()221a f c f c =---⎡⎤⎡⎤⎣⎦⎣⎦29=-,()()323227a f c f c =---=-⎡⎤⎡⎤⎣⎦⎣⎦ ..................2分 又数列{}n a 成等比数列，22134218123327aa c a ===-=-- ，所以 1c =...........3分又公比2113a q a ==，所以12112333n nn a -⎛⎫⎛⎫=-=- ⎪⎪⎝⎭⎝⎭*n N ∈ ..................4分1n n S S --==Q ()2n ≥又0n b >0>, 1=......................................5分数列构成一个首相为1公差为1()111n n =+-⨯= ， 2n S n =当2n ≥， ()221121n n n b S S n n n -=-=--=-又满足11b c ==21n b n ∴=-(*n N ∈)...............................6分 (2)12233411111n n n T b b b b b b b b +=++++L ()1111133557(21)21n n =++++⨯⨯⨯-⨯+K 8分由1000212012n n T n =>+得100012n >，满足10002012n T >的最小正整数为84........12分21 解: ∵)(x f 在2=x 时取得极值，022=-∴a ，4=∴a ...................2分此时xx x xx xx x f )2)(2(44)(2+-=-=-='.()f x Q 的定义域是}0|{>x x ，∴当20<<x 时，0)(<'x f ；当2>x 时，0)(>'x f .∴当4=a 时，2=x 是)(x f 的极小值点，4=∴a .........................4分（2）()a f x x x'=-Q 且()f x 的定义域是}0|{>x x ................6分当0≤a 时，)(x f 的单调递增区间为),0(+∞..................7分当0>a 时，xa x a x xa x xa x x f ))(()(2+-=-=-='，令0)(>'x f 有a x >，∴函数)(x f 的单调递增区间为),(+∞a ；令0)(<'x f 有a x <<0，∴函数)(x f 的单调递减区间为),0(a ...........8分（3）设x x x x g ln 2132)(23--=，xx x x g 12)(2--='，..............9分Q 当1>x 时，0)12)(1()(2>++-='xx x x x g ....................10分)(x g ∴在),1(+∞上是增函数，∴061)1()(>=>g x g ...................12分∴当1>x 时，3232ln 21x x x <+ .........13分22．解：(1)设椭圆方程为22221x y ab+=(a>b>0)，11(,)E x y 22(,)F x y2c e a==令2,a t c == 则b t = 222214xy tt∴+=…………２分由22244220x y t x y ⎧+=⎨-+=⎩得:222210y y t -+-= ……………………………… 4分 2442(1)0t ∆=-⨯-> 212t ∴>12EF y y =-==21t ∴=椭圆C 的方程是:2214xy += …………………………………… 7分(2) 当直线l 不垂直于x 轴时,设A B ：y kx m =+ 11(,)A x y 22(,)B x y22244x y t y kx m⎧+=⎨=+⎩得222(14)84(1)0k x km x m +++-= 1222121212(2)(2)(1)(2)()4PA PB x x y y k x x km x x m =+++=++++++=222224(1)8(1)(2)401414m km k km m kk--+++++=++ …………………… 10分22125160k m km ∴+-= 即 (65)(2)0k m k m --=625m k m k ∴==或当65m k =时，6:5AB y kx k =+恒过定点6(,0)5-当2m k =时，:2AB y kx k =+恒过定点(2,0)-，不符合题意舍去 … 12分 当直线l 垂直于x 轴时，若直线AB ：65x =-则AB 与椭圆Ｃ相交于64(,)55A --，64(,)55B - 24444444(,)(,)()()()5555555P AP B ∴=-=+-= P A P B ⊥ ，满足题意综上可知，直线A B 恒过定点，且定点坐标为6(,0)5-……………… 13分。

山东省济南市2013届高三高考模拟考试文科数学试题本试题分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共4页. 考试时间120分钟，满分150分，考试结束后，将本试卷和答题卡一并交回.注意事项：1.答题前，考生务必用0.5毫米黑色签字笔将自己的姓名、座号、考生号、县区和科类写在答题卡和试卷规定的位置上.2.第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号，答案不能答在试卷上.3.第Ⅱ卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.4.填空题请直接填写答案，解答题应写出文字说明、证明过程或演算步骤. 参考公式：1.锥体的体积公式：1V S 3h =，其中S 是锥体的底面积，h 是锥体的高; 2.方差],)()()[(1222212x x x x x x ns n -++-+-=其中x 为n x x x ,,,21 的平均数. 第I 卷（选择题 共60分）一、选择题：本大题共12个小题，每小题5分，共60分.每小题给出的四个选项中只有一项是符合题目要求的.1. 已知全集}6,5,4,3,2,1,0{=U ，集合{1,2}A =，}5,2,0{=B ，则集合=B A C U )(A ．{3，4，6}B ．{3，5}C ．{0，5}D ．{0，2，4}【答案】C{0,3,4,5,6}U A =ð，所以(){0,5}U A B = ð，选C.2. 设复数(34)(12)z i i =-+（i 是虚数单位），则复数z 的虚部为 A ．2- B. 2 C. i 2- D. i 2【答案】B由(34)(12)52z i i i =-+=-+，所以复数z 的虚部为2，选B. 3. 若6.03=a ，2.0log 3=b ，36.0=c ，则A ．b c a >> B. c b a >> C. a b c >> D. a c b >>【答案】A0.6331,log 0.20><,300.61<<，所以a c b >>。

2013年普通高等学校招生全国统一考试（全国II ）数学（文科）第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的． （1）【2013年全国Ⅱ，文1，5分】已知集合{|31}M x x =-<<，{3,2,1,0,1}N =---，则M N = （ ）（A ）{2,1,0,1}-- （B ）{3,2,1,0}--- （C ）{2,1,0}-- （D ）{3,2,1}--- 【答案】C【解析】因为{31}M x x =-<<，{3,2,1,0,1}N =---，所以M N {2,1,0}=--，故选C ． （2）【2013年全国Ⅱ，文2，5分】21i=+（ ） （A） （B ）2 （C（D ）1 【答案】C【解析】22(1i)2(1i)1i 1i (1i)(1i)2--===-+-+，所以21i=+C ． （3）【2013年全国Ⅱ，文3，5分】设,x y 满足约束条件10103x y x y x -+≥⎧⎪+-≥⎨⎪≤⎩，则23z x y =-的最小值是（ ）（A ）7- （B ）6- （C ）5- （D ）3- 【答案】B【解析】由23z x y =-得32y x z =-，即233z y x =-．作出可行域如图，平移直线233zy x =-，由图象可知当直线233z y x =-经过点B 时，直线233zy x =-的截距最大，此时z 取得最小值，由103x y x -+=⎧⎨=⎩得34x y =⎧⎨=⎩，即(3,4)B ，代入直线23z x y =-得32346z =⨯-⨯=-，故选B ．（4）【2013年全国Ⅱ，文4，5分】ABC ∆的内角,,A B C 的对边分别为,,a b c ，已知2b =，6B π=，4C π=，则ABC ∆的面积为（ ）（A）2 （B1 （C）2 （D1【答案】B【解析】因为,64B C ππ==，所以712A π=．由正弦定理得sin sin 64b c =，解得c =．所以三角形的面积为117sin 22212bc A π=⨯⨯．因为7231s i n s i n (()1232222πππ=++，所以13s i n ()312b c A =++，故选B ． （5）【2013年全国Ⅱ，文5，5分】设椭圆2222:1x y C a b+=(0)a b >>的左、右焦点分别为12,F F ，P 是C 上的点，212PF F F ⊥，1230PF F ∠=，则C 的离心率为（ ）（A（B ）13（C ）12 （D【答案】D【解析】因为21212,30PF F F PF F ⊥∠=，所以212tan 30,PF c PF ===．又122PF PF a +==，所以c a ==，故选D ．（6）【2013年全国Ⅱ，文6，5分】已知2sin 23α=，则2cos ()4πα+=（ ）（A ）16 （B ）13（C ）12 （D ）23【答案】A【解析】因为21cos2()1cos(2)1sin 242cos ()4222ππααπαα++++-+===，所以2211sin 213cos ()4226παα--+===，故选A ．（7）【2013年全国Ⅱ，文7，5分】执行右面的程序框图，如果输入的4N =，那么输出的S =（ ）（A ）1111234+++ （B ）1111232432+++⨯⨯⨯ （C ）111112345++++ （D ）111112324325432++++⨯⨯⨯⨯⨯⨯ 【答案】B【解析】第一次循环，1,1,2T S k ===；第二次循环，11,1,322T S k ==+=；第三次循环，111,1,423223T S k ==++=⨯⨯，第四次循环，1111,1,5234223234T S k ==+++=⨯⨯⨯⨯⨯，此时满足条件输出1111223234S =+++⨯⨯⨯，故选B ． （8）【2013年全国Ⅱ，文8，5分】设3log 2a =，5log 2b =，2log 3c =，则（ ）（A ）4 （B ）5 （C ）6 （D ）7 【答案】D【解析】因为321lo g 21lo g 3=<，521log 21log 5=<，又2log 31>，所以c 最大．又221log 3log 5<<，所以2211log 3log 5>，即a b >，所以c a b >>，故选D ． （9）【2013年全国Ⅱ，文9，5分】一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是()1,0,1，()1,1,0，()0,1,1，()0,0,0，画该四面体三视图中的正视图时，以zOx 平面为投影面，则得到的正视图可以为（ ）（A ） （B ） （C ） （D ）【答案】A【解析】在空间直角坐标系中，先画出四面体O ABC -的直观图，以zOx 平面为投影面，则得到正视图(坐标系中红色部分)，故选A ．（10）【2013年全国Ⅱ，文10，5分】设抛物线2:4C y x =的焦点为F ，直线l 过F 且与C 交于A ，B 两点．若||3||AF BF =，则l 的方程为（ ） （A ）1y x =-或1y x =-+ （B）1)y x =-或1)y x =- （C）1)y x -或1)y x =- （D）1)y x =-或1)y x =-【答案】C【解析】抛物线24y x =的焦点坐标为10（,），准线方程为1x =-，设11A x y （，），22B x y （，），则因为3AF BF =，所以12131x x +=+（），所以1232x x =+，因为123y y =，129x x =，所以13x =，213x =，当13x =时，2112y =，所以此时1y ==±，若1y =1(,3A B ，此时AB k =线方程为1)y x -．若1y =-，则1(3,),()3A B -，此时AB k =，此时直线方程为1)y x =-．所以l 的方程是1)y x -或1)y x =-，故选C ．（11）【2013年全国Ⅱ，文11，5分】已知函数32()f x x ax bx c =+++，下列结论中错误的是（ ）（A ）0x R ∃∈，0()0f x = （B ）函数()y f x =的图象是中心对称图形 （C ）若0x 是()f x 的极小值点，则()f x 在区间0(,)x -∞单调递减（D ）若0x 是()f x 的极值点，则0'()0f x = 【答案】C【解析】若0c =则有(0)0f =，所以A 正确．由32()f x x ax bx c =+++得32()f x c x ax bx -=++，因为函数32y x ax bx =++的对称中心为0,0（），所以32()f x x ax bx c =+++的对称中心为(0,)c ，所以B 正确．由三次函数的图象可知，若0x 是()f x 的极小值点，则极大值点在0x 的左侧，所以函数在区间0,x -∞（）单调递减是错误的，D 正确，故选C ．（12）【2013年全国Ⅱ，文12，5分】若存在正数x 使2()1x x a -<成立，则a 的取值范围是（ ） （A ）(,)-∞+∞ （B ）(2,)-+∞ （C ）(0,)+∞ （D ）(1,)-+∞【答案】D【解析】解法一：因为20x >，所以由2()1x x a -<得122x x x a --<=，在坐标系中，作出函数 (),()2xf x x ag x -=-=的图象，当0x >时，()21x g x -=<，所以如果存在0x >，使2()1x x a -<，则有1a -<，即1a >-，故选D ．解法二：由题意可得，()102xa x x ⎛⎫>-> ⎪⎝⎭．令()12xf x x ⎛⎫=- ⎪⎝⎭，该函数在(0)∞，＋上为增函数，可知()f x 的值域为()1∞－，＋，故1a >-时，存在正数x 使原不等式成立，故选D ．第II 卷本卷包括必考题和选考题两部分．第（13）题~第（21）题为必考题，每个试题考生都必须作答．第（22）题~第（24）题为选考题，考生根据要求作答．二、填空题：本大题共4小题，每小题5分，共20分．把答案填在题中横线上 （13）【2013年全国Ⅱ，文13，5分】从1,2,3,4,5中任意取出两个不同的数，其和为5的概率是______．【答案】15【解析】从5个正整中任意取出两个不同的数，有2510C =种，若取出的两数之和等于5，则有(1,4),(2,3)，共有2个，所以取出的两数之和等于5的概率为21105=．（14）【2013年全国Ⅱ，文14，5分】已知正方形ABCD 的边长为2，E 为CD 的中点，则AE BD ⋅=__ ____． 【答案】2【解析】在正方形中，12AE AD DC =+ ，BD BA AD AD DC =+=-，所以2222111()()222222AE BD AD DC AD DC AD DC ⋅=+⋅-=-=-⨯= ．（15）【2013年全国Ⅱ，文15，5分】已知正四棱锥O ABCD -则以O 为球心，OA 为半径的球的表面积为_______．【答案】24π【解析】设正四棱锥的高为h ，则213h ⨯=，解得高h =．所以OA =2424ππ=． （16）【2013年全国Ⅱ，文16，5分】函数cos(2)()y x ϕπϕπ=+-≤≤的图象向右平移2π个单位后，与函数sin(2)3y x π=+的图象重合，则ϕ=_______．【答案】56π【解析】函数cos(2)y x ϕ=+，向右平移2π个单位，得到sin(2)3y x π=+，即sin(2)3y x π=+向左平移2π个单位得到函数cos(2)y x ϕ=+，sin(2)3y x π=+向左平移2π个单位，得sin[2()]sin(2)233y x x ππππ=++=++sin(2)cos(2)323x x πππ=-+=++5cos(2)6x π=+，即56πϕ=． 三、解答题：解答应写出文字说明，证明过程或演算步骤．（17）【2013年全国Ⅱ，文17，12分】已知等差数列{}n a 的公差不为零，125a =，且11113,,a a a 成等比数列．（1）求{}n a 的通项公式； （2）求14732+n a a a a -++⋅⋅⋅+．解：（1）设{}n a 的公差为d ．由题意，211113a a a =，即2111()1012()a d a a d ＋＝＋．于是1225(0)d a d ＋＝．又125a ＝，所以0d ＝ (舍去)，2d =-．故227n a n =-+．（2）令14732n n S a a a a -=+++⋯+．由（1）知32631n a n -=-+，故32{}n a -是首项为25，公差为6-的等差数列．从而()()2132656328n n S a a n n n -=+=-+=-+．（18）【2013年全国Ⅱ，文18，12分】如图，直三棱柱111ABC A B C -中，D ，E 分别是AB ，1BB 的中点．（1）证明：1//BC 平面11A CD ；（2）设12AA AC CB ===，AB =1C A DE -的体积．解：（1）连结1AC 交1A C 于点F ，则F 为1AC 中点．又D 是AB 中点，连结DF ，则1//BC DF ．因为DF ⊂平面1A CD ，1BC ⊄平面1A CD ，所以1//BC 平面1A CD ．（2）因为111ABC A B C -是直三棱柱，所以1AA CD ⊥．由已知AC CB =，D 为AB 的中点，所以CD AB ⊥．又1AA AB A = ，于是CD ⊥平面11ABB A ．由12AA AC CB ===，AB =得90ACB ∠=︒，CD1A D =DE =13A E =，故22211A D DE A E +=，即1D E A D ⊥．所以111132C A DE V -⨯=．（19）【2013年全国Ⅱ，文19，12分】经销商经销某种农产品，在一个销售季度内，每售出1 t 该产品获利润500元，未售出的产品，每1 t 亏损300元．根据历史资料，得到销售季度内市场需求量的频率分布直方图，如图所示．经销商为下一个销售季度购进了130 t 该农产品．以X (单位：t ，100150X ≤≤)表示下一个销售季度内的市场需求量，T (单位：元)表示下一个销售季度内经销该农产品的利润 （1）将T 表示为X 的函数；（2）根据直方图估计利润T 不少于57000元的概率．1解：（1）当[)100,130X ∈时，()50030013080039000T X X X =--=-，当[]130,150X ∈时，50013065000T =⨯=． 所以80039000,10013065000,130150X X T X -≤<⎧=⎨≤≤⎩．（2）由（1）知利润T 不少于57000元当且仅当120150X ≤≤．由直方图知需求量[]120,150X ∈的频率为0.7，所以下一个销售季度内的利润T 不少于57000元的概率的估计值为0.7．（20）【2013年全国Ⅱ，文20，12分】在平面直角坐标系xOy 中，已知圆P 在x轴上截得线段长为在y 轴上截得线段长为．（1）求圆心P 的轨迹方程；（2）若P 点到直线y x =P 的方程． 解：（1）设()P x y ，，圆P 的半径为r ．由题设222y r +=，223x r +=．从而2223y x +=+．故P 点的轨迹方程为221y x -=． （2）设00()P x y ，=．又P 点在双曲线221y x -=上，从而得002210||11x y y x -=⎧⎨-=⎩ 由00220011x y y x -=⎧⎨-=⎩得0001x y =⎧⎨=-⎩，此时，圆P 的半径r =3．由00220011x y y x -=-⎧⎨-=⎩得001x y =⎧⎨=⎩，此时，圆P的半径r =．故圆P 的方程为()2213x y +-=或()2213x y ++=．（21）【2013年全国Ⅱ，文21，12分】已知函数2()x f x x e -=．（1）求()f x 的极小值和极大值；（2）当曲线()y f x =的切线l 的斜率为负数时，求l 在x 轴上截距的取值范围．解：（1）()f x 的定义域为()-∞+∞，，()()2x f x e x x -'=--．① 当)0(x ∈-∞，或2()x ∈+∞，时，()0f x '＜； 当)2(0x ∈,时，()0f x '＞．所以()f x 在()0-∞,，(2)+∞，单调递减，在(0)2,单调递增．故当0x =时，()f x取得极小值，极小值为()00f =；当2x =时，()f x 取得极大值，极大值为()224f e -=．（2）设切点为()()t f t ，，则l 的方程为()()()y f t x t f t ='-+．所以l 在x 轴上的截距为()()223'()22f t t t t t f t t m t t -=+=-++--=．由已知和①得()02()t ∈-∞+∞ ，，．令()()20h x x x x+=≠， 则当0()x ∈+∞，时，()h x的取值范围为⎡⎤+∞⎣⎦；当2()x ∈-∞-，时，()h x 的取值范围是()3-∞-，． 所以当()02()t ∈-∞+∞ ，，时，()m t的取值范围是0()3,⎡⎤-+∞⎦∞⎣ ，． 综上，l 在x轴上的截距的取值范围是0()3,⎡⎤-+∞⎦∞⎣ ，．请考生在（22）、（23）、（24）三题中任选一题作答．注意：只能做所选定的题目．如果多做，则按所做第一个题目计分，做答时请写清题号． （22）【2013年全国Ⅱ，文22，10分】（选修4-1：几何证明选讲）如图，CD 为ABC ∆外接圆的切线，AB 的延长线交直线CD 于点D ，E ，F 分别为弦AB 与弦AC 上的点，且··BC AE DC AF =，B ， E ，F ，C 四点共圆．（1）证明：CA 是ABC ∆外接圆的直径；（2）若DB BE EA ==，求过B ，E ，F ，C 四点的圆的面积与ABC ∆外接圆面积的比值．解：（1）因为CD 为ABC ∆外接圆的切线，所以DCB A ∠=∠，由题设知BC DCFA EA=，故CDB AEF ∆∆∽， 所以DBC EFA ∠=∠．因为B ，E ，F ，C 四点共圆，所以CFE DBC ∠=∠，故90EFA CFE ∠=∠=︒． 所以90CBA ∠=︒，因此CA 是ABC ∆外接圆的直径．（2）连结CE ，因为90CBE ∠=︒，所以过B ，E ，F ，C 四点的圆的直径为CE ，由D B B E =，有CE DC =又22·2BC DB BA DB ==，所以222246CA DB BC DB =+=．而22·3DC DB DA DB ==，故过B ，E ，F ， C 四点的圆的面积与ABC ∆外接圆面积的比值为12．（23）【2013年全国Ⅱ，文23，10分】（选修4-4：坐标系与参数方程）已知动点P Q 、都在曲线2cos :2sin x tC y t=⎧⎨=⎩（t 为参数）上，对应参数分别为=t α与=2t α（02απ<<），M 为PQ 的中点． （1）求M 的轨迹的参数方程；（2）将M 到坐标原点的距离d 表示为α的函数，并判断M 的轨迹是否过坐标原点．解：（1）依题意有2cos (n )2si P αα，，2cos2(2)2sin Q αα，，因此cos cos ()2sin sin2M αααα++，． M 的轨迹的参数方程为cos cos 2sin sin 2x y αααα=+⎧⎨=+⎩(α为参数，02απ<<)．（2）M 点到坐标原点的距离)02d απ<<．当απ=时，0d =，故M 的轨迹过坐标原点．（24）【2013年全国Ⅱ，文24，10分】（选修4-5：不等式选讲）设a ，b ，c 均为正数，且1a b c ++=，证明：（1）13ab bc ac ++≤；（2）2221a b cb c a ++≥．解：（1）由222a b ab +≥，222b c bc +≥，222c a ca +≥，得222a b c ab bc ca ++≥++．由题设得()21a b c ++=，即2222221a b c a b b c c a +++++=．()31ab bc ca ∴++≤，即13a b b c c a ++≤．（2）因为22a b a b +≥，22b c b c +≥，22c a c a +≥，故()222(2)a b ca abc c a b c b +≥++++++，即222a b c a b c b c a ≥++++．所以2221a b cb c a++≥．。

山东省2013届高三最新文科模拟试题精选分类汇编14：导数 1 ．设曲线11x y x +=-在点(3,2)处的切线与直线10ax y ++=垂直,则a =（ ）A ．-2B ．2C ．12- ( D)122 ．若曲线()cos f x a x =与曲线()21g x x bx =++在交点()0,m 处有公切线,则a b +=（ ）A ．1-B ．0C ．1D ．23 ．设函数()()3402f x x x a a =-+<<有三个零点1x 、x 2、x 3,且123,x x x <<则下列结论正确的是（ ）A ．11x >-B ．20x <C ．32x >D ．201x <<4 ．定义在R 上的函数()f x 的导函数为'()f x ,已知(1)f x +是偶函数，(1)'()0x f x -<. 若12x x <,且122x x +>,则1()f x 与2()f x 的 大小关系是 （ ）A ．12()()f x f x <B ．12()()f x f x =C ．12()()f x f x >D ．不确定5 ．已知函数()f x 对定义域R 内的任意x 都有()f x =(4)f x -,且当2x ≠时其导函数()f x '满足()2(),xf x f x ''>若24a <<则（ ）A ．2(2)(3)(log )af f f a << B ．2(3)(log )(2)af f a f << C ．2(log )(3)(2)af a f f <<D ．2(log )(2)(3)af a f f <<6 ．若直线l 与幂函数ny x =的图象相切于点A (2,8),则直线l 的方程为（ ）A ．12160x y --=B ．40x y -=C ．12160x y +-=D ．640x y --=7 ．已知f ′()x 是函数()f x 的导函数,如果f ′()x 是二次函数,f ′()x 的图象开口向上,顶点坐标为,那么曲线()y f x =上任一点处的切线的倾斜角α的取值范围是（ ）A ．0,3π⎛⎤ ⎥⎝⎦B ．,32ππ⎡⎫⎪⎢⎣⎭C ．2,23ππ⎛⎤⎥⎝⎦ D ．,3π⎡⎫π⎪⎢⎣⎭8 ．已知R 上可导函数()f x 的图象如图所示,则不等式2(23)()0x x f x '-->的解集为（ ）A ．(,1)(1,0)(2,)-∞-⋃-⋃+∞B ．(,1)(1,1)(3,)-∞-⋃-⋃+∞C ．(,2)(1,2)-∞-⋃D ．(,2)(1,)-∞-⋃+∞9 ．已知函数()y f x =的图象关于y 轴对称,且当(,0),()'()0x f x xf x ∈-∞+<成立a=(20.2)·0.2(2),(13)f b og π=·3(13),(19)f og c og π=·3(19)f og ,则a,b,c 的大小关系是（ ）A ．b a c >>B ．c a b >>C ．c b a >>D ．a c b >>10．已知函数332y x x c =-+的图像与x 轴恰有两个公共点,则c 的值为（ ）A ．2或2-B ．3-或1C ．1或1-D ．3或9-11．设曲线y=11x x +-在点(3,2)处的切线与直线ax+y+3=0垂直,则a= （ ）A ．2B ．-2C ．12D ．-1212．若曲线1f (x )x sin x =+在2x π=处的切线与直线a x +2y +1=0互相垂直,则实数a 的值为 （ ）A ．-2B ．-lC ．1D ．213．已知f(x)为R 上的可导函数,且x ∀∈R,均有f(x)()f x '>,则有（ ）A ．e 2013 f(-2013)<f(0),f(2013)>e 2013f(0)B ．e2013f(-2013)< f(0),f(2013)<e 2013f(0)C ．e 2013 f(-2013)>f(0),f(2013)>e 2013f(0)D ．e 2013 f(-2013)>f(0),f(2013)<e 2013f(0)14．若函数22()1xf x x =+在点(2,(2))f 处的切线为l ,则直线l 与y 轴的交点坐标为_____________. 15．直线l 过点(-1,3),且与曲线12y x =-在点(1,-1)处的切线相互垂直,则直线l 的方程为_______________________16．函数220410ln x x x,x f (x )x ,x ⎧-+>=⎨+≤⎩的零点个数是____.17．已知函数()3e xf x a =+(e 2.71828=是自然对数的底数)的最小值为3.(Ⅰ)求实数a 的值;10题(Ⅱ)已知b ∈R 且0x <,试解关于x 的不等式 22()3(21)3lnf x ln x b x b -<+--;(Ⅲ)已知m Z ∈且1m >.若存在实数[1,)t ∈-+∞,使得对任意的[1,]x m ∈,都有()3e f x t x +≤,试求m 的最大值.18．已知函数x a x g ln )2()(-=,2ln )(ax x x h +=)(R a ∈,令)()()('x h x g x f +=.(Ⅰ)当0=a 时,求)(x f 的极值; (Ⅱ)当2-<a 时,求)(x f 的单调区间;(Ⅲ)当23-<<-a 时,若对]3,1[,21∈∀λλ,使得3ln 2)3ln (|)()(|21-+<-a m f f λλ恒成立, 求m 的取值范围.19．已知函数()3213f x x ax bx =++()R a,b ∈.(Ⅰ)若曲线()C :y f x =过点()12P ,,曲线C 在点P 处的切线与直线2140x y +-=垂直,求a,b 的值;(Ⅱ)在(Ⅰ)的条件下,试求函数()()()2713g x m f x x ⎡⎤=--⎢⎥⎣⎦(m 为实常数,1m ≠±)的极大值与极小值之差;(Ⅲ)若()f x 在区间()12,内存在两个不同的极值点,求证:02a b <+<.20．设21xf (x )e (ax x )=++.(I)若a>0,讨论f (x )的单调性;(Ⅱ)x =1时,f (x )有极值,证明:当θ∈[0,2π]时,2|f (cos )f (sin )|θθ-<21．已知函数()()()(),0ln xg x f x g x ax a x==->. (I)求函数()g x 的单调区间;(II)若函数()()1,f x +∞在上是减函数,求实数a 的最小值;(III)若212,,x x e e ⎡⎤∃∈⎣⎦,使()()12f x f x a '≤+成立,求实数a 的取值范围.22．已知函数21()122f x nx ax x =--(1)若函数()f x 在x=2处取得极值,求实数a 的值; (2)若函数()f x 在定义域内单调递增,求a 的取值范围; (3)若12a =-时,关于x 的方程1()2f x x b =-+在[1,4]上恰有两个不相等的实数根,求实数b 的取值范围.23．某分公司经销某种品牌产品,每件产品的成本为30元,并且每件产品须向总公司缴纳a 元(a 为常数,2≤a≤5)的管理费,根据多年的统计经验,预计当每件产品的售价为x 元时,产品一年的销售量为x ke(e 为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x 最低不低于35元,最高不超过41元.(1)求分公司经营该产品一年的利润L(x)万元与每件产品的售价x 元的函数关系式; (2)当每件产品的售价为多少元时,该产品一年的利润L(x)最大,并求出L(x)的最大值. 参考公式:24．已知函数()2ln g x ax x =-(I)若a>0,求函数()g x 的最小值 (Ⅱ) 若函数()()af xg x x=-在其定义域内为单调函数,求实数a 的取值范围; 25．已知函数()ln(1)(xf x e a a =++为常数)是实数集R 上的奇函数.(Ⅰ)求实数a 的值;(Ⅱ)若函数()()sin g x f x x λ=+在区间[]1,1-上是减函数,求实数λ的最大值; (Ⅲ)若关于x 的方程2ln 2()xx ex m f x =-+有且只有一个实数根,求m 的值. 26．设函数321()(4),()ln(1)3f x mx m xg x a x =++=-,其中0a ≠.( I )若函数()y g x =图象恒过定点P,且点P 在()y f x =的图象上,求m 的值;(Ⅱ)当8a =时,设()'()()F x f x g x =+,讨论()F x 的单调性;(Ⅲ)在(I)的条件下,设(),1()(),1f x x G xg x x ≤⎧=⎨>⎩,曲线()y G x =上是否存在两点P 、Q,使△OPQ(O 为原点)是以O 为直角顶点的直角三角形,且该三角形斜边的中点在y 轴上?如果存在,求a 的取值范围;如果不存在,说明理由.27．已知函数31()(2)3f x ax a x c =+-+的图象如右图所示.(1)求函数)(x f y =的解析式; (2)若()()2ln kf x g x x x'=-在其定义域内为增函数,求实数k 的取值范围.28．已知函数2(1)()a x f x x-=,其中0a >. (Ⅰ)求函数()f x 的单调区间;(Ⅱ)若直线10x y --=是曲线()y f x =的切线,求实数a 的值;(Ⅲ)设2()ln ()g x x x x f x =-,求()g x 在区间[1,e]上的最小值.(其中e 为自然对数的底数)29．设函数f(x)=m(x 1x -)-21nx,g(x)= 2e x(m 是实数,e 是自然对数的底数). (1)当m=2e 时,求f(x)+g(x)的单调区间;(2)若直线l 与函数f(x),g(x)的图象都相切,且与函数f(x)的图象相切于点(1,0),求m 的值.30．已知函数()ln ,()xf x ax xg x e =+=.(I)当0a ≤时,求()f x 的单调区间(Ⅱ)若不等式()g x <有解,求实数m 的取值菹围; (Ⅲ)证明:当a=0时,()()2f x g x ->.31．已知函数()()21.xf x ax x e =++(I)若曲线()1y f x x ==在处的切线与x 轴平行,求a 的值,并讨论()f x 的单调性;(2)当0a =时,是否存在实数m 使不等式()214121mx x x f x mx +≥-++≥+和对任意[)0,x ∈+∞恒成立?若存在,求出m 的值,若不存在,请说明理由32．已知函数a f (x )ln x x=-. (I)若a >0,试判断f (x )在定义域内的单调性; (Ⅱ)若f (x )在[1,e]上的最小值为32,求a 的值; (III)若2f (x )x <在(1,+∞)上恒成立,求a 的取值范围33．已知函数x x a x f ln )1()(2++=.(Ⅰ)讨论函数)(x f 的单调性;(Ⅱ)若对任意)2,4(--∈a 及]3,1[∈x 时,恒有()2a x f ma >-成立,求实数m 的取值范围.34．设函数2()ln ()f x x a x a x=--∈R . (Ⅰ)当3a =时,求()f x 的极值;(Ⅱ)讨论函数()f x 的单调性.35．设1)(--=ax x f ex(Ⅰ)若0,()0a f x >≥对一切x R ∈恒成立,求a 的最大值. (Ⅱ)设()()xag x f x e =+,且112212(,),(,)()A x y B x y x x ≠是曲线()y g x =上任意两点,若对任意的1a ≤-,直线AB 的斜率恒大于常数m ,求m 的取值范围;36．已知函数()ln (1)ln 2e f x x f x '=-⋅+,32()()2x g x f x x=--.(1)求()f x 的单调区间;(2)设函数2()4h x x mx =-+,若存在1(0,1]x ∈,对任意的2[1,2]x ∈,总有12()()g x h x ≥成立,求实数m 的取值范围.37．已知(),P x y 为函数1ln y x =+图象上一点,O 为坐标原点,记直线OP 的斜率()k f x =.(I)若函数()f x 在区间1,3m m ⎛⎫+ ⎪⎝⎭()0m >上存在极值,求实数m 的取值范围; (II)当 1x ≥时,不等式()1tf x x ≥+恒成立,求实数t 的取值范围. 38．已知函数21()(21)2ln 2f x ax a x x =-++,其中常数0a >. (1)求()f x 的单调区间;(2)如果函数(),(),()f x H x g x 在公共定义域D 上,满足()()()f x H x g x <<,那么就称()H x 为()f x 与()g x 的“和谐函数”.设2()4g x x x =-,求证:当522a <<时,在区间(0,2]上,函数()f x 与()g x 的“和谐函数”有无穷多个.39．某工厂共有10台机器,生产一种仪器元件,由于受生产能力和技术水平等因素限制,会产生一定数量的次品.根据经验知道,若每台机器产生的次品数P(万件)与每台机器的日产量()()412x x ≤≤万件之间满足关系:20.1 3.2ln 3.P x x =-+已知每生产1万件合格的元件可以盈利2万元,但每产生1万件装次品将亏损1万元.(利润=盈利—亏损)(I)试将该工厂每天生产这种元件所获得的利润y (万元)表示为x 的函数; (II)当每台机器的日产量x (万件)写为多少时所获得的利润最大,最大利润为多少?40．已知函数f(x)=a(x 2-2x +1)+1nx+1.(I)当a=14-时,求函数f(x)的单调区间; (Ⅱ)若对[)1,()x f x x ∀∈+∞≥恒成立,求实数a 的取值范围.41．已知函数2()(1)xf x ax x e =+-,其中e 是自然对数的底数,a R ∈.(1)若1=a ,求曲线)(x f 在点))1(,1(f 处的切线方程; (2)若0<a ,求()f x 的单调区间;(3)若1-=a ,函数)(x f 的图象与函数m x x x g ++=232131)(的图象有3个不同的交点,求实数m 的取值范围.。